Utility-Centric Service Provisioning in Multi-Access Edge Computing

Abstract

Recently, multi-access edge computing (MEC) is a promising paradigm to offer resource-intensive and latency-sensitive services for IoT devices by pushing computing functionalities away from the core cloud to the edge of networks. Most existing research has focused on effectively improving the use of computing resources for computation offloading while neglecting non-trivial amounts of data, which need to be pre-stored to enable service execution (e.g., virtual/augmented reality, video analytics, etc.). In this paper, we, therefore, investigate service provisioning in MEC consisting of two sub-problems: (i) service placement determining services to be placed in each MEC node under its storage capacity constraint, and (ii) request scheduling determining where to schedule each request considering network delay and computation limitation of each MEC node. The main objective is proposed to ensure the quality of experience (QoE) of users, which is also yet to be studied extensively. A utility function modeling user perception of service latency is used to evaluate QoE. We formulate the problem of service provisioning in MEC as an Integer Nonlinear Programming (INLP), aiming at maximizing the total utility of all users. We then propose a Nested-Genetic Algorithm (Nested-GA) consisting of two genetic algorithms, each of whom solves a sub-problem regarding service placement or request scheduling decisions. Finally, simulation results demonstrate that our proposal outperforms conventional methods in terms of the total utility and achieves close-to-optimal solutions.

1. Introduction

Presently, together with the population explosion of the Internet of Things (IoT) devices, many new services are constantly emerging and attracting a lot of attention, including virtual/augmented reality (VR/AR), industrial robotics, face recognition, natural language processing, etc. These services are usually compute-intensive and/or data-intensive while IoT devices have certain limitations in terms of processing and storage capacity, battery life, and network resources. The emergence of mobile cloud computing (MCC) [1] supported IoT devices by enabling offloading heavy computing service requests up to the centralized cloud and providing huge data storage capabilities to the services. For example, in the healthcare sector, clinical centers are paying attention to the IoT and MCC technologies to develop next-generation pervasive healthcare solutions [2,3,4]. Based on MCC infrastructure, physiological parameters and vital signs collected from wireless sensor body networks in the form of wearable accessories or devices attached to the human body could be transmitted to a centralized and powerful computing platform in the cloud for aggregation, analysis, and storage. Accordingly, MCC-based healthcare systems not only facilitate information sharing among patients, caregivers, and physicians in a structured and cost-effective manner but also enable advanced big data analytics and machine learning techniques to derive insights from sensor data, thereby providing better treatment and assistant services (e.g., telemonitoring, ambient assisted living, electronic health record, and multi-agent medical consultation, etc.) to patients and disabled people in their everyday life [5,6,7]. However, the far distance between the end-users and the centralized cloud is perceived to be a major barrier to meeting the diverse quality requirements of emerging services. Services with strict latency requirements cannot tolerate the high network latency incurred to reach the remote cloud. For example, in real-time medical services that require immediate feedback, such as real-time cardiac monitoring, fall detection, emergency medical services, just a little delay or lack of service availability due to any reason (e.g., loss of Internet connectivity or cloud failure) may put patients’ health at risk. Moreover, transmitting a large amount of data from IoT devices to the remote cloud will pose a substantial burden on the backhaul links, degrade network performance, and increase energy consumption.

To address the above issues, a new paradigm named multi-access edge computing (MEC) [8] or formerly mobile edge computing was proposed as the extension of cloud computing to the edge of networks. The main idea of MEC is to bring computing power and storage resources close to end-users by attaching small servers (a.k.a, MEC servers) to WiFi access points or mobile base stations (BS) at the network edge. By this way, MEC is expected to fill the gap between the centralized cloud and the IoT. The combination of MEC and the IoT recently opened many new frontiers for service providers and telecom operators to deploy versatile services on IoT applications (e.g., industrial internet, smart city, connected car, telehealth, etc.) [9,10]. The reasons are as follows. First, MEC can help alleviate the network traffic congestion by aggregating and preprocessing data of massive IoT applications at the network edge, saving the time and cost of transmitting data to the centralized cloud. Second, due to the reduced communication distance, MEC can facilitate ultra-reliable and low-latency services, which is very critical for IoT applications. Third, MEC can help IoT devices (limited and unstable power supply, e.g., energy harvesting sensor nodes) mitigate computational and communication overhead by offloading their heavy workloads to MEC servers [11]. In doing so, the lifetime of IoT devices or even the entire IoT network could be enhanced. Finally, a distributed computing environment like MEC can eliminate the problem of a single point of failure that the centralized cloud is facing. In MEC, if there is a failure, data can be rerouted through other multiple pathways, such that IoT devices can retain access to the services they need. Therefore, MEC ensures better resilience in the IoT network. For those unparalleled benefits, MEC is recognized as a key enabler for the development of future IoT ecosystems [12]. Inversely, IoT also energizes MEC by expanding MEC services to all types of smart objects ranging from sensors and actuators to smart vehicles.

Despite the promising benefits brought by MEC, the service provisioning in MEC remains challenging. Compared to the centralized cloud, a MEC node is much more limited in computing resources, and may not always be possible to serve all service requests at the same time. Hence, there have been researching initiatives to create an open MEC environment, such that distributed MEC nodes within the same geographical region do not work independently, but collaborate to form a shared resource pool allowing service requests to be served by any appropriate MEC nodes in the system [13,14,15]. On the other hand, the MEC nodes are also able to cooperate with the central cloud in case of a need for higher computation power for service requests, resulting in a hierarchical computation offloading architecture combining the MEC nodes and the central cloud. It naturally raises the question of determining the appropriate computing node (i.e., local MEC, a nearby MEC, or the central cloud) for each service request originated from each MEC. Many previous studies solved this problem under the theme of computation offloading [13,14,15,16,17,18,19,20]. However, most of them focused on effectively improving the use of computing resources while neglecting non-trivial amounts of data, which need to be pre-stored to enable service execution, especially for data-intensive services. For example, in an AR service, the MEC node needs to store the object database and the trained machine learning models to run image classification and object recognition tasks before returning the results to the users [21]. Meanwhile, MEC is typically limited in terms of storage capacity, and thus allows only a very small set of services to be placed at a time. Which services are placed on a MEC determines which service requests can be scheduled to that MEC, thereby significantly affecting the MEC performance.

As such, the service provisioning problem in MEC should jointly consider two sub-problems: (i) service placement, which determines services (including server code and related libraries/databases) to place in each MEC so as to better use its available storage capacity, and (ii) request scheduling, which determines where to schedule each service request considering the network delay and computation limitation of MEC. In the literature, different service provisioning policies were investigated but mostly focused on the quality of service (QoS) metrics (e.g., latency, bandwidth, packet loss ratio, etc.) [22,23]. However, it is observed that the QoS cannot always guarantee the actual service quality that is experienced by the users. Hence, Quality of Experience (QoE) emerged as an extension of the QoS by including more subjective and also service-specific measures beyond traditional technical parameters to reflect the degree of satisfaction of the end-user [24]. Over the past few years, QoE has become one of the prime importance to the service provisioning policies of infrastructure and service providers. Higher QoE promises a happier user experience, thereby enhancing user loyalty and reducing service relinquish rate [25]. In a distributed environment like MEC, services, devices, and resources may not only be spread in various locations but they are of diversified nature too. In such an environment, developing efficient QoE-aware service provisioning policies while considering storage and computation resource limitations of MEC remains a challenging task, which is yet to be investigated extensively and holistically.

Motivated by the above facts, in this paper, we investigate a utility-centric approach to the problem of service provisioning in MEC, using utility score as QoE assessment [26]. Specifically, we take measurements of an objective QoS parameter (e.g., service latency), which is then mapped onto subjective mean opinion score (MOS) using a utility function. The utility function is derived from [27,28] based on the observation that user perception of service latency does not advance beyond a certain threshold. For example, experimental results in [29] show that in VR services, service latency values smaller than 20 ms are not perceived by the users, and thus no difference in terms of user experience while in some cloud-based interactive games [30], only latencies above 50 ms affect the gaming experience.

In brief, the main contributions of this paper are summarized as follows.

• We formulate the problem of service provisioning as an Integer Nonlinear Programming (INLP) problem that jointly optimizes the service placement decisions and request scheduling decisions so as to maximize the total utility (or satisfaction) of all users within both the storage and computation resource constraints in MEC systems.
• We then propose a Nested-Genetic algorithm (Nested-GA) that consists of two genetic algorithms (outer and inner), each of whom solves a sub-problem (i.e., service placement or request scheduling).
• We justify the efficiency of our proposed algorithm by extensive simulations. The experimental results show that our proposal consistently outperforms baselines in terms of the total utility and can provide close-to-optimal solutions.

The remainder of this paper is structured as follows. We start by reviewing some relevant research works in Section 2. In Section 3, the system model and problem formulation are presented. We then introduce our proposed algorithm in Section 4. Simulation results are shown and discussed in Section 5, followed by our conclusions in Section 6.

2. Related Work

The problem of edge workload scheduling or computation offloading is an attractive and challenging topic in MEC, which decides whether/how to schedule/offload users’ tasks (requests) from their devices to the appropriate computing nodes in the MEC or the cloud. Various aspects of this problem were investigated in the literature, considering different objectives (e.g., minimizing the makespan [16] or the energy [17] or the cost [18]), workload models (e.g., independent atomic tasks [19], composite applications/workflows [20]), and MEC architectures and offloading schemes (e.g., non-collaborative [18] versus collaborative [14], flat versus hierarchical [15]). However, in these works, MEC nodes are implicitly assumed to execute any types of computation tasks without considering whether the corresponding services are available on the MEC nodes.

Content placement in cache networks is another line of related work, considering storage resources sharable among requests of the same type. Caching popular contents at the network edgecannot only reduce network latency and energy consumption but also prevent redundant transmissions of the same content, and thus save network traffic. Various content caching policies have been introduced. Least frequently used (LFU) and least recently used (LRU) are the most widely used caching policies in the literature [31]. User preference profile (UPP)-based caching policy was proposed in [32] based on the observation that a user typically has a strong preference toward specific content categories. Meanwhile, based on machine learning technology, the authors in [33] introduced learning-based content caching policy for wireless networks with a priori unspecified content dissemination. Also, the caching policies can decide the content to cache at each MEC without considering the cooperation among the MEC nodes [32] or in a cooperative manner [34]. The problem of joint request routing and content caching in heterogeneous cache networks was also investigated in [35]. Nevertheless, research on content placement problem only concerns storage resources while neglecting other types of resources (e.g., CPU).

Meanwhile, the service provisioning problem in MEC has to take into account both computing and storage constraints as well as jointly optimize the service placement and request scheduling decisions to maximize the overall system performance. For examples, Zhao et al. [36] addressed the problems of VM placement and task distribution for supporting multiple applications in MEC, in which the objective is to minimize the average latency of a request. However, this work does not take into account the deadline requirement of the latency, especially for latency-sensitive applications. In [37], a dynamic service placement and workload scheduling algorithm based on Lyapunov optimization framework was proposed, but there is no hard constraint on computation resources. In [22], a genetic algorithm was developed for the load distribution and placement problem of IoT services to minimize the potential violation of their QoS requirements considering both computation and storage constraints of edge resources. However, the authors neglect the storage demand of data-intensive services (e.g., VR/AR, video analytics, distributed machine learning, etc.), which requires a pre-stored library/dataset shareable among requests of the same type. Until recently, few studies [38,39] have addressed this limitation to serve data-intensive services from the edge. They jointly optimized the service placement and request scheduling decisions while considering both shareable (i.e., storage) and non-shareable resources (i.e., CPU). In [23], FogPlan, a QoS-aware service provision framework, was proposed to deliver fog services to edge devices or the cloud to minimize the resource cost while meeting the latency and QoS constraints. However, we note that these works focus on the QoS metrics rather than the user experience or satisfaction in the service provisioning process.

In contrast to the mentioned papers, our paper studies the utility-centric service provisioning in MEC. The utility is a measure of user satisfaction and is defined as a non-increasing function of service latency (both network latency and processing latency) [27,28]. Based on this utility function, in [27], the authors presented utilitarian server selection, a new method to facilitate service placement and to select the best service replica for each user request while satisfying network transit cost constraints. In [28], the authors addressed composite service placement problems and propose utility-maximizing solutions based on genetic algorithm. However, in these works, they target the cloud data centers, in which there are no hard constraints on both storage and computation resources. Moreover, they do not jointly take into account the service placement and request scheduling problems. Meanwhile, our work studies utility-centric service provisioning in MEC, which jointly optimize service placement and request scheduling decisions within both the storage and computation resource constraints in MEC systems.

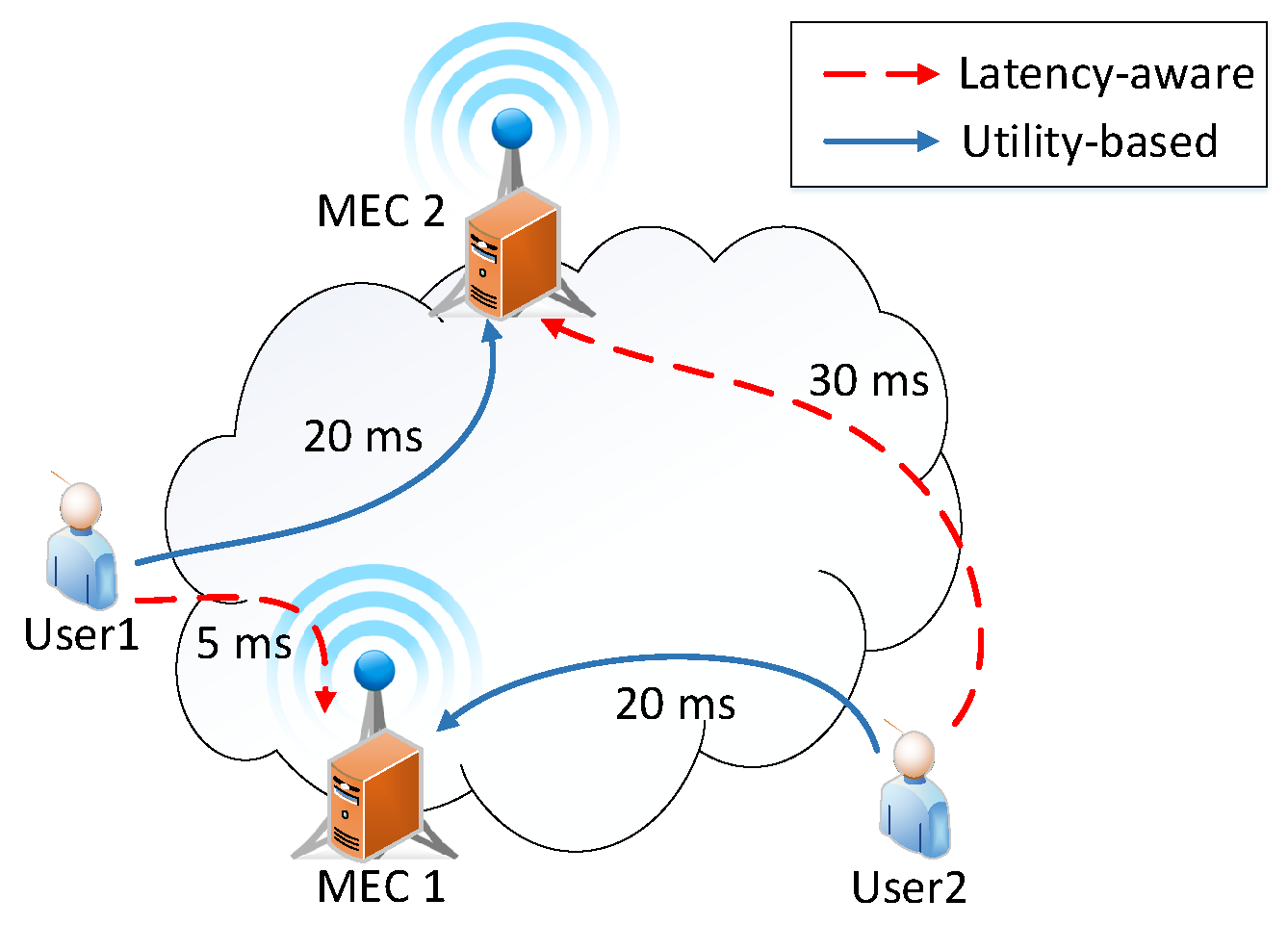
3. System Model and Problem Formulation

3.1. Scenario Description

As illustrated in Figure 1, the MEC system consists of IoT devices, multiple computing nodes (MEC servers and the core cloud), and networks connecting them. Several services can be deployed and executed in different computing nodes, where the infrastructure and service providers define the placement locations of these services. In our proposal, each MEC server is attached to a base station or Wifi access point covering a local area to provide services to the registered IoT devices or users. Moreover, all MEC nodes are connected by backhaul links to form a resource pool (a.k.a, collaboration space) that serves users collaboratively. At a time slot, users send their diverse types of service requests to the MEC system. We assume that each user is directly associated with only one MEC node (non-overlapping), referred to as its connected MEC. The connected MEC of a user can admit its request into the system, but any MEC in the collaboration space can be chosen as the processing node of the request provided that the requested service is already placed on that MEC and the service performance is guaranteed. Two types of MEC resource constraints are considered: (i) the storage constraint restricts the number of services each MEC can offer, and (ii) the computation constraint restricts the number of requests each MEC can effectively process. Within these resource constraints, the service provisioning problem consists of service placement, deciding which services to place at each MEC, and request scheduling, deciding where to schedule users’ requests. Please note that requests not scheduled to any MEC node will be “dropped” (e.g., the yellow request in Figure 1). “Dropping” a request only implies not processing it from the MEC, the dropped request can be processed by the core cloud, which is assumed to host all services. Accessing the core cloud, however, may cause high network latency, and thus should be avoided.

In order to enable the service placement and request scheduling among the MEC nodes, we assume that all MEC nodes in the collaboration space are managed by a SDN-based MEC controller, in which the major components are described as follows.

MEC Resource and Service Monitoring Database module maintains a MEC resource table, service information table, and service map table. The MEC resource table includes the available resources (e.g., storage and computation) of each MEC in the collaboration space. The service information table includes the demand of the services to be placed, such as the amount of storage of required libraries and databases, amount of processing to get a response to a request of a service, and QoS parameters (e.g., tolerable delay) of each service. The service map table is used to keep/store the list of currently processed services and their placement location.

Traffic Monitor module, such as that of a Software Defined Networking (SDN) controller, is responsible for collecting and managing the service requests from IoT devices to each MEC node. Commercial SDN controller, such as OpenDaylight, supports OpenFlow protocol to enable communication between the SDN controller and the network devices for monitoring the service-level traffic [40]. All scheduling rules are calculated at the SDN controller and applied to the request flow tables of each MEC node in the system. The action sets in a flow table can be forward, drop, and so on, to control the behaviors of request flows.

Based on the profiles of MEC nodes, services and requests from users provided by the above modules, the Provision Planner module will solve the problem of service provisioning in MEC periodically. The main objective is to maximize the total utility of all users within the resource constraints. According to the service placement and request scheduling decisions obtained from Provision Planner, each MEC node will trigger corresponding actions. Please note that these decisions are made for a certain period during which the user demand is fixed and forecast. Since the demand may change over time (e.g., after some hours), the Provision Planner will have to periodically forecast new demand and adjust the policy accordingly. The adaptation of service placement requires service migration, which causes the cost of replicating service data through the network. Services may migrate/replicate between MEC nodes, or from the core cloud to a MEC node.

In the scope of this paper, we investigate the service provisioning problem in an offline setting, which does not consider service migration cost and user mobility. In addition, the user demand is assumed to be predicted in advance and remains unchanged during the placement period. The online setting, which includes service migration, user mobility and other dynamic changes in the network can be considered to be future work.

3.2. Notation and Variable

To formulate the service provisioning problem in MEC, we first introduce some notations. Let $\mathcal{N}=\{1,2,3,\dots ,N\}$ denote the set of MEC nodes, l denote the core cloud, $\mathcal{S}=\{1,2,3,\dots ,S\}$ denote the set of services, and $\mathcal{U}=\{1,2,3,\dots ,U\}$ denote of the set of users. Each MEC node $n\in \mathcal{N}$ has a storage capacity $R_n$, and a CPU of computation capacity $F_n$. Each service $s\in \mathcal{S}$ is represented by a tuple of five parameters as <$im{g}_s$, $d_s$, $w_s$, $T_s^{min}$, $T_s^{max}$>, where $im{g}_s$ is the size of service image containing libraries and databases associated with service s, $d_s$ is the input data size for service s per request, $w_s$ is the required amount of processing for service s per request, $T_s^{min}$ and $T_s^{max}$ are two latency thresholds associated with service s to evaluate the utility function. For the sake of simplicity, we assume that at a time slot, each user $u\in \mathcal{U}$ performs only one request for a service. We will refer to a user request as a user. Let $n_u\in \mathcal{N}$ denote the connected MEC node (i.e., directly covering) of user u, and $s_u\in \mathcal{S}$ denote the service requested by user u.

The main decision variables of the service provisioning problem are the following two sets of optimization variables. We define the service placement profile as $\mathbf{x}=\left\{x_{sn}\right|s\in \mathcal{S},n\in \mathcal{N}\cup \left\{l\right\}\}$, in which $x_{sn}=1$ indicates that service s is placed at node n, and $x_{sn}=0$, otherwise. Similarly, the request scheduling profile is defined as $\mathbf{y}=\left\{y_{un}\right|u\in \mathcal{U},n\in \mathcal{N}\cup \left\{l\right\}\}$, in which $y_{un}=1$ indicates that user u is scheduled to node n, and $y_{un}=0$, otherwise. Here, $x_{sl}=1,\forall s\in \mathcal{S}$ since we assume that the core cloud hosts all services.

3.3. Service Latency Estimation

In this section, we present an estimation to determine the service latency of a user. Typically, it is defined as the total time from when the user sends its service request until receiving the result. Suppose user u is scheduled to a computing node n ($n\in \mathcal{N}\cup \left\{l\right\}$). Serving user u at node n causes communication latency for transferring input/output data between the user and node n, and processing latency at node n. Each latency will be described in the following subsections.

3.3.1. Communication Latency

The communication latency of user u at node n consists of two parts: (i) the network latency between user u and its connected MEC $n_u$, denoted as ${\tau }_{u,n_u}^{comm}$, and (ii) the network latency between the connected MEC $n_u$ (i.e., source node) and the selected node n for executing the user request (i.e., target node), denoted as ${\tau }_{n_u,n}^{comm}$. Each network latency is composed of transmission delay and propagation delay. It is noteworthy that a user’s connected MEC can host the service and process its request (i.e., $n=n_u$), and in this case ${\tau }_{n_u,n}^{comm}=0$. Hence, let ${\tau }_{u,n}^{comm}$ denote the communication latency of user u at node n. Then it is estimated as

$${\tau }_{u,n}^{comm}={\tau }_{u,n_u}^{comm}+{\tau }_{n_u,n}^{comm}=\left\{\begin{array}{c}\frac{d_{s_u}}{r_{u,n_u}}+D_{u,n_u},\mathrm{if}n=n_u\hfill \\ \frac{d_{s_u}}{r_{u,n_u}}+D_{u,n_u}+\frac{d_{s_u}}{r_{n_u,n}}+D_{n_u,n},\mathrm{otherwise}\hfill \end{array}\right.$$

(1)

where $r_{u,n_u}$ and $D_{n_u,n}$ are the transmission rate and round-trip propagation delay between the user u and its connected MEC $n_u$, respectively; $r_{n_u,n}$ and $D_{n_u,n}$ are the transmission rate and the round-trip propagation delay of the network links between node $n_u$ and n, respectively. Here, we omit the time cost for transferring the computation result back to the user since the size of the computation outcome is much smaller than that of the input data [41,42].

3.3.2. Processing Latency

In our model, the processing units of MEC nodes are assumed to be allocated based on weighted proportional allocation [13,43]. Each user receives a fraction of computation resources at the target MEC node n based on its demand. Let $f_{un}$ be the computation resource allocated to user u by node n. It is calculated as

$$f_{un}=\frac{w_{s_u}}{{\displaystyle \sum _{u^{\prime }\in \mathcal{U}}}{y}_{u^{\prime }n}{w}_{s_{u^{\prime }}}}{F}_n$$

(2)

Then the processing time of user u at MEC node n, denoted as ${\tau }_{u,n}^{proc}$, is given by

$${\tau }_{u,n}^{proc}=\frac{w_{s_u}}{f_{un}}$$

(3)

In case the request of user u is not scheduled to any MEC node in the collaboration space, it will be sent to the core cloud l. Here, since the core cloud is generally equipped with abundant computation resources, the processing time at cloud can be ignored [14,22]. However, serving the user at the core cloud, which is assumed to be located far away, causes much higher propagation delay than that of serving it by a MEC (i.e., $D_{n_u,l}>>D_{n_u,n},\forall n_u,n\in \mathcal{N}$).

3.3.3. Service Latency

Combining communication and processing latency, the service latency of user u, denoted as $t_u$, can be expressed as follows.

$$t_u=\sum _{n\in \mathcal{N}\cup \left\{l\right\}}{y}_{un}\left({\tau }_{u,n}^{comm}+{\tau }_{u,n}^{proc}\right),\forall u\in \mathcal{U}$$

(4)

Service latency is a vital factor that greatly affects users’ QoE. In our work, instead of using raw service latency, we convert it to a MOS by means of a utility function, which is presented in the next section.

3.4. Utility Model

The utility function is adapted from [27,28], which shows that the user perception of service latency does not advance beyond a certain threshold. Figure 2 depicts the utility function, which is a non-decreasing piecewise linear utility function of service latency of users. Based on the two latency thresholds: $T^{min}$ and $T^{max}$, the utility function maps each data point of service latency t to one of the utility levels of excellent, good, fair, poor, bad/dissatisfied as follows.

• $t\le T^{min}$: Depending on the service type, the quality perception of users is the best at a pre-defined threshold $T^{min}$, and no further improvement in quality can be perceived by users of that service even if the latency t reduces below this value. In this case, the utility remains unchanged ($W^{max}=1$)
• $T^{min}<t\le T^{max}$: The service latency t is within an acceptable range. User experience reduces as t increases, and the utility get a value between 0 and 1 ($0\le W<1$). In this case, it is possible to define an optional point ($T^{fair}$) from which the users begin to feel the quality drops clearly to a poor experience.
• $t>T^{max}$: The service quality is really bad and beyond the acceptable range. In this case, the utility has a negative value ($W^b<0$).

Given these definitions, the utility function of user u requesting service $s_u$ is formulated as

$$W_u=\left\{\begin{array}{c}1,\mathrm{if}{t}_u\le T_{s_u}^{min},\hfill \\ 0\le \frac{T_{s_u}^{max}-t_u}{T_{s_u}^{max}-T_{s_u}^{min}}<1,\mathrm{if}{T}_{s_u}^{min}<t_u\le T_{s_u}^{max}\hfill \\ W^b<0,otherwise\hfill \end{array}\right.$$

(5)

Or it can be rewritten in a shorten form as follows.

$$W_u=\frac{T_{s_u}^{max}-T_{s_u}^{min}-max(0,t_u-T_{s_u}^{min})}{T_{s_u}^{max}-T_{s_u}^{min}}=1-\frac{max(0,t_u-T_{s_u}^{min})}{T_{s_u}^{max}-T_{s_u}^{min}}$$

(6)

The mentioned thresholds are set by the service providers depending on services via MOS estimation models. For the example of VR services, [29] shows that the ideal latency is equal to or below 20 ms. If this latency exceeds 20 ms, the user experience will decrease and when it reaches about 50 ms, users will be disturbed by a noticeable lag when moving in the virtual world. In addition, it is said to be too slow if the latency exceeds 100 ms. Hence, for VR services, we can set $T^{min}=20$ ms, $T^{fair}=50$ ms and $T^{max}=100$ ms. Similarly, a latency of $T^{min}=50$ ms is the limit for user to feel the instant feedback and $T^{max}=150$ ms is the acceptable maximum latency of some interactive games [30].

We also illustrate an example that captures the concept of the utility function based on the service latency of users as shown in Figure 3. Two users request a VR service, which is supposed to be available in both MEC 1 and MEC 2. However, due to the computation resource constraint, each MEC can effectively serve only one user at a time. The traditional latency-aware task/request scheduling policies [16,36,44] would minimize the average service latency (i.e., 17.5 ms) and lead to solution: (user 1 -> MEC 1; user 2 -> MEC 2). In this case, user 1 will perceive excellent quality while user 2 perceives the decline of service quality. Meanwhile, by using the proposed utility function, we obtain a better solution, (user 1 -> MEC 2; user 2 -> MEC 1), where both of them get the best experience with a latency of 20 ms.

3.5. Problem Formulation

The objective of our work is to determine optimal service placement and request scheduling decisions in order to maximize the total utility of all users while taking into account both storage and computation resource constraints in MEC systems. For a given service placement profile x, and request scheduling profile y, the optimization problem of joint service placement and request scheduling (JSPRS) can be expressed as follows.

$$\begin{array}{cc}\hfill \underset{\mathbf{x},\mathbf{y}}{\max .}& \sum _{u\in \mathcal{U}}{W}_u\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \end{array}$$

(7)

$$\begin{array}{cc}\hfill & \sum _{n\in \mathcal{N}\cup \left\{l\right\}}{y}_{un}=1,\forall u\in \mathcal{U},\hfill \end{array}$$

(7a)

$$\begin{array}{cc}\hfill & \sum _{s\in \mathcal{S}}{x}_{sn}im{g}_s\le R_n,\forall n\in \mathcal{N},\hfill \end{array}$$

(7b)

$$\begin{array}{cc}\hfill & \sum _{u\in \mathcal{U}}{y}_{un}{f}_{un}\le F_n,\forall n\in \mathcal{N},\hfill \end{array}$$

(7c)

$$\begin{array}{cc}\hfill & y_{un}\le x_{s_{u}n},\forall u\in \mathcal{U},s_u\in \mathcal{S},n\in \mathcal{N},\hfill \end{array}$$

(7d)

$$\begin{array}{cc}\hfill & x_{sn},y_{un}\in \left\{0,1\right\},\forall u\in \mathcal{U},s\in \mathcal{S},n\in \mathcal{N}\cup \left\{l\right\}\hfill \end{array}$$

(7e)

The constraint in Equation (7a) indicates that each user is scheduled to exactly one computing node, i.e., either a MEC server or the core cloud. The constraint in Equation (7b) guarantees that the total amount of data of services placed in a MEC node do not exceed its storage capacity. The constraint in Equation (7c) guarantees that the computing resources allocated to users at each MEC node do not exceed its computation capacity. The constraint in Equation (7d) states that a MEC node can only serve a user u if the requested service $s_u$ is already placed on that MEC. In addition, the constraint in Equation (7e) denotes x, and y are binary vectors.

4. Proposed Nested-Genetic Algorithm

The JSPRS problem is an Integer Nonlinear Programming (INLP) problem, which has been shown as NP-hard [45]. In this section, we introduce a metaheuristic solution based on genetic algorithm (GA) due to the popularity of GA in solving service provisioning problems [22,28]. The major benefit of GAs is that they enable browsing a large search space to derive a global high-quality solution in polynomial time.

As the name implies, GA is inspired by natural evolution, which is the differential survival and reproduction of individuals over generations. Specifically, GA is an iterative process, in which each iteration is called a generation. Each generation consists of a population of individuals (or candidate solutions). Each individual is represented by its own chromosome, which is characterized by a set of variable components known as genes. The quality of an individual in the population is determined by a fitness function whose value specifies how fit the individual is compared to others in the population. Fitter individuals are given a higher chance to mate and produce offspring for the next generation while individuals with least fitness values are discarded to provide space for new offspring. By applying three genetic operators (selection, crossover, and mutation), an old generation can evolve into a new one with a population of both the elite (i.e., the individuals with the best fitness values) and offspring. This process is repeated until the population converges or reaching the maximum number of generations.

The JSPRS problem includes two sub-problems: service placement and request scheduling, which are coupled since the MEC node, to which a request is scheduled, must have a replica of the requested service. To solve the JSPRS problem, we propose a Nested-Genetic Algorithm (Nested-GA) that consists of two genetic algorithms: Outer-GA and Inner-GA. The Outer-GA addresses service placement sub-problem while the Inner-GA addresses request scheduling sub-problem. Specifically, given a service placement x, we can obtain the optimal request scheduling solution y* that maximizes the total utility of users by using the Inner-GA as shown in Algorithm 2. Based on this optimal y*, the optimal service placement solution x* can be obtained by the outer-GA of the Nested-GA as shown in Algorithm 1. The optimal result (x*, y*) represents service placement and request scheduling policy. In the following, we will describe the concrete implementation of our proposed Nested-GA to solve the JSPRS problem.

Algorithm 1: Nested-Genetic Algorithm (Nested-GA)

Input: Input parameters of Equation (7); the parameters of the outer-GA $popSizeX$,

$outerMaxIter$, $eliteSizeX$, $tourSizeX$, $p_{xm}$; and the parameters of the Inner-GA.

Output: Optimal service placement and request scheduling solution (x*, y*).

1. Generate initial population of individuals for the JSPRS problem.

1.a. Initialize a population of $popSizeX$ number of service placement individuals

under the constraint Equation (7b), denoted as $X\_POP$.

1.b. For each x in $X\_POP$, conduct the Inner-GA (Algorithm 2) to find the optimal

request scheduling y*, thus producing a complete solution (x, y*) for the problem

Equation (7).

2. REPEAT /Search for optimal service placement x*/

2.a. Find the $eliteSizeX$ best individuals to be preserved (elitism mechanism). Add

them to the parent set.

2.b. Select some other parents according to the principles of tournament selection with

tournament size of $tourSizeX$.

2.c. Choose two service placement x1 and x2 of the parent set randomly. Then apply

the crossover operation to create two new offspring. Repeat this step until the number

of offspring is equal to ($popSizeX-eliteSizeX$).

2.d. For each offspring x (service placement), do the mutation operation with the

mutation probability $p_{xm}$. Then if the mutated x does not exist in the population,

conduct the Inner-GA (Algorithm 2) to find the best request scheduling y* for the new x.

2.e. Replace the current generation with the new one filled by both the elite and

offspring.

UNTIL the population converges or reaching the maximum number of iterations

$outerMaxIter$.

Algorithm 2: Inner Genetic Algorithm (Inner-GA)

Input: Input parameters of Equation (7); a service placement x; and the parameters of the

Inner-GA $popSizeY$, $innerMaxIter$, $eliteSizeY$, $tourSizeY$, $p_{ym}$.

Output: Optimal request schedule y* for a service placement x.

1. Initialize a population of $popSizeY$ number of request scheduling individuals according to

the service placement x (i.e., all request must be scheduled to nodes at which the required

service is stored).

2. REPEAT

2.a. Compute the fitness of each individual according to the objective function in

Equation (7).

2.b. Find the $eliteSizeY$ best individuals to be preserved (elitism mechanism). Add

them to the parent set.

2.c. Select some other parents according to the principles of tournament selection with

tournament size of $tourSizeY$.

2.d. Choose two individuals y1 and y2 of the parent set randomly. Then apply the

crossover operation to create two new offspring. Repeat this step until the number of

offspring is equal to ($popSizeY-eliteSizeY$).

2.e. For each offspring y (request scheduling), do the mutation operation with the

mutation probability $p_{ym}$.

2.f. Replace the current generation with the new generation filled by both the elite and

offspring.

UNTIL the population converges or reaching the maximum number of iterations

$innerMaxIter$.

4.1. Chromosome and Initialization

In our algorithm, the chromosome of a service placement individual $\mathbf{x}=\{x_{sn}\in \{0,1\}|s\in \mathcal{S},n\in \mathcal{N}\}$ is represented by $\left|\mathcal{N}\right|$ blocks of $\left|\mathcal{S}\right|$ bits each, one block for each MEC node $n\in \mathcal{N}$, and one bit for each service $s\in \mathcal{S}$. As such, it can be encoded as a binary vector of size $\left|\mathcal{N}\right|\ast \left|\mathcal{S}\right|$, where the value of gene $x_{sn}$ located at $(n-1)\ast \left|\mathcal{S}\right|+s$ indicates whether service s is placed on MEC node n (1) or not (0). Meanwhile, the chromosome of a request scheduling individual y is encoded as an integer vector of size $\left|\mathcal{U}\right|$, in which the value of gene $y_u$ specifies where to schedule the user $u\in \mathcal{U}$. The chromosome of a service placement and a request scheduling individual are shown in Figure 4a and Figure 4b, respectively.

The initial population (i.e., initialization in Algorithms 1 and 2) is generated randomly but within the constraints of Equation (7). Specifically, the Outer-GA in Algorithm 1 initializes the population of service placement individuals within the storage constraint Equation (7b). We loop over each block (MEC) of the vector and assign value 0 or 1 randomly to each bit (service) of the block until the storage demand of services assigned value 1 exceeds the capacity of the MEC. Then the remaining bits in the block is assigned value 0. The Inner-GA (i.e., Algorithm 2) initializes the population of request scheduling individuals according to a given service placement solution. Let ${\mathcal{H}}_u=\left\{0\right\}\cup \{n\in \mathcal{N}|x_{s_{u}n}=1\}$ denote the set of hosting nodes of the service $s_u$ requested by user u. Here, $\left\{0\right\}$ represents the core cloud, which is assumed to host all services. Then in the chromosome of y, each gene $y_u$ takes a random element from the corresponding set ${\mathcal{H}}_u$.

A complete solution to the JSPRS problem contains a service placement and a request scheduling individual. To evaluate how fit each solution is, the fitness function is defined according to the objective function in Equation (7), which is to maximize the total utility of all users. Hence, $Fitness={\displaystyle \sum _{u\in \mathcal{U}}}{W}_u$.

Once the initial population is created, the GA evolves the generation iteratively by applying the GA operators, i.e., selection, crossover, and mutation for the reproduction process. In each iteration, the selection operator is applied to maintain the parents, and then the crossover and mutation operators are applied to the parents to produce the offspring. These operators will be described in detail next.

4.2. Selection

For the selection operation, we adopt tournament selection, which is the most popular selection method in GA due to its efficiency and ease of implementation [46]. In tournament selection, we pick a few individuals at random from the population, and these individuals compete against each other. The one with the best fitness wins and is selected as a parent for producing offspring. The number of individuals competing in a tournament is referred to as tournament size. We also adopt elitism mechanism, which allows the fittest individuals from the current generation to carry over to the next, unchanged. While the elitism ensures that the solution quality obtained by the GA will not decrease in the reproduction process, the tournament selection maintains sufficient diversity and avoids premature convergence. Hence, the performance of GA can be improved.

4.3. Crossover and Mutation

The next step is to generate the successive generation from the parents through a combination of genetic operators, i.e., crossover and mutation. The crossover and mutation operations help GA extend searching region and enhance population diversity so as to avoid falling into the local optimal point.

For the crossover operation, two randomly selected parents exchange their segments to create two new offspring. This process repeats until the population size of the successive generation is equal to that of the current. Here, we apply two-point crossover, in which two crossover points are picked randomly from the parents, and then the segments in between the two points are swapped between the parents. The two-point crossover operation on service placement individuals and request scheduling individuals are shown in Figure 5a and Figure 5b, respectively. It is noteworthy that for service placement individuals (Figure 5a), although the crossover points are selected randomly, they must be selected delicately at the points of MEC blocks, which do not mix up the service placement decisions on each MEC.

For the mutation operation, an individual is selected with a predefined mutation probability firstly, and then one or more random genes of the selected chromosome alter their current values to produce a new offspring. For the service placement individuals, we choose a random block (MEC) and apply bit-flip mutation (i.e., 1 to 0 and vice versa) to two random genes (services) of the block such that the storage constraint is not violated. For the request scheduling individuals, we choose two random users and replace the current hosting node of each user u with a random node within the set ${\mathcal{H}}_u$ of the requested service $s_u$.

At the end of each iteration, the current generation is replaced by the new one including the current fittest individuals (elitism) and offspring. This new generation is then inputted to the next iteration. The process continues until there is no improvement in the fitness value of the best solution (i.e., the population converges) or the maximum number of iterations is reached.

5. Performance Evaluation and Discussion

In this section, we carry out experiments to verify the performance of the proposed algorithm under different configurations of MEC nodes.

5.1. Simulation Settings

For the network topology, we extract user and MEC locations from real-world data traces. For MEC locations, we collect the information (e.g., cell ID, longitude, latitude) of base stations (BSs) in Phoenix city, USA via the publicly available OpenCellid database [47]. We assume a MEC server is attached to each BS to form a MEC node. Meanwhile, user locations are extracted from a Twitter user dataset [48], which contains the record of over 20,000 users. We prune the dataset keeping only the users from Phoenix city. Based on the locations of users and BSs, we match the users to their corresponding BSs. Suppose that the communication coverage of each BS is about 2000 m, the users are assumed to be connected to their nearest BS within the range of 2000 m. For our experiment, we choose a sampled map of $\left|\mathcal{N}\right|=5$ BSs (non-overlapping) located close to each other to form a collaboration space, and $\left|\mathcal{U}\right|=100$ users, each of whom is directly connected to one of these BSs. The users are observed to be uniformly distributed in the collaboration space. Moreover, the core cloud data center is assumed to be located in Knoxville city, USA. The propagation delay between any two computing nodes can be estimated by the round-trip time of small packets and provided by [49]. As such, the propagation delay between the MEC nodes ranges from 1 to 10 ms, and between the MEC nodes and the core cloud ranges from 100 to 120 ms. We omit the propagation delay between users and their connected MEC due to the close distance between them. For the sake of simplicity, we set the transmission rate of the network link between any two computing nodes to $r_{n_u,n}=1$ Gbps ($\forall n_u\in \mathcal{N},n\in \mathcal{N}\cup \left\{l\right\}$), and the wireless transmission rate between users and their connected MEC to $r_{u,n_u}=100$ Mbps ($\forall u\in \mathcal{U},n_u\in \mathcal{N}$).

In the simulation, each user performs only one request for a service drawn from a set of $\left|\mathcal{S}\right|=20$ services. The service popularity follows the Zipf distribution with exponent $\alpha =0.8$. For each service s, the storage demand of service image $im{g}_s$ is set randomly within [10, 100] GB. The required input data size per request $d_s$ and computation intensity per request $w_s$ take value within [50, 300] KB and [10, 200] Megacycles, respectively. In addition, each service s has different latency requirements including two thresholds: $T^{min}$, $T^{max}$. For example, latency-sensitive services such as VR require $T^{min}=20$ ms and $T^{max}=100$ ms [29]; some cloud-based interactive games require $T^{min}=50$ ms and $T^{max}=150$ ms [28,30]; for latency-tolerant services such as simple web services, web search, $T^{min}=100$ ms and $T^{max}=1000$ ms [50]. In our experiment, we consider services of these categories, and thus ($T^{min}$, $T^{max}$) of each service s is set randomly within {(20, 100), (50, 150), (100, 1000)} ms.

For each MEC node n, unless otherwise stated, the storage capacity and the computation capacity are set as $R_n=500$ GB and $F_n=20$ GHz, respectively. Yet, during the evaluations, we vary these parameters to show their influence on the system performance. Other simulation settings related to the parameters of the proposed GA are described in

Table 1. Nested-GA parameters.

Parameter	Value
Population size of service placement individuals (Outer-GA), $popSizeX$	60
Population size of request scheduling individuals (Inner-GA), $popSizeY$	100
Number of the elite for the Outer-GA, $eliteSizeX$	$10\%\ast popSizeX$
Number of the elite for the Inner-GA, $eliteSizeY$	$10\%\ast popSizeY$
Tournament size of the Outer-GA, $tourSizeX$	3
Tournament size of the Inner-GA, $tourSizeY$	5
Mutation probability of the Outer-GA, $p_{xm}$	0.1
Mutation probability of the Inner-GA, $p_{ym}$	0.2
Maximum number of iterations for Outer-GA, $outerMaxIter$	100
Maximum number of iterations for Inner-GA, $innerMaxIter$	100

.

To evaluate the performance of the proposed algorithm, we compare the Nested-GA with other baseline methods as follows.

• The optimal solution of Equation (7) using BONMIN solver in the COIN-OR toolbox, which is a well-known open-source optimization tool for solving non-linear programming. BONMIN solver uses IPOPT package, which implements an interior point line search filter method to find relaxed solutions for the NLP problems.
• Top-R service placement with Nearest-based request scheduling (abbr., Top-R Nearest) algorithm, which first places services at each MEC $n\in \mathcal{N}$ in descending order of service popularity until reaching the storage capacity $R_n$ (i.e., the Top-R most popular services are placed), and then schedules each user request to the nearest (i.e., smallest network latency) hosting node of the requested service.
• Top-R service placement with Genetic-based request scheduling (abbr., Top-R Genetic) algorithm, in which the service placement strategy is similar to the Top-R Nearest, and the request scheduling strategy follows the Inner-GA (Algorithm 2). In other words, the service placement and request scheduling decisions are addressed separately, and only the request scheduling is optimized.

5.2. Simulation Results

First, we investigate the convergence of the proposed Nested-GA. Figure 6a displays the convergence of the Inner-GA of the Nested-GA. We observe that the total utility keeps increasing for about 62 iterations and becomes constant for the rest of the iterations. Meanwhile, Figure 6b plots the convergence of the Outer-GA of the Nested-GA. We observe that the Outer-GA even has a faster convergence rate than the Inner-GA and converges within 34 iterations due to smaller search space. These results show that our proposal can converge in a reasonable time.

Next, we compare the performance of the proposed Nested-GA with the other algorithms in terms of the total utility of all users when varying different input parameters, one at a time. In Figure 7, we show the impact of increasing the storage capacity of MEC $R_n,\forall n\in \mathcal{N}$ on the total utility, cloud load (i.e., percentage of users scheduled to the core cloud) and percentage of dissatisfied users (i.e., $W_u<0$). In general, when $R_n$ increases, the total utility achieved by all algorithms (except Top-R Nearest) increases (Figure 7a). Meanwhile, the cloud load of all algorithms and the percentage of dissatisfied users of all algorithms (except Top-R Nearest) decrease as shown in Figure 7b and Figure 7c, respectively. It is because when $R_n$ becomes larger, more services can be placed at the MEC nodes, and more users can be served by the MEC nodes with low network latency, resulting in the improvement of user experience. However, at the same time, due to the computing resource limitation of MEC, the more users scheduled to the MEC nodes, the less the amount of computing resource assigned to each user. Hence, the processing latency of users becomes larger and affects the user experience. It can be observed from Figure 7a that when $R_n$ increases, the total utility of all algorithms increases dramatically at first but then slows down. Among the algorithms, Top-R Nearest, which always schedules each user to the nearest MEC node hosting the corresponding service, performs the worst in all cases of storage capacity. As $R_n$ increases, Top-R Nearest tends to only use the MEC computing resource to serve users (i.e., the cloud load gradually decreases to 0). Hence, when the storage capacity exceeds 700 GB, due to the computing resource bottleneck of the MEC nodes, the total utility of Top-R Nearest even decreases slightly and the percentage of dissatisfied users increases from 3% to 6% (Figure 7c). Compared to Top-R Nearest, Top-R Genetic better uses the cloud and MEC computing resources by scheduling the users to appropriate computing nodes (a MEC or the core cloud) based on Algorithm 2. Hence, the total utility of Top-R Genetic becomes much better than that of Top-R Nearest as $R_n$ increases. Meanwhile, our proposed Nested-GA considerably outperforms the above algorithms by optimizing both the service placement and request scheduling decisions. It is noteworthy that when the storage capacity of each MEC is large enough to store all services ($R_n=900$ GB), the only problem is the optimal request scheduling or task offloading; and hence, the performance of Top-R Genetic can reach that of Nested-GA. In this case, the cloud load of both algorithms reduces to a stable value of 29% (Figure 7b) and the percentage of dissatisfied users reduces to 0% (Figure 7c). Moreover, the performance of Nested-GA is very close to the optimal solution provided by Bonmin solver. In general, as $R_n$ increases, the total utility of our proposal is improved by 23.14% and 10.14% on average compared to Top-R Nearest and Top-R Genetic, respectively while it is only 1.29% smaller on average than the optimal value.

Figure 8 illustrates the impact of increasing computation capacity $F_n,\forall n\in \mathcal{N}$ on the total utility, cloud load and percentage of dissatisfied users. Similarly, as $F_n$ increases, the total utility increases (Figure 8a) while the cloud load (except in the case of Top-K Nearest) and the percentage of dissatisfied users decrease (Figure 8b,c). Taking a closer look by comparing the performance of different algorithms for the same computation capacity, Top-R Nearest still performs the worst in all cases of $F_n$. When $F_n$ is small ($F_n=5$ GHz), the total utility of all users of Top-K Nearest is very small, and many users are dissatisfied (Figure 8c) due to the computing resource bottleneck of MEC. We also note that with fixed storage capacity (here, $R_n=500$ GB), the variation of computation capacity of MEC does not affect the cloud load of Top-R Nearest (Figure 8b). Compared to Top-R Nearest, Top-R Genetic performs much better when $F_n$ is small since it schedules most users to the core cloud. However, as $F_n$ increases, serving users at the MEC nodes is more benefit, and thus the performance of Top-R Nearest increases rapidly and can reach close to that of Top-R Genetic when $F_n$ is large enough. In this case, it can be observed from Figure 8b and Figure 8c that the cloud load and percentage of dissatisfied users of both algorithms are kept stable at 15% and 3%, respectively. Meanwhile, the proposed Nested-GA can always get better total utility than the above two methods by performing optimal service placement and request scheduling on MEC and cloud resources. Specifically, our proposal can achieve an average improvement of 192.59% over Top-R Nearest and 8.30% over Top-R Genetic. Figure 8c also shows the percentage of dissatisfied users of our proposal is also lower and reduces to 0 as $F_n$ increases. Furthermore, similar to the previous experiment, the performance of our algorithm is approximate to the optimal solution with the average difference of 2.02%.

Based on these experimental results, we can conclude that the proposed Nested-GA consistently outperforms the two baseline methods, Top-R Nearest and Top-R Genetic, in all configurations of storage capacity $R_n$ and computation capacity $F_n$. Moreover, the performance of Nested-GA is very close to the optimal solution provided by Bonmin solver while reducing the running time significantly. The solver takes an average of 4.6 h while only 1425 s on average is needed for Nested-GA to find near-optimal solutions.

5.3. Discussion

From the above observations, there are many interesting research directions to extend the proposed service provisioning policy as follows.

(i)

The policy can handle user demand changes over time more effectively by considering migration cost. Typically, a small change in the user demand may make the current solution no longer optimal; and hence, the policy must be adapted accordingly. The adaptation of service placement requires service migration between MEC nodes or from the core cloud to a MEC node. In the worst case, major migrations may cause a tremendous amount of data to move back and forth between computing nodes, thereby overloading the backhaul links. To avoid it, we can impose a budget constraint on the migration cost, allowing only incremental adjustments.

(ii)

The energy consumption of both the centralized cloud and MEC nodes may be soaring while processing a large volume of service requests. Hence, an energy-efficient service provisioning policy is needed while guaranteeing QoE is still a challenge.

(iii)

In some cases, the service provisioning may have to consider the monetary cost of using resources. For example, the centralized cloud and the MEC nodes are managed on different administration domains. A cloud service provider (CSP) does not have MEC infrastructure, and thus rents the MEC resources of network operators (e.g., computing, storage, network) to deploy services closer to the IoT devices or end-users. Due to the wide geographical distribution of IoT devices, the MEC resources may be offered from different parties with diverse prices. In this case, the objective of service provisioning policy is to maximize the total utility of all users under the budget constraint of the CSP in using MEC resources.

(iv)

It is also necessary to design provision policy for composite services consisting of multiple interdependent components. In this case, it becomes the problem of mapping task graphs onto a processor graph. In particular, the task graph represents service components and communication among these components while the processor graph represents the computing nodes and communication links in the physical system.

6. Conclusions

In this paper, we investigated the utility-centric service provisioning considering service placement and request scheduling under both the storage and computation resource constraints in MEC systems. The major objective of the research is to maximize the total utility of all users, and thus provide a service provisioning policy that effectively guarantees the QoE of users. We formulate the problem as an INLP and then propose a metaheuristic algorithm, namely Nested Genetic Algorithm (Nested-GA), which consists of two genetic algorithms, each of whom solves a sub-problem regarding service placement or request scheduling decisions. Finally, we verify the efficiency of the Nested-GA through experiments. The results indicate that our proposal achieves better total utility than other baseline methods and can achieve close-to-optimal solutions in reasonable running time. In future work, it is more robust to take into account the migration cost, energy consumption, resource cost, or composite services in the service provisioning policy.