Experimental Measurements of the Natural Frequencies and Mode Shapes of Rotating Disk-Blades-Disk Assemblies from the Stationary Frame
Abstract
:1. Introduction
2. Diametrical Mode Shapes of Rotating Disk-Blades-Disk Like Structures from the Rotating Frame
2.1. Simple Disk Case
2.2. Disk-Blades-Disk Structures
3. Decomposition of the Diametrical Mode Shapes for Disk-Blade-Disk Configuration
- It is assumed that the response is measured in N’ equidistant points.
- In order to get a good resolution in the diametrical components information, this deformation is virtually elongated λ times (10 times in this example) in space. The first and the last point of the final sequence correspond to the displacement at angle 0° (Figure 5b).
- The FFT is applied to the resulting peripheral deformation. The transform is according to the following equation:
- In this equation is the sequence of points of the elongated periphery that has N points. is the sequence of complex values after the transformation (Figure 5c).
- The first N/2 values of the sequence are plotted in Magnitude against the diametrical components. To do this, the following transformation with the index k has to be done.n represents the diametrical components. In this case, λ = 10 is considered, because the peripheral deformation is elongated 10 times. The magnitude is represented in terms of 0-peak value and, therefore, to obtain from the -values:
- The resolution in the diametrical components is 1/λ, where λ is the number of times that the peripheral deformation is virtually elongated. To accurately see the diametrical components, λ should be higher or equal to 2 (λ ≥ 2).
- The maximum diametrical component that can be detected on the mode shape depends on the number of measured points on the periphery (equidistant points). where is the number of measured points on the periphery.
Application of the Decomposition in a Real Prototype Disk-Blades-Disk Structure
4. Diametrical Mode Shapes of a Rotating Disk-Blades-Disk Structure Observed from a Stationary Point of View and Its Relation to Mode Shape Decomposition
5. Experimental Test
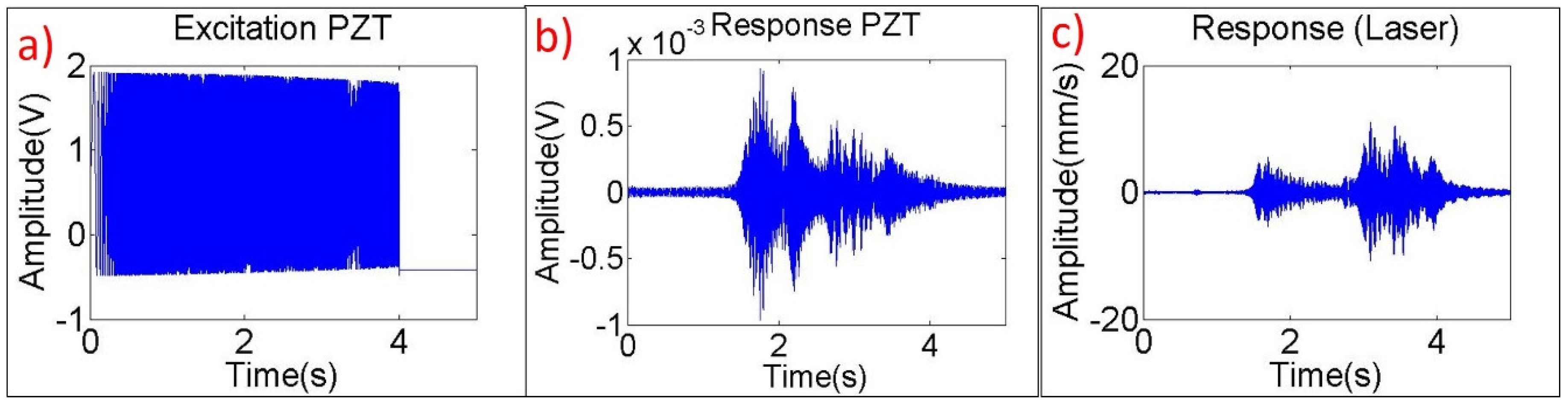
5.1. Test Setup
5.2. Mode Shape Decomposition of the Diametrical Modes for the Standing Disk-Blades-Disk Structure
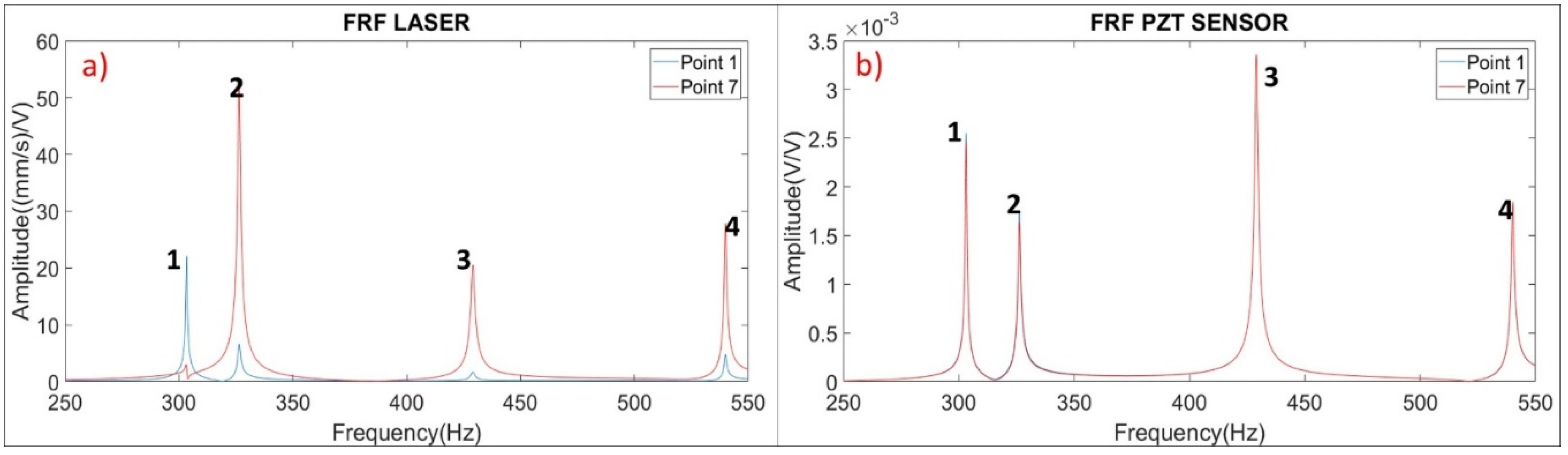
5.3. Tests with the Disk-Blades-Disk Structure Rotating and Detection of Natural Frequencies with LDV from the Stationary Frame
5.4. Limitation of Standard Numerical Codes For Non-Axisymmetric Rotating Structures Analyzed in the Stationary Frame
5.5. Validity of the Relationship between the Mode Shape Decomposition and the Frequencies Detected from the Stationary Frame and Future Work
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ewins, D.J. Modal Testing: Theory and Practice; Research Studies Press Letchworth: Letchworth Garden City, UK, 1984; Volume 15. [Google Scholar]
- Heylen, W. Modal Analysis Theory and Testing; Katholieke Universiteit Leuven: Leuven, Belgium, 2007. [Google Scholar]
- Bucher, I. Transforming and separating rotating disk vibrations using a sensor array. J. Sound Vib. 2011, 330, 1244–1264. [Google Scholar] [CrossRef]
- Legrand, M.; Pierre, C.; Cartraud, P.; Lombard, J.-P. Two-dimensional modeling of an aircraft engine structural bladed disk-casing modal interaction. J. Sound Vib. 2009, 319, 366–391. [Google Scholar] [CrossRef] [Green Version]
- Singh, M.P.; Thakur, B.K.; Sullivan, W.E.; Donald, G. Resonance identification for impellers. In Proceedings of the 32nd Turbomachinery Symposium, College Station, TX, USA, 8–11 September 2003; A&M University. Turbomachinery Laboratories: College Station, TX, USA, 2003. [Google Scholar]
- Egusquiza, E.; Valero, C.; Presas, A.; Huang, X.; Guardo, A.; Seidel, U. Analysis of the dynamic response of pump-turbine impellers. Influence of the rotor. Mech. Syst. Signal Process. 2016, 68–69, 330–341. [Google Scholar] [CrossRef]
- Southwell, R.V. On the free transverse vibrations of a uniform circular disc clamped at its centre and on the effects of rotation. Proc. R. Soc. Lond. 1922, 101, 133–153. [Google Scholar] [CrossRef]
- Belvins, R. Formulas for Natural Frequency and Mode Shape; Krieger Publishing Company: Malabar, FL, USA, 1984. [Google Scholar]
- Leissa, A.W. Vibration of Plates; Goverment Printing Office: Washington, DC, USA, 1969. [Google Scholar]
- Vogel, S.; Skinner, D. Natural frequencies of transversely vibrating uniform annular plates. J. Appl. Mech. 1965, 32, 926–931. [Google Scholar] [CrossRef]
- Rao, S.S.; Prasad, A. Vibrations of annular plates including the effects of rotatory inertia and transverse shear deformation. J. Sound Vib. 1975, 42, 305–324. [Google Scholar] [CrossRef]
- Weisensel, G. Natural frequency information for circular and annular plates. J. Sound Vib. 1989, 133, 129–137. [Google Scholar] [CrossRef]
- Leissa, A.; Narita, Y. Natural frequencies of simply supported circular plates. J. Sound Vib. 1980, 70, 221–229. [Google Scholar] [CrossRef]
- Amabili, M.; Forsali, G.; Kwak, M.K. Free vibrations of annular plates coupled with fluids. J. Sound Vib. 1996, 191, 825–846. [Google Scholar] [CrossRef]
- Amabili, M. Effect of finite fluid depth on the hydroelastic vibration of circular and annular plate. J. Sound Vib. 1996, 193, 909–925. [Google Scholar] [CrossRef]
- Mehdigholi, H. Forced Vibration of Rotating Discs and Interaction with Non-Rotating Structures. Ph.D. Thesis, Imperial College, London, UK, 1991. [Google Scholar]
- Ahn, T.K.; Mote, C.D. Mode Identification of a Rotating Disk. Exp. Mech. 1998, 38, 250–254. [Google Scholar] [CrossRef]
- Chung, J.; Kang, N.-C.; Lee, J.M. A study on free vibration of a spinning disk. KSME J. 1996, 10, 138–145. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Seidel, U. On the detection of natural frequencies and mode shapes of submerged rotating disk-like structures from the casing. Mech. Syst. Signal Process. 2015, 60, 547–570. [Google Scholar] [CrossRef]
- Ewins, D. Vibration characteristics of bladed disc assemblies. J. Mech. Eng. Sci. 1973, 15, 165–186. [Google Scholar] [CrossRef]
- Castanier, M.P.; Pierre, C. Modeling and analysis of mistuned bladed disk vibration: Current status and emerging directions. J. Propuls. Power 2006, 22, 384–396. [Google Scholar] [CrossRef]
- Ottarsson, G.; Castanier, M.; Pierre, C. A reduced-order modeling technique for mistuned bladed disks. In Proceedings of the 35th Structures, Structural Dynamics, and Materials Conference, Hilton Head, SC, USA, 18–20 April 1994; p. 1640. [Google Scholar]
- Jacquet-Richardet, G.; Ferraris, G.; Rieutord, P. Frequencies and modes of rotating flexible bladed disc-shaft assemblies: A global cyclic symmetry approach. J. Sound Vib. 1996, 191, 901–915. [Google Scholar] [CrossRef]
- Lemeš, S.; Zaimović-Uzunović, N. Mode shapes of centrifugal pump impeller. In Proceedings of the 6th International Research/Expert Conference on Trends in the Development of Machinery and Associated Technology (TMT 2002), Neum, Bosnia and Herzegovina, 18–22 September 2002. [Google Scholar]
- Wang, Q.; Bartos, J.C.; Houston, R.A. Methodology of open bladed impeller resonance indentification. In Proceedings of the 28th Turbomachinery Symposium, College Station, TX, USA, September 1999; A&M University. Turbomachinery Laboratories: College Station, TX, USA, 1999. [Google Scholar]
- Lais, S.; Liang, Q.; Henggeler, U.; Weiss, T.; Escaler, X.; Egusquiza, E. Dynamic Analysis of Francis Runners—Experiment and Numerical Simulation. Int. J. Fluid Mach. Syst. 2009, 2, 303–314. [Google Scholar] [CrossRef]
- Tanaka, H. Vibration Behavior and Dynamic Stress of Runners of Very High Head Reversible Pump-turbines. Int. J. Fluid Mach. Syst. 2011, 4, 289–306. [Google Scholar] [CrossRef]
- Kubota, Y.; Susuki, T.; Tomita, H.; Nagafuji, T.; Okamura, T. Vibration of rotating bladed disc excited by stationary distributed forces. Bull. JSME 1985, 26, 1952–1957. [Google Scholar] [CrossRef]
- Kubota, Y.; Ohashi, H. A study on the natural frequencies of hydraulic pumps. In Proceedings of the 1st ASME Joint International Conference on Nuclear Engineering, Tokyo, Japan, 4–7 November 1991; pp. 589–593. [Google Scholar]
- Egusquiza, E.; Valero, C.; Huang, X.; Jou, E.; Guardo, A.; Rodriguez, C. Failure investigation of a large pump-turbine runner. Eng. Fail. Anal. 2012, 23, 27–34. [Google Scholar] [CrossRef] [Green Version]
- Escaler, X.; Hütter, J.K.; Egusquiza, E.; Farhat, M.; Avellan, F. Modal behavior of a reduced scale pump-turbine impeller. Part 1: Experiments. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Timişoara, Romania, 20–24 September 2010; Iop Publishing: Bristol, UK, 2012; Volume 12, p. 012116. [Google Scholar]
- Valero, C.; Huang, X.; Egusquiza, E.; Farhat, M.; Avellan, F. Modal behavior of a reduced scale pump turbine impeller. Part II: Numerical simulation. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Timişoara, Romania, 20–24 September 2010; Iop Publishing: Bristol, UK, 2012; Volume 12, p. 012117. [Google Scholar]
- Huang, X.X.; Egusquiza, E.; Valero, C.; Presas, A. Dynamic behaviour of pump-turbine runner: From disk to prototype runner. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Beijing, China, 19–22 September 2013; IOP Publishing: Bristol, UK, 2013; Volume 52, p. 022036. [Google Scholar]
- De Siervo, F.; De Leva, F. Modern trends in selecting and designing Francis turbines. Water Power Dam Constr. 1976, 28, 28–35. [Google Scholar]
- Zobeiri, A. Investigations of Time Dependent Flow Phenomena in a Turbine and a Pump-Turbine of Francis Type: Rotor Stator Interactions and Precessing Vortex Rope. Ph.D. Thesis, École polytechnique fédérale de Lausanne (EPFL), Lausanne, France, 2009. [Google Scholar]
- Nicolet, C.; Ruchonnet, N.; Avellan, F. One-dimensional modeling of rotor stator interaction in Francis Pump-Turbine. In Proceedings of the 23rd IAHR Symposium, Yokohama, Japan, 17–21 October 2006. [Google Scholar]
- Inc, A. ANSYS Mechanical APDL Theory Reference; ANSYS, Inc.: Canonsburg, PA, USA, 2016; Volume 17. [Google Scholar]
- Software, M. MSC Nastran 2016. Rotordynamics User’s Guide; MSC: Newport Beach, CA, USA, 2016. [Google Scholar]
- Chandraker, A. Runner Blade for Low Specific Speed Francis Turbine. US7210904B2, 1 May 2007. [Google Scholar]
- Presas, A.; Valero, C.; Huang, X.; Egusquiza, E.; Farhat, M.; Avellan, F. Analysis of the Dynamic Response of Pump-Turbine Runners-Part I: Experiment. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Beijing, China, 13–23 August 2012; IOP Publishing: Bristol, UK, 2012; p. 052015. [Google Scholar]
- Anagnostopoulos, J.S. CFD analysis and design effects in a radial pump impeller. WSEAS Trans. Fluid Mech. 2006, 1, 763. [Google Scholar]
- Richards, S.K.; Ramakrishnan, K.; Shieh, C.M.; Moyroud, F.; Picavet, A.; Ballarini, V.; Michelassi, V. Unsteady acoustic forcing on an impeller due to coupled blade row interactions. J. Turbomach. 2012, 134, 061014. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Seidel, U. Influence of the rotation on the natural frequencies of a submerged-confined disk in water. J. Sound Vib. 2015, 337, 161–180. [Google Scholar] [CrossRef]
- Lamb, H.; Southwell, R.V. The vibrations of spinning discs. Proc. R. Soc. Lond. 1921, 99, 272–280. [Google Scholar] [CrossRef]
- Oppenheim, A.V. Discrete-Time Signal Processing; Pearson Education India: Chennai, India 1999. [Google Scholar]
- Heath, S.; Imregun, M. A Review of Analysis techniques for blade tip-timing measurements. In Proceedings of the ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition, Orlando, FL, USA, 2–5 June 1997. [Google Scholar]
- Bi, S.; Ren, J.; Wang, W.; Zong, G. Elimination of transducer mass loading effects in shaker modal testing. Mech. Syst. Signal Process. 2013, 38, 265–275. [Google Scholar] [CrossRef]
- Egusquiza, E.; Valero, C.; Valentin, D.; Presas, A.; Rodriguez, C.G. Condition monitoring of pump-turbines. New challenges. Measurement 2015, 67 (Suppl. C), 151–163. [Google Scholar] [CrossRef] [Green Version]
- Bauer, H.F.; Eidel, W. Transverse vibration and stability of spinning circular plates of constant thickness and different boundary conditions. J. Sound Vib. 2007, 274, 877–895. [Google Scholar] [CrossRef]
- Vass, J.; Šmíd, R.; Randall, R.; Sovka, P.; Cristalli, C.; Torcianti, B. Avoidance of speckle noise in laser vibrometry by the use of kurtosis ratio: Application to mechanical fault diagnostics. Mech. Syst. Signal Process. 2008, 22, 647–671. [Google Scholar] [CrossRef]
- Martin, P.; Rothberg, S.J. Pseudo-vibration sensitivities for commercial laser vibrometers. Mech. Syst. Signal Process. 2011, 25, 2753–2765. [Google Scholar] [CrossRef] [Green Version]
- Rothberg, S. Numerical simulation of speckle noise in laser vibrometry. Appl. Opt. 2006, 45, 4523–4533. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rothberg, S.J.; Halkon, B.J.; Tirabassi, M.; Pusey, C. Radial vibration measurements directly from rotors using laser vibrometry: The effects of surface roughness, instrument misalignments and pseudo-vibration. Mech. Syst. Signal Process. 2012, 33, 109–131. [Google Scholar] [CrossRef] [Green Version]
- Valentín, D.; Presas, A.; Egusquiza, E.; Valero, C. On the Capability of Structural–Acoustical Fluid–Structure Interaction Simulations to Predict Natural Frequencies of Rotating Disklike Structures Submerged in a Heavy Fluid. J. Vib. Acoust. 2016, 138, 034502. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Seidel, U. Dynamic response of a rotating disk submerged and confined. Influence of the axial gap. J. Fluids Struct. 2016, 62, 332–349. [Google Scholar] [CrossRef] [Green Version]
- Vagnoni, E.; Andolfatto, L.; Avellan, F. On the sloshing free surface in the draft tube cone of a Francis turbine operating in synchronous condenser mode. J. Phys. Conf. Ser. 2017, 813, 012034. [Google Scholar] [CrossRef] [Green Version]
- Vagnoni, E.; Favrel, A.; Andolfatto, L.; Avellan, F. Experimental investigation of the sloshing motion of the water free surface in the draft tube of a Francis turbine operating in synchronous condenser mode. Exp. Fluids 2018, 59, 95. [Google Scholar] [CrossRef]






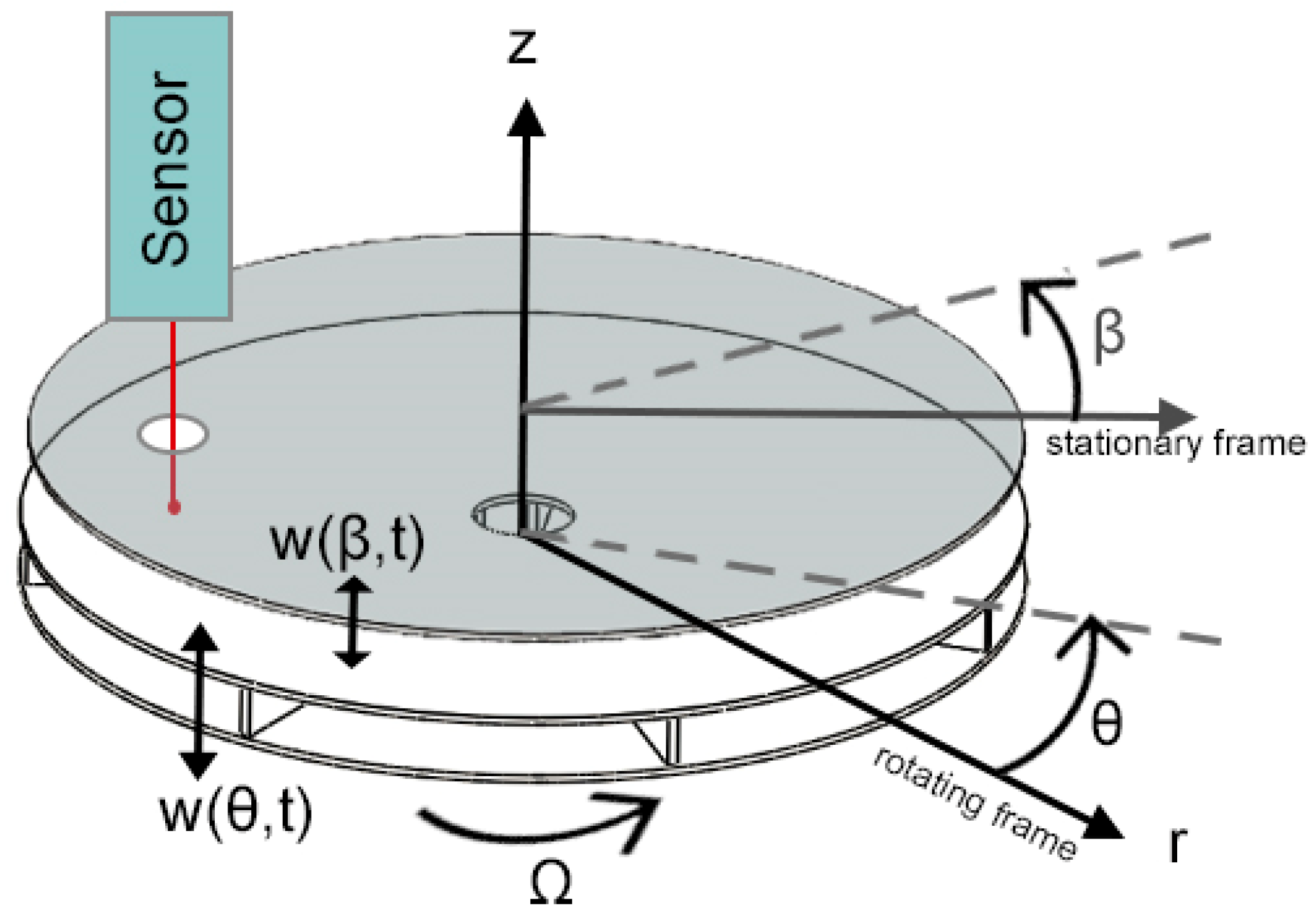








| Stationary Frame | Rotating Frame |
|---|---|
| Rotating structure has to be axisymmetric around the rotating axis | Rotating structure can be not axisymmetric around the rotating axis |
| Rotating structure can be connected to stationary structures | Only rotating structure can be considered in the analysis |
| More than one rotating structure | Only a single rotating structure |
| Campbell diagrams for computing rotor critical speeds are possible | Campbell diagrams are not applicable |
| Cyclic-symmetric analysis can be used |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Presas, A.; Valentin, D.; Valero, C.; Egusquiza, M.; Egusquiza, E. Experimental Measurements of the Natural Frequencies and Mode Shapes of Rotating Disk-Blades-Disk Assemblies from the Stationary Frame. Appl. Sci. 2019, 9, 3864. https://doi.org/10.3390/app9183864
Presas A, Valentin D, Valero C, Egusquiza M, Egusquiza E. Experimental Measurements of the Natural Frequencies and Mode Shapes of Rotating Disk-Blades-Disk Assemblies from the Stationary Frame. Applied Sciences. 2019; 9(18):3864. https://doi.org/10.3390/app9183864
Chicago/Turabian StylePresas, Alexandre, David Valentin, Carme Valero, Monica Egusquiza, and Eduard Egusquiza. 2019. "Experimental Measurements of the Natural Frequencies and Mode Shapes of Rotating Disk-Blades-Disk Assemblies from the Stationary Frame" Applied Sciences 9, no. 18: 3864. https://doi.org/10.3390/app9183864






