Issues on the Vibration Analysis of In-Service Laminated Glass Structures: Analytical, Experimental and Numerical Investigations on Delaminated Beams
Abstract
1. Introduction
2. Classical Analytical Formulation for Frequency Calculations
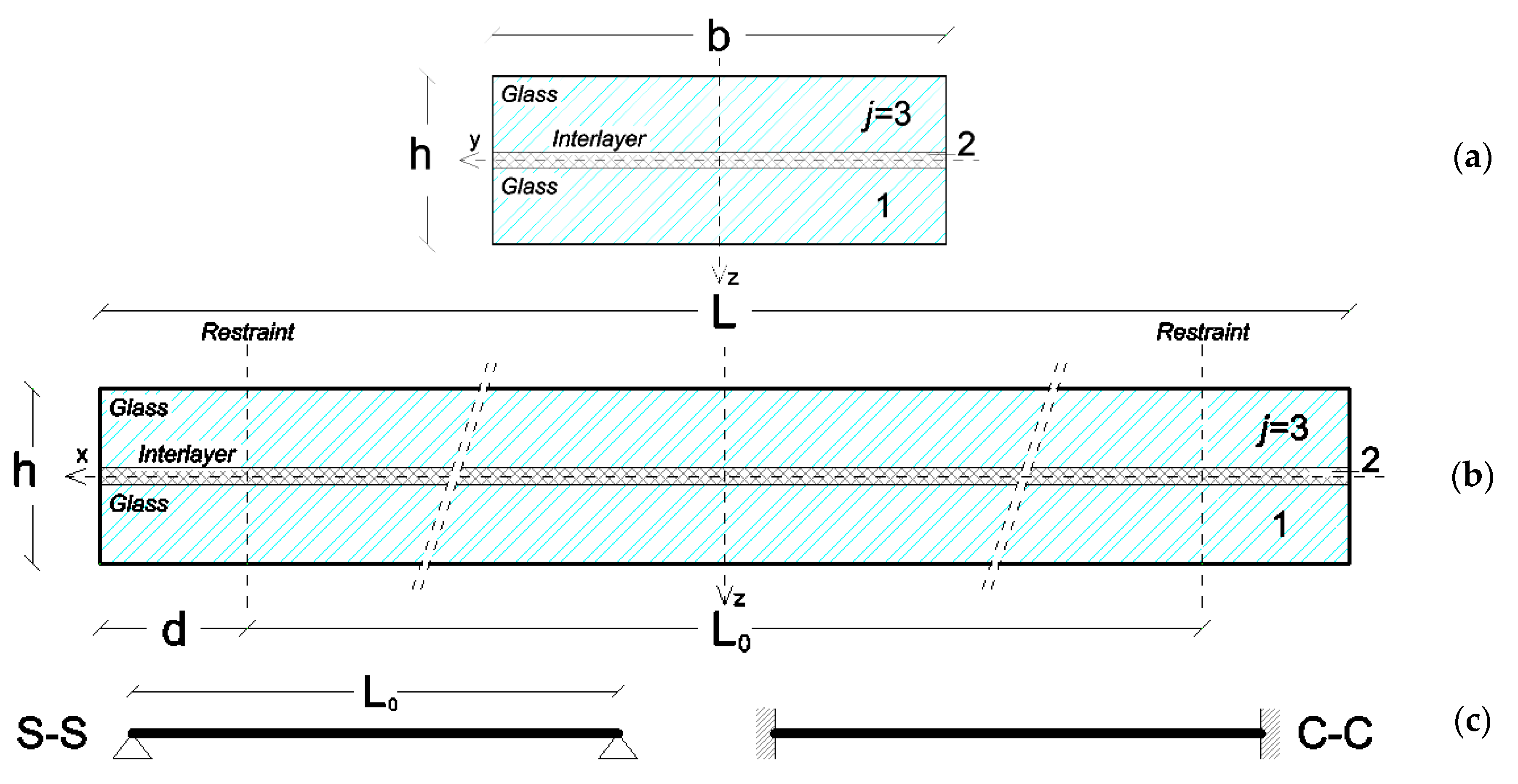
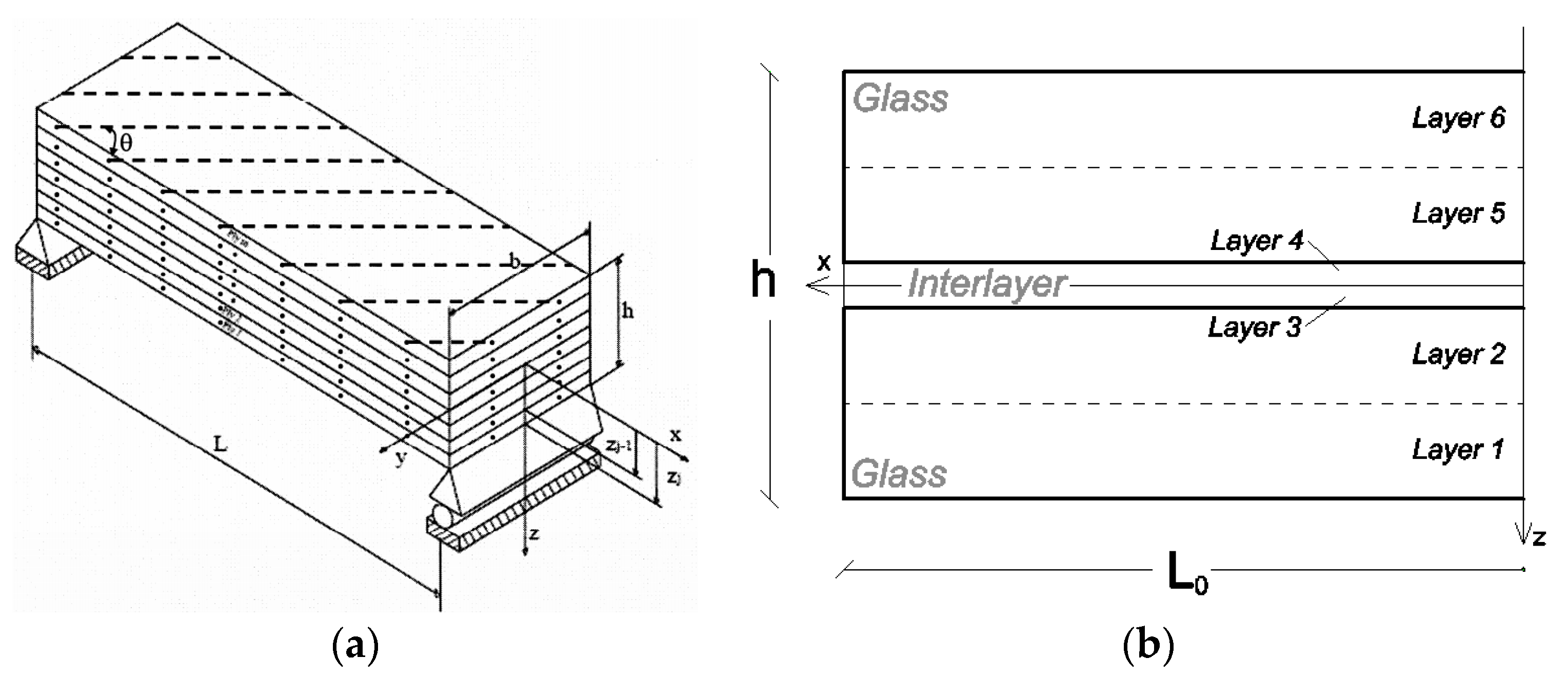
2.1. Reference System
2.2. Existing Closed-Form Solutions
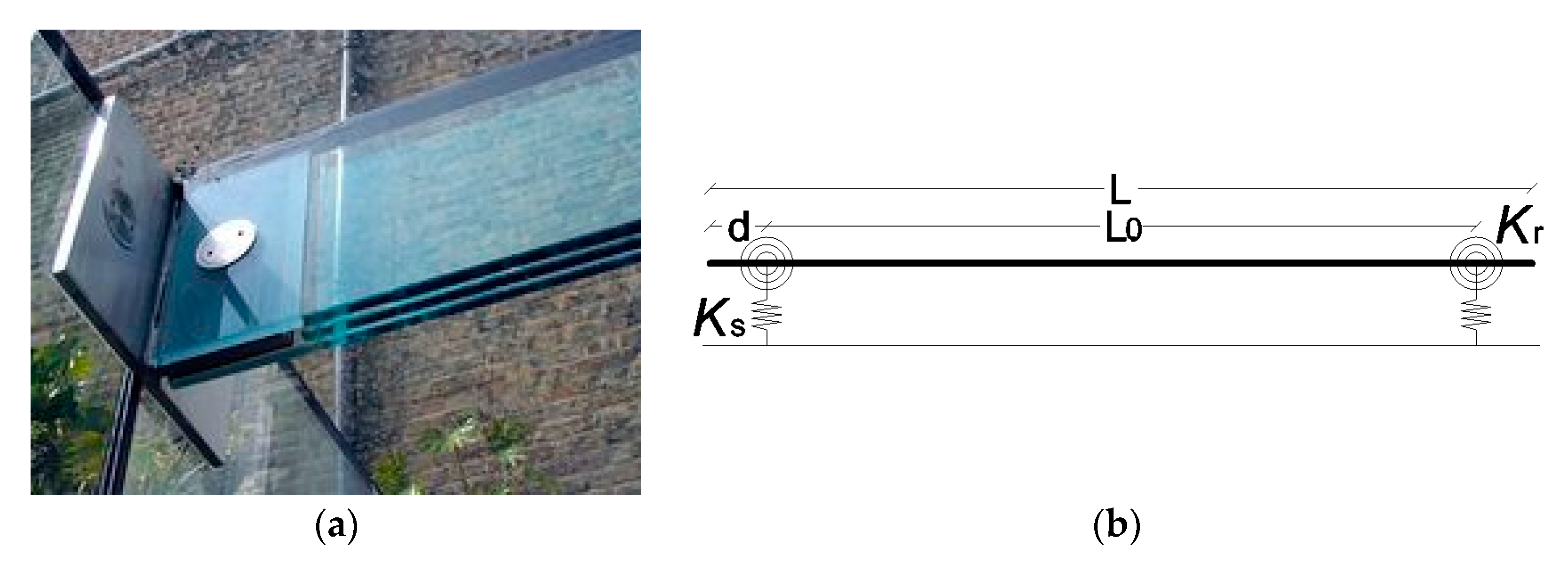
2.3. Restraints and Delaminations for In-Service LG Systems
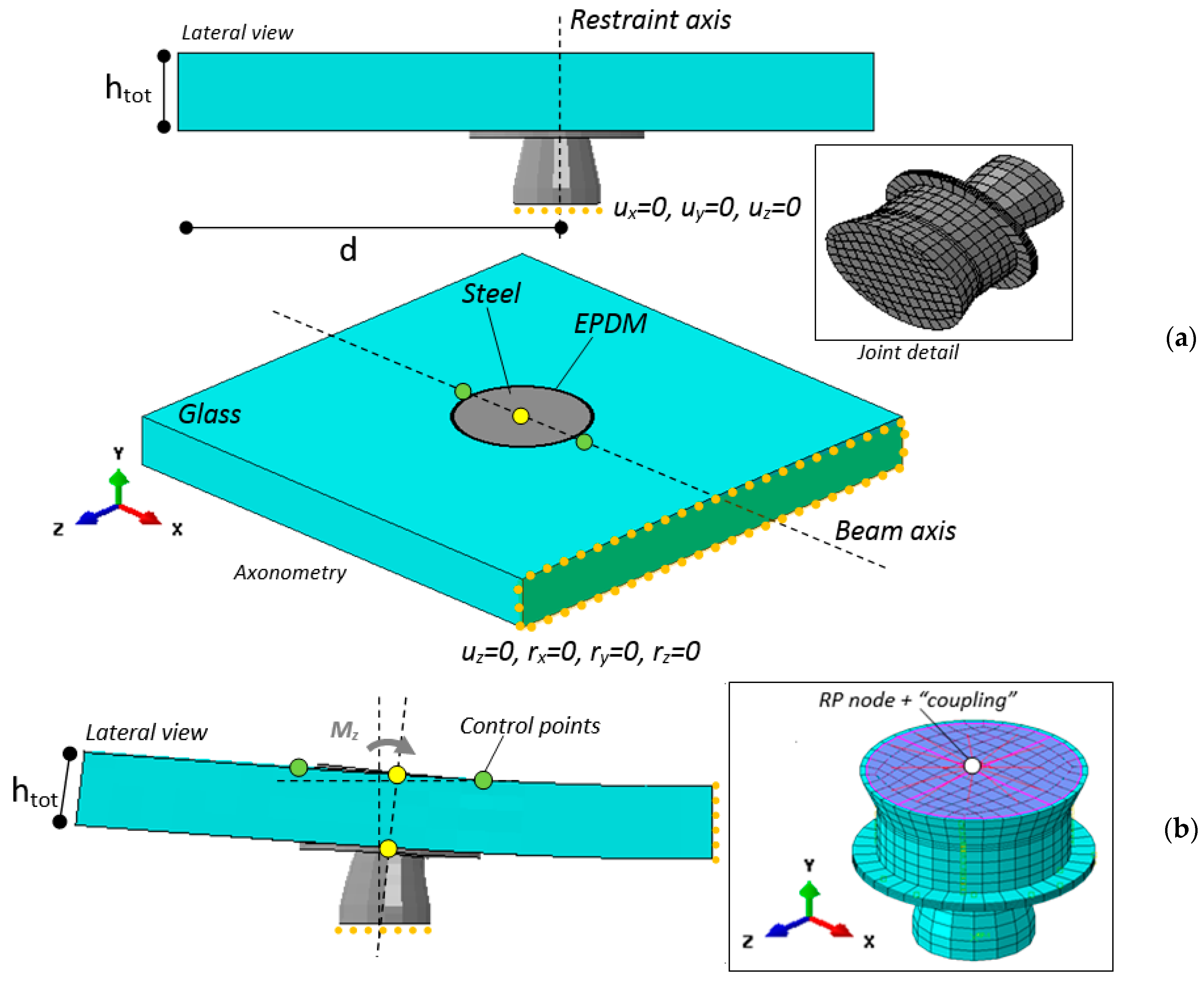
3. Experimental Study on In-Service LG Beams
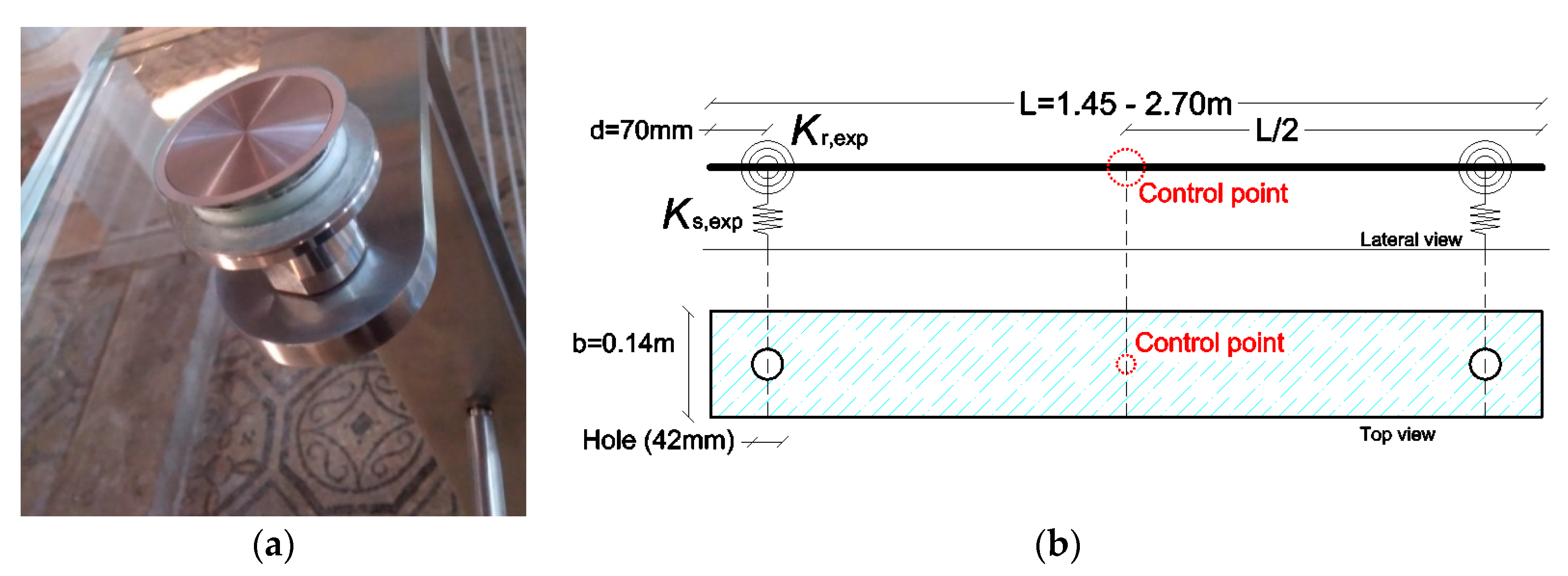
3.1. Specimens and Test Methods
3.2. Derivation of Experimental Fundamental Frequencies
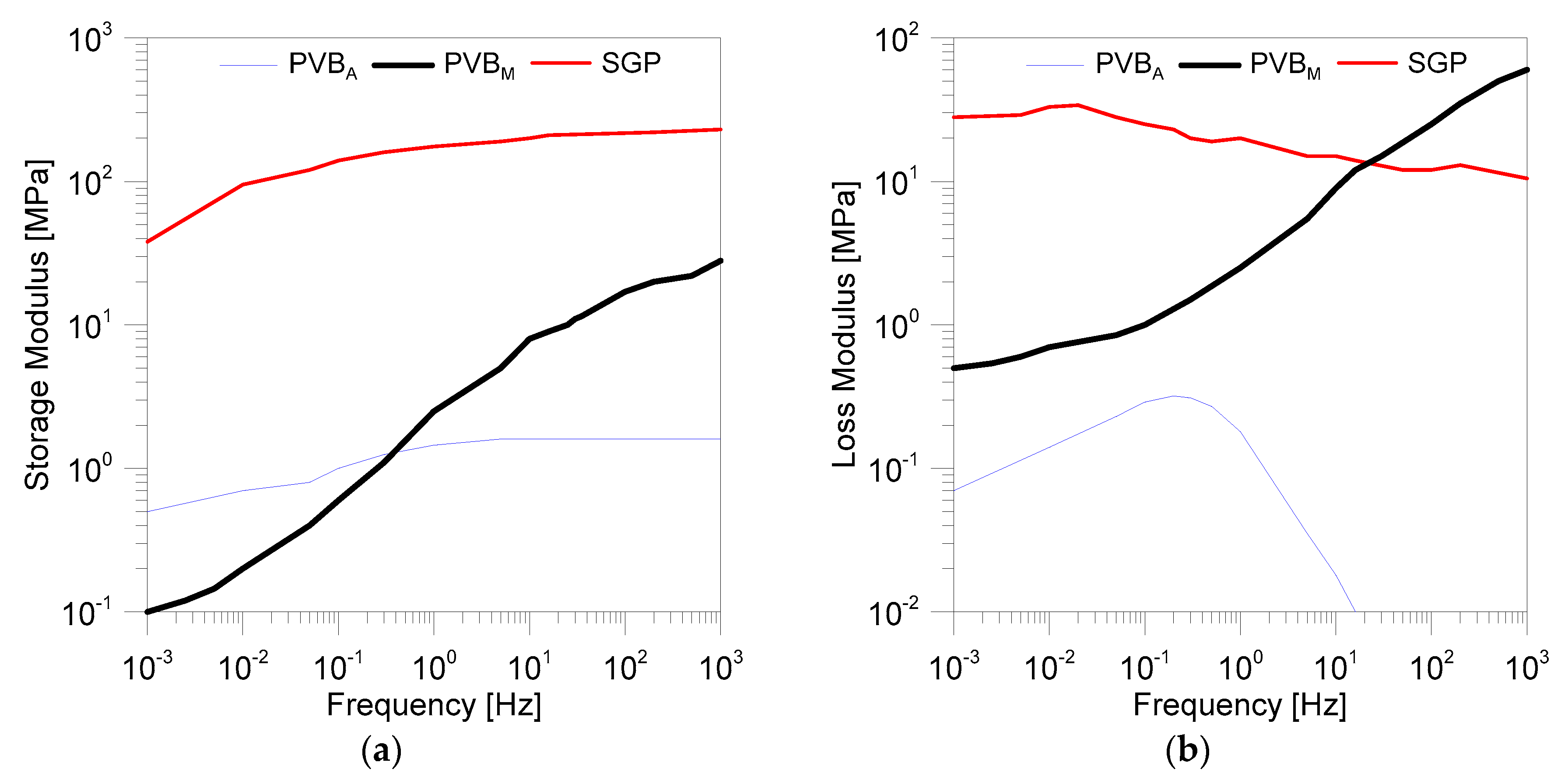
4. Analysis of Relevant Influencing Parameters
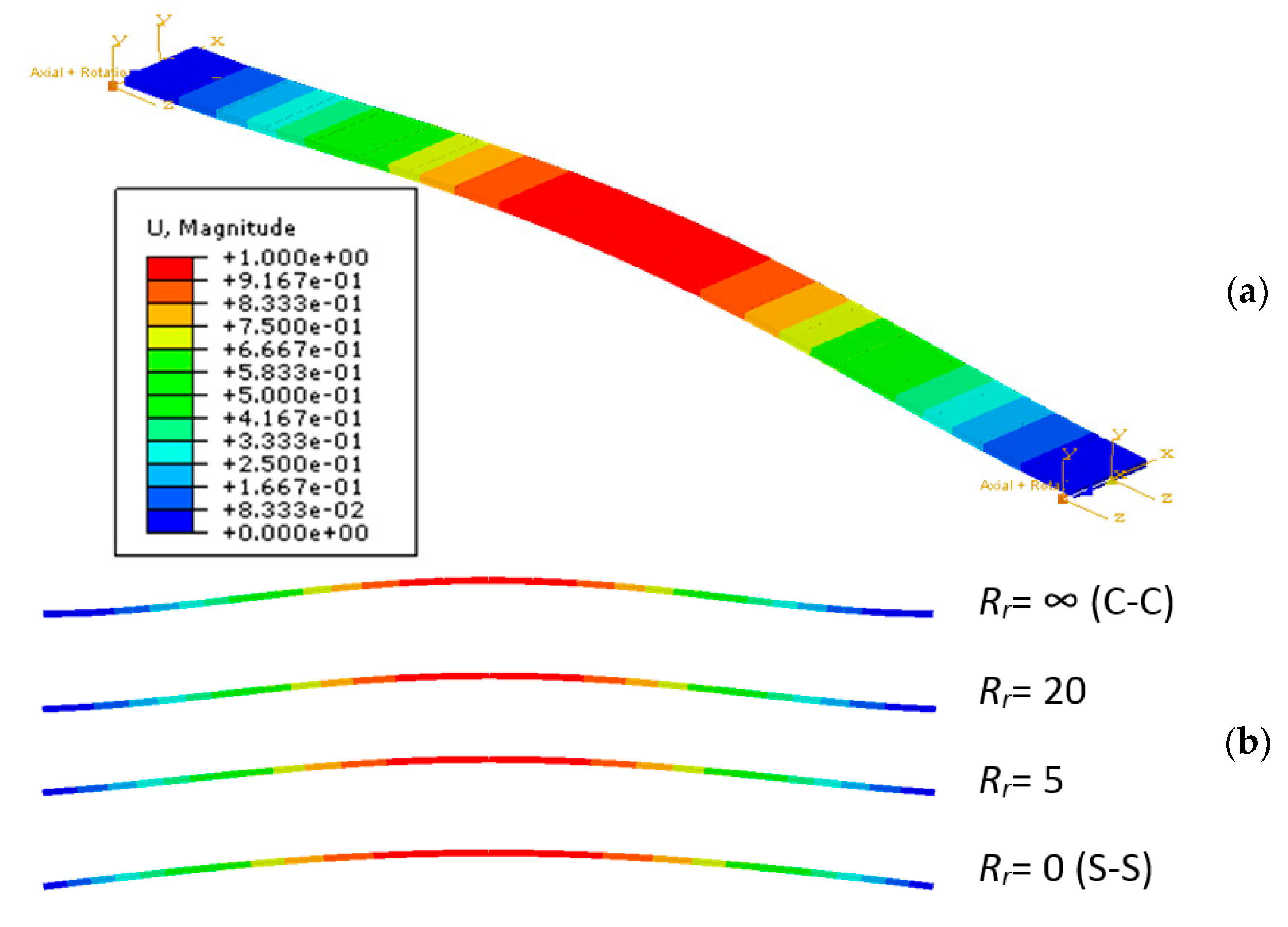
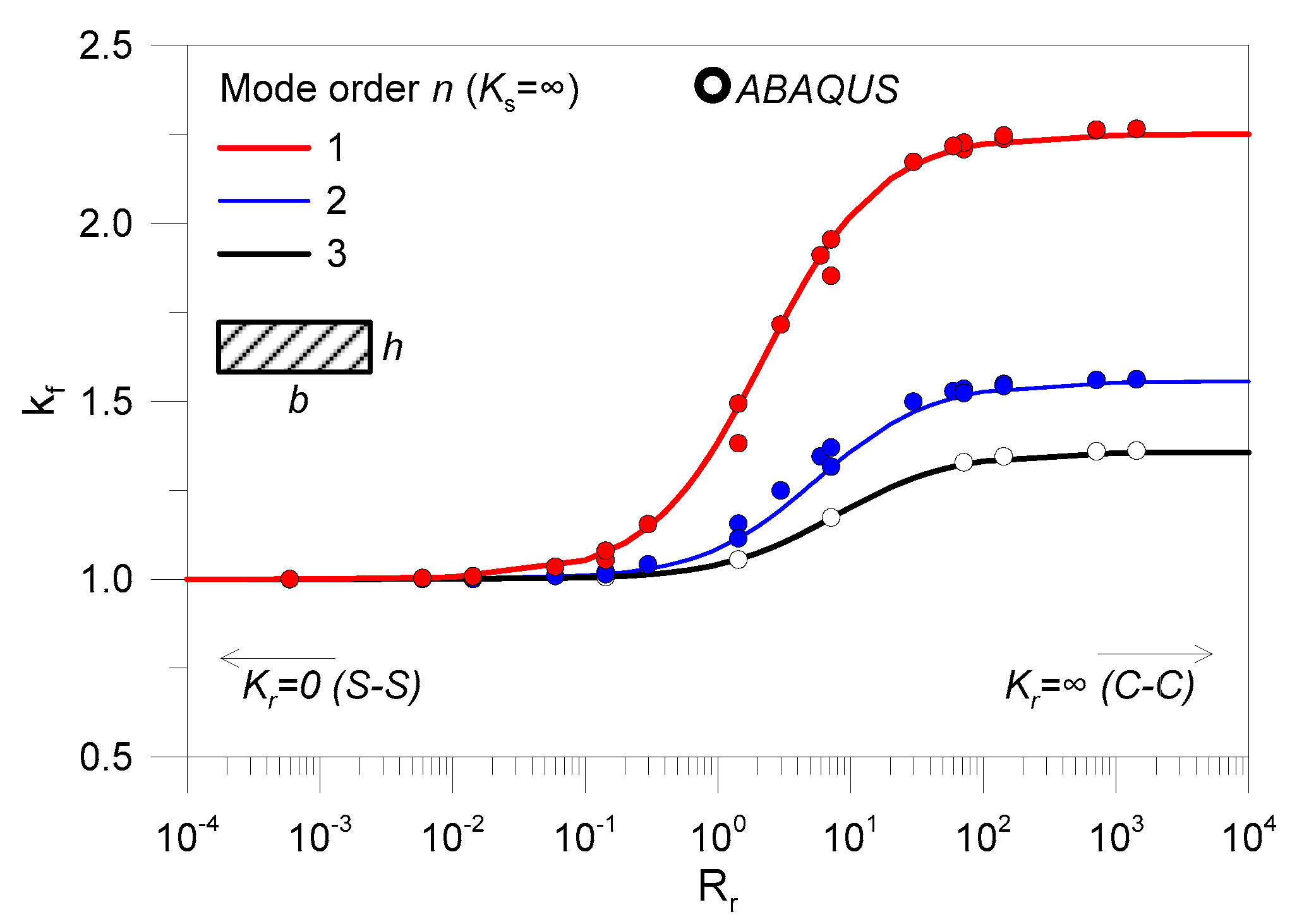
4.1. Stiffness Contribution of Point-Fixings
4.2. Derivation of Practical Fitting Curves for LG Members with Flexible Restraints
4.3. Effect of Delaminations
4.3.1. Analytical Description of the Problem
- Ezd—is the longitudinal MoE of a totally delaminated section (along one or more interfaces), representative of the so-called imperfect effective MoE;
- S—is the number of sub-layers detected by the delamination;
- zj—represents the thickness of the j-th sub-layers; and,
- Ad, At—are respectively the delaminated and total interfacial area between the bonded layers.
- (1)
- Plane sections are initially normal to the longitudinal axis of the glass beam, and remain plane and normal also during flexure;
- (2)
- The beam has symmetrical properties about the neutral axis (both geometrical and mechanical);
- (3)
- The sandwich beam section is composed of layers with a linear elastic behaviour; and,
- (4)
- Shear coupling between each ply can be disregarded.
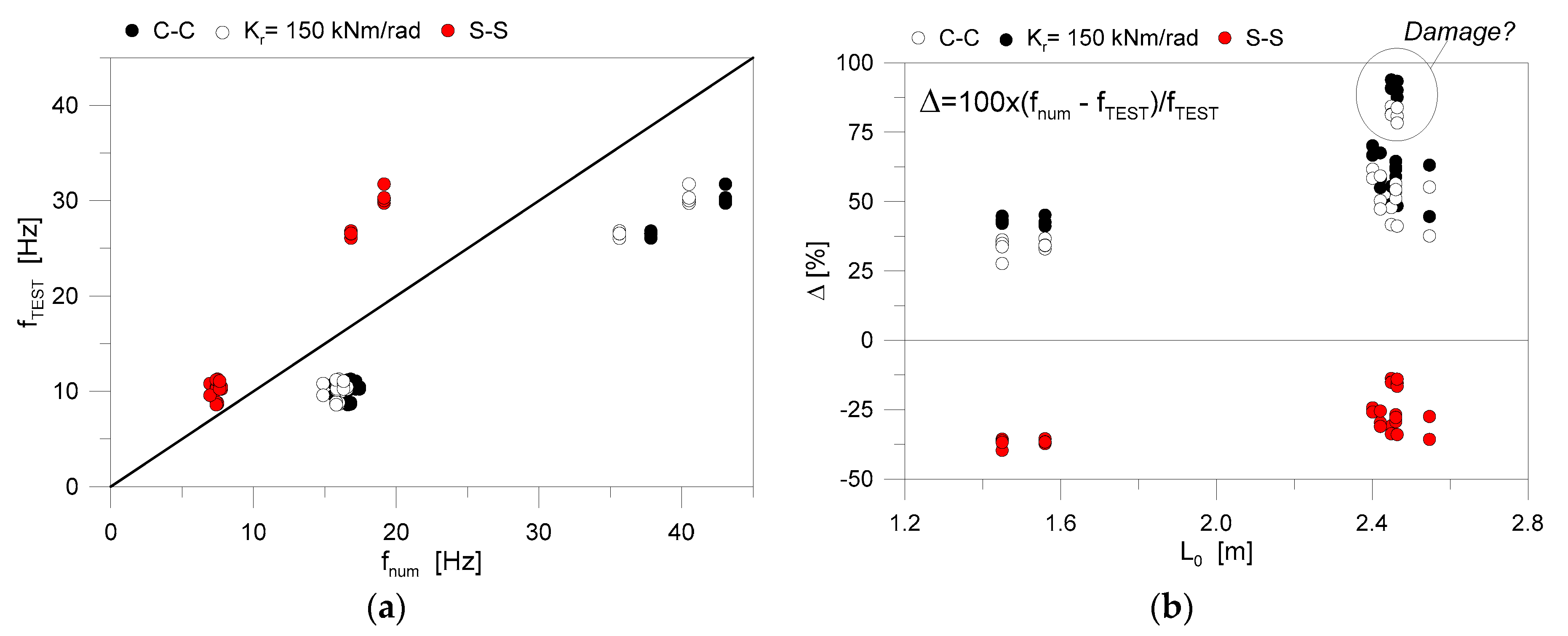
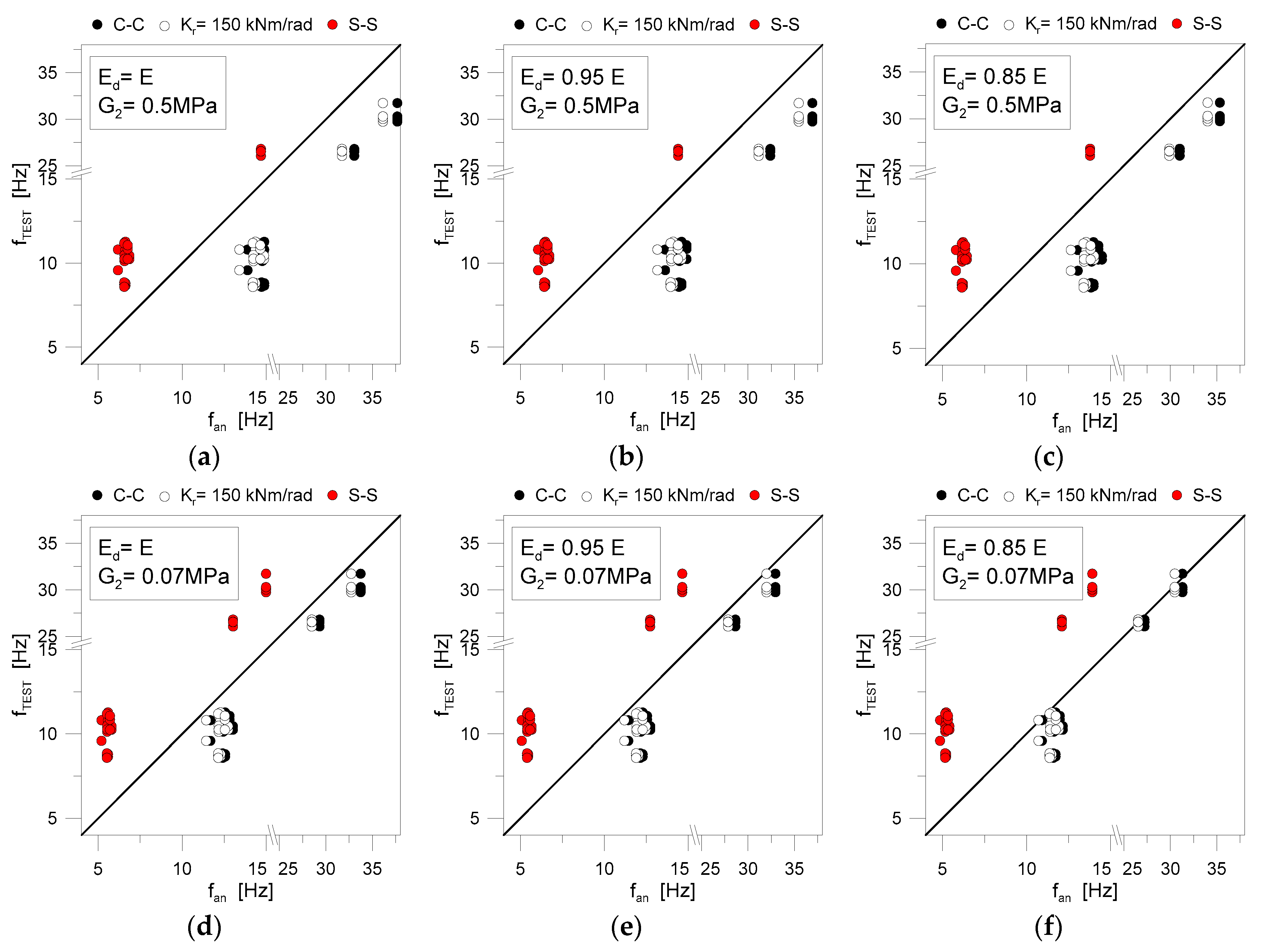
4.3.2. Reliability of Frequency Calculations for Delaminated LG Specimens
- -
- Scheme D1: Ad,tot = 2Ad,1 delaminated surface close to each restraint, where Ad,1 = b × d;
- -
- Scheme D2: similar to D1, but with Ad,tot = 2Ad,2 and Ad,2 = b × 2d close to each restraint;
- -
- Scheme D3: like D2, with Ad,tot = 2Ad,2 + 2Ad,3 and Ad,3 = s × b (s = 30, 60 and 90 mm); and,
- -
- Scheme D4: inclusive of delamination along the longitudinal edges, thus Ad,tot = 2Ad,2 + 2Ad,4, with Ad,4 = t × L0 (t = 15, 30, 45 mm, that is ≈b/10, ≈b/5 and ≈b/3 for the selected specimens).
- -
- The analytical method recalled from [51] and extended to the adjusted dynamic thickness for viscoelastic LG beams could be rationally used for preliminary frequency estimates, especially when refined methods of analysis or dedicated experimental investigations are not available;
- -
- The presence of even slight delaminations along the edges of LG beams (i.e., with limited thickness, with respect to the beam width b) can have marked effects on the bending stiffness of the composite LG sections, thus on the corresponding frequency calculations; and,
- -
- On the other side, the simplified assumptions of Equations (12)–(14) gave evidence of a certain scatter from the corresponding FE calculations, with respect to a given Ad/At ratio. Such an effect can be also observed in Figure 20b, for selected LG configurations. As a general trend, the analytical formulation for delaminated LG beams was found to clearly overestimate the FE frequency variations, thus providing even more conservative predictions.
4.3.3. Final Remarks on Practical Analytical Calculations for Design
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haldimann, M.; Luible, A.; Overend, M. Structural Use of Glass; IABSE: Zurich, Switzerland, 2008; ISBN 978-3-85748-119-2. [Google Scholar]
- Feldmann, M.; Kasper, R.; Abeln, B.; Cruz, P.; Belis, J.; Beyer, J.; Geßler, A.; Colvin, J.; Ensslen, F.; Eliasova, M.; et al. Guidance for European Structural Design of Glass Components—Support to the Implementation, Harmonization and Further Development of the Eurocodes; Dimova, P., Feldmann, D., Eds.; Report EUR 26439; European Union: Luxembourg, 2014. [Google Scholar]
- Peroni, M.; Solomos, G.; Pizzinato, V.; Larcher, M. Experimental investigation of high strain-rate behaviour of glass. Appl. Mech. Mater. 2011, 82, 63–68. [Google Scholar] [CrossRef]
- Del Linz, P.; Wang, Y.; Hooper, P.A.; Arora, H.; Smith, D.; Pascoe, L.; Cormie, D.; Blackman, B.R.K.; Dear, J.P. Determining material response for Polyvinyl Butyral (PVB) in blast loading situations. Exp. Mech. 2016, 56, 1501–1517. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, H.; Wang, Z. Experimental study of laminated glass window responses under impulsive and blast loading. Int. J. Impact Eng. 2015, 78, 1–19. [Google Scholar] [CrossRef]
- Bedon, C.; Kalamar, R.; Eliasova, M. Low velocity impact performance investigation on square hollow glass columns via full-scale experiments and Finite Element analyses. Compos. Struct. 2017, 182, 311–325. [Google Scholar] [CrossRef]
- Mohagheghian, I.; Wang, Y.; Jiang, L.; Zhang, X.; Guo, X.; Yan, Y.; Kinloch, A.; Dear, J. Quasi-static bending and low velocity impact performance of monolithic and laminated glass windows employing chemically strengthened glass. Eur. J. Mech. 2017, 63, 165–186. [Google Scholar] [CrossRef]
- Biolzi, L.; Bonati, A.; Cattaneo, S. Laminated glass cantilevered plates under static and impact loading. Adv. Civ. Eng. 2018, 2018, 7874618. [Google Scholar] [CrossRef]
- Xue, L.; Coble, C.R.; Lee, H.; Yu, D.; Chaparala, S.; Park, S. Dynamic analysis of thin glass under ball drop impact with new metrics. In Proceedings of the ASME 2013—International Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Microsystems, Burlingame, CA, USA, 16–18 July 2013. [Google Scholar] [CrossRef]
- Behr, R.; Minor, J.; Kremer, P. Effects of Accelerated Weathering on Architectural Laminated Glass in a Windstorm Environment. In Science and Technology of Building Seals, Sealants, Glazing, and Waterproofing: Sixth Volume; Myers, J., Ed.; ASTM International: West Conshohocken, PA, USA, 1996; pp. 27–45. [Google Scholar]
- Santarsiero, M.; Bedon, C.; Moupagitsoglou, K. Energy-based considerations for the seismic design of ductile and dissipative glass frames. Soil Dyn. Earthq. Eng. 2019, 125, 105710. [Google Scholar] [CrossRef]
- Lenci, S.; Consolini, L.; Clementi, F. On the experimental determination of dynamic properties of laminated glass. Ann. Solid Struct. Mech. 2015, 7, 27–43. [Google Scholar] [CrossRef]
- Bedon, C.; Fasan, M.; Amadio, C. Vibration analysis and dynamic characterization of structural glass elements with different restraints based on Operational Modal Analysis. Buildings 2019, 9, 13. [Google Scholar] [CrossRef]
- Aenlle, M.L.; Pelayo, F.; Ismael, G. An effective thickness to estimate stresses in laminated glass beams under dynamic loadings. Compos. Part B Eng. 2015, 82, 1–12. [Google Scholar] [CrossRef]
- Bedon, C. Diagnostic analysis and dynamic identification of a glass suspension footbridge via on-site vibration experiments and FE numerical modelling. Compos. Struct. 2019, 216, 366–378. [Google Scholar] [CrossRef]
- Bedon, C.; Fasan, M. Reliability of field experiments, analytical methods and pedestrian’s perception scales for the vibration serviceability assessment of an in-service glass walkway. Appl. Sci. 2019, 9, 1936. [Google Scholar] [CrossRef]
- Zemanova, A.; Zeman, J.; Janda, T.; Schmidt, J.; Sejnoha, M. On modal analysis of laminated glass: Usability of simplified methods and Enhanced Effective Thickness. Compos. Part B 2018, 151, 92–105. [Google Scholar] [CrossRef]
- ABAQUS Computer Software; Simulia: Dassault, RI, USA, 2019.
- EN 572–2:2004. Glass in Buildings-Basic Soda Lime Silicate Glass Products; CEN: Brussels, Belgium, 2004. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamics of Structures; McGraw-Hill: New York, NY, USA, 1993; ISBN 0-07-011394-7. [Google Scholar]
- Galuppi, L.; Royer-Carfagni, G. Effective thickness of laminated glass beams: New expression via a variational approach. Eng. Struct. 2012, 38, 53–67. [Google Scholar] [CrossRef]
- Andreozzi, L.; Bati, S.B.; Fagone, M.; Ranocchiai, G.; Zulli, F. Dynamic torsion tests to characterize the thermo-viscoelastic properties of polymeric interlayers for laminated glass. Constr. Build. Mater. 2014, 65, 1–13. [Google Scholar] [CrossRef]
- Bennison, S.J.; Jagota, A.; Smith, C. Fracture of glass/poly(vinyl butyral) (Butacite®) laminates in biaxial flexure. J. Am. Ceram. Soc. 1999, 82, 1761–1770. [Google Scholar] [CrossRef]
- Hooper, P.A.; Blackman, B.R.K.; Dear, J.P. The mechanical behaviour of poly(vinyl butyral) at different strain magnitudes and strain rates. J. Mater. Sci. 2012, 47, 3564–3576. [Google Scholar] [CrossRef]
- Ensslen, F. Influences of laboratory and natural weathering on the durability of laminated safety glass. In Proceedings of the Glass Performance Days, GDP 2007, Tampere, Finland, 15–18 June 2007; 7p. [Google Scholar]
- Hana, T.; Janda, T.; Schmidt, J.; Zemanova, A.; Sejnoha, M.; Eliasova, M.; Vokac, M. Experimental and numerical study of viscoelastic properties of polymeric interlayers used for laminated glass: Determination of material parameters. Materials 2019, 12, 2214. [Google Scholar] [CrossRef]
- Froli, M.; Lani, L. Adhesion, creep and relaxation properties of PVB in laminated safety glass. In Proceedings of the Glass Performance Days, GPD 2011, Tampere, Finland, 17–20 June 2011; 4p. [Google Scholar]
- Serafinavicius, T.; Lebet, J.P.; Louter, C.; Lenkimas, T.; Kuranovas, A. Long-term laminates glass four point bending test with PVB, EVA and SG interlayers at different temperatures. Procedia Eng. 2013, 57, 996–1004. [Google Scholar] [CrossRef]
- Xu, X.; Liu, B.; Li, Y. Experimental studies on viscoelasticity of film materials in laminated glass sheets. Sae Int. J. Mater. Manuf. 2015, 8, 922–931. [Google Scholar] [CrossRef]
- Rodrigues, T.; Jordão, S.; Bedon, C. Long-term effects on structural glass beams. In Proceedings of the XI CMM Conference—Congresso de Construção Metálica e Mista, Coimbra, Portugal, 23 November 2017; pp. 933–942. [Google Scholar]
- Stevels, W.; D’Haene, P.; Zhang, P.; Haldeman, S. A comparison of different methodologies for PVB interlayer modulus characterization. In Proceedings of the Challenging Glass 5—Conference on Architectural and Structural Applications of Glass, Ghent, Belgium, 16–17 June 2016; ISBN 978-909-825-2680-6. [Google Scholar]
- Lopez-Aenlle, M.; Noriega, A.; Pelayo, F. Mechanical characterization of polyvinyl butyral from static and modal tests on laminated glass beams. Compos. Part B Eng. 2019, 169, 9–18. [Google Scholar] [CrossRef]
- Carrot, C.; Bendaoud, A.; Pillon, C. Polyvinyl Butyral. In Handbook of thermoplastics; Olabisi, O., Adewale, K., Eds.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Chapuis, V.; Pelisset, S.; Raeis-Barneoud, M.; Li, H.Y.; Ballif, C.; Perret-Aebi, L.E. Compressive-shear adhesion characterization of polyvinyl-butyral and ethylene-vinyl acetate at different curing times before and after exposure to damp-heat conditions. Prog. Photovolt. Res. Appl. 2014, 22, 405. [Google Scholar] [CrossRef]
- Liang, R.H.; Gupta, A.; di Stefano, S. Photothermal Characterization of Encapsulated Materials for Photovoltaic Modules. 1982. Available online: https://www2.jpl.nasa.gov/adv_tech/photovol/2016ENG/Phototherm%20Char%20of%20Encap%20Mtls_5101-210_JPL1982.pdf (accessed on 13 September 2019).
- Kuraray. Edge Stability, Durability and Weathering. Document Ref. GLS-TECBU-2014-04. 2014. Available online: https://www.trosifol.com/fileadmin/user_upload/Kuraray_4_4_Edge_Stability.pdf (accessed on 13 September 2019).
- CPNI EPB 04/13. Guidance note—Influence of Delamination of Laminated Glass on Its Blast Performance. Centre for the Protection of National Infrastructure. 2013. Available online: https://www.cpni.gov.uk/system/files/documents/4d/8f/Delamination-of-laminated-glass.pdf (accessed on 13 September 2019).
- Dural, E. Experimental and numerical treatment of delamination in laminated glass plate structures. J. Reinf. Plast. Compos. 2016, 35, 56–70. [Google Scholar] [CrossRef]
- Dural, E. Analysis of delaminated glass beams subjected to different boundary conditions. Compos. Part B 2016, 101, 132–146. [Google Scholar] [CrossRef]
- Jaskowiec, J. Numerical modelling mechanical delamination in laminated glass by XFEM. Procedia Eng. 2015, 487, 181–184. [Google Scholar]
- Vedrtnam, A. Experimental and simulation studies on delamination strength of laminated glass composites having polyvinyl butyral and ethyl vinyl acetate inter-layers of different critical thicknesses. Def. Technol. 2018, 14, 313–317. [Google Scholar] [CrossRef]
- Bedon, C.; Bergamo, E.; Izzi, M.; Noè, S. Prototyping and validation of MEMS accelerometers for structural health monitoring—The case study of the Pietratagliata cable-stayed bridge. J. Sens. Actuator Netw. 2018, 7, 18. [Google Scholar] [CrossRef]
- De Rosa, M.A.; Auciello, N.M. Free vibrations of tapered beams with flexible ends. Comput. Struct. 1996, 60, 197–202. [Google Scholar] [CrossRef]
- Lee, J. Free vibration analysis of delaminated composite beams. Comput. Struct. 2000, 74, 121–129. [Google Scholar] [CrossRef]
- Della, C.N.; Shu, D. Free vibration analysis of composite beams with overlapping delaminations. Eur. J. Mech. A/Solids 2005, 24, 491–503. [Google Scholar] [CrossRef]
- Ramtekkar, G.S. Free vibration analysis of delaminated beams using mixed finite element model. J. Sound Vib. 2009, 328, 428–440. [Google Scholar] [CrossRef]
- Callioglu, H.; Atlihan, G. Vibration analysis of delaminated composite beams using analytical and FEM models. Indian J. Eng. Mater. Sci. 2011, 18, 7–14. [Google Scholar]
- Zhang, Z.; Shankar, K.; Morozov, E.V.; Tahtali, M. Vibration-based delamination detection in composite beams through frequency changes. J. Vib. Control 2016, 22, 496–512. [Google Scholar] [CrossRef]
- Krawczuk, M.; Ostachowicz, W.; Zuk, A. Analysis of natural frequencies of delaminated composite beams based on finite element method. Struct. Eng. Mech. 1996, 4, 243–255. [Google Scholar] [CrossRef]
- Tate, I.V.; Roy, S.; Jagtap, K.R. Delamination detection of composite cantilever beam coupled with piezoelectric transducer using natural frequency deviation. Procedia Eng. 2014, 97, 1293–1304. [Google Scholar] [CrossRef]
- Gibson, R.F. Principles of Composite Material Mechanics; CRC Press: Philadelphia, PA, USA, 1994. [Google Scholar]
- AGC Glass Europe. Material Properties of PVB Interlayers Used in Stratobel and Stratobel Strong Laminated Glass. 2018. Available online: https://www.agc-yourglass.com/sites/default/files/technical_documents/original/STRATOBEL_PROPERTIES44907Material%20Properties%20of%20PVB_Stratobel_June2018_ENG.pdf (accessed on 13 September 2019).











| Beam Restraints | βn | Ψ | ||||
|---|---|---|---|---|---|---|
| Mode Order n | Mode Order n | |||||
| 1 | 2 | 3 | 1 | 2 | 3 | |
| Simply supports (S-S) | π/L0 | 2π/L0 | 3π/L0 | π/L02 | (2π)2/L0 | (3π)2/L0 |
| Clamps (C-C) | 4.73/L0 | 7.8532/L0 | 10.996/L0 | 40.7/L02 | 82.6/L02 | 148/L02 |
| Mode Order n | |||
|---|---|---|---|
| 1 | 2 | 3 | |
| A | 5.4 | 9.9 | 21.5 |
| B | 0.8 | 1.8 | 2.8 |
| C | 1.0 | 1.0 | 1.0 |
| Delamination Severity (Equation (13))—Ed/E | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.95 | 0.85 | |||||||
| Restraint | C-C | Kr | S-S | C-C | Kr | S-S | C-C | Kr | S-S |
| G2 = 0.5 MPa | +40.8 | +35.6 | −37.4 | +32.2 | +30.1 | −38.7 | +38.1 | +27.8 | −41.2 |
| G2 = 0.07 MPa | +20.6 | +17.7 | −46.2 | +17.9 | +15.3 | −47.5 | +15.5 | +10.1 | −49.9 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedon, C. Issues on the Vibration Analysis of In-Service Laminated Glass Structures: Analytical, Experimental and Numerical Investigations on Delaminated Beams. Appl. Sci. 2019, 9, 3928. https://doi.org/10.3390/app9183928
Bedon C. Issues on the Vibration Analysis of In-Service Laminated Glass Structures: Analytical, Experimental and Numerical Investigations on Delaminated Beams. Applied Sciences. 2019; 9(18):3928. https://doi.org/10.3390/app9183928
Chicago/Turabian StyleBedon, Chiara. 2019. "Issues on the Vibration Analysis of In-Service Laminated Glass Structures: Analytical, Experimental and Numerical Investigations on Delaminated Beams" Applied Sciences 9, no. 18: 3928. https://doi.org/10.3390/app9183928
APA StyleBedon, C. (2019). Issues on the Vibration Analysis of In-Service Laminated Glass Structures: Analytical, Experimental and Numerical Investigations on Delaminated Beams. Applied Sciences, 9(18), 3928. https://doi.org/10.3390/app9183928





