Theoretical Description of Carbon Felt Electrical Properties Affected by Compression

Featured Application

Vanadium and other electrolyte flow batteries.

Abstract

Electro-conductive carbon felt (CF) material is composed by bonding together different lengths of carbon filaments resulting in a porous structure with a significant internal surface that facilitates enhanced electrochemical reactions. Owing to its excellent electrical properties, CF is found in numerous electrochemical applications, such as electrodes in redox flow batteries, fuel cells, and electrochemical desalination apparatus. CF electro-conductivity mostly arises from the close contact between the surface of two electrodes and the long carbon fibers located between them. Electrical conductivity can be improved by a moderate pressing of the CF between conducting electrodes. There exist large amounts of experimental data regarding CF electro-conductivity. However, there is a lack of analytical theoretical models explaining the CF electrical characteristics and the effects of compression. Moreover, CF electrodes in electrochemical cells are immersed in different electrolytes that affect the interconnections of fibers and their contacts with electrodes, which in turn influence conductivity. In this paper, we investigated both the role of CF compression, as well as the impact of electrolyte characteristics on electro-conductivity. The article presents results of measurements, mathematical analysis of CF electrical properties, and a theoretical analytical explanation of the CF electrical conductivity which was done by a stochastic description of carbon filaments disposition inside a CF frame.

1. Introduction

Carbon Felt (CF) is used as electrode material in a variety of electrochemical applications [1,2,3,4,5,6,7]. Currently, its most prominent utilization is in the vanadium redox and other flow type batteries owing to its good electrical conductivity, hydraulic permeability, and durability in strong acid and alkali electrolytes. In particular, good electrical conductivity arises from the movement of electrons through the carbon filaments to reach the electrolyte [8,9,10,11,12,13,14,15,16,17,18,19,20].

CF conductivity is determined by the carbon fibers comprising the felt structure and which connect simultaneously to both electrodes. Conductivity is well known to be improved by felt compression. With slight pressure on a felt, the density of the fibers is increased, producing additional self-interconnections of fibers and better contact with the substrate of the electrodes. However, felt compression also decreases the interstitial volume, and therefore, reduces the average cross-section of micro-channels linking pores inside a felt framework. The result is an increase in the CF hydraulic resistance obstructing electrolyte flow through the electrode. Electrochemical researchers, design engineers, and others need to consider both the electrical and physical properties of CF for optimal performance in many electrochemical applications.

A tremendous amount of research work [21,22,23,24,25,26,27,28,29,30] has been carried out to investigate and measure the properties of CF. Weber et al. [31], for example, suggested a ladder circuit comprising multiple equal resistances that model resistivity for the explanation CF conductivity. However, this model does not explain sufficiently the decrease of CF resistivity during its compression.

Choe et al. [32] measured physical parameters of rayon-based CF manufactured by Mersen Co in large sheets with a width of several mm to a few cm.

The structure of CF exhibits a significant stochastic framework; therefore, theoretical analyses previously developed, as a rule, used many simplifying assumptions. Thus, results and conclusions required correction coefficients and frequently differed from experimental test results. Moreover, it proved difficult to generalize results to other similar cases. Therefore, many investigations concerning electrical conductivity of CF were conducted for specific applications with the generalization obtained by results from mathematical formulations. For example, measurements of CF electrical resistivity (conductivity) were carried out for furnace heating elements [3].

Among the reports, work by Johan et al. [26] was the first to examine conductivity of CFs used in electrochemical applications. These authors studied a new bipolar cell with a proton-exchange membrane, where flat electrodes were made of long carbon fiber assemblies like CF structure to facilitate electrical current flow. The main aim of the investigation was the amplification of the cell current that could be enhanced by the increase of electrodes conductivity. They found a two-fold increase of stress on the electrodes which causes a 2.5-times increase of CF conductivity and current, which in turn led to enhanced electrochemical reactions. At the same time, oxidative reactions are enhanced at the anode electrode, and reduction reactions are enhanced at the cathode. Accordingly, electrodes resistivity were measured based on the area-specific resistance (ASR), which represents the specific resistance in the perpendicular-plane direction of CF electrodes. ASR was found to be a function of the compression of felt, and it allows the resistance estimation of any electrode having its own specific dimensions. It is important to emphasize the usefulness of ASR for describing CF conductivity appearing in this work for the first time. The usefulness of ASR is witnessed by its usage in multiple published studies [27,28,29,30].

The sharp decrease of CF ASR during compression was observed in all experiments. The only difference could be observed in heterogeneous mathematical formulations for describing CF conductivity. ASR magnitude was characterized [26], for example, by an exponential function. Subsequent results of ASR versus CF compression coefficient were obtained [27]. Since CF could be bound to the surface of the electrode either by simple mechanical contact or by adhesives, the influences on ASR of these materials were investigated. Assemblies of different electrode plates were examined. The same sharp diminishing of resistance versus compression pressure was detected, which may be described by an exponential formula, although with different exponent coefficients. Predictably, these coefficients depend on the type of adhesive used; however, the significant achievement of Johan et al.’s work [26] is that for the first time their values were represented as a function of the kind of adhesive and the type of electrodes design.

More recent reports have focused on experimental measurements of CF conductivity [28,29,30] and have shown influences of felt porosity and specific resistivity of the carbon material. For example, the analytical expression of ASR (named as a specific electrical resistivity and denoted as ${\rho }_{felt}$ [28]) was defined by the following expression:

$${\rho }_{felt}=\frac{4}{\left(1-\lambda \right)}{\rho }_{carbon},$$

(1)

where λ signifies relative felt porosity and is equal to the volume ratio of its empty space to the total felt. Expression (1) was found to be in good agreement with the experimental results.

Experimental measurements of ASR for CF electrodes used in vanadium redox batteries were carried out in [32]. ASR, in this work, is denoted as R_ASR. R_ASR with units of mΩ·cm⁻² was estimated by Equation (2) below, where V_f denotes the percentage of fiber volume. Notably, V_f is expressed by the porosity (λ), i.e., V_f/100 = 1 − λ. Then

$$R_{ASR}=144.456\cdot {\left(3-\frac{10}{V_f}\right)}^{-1.117},$$

(2)

The exponential type of expression (2) is valid for various electrochemical applications. However, all the specific constants in Equation (2) are only applicable to the description of resistance of electrodes used in special vanadium redox batteries. The use of this expression in other applications will lead to considerable loss of accuracy. This is because an actual type of carbon material and the manufacturing process of CF were neglected in this work. Therefore, this circumstance significantly diminishes the value of the presented results. Furthermore, resistance measurements were carried out in dry conditions, i.e., in the air only. However, supplementary investigations performed by the authors [21] showed the effects of liquid dielectric constant (relative permittivity) on CF conductivity. The electrical conductivity of CF seems to be influenced by the properties of these liquids conducive to the penetration of fluid between fibers and their separation or conversely, to their convergence and additional contacts. The resistance of CF is known to increase through a diminishing interconnection of density of fibers. On the other hand, the resistance is diminished by additional interconnections [21]. It is possible to summarize that currently, many results regarding CF electrical conductivity have been obtained, processed, and described. However, a strict analytical explanation of the CF electrical resistance phenomena has not been propounded. This could be explained by the significantly stochastic structure of felt that was not considered in previous works. Known theoretical approaches used relatively simplified assumptions, reducing the applicability of their results. The requirement to find a more comprehensive analytical explanation of CF conductivity remains an actual and important task.

The present work is aimed at developing a rigorous analytical model of felt conductivity by considering the stochastic character of filaments dimensions and dispositions inside CF, as well as their random contacts. In addition, a parallel study of electrical properties of a CF immersed in different dielectric liquids was conducted. The experimental measurements were compared with the results of the developed theoretical model.

2. Methodology of Experimental Research

The main objective of this research was to investigate and determine the electrical properties of CFs in a wide range of external conditions.

2.1. Characteristics of CF

In this work, rayon-based CF material made from high-quality carbon fibers, acquired from Mersen Corp (Mersen, Greenville, MI, USA) [33], was used. A micrograph showing the structure of the CF is depicted in Figure 1. Additional characteristics of this CF are tabulated in

Table 1. Mechanical properties of a CF.

Fiber Diameter, µm	Average	Standard Deviation
	19.2	1.66
Felt density, [kg/m3], ρf	88	-
Carbon density, [kg/m3], ρc	1954	-
Porosity, [%], λ	95.5	-
Relative carbon volume, p.u. [%], V	0.045 (4.5%)	-
Specific felt surface, [m−1], S	9.8·103	-

[33].

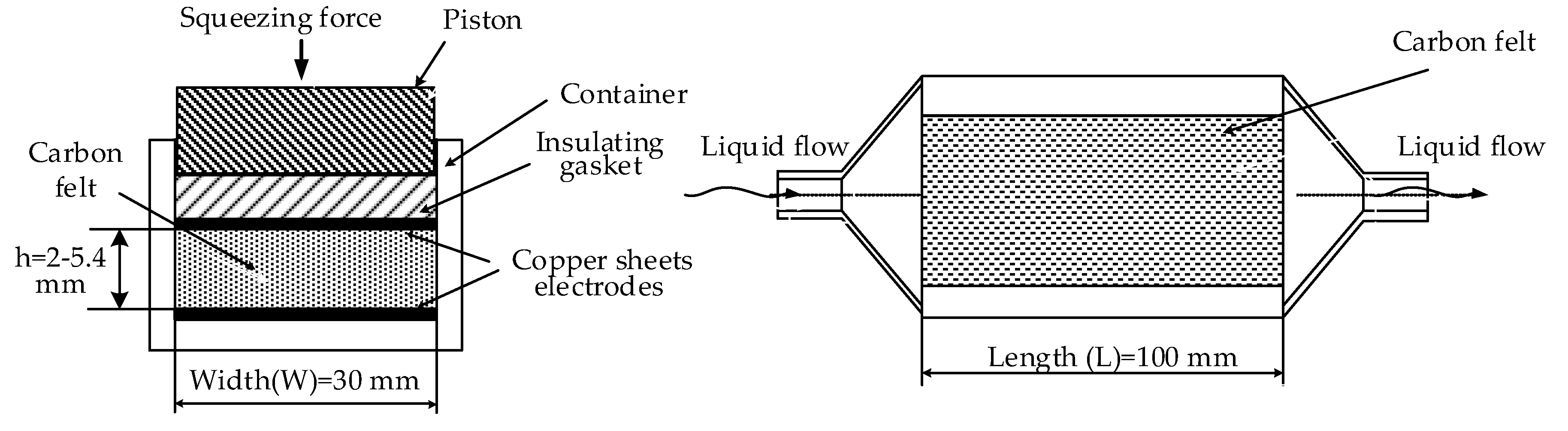
A special cell for testing was fabricated (Figure 2); the design allows measurements of electrical conductivity for compressed CF. Cell dimensions (Figure 3) for felt samples were of 30 × 100 mm. Each felt sample was placed between two identical thin copper sheets of a similar size to that of the felt sample. These copper sheets are placed below and over CF as it seems in Figure 2. Felt thicknesses, denoted as h, diminished from 6.6 to 1.2 mm by tightening four screw nuts. The uniformity of the felt thickness is measured by an electronic caliber having 0.01 mm accuracy.

Electrical conductivity was measured between copper sheets simulating electrode substrates.

The electrical conductivity of compressed CFs was initially measured in dry conditions. This was then repeated after immersing CFs in three different liquids of dissimilar electrical permittivity including glycerol, ethanol (96% strength) and cyclohexane. Conductivity estimation was provided by a bench-type four-probe R/L/C METER IX 3131B (Metrix Co., Dubuque, IA, USA) able to measure resistance (R_ac) by applying 100 Hz, 120 Hz, 1 kHz, and 10 kHz AC frequencies with an error of ~0.6%. In addition, the resistance (R_dc), by applying DC voltage, was measured by a Fluke multimeter.

2.2. Conductivity Measurements

The results of resistance measurements are presented here both for dry felt electrodes and for those immersed in several dielectric (nonconductive) liquids. Dielectric liquids were used in order to eliminate the influences of the ionic conductivity of the liquid itself on the resistance of the felt. A major assumption for the conductivity description was that the resistance of the felt is determined mainly by the density of filament interconnections within the felt along with the density of filament contacts with the electrode surfaces.

Three dissimilar dielectric liquids were chosen: glycerol, ethanol, and cyclohexane, with significantly different values of relative electric permittivity’s (dielectric constant) ɛ_r. Below is

Table 2. Physical parameters of glycerol, alcohol, and cyclohexane.

Parameter	Liquid
	Glycerol	Ethanol	Cyclohexane
Density, [g/cm3] (25 °C)	1.26	0.789	0.8
Relative permittivity, εr, (0.57 MHz, 25 °C)	~42.5	~21.6	~2.02
Specific electrical conductivity, [(Ω·cm)−1], 25 °C	5·10−8	~1·10−6	<5 × 10−9
Viscosity, [Pa·s], 20 °C (30 °C)	141 (61.2)	~0.11	0.61

, which represents the most important physical parameters of each. It should be noted that resistance properties of carbon material used for CF producing are represented in Table 2 by specific electrical conductivity measured in (Ω·cm)⁻¹.

Resistance values of dry CF are shown in

Table 3. Resistance of dry CF.

Parameter		h, mm
		6.3	6.1	4.9	4.45	3.7	1.55	1.1
		Volume decrease, %
		0	3	22	29	41	75	83
Rdc, Ω		0.65	0.22	0.13	0.1	0.09	0.07	0.08
Rac, Ω	100 Hz	0.74	0.17	0.098	0.092	0.08	0.059	0.059
	120 Hz	0.737	0.168	0.095	0.095	0.082	0.061	0.058
	1 kHz	0.737	0.17	0.101	0.093	0.086	0.061	0.057
	10 kHz	0.665	0.163	0.095	0.091	0.08	0.063	0.058
Rrel, p,u.		1.000	0.252	0.147	0.133	0.118	0.089	0.088
ASCDC, 1/(Ω·cm2)		0.051	0.152	0.256	0.333	0.370	0.476	0.417
ASCAC, 1/(Ω·cm2)	100 Hz	0.045	0.196	0.340	0.362	0.417	0.565	0.565
	120 Hz	0.045	0.198	0.351	0.351	0.407	0.546	0.575
	1 kHz	0.045	0.196	0.330	0.358	0.388	0.546	0.585
	10 kHz	0.050	0.204	0.351	0.366	0.417	0.529	0.575
Average ASC, 1/(Ω·cm2)		0.0474	0.1893	0.3257	0.3543	0.3996	0.5326	0.5432

measured in AC and DC currents. For ensuring the exactness of tests, the conductivity of each liquid (without a CF presence in the cell) was measured preliminary. Only if the conductivity had a zero value (in accordance with the exactness of applied devices), the following experiments with CF were produced.

As a measure of felt conductivity the average square conductivity (ASC) (1/(Ω∙cm²) parameter was chosen equal to the reciprocal of the total resistance of the felt in the experimental cell multiplied by its area. The indicator of conductivity was taken its average value obtained for alternating and direct currents.

Where: h-current CF width, mm; R_dc – resistance is measured by direct current (DC), Ω; R_ac – resistance is measured by alternate current (AC), Ω.

The measurements of CF resistivity, whose results are shown in Table 3, confirm the decrease of CF resistivity during compression applied perpendicular to the surface. Initially, CF resistivity falls precipitously; subsequently, the resistance decrease slows. The measurements results for CF immersed in glycerol, alcohol, and cyclohexane are placed in Appendix A. The typical change of relative resistivity for CF in ethanol is presented in Figure 4. Further analysis is given in the following section.

3. Interpretation of Experimental Data

We suggest representing the CF ability to conduct electric current by the average surface conductance (ASC) instead of the well-known use of ASR, which is the inverse of ASC. The advantages of such representation will be seen later. The values of CF ASC immersed in different liquids are placed in Appendix B.

A typical graph of CF ASC in the air versus felt compression D, [%], is shown in Figure 5.

Similar graphs were obtained for CF in glycerol, alcohol, and cyclohexane. The behavior of ASC measured in [$\frac{1}{\Omega ·c{m}^2}]$ units can be satisfactorily described by an exponential function (3) approximating actual data with a criterion of a precision R² = 0.986:

$$ASC=a\cdot \left(1-e^{-b\cdot D}\right)+c$$

(3)

Table 4. Coefficients of the approximating function of the relative increase of filaments interconnections for ASC.

εr	ASC	ASC=a*(1-exp(-b·D)) +c			Coefficient R2
		a	b	c
1	dry	0.5071	0.02488	0.0933	0.969
2.02	cyclohexane	0.5024	0.02008	0.2116	0.988
21.6	ethanol	0.4269	0.02377	0.322	0.982
42.5	glycerol	0.9134	0.01278	0.0996	0.967

tabulated values of coefficients a, b and c for approximating dependence of CF ASC versus compression ratio in different liquids. The precision of the theoretical approximation to experimental data is estimated by a coefficient of determination R² having a significantly high value (see Table 4). Relative dielectric constant values ε_r for all environments in which measurements for CF ASC were made, are represented in the first column of Table 4.

It should be noted good conformity of approximating function (3) to measured data. A tendency of coefficient a and b changings versus alteration of liquid dielectric constant can be observed. The first one is grows up with the increase of the dielectric constant whereas the second one goes down. Coefficient c has no strict propensity and variates around its average magnitude only.

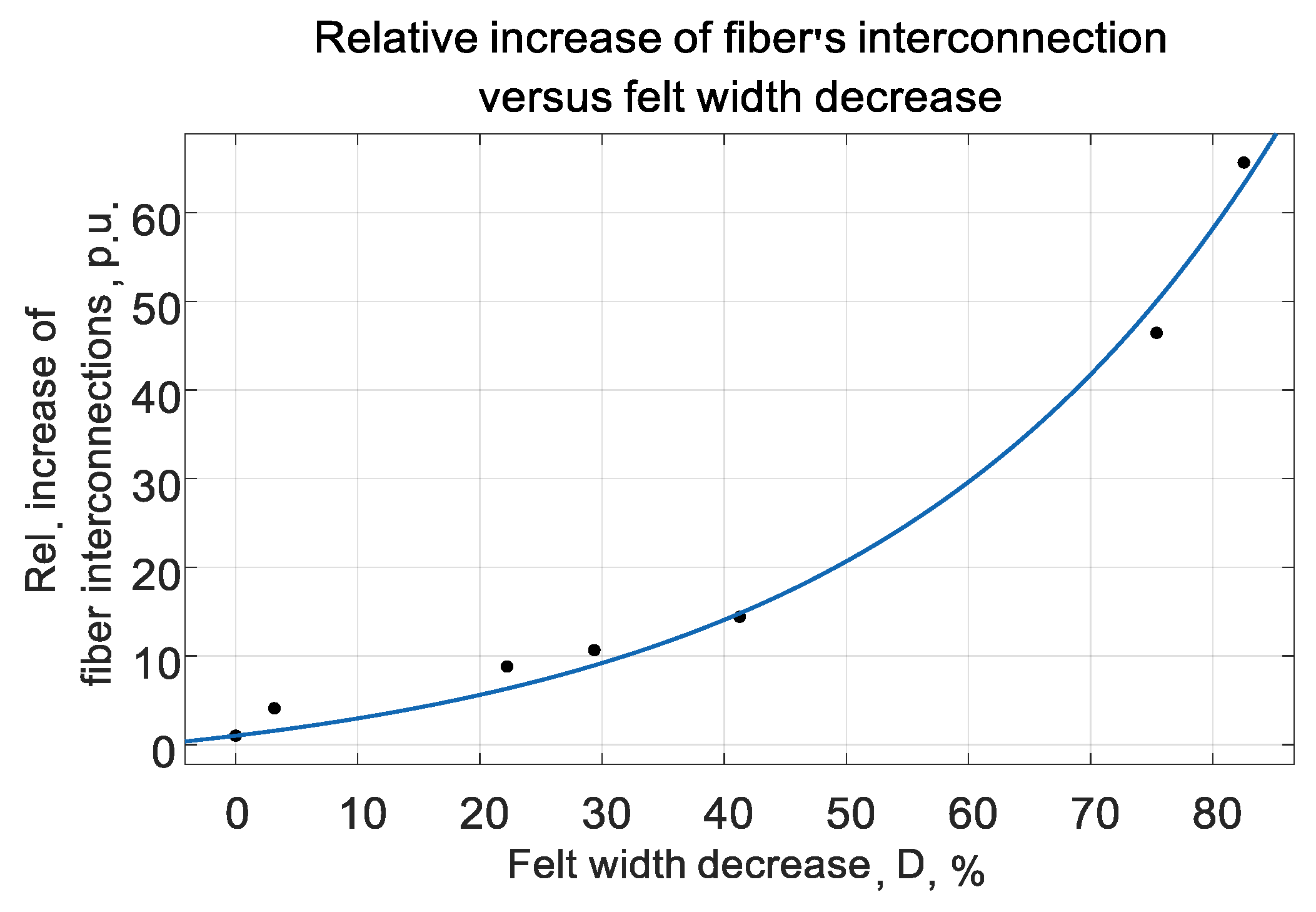
Notably, ASC appears to be dependent on liquid dielectric parameters. Obviously, higher electric permittivity ε positively influences CF conductivity. CF conductivity increases as a function of ε_r, which could be explained by the increase of the density on internal filaments interconnections both between themselves and with electrodes surfaces. Assuming the density of the interconnections between the carbon filaments is the main felt conductance factor, its relative increase (K_inc)_rel was calculated as:

$${\left(K_{inc}\right)}_{rel}=\frac{{\left(ASC\right)}_{Di}}{{\left(ASC\right)}_{D_0}}\cdot \frac{\left(V_0\right)}{\left(V_i\right)}$$

(4)

where (ASC)_Di and (ASC)_D0 are average specific conductance for CF having an initial width D₀ and the width D_i at time t. V₀ designates initial felt and V_i its volume at time t. A felt width (or equivalently, felt volume) decrease was observed as a result of felt compression. Data of interconnection increase of the CF ASC were calculated in accordance with expression (4) and are placed in Appendix C. The persistent increase of interconnection density can be observed that is witnessing the correctness of the proposed model of CF increased conductivity versus its compressing.

K_incr could be approximated rather exactly by the expression (5) for all liquids. The choice of such exponential function was dictated by its good correlation to measured data. The typical graphic interpretation of (5) is given in Figure 6.

$${\left(K_{inc}\right)}_{rel}=A\cdot \left(e^{B\cdot D}-1\right)+1$$

(5)

Comparison of the measurements results with those obtained for a K_incr from the approximation function (5) for each liquid are shown in

Table 5. Coefficients in approximating function (5) defining a relative increase of filaments interconnections during felt compression.

εr	Liquid	Kincr = A(eB·D-1) + 1		coeff. R2
		A	B
1	dry	5.499	0.03042	0.991
42.5	glycerol	2.832	0.0322	0.98
21.6	ethanol	0.5523	0.05052	0.996
2.02	cyclohexane	0.8402	0.03486	0.986

.

3.1. Analytical Model of CF conductivity

The electrical conductivity of CF is achieved with carbon (graphite) filaments. More detailed analysis of the CF electrical conductivity leads to a rigorous conclusion that only those carbon filaments which simultaneously contact both electrodes of the cell sustain electron flow. Therefore, CF conductivity may be assessed as a sum of individual filaments conductivity comprising the total current flow between electrodes. Any individual random disposition of filaments in a CF structure (Figure 7 could be represented by a diagonal of parallelepiped ABCDA^*B^*C^*D^*, as in Figure 7. For simplicity, individual fibers are considered as thin rods having similar diameters, and therefore, equal cross-sections. This circumstance follows from the data in Table 1. The edge CC^* in the parallelepiped is equal to $C{C}^{\ast }=L\cdot \sin \phi$ and symbolizes a height of a filament having length L and polar disposition angle φ. In accordance with the working hypothesis, only those filaments contacting both electrodes are participating in current flow; therefore, they must have heights greater than the width (denoted as W) of the CF. Thus, the totality of fibers whose edge CC^* >= W contribute to the total electrical conductivity of CF.

Considering a stochastic length and disposition of filaments in the space of the CF frame, the summing of conductivities can be performed only by a probabilistic approach. Firstly, a stochastic distribution of their lengths (Figure 8a) was measured by a microscope and described by truncated Gauss function. The appropriate parameters were found to include the average length of L_av = 25 mm, with a standard deviation (STD) of 11 mm.

The measurement of the angle φ presents a significant technical problem. It was suggested to measure horizontal (α) and vertical (β) angles separately by the same optical microscope approach. The histograms of their distributions are shown in Figure 8b,c. In addition, for the simplification of succeeding calculations, it was assumed that both these angles and their distributions are independent. Knowing the horizontal and vertical angles allows calculating the polar angle φ as:

$$\phi =\arccos \left(\frac{\cos \beta }{\sqrt{{\cos }^2\alpha +{\sin }^2\alpha \cdot {\cos }^2\beta }}\right)$$

(6)

Considering the distribution of horizontal and vertical angles obtained in optical measurements, a Gamma function was selected to describe their probabilities. The expression of the Gamma function (7) includes two parameters (a and b) which determine an exact curve of a probability function p of a variable x, it’s mean and standard deviation (STD) values.

$$p\left(x|a,b\right)=\{\begin{array}{ll}\frac{1}{b^a\mathsf{\Gamma }\left(a\right)}{x}^{a-1}{e}^{-\frac{x}{b}},& x\ge 0\\ 0,& x<0\end{array},$$

(7)

The horizontal angle α distribution is described by parameters a = 1 and b = 22. Whereas for angle β: a = 1.4, b = 20.

Stochastic distributions of polar angles are illustrated in Figure 8a,b. Where: W denotes the width, L the length, and H the height of a CF in a cell.

Typical histograms of filaments lengths, horizontal, and vertical angles probability distributions that were obtained by optical measurements (see Appendix D) are shown in Figure 9.

The comparison between the experimental and fitted (gamma distribution) angle spreading is shown in Figure 10.

Knowing the distributions of both horizontal α and vertical β angles and considering their independence, the distribution of a polar angle φ can be obtained. The simplest way, for example, is a numerical simulation (see Figure 11) based on the Monte–Carlo approach.

Bearing in mind the above-mentioned, a total conductance (G) of a CF can be assessed by the integral is considering conductivities of those filaments, which are connecting both of cell electrodes:

$$G\left(h\right)=g_{carbon}\cdot A\cdot L_T{\displaystyle \underset{h}{\overset{\infty }{\int }}\left({\displaystyle \underset{\arcsin \frac{h}{l}}{\overset{\frac{\pi }{2}}{\int }}{p}_{\phi }d\phi }\right)}{p}_l\frac{dl}{l}=g_{carbon}\cdot \frac{V_{carbon}}{{\rho }_{carbon}}{\displaystyle \underset{h}{\overset{\infty }{\int }}\left({\displaystyle \underset{\arcsin \frac{h}{l}}{\overset{\frac{\pi }{2}}{\int }}{p}_{\phi }d\phi }\right)}{p}_l\frac{dl}{l},$$

(8)

where h is the current thickness of a CF; A—the cross-section of carbon filaments; L_T—the total length of all filaments together; V_carbon—the total volume of all filaments; g_carbon—the specific conductivity of a carbon material, p_φ, p_l—the probability of a polar angle φ and a filament length being equal to l; dφ and dl—two variables of integration.

Using a numerical approach, the ASC of a CF versus its volume decrease (expressed by its relative squeezing) was obtained that is represented in Figure 12. Dots in Figure 12 denominate ASC values, which were obtained from an integral of conductivity. The solid line represents ASC approximating values obtained from the expression (3) where coefficients are equal to their average magnitudes from Table 4.

The comparison between the measured and theoretically based values shows an accuracy that is represented by R² = 0.984. This witnesses good applicability of the developed approach.

4. Results

(1) The comprehensive investigation of CF electrical conductivity properties was carried in the present article.

(2) The dependence of resistivity versus compressing rate was obtained as in dry conditions (in air) and when CF is immersed in different dielectric liquids.

(3) Electronic resistivity was measured by applying a DC current and an AC current at several specific frequencies (100 Hz, 120 Hz, 1 kHz and 10 kHz), respectively.

(4) Considering the requirement to verify the influence of dielectric liquid parameters on CF conductivity, four sets of tests were performed. Resistance was measured in dry conditions and with the CF immersed in different (glycerol, alcohol, and cyclohexane) non-conducting (dielectric) liquids. The use of dielectric liquids instead of real electrolytes was justified to prevent the influence of electrolyte ionic conductivity on the measurement results.

(5) Approximating function with their specific coefficients for description average surface conductivity of CF was found. The proximity of this function to the real data was determined.

(6) Stochastic dispersion of individual carbon filaments and their disposition angles (vertical and horizontal) were established and were described further by a gamma-distribution function.

(7) Analytical description of CF conductivity based on a stochastic approach and represented by the integral of conductivity was developed.

5. Discussion

The results of CF electrical resistivity properties are extremely important for practical use, as well as for new developments, and research work. Knowing the analytical description of a conductivity paves the way to finding an optimal design of a CF structure able to minimize as an electrical and hydrodynamic resistances. The last may lead to new CF electrodes for different electrochemical application more efficient and useful.

6. Conclusions

(1) CF material has widespread requests in different applications, including heating elements and diverse electrochemical cells.

(2) Electrical (electronic) conductivity of CF plays a crucial role for electrons to reach the surface of the electrodes and to participate in reactions. Likewise, electrical resistivity (the inverse of electrical conductivity) plays a significant role in generating heat and causing electrical losses, thus diminishing the efficiency of electrochemical equipment.

(3) Owing to the significant importance of CF resistivity and conductivity for different electrochemical applications, a special comprehensive investigation was carried out aiming to find the magnitudes of these parameters.

(4) It was observed that electrical resistivity was diminished during felt compression, having a non-linear relation versus volume decrease like the negative exponential function. In the initial stage of volume decrease, the resistance drops quickly. However, after 80–60% of its initial value, additional compression has a negligible effect on conductivity.

(5) Electrical conductivity moderately depends on liquid permittivity properties. Dielectric constant (ε), among other liquid parameters, obviously has the main role influencing the quantity of interconnection between carbon filaments and electrodes. The increase of ε causes a slight improvement in CF conductivity.

(6) The theoretical approach based on the stochastic distributions of filaments lengths and their stochastic dispositions inside the felt frame was developed. The conductivity for each current felt thickness was estimated by an integral which summarizes the conductivities of all filaments that this time are connecting both of the cell electrodes.

(7) It could be assumed that the type of lengths and angles distribution inside a frame plays a significant role in defining CF conductivity and should be investigated in future research work.