Theoretical Study on Geometries of Electrodes in Laboratory Electrical Resistivity Measurement
Abstract
:Featured Application
Abstract
1. Introduction
2. Theoretical Background
2.1. Electric Potential from a Point Electrode
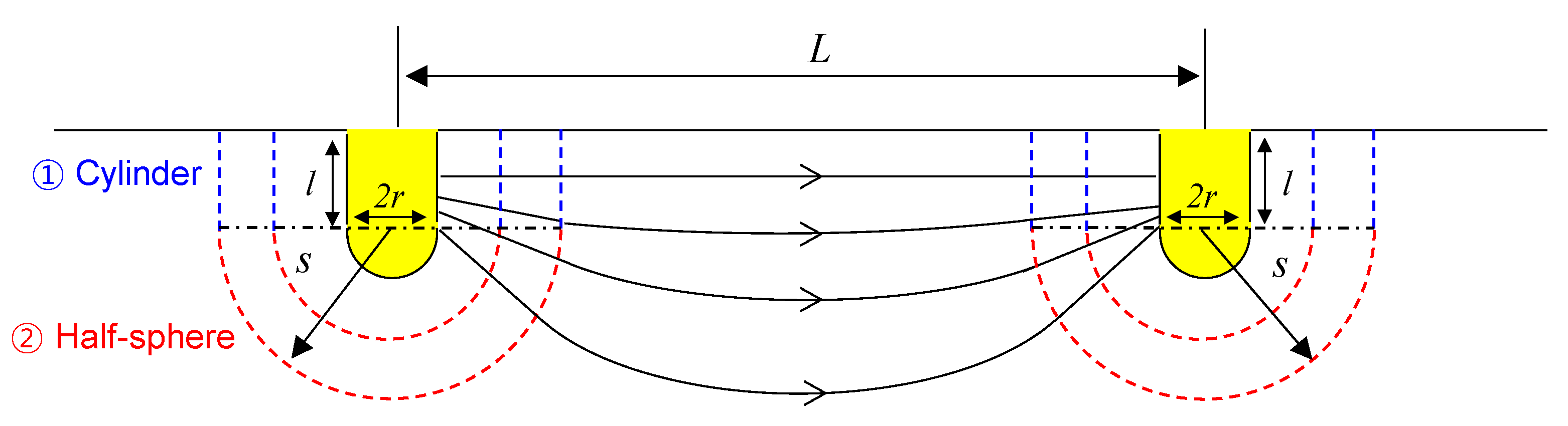
2.2. Electrical Resistance Measured between Two Cylindrical Electrodes
2.3. Two Cylindrical Electrodes in the Container
3. Experimental Tests and Results
4. Discussion
4.1. Electrical Resistance Measured between Two Half-Buried Spherical Electrodes
4.2. Parametric Study: Influence of the Electrode Geometry on Boundary Effect
5. Conclusions
- The theoretical electrical resistance, between two cylindrical electrodes with rounded tips, is represented as a function of the radius (r) and penetration depth (l) of the electrodes and the distance (L) between the two electrodes. The electrical resistance increases when the electrical resistivity of the material and the distance between the electrodes increase and the radius and penetration depth decrease.
- Over short distances, the measured electrical resistance between two cylindrical electrodes shows a similar tendency to values predicted by the theoretical equation. However, as the distances increase, the electrodes are situated closer to the non-conductive (acrylic) walls of the container and the measured electrical resistance is higher than the predicted values. This boundary effect is caused by the distortion of the current flow near the non-conductive materials and it starts in about a quarter of the container width from the container wall. The boundary effect is adjusted by adopting the method of image charges.
- It is verified that the electrical resistance between two cylindrical electrodes becomes identical to the electrical resistance between two half-buried spherical electrodes as the penetration depth becomes shallow. The cylindrical electrodes can be treated as half-buried spherical electrodes with the allowable error range. If the allowable error of the measured electrical resistance is 2%, the ratio between penetration depth and the radius is less than unity.
- The parametric study shows that the boundary effect can be reduced when the ratio between the penetration depth and the radius (l/r) and the spacing and the penetration depth (L/l) are large. Therefore, it is recommended to employ slender electrodes or a short distance between two electrodes to avoid the boundary effect in a fixed size container.
Author Contributions
Funding
Conflicts of Interest
References
- Wenner, F. The four-terminal conductor and the Thomson bridge. Bull. Bur. Stand. 1912, 8, 559–610. [Google Scholar] [CrossRef]
- Tagg, G.F. Earth Resistances; Pitman Pub. Corp.: New York, NY, USA, 1964. [Google Scholar]
- Telford, W.M.; Geldart, L.P.; Sheriff, R.E. Applied Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Byun, Y.K.; Hong, W.T.; Yoon, H.K. Characterization of cementation factor of unconsolidated granular materials through time domain reflectrometry with variable saturated conditions. Materials 2019, 12, 1340. [Google Scholar] [CrossRef] [PubMed]
- Rücker, C.; Günther, T. The simulation of finite ERT electrodes using the complete electrode model. Geophysics 2011, 76, 227–238. [Google Scholar] [CrossRef]
- Rooney, W.J.; Gish, O.H. Results of Earth-resistivity surveys near Watheroo, Western Australia, and at Ebro, Spain. Terr. Magn. Atmos. Electr. 1927, 32, 49–63. [Google Scholar] [CrossRef]
- Ingeman-Nielsen, T.; Tomaškovičová, S.; Dahlin, T. Effect of electrode shape on grounding resistances—Part 1: The focus-one protocol. Geophysics 2016, 81, WA159–WA167. [Google Scholar] [CrossRef]
- Daily, W.; Ramirez, A.; Binley, A. Remote monitoring of leaks in storage tanks using electrical resistance tomography: Application at Hanford site. J. Environ. Eng. Geophys. 2004, 9, 11–24. [Google Scholar] [CrossRef]
- Rücker, C.; Günther, T.; Spitzer, K. Three-dimensional modelling and inversion of dc resistivity data incorporating topography—I. Modelling. Geophys. J. Int. 2006, 166, 495–505. [Google Scholar] [CrossRef]
- Binley, A.; Henry-Poulter, S.; Shaw, B. Examination of solute transport in an undisturbed soil column using electrical resistance tomography. Water Resour. Res. 1996, 32, 763–769. [Google Scholar] [CrossRef]
- Igel, J. On the Small-Scale Variability of Electrical Soil Properties and its Influence on Geophysical Measurements; University of Frankfurt/Main: Frankfurt, Germany, 2007. [Google Scholar]
- Flechsig, C.; Fabig, T.; Rücker, C.; Schütze, C. Geoelectrical investigations in the Cheb Basin/W-Bohemia: An approach to evaluate the near-surface conductivity structure. Stud. Geophys. Geod. 2010, 54, 443–463. [Google Scholar] [CrossRef]
- Baishiki, R.S.; Osterberg, C.K.; Dawalibi, F. Earth Resistivity Measurements Using Cylindrical Electrodes at Short Spacings. IEEE Trans. Power Deliv. 1987, 2, 64–71. [Google Scholar] [CrossRef]
- Taiwo, S.M.; Lee, J.S.; Yoon, H.K. Analytical and experimental studies to obtain electrical resistivity in a small-scaled laboratory test. Geophysics 2017, 82, 267–275. [Google Scholar] [CrossRef]
- Park, J.; Lee, K.H.; Seo, H.; Ryu, J.; Lee, I.M. Role of induced electrical polarization to identify soft ground/fractured rock conditions. J. Appl. Geophys. 2017, 137, 63–72. [Google Scholar] [CrossRef]
- Van Nostrand, R.G.; Cook, K.L. Interpretation of Resistivity Data; United States Government Printing Office: Washington, DC, USA, 1966. [Google Scholar]
- Glover, P.W.; Hole, M.J.; Pous, J. A modified Archie’s law for two conducting phases. Earth Planet. Sci. Lett. 2000, 180, 369–383. [Google Scholar] [CrossRef]
- McCarter, W.J.; Starrs, G.; Kandasami, S.; Jones, R.; Chrisp, T. Electrode configurations for resistivity measurements on concrete. Aci. Mater. J. 2009, 106, 258–264. [Google Scholar]
- Jaschinsky, P.; Wensorra, J.; Lepsa, M.I.; Mysliveček, J.; Voigtländer, B. Nanoscale charge transport measurements using a double-tip scanning tunneling microscope. J. Appl. Phys. 2008, 104, 094307. [Google Scholar] [CrossRef] [Green Version]
- Blythe, A. Electrical resistivity measurements of polymer materials. Polym. Test. 1984, 4, 195–209. [Google Scholar] [CrossRef]
- Ryu, H.H. Development of Tunnel Electrical Resistivity Prospecting System and its Application; Korea Advanced Institute of Science and Technology (KAIST): Daejeon, Korea, 2010. [Google Scholar]
- Moussa, A.H.; Dolphin, L.T.; Mokhtar, G. Applications of Modern Sensing Techniques to Egyptology; A report of the 1977 Field Experiments by a Joint Team; SRI International: Menlo Park, CA, USA, 1977. [Google Scholar]
- Athanasiou, E.; Tsourlos, P.; Vargemezis, G.; Papazachos, C.; Tsokas, G. Non-destructive DC resistivity surveying using flat-base electrodes. Near Surf. Geophys. 2007, 5, 263–272. [Google Scholar] [CrossRef] [Green Version]
- Won, I. The geometrical factor of a marine resistivity probe with four ring electrodes. IEEE J. Ocean. Eng. 1987, 12, 301–303. [Google Scholar] [CrossRef]
- Ridd, P. Electric potential due to a ring electrode. IEEE J. Ocean. Eng. 1994, 19, 464–467. [Google Scholar] [CrossRef]

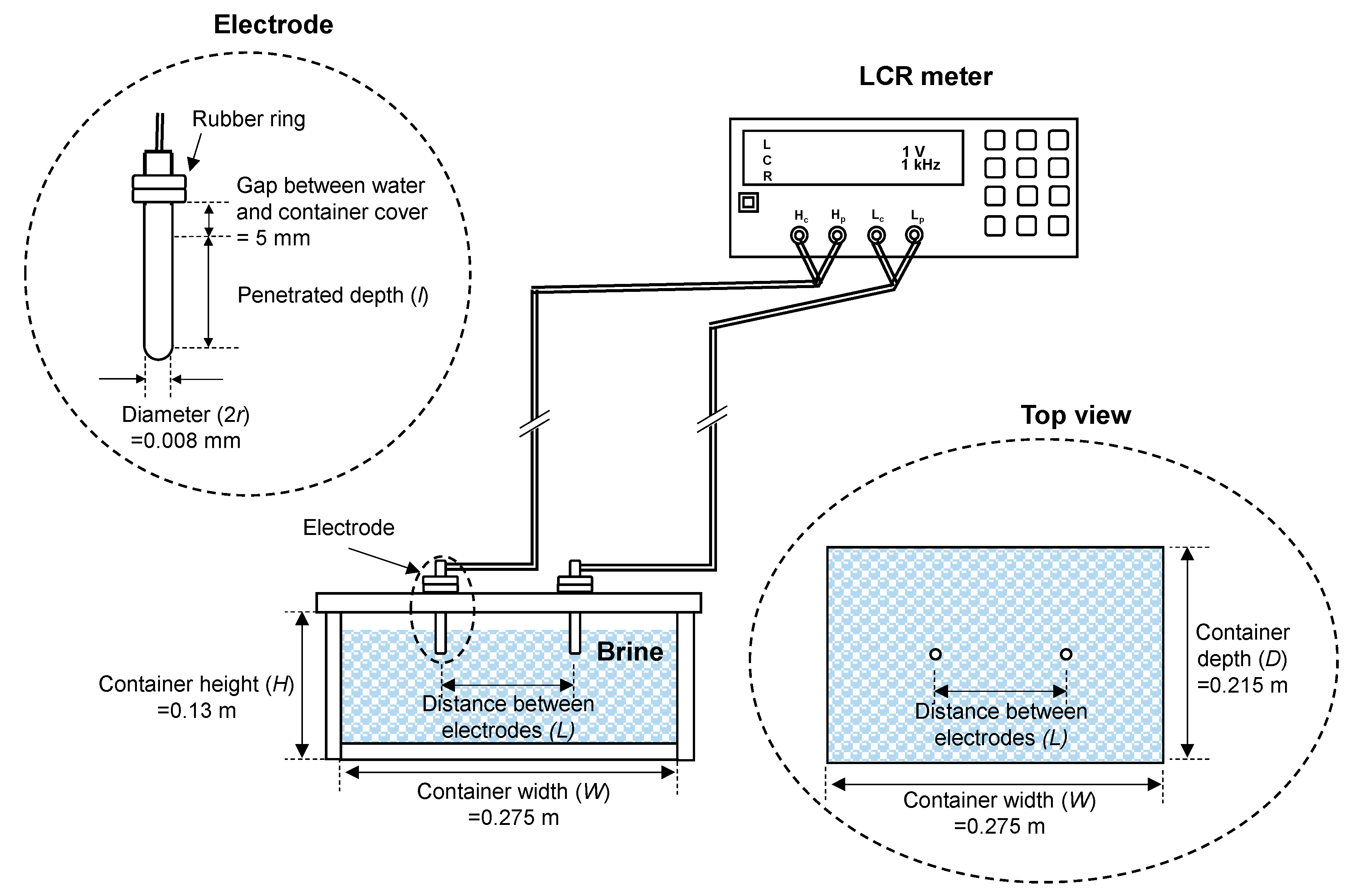





| Electrical Resistivity, ρ (Ωm) | Penetration Depth, l (mm) | Distance between Two Electrodes, L (m) |
| 18.88 | 0 | 0.015 |
| 0.045 | ||
| 4 | 0.085 | |
| 4.78 | 8 | 0.125 |
| 0.165 | ||
| 16 | 0.205 | |
| 0.245 |
| l/r (-) | L/l (-) |
|---|---|
| 1 1.5 2.5 5 10 20 | 3 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, C.-H.; Chong, S.-H.; Cho, G.-C. Theoretical Study on Geometries of Electrodes in Laboratory Electrical Resistivity Measurement. Appl. Sci. 2019, 9, 4167. https://doi.org/10.3390/app9194167
Hong C-H, Chong S-H, Cho G-C. Theoretical Study on Geometries of Electrodes in Laboratory Electrical Resistivity Measurement. Applied Sciences. 2019; 9(19):4167. https://doi.org/10.3390/app9194167
Chicago/Turabian StyleHong, Chang-Ho, Song-Hun Chong, and Gye-Chun Cho. 2019. "Theoretical Study on Geometries of Electrodes in Laboratory Electrical Resistivity Measurement" Applied Sciences 9, no. 19: 4167. https://doi.org/10.3390/app9194167
APA StyleHong, C.-H., Chong, S.-H., & Cho, G.-C. (2019). Theoretical Study on Geometries of Electrodes in Laboratory Electrical Resistivity Measurement. Applied Sciences, 9(19), 4167. https://doi.org/10.3390/app9194167






