Research on Polarization and Phase Fading Compensation in Michelson Interferometer Based on 3 × 3 Coupler and Novel Probe with Built-in Faraday Rotator
Abstract
:1. Introduction
2. Materials and Methods
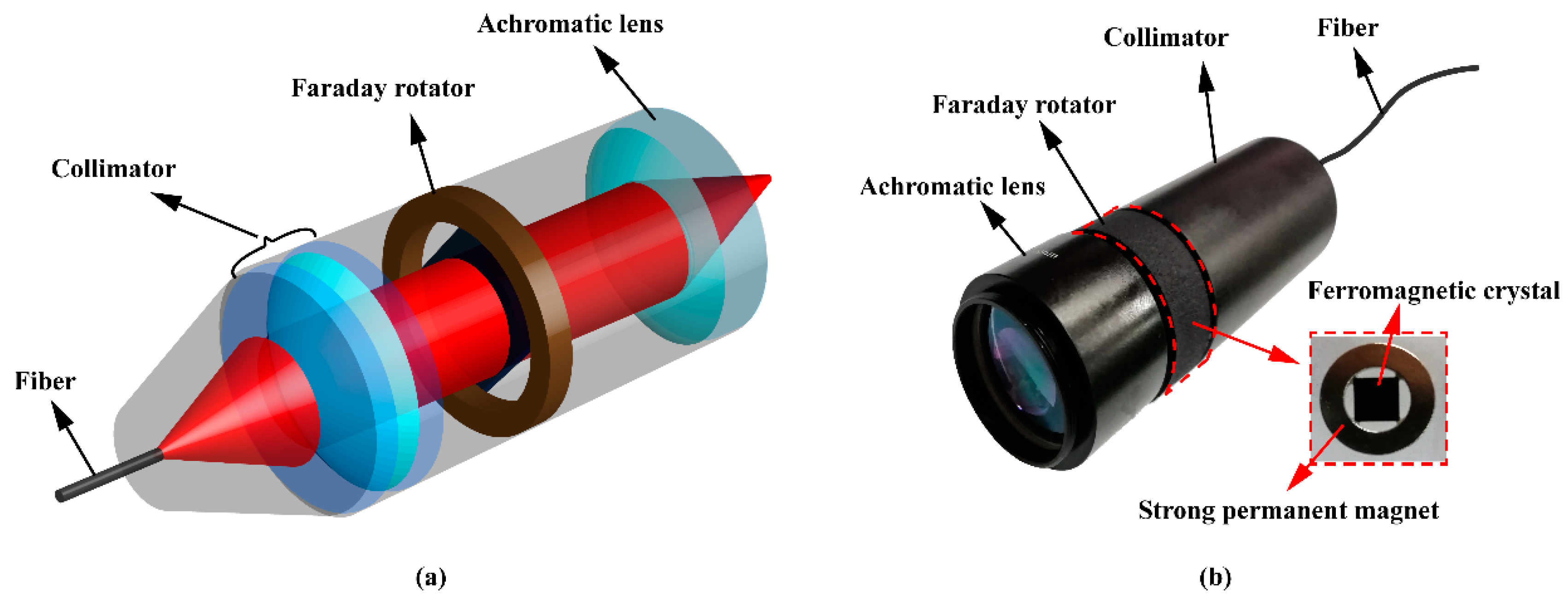
2.1. Depolarization Fading System Model Based on Probe with Built-in Faraday Rotator
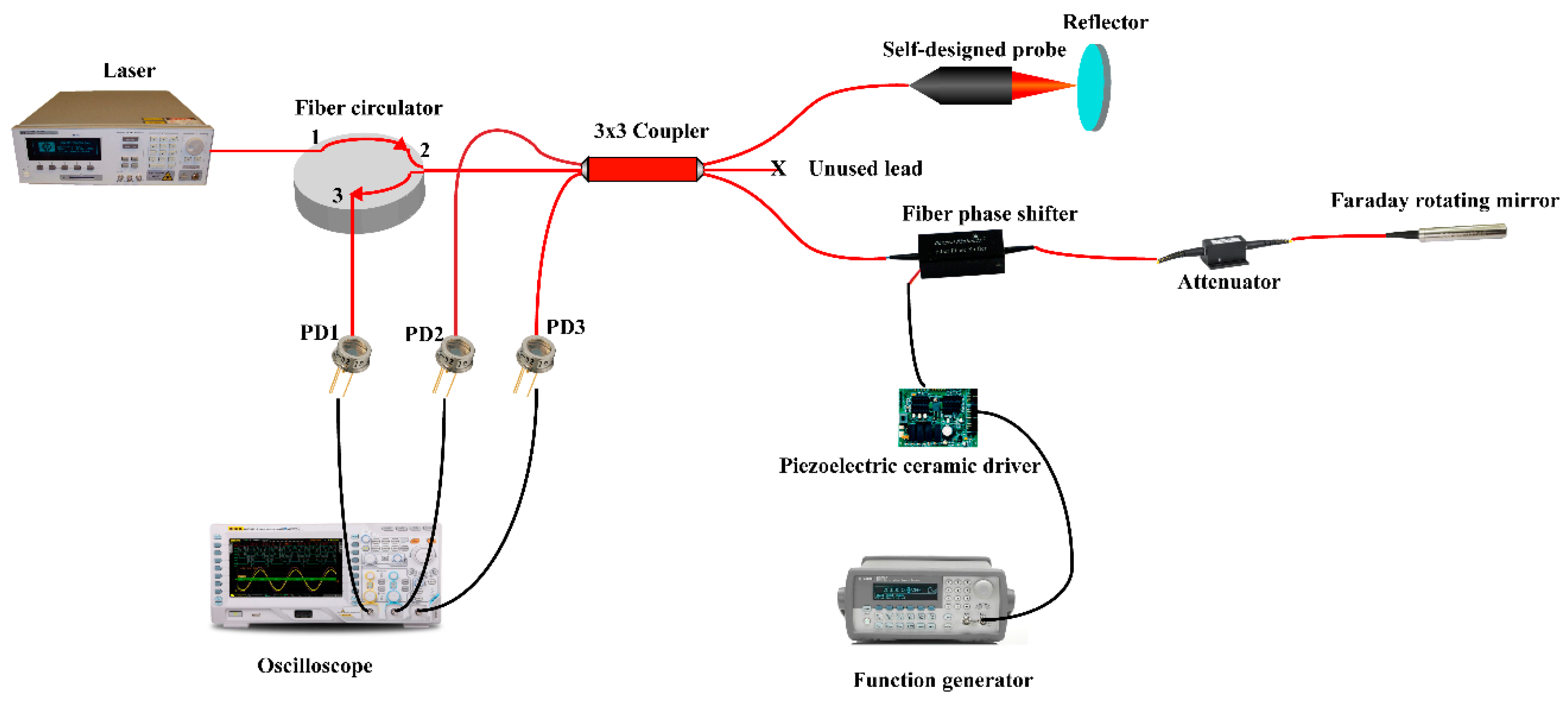
2.2. Experimental Interferometer System with Phase Feedback Control Scheme
3. Results
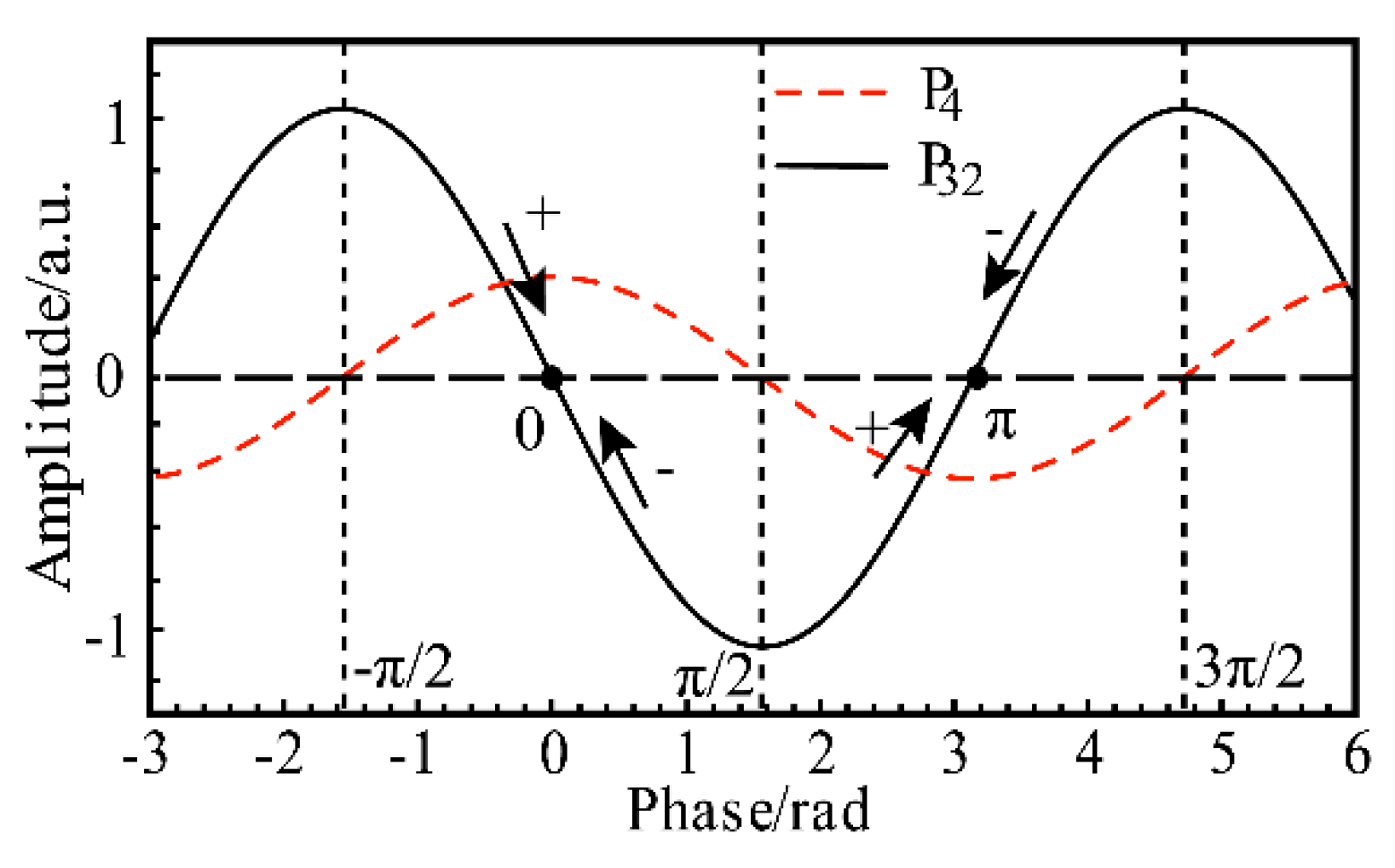
3.1. Performance of Depolarization Fading with Self-Designed Probe
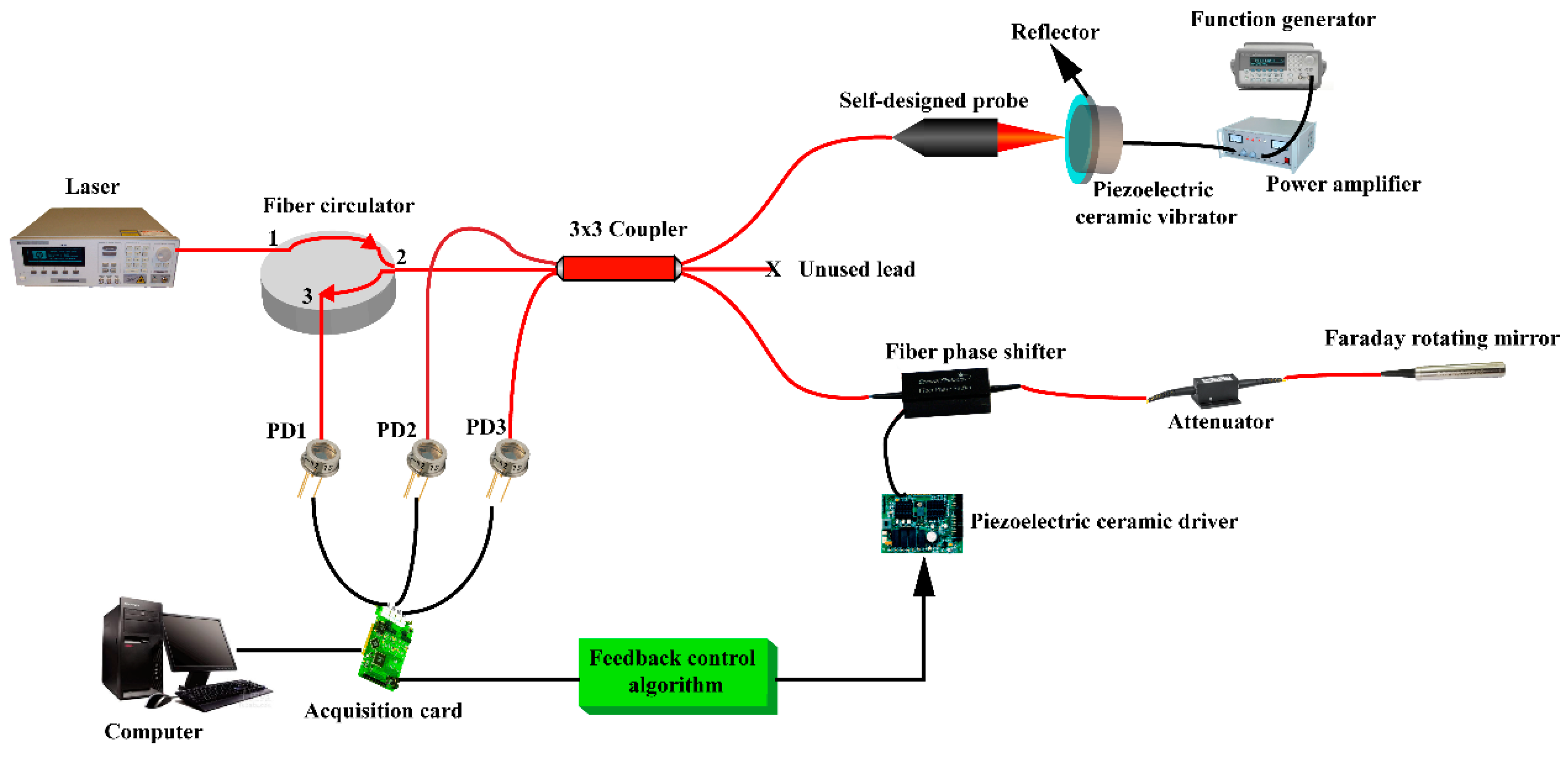
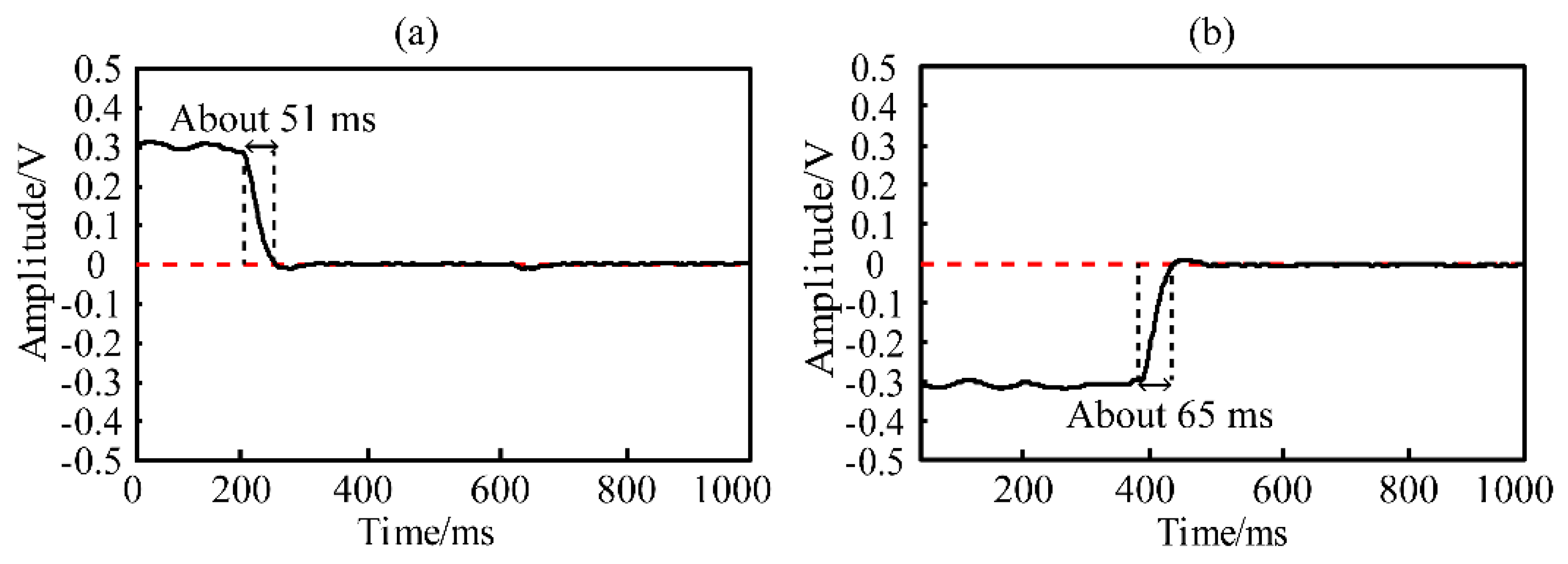
3.2. Performance of Feedback Control Scheme for Phase Fading
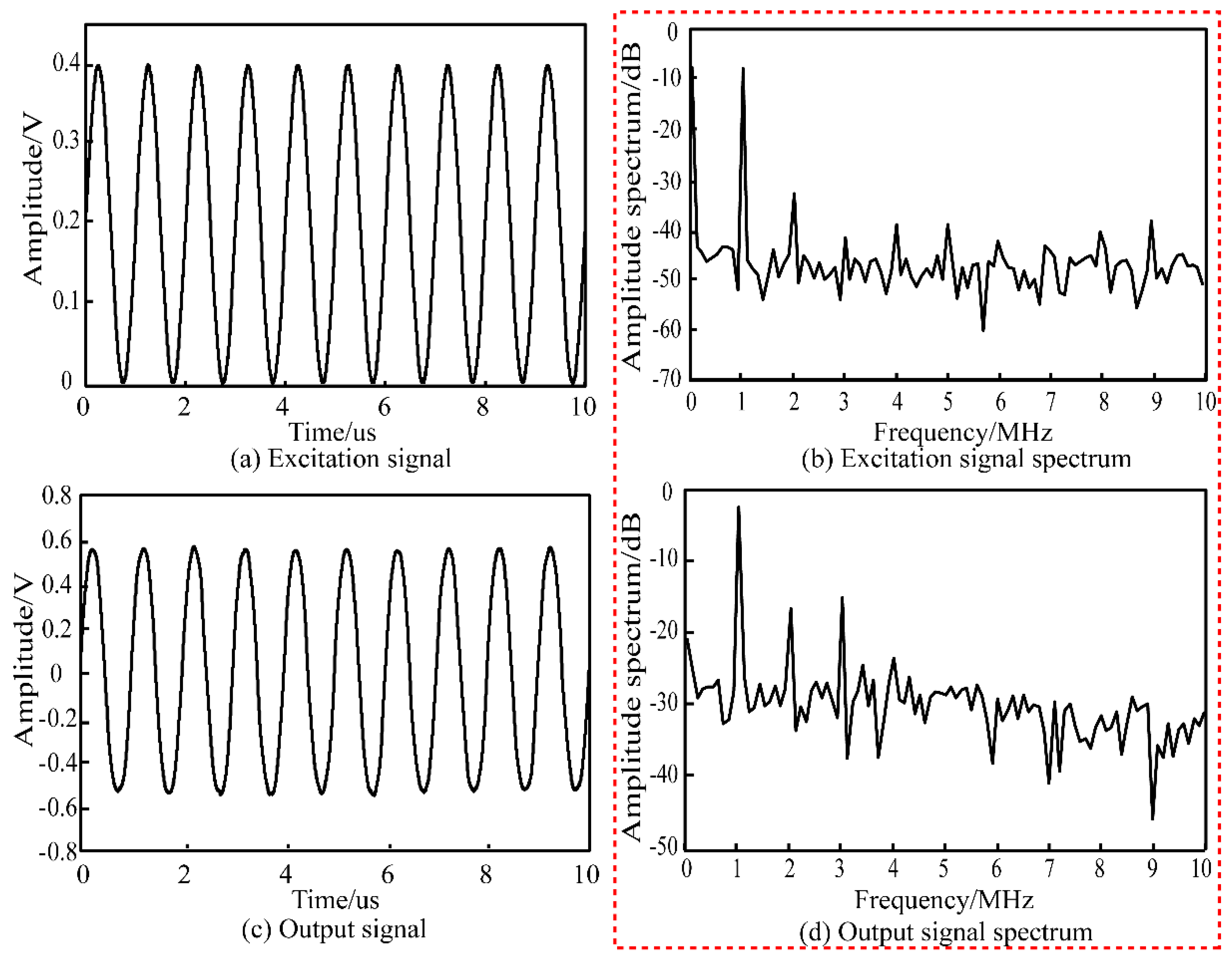
3.3. Detection Performance of the Interferometer
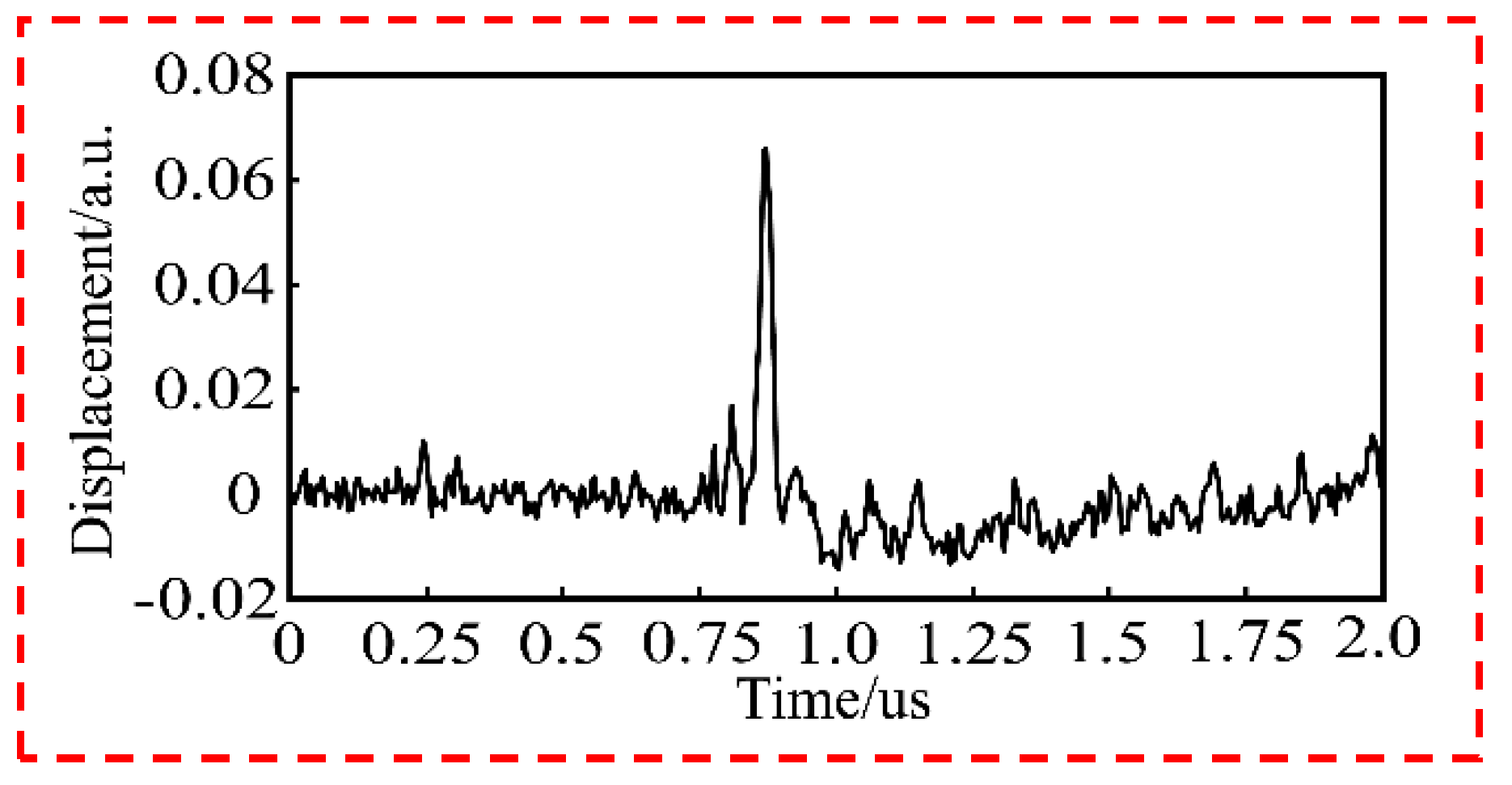
4. Application in Photoacoustic Detection
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Han, M.; Wang, X.W.; Xu, J.C.; Cooper, K.L.; Wang, A.B. Diaphragm-based extrinsic fabry-perot interferometric optical fiber sensor for acoustic wave detection under high background pressure. Opt. Eng. 2005, 44, 060506. [Google Scholar] [CrossRef]
- Yan, L.; Gui, Z.G.; Wang, G.J.; An, Y.Q.; Gu, J.Y.; Zhang, M.Q.; Lin, X.L.; Wang, Z.B.; Wang, G.; Jia, P.G. A micro bubble structure based fabry–perot optical fiber strain sensor with high sensitivity and low-cost characteristics. Sensors 2017, 17, 555. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.A.; Yuan, L.; Lan, X.W.; Kaur, A.; Huang, J.; Xiao, H. High-temperature fiber-optic Fabry-Perot interferometric pressure sensor fabricated by femtosecond laser. Opt. Lett. 2013, 38, 4609–4612. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.S.; Xiong, S.S.; Gao, S.C.; Zhang, H.; Wan, L.; Huang, X.C.; Huang, B.S.; Feng, Y.H.; Liu, W.P.; Li, Z.H. High-temperature sensor based on fabry-perot interferometer in microfiber tip. Sensors 2018, 18, 202. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.J.; Jiang, X.Q.; Xie, F.; Zhang, W.; Zhang, L.; Bennion, L. High stability multiplexed fiber interferometer and its application on absolute displacement measurement and on-line surface metrology. Opt. Express 2004, 12, 5729–5734. [Google Scholar] [CrossRef] [PubMed]
- Xiong, W.; Xiao, G.Z.; Han, X.; Chen, X.L.; Yang, K.Y.; Luo, H. All-fiber interferometer for displacement and velocity measurement of a levitated particle in fiber-optic traps. Appl. Opt. 2019, 58, 2081–2084. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Xiao, H.; May, R.G.; Wang, J.; Zhao, W.; Deng, J.; Zhang, P.; Pickrell, G.R. Optical fiber sensors for harsh environments. Proc. SPIE Int. Soc. Opt. Eng. 2000, 4077, 2–6. [Google Scholar]
- Rong, Q.Z.; Zhou, R.X.; Hao, Y.X.; Yin, X.L.; Shao, Z.H.; Gang, T.T.; Qiao, X.G. Ultrasonic sensitivity-improved Fabry-Perot interferometer using acoustic focusing and its application for noncontact imaging. IEEE Photonics J. 2017, 9, 7011210. [Google Scholar] [CrossRef]
- Eom, J.; Park, S.J.; Lee, B.H. Noncontact photoacoustic tomography of in vivo chicken chorioallantoic membrane based on all-fiber heterodyne interferometry. J. Biomed. Opt. 2015, 20, 106007. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.J.; Yang, S.H.; Wang, Y.; Xing, D. Noncontact broadband all-optical photoacoustic microscopy based on a low-coherence interferometer. Appl. Phys. Lett. 2015, 106, 043701. [Google Scholar] [CrossRef]
- Hochreiner, A.; Bauer-Marschallinger, J.; Burgholzer, P.; Jakoby, B.; Berer, T. Non-contact photoacoustic imaging using a fiber based interferometer with optical amplification. Biomed. Opt. Express. 2013, 4, 2322–2331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martinelli, M. A universal compensator for polarization changes induced by birefringence on a retracing beam. Opt. Commun. 1989, 72, 341–344. [Google Scholar] [CrossRef]
- Zhang, R.X.; Yao, X.S.; Liu, T.G.; Li, L. The effect of linear birefringence on fiber optic current sensor based on Faraday mirror. In Proceedings of the SPIE—The International Society for Optical Engineering, Beijing, China, 9–11 October 2014. [Google Scholar]
- Zhang, C.; Duan, F.J. Phase stepping methods based on PTDC for Fiber-Optic Projected-Fringe Digital Interferometry. Opt. Laser. Technol. 2012, 44, 1089–1094. [Google Scholar]
- Lundin, P.; Guan, Z.G.; Svanberg, S. Active feedback regulation of a Michelson interferometer to achieve zero-background absorption measurements. Appl. Opt. 2011, 50, 373–378. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Gao, Y.Z.; Ma, Z.H.; Zhou, H.X.; Wang, R.K.K.; Wang, Y. In vivo photoacoustic imaging of blood vessels using a homodyne interferometer with zero-crossing triggering. J. Biomed. Opt. 2017, 22, 036002. [Google Scholar] [CrossRef] [PubMed]
- Elezov, M.S.; Scherbatenko, M.L.; Sych, D.V.; Goltsman, G.N. Active and passive phase stabilization for the all-fiber Michelson interferometer. J. Phys. 2018, 1124, 051014. [Google Scholar] [CrossRef]
- Lutzweiler, C.; Razansky, D. Optoacoustic imaging and tomography: Reconstruction approaches and outstanding challenges in image performance and quantification. Sensors 2013, 13, 7345–7384. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.H.; Hu, S. Photoacoustic tomography: In vivo imaging from organelles to organs. Science 2012, 335, 1458. [Google Scholar] [CrossRef] [PubMed]
- Kersey, A.D.; Marrone, M.J.; Davis, M.A. Polarization-insensitive fiber optic Michelson interferometer. Electron. Lett. 1991, 27, 518–520. [Google Scholar] [CrossRef]


| Output Signal | Normalized Result | |||
|---|---|---|---|---|
| 0.09 | 0.18 | 0.30 | 0.56 | 1.86 |
| 0.09 | 0.15 | 0.22 | 0.42 | 1.91 |
| 0.09 | 0.11 | 0.14 | 0.27 | 1.92 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, S.; Rong, J.; Tian, J. Research on Polarization and Phase Fading Compensation in Michelson Interferometer Based on 3 × 3 Coupler and Novel Probe with Built-in Faraday Rotator. Appl. Sci. 2019, 9, 4173. https://doi.org/10.3390/app9194173
Jing S, Rong J, Tian J. Research on Polarization and Phase Fading Compensation in Michelson Interferometer Based on 3 × 3 Coupler and Novel Probe with Built-in Faraday Rotator. Applied Sciences. 2019; 9(19):4173. https://doi.org/10.3390/app9194173
Chicago/Turabian StyleJing, Shuaiqi, Jian Rong, and Jiayan Tian. 2019. "Research on Polarization and Phase Fading Compensation in Michelson Interferometer Based on 3 × 3 Coupler and Novel Probe with Built-in Faraday Rotator" Applied Sciences 9, no. 19: 4173. https://doi.org/10.3390/app9194173
APA StyleJing, S., Rong, J., & Tian, J. (2019). Research on Polarization and Phase Fading Compensation in Michelson Interferometer Based on 3 × 3 Coupler and Novel Probe with Built-in Faraday Rotator. Applied Sciences, 9(19), 4173. https://doi.org/10.3390/app9194173





