Direct Sailing Variable Acceleration Dynamics Characteristics of Water-Jet Propulsion with a Screw Mixed-Flow Pump
Abstract
:1. Introduction
2. Research Method for Investigating the Variable Acceleration Motion of a Submersible
3. Water-Jet Propulsion Dynamics Modeling
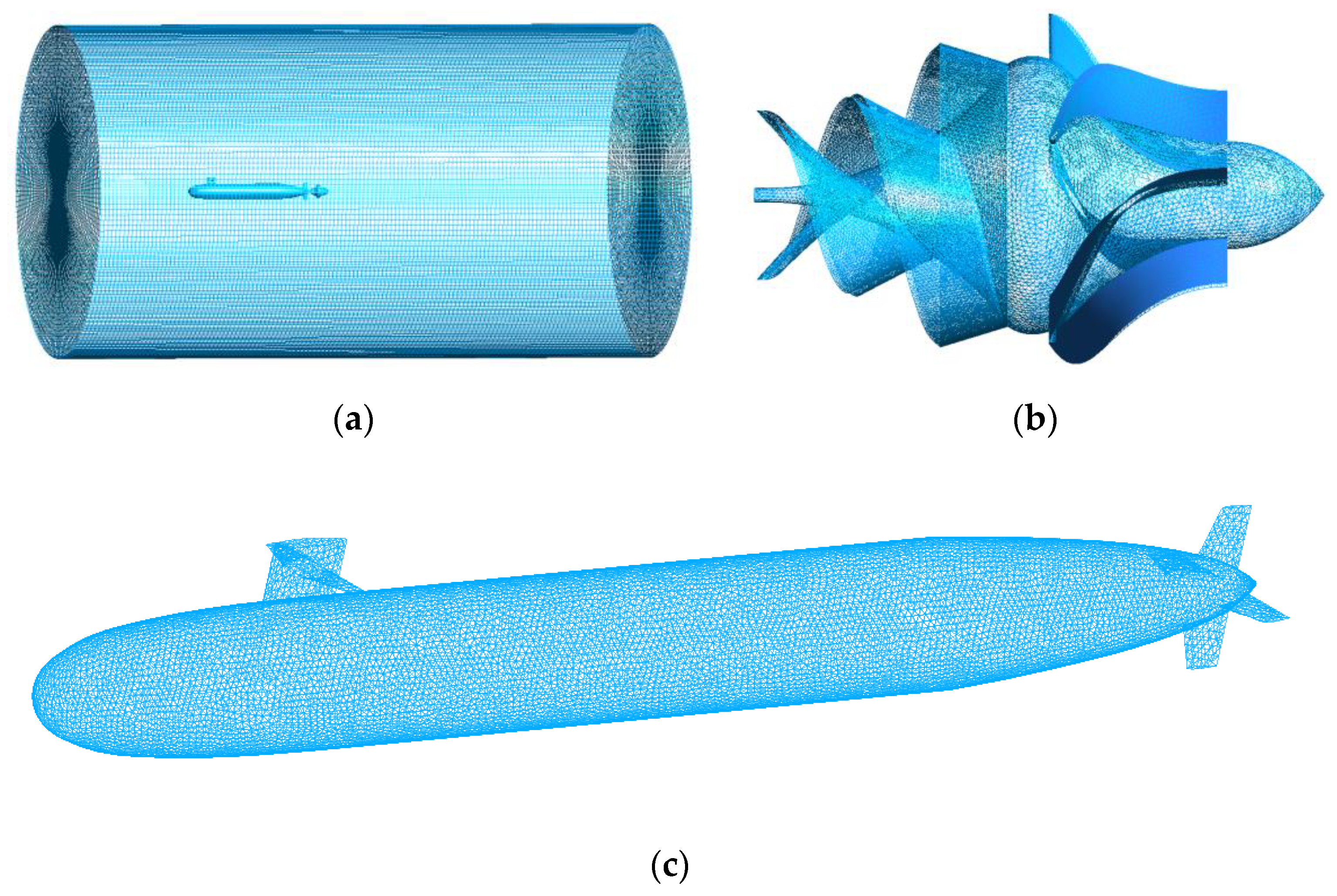
3.1. Geometric Models and Meshing
3.1.1. Submersible Geometry Model
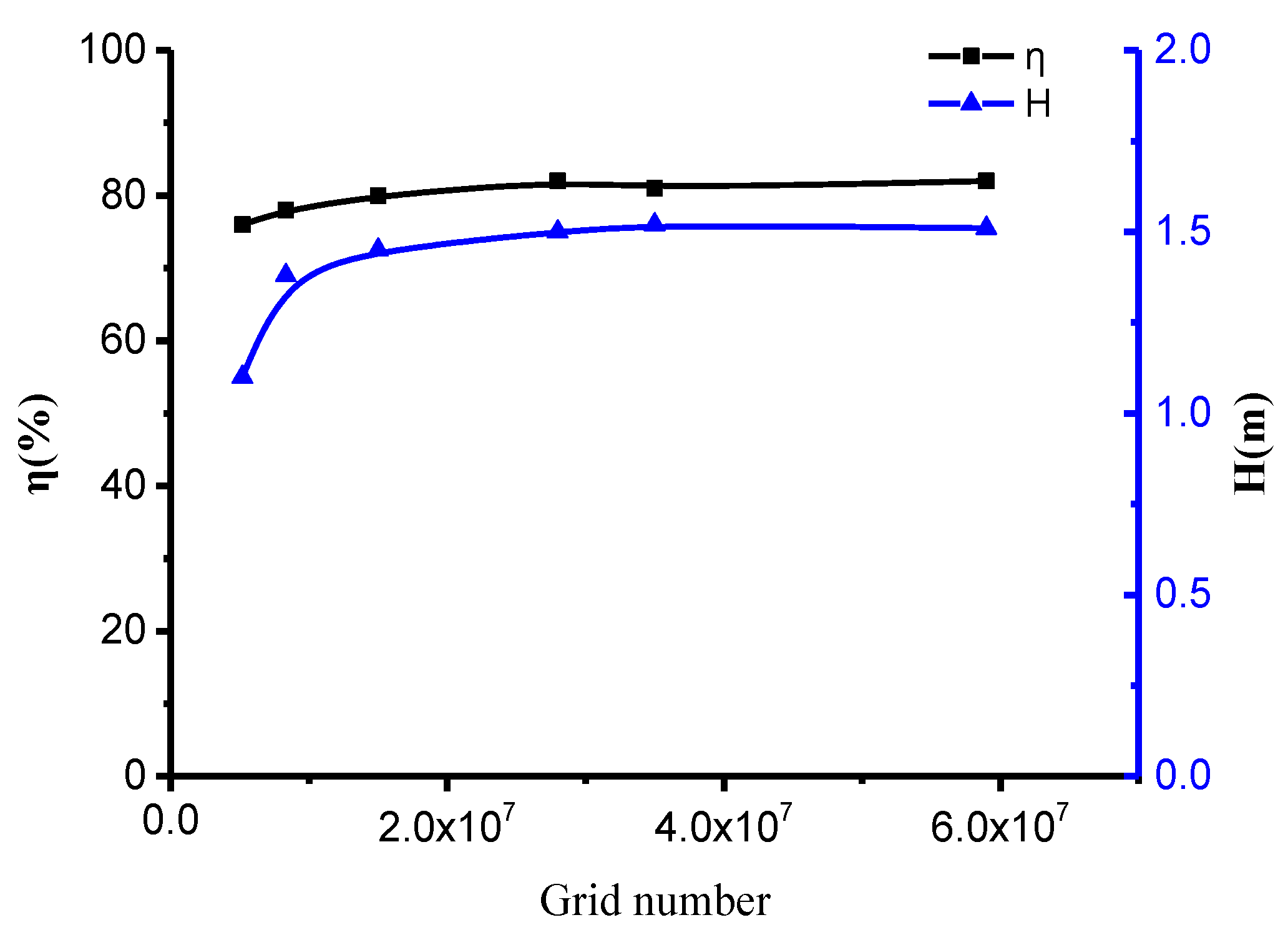
3.1.2. Determining and Meshing the Flow Region
3.1.3. Numerical Calculation Methods and Boundary Conditions
3.2. A Dynamics Model of Direct Sailing Variable Acceleration Motion
3.2.1. Basic Assumptions
3.2.2. Model of Thrust Provided by the Water-Jet Pump
3.2.3. A Dynamics Model of Variable Acceleration Motion
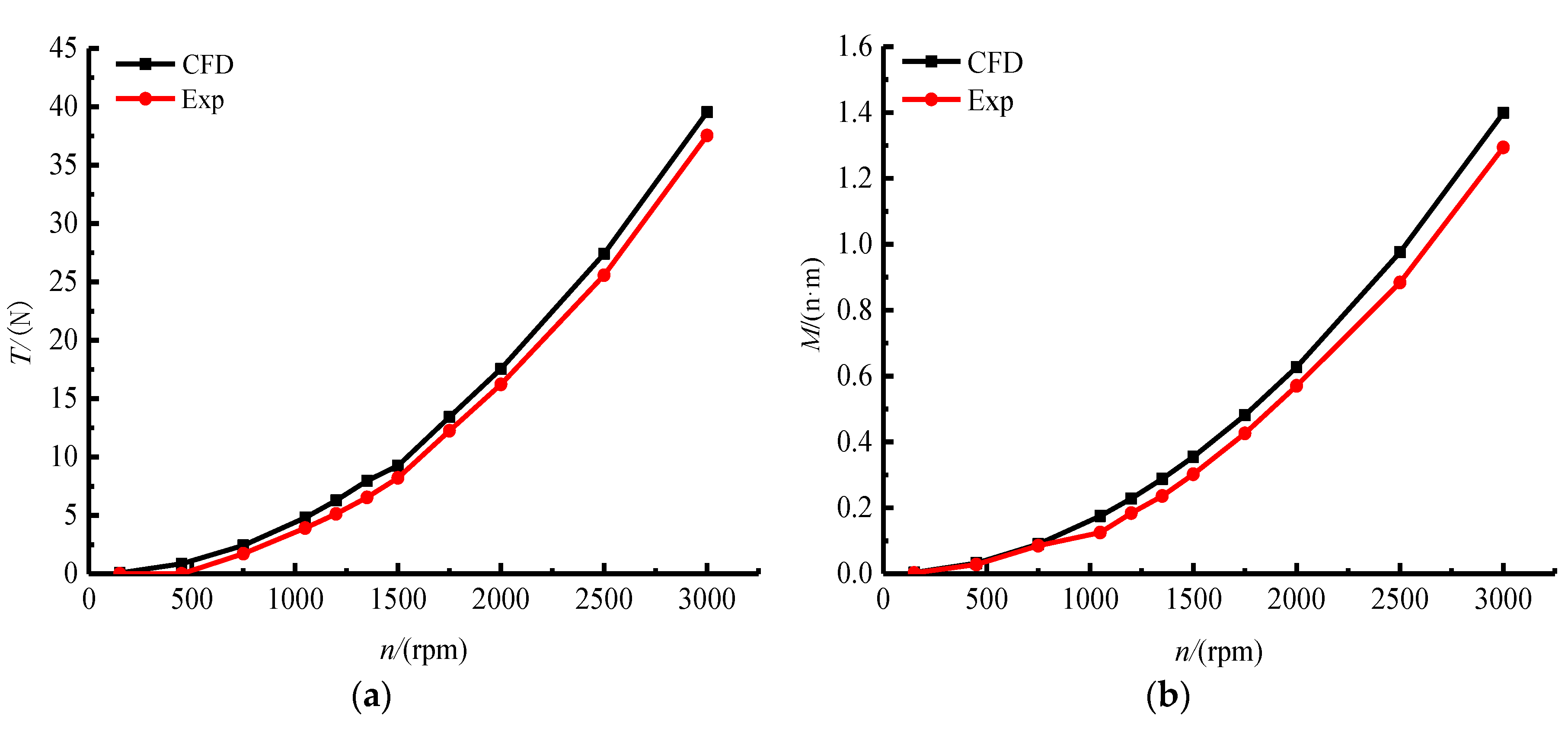
4. Water-Jet Propulsion Experiments
4.1. Test Platform and Main Equipment
4.2. Test Results
5. Calculation Results and Analysis
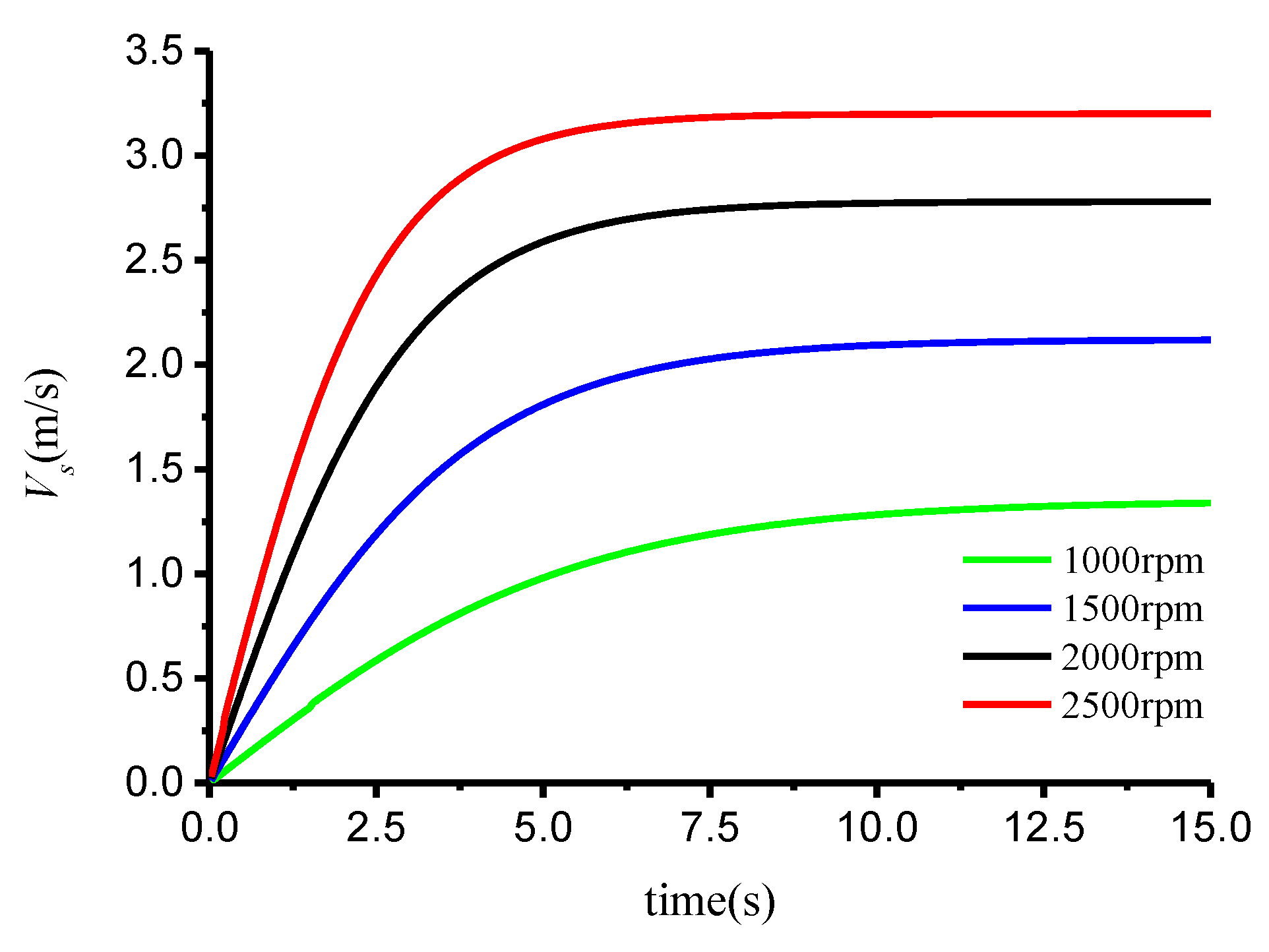
5.1. Analytic Solutions of the Submerged Speed
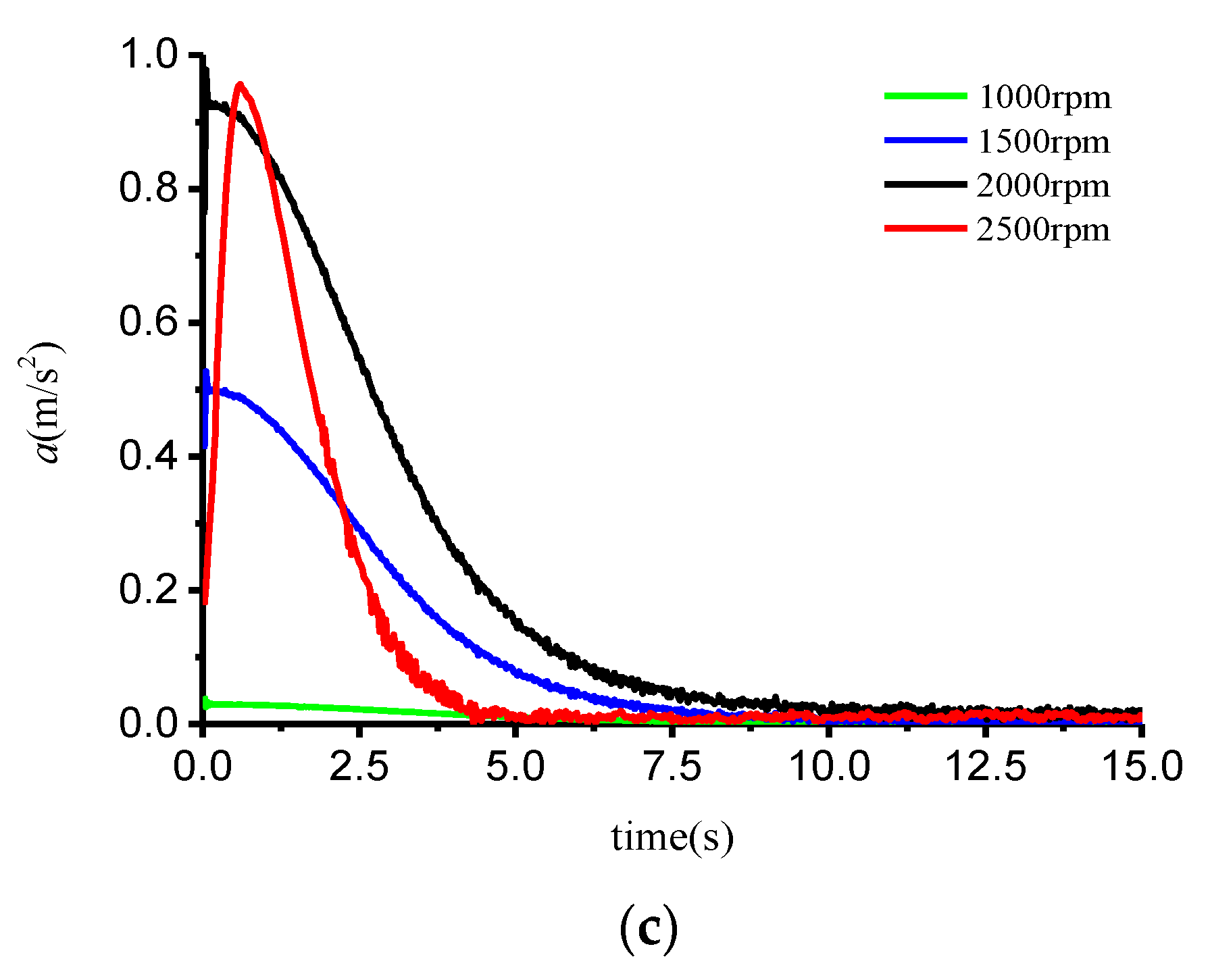
5.2. Analysis of the Results of Accelerated Motion from Propulsion
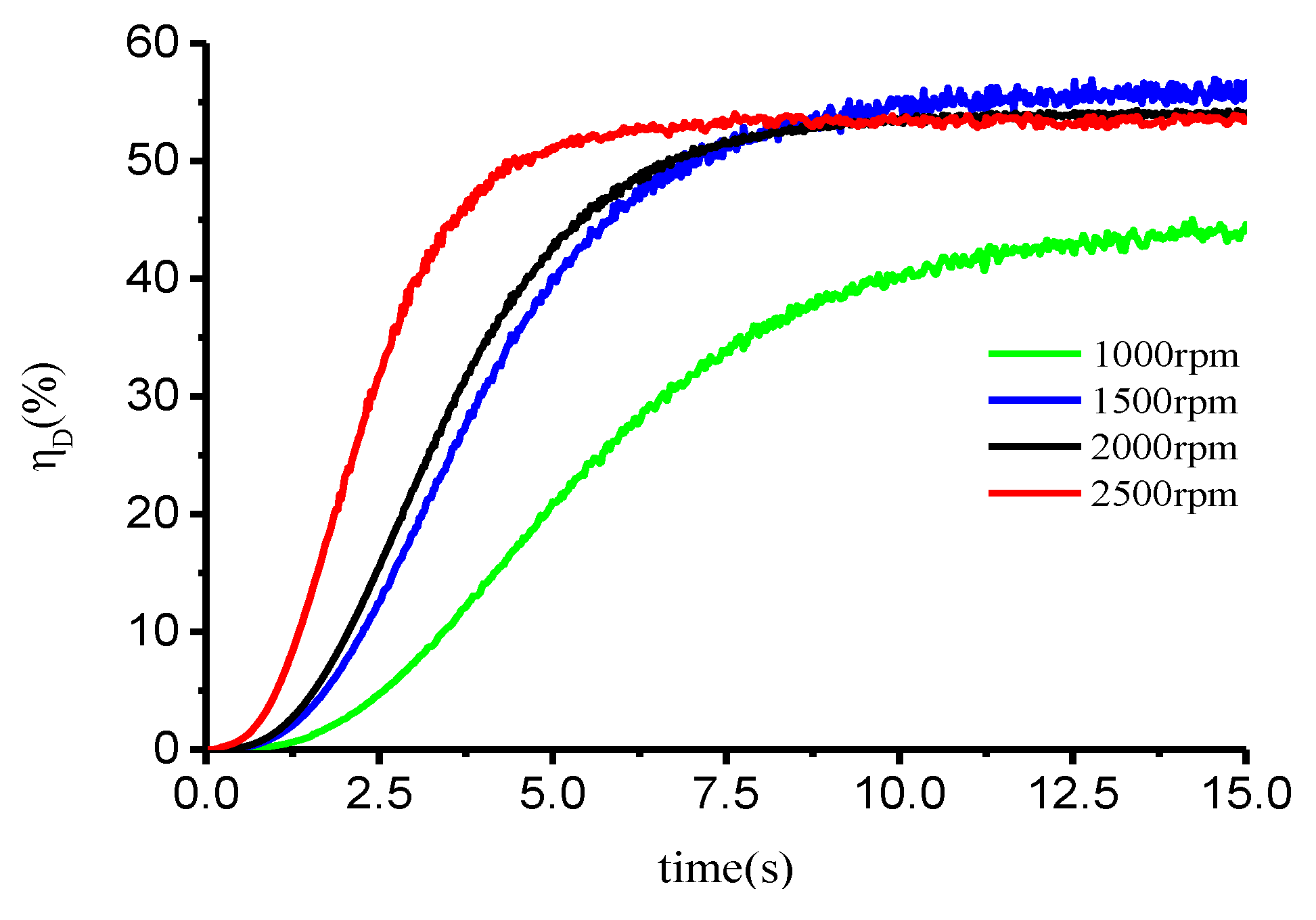
5.3. Analysis of Water-Jet Pump Performance During Acceleration
6. Conclusions
- (1)
- Based on the momentum theorem, a dynamics model of water-jet propulsion with a screw mixed-flow pump under the conditions of direct sailing variable acceleration coupled with pump geometry and hydraulic parameters was established. The analytical solution of the submerged speed of a submersible in variable acceleration motion with respect to time was obtained, and the variation of the submerged speed with respect to time satisfied a hyperbolic tangent function distribution.
- (2)
- The variation of the submerged speed with respect to time was considered the initial condition of the numerical calculation of other dynamics parameters, realized via a UDF. Utilizing this method, the strongly nonlinear relationships between the acceleration, drag, net thrust, propulsion torque, and efficiency with respect to time were revealed.
- (3)
- The values of submerged speed with respect to time satisfied a hyperbolic tangent function distribution. The variation of the submerged drag with time was similar to the step response of a second-order system with critical damping. The net thrust and acceleration increased sharply at the beginning and then decreased gradually to zero, especially at different rotation speeds of the water-jet pump.
- (4)
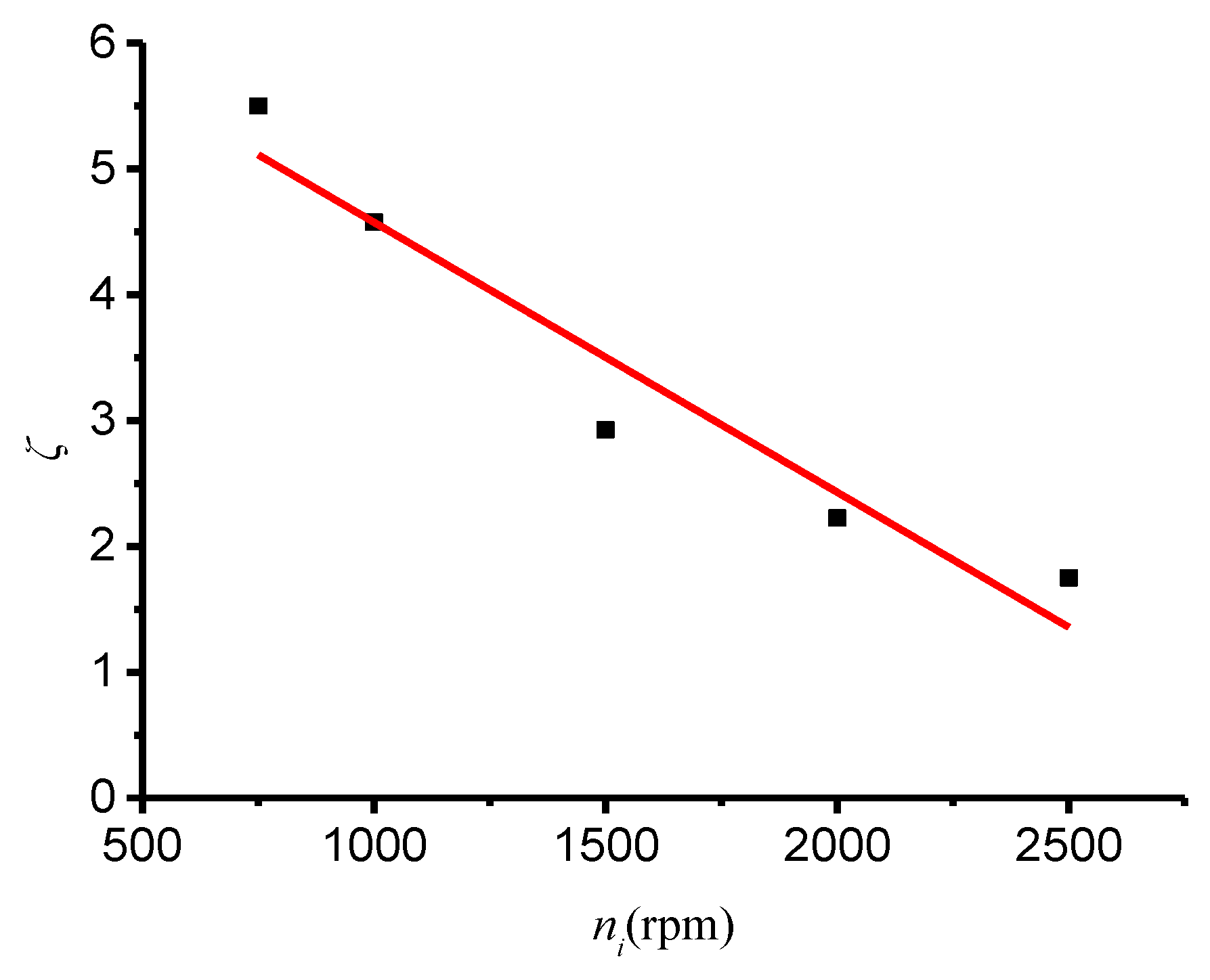
- Based on the principle of automatic control, the relationship between the submerged speed and time of the submersible was found to be similar to the step transient response of the first-order system, and the time constant ζ was related with the rotation speed of the water-jet pump.
Author Contributions
Funding
Conflicts of Interest
References
- Sherbrooke, Q.; Simon, F.; Stéphane, M. Alain Desrochers. 3D Unsteady simulation of a planning hull propelled by a water-jet pump system. In Proceedings of the ASME 2012 Fluids Engineering Summer Meeting FEDSM2012, Rio Grande, Puerto Rico, 8–12 July 2012. [Google Scholar]
- Eslamdoost, A.; Larsson, L. Water-jet Propulsion and Thrust Deduction. J. Ship Res. 2014, 58, 201–215. [Google Scholar] [CrossRef]
- Weinblum, G.P. The Thrust Deduction. Nav. Eng. J. 1951, 63, 363–380. [Google Scholar] [CrossRef]
- Sun, C.L.; Wang, Y.S. Mechanism of negative thrust deduction factor of water-jet hull. Chin. J. 2011, 26, 177–185. [Google Scholar]
- Shen, H.C.; Yao, H.Z.; Yang, R.Y. Model experiments of ship hull integrated propulsor hydrodynamic interactions and assessment analysis of thrust deduction characteristics. J. Ship Mech. 2007, 4, 487–497. [Google Scholar]
- Beveridge, J.L. Analytical prediction of thrust deduction for submarines and surface ships. J. Anal. Predict. Thrust Deduc. Submar. Surf. Ships 1969. [Google Scholar]
- Lin, T.Y.; Kouh, J.S. On the scale effect of thrust deduction in a judicious self-propulsion procedure for a moderate-speed containership. J. Mar. Sci. Technol. 2015, 20, 373–391. [Google Scholar] [CrossRef]
- Bazhenov, V.A.; Pogorelova, O.S.; Postnikova, T.G. Intermittent transition to chaos in vibroimpact system. J. Appl. Math. Nonlinear Sci. 2018, 3, 475–486. [Google Scholar] [CrossRef] [Green Version]
- Bazhenov, V.A.; Lizunov, P.P.; Pogorelova, O.S. Stability and Bifurcations Analysis for 2-DOF Vibroimpact System by Parameter Continuation Method. Part I: Loading Curve. J. Appl. Nonlinear Dyn. 2015, 11, 3. [Google Scholar] [CrossRef]
- Yong, Q.; Yuyan, L.; Jingru, L. Simulation analysis of resource-based city development based on system dynamics: A case study of Panzhihua. J. Appl. Math. Nonlinear Sci. 2018, 3, 115–126. [Google Scholar] [Green Version]
- Akkerman, I.; Dunaway, J.; Kvandal, J. Toward free-surface modeling of planning vessels: Simulation of the Fridsma hull using ALE-VMS. J. Comput. Mech. 2012, 50, 719–727. [Google Scholar] [CrossRef]
- Fridsma, G.A. Systematic study of the rough-water performance of planning boats. Irregul. Waves-Part II J. 1971, 11–12. [Google Scholar]
- Sun, H.; Faltinsen, O.M. Dynamic motions of planing vessels in head seas. J. Mar. Sci. Technol. 2011, 16, 168–180. [Google Scholar] [CrossRef]
- Minisci, E.; Vasile, M.; Liqiang, H. Multidisciplinary Design of a Micro-USV for Reentry Operations. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar] [CrossRef]
- Xiong, J.; Li, D.; He, Y. Active Quasi-LPV Modeling and Identification for a Water-Jet Propulsion USV: An Experimental Study. J. IFAC-Pap. OnLine. 2015, 48, 1359–1364. [Google Scholar] [CrossRef] [Green Version]
- Han, J.D.; Xiong, J.F.; He, Y.Q. Nonlinear Modeling for a Water-Jet Propulsion USV: An Experimental Study. IEEE Trans. Ind. Electron. 2017, 64, 3348. [Google Scholar] [CrossRef]
- Fan, S.Y.; Peng, Y.S. Maneuverability calculation of nonlinear ships. J. Ship Eng. 1982, 14, 19–26. [Google Scholar]
- Zhanyi, L.; Baowei, S.; Qiaogao, H. Applying CFD Technique to Calculating Successfully Hydrodynamic Performance of Water-Jet Pump. J. Northwestern Polytech. Univ. 2010, 28, 724–729. [Google Scholar]
- Gao, H.; Lin, W.; Du, Z. Numerical flow and performance analysis of a water-jet axial flow pump. J. Ocean Eng. 2008, 35, 1604–1614. [Google Scholar] [CrossRef]
- Shibin, J.; Puyu, C.; Yang, W. Numerical analysis on velocity field of water-jet pump under non-uniform inflow. J. Drain. Irrig. Mach. Eng. 2016, 34, 115–121. [Google Scholar]
- Qiongfang, Y. Computational Fluid Dynamics Analysis of Effects of Number of Pump Blades on Water-jet Propeller Performance. J. Mech. Eng. 2009, 45, 222–228. [Google Scholar]
- Shih, T.; Liou, W.; Shabbir, A. A New Kappa-Epsilon Eddy Viscosity Model for High Reynolds-Number Turbulent Flows; NASA Center for AeroSpace Information: Linthicum Heights, MD, USA, 1995.
- Zhian, R.; Dian, H.; Hongjie, X. Several turbulence models and their application in FLUENT. J. Chem. Ind. Equip. Technol. 2009, 30, 38–40. [Google Scholar]
- Haiwen, T.; Jianglong, S. Numerical calculation of submarine resistance and flow field based on CFD. J. Ship Sci. Technol. 2012, 34, 19–25. [Google Scholar]
- Han, Z.; Reitz, R.D. Turbulence Modeling of Internal Combustion Engines Using RNG κ-ε Models. J. Combust. Sci. Technol. 1995, 106, 267–295. [Google Scholar] [CrossRef]
- Qingping, L.; Dunsong, X. Experimental study on external characteristics of helical axial flow multiphase pumps. J. Eng. Thermophy. 2000, 21, 451–455. [Google Scholar]
- Wei, H. Numerical Research on Multiphase Flow Characteristics and Flotation Dynamics in Flotation Machine. Ph.D. Thesis, Lanzhou University of Technology, Lanzhou, China, 2009. [Google Scholar]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Xin, B.; Xiaohui, L.; Zhaocun, S. A vectored water-jet propulsion method for autonomous underwater vehicles. J. Ocean Eng. 2013, 74, 133–140. [Google Scholar] [CrossRef]
- Qiongfang, Y.; Yongsheng, W. Low Noise Design Mechanism and Design Application of Pump-Jet Propeller; Huazhong University of Science and Technology Press: Wuhan, China, 2016. [Google Scholar]
- Wenjun, J. Fluid Mechanics Study on The Coefficients of Sea Resistance. J. Mar. Sci. Technol. 2002, 20, 17–20. [Google Scholar]
- Jingping, X.; Ying, W. Development and application of comprehensive experimental equipment for automatic control principle. J. Exp. Technol. Manage 2017, 34, 104–108. [Google Scholar]
- Shoujun, X. National Defense Science and Technology Nomenclature, Ship; Atomic Energy Press: Beijing, China, 2002. [Google Scholar]

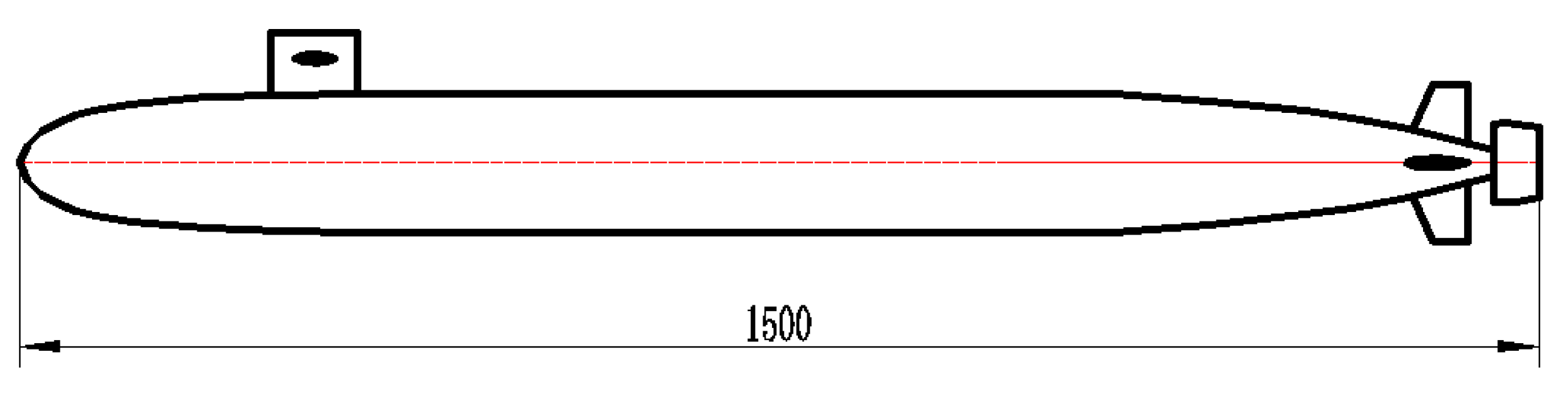





| Parameters | Ls/(mm) | Rmax/(mm) | Lc/(mm) | Lw/(mm) | Lh/(mm) |
|---|---|---|---|---|---|
| Value | 1500 | 136 | 247.5 | 746.5 | 76.66 |
| Parameters | Q0/(m3/s) | H0/(m) | η0/(%) | n0/(rpm) | ns |
|---|---|---|---|---|---|
| Value | 0.00383 | 1.303 | 80 | 1500 | 277.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, W.; Shang, T.; Su, M.; Gong, C.; Li, R.; Meng, B. Direct Sailing Variable Acceleration Dynamics Characteristics of Water-Jet Propulsion with a Screw Mixed-Flow Pump. Appl. Sci. 2019, 9, 4194. https://doi.org/10.3390/app9194194
Han W, Shang T, Su M, Gong C, Li R, Meng B. Direct Sailing Variable Acceleration Dynamics Characteristics of Water-Jet Propulsion with a Screw Mixed-Flow Pump. Applied Sciences. 2019; 9(19):4194. https://doi.org/10.3390/app9194194
Chicago/Turabian StyleHan, Wei, Ting Shang, Min Su, Chengyong Gong, Rennian Li, and Bin Meng. 2019. "Direct Sailing Variable Acceleration Dynamics Characteristics of Water-Jet Propulsion with a Screw Mixed-Flow Pump" Applied Sciences 9, no. 19: 4194. https://doi.org/10.3390/app9194194
APA StyleHan, W., Shang, T., Su, M., Gong, C., Li, R., & Meng, B. (2019). Direct Sailing Variable Acceleration Dynamics Characteristics of Water-Jet Propulsion with a Screw Mixed-Flow Pump. Applied Sciences, 9(19), 4194. https://doi.org/10.3390/app9194194




