1. Introduction
Grid-connected photovoltaic (PV) systems have acquired quite a good proportion of usage among different renewable energy sources. Every year, the amount of grid-feeding PV systems in use is increasing. As a result, it is becoming highly required that the grid-connected PV systems operate optimally to perform stable grid operation and meet user demand.
One of the primary models for grid-connected solar PV is single-stage model that uses only a single converter. Such converters either can be voltage source or current source inverters. The control of the converters requires inner current control loops and an outer voltage control loop. The reference of the outer voltage control loop can be found by maximum power point tracking (MPPT) technique, and the output of the voltage control loop can be used a reference for the inner current control loop. These controllers require tuning of their respective parameters for optimal operation of the system. Development of different controllers for optimal operation of grid-connected distributed generation or PV systems has been widely described in different literature. Touqeer et al. [
1] proposed a grasshopper optimization algorithm-based optimal power flow controller for a grid-connected Distributed Generation (DG) system. The authors only tuned the outer control loop while keeping fixed internal loop values, which makes the system difficult to tune when the values of internal loop gain parameters are unknown. Sharifian et al. [
2] proposed a reactive power control and adaptive predictive current control strategy, where the Reactive Power controller (RPC) generates the reactive current using a PI controller. Tafti et al. [
3] proposed a three-level neutral point clamped inverter instead of a two-level Voltage Source Inverter (VSI) with voltage-oriented control strategy using proportional resonant (PR) controller. A fictitious reference iterative tuning method using particle swarm optimization for tuning a DC link voltage controller was proposed in [
4]. In [
5] authors discussed single-stage topology with a current source inverter (CSI) with MPPT and double tuned resonant filter. They also proposed series addition of a small DC link inductor with double-tuned resonant filter to eliminate harmonics. The authors used proportional resonant controller for voltage and current control loop. Touil et al. [
6] proposed sliding mode control to force the output voltage of the PV and grid power factor to follow a certain trajectory reference. This requires rigorous calculation for determination of control law. Azghandi et al. presented a precise phasor model and employed an active power loop cascaded with an inner reactive power loop [
7]. Few works also proposed methodologies to work under fault conditions. DC link voltage control of a grid-connected PV system with enhanced fault ride through capability enhancement was proposed by Mohamed et al. [
8]. The proposed control scheme includes control without MPPT which activates when DC link voltage exceeds the nominal value. In [
9], Khawla et al. proposed a three-phase grid-connected PV system working with MPPT and non-MPPT mode to work under grid fault mode. Recently, Islam et al. [
10] designed a proportional resonant controller with resonant harmonic compensator for a grid-connected photovoltaic system. The authors have also proposed a switch-type fault current limiter for fault ride through a capability which can work under asymmetrical faults also.
Although different methodologies have been proposed by different authors, almost all of them have considered the controllers with internal gain parameters; these works have rarely discussed any systematic approach for tuning of those parameters irrespective of the controller type, which is one of the most important issues while designing a successful controller. Because trial-and-error or Ziegler–Nichols methods often suffer from huge time consumption and optimal parameter selection uncertainty, it is highly required to discover a systematic optimal tuning process which can guarantee satisfactory results within minimum time and computation effort. Also, as the outer voltage control loop and the inner current loop are cascaded in nature, separate tuning will take time to get optimal results. Hence, simultaneous tuning is required to tune optimally. Moreover, the system response can be suboptimal when applying a conventional PI controller due to the fixed-order integrator. Hence the system can be more sophisticated by applying a well-tuned fractional order PI (FOPI) controller due to its capability of dealing with fractional order integrators. Again, this needs a systematic approach to tune the respective parameters.
Thus, in this work, a novel plant propagation algorithm (PPA)-based simultaneous and cascaded outer DC link voltage and inner current loop controller is proposed. The proposed method is applied with fractional order PI controller instead of the conventional PI controller due to its increase in degree of freedom to control more precisely. The considered objective function consists of two terms (integral of absolute time error and peak difference) which effectively reduces the overshoot, settling time and steady-state error if the controller is tuned properly. The proposed controller is also compared with two other metaheuristic algorithms, namely particle swarm optimization (PSO) and elephant herding optimization (EHO). Using PSO, conventional PI is tuned; using EHO, FOPI is tuned. The differences in results and reasonings are covered in detail to understand the science behind better results with PPA over PSO and EHO. As systems are becoming more and more digitized, the real-time simulation is also required to develop appropriate digital twins to emulate physical systems in the cyber domain. A successful development of an optimal controller in real-time simulators can lead to such achievements proficiently. Thus, the proposed controllers were tested in real-time simulator OPAL-RT. The performance of the proposed controller was also extended by analysis of the total harmonic distortion (THD) of the inverter current and performance during voltage sags and varied irradiance in grid-connected mode.
The paper is arranged in the following order.
Section 2 describes the system, system components, and mathematical modeling of the considered system along with perturbation-and observation-based MPPT algorithm. In
Section 3 the objective function, working flow chart, and algorithms are discussed in detail.
Section 4 deals with the experimental setup, parameter selection, and simulation results. Analyses of results and comparative analysis of the experimented optimization methods are also covered in the same section. In
Section 5, performance of the selected controller is also tested under varied conditions and in terms of THD criteria. Finally,
Section 6 concludes and summarizes the paper with a direction to future prospective work.
3. Objective Function
The system consists of cascaded outer voltage and inner d-axis current and reactive power/q-axis current control loops. Due to the cascaded nature of the control system, it is highly required that the inner loop of the designed controller must follow the outer loop with a minimum amount of error. Generally, the errors are calculated using four renowned methods known as IAE, ISE, ITSE, and ITAE [
15]. IAE and ISE put equal importance on error irrespective of the time, but ITSE and ITAE put different weight on error with respect to time due to the presence of time in the objective function. In ITSE, due to presence of square term, error drops drastically as the error converges to zero. ITAE is free from such a problem, as it puts different weight to error with respect to time without squaring the error. However, only using such criterions sometimes does not guarantee lesser peak overshoot. Hence, a peak difference term is also added in the objective function to minimize the peak overshoot along with ITAE.
The proposed objective function is as follows:
where
Each portion of the Equation (10) is comprised of three PI/FOPI controllers’ responses. That means three peak differences are calculated for outer voltage and inner current control loops (d- and q-axis), and that three ITAE are calculated as well.
3.1. Optimization Process
To begin the optimization, the initialization of the system parameters and parameters associated with optimization algorithms must be initiated. Once the initialization is done, the system will be directly simulated in the RTLAB-based Simulink environment, the system responses will be sent to the MATLAB environment, and then optimization algorithms will update the next iteration solutions and feed them into the Simulink environment again. The whole system operates in an iterative manner until the termination criteria or maximum number of generation (iterations) is reached.
Figure 6 describes the operational flowchart for finding the optimal values. The core of the process is the optimization algorithm. In the next section, a brief introduction of three applied optimization algorithms are given.
3.2. Particle Swarm Optimization
Particle swarm optimization (Algorithm 1) [
16] is a population-based stochastic optimization technique developed by Eberhart and Kennedy in 1995. The essence of the PSO can be understood by the following equations and the pseudocode:
where
and
are particle positions in the g
and
generations, respectively.
and
are particle velocities in g
and
generations, respectively.
is known as inertia and generally varies within 0 to 1.
and
are known as cognitive and social parameters, respectively, and are generally within the range of 0–2.
is a random number within the range of 0–1.
and
are best-remembered individual and swarm positions, respectively.
| Algorithm 1. PSO |
| 1: Initialize X = Particle/Solution and v = Velocity |
| 2: while gen < max_gen |
| 3: for each particle x in X do |
| 4: fx = f(x) |
| 5: if fx is better than f(xBest) |
| 6: xBest = x; |
| 7: end |
| 8: gBest = best x in X |
| 9: for each particle x in X do |
| 10: update velocity and particle position using Equations (11) and (12) |
| 11: end for |
| 12: end while |
3.3. Elephant Herding Optimization
Elephant herding optimization (Algorithm 2) [
17] was proposed by Gai-Ge Wang, Suash Deb and Leandro dos S. Coelho in 2015. The algorithm is inspired by the herding behavior of the elephant group. Elephants of different clans live together under the leadership of a matriarch, and male elephants leave the group when they become adults. These two behaviors are modeled into this algorithm, known as clan updating and separating operators. The position of an elephant updates the updating operator. Next, the population diversity is created by separating the operator. The required equations for this optimization given below.
Clan updating operator:
where
and
are updated and previous positions of elephant
j in clan
ci.
is a scale factor.
is the matriarch in the clan.
is a uniformly distributed random number.
The fittest elephant in each clan should be updated using Equation (14):
where
and
.
Separating Operator:
where
.
| Algorithm 2. EHO |
| 1: Initialize X=Particle/Solution |
| 2: while gen < max_gen |
| 3: Sort all the elephants according to the fitness |
| 4: Implement Clan updating operator by Equations (13) and (14) |
| 5: Implement Separating operator using Equation (15) |
| 6: Evaluate the population by updated positions |
| 7: gen = gen + 1; |
| 8: end while |
3.4. Plant Propagation Algorithm
The plant propagation algorithm (Algorithm 3) [
18] is inspired by propagating plants akin to strawberry plants (Salhi and Fraga, 2011). PPA resembles the way plants, particularly strawberry plants propagate. PPA consists of four simple steps. In step 1, fitness values are normalized using the following equation:
where
j represents the corresponding population. In the next step, few offspring are made to explore the decision space. The number of runners (offspring) created by a solution is proportionate to its normalized fitness value and it is calculated as:
where
and
indicates the ceiling of
x.
Next, the distance between the original and the new solutions is calculated as follows:
where
is the dimension of the problem.
Then, this distance is used to generate new solutions as follows:
where
and
are upper and lower bounds of the solution variable, respectively.
| Algorithm 3. PPA |
| 1: Initialize X = Particle/Solution |
| 2: while gen < max_gen |
| 3: evaluate the fitness value of solutions |
| 4: for j = 1 to M |
| 5: evaluate normalized fitness using Equation (16) |
| 6: evaluate the number of new solutions generated by Equation (17) |
| 7: for i = 1 to N |
| 8: evaluate the length of the offspring by Equation (18) |
| 9: end for |
| 10: for r = 1 to |
| 11: for i = 1 to N |
| 12: evaluate the decision variable ith of new solution rth generated by Equation (19) |
| 13: end for |
| 14: end for |
| 15: end for |
| 16: Reform the new population with M best solutions |
| 17: end while |
Each of the above algorithms requires an initial value of candidate solutions; an initial velocity is also required for PSO. This can be written as a matrix for ease of computation procedure:
where,
=
jth solution, i = population size, and
N = problem dimension.
4. Experimental Setup and Simulation Results
The experiment was set up with the data given in
Table 1. For the machine-In-loop experiment, the help of OPAL-RT (OP5600) real-time digital simulator was taken. The model was built in RTLAB using Simulink-based toolbox, and optimization source-codes were written in MATLAB script. The experimental setup is shown in
Figure 7.
For a global solution, a closed search space is required, or in other words, the solutions must be bounded within where the optimal value can be tracked. Mathematically,
However, in some systems if the search space boundary is unknown then it is difficult to find an initial value for starting the optimization. Hence, before conducting the actual optimization process, we randomly ran the simulation 30 times with a random data range to find a valid search space within where we can find the optimal solution. After such trials, the following range was found for each of the parameters given in
Table 2.
In every metaheuristic algorithm, it is required to deal with some parameters to control the convergence speed of the algorithm. These parameters are generally user-defined parameters, which means the user can set those parameters and examine for which set of values optimal results are achieved. For example, for PPA algorithm the only such parameter is
, which controls the number of runners created by a solution. If this number increases, a solution will create more runners, but simulation time will increase. Hence it should be chosen in such a way that optimal result is found under minimum possible simulation time. For the considered algorithms, the parameters and their values are given in
Table 3.
Also, the population number and number of generation were taken as 20 and 30, respectively.
In
Figure 8, the simulation figure in the RT-LAB environment has been shown. Unlike Simulink environment, RTLAB-based simulator requires two different blocks for real-time operation. The first block is sm_computation block, where the main system and corresponding controllers were developed. In the second block, sc_user_interface, the input for the system and data visualization blocks are drawn. Fractional order PI controller has been implemented using FOMCON toolbox. The inputs of the system were the solar irradiance and temperature.
After the completion of the simulation, the best fitness value can be obtained from
Figure 9 and it can be understood that PPA outperforms EHO- and PSO-based controllers. For PSO, conventional PI controller was used; for EHO and PPA, FOPI was used. The reason behind the better solution from PPA is due to the creation of multiple runners from each solution (Equation (17)) and storing only the best population in each generation. In this problem we have chosen maximum value of
as No. of population/5, i.e., 20/5 = 4.
Hence each of the solutions can generate a maximum of four different solutions from its original solution. As a result, in each generation, the total number for population can vary from 20–80. But to maintain uniformity, after completion of each generation only the 20 best populations are chosen from the 20–80 populations. The process repeats in each iteration.
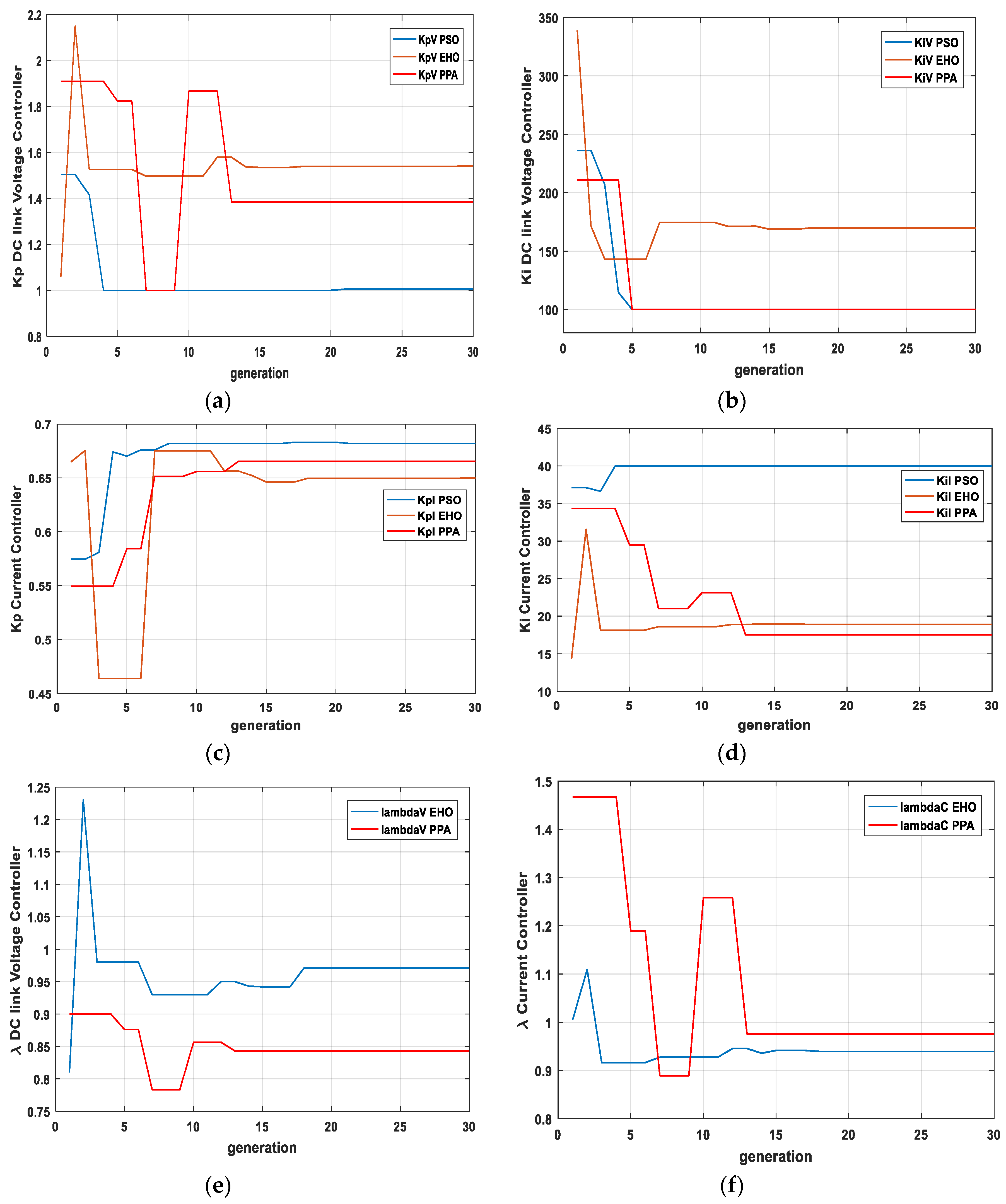
Figure 10 shows the gain parameter trajectory over time. For PSO
Kp (DC link voltage controller) gain value changes until the 21st generation, But
Ki (DC link voltage controller) gain reaches the minimum value of the range at the fifth generation and could not improve further.
Kp (current control loop) for PSO finally stops changing at iteration 21, whereas
Ki (current control loop) reaches the maximum value at the fourth generation.
For EHO, there is no such incident of reaching the maximum or minimum values without further improvement.
In the case of PPA, there is only such a case (Ki (DC link voltage controller)) where it reaches the minimum value and could not improve further. However, due to the increase of the degree of freedom in control action with the help of parameter, it still improves the overall response and hence reduces the error.
Table 4 represents the optimal values of the controller parameters, in other words, the final values of the gain parameters from the trajectory plot of
Figure 10.
The optimal response of the DC link voltage controller, d-axis current and reactive power/q-axis current control loop is given in
Figure 11. Optimization was done under the maximum irradiance of 1000 w/m
2 and a fixed temperature of 25 °C. In
Figure 11b, unlike
Figure 11a,c, there are different individual reference values for each of the optimization algorithms. This is because the reference value for the d-axis current controller comes from the output of the DC link voltage controller. As responses from different optimization techniques provide different outputs from the DC link voltage controller, the reference value also changes for the d-axis current controller.
The settling time was calculated by finding the response when it comes to the
band of the desired response. The peak overshoot was calculated using:
As the reference value for the reactive power controller is 0 (unity power factor condition), hence the percent peak overshoot for this term was calculated using a modified equation as follows:
The value of
is an arbitrary small number, which should be the same, irrespective of the algorithm to maintain uniformity. The time responses of
Figure 11, the objective function, and convergence speed are listed in
Table 5.
From
Table 5, in terms of objective function, PPA shows a better result over PSO and EHO. However, at the molecular level (settling time and peak overshoot) the performance can be varied. For example, settling time for DC link voltage controller and Iq/Q controller in terms of PPA is greater than PSO and EHO. Also, peak overshoot of Iq/Q for PPA-based controller is greater than PSO- and EHO-based controllers. Hence, it is difficult to say that PPA is better than EHO and PSO from the tabular analysis only. So, a spider graph-based [
19] approach is proposed to compare the indexes to find out the best algorithm.
4.1. Index Comparison
For index-based performance analysis, we have considered eight indexes where three are for settling time, three are for peak overshoot, one is for the objective function, and the remaining is for converge speed of the optimization algorithms. As the indexes have different ranges, we have normalized them using their maximum values and plotted them in the spider graph to compare the indexes. The normalized index value is calculated using the following equation:
From the above equation, it can be understood that any value which is closer to 1 represents the maximum value. As this is a minimization problem, the lesser the value is, the better the index is. Hence, the smaller boundary inside the solid line represents the better solution.
Also, from
Figure 12, it can be easily seen that although for some indexes PPA reaches the maximum value, extremely smaller values in other indexes makes the inner area smaller compared to other algorithms. So, it can be said that PPA outperforms PSO and EHO in this problem.
4.2. Boxplot Analysis for Global Optimization Analysis
The boxplot in
Figure 13. represents the fitness function values corresponding to the population at the final iteration (generation). The fitness functions for EHO and PPA are distributed over a narrow range, except for a few far points (red + markers) for EHO. Also, the means for PPA and EHO are much less than for PSO. The lowest value of the objective function is found using the PPA-based algorithm which validates the result from
Figure 9. The smaller range of objective function signifies that all the population has reached the global optimal solution.