A Steam Ejector Refrigeration System Powered by Engine Combustion Waste Heat: Part 1. Characterization of the Internal Flow Structure
Abstract
:1. Introduction
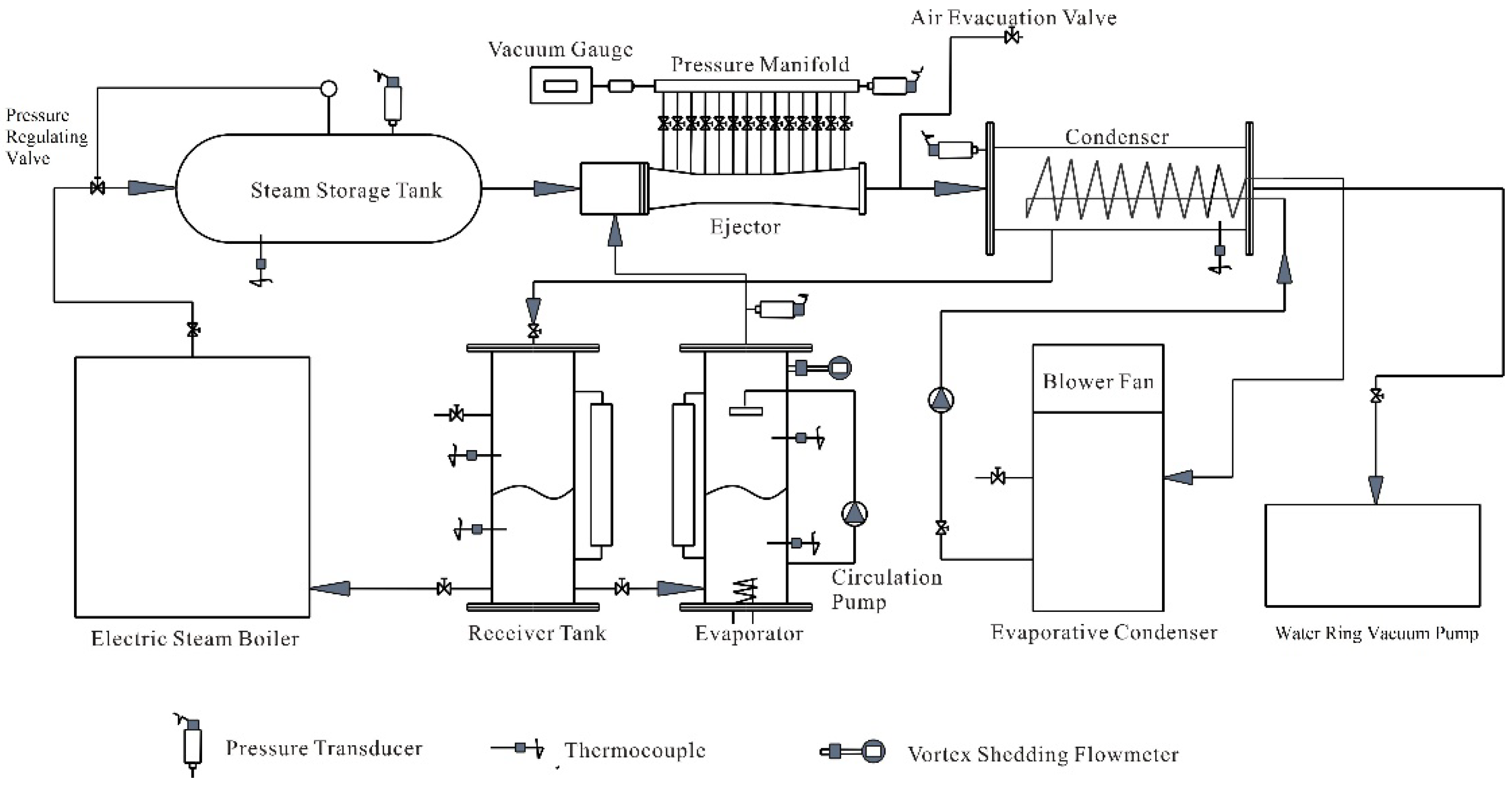
2. Experiment Instrumentation
3. Numerical Analysis of Flow Behaviour inside the Steam Ejector
3.1. Numerical Simulation Method
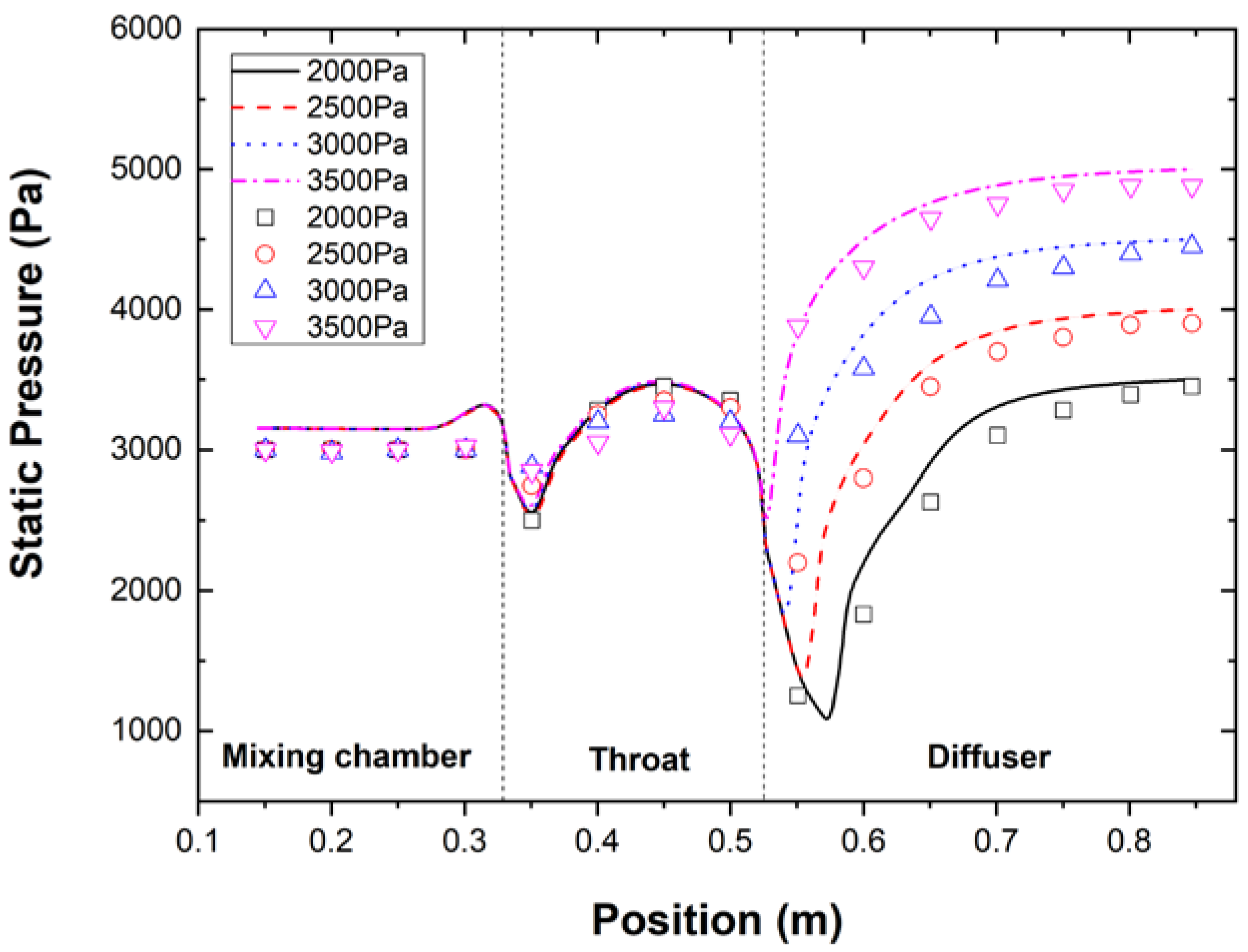
3.2. CFD Model Validation
3.3. Analysis of the Flow Structure inside the Steam Ejector
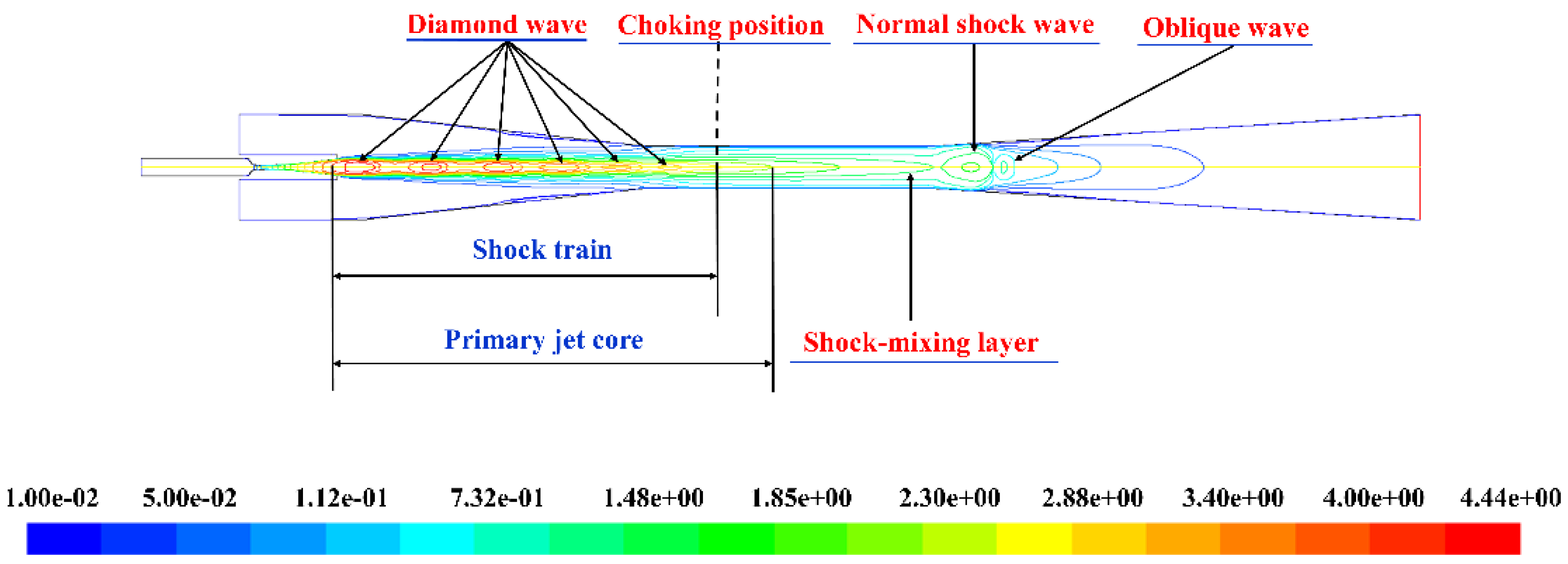
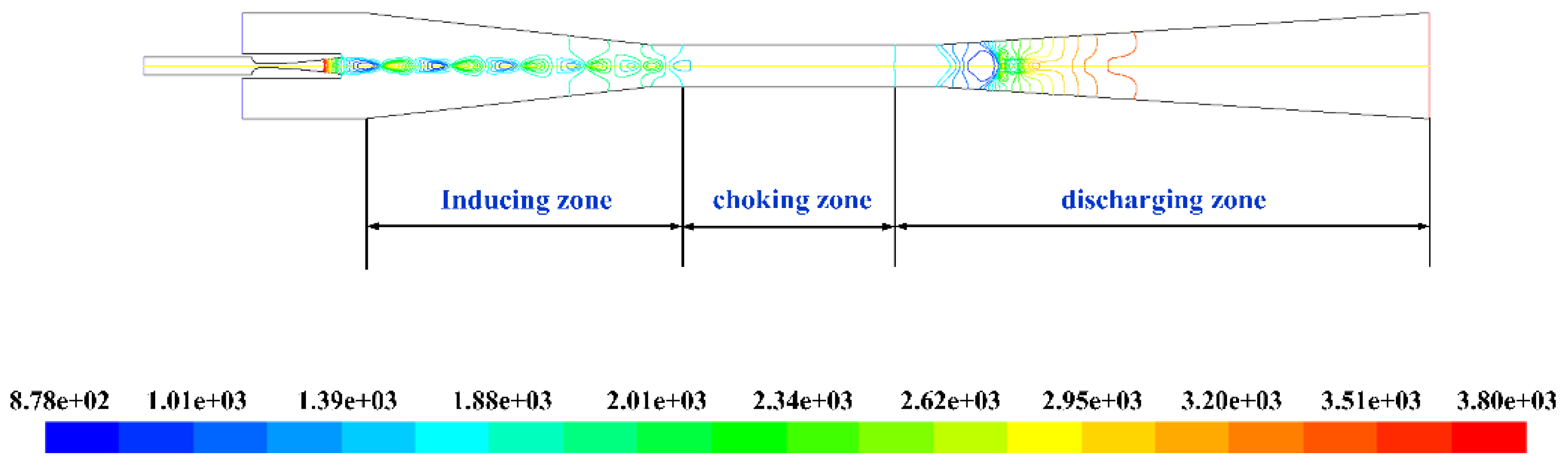
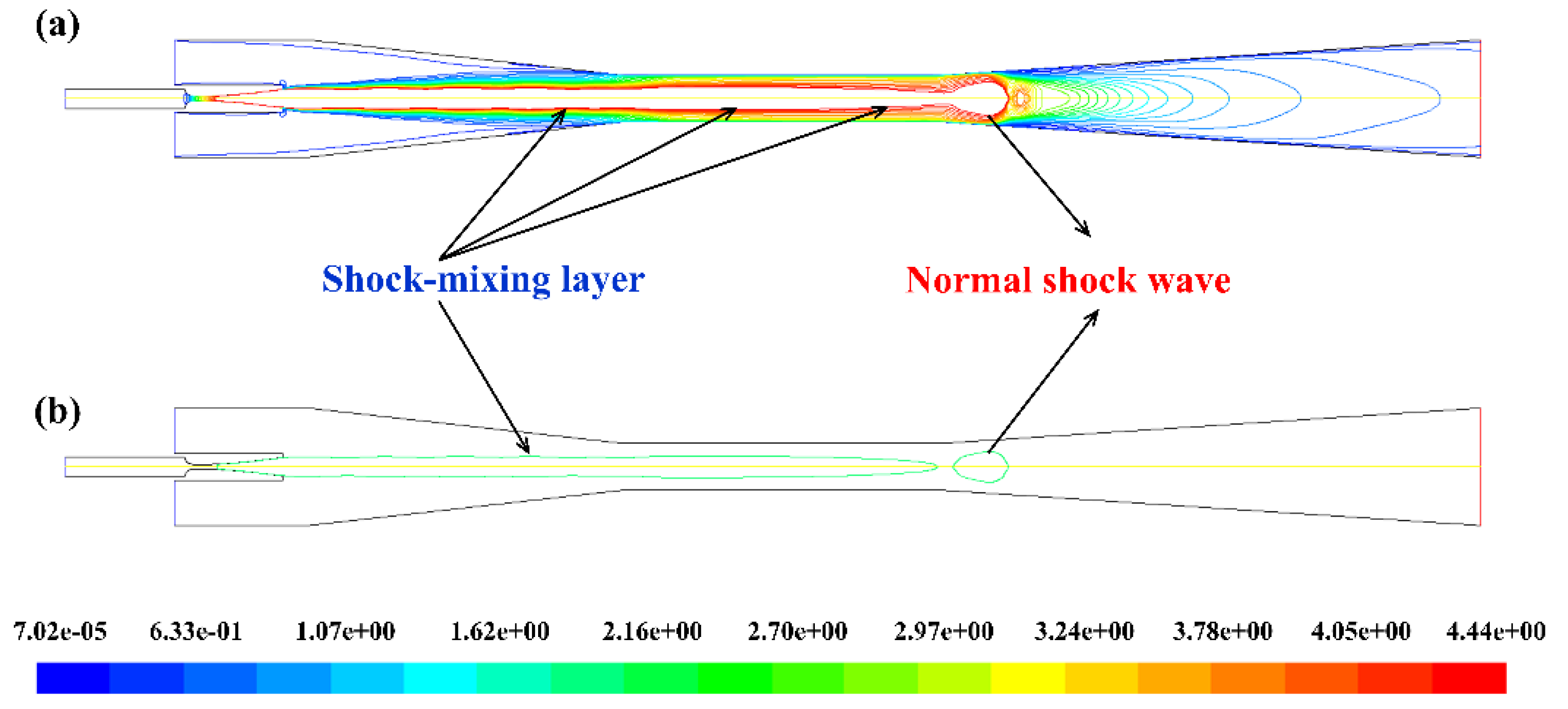
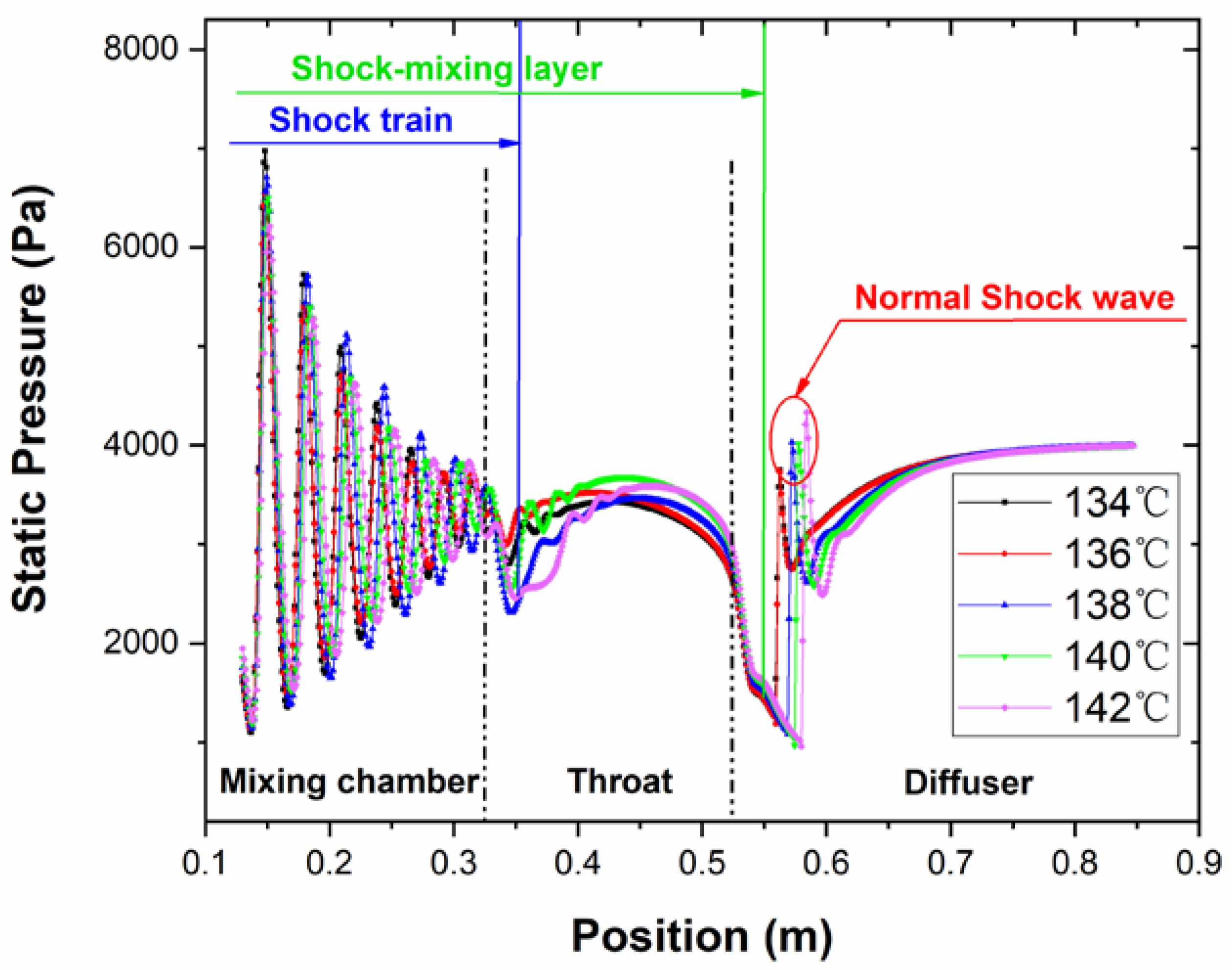
3.3.1. The Division of the Entire Flow Region
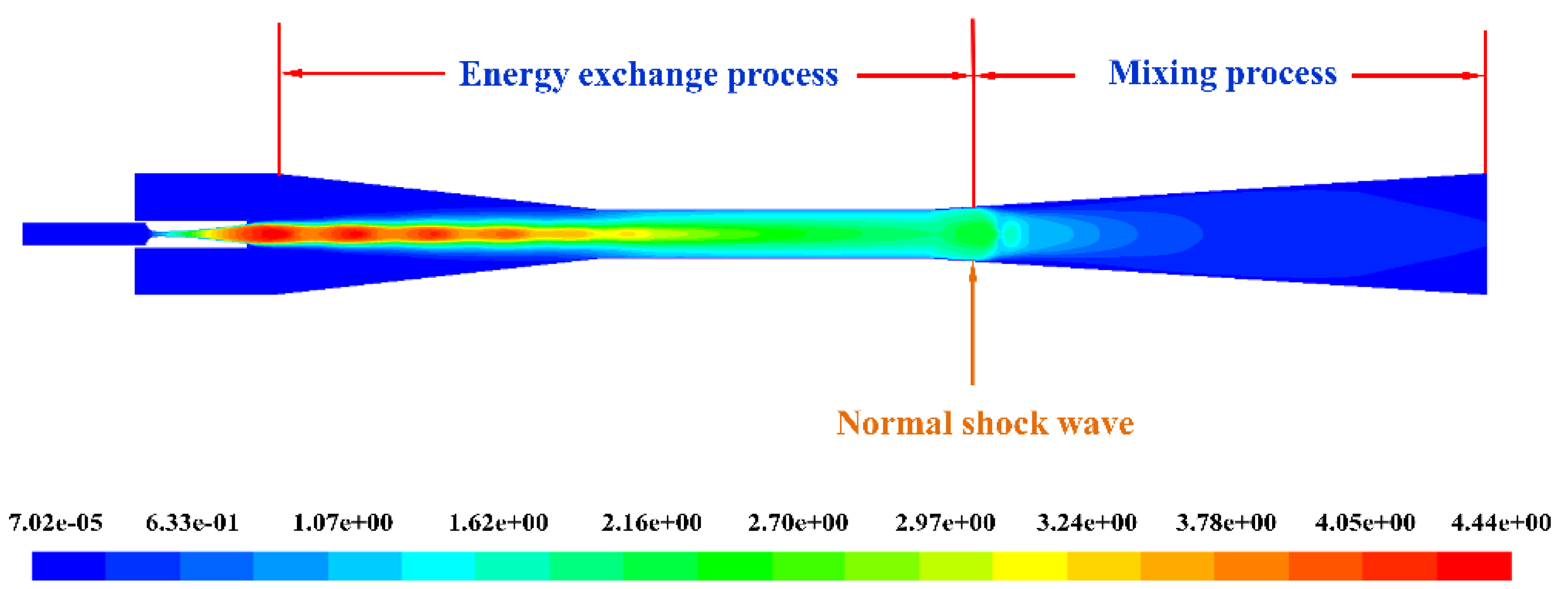
3.3.2. The Shock-Mixing Layer
4. Results and Discussion
4.1. The Influence of the Primary Fluid Temperature
4.2. The Influence of the Secondary Fluid Temperature
4.3. The Influence of the Back Pressure
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, L.; Cai, W.; Zhao, H.; Lin, C.; Yan, J. Experimentation and cycle performance prediction of hybrid A/C system using automobile exhaust waste heat. Appl. Therm. Eng. 2016, 94, 314–323. [Google Scholar] [CrossRef]
- Li, A.; Yuen, A.Y.C.; Chen, T.B.Y.; Wang, C.; Liu, H.L.; Cao, R.F.; Yang, W.; Yeoh, G.H.; Timchenko, V. Computational Study of Wet Steam Flow to Optimize Steam Ejector Efficiency for Potential Fire Suppression Application. Appl. Sci. 2019, 9, 1486. [Google Scholar] [CrossRef]
- Wu, H.; Liu, Z.; Han, B.; Li, Y. Numerical investigation of the influences of mixing chamber geometries on steam ejector performance. Desalination 2014, 353, 15–20. [Google Scholar] [CrossRef]
- Sumeru, K.; Martin, L.; Ani, F.N.; Nasution, H. Energy savings in air conditioning system using ejector: An overview. Appl. Mech. Mater. 2014, 493, 93–98. [Google Scholar] [CrossRef]
- Hamner, R.M. An Alternate Source of Cooling- the Ejector-Compression Heat-Pump. Ashrae J.-Am. Soc. Heat. Refrig. Air-Cond. Eng. 1980, 22, 62–66. [Google Scholar]
- Passengers, I. Determination of the ejector dimensions of a bus air-conditioning system using analytical and numerical methods. Appl. Therm. Eng. 2015, 90, 110–119. [Google Scholar]
- Chunnanond, K.; Aphornratana, S. Ejectors: Applications in refrigeration technology. Renew. Sustain. Energy Rev. 2004, 8, 129–155. [Google Scholar] [CrossRef]
- Poirier, M.; Giguère, D.; Sapoundjiev, H. Experimental parametric investigation of vapor ejector for refrigeration applications. Energy 2018, 162, 1287–1300. [Google Scholar] [CrossRef]
- Haghparast, P.; Sorin, M.V.; Nesreddine, H. The impact of internal ejector working characteristics and geometry on the performance of a refrigeration cycle. Energy 2018, 162, 728–743. [Google Scholar] [CrossRef]
- Sriveerakul, T.; Aphornratana, S.; Chunnanond, K. Performance prediction of steam ejector using computational fluid dynamics: Part 1. Validation of the CFD results. Int. J. Therm. Sci. 2007, 46, 812–822. [Google Scholar] [CrossRef]
- Wang, X.; Dong, J.; Li, A.; Lei, H.; Tu, J. Numerical study of primary steam superheating effects on steam ejector flow and its pumping performance. Energy 2014, 78, 205–211. [Google Scholar] [CrossRef]
- Riffat, S.B.; Jiang, L.; Gan, G. Recent development in ejector technology—A review. Int. J. Ambient Energy 2005, 26, 13–26. [Google Scholar] [CrossRef]
- Stoecker, W.F. Steam-Jet Refrigeration; McGraw-Hill: Boston, MA, USA, 1958. [Google Scholar]
- Chen, J.; Jarall, S.; Havtun, H.; Palm, B. A review on versatile ejector applications in refrigeration systems. Renew. Sustain. Energy Rev. 2015, 49, 67–90. [Google Scholar] [CrossRef]
- Besagni, G.; Mereu, R.; Inzoli, F. Ejector refrigeration: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 53, 373–407. [Google Scholar] [CrossRef] [Green Version]
- Sanaye, S.; Emadi, M.; Refahi, A. Thermal and economic modeling and optimization of a novel combined ejector refrigeration cycle. Int. J. Refrig. 2019, 98, 480–493. [Google Scholar] [CrossRef]
- Ahmadzadeh, A.; Salimpour, M.R.; Sedaghat, A. Thermal and exergoeconomic analysis of a novel solar driven combined power and ejector refrigeration (CPER) system. Int. J. Refrig. 2017, 83, 143–156. [Google Scholar] [CrossRef]
- Li, A.; Yeoh, G.H.; Timchenko, V.; Yuen, A.C.Y.; Wang, X. Numerical Study of Condensation Effect on a Steam Ejector by Wet Steam Model. In Proceedings of the Thirteenth International Conference on Flow Dynamics (ICFD2016), Sendai, Japan, 10–12 October 2016; Volume 12, pp. 492–493. [Google Scholar]
- Yang, Y.; Zhu, X.; Yan, Y.; Ding, H.; Wen, C. Performance of supersonic steam ejectors considering the nonequilibrium condensation phenomenon for e ffi cient energy utilisation. Appl. Energy 2019, 242, 157–167. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X.; Wang, D.; Jin, Z.; Qin, X. Performance evaluation and operation optimization of the steam ejector based on modified model. Appl. Therm. Eng. 2019, 163, 114388. [Google Scholar] [CrossRef]
- Wang, X.; Dong, J.; Zhang, G.; Fu, Q.; Li, H.; Han, Y.; Tu, J. The primary pseudo-shock pattern of steam ejector and its influence on pumping efficiency based on CFD approach. Energy 2019, 167, 224–234. [Google Scholar] [CrossRef]
- Han, Y.; Wang, X.; Sun, H.; Zhang, G.; Guo, L.; Tu, J. CFD simulation on the boundary layer separation in the steam ejector and its influence on the pumping performance. Energy 2019, 167, 469–483. [Google Scholar] [CrossRef]
- Glushniova, A.V.; Saveliev, A.S.; Son, E.E.; Tereshonok, D.V. Shock wave-boundary layer interaction on the non-adiabatic ramp surface. High Temp. 2014, 52, 220–224. [Google Scholar] [CrossRef]
- Bartosiewicz, Y.; Aidoun, Z.; Mercadier, Y. Numerical assessment of ejector operation for refrigeration applications based on CFD. Appl. Therm. Eng. 2006, 26, 604–612. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, P. Experimental and analytical studies on the shock wave length in convergent and convergent-divergent nozzle ejectors. Energy Convers. Manag. 2014, 88, 907–914. [Google Scholar] [CrossRef]
- Zhu, Y.; Cai, W.; Wen, C.; Li, Y. Shock circle model for ejector performance evaluation. Energy Convers. Manag. 2007, 48, 2533–2541. [Google Scholar] [CrossRef]
- Varga, S.; Oliveira, A.C.; Diaconu, B. Numerical assessment of steam ejector efficiencies using CFD. Int. J. Refrig. 2009, 32, 1203–1211. [Google Scholar] [CrossRef]
- Jeong, H.; Utomo, T.; Ji, M.; Lee, Y.; Lee, G.; Chung, H. CFD analysis of flow phenomena inside thermo vapor compressor influenced by operating conditions and converging duct angles. J. Mech. Sci. Technol. 2009, 23, 2366–2375. [Google Scholar] [CrossRef]
- Ruangtrakoon, N.; Thongtip, T.; Aphornratana, S.; Sriveerakul, T. CFD simulation on the effect of primary nozzle geometries for a steam ejector in refrigeration cycle. Int. J. Therm. Sci. 2013, 63, 133–145. [Google Scholar] [CrossRef]
- Sankarlal, T.; Mani, A. Experimental studies on an ammonia ejector refrigeration system. Int. Commun. Heat Mass Transf. 2006, 33, 224–230. [Google Scholar] [CrossRef]
- Ramesh, A.S.; Joseph Sekhar, S. Experimental Studies on the Effect of Suction Chamber Angle on the Entrainment of Passive Fluid in a Steam Ejector. J. Fluids Eng. 2017, 140, 011106. [Google Scholar] [CrossRef]
- Ramesh, A.S.; Sekhar, S.J. Experimental and numerical investigations on the effect of suction chamber angle and nozzle exit position of a steam-jet ejector. Energy 2018, 164, 1097–1113. [Google Scholar] [CrossRef]
- Fu, W.; Liu, Z.; Li, Y.; Wu, H.; Tang, Y. Numerical study for the influences of primary steam nozzle distance and mixing chamber throat diameter on steam ejector performance. Int. J. Therm. Sci. 2018, 132, 509–516. [Google Scholar] [CrossRef]
- Bartosiewicz, Y.; Aidoun, Z.; Desevaux, P.; Mercadier, Y. Numerical and experimental investigations on supersonic ejectors. Int. J. Heat Fluid Flow 2005, 26, 56–70. [Google Scholar] [CrossRef]
- Ariafar, K.; Buttsworth, D.; Al-Doori, G.; Sharifi, N. Mixing layer effects on the entrainment ratio in steam ejectors through ideal gas computational simulations. Energy 2016, 95, 380–392. [Google Scholar] [CrossRef]
- Sharifi, N.; Sharifi, M. Reducing energy consumption of a steam ejector through experimental optimization of the nozzle geometry. Energy 2014, 66, 860–867. [Google Scholar] [CrossRef]
- Matsuo, S.; Kanesaki, K.; Nagao, J.; Khan, M.T.I.; Setoguchi, T.; Kim, H.D. Effects of Supersonic Nozzle Geometry on Characteristics of Shock Wave Structure. Open J. Fluid Dyn. 2012, 2, 181–186. [Google Scholar] [CrossRef]
- García Del Valle, J.; Sáiz Jabardo, J.M.; Castro Ruiz, F.; San José Alonso, J. A one dimensional model for the determination of an ejector entrainment ratio. Int. J. Refrig. 2012, 35, 772–784. [Google Scholar] [CrossRef]
- Sriveerakul, T.; Aphornratana, S.; Chunnanond, K. Performance prediction of steam ejector using computational fluid dynamics: Part 2. Flow structure of a steam ejector influenced by operating pressures and geometries. Int. J. Therm. Sci. 2007, 46, 823–833. [Google Scholar] [CrossRef]
- Pianthong, K.; Seehanam, W.; Behnia, M.; Sriveerakul, T.; Aphornratana, S. Investigation and improvement of ejector refrigeration system using computational fluid dynamics technique. Energy Convers. Manag. 2007, 48, 2556–2564. [Google Scholar] [CrossRef]
- Eames, I.W.; Aphornratana, S.; Haider, H. A theoretical and experimental study of a small-scale steam jet refrigerator. Int. J. Refrig. 1995, 18, 378–386. [Google Scholar] [CrossRef]
- Yuen, A.C.Y.; Yeoh, G.H.; Cheung, S.C.P.; Chan, Q.N.; Chen, T.B.Y.; Yang, W.; Lu, H. Numerical study of the development and angular speed of a small-scale fire whirl. J. Comput. Sci. 2018, 27, 21–34. [Google Scholar] [CrossRef]
- Yuen, A.C.Y.; Chen, T.B.Y.; Yeoh, G.H.; Yang, W.; Cheung, S.C.P.; Cook, M.; Yu, B.; Chan, Q.N.; Yip, H.L. Establishing pyrolysis kinetics for the modelling of the flammability and burning characteristics of solid combustible materials. J. Fire Sci. 2018, 36, 494–517. [Google Scholar] [CrossRef] [Green Version]
- Huang, B.J.; Chang, J.M.; Wang, C.P.; Petrenko, V.A. 1-D analysis of ejector performance. Int. J. Refrig. 1999, 22, 354–364. [Google Scholar] [CrossRef]
- Selvaraju, A.; Mani, A. Analysis of a vapour ejector refrigeration system with environment friendly refrigerants. Int. J. Therm. Sci. 2004, 43, 915–921. [Google Scholar] [CrossRef]
- Sharifi, N.; Boroomand, M.; Sharifi, M. Numerical assessment of steam nucleation on thermodynamic performance of steam ejectors. Appl. Therm. Eng. 2013, 52, 449–459. [Google Scholar] [CrossRef]
- Sharifi, N.; Boroomand, M.; Kouhikamali, R. Wet steam flow energy analysis within thermo-compressors. Energy 2012, 47, 609–619. [Google Scholar] [CrossRef]
- Ariafar, K.; Buttsworth, D.; Al-Doori, G.; Malpress, R. Effect of mixing on the performance of wet steam ejectors. Energy 2015, 93, 2030–2041. [Google Scholar] [CrossRef]
- Aphornratana, S.; Eames, I.W. A small capacity steam-ejector refrigerator: Experimental investigation of a system using ejector with movable primary nozzle. Int. J. Refrig. 1997, 20, 352–358. [Google Scholar] [CrossRef]
- Yuen, A.C.Y.; Yeoh, G.H.; Timchenko, V.; Chen, T.B.Y.; Chan, Q.N.; Wang, C.; Li, D.D. Comparison of detailed soot formation models for sooty and non-sooty flames in an under-ventilated ISO room. Int. J. Heat Mass Transf. 2017, 115, 717–729. [Google Scholar] [CrossRef]
- Yuen, A.C.Y.; Yeoh, G.H.; Timchenko, V.; Cheung, S.C.P.; Barber, T.J. Importance of detailed chemical kinetics on combustion and soot modelling of ventilated and under-ventilated fires in compartment. Int. J. Heat Mass Transf. 2016, 96, 171–188. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new κ-ε eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Yang, X.; Long, X.; Yao, X. Numerical investigation on the mixing process in a steam ejector with different nozzle structures. Int. J. Therm. Sci. 2012, 56, 95–106. [Google Scholar] [CrossRef]
- Yuen, A.C.Y.; Yeoh, G.H. Numerical Simulation of an Enclosure Fire in a Large Test Hall. Comput. Therm. Sci. 2013, 5, 459–471. [Google Scholar] [CrossRef]
- Yuen, A.C.Y.; Yeoh, G.H.; Timchenko, V.; Cheung, S.C.P.; Chan, Q.N.; Chen, T. On the influences of key modelling constants of large eddy simulations for large-scale compartment fires predictions. Int. J. Comput. Fluid Dyn. 2017, 31, 324–337. [Google Scholar] [CrossRef]
- Dvorak, V.; Safarik, P. Transonic instability in entrance part of mixing chamber of high-speed ejector. J. Therm. Sci. 2005, 14, 258–264. [Google Scholar] [CrossRef]
- Monday, J.T.; Bagster, D.F. A New Ejector Theory Applied to Steam Jet Refrigeration. Ind. Eng. Chem. Process Des. Dev. 1977, 16, 442–449. [Google Scholar] [CrossRef]









| Geometrical Parameters | Value |
|---|---|
| Diameter of the nozzle inlet | 12 mm |
| Diameter of the nozzle outlet | 11 mm |
| Diameter of the nozzle throat | 2.5 mm |
| Expand the angle of the nozzle | 10° |
| Nozzle exit position | 10 mm |
| Diameter of mixing chamber inlet | 70 mm |
| Diameter of throat | 28 mm |
| Length of mixing chamber | 122.2 mm |
| Length of throat | 90 mm |
| Length of diffuser | 210 mm |
| Boundary Conditions | Value |
|---|---|
| Primary fluid temperature | 134 °C~146 °C |
| Secondary fluid temperature Back pressure | 5 °C~20 °C 3000 Pa~5000 Pa |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Guo, L.; Wang, X.; Yuen, A.C.Y.; Li, C.; Cao, R.; Liu, H.; Chen, T.B.Y.; Tu, J.; Yeoh, G.H. A Steam Ejector Refrigeration System Powered by Engine Combustion Waste Heat: Part 1. Characterization of the Internal Flow Structure. Appl. Sci. 2019, 9, 4275. https://doi.org/10.3390/app9204275
Han Y, Guo L, Wang X, Yuen ACY, Li C, Cao R, Liu H, Chen TBY, Tu J, Yeoh GH. A Steam Ejector Refrigeration System Powered by Engine Combustion Waste Heat: Part 1. Characterization of the Internal Flow Structure. Applied Sciences. 2019; 9(20):4275. https://doi.org/10.3390/app9204275
Chicago/Turabian StyleHan, Yu, Lixin Guo, Xiaodong Wang, Anthony Chun Yin Yuen, Cuiling Li, Ruifeng Cao, Hengrui Liu, Tim Bo Yuan Chen, Jiyuan Tu, and Guan Heng Yeoh. 2019. "A Steam Ejector Refrigeration System Powered by Engine Combustion Waste Heat: Part 1. Characterization of the Internal Flow Structure" Applied Sciences 9, no. 20: 4275. https://doi.org/10.3390/app9204275







