Validating the Comparison Framework for the Finite Dimensions Model of Concentric Ring Electrodes Using Human Electrocardiogram Data

Abstract

While progress has been made in design optimization of concentric ring electrodes maximizing the accuracy of the surface Laplacian estimation, it was based exclusively on the negligible dimensions model of the electrode. Recent proof of concept of the new finite dimensions model that adds the radius of the central disc and the widths of concentric rings to the previously included number of rings and inter-ring distances provides an opportunity for more comprehensive design optimization. In this study, the aforementioned proof of concept was developed into a framework allowing direct comparison of any two concentric ring electrodes of the same size and with the same number of rings. The proposed framework is illustrated on constant and linearly increasing inter-ring distances tripolar concentric ring electrode configurations and validated on electrocardiograms from 20 human volunteers. In particular, ratios of truncation term coefficients between the two electrode configurations were used to demonstrate the similarity between the negligible and the finite dimension models analytically (p = 0.077). Laplacian estimates based on the two models were calculated on electrocardiogram data for emulation of linearly increasing inter-ring distances tripolar concentric ring electrode. The difference between the estimates was not statistically significant (p >> 0.05) which is consistent with the analytic result.

1. Introduction

Surface bioelectric signals, such as an electrocardiogram (ECG) or electroencephalogram became an essential tool in clinical diagnosis. When recorded with conventional disc electrodes surface bioelectric signals have an outstanding temporal resolution but poor spatial one because of the blurring effect. It is due to the configuration of conventional disc electrodes and different conductivities of the body volume conductor [1,2]. To overcome this drawback, surface Laplacian estimation was proposed. Surface Laplacian is the second spatial derivative of the surface potentials that acts as a high-pass spatial filter [3] and allows diminishing the blurring effect of the volume conduction [4,5]. Laplacian estimation allows an improvement in picking up the bioelectric dipoles closest to the electrodes and rejection of distant bioelectric dipole sources when compared to bipolar signals from conventional disc electrodes [6].

Initially, Laplacian was estimated based on the surface potentials recorded via multiple single pole electrodes and the application of discretization techniques such as the five-point method [7], Laplacian triangular estimation [8] or the nine-point method [9]. Next, concentric ring electrodes (CREs) were developed in different configurations (bipolar, quasi-bipolar, and tripolar) allowing direct estimation of the surface Laplacian at each electrode by combining signals from all the recording surfaces. Specifically, tripolar CREs (TCREs) allows more accurate surface Laplacian estimation when compared to quasi-bipolar and bipolar configurations with increased spatial resolution [10,11]. CREs implemented on rigid and later on flexible substrates [12,13] were used to record a wide variety of human bioelectric signals such as electroencephalograms [14,15], electroenterograms [16,17], electrohysterograms [18], and ECGs [19,20] that provide information regarding the electrical conduction in the heart and the heart rate, enabling the diagnosis of a large range of cardiac pathologies. Specifically, 12-lead short-term ECG recordings with conventional disc electrodes are broadly used in clinics with benchtop equipment to diagnose a wide range of cardiac pathologies that can be dangerous and even deadly such as bundle branch block, AV blocks, sinus bradycardia or tachycardia and atrial/ventricular fibrillation [21].

This paper continues a series of works concentrating on further improving the accuracy of Laplacian estimation via CREs by optimizing the number of concentric rings [22] and inter-ring distances (distances between the consecutive rings) [23,24]. Analytic results from [22,23,24] have been validated using finite element method modeling. Moreover, in [12] stencil printed TCRE prototypes resembling the linearly increasing inter-ring distances (LIIRD) design proposed in [23] were assessed on human electroencephalogram, ECG, and electromyogram data with obtained results suggesting enhanced spatial resolution and localization of signal sources. However, in [12] physical TCRE prototype had a 1:3 ratio of inter-ring distances compared to the 1:2 ratio in the LIIRD design proposed in [23]. More importantly, the Laplacian estimate equation used in [12] corresponded to a constant inter-ring distances (CIRD) TCRE with 1:1 ratio of inter-ring distances. Furthermore, an inherent limitation of [22,23,24] is the use of the negligible dimensions model (NDM) of a CRE where the widths of concentric rings and the radius of the central disc are assumed to be negligible. In order to optimize all of the CRE parameters simultaneously, these parameters need to be included in the general optimization problem similar to the NDM based one in [24] along with the number of rings and the inter-ring distances. Such a comprehensive finite dimensions model (FDM) of a CRE would build and improve upon all the previous NDM based findings from [22,23,24] and could be used to optimize future CRE designs maximizing the accuracy of the surface Laplacian estimation. The first step toward FDM has been taken in [25] by deriving a Laplacian estimate for a proof of concept TCRE with nonnegligible radius of the central disc and widths of the concentric rings. This was accomplished by representing the central disc of the TCRE as a cluster of points with specific radius as opposed to the NDM representation via a single point [25]. Both concentric rings were also represented by clusters of points with specific widths as opposed to the NDM representation via concentric circles [25]. In this study, the FDM proof of concept from [25] was developed into a framework allowing direct comparison of any two CRE configurations of the same size and with the same number of rings in terms of their accuracy of Laplacian estimation. This framework was applied to two FDM based TCRE configurations: CIRD and LIIRD. Moreover, CIRD/LIIRD ratios of truncation term coefficients for FDM based Laplacian estimates were compared to respective ratios obtained for NDM based estimates in [23]. No statistically significant difference between the FDM and NDM based ratios was found once they were adjusted to make the FDM and NDM TCRE configurations comparable in terms of a relation between absolute change between CIRD and LIIRD configurations and the size of TCRE. Finally, this analytic result has been validated on human ECG data (N = 20) using FDM and NDM based Laplacian estimate equations derived for a real life LIIRD TCRE. Comparison between both the estimate equations and metrics calculated on resulting Laplacian estimate signals has been drawn. No statistically significant differences have been found confirming the analytic result of consistency between the FDM and the NDM for CIRD and LIIRD TCREs considered.

2. Materials and Methods

2.1. Preliminaries

In Figure 1, the diagram represents two configurations of the FDM based TCREs: CIRD and LIIRD ones. Both configurations are subdivided into 9 intervals equal to r, both central discs have a radius of r, and all the concentric rings have a width of r. The CIRD configuration has each ring evenly spaced with inter-ring distances of 3r. For the LIIRD configuration, the distance between the central disc and the middle ring is 2r and the distance between the middle ring and the outer ring is two times larger at 4r.

Table 1. Taylor series for concentric circles.

Concentric Circle Radius	Taylor Series for Concentric Circle
r	$v_r\cong v_0+\frac{2\cdot 1^2}{4\cdot 2!}{r}^2\Delta v_0+\frac{2\cdot 1^4}{4\cdot 4!}{r}^4{T}_4+\frac{2\cdot 1^6}{4\cdot 6!}{r}^6{T}_6$
2r	$v_{2r}\cong v_0+\frac{2\cdot 2^2}{4\cdot 2!}{r}^2\Delta v_0+\frac{2\cdot 2^4}{4\cdot 4!}{r}^4{T}_4+\frac{2\cdot 2^6}{4\cdot 6!}{r}^6{T}_6$
3r	$v_{3r}\cong v_0+\frac{2\cdot 3^2}{4\cdot 2!}{r}^2\Delta v_0+\frac{2\cdot 3^4}{4\cdot 4!}{r}^4{T}_4+\frac{2\cdot 3^6}{4\cdot 6!}{r}^6{T}_6$
4r	$v_{4r}\cong v_0+\frac{2\cdot 4^2}{4\cdot 2!}{r}^2\Delta v_0+\frac{2\cdot 4^4}{4\cdot 4!}{r}^4{T}_4+\frac{2\cdot 4^6}{4\cdot 6!}{r}^6{T}_6$
5r	$v_{5r}\cong v_0+\frac{2\cdot 5^2}{4\cdot 2!}{r}^2\Delta v_0+\frac{2\cdot 5^4}{4\cdot 4!}{r}^4{T}_4+\frac{2\cdot 5^6}{4\cdot 6!}{r}^6{T}_6$
6r	$v_{6r}\cong v_0+\frac{2\cdot 6^2}{4\cdot 2!}{r}^2\Delta v_0+\frac{2\cdot 6^4}{4\cdot 4!}{r}^4{T}_4+\frac{2\cdot 6^6}{4\cdot 6!}{r}^6{T}_6$
7r	$v_{7r}\cong v_0+\frac{2\cdot 7^2}{4\cdot 2!}{r}^2\Delta v_0+\frac{2\cdot 7^4}{4\cdot 4!}{r}^4{T}_4+\frac{2\cdot 7^6}{4\cdot 6!}{r}^6{T}_6$
8r	$v_{8r}\cong v_0+\frac{2\cdot 8^2}{4\cdot 2!}{r}^2\Delta v_0+\frac{2\cdot 8^4}{4\cdot 4!}{r}^4{T}_4+\frac{2\cdot 8^6}{4\cdot 6!}{r}^6{T}_6$
9r	$v_{9r}\cong v_0+\frac{2\cdot 9^2}{4\cdot 2!}{r}^2\Delta v_0+\frac{2\cdot 9^4}{4\cdot 4!}{r}^4{T}_4+\frac{2\cdot 9^6}{4\cdot 6!}{r}^6{T}_6$

displays the average potentials v_kr on each concentric circle with radius kr with k ranging from 1 to 9 (Figure 1) based on Huiskamp’s calculation of the Laplacian potential using Taylor series expansion from [9] (see [25] for more details on its derivation):

$$v_{kr}\cong v_0+\frac{2\cdot k^2}{4\cdot 2!}{r}^2\Delta v_0+\frac{2\cdot k^4}{4\cdot 4!}{r}^4{T}_4+\frac{2\cdot k^6}{4\cdot 6!}{r}^6{T}_6$$

(1)

where

$$\Delta v_0=\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}$$

(2)

$$T_4=\frac{{\partial }^{4}v}{\partial x^4}+\frac{{\partial }^{4}v}{\partial y^4}$$

(3)

$$T_6=\frac{{\partial }^{6}v}{\partial x^6}+\frac{{\partial }^{6}v}{\partial y^6}$$

(4)

The following notations are used in Equation (1) and in Table 1: Δv₀ is the surface Laplacian potential at the point with potential v₀ (Equation (2)) and T₄ and T₆ are the fourth (Equation (3)) and the sixth (Equation (4)) order truncation terms respectively.

2.2. Deriving Laplacian Estimates for Real Life Linearly Increasing Inter-ring Distances (LIIRD) Tripolar Concentric Ring Electrode (TCRE) Based on Negligible Dimensions Model (NDM) and Finite Dimensions Model (FDM)

For the case of NDM, in [24] the method of optimal surface Laplacian estimation was proposed for a TCRE with concentric ring radii αr and r where coefficient α satisfies 0 < α < 1. The method is based on using the matrix of truncation term coefficients (α⁴ 1) to solve for its null space vector (−1/ α⁴, 1) followed by linearly combining two bipolar signals corresponding to differences between concentric ring and central disc potentials into a Laplacian estimate with the null space vector used as linear combination coefficients [24]. For the physical LIIRD TCRE we applied this method to actual TCRE measurements including middle ring radii (9.6 mm inner and 10.8 mm outer,

Table 2. Concentric ring electrode (CRE) dimensions and nomenclature of the biopotentials used for Laplacian estimation.

	Radius (mm)		Biopotential	Laplacian Estimate
	Inner	Outer
Central disc	N/A	4.8	U1	LIIRD TCRE
Hook 1	9.6	10.8	U2	LIIRD TCRE
Hook 2	15.6	16.8	U3	-
Hook 3	21.6	22.8	U4	LIIRD TCRE
Hook 4	27.6	28.8	U5	- (analog ground)

LIIRD: linearly increasing inter-ring distances; TCRE: tripolar concentric ring electrode.

) and outer ring radii (21.6 mm inner and 22.8 mm outer, Table 2) as well as to radii corresponding to the center of each ring (10.2 mm for the middle ring and 22.2 mm for the outer one).

For the case of FDM, steps similar to the ones in Section 3.1 below were used to find the coefficients of the Laplacian estimate.

2.3. Human Electrocardiogram (ECG) Data Collection and Processing

2.3.1. Sensor Node

A wireless sensor node was used to pick up bipolar ECG signals. The node consisted of a flexible disposable CRE and electronic circuitry performing processing, digitization, and transmission of three bipolar ECG analogue signals [26]. The CRE consisted of a central disc and four hooks (analogous to the concentric rings) in a bilayer design (Figure 2). The CRE dimensions were chosen based on the distance between the chest surface and the heart wall is equal to approximately 3–5 cm [27,28]. Screen-printing technology was employed to produce the electrodes, printing a biocompatible silver paste onto a flexible polyester film [26].

The sensor node from Figure 2 provided three bipolar ECG signals from the CRE including U₂ − U₁, U₃ − U₁, and U₄ − U₁ where U₁, U₂, U₃, and U₄ were the biopotentials captured by the disc and the three central hooks from inside to outside respectively (Table 2). To reduce common mode interference, the outer hook was connected to the analog ground. No external reference electrode was used. The analog signal processing consisted of amplification of 4084 V/V and bandpass filtering between 0.3 and 150 Hz. Then signals were digitized at 500 Hz with 24-bit resolution. The sensor node permitted storing the signals locally on a microSD card or transmitting them wirelessly via Bluetooth. The sensor node was powered by a 3.7 V rechargeable battery.

2.3.2. ECG Signal Recording Protocol

ECG recordings were carried out at the Juana Portaceli Health Center of the Universitat Politècnica de València on twenty volunteers: 17 males and three females with ages between 20 and 70 years old (mean ± standard deviation: 36 ± 14.1) and body mass indices between 19 and 33 Kg/m² (mean ± standard deviation: 25.1 ± 3.2 Kg/m²) who attended routine check-ups, some of them healthy and others with cardiac pathologies. The study was approved by the institutional Ethics Committee (project identification code P4_20_02_19) and adheres to the Declaration of Helsinki. Volunteers were informed of the aim of the study, briefed on the recording protocol, and signed the informed consent forms.

Recordings were conducted with volunteers at rest, lying on a stretcher in a supine position. The sensor node was placed at CMV1 (location comparable to conventional precordial V1, 4th intercostal space to the right of the sternum) for each patient as shown in Figure 3. This location was chosen to make picking up electrical signals from both atria and ventricle easier since the atrial activity is noticeably weaker than that of the ventricle. Previously, to reduce contact impedance, the skin area was slightly exfoliated (Nuprep, Weaver and Company, Aurora, CO, USA) and, in the case of male volunteers, shaved. Five minutes of bipolar ECG signals were recorded for each volunteer.

2.3.3. ECG Data Analysis

Two bipolar ECG signals selected to emulate LIIRD TCRE (U₂ − U₁ and U₄ − U₁) were digitally high pass filtered (0.3 Hz, fifth-order zero-phase Butterworth filter) to reduce remaining baseline drifts. Subsequently, two surface Laplacian estimates were obtained, one for the NDM and one for the FDM, according to equations derived in Section 3.4 below.

ECG fiducial points were identified by detecting the R-wave in both Laplacian estimate signals using Hamilton & Tompkins algorithm [29]. The average beat ($\overline{ECG}$) for each subject was computed in a 60 s window, covering from 250 ms prior to 375 ms after the R-wave. To compare the two Laplacian estimates the average values of the following parameters were computed for each recording session:

• The amplitude of the QRS complex of $\overline{ECG}$, computed as the peak-to-peak amplitude of $\overline{ECG}$ in the interval [−90 ms, +90 ms] of the detected R-wave.
• Normalized amplitude of the P- and T-waves with respect to the peak to peak amplitude of QRS [30]. P- and T-wave amplitude computed as the peak-to-peak amplitude of $\overline{ECG}$ in the interval [−250 ms, −90 ms] and [+90 ms, 375 ms] of the detected R-wave. The higher the normalized amplitude of the wave, the easier it is to identify and to assess its morphology, which is helpful for diagnosis of cardiac pathologies,
• Signal-to-noise ratio: the ratio of the peak-to-peak amplitude value of $\overline{ECG}$ and the root mean square value of the noise during the isoelectric interval between beats, the latter being computed for all the isoelectric intervals in the 60 s window.

  $$SNR \left(dB\right)=20·lo{g}_{10}\left(\frac{v_{PP}\left(\overline{ECG}\right)}{v_{RMS}\left(noise\right)}\right)$$

  (5)

3. Results

3.1. Establishing the Comparison Framework

To establish the comparison framework under the FDM the surface Laplacian estimates for the two TCRE configurations from Figure 1 are derived first. The derivation starts with calculating the three potentials on the TCRE surfaces: the central disc, middle ring, and outer ring.

The potential on the central disc v_CD with a radius equal to r (Figure 1) is equal to the average of the potential v₀ at the center of the disc and the potential v_r on the concentric circle with radius r. The central disc potential is the same for both CIRD and LIIRD TCRE configurations as shown in Figure 1.

$$v_{CD}=\frac{v_0+v_r}{2}\cong v_0+\frac{1}{8}{r}^2\Delta v_0+\frac{1}{96}{r}^4{T}_4+\frac{1}{2880}{r}^6{T}_6$$

(6)

CIRD and LIIRD middle ring potentials are different. In Figure 1 the CIRD configuration places the middle ring between concentric circles with radii of 4r and 5r so the average of v_4r and v_5r is calculated.

$$v_{MR}^{CIRD}=\frac{v_{4r}+v_{5r}}{2}\cong v_0+\frac{41}{8}{r}^2\Delta v_0+\frac{881}{96}{r}^4{T}_4+\frac{19721}{2880}{r}^6{T}_6$$

(7)

However, for the LIIRD configuration, the average of potentials v_3r and v_4r is calculated instead.

$$v_{MR}^{LIIRD}=\frac{v_{3r}+v_{4r}}{2}\cong v_0+\frac{25}{8}{r}^2\Delta v_0+\frac{337}{96}{r}^4{T}_4+\frac{965}{576}{r}^6{T}_6$$

(8)

Next, for both LIIRD and CIRD configurations the outer ring potential v_OR is calculated as the average of the potentials on concentric circles with radii of 8r and 9r.

$$v_{OR}=\frac{v_{8r}+v_{9r}}{2}\cong v_0+\frac{145}{8}{r}^2\Delta v_0+\frac{10657}{96}{r}^4{T}_4+\frac{158717}{576}{r}^6{T}_6$$

(9)

Finally, v₀ is canceled out. This is accomplished by taking the bipolar difference between v_CD and v_MR. Since there are two different equations for the middle ring potential, the CIRD configuration is considered first.

$$v_{MR}^{CIRD}-v_{CD}\cong 5r^2\Delta v_0+\frac{55}{6}{r}^4{T}_4+\frac{493}{72}{r}^6{T}_6$$

(10)

Followed by the LIIRD configuration.

$$v_{MR}^{LIIRD}-v_{CD}\cong 3r^2\Delta v_0+\frac{7}{2}{r}^4{T}_4+\frac{67}{40}{r}^6{T}_6$$

(11)

Bipolar difference between the outer ring potential v_OR and the central disc potential v_CD which is the same for both configurations is taken as well.

$$v_{OR}-v_{CD}\cong 18r^2\Delta v_0+111r^4{T}_4+\frac{5511}{20}{r}^6{T}_6$$

(12)

These three bipolar differences are combined linearly to cancel out the 4th order truncation term T₄ and provide the surface Laplacian estimates for CIRD and LIRD configurations.

$$\Delta v_0^{CIRD}\cong \frac{1}{r^2}\left[\frac{37}{130}\left(v_{MR}^{CIRD}-v_{CD}\right)-\frac{11}{468}\left(v_{OR}-v_{CD}\right)\right]+\frac{163}{36}{r}^4{T}_6$$

(13)

$$\Delta v_0^{LIIRD}\cong \frac{1}{r^2}\left[\frac{37}{90}\left(v_{MR}^{LIIRD}-v_{CD}\right)-\frac{7}{540}\left(v_{OR}-v_{CD}\right)\right]+\frac{173}{60}{r}^4{T}_6$$

(14)

Considering the ratio of the respective 6th order truncation term (T₆) coefficients for CIRD and LIIRD configurations the truncation error corresponding to the CIRD configuration is estimated to be 1.57 times greater than that of the LIIRD configuration.

$$\frac{163}{36}÷\frac{173}{60}=\frac{815}{519}=1.57$$

(15)

Such ratios of truncation term coefficients for the lowest remaining truncation term order allow comparing any two TCRE configurations of the same size and with the same number of rings directly in terms of truncation error since according to [31] for Taylor series “higher-order terms usually contribute negligibly to the final sum and can be justifiably discarded.”

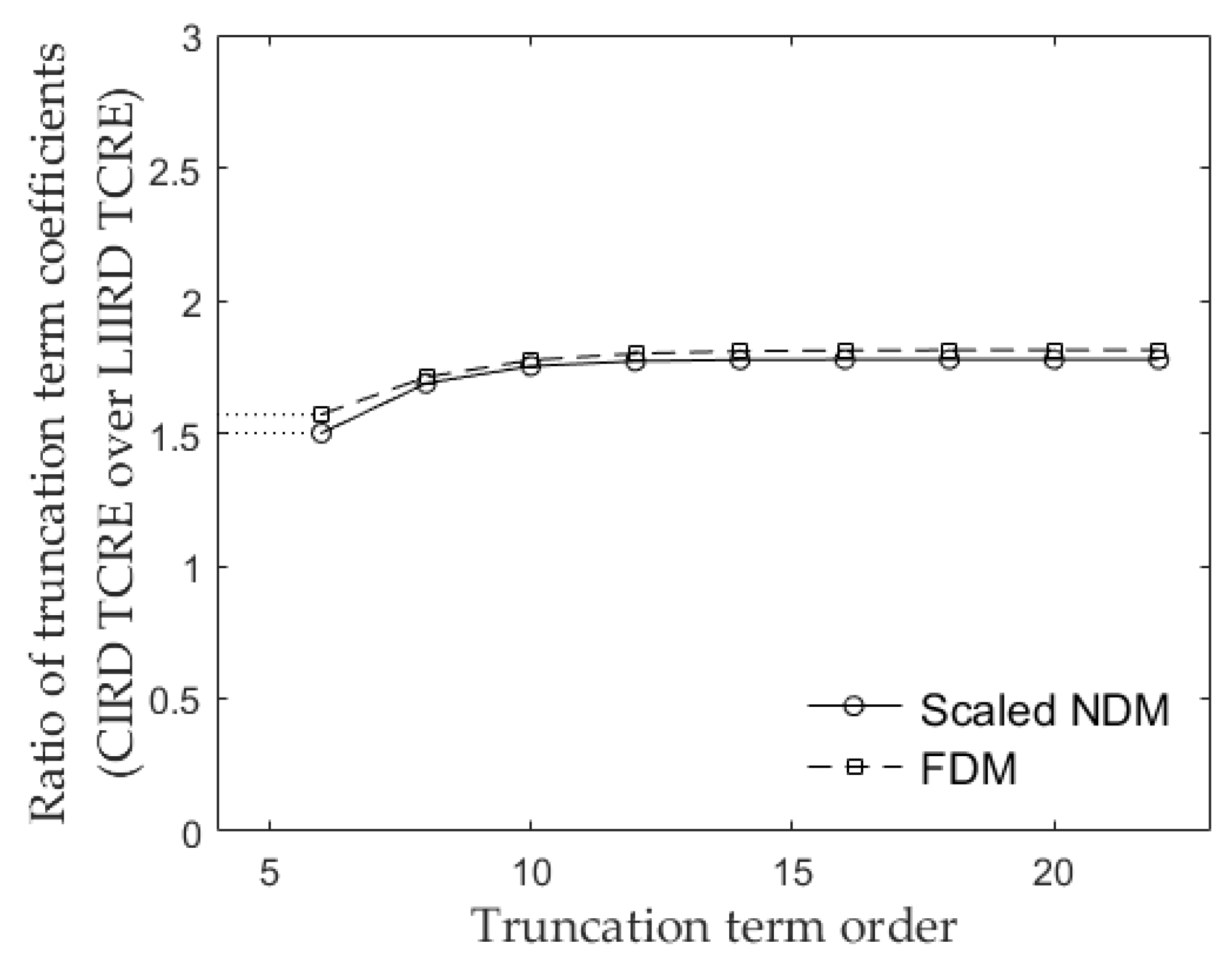
3.2. Comparing Truncation Term Coefficient Ratios for the NDM and the FDM

FDM based coefficients for truncation terms of orders ranging from 8 to 22 were calculated in a manner identical to that of the sixth order truncation term coefficients [Equations (6)–(15)] above. Coefficient ratios (CIRD over LIIRD) for the full range of truncation term orders (6 to 22) were compared to the respective NDM based ratios calculated in [23]. The resulting comparison is presented in Figure 4.

3.3. Relating the Difference in Truncation Term Coefficient Ratios to the Difference in TCRE Configurations Between the NDM and the FDM

As seen in Figure 4, while the general shapes of the curves corresponding to the truncation term coefficient ratios based on the NDM and the FDM are consistent, there is a substantial difference in scale. This difference arises because the ratios for the NDM were based on TCRE setups presented in Figure 5 [23].

Comparing Figure 1 and Figure 5 it can be noticed that the difference between the middle rings in two TCRE configurations (CIRD versus LIIRD) is equivalent to a distance of r. However, while in Figure 1 that distance represents 1/9 of the radius of the TCRE (equal to 9r), in Figure 5 it represents 1/6 of the radius of the TCRE (equal to 6r). To make CRE configurations for the NDM and the FDM comparable, the latter would need to be scaled by a factor of 2/3 since (1/6) · (2/3) = 1/9. The revised comparison from Figure 4 with the curve corresponding to the NDM based truncation term coefficient ratios scaled by a factor of 2/3 is presented in Figure 6.

As shown in Figure 6, once the scale is adjusted for the NDM to make CRE configurations in Figs. 1 and 5 directly comparable, respective ratios of truncation term coefficients for the scaled NDM and the FDM differ by less than 5%. Non parametric Wilcoxon rank sum test (equivalent to a Mann-Whitney U-test) has been used to confirm that there is no statistically significant difference between the aforementioned ratios (p = 0.077) after confirming that data did not come from a normal distribution using Lilliefors test.

3.4. NDM and FDM Based Laplacian Estimates for Real Life LIIRD TCRE

Laplacian estimate coefficients are not unique for both NDM and FDM. For NDM they are determined as a null space vector of a truncation term coefficient matrix and therefore are not unique [22]. For FDM, as shown in Section 3.1 they are also a solution of a system of linear equations. Since in both cases Laplacian estimate coefficients are determined up to (multiplication by) a constant factor they were scaled both for the NDM and for the FDM to a unit value of the first coefficient to allow direct comparison.

Since one of the main limitations of the NDM is the negligible widths of the concentric rings, the Laplacian estimate coefficients were calculated as null spaces of the respective truncation term coefficient matrices [24] for three scenarios: separately for inner and outer radii of the two rings and for radii corresponding to the center of each ring since if each ring had to be represented as a circle with negligible width then the natural point estimate would have been the average of ring’s inner and outer radii. The average of the coefficients obtained for the three scenarios yielded coefficients (1, −0.0446417) for the LIIRD TCRE case equivalent to the following NDM based Laplacian estimate:

$$\begin{array}{l}\Delta v_0^{NDM}\cong 1·\left(v_{MR}-v_{CD}\right)-0.0446417·\left(v_{OR}-v_{CD}\right)\\ =(U_2-U_1)-0.0446417·\left(U_4-U_1\right)\end{array}$$

(16)

For the FDM Laplacian estimate, first, the outer radius of the outer ring (radius of the LIIRD TCRE) was set equal to a large arbitrary numeric constant (e.g., 50,000). Next, the radius of the central disc and inner and outer radii of both concentric rings were expressed as integer fractions of this constant based on their actual dimensions from Table 2. For example, the radius of the central disc was set equal to 4.8 × 50,000/22.8 ≈ 10,526. Finally, potentials on all the recording surfaces were calculated as averages of potentials on all the concentric circles included in them. For example, the potential on the central disc was calculated as the arithmetic mean of 10,527 potentials including one at the center of the disc and potentials on concentric circles with radii up to 10,526. Potentials on the recording surfaces were combined in the manner identical to the Equations (10)–(15) from Section 3.1 above to obtain coefficients (1, −0.0443895) for the LIIRD TCRE case equivalent to the following FDM based Laplacian estimate:

$$\begin{array}{l}\Delta v_0^{FDM}\cong 1·\left(v_{MR}-v_{CD}\right)-0.0443895·\left(v_{OR}-v_{CD}\right)\\ =(U_2-U_1)-0.0443895·\left(U_4-U_1\right)\end{array}$$

(17)

It can be seen that the two resulting Laplacian estimates for the LIIRD TCRE based on the NDM and the FDM (Equations (16) and (17) respectively) are virtually identical with the coefficient at (U₄ − U₁) differing by less than 0.6%.

3.5. Assessing NDM and FDM Based Laplacian Estimates for Real Life LIIRD TCRE on Human ECG Data

Figure 7 shows 5 s of ECG signals recorded at CMV1. The bipolar signals (U₂ − U₁ and U₄ − U₁) needed for the computation of the Laplacian estimates for emulation of LIIRD TCRE are shown in black in the top and middle panels. Laplacian estimates based on NDM (dotted line) and FDM (dashed line) models are shown in the bottom panel. Signals are of low amplitude (tens of microvolts). The P- and T-waves and the QRS complex can be clearly observed in all panels. In fact, the P1- and P2-waves of left and right atrial activity can be identified. As expected based on the Equations (16) and (17), Laplacian estimates based on NDM and FDM are virtually identical.

Laplacian estimate signal metrics are summarized in

Table 3. Laplacian estimate signal metrics (mean ± standard deviation, N = 20).

∆v0	Amplitude QRS (µV)	Normalized Amplitude P-Wave	Normalized Amplitude T-Wave	Signal-to-Noise Ratio (dB)
NDM	18.59 ± 28.40	0.256 ± 0.145	0.367 ± 0.260	20.05 ± 8.29
FDM	18.60 ± 28.40	0.253 ± 0.141	0.362 ± 0.264	19.94 ± 8.48

. Estimates based on NDM and FDM presented very similar results with no statistically significant differences (Wilcoxon test following Lilliefors test to assess normality, p >> 0.05). The mean QRS amplitude is low (18.6 µV) and presents high variability (28.4 µV). A mean signal-to-noise ratio of around 20 dB was obtained for both signals. Mean normalized P-wave amplitude was equal to 0.256 and 0.253 for NDM and FDM based Laplacian estimates respectively. The normalized amplitude for T-wave was also similar (0.37 and0.36) for both estimates.

4. Discussion

Steps similar to the ones in [25] can be used to estimate the Laplacian for any multipolar CRE configuration where the widths of concentric rings and the radius of the central disc are nonnegligible (FDM). In this study, the proof of concept from [25] has been developed into a framework for direct comparison of any two specific CRE configurations of the same size and with the same number of concentric rings. Ratios of the lowest remaining order truncation term coefficients were used as a measure to base the comparison on since in [23] and [24] these ratios have been shown (using finite element method modeling) to be a predictor of the corresponding Laplacian estimation error. Namely, differences of less than 5% between the modeling derived ratios of Relative and Maximum Errors of Laplacian estimation and respective analytic ratios of truncation term coefficients have been reported for combinations of LIIRD, CIRD, and linearly decreasing inter-ring distances TCREs and quadripolar CREs [23] as well as for their quadratically increasing inter-ring distances counterparts [24]. The proposed comparison framework is implemented for the LIIRD and CIRD TCRE configurations. Obtained results confirm that a relatively small change in the geometry of the TCRE (moving the middle ring from 3r–4r to 4r–5r for a TCRE with radius of 9r in Figure 1) increases the Laplacian estimation error by more than 50% (approximately 1.57 times greater for the CIRD TCRE compared to the LIIRD one).

Moreover, this study directly compared the truncation term coefficient ratios obtained for the FDM TCRE configurations with the respective ratios obtained for the NDM in [23]. Once the scale was adjusted to make the TCRE configurations for the FDM (Figure 1) and the NDM (Figure 5) comparable there was no statistically significant difference between the truncation term coefficient ratios from Figure 6. This comparison provides insight into the effect of including additional parameters such as the radius of the central disc and the widths of concentric rings into the CRE model. The fact that for TCRE configurations assessed in the current study the ratios of truncation term coefficients corresponding to FDM and NDM respectively differed by less than 5% suggests consistency between the two models. This is to be expected since FDM and NDM are also consistent in terms of the highest truncation term order (2n) that can be cancelled out for a CRE with n rings as was shown in [22] and [25] respectively. However, an argument can be made that this may change for CRE designs that are drastically different from the NDM. For example, CRE design with variable widths of individual concentric rings that are significant compared to the total radius of the CRE. For such a CRE design only FDM is likely to produce meaningful results.

Finally, an intuitive result that larger differences between CRE configurations may result in larger differences in respective Laplacian estimation errors was suggested. For example, difference between the CIRD and the LIIRD configurations equivalent to 1/9 of the radius of the TCRE in case of FDM (Figure 1) resulted in a smaller CIRD over LIIRD error ratio of 1.57 while a more substantial difference of 1/6 of the radius of the TCRE between the same two TCRE configurations in case of NDM (Figure 5) resulted in a larger CIRD over LIIRD error ratio of 2.25.

Reported Laplacian ECG signals via LIIRD TCRE emulation were of low amplitude (tens of microvolts) as reported by other authors [20,28] but of good quality, as described below. As reported in [26], differences in the physiological constitution and variability of the relative position and orientation of the heart with respect to the CRE for different subjects, exacerbated by enhanced spatial resolution of CREs in comparison with conventional disc electrodes, are likely to be responsible for high standard deviation of the amplitude of cardiac vectors. The signal-to-noise ratio was of about 20dB, similar to other studies on bipolar ECG signals via CREs on textiles [13] and polyester [26] substrates. The main cardiac vectors were easily identifiable visually. The visualization of the PQRST peaks is very important for clinical diagnosis. The P-waves which are associated with the atrial activity are the lowest ECG peaks and the most challenging to identify. This is because the atrial activation involves fewer cardiac cells than the ventricular ones. In this context, the position of the recording electrode and its spatial resolution play an important role in providing a good contrast in the monitoring of atrial cardiac activity. Normalized P-wave amplitude to the full ECG peak-to-peak amplitude or to the QRS amplitude are commonly used to quantify this contrast. In traditional 12-lead ECG recordings, the highest normalized P-wave amplitudes are obtained in Lead I, Lead III, and V1 [30], with values between 0.09 and 0.14. In the case of CREs, the highest contrast is obtained in position equivalent to V1. Bipolar ECG signals picked up at that area have yielded normalized P-wave values of 0.18 [12] and 0.16 [20] with electrodes of external diameter equal to 15 mm and 42 mm respectively. In this study, normalized P-wave amplitude of 0.25 was obtained for LIIRD TCRE emulation with external diameter equal to 45.6 mm. Although a larger electrode size corresponds to worse spatial resolution associated with a given recording configuration (bipolar, tripolar,...) [26,27], the greater contrast obtained in the P-wave with the LIIRD TCRE configuration suggests better spatial resolution of this configuration compared to the bipolar one which is consistent with the finite element method modeling results from [23]. This improved ability to capture atrial activity facilitates its study, providing a tool of great clinical interest. LIIRD TCRE could provide more accurate cardiac activation patterns over bipolar concentric ECG and 12-lead ECG, and facilitate the diagnosis of atrial fibrillation in which a standard 12-lead ECG is insufficient to guide clinical management [32]. In fact, in a very recent study LIIRD TCRE provided the highest P-wave contrast (normalized amplitude) compared to bipolar, linearly decreasing inter-ring distances TCRE and quadripolar Laplacian estimates at CMV1 with significant differences from all the 12-lead standard ECG signals [33]. This ability is not compromised by obtaining the LIIRD TCRE Laplacian estimate using NDM or FDM, since they provide almost identical results in the equation coefficients and, therefore, in estimate signals obtained using Equations (16) and (17) respectively. On the other hand, having used a high-pass filter for the elimination of baseline drifts may have slightly reduced the relative amplitude of the low frequency cardiac components such as the P-wave and the T-wave. The use of more modern signal processing techniques [34], that respect to a greater extent the cardiac components, could lead to greater contrast in the study of these waves.

The limitation of this study is that, for the validation of human ECG data, emulation of CIRD TCRE of the same size as the emulation of LIIRD TCRE using the real life CRE in Figure 2 was not feasible. The only other TCRE configuration of the same size that could be emulated was the linearly decreasing inter-ring distances one (using bipolar ECG signals U₃ − U₁ and U₄ − U₁) from [23]. However, with the NDM and FDM based Laplacian estimates for LIIRD TCRE being virtually identical there is no reason to expect the NDM and FDM based Laplacian estimates for CIRD TCRE to be significantly different. Therefore, the CIRD over LIIRD truncation term coefficient ratios (based on NDM and FDM) corresponding to the ratios of truncation and, therefore, of Laplacian estimation errors will also be virtually identical in case when both the numerators and the denominators are. This human ECG data based result is consistent with the analytic result from Figure 6.

In the future, this comparison framework will be developed into a comprehensive optimization problem including and directly comparing all the possible CRE designs of the same size and with the same number of rings. If this FDM based optimization problem cannot be solved analytically it will be solved numerically as was the NDM based one in [24] for a wider range of numbers of rings and percentile values. Solutions of this problem could inform the design of CREs by maximizing the accuracy of their Laplacian estimates and could be particularly useful for designs dissimilar to the overly simplified NDM. The second direction of future work is related to investigating the potential of using fractional Laplacian for electrophysiological measurement applications instead of currently used regular Laplacian [35].

5. Conclusions

In this study, a CRE comparison framework was proposed and validated on human ECG data. This analytic framework is based on FDM and allows direct comparison of any two CRE configurations of the same size and with the same number of rings but with different inter-ring distances, radii of the central disc, and the widths of concentric rings in terms of the accuracy of their respective Laplacian estimates. The main advantage of such a framework stems from its potential to form the basis for future comprehensive optimization of CRE design where all the possible CRE configurations of the same size and with the same number of rings are compared to select configurations providing the highest accuracy of Laplacian estimation. With the ability to estimate the Laplacian accurately at each electrode constituting the primary biomedical significance of CREs, reported human Laplacian ECG signals from 20 volunteers were not just consistent with the analytic results but also showed high P-wave contrast suggesting an improved spatial resolution. Resulting in better ability to capture atrial activity could facilitate its study and reduce the need for digital processing for further improvement, thus being of interest for real-time clinical diagnosis systems.