Command-Filtered Backstepping Integral Sliding Mode Control with Prescribed Performance for Ship Roll Stabilization

Abstract

In this paper, a novel, robust fin controller based on the backstepping control strategy and sliding mode control is proposed to handle the problem of ship roll stabilization. First, the mathematical model of the fin control system is established, including the modeling errors and the external disturbances generated by sea waves. In order to address the side effects caused by differential expansion, a command-filter is implemented within the backstepping controller design. By introducing a new performance function and a corresponding error transformation, the compensated tracking error can be bounded to achieve the desired prescribed dynamic and steady-state responses. The sliding mode disturbance rejection control with prescribed performance is realized by combining the disturbance observer. Simulations are presented to demonstrate the effectiveness of the proposed control scheme.

1. Introduction

During recent decades, the problem of ship roll stabilization has been increasingly tackled by researchers due to a demand for higher cargo safety, on-board staff effectiveness, passenger comfort, and on-board equipment operation [1,2,3]. In order to reduce the effect of roll motion, several solutions have been devised. Examples include bilge keels, gyroscopic stabilizers, anti-rolling tanks, active fins, and rudder roll stabilization [3]. Among these promising techniques, the fin stabilizer is one of the most interesting devices due to its reliability, engineering feasibility and high efficiency. The effectiveness of the fin stabilizer is demonstrated especially when the ship navigates at higher speeds, as it can provide considerable damping to the ship roll angle and the corresponding roll rate [4].

As a key problem in sailing, environmental disturbances, such as waves, sea winds and underwater currents, will damage the stability of the system and induce rolling. Some attempts to deal with these disturbances can be found in [3,4,5,6,7,8]. Due to the difficulty in predicting the value of external disturbances, Sun et al. [3] decoupled the fin hydrodynamic force and severe disturbances using a force sensor and a novel mechanical decoupling method. Ghaemi et al. [4] reduced the impact caused by unknown disturbances using a robust control method when the discrete fin stabilizer system model is confronted with bounded additive disturbances. In [5], a self-tuning proportion-integration-differentiation (PID) controller, based on two multilayer neural networks, was constructed for suppressing the impact of the external disturbance with self-tuning PID gains. In order to eliminate the moments induced by disturbance, in [6] a lift-feedback control of fin stabilizers based on a new measuring lift device was proposed. In [7], the simulation of the multi-island genetic algorithm (MIGA) PID controller showed that the fin stabilizer is an effective method of roll angle reduction in the presence of external disturbances. However, the aforementioned methods will inevitably increase the controller design difficulty and the computational complexity of the control system. In addition, the disturbance observer is capable of estimating the unknown disturbance while integrated with other advanced control techniques. In [9], a nonlinear disturbance observer is proposed the multilink robotic manipulators; this observer relaxes the constraints on the prior knowledge of the acceleration signals. Zhang et al. [10] investigated the combination of the disturbance observer and the prescribed performance control methods, which eliminate the impact of these external disturbances effectively. In this study, the impact of the external disturbance was also suppressed through the adoption of a nonlinear disturbance observer.

When performing certain tasks, the roll angle of a ship should be adjusted through an expected dynamic process and the steady-state working performance. The controllers that are capable of providing this desired dynamic process and steady-state performance are usually based on the prescribed performance control [11,12,13,14,15,16]. In [11], a robust controller for a multi-input multi-output (MIMO) system was proposed based on adaptive control with respect to the prescribed performance. Bechlioulis et al. [12] proposed an adaptive prescribed performance controller where the error convergence trajectory, the overshoot, and the steady-state error are constrained by a prescribed performance function. The corresponding studies also investigated some actual systems, such as flexible air-breathing hypersonic vehicles [13], variable stiffness actuated robots [14], and unknown high-order nonlinear multi-agent systems [16]. Considering the superior characteristics of the prescribed performance control, it may be one of the most effective strategies to provide an expected performance for the ship rolling system.

To simplify the controller design process with prescribed performance, many researchers focus on the backstepping control strategy [17,18,19,20,21,22,23,24,25]. A novel backstepping control method was developed in [17] for a class of uncertain system, and the stability of the system was examined under the impact of artificial delays. In [18], an adaptive backstepping approach was proposed for the nonlinear systems with quantized states to solve the discontinuity problem brought by state quantization. However, the above backstepping methods inevitably have the problem of differential expansion, which will damage the control performance and affect the stability of the system, especially for high-order systems. In addition, the differential signals are easily affected by high-frequency disturbances or uncertainties. In order to address this problem, Farrell et al. [20,21] utilized a compensated tracking error signal to introduce the concept of the command filter so that the problem can be addressed. In [25], modified error compensation signals were proposed along with new virtual control signals so as to ensure the finite-time tracking performance for a class of nonlinear systems. Besides, the backstepping control was applied to practical engineering by combining other advanced control methods like sliding mode control for better control performance, which has been investigated by researchers [19,22]. In [19], the proposed backstepping control strategy was incorporated with a predictive model control method to maintain the DC-bus voltage in the photovoltaic (PV) grid-connected system. Xu et al. [22] integrated adaptive sliding mode control with the command filter-based backstepping control strategy for the linear induction motor with end effects, uncertain parameters and external disturbances to solve its speed control problem. However, they have no assurance of the control performance and range of tracking error.

Motivated by the aforementioned studies, an adaptive command filter-based backstepping controller (CBC) is presented for the ship roll stabilization in this paper. The dynamic performance and the steady-state of the compensated tracking error is guaranteed through the implementation of the prescribed performance control strategy. To offset the impact caused by external disturbances, a nonlinear disturbance observer is constructed and the stability of the whole system is examined via Lyapunov stability criterion. Due to the time-delay in the estimation, a disturbance estimation error may exist in the design of the proposed command-filter based backstepping controller. To eliminate the impact caused by this error, an adaptive control method is integrated with the design of the prescribed performance controller. The main contributions of this study are as follows:

• To the best of the author’s knowledge, the result in this paper is the first attempt to incorporate a prescribed performance control strategy in the ship rolling system control with adaptive sliding mode control.
• Compared to some existing methods, the impact caused by the external disturbances and the system uncertainty is taken into account, even with the estimation delay problem that is eliminated by the adaptive control strategy.

This paper is organized as follows: In Section 2, the system dynamics, command filter and the background knowledge for the prescribed performance control strategy are presented. In Section 3, the command-filter based controller with prescribed performance is constructed and the effectiveness of the disturbance observer is analyzed. Section 4 demonstrates the simulation results. Conclusions and future work are presented in Section 5.

2. Problem Formulation

2.1. System Dynamic

We note that the ship roll angles may have a large range. As a result, the traditional ship motion mathematical model, which is based on Conolly’s theory, is no longer applicable. According to some reasonable simplifications, the ship roll dynamic equation in [1,26] is formulated as follows

$$\dot{\varphi }=p^{\prime }\frac{U}{L}$$

(1)

$$\left(I_x^{\prime }+J_x^{\prime }\right){\dot{p}}^{\prime }-A^{\prime }{p}^{\prime }-B^{\prime }\left|p^{\prime }\right|p^{\prime }+W^{\prime }G{M}^{\prime }\varphi =K^{\prime }-2A_F^{\prime }{C}_L{\alpha }_f{l}_f^{\prime }$$

(2)

where $\varphi$ is the rolling angle of the ship, $I_x^{\prime }$ is the moments of inertia, $J_x^{\prime }$ is the added inertia moments, $A^{\prime }$ and $B^{\prime }$ are the so-called roll motion damping coefficients, $GM$ is the initial metacentric height, ${\alpha }_f$ is the control moment generated by the fin stabilizer, K is the moment caused by the sea wave, L is the ship length between ship perpendiculars, g is the gravity acceleration constant, $\rho$ is the water density, U is the ship speed, $A_f$ is the fin area, $l_f$ is the acting force arm of the fin stabilizer, and $C_L$ is the slope of lift coefficient. Symbol ‘${}^{\prime }$’ denotes dimensionless variables. According to Equations (1) and (2), the dynamic equation of the rolling angle can be rewritten in the following way,

$$\dot{p^{\prime }}=a_1\varphi +a_2{p}^{\prime }+a_3{p}^{\prime }\left|p^{\prime }\right|+b{\alpha }_f+F$$

(3)

where $a_1=-W^{\prime }G{M}^{\prime }/(I_x^{\prime }+J_x^{\prime })$, $a_2=A^{\prime }/(I_x^{\prime }+J_x^{\prime })$, $a_3=B^{\prime }/(I_x^{\prime }+J_x^{\prime })$, $b=-2A_F^{\prime }{C}_L{l}_f^{\prime }/(I_x^{\prime }+J_x^{\prime })$ and $F=K^{\prime }/(I_x^{\prime }+J_x^{\prime })$.

We define $x={[x_1,x_2]}^T={[\varphi ,p^{\prime }]}^T$ as the state vector, $y=\varphi =x_1$ as the output and $u={\alpha }_f$ as the control input. Considering the unknown part in the modeling process and the uncertainty caused by the external sea wave, the dynamic Equation (3) can be written as

$${\dot{x}}_1=\frac{U}{L}{x}_2$$

(4)

$${\dot{x}}_2=a_1{x}_1+a_2{x}_2+a_3{x}_2\left|x_2\right|+bu+F$$

(5)

$$y=x_1.$$

(6)

Denoting $f\left(x\right)=a_1{x}_1+a_2{x}_2+a_3{x}_2\left|x_2\right|$, $c=U/L$. The system dynamic equation can be simplified as follows

$${\dot{x}}_1=c{x}_2$$

(7)

$${\dot{x}}_2=f\left(x\right)+bu+F.$$

(8)

2.2. Command Filter

In order to mitigate the impact of the differential expansion as well as of the input saturation problem, Farrell et al. [20,21] introduced a constrained command filter in the design of the backstepping control strategy. The corresponding command filter, which is depicted in Figure 1 is as follows

$$\left[\begin{array}{c}{\dot{q}}_1\\ {\dot{q}}_2\end{array}\right]=\left[\begin{array}{c}{q}_2\\ 2\xi {\omega }_n\left[S_R\left(\frac{{\omega }_n^2}{2\xi {\omega }_n}\left(S_M\left(u\right)-q_1\right)\right)-q_2\right]\end{array}\right]$$

(9)

where

$$\left[\begin{array}{c}{q}_1\\ q_2\end{array}\right]=\left[\begin{array}{c}{x}^c\\ {\dot{x}}^c\end{array}\right],u=x^d$$

and $\xi$ and ${\omega }_n$ are the damping and the bandwidth of the filter, respectively, $S_R(·)$ and $S_M(·)$ represent the rate and the magnitude limits, respectively.

2.3. Prescribed Performance Control and Error Transformation

To guarantee the transient and steady-state performance, the prescribed performance control strategy is adopted here. The objective is to translate the prescribed performance into tracking error constraints and cause the compensated tracking error signals ${\overline{z}}_1$(defined later) to exhibit the desired transient and steady-state performance.

In order to achieve the desired control objective, the so-called performance function is proposed, which bounds the system’s performance. The definition of the performance function is as follows:

Definition 1

([11]). A smooth function $\rho \left(t\right):{\mathcal{R}}^{+}\to {\mathcal{R}}^{+}$ will be called as a performance function if it satisfies

(1) 

$\rho \left(t\right)$ is positive and decreasing

(2) 

${lim}_{t\to \infty }\rho \left(t\right)={\rho }_{\infty }>0$.

The function $\rho \left(t\right)$ is conventionally selected as

$$\rho \left(t\right)=({\rho }_0-{\rho }_{\infty })e^{-lt}+{\rho }_{\infty }$$

(10)

where ${\rho }_0$, ${\rho }_{\infty }$ and l are positive scalars. By using the performance function, the compensated tracking error ${\overline{z}}_1$ is bounded by the following constraints,

$$\left\{\begin{array}{cc}-M\rho \left(t\right)<{\overline{z}}_1\left(t\right)<\rho \left(t\right),\hfill & {\overline{z}}_1\left(0\right)>0\hfill \\ -\rho \left(t\right)<{\overline{z}}_1\left(t\right)<M\rho \left(t\right),\hfill & {\overline{z}}_1\left(0\right)<0\hfill \end{array}\right.$$

(11)

where $0\le M\le 1$. According to the performance function (10) and the performance constraints (11), if the initial value of the compensated tracking error ${\overline{z}}_1$ satisfies $0\le |{\overline{z}}_1\left(0\right)|<{\rho }_0$, the behavior of ${\overline{z}}_1\left(t\right)$ will be governed by the performance function $\rho \left(t\right)$ and the convergence speed of the compensated tracking error can be bounded by the performance function as well.

In order to transform the constrained system performance into an equivalent unconstrained one, an error transformation is proposed here with respect to the system dynamics, the compensated tracking error and the performance constraints in (11). More specifically, the error transformation function is defined as

$${\overline{z}}_1\left(t\right)=\rho \left(t\right)\mathcal{L}\left(\epsilon \left(t\right)\right)$$

(12)

where $\epsilon \left(t\right)$ is the transformed error and $\mathcal{L}(·)$ is a smooth, strictly increasing and invertible function. In addition, $\mathcal{L}(·)$ possesses the following properties.

$$-M<\mathcal{L}\left(\epsilon \right)<1,{\overline{z}}_1\left(0\right)>0$$

(13)

$$-1<\mathcal{L}\left(\epsilon \right)<M,{\overline{z}}_1\left(0\right)<0$$

(14)

$$\left\{\begin{array}{c}\underset{\epsilon \to -\infty }{lim}\mathcal{L}\left(\epsilon \right)=-M,\hfill \\ \underset{\epsilon \to \infty }{lim}\mathcal{L}\left(\epsilon \right)=1,\hfill \end{array}\right.{\overline{z}}_1\left(0\right)>0$$

(15)

$$\left\{\begin{array}{c}\underset{\epsilon \to -\infty }{lim}\mathcal{L}\left(\epsilon \right)=-1,\hfill \\ \underset{\epsilon \to \infty }{lim}\mathcal{L}\left(\epsilon \right)=M,\hfill \end{array}\right.{\overline{z}}_1\left(0\right)<0.$$

(16)

A function $\mathcal{L}$, which satisfies all the constraints, can be selected as

$$\mathcal{L}\left(\epsilon \right)=\left\{\begin{array}{cc}\frac{e^{\epsilon }-M{e}^{-\epsilon }}{e^{\epsilon }+e^{-\epsilon }},\hfill & \mathrm{if}{\overline{z}}_1\left(0\right)>0\hfill \\ \frac{M{e}^{\epsilon }-e^{-\epsilon }}{e^{\epsilon }+e^{-\epsilon }},\hfill & \mathrm{if}{\overline{z}}_1\left(0\right)<0.\hfill \end{array}\right.$$

(17)

From the error transformation function (12) and the definition of function $\mathcal{L}$, the transformation error can be rewritten as

$$\epsilon \left(t\right)={\mathcal{L}}^{-1}\left(\frac{{\overline{z}}_1\left(t\right)}{\rho \left(t\right)}\right).$$

(18)

Remark 1.

Once ε remains bounded, whenever ${\overline{z}}_1\left(0\right)>0$, it can be obtained that $-M<\mathcal{L}\left(\epsilon \right)<1$. From $\rho \left(t\right)>0$ and (12), it can be found that $-M\rho \left(t\right)<{\overline{z}}_1\left(t\right)<\rho \left(t\right)$. Otherwise, whenever ${\overline{z}}_1\left(0\right)<0$, it can be obtained that $-\rho \left(t\right)<{\overline{z}}_1\left(t\right)<M\rho \left(t\right)$. Therefore, the error transformation function can guarantee the prescribed performance of the whole system.

2.4. Problem Formulation

In this paper, a novel command-filter backstepping control method is investigated for the ship rolling system in the following aspects:

(1)

By designing a proper backstepping control method that integrates the command-filter technique, the system output $x_1$, namely the rolling angle, can be uniformly ultimately bounded.

(2)

The compensated tracking error ${\overline{z}}_1$ can obtain the prescribed transient and steady-state performance with respect to the proposed control strategy.

(3)

In order to offset the impact caused by external disturbances, a disturbance observer is proposed in this paper to provide the estimation of the external disturbances during the design of the command-filter backstepping controller.

For the development of the prescribed performance controller with command-filter backstepping method, the following assumptions are required:

Assumption 1

([11]). The rolling angle φ, its derivative $\dot{\phi }$ and the acceleration of the rolling angle $\ddot{\phi }$ are bounded.

Assumption 2

([9]). The disturbance is bounded and it satisfies $\left|F\right|\le \overline{F}$, where $\overline{F}$ is a positive scalar.

3. Main Result

3.1. Command-Filter Based Controller Design with Prescribed Performance

In this section, a command-filter based backstepping controller with prescribed performance is designed. Firstly, some new error variables are defined as follows,

$$z_1=x_1-x_1^c$$

(19)

$$z_2=x_2-x_2^c$$

(20)

where the definitions of $x_1^c$ and $x_2^c$ are along with the classic command-filter backstepping controller design in [22]. In addition, $x_1^c=x_1^d$ and $x_1^d$ is the desired rolling angle signal. $x_2^c$ is the output of the command-filter. The compensated tracking error ${\overline{z}}_1$ is defined as

$${\overline{z}}_1=z_1-{\zeta }_1$$

(21)

and the ${\zeta }_1$ signal is chosen as

$$\dot{{\zeta }_1}=-k_1{\zeta }_1+(x_2^c-x_2^d)$$

(22)

where $x_2^d$ is the desired value of $x_2$, which can be utilized to stabilize the outer loop.

In order to obtain the prescribed performance, the stability of the transformation error $\epsilon \left(t\right)$ should be validated. By taking the derivation of $\epsilon \left(t\right)$ with respect to time, it yields

$$\begin{array}{cc}\hfill \dot{\epsilon }& =\frac{\partial {\mathcal{L}}^{-1}}{\partial ({\overline{z}}_1/\rho )}\frac{1}{\rho }\left({\dot{x}}_1-{\dot{x}}_1^c-{\dot{\zeta }}_1-\frac{\dot{\rho }{\overline{z}}_1}{\rho }\right)\hfill \\ \hfill & =r(c{x}_2-{\dot{x}}_1^c-{\dot{\zeta }}_1+\nu )\hfill \end{array}$$

(23)

where $r=\frac{\partial {\mathcal{L}}^{-1}}{\partial ({\overline{z}}_1/\rho )}\frac{1}{\rho }$, $\nu =-\frac{\dot{\rho }{\overline{z}}_1}{\rho }$. And for the inner loop, an integral sliding mode surface is given as follows

$$s=z_2+a{\int }_0^t{z}_2^{m/n}dt$$

(24)

where a is a positive scalar, m and n are add integers satisfying $n>m>0$. The reaching law for the sliding mode surface is selected as

$$\dot{s}=-k_{3}s-\tau sign\left(s\right)$$

(25)

where $k_3>0$ and $\tau >0$ are two positive real scalars. Before presenting the first main result of this study, the desired virtual controller $x_2^d$ is selected as

$$x_2^d=-k_1{\zeta }_1+{\dot{x}}_1^c-\nu -k_2\epsilon$$

(26)

and the controller $u^d$ is chosen as

$$u=b^{-1}\left(-f\left(x\right)+{\dot{x}}_2^c-a{z}_2^{m/n}-k_{3}s-\tau sign\left(s\right)-\overline{F}sign\left(s\right)\right).$$

(27)

Theorem 1.

For the rolling angle dynamic system (7) and (8), suppose that Assumptions 1 and 2 hold, the transformation error $\epsilon \left(t\right)$ and $z_2$ are asymptotically stable by the proposed virtual controller (26) and the sliding mode controller (27) while ${\overline{z}}_1$ converges to the neighbor domain of 0 with the prescribed performance.

Proof of Theorem 1.

In this position, the Lyapunov function is selected as

$$V_1=\frac{1}{2r}{\epsilon }^2+\frac{1}{2}{s}^2$$

(28)

Taking the derivation of $V_1$ with respect to time, it yields

$$\begin{array}{cc}\hfill {\dot{V}}_1& =\epsilon ·\left(x_2-{\dot{x}}_1^c-{\dot{\zeta }}_1+\nu \right)+s\left({\dot{z}}_2+a{z}_2^{m/n}\right)\hfill \\ \hfill & =\epsilon ·\left(x_2-{\dot{x}}_1^c+k_1{\zeta }_1-x_2^c+x_2^d+\nu \right)+s\left({\dot{z}}_2+a{z}_2^{m/n}\right).\hfill \end{array}$$

(29)

Substituting (26) into (29), it can be obtained that

$${\dot{V}}_1=-k_2·{\epsilon }^2+\epsilon z_2+s\left(f\left(x\right)+bu+F-{\dot{x}}_2^c+a{z}_2^{m/n}\right),$$

(30)

and the following relationship holds as

$$\epsilon ·z_2\le \frac{1}{2}{\epsilon }^2+\frac{1}{2}{z}_2^2\le \frac{1}{2}{\epsilon }^2+\frac{1}{2}{s}^2.$$

Substituting the sliding mode controller (27) into (30),

$$\begin{array}{cc}\hfill {\dot{V}}_1& \le -\left(k_2-\frac{1}{2}\right)·{\epsilon }^2+\frac{1}{2}{s}^2+s\left(f\left(x\right)+bu+F-{\dot{x}}_2^c+a{z}_2^{m/n}\right)\hfill \\ \hfill & \le -\left(k_2-\frac{1}{2}\right)·{\epsilon }^2-\left(k_3-\frac{1}{2}\right)s^2+s\left(F-\overline{F}sign\left(s\right)\right)-\tau \left|s\right|\hfill \\ \hfill & \le -\left(k_2-\frac{1}{2}\right)·{\epsilon }^2-\left(k_3-\frac{1}{2}\right)s^2\le 0.\hfill \end{array}$$

(31)

This implies that, with the implement of the proposed virtual controller, the transformation errors $\epsilon$ and $z_2$ are asymptotically stable. Meanwhile, the dynamic and steady-state response of the compensated tracking error ${\overline{z}}_1$ is guaranteed through the prescribed performance by selecting a proper value of M. This completes the proof. □

Remark 2.

In Theorem 1, it can be seen found that the transformation ε is asymptotically stable and this guarantees that ε will converge to 0. However, the value of M cannot be set to 0 as as $\epsilon \left(t\right)$ will become infinite. Therefore, the time response of ${\overline{z}}_1$ is uniformly ultimately bounded.

Remark 3.

For the design of the proposed sliding mode controller, the upper bound of the disturbance F should be known in advance. This reduces the applicability of the proposed control strategy in real industrial processes. This drawback will be eliminated in the following subsection.

3.2. Command-Filter Based Controller Design with Prescribed Performance and Disturbance Observer

In this subsection, a disturbance observer is proposed in order to provide a better estimation of the disturbance in the design of the command-filter based controller with prescribed performance. The structure of command-filtered backstepping integral sliding mode control with prescribed performance for ship roll stabilization strategy developed in this study is shown in Figure 2.

From (8), it can be obtained that

$$F=-f\left(x\right)+bu+{\dot{x}}_2.$$

(32)

Therefore, the disturbance observer for (32) is designed as follows

$$\widehat{F}=\lambda +l_f(x_1,x_2)$$

(33)

$$\dot{\lambda }=-l_o\lambda +l_o\left(-f\left(x\right)+bu-l_f(x_1,x_2)\right)$$

(34)

where $l_f(x_1,x_2)=l_o{x}_2$ and $l_o$ is a positive scalar. In addition, the estimation error $\tilde{F}$ is defined as $\tilde{F}=F-\widehat{F}$. With the implement of the disturbance observer, the impact caused by disturbance can be offset.

Due the estimation time delay, the estimation error still exists before the disturbance observer can give an accurate estimation of the disturbance. It is reasonable to assume that the estimation error $\tilde{F}$ satisfies that $|\tilde{F}|\le \kappa$. The proposed controller is modified as

$$u=b^{-1}\left(-f\left(x\right)+{\dot{x}}_2^c-a{z}_2^{m/n}-k_{3}s-\tau sign\left(s\right)-\widehat{F}-\widehat{\kappa }sign\left(s\right)\right)$$

(35)

$$\dot{\widehat{\kappa }}=ϵs·sign\left(s\right)$$

(36)

where $\kappa$ and $ϵ$ are positive scalars.

Theorem 2.

For the rolling angle dynamic system (7) and (8), suppose that Assumptions 1–2 hold, the transformation error $\epsilon \left(t\right)$ and $z_2$ are asymptotically stable by the proposed virtual controller (26) and the sliding mode controller (35) with the disturbance observer (33) while ${\overline{z}}_1$ converges to the neighbor domain of 0 with the prescribed performance.

Proof of Theorem 2.

Considering the following Lyapunov function

$$V_2=\frac{1}{2r}{\epsilon }^2+\frac{1}{2}{s}^2+\frac{1}{2}{\tilde{F}}^2+\frac{1}{2ϵ}{\tilde{\kappa }}^2,$$

(37)

denoting $\tilde{\kappa }=\kappa -\widehat{\kappa }$, it can be obtained

$$\begin{array}{cc}\hfill {\dot{V}}_2& \le -\left(k_2-\frac{1}{2}\right)·{\epsilon }^2+\frac{1}{2}{s}^2+s\left(f\left(x\right)+bu+F-{\dot{x}}_2^c+a{z}_2^{m/n}\right)-\tilde{F}\dot{\widehat{F}}-\tilde{\kappa }\dot{\widehat{\kappa }}\hfill \\ \hfill & \le -\left(k_2-\frac{1}{2}\right)·{\epsilon }^2-\left(k_3-\frac{1}{2}\right)s^2+s\left(F-\widehat{F}-\widehat{\kappa }sign\left(s\right)\right)-\tilde{\kappa }s·sign\left(s\right)\hfill \\ \hfill & -\tilde{F}\left(-l_o\lambda +l_o\left(-f\left(x\right)+bu-l_f(x_1,x_2)\right)+{\dot{l}}_f(x_1,x_2).\right)\hfill \end{array}$$

(38)

Due to (32)–(34),

$$\begin{array}{cc}\hfill {\dot{V}}_2& \le -\left(k_2-\frac{1}{2}\right)·{\epsilon }^2-\left(k_3-\frac{1}{2}\right)s^2+s\left(\tilde{F}-\widehat{\kappa }sign\left(s\right)\right)-\tilde{\kappa }s·sign\left(s\right)\hfill \\ \hfill & -\tilde{F}\left(-l_o\widehat{F}+l_o\left(-f\left(x\right)+bu)\right)+{\dot{l}}_f(x_1,x_2)\right)\hfill \\ \hfill & \le -\left(k_2-\frac{1}{2}\right)·{\epsilon }^2-\left(k_3-\frac{1}{2}\right)s^2+s\left(\tilde{F}-\kappa ·sign\left(s\right)\right)+s\kappa ·sign\left(s\right)\hfill \\ \hfill & -s\widehat{\kappa }·sign\left(s\right)-\tilde{\kappa }s·sign\left(s\right)-\tilde{F}\left(-l_o\widehat{F}+l_{o}F\right)\hfill \\ \hfill & \le -\left(k_2-\frac{1}{2}\right)·{\epsilon }^2-\left(k_3-\frac{1}{2}\right)s^2-l_o{\tilde{F}}^2.\hfill \end{array}$$

(39)

□

Remark 4.

It implies that the error system still can be stable while the upper bound of the lumped disturbance is no longer needed here. It implies that the proposed prescribed performance control strategy possesses the real industrial potential in the ship stabilizer design with the implement of the nonlinear disturbance observer.

Remark 5.

In order to eliminate the chattering phenomenon in the simulation verification phase, the discontinuous terms $sign\left(s\right)$ in (27) and (35) are replaced by the saturation functions $sat(s/\delta )$, where δ is known as the boundary layer thickness of saturation function.

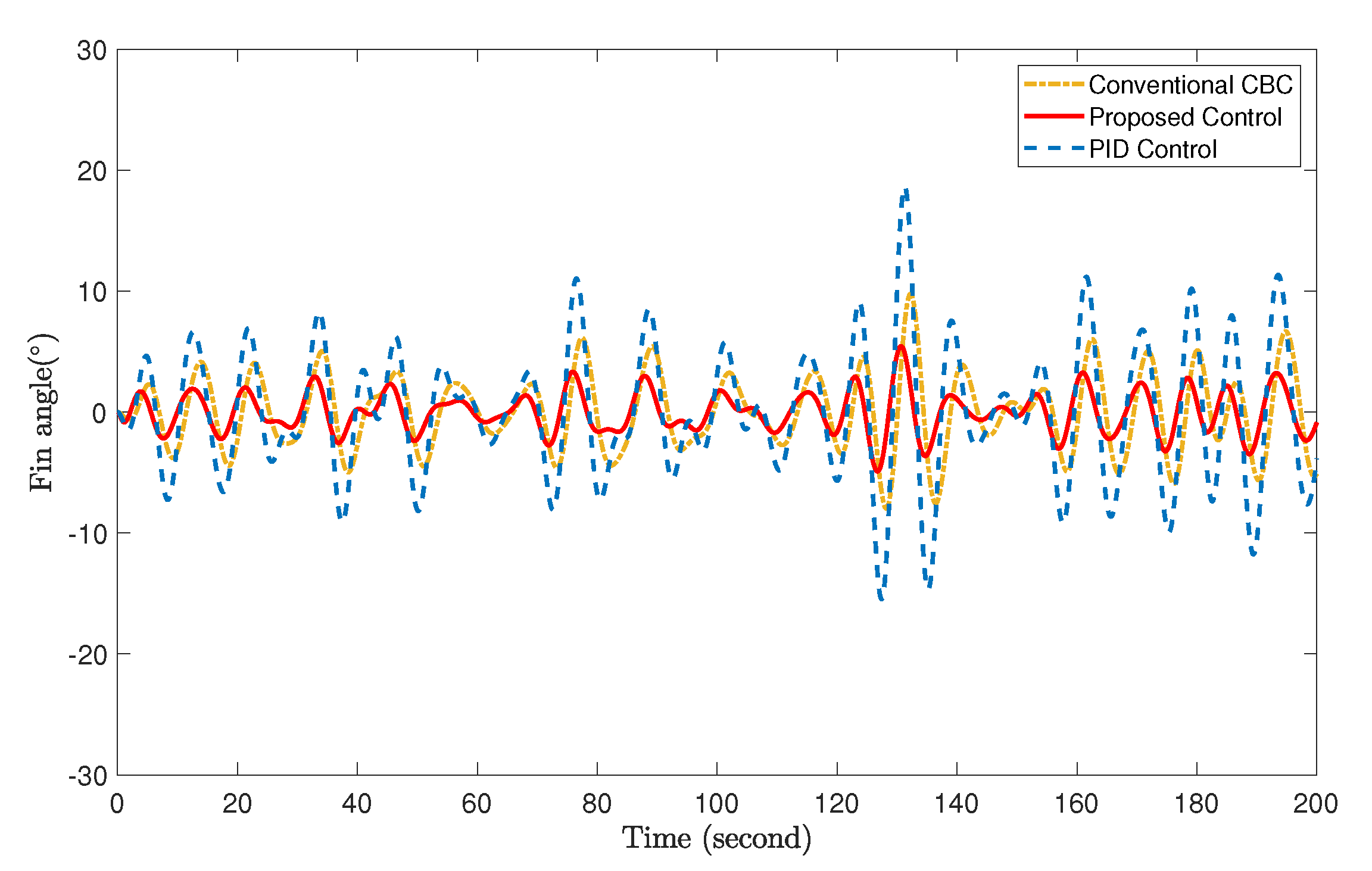
4. Simulation

To validate the proposed command-filter based sliding mode controller and evaluate prescribed performance of the compensated tracking error, the corresponding simulation is carried out and the roll stabilization performance is also tested, as shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 in this section. The particulars of the ship are shown as follows: the ship length is 175 $\mathrm{m}$, the ship speed is 12.43 Kn, the fin area is 12 ${\mathrm{m}}^2$, the acting force arm of the stabilizer fin is 16 $\mathrm{m}$, the lift coefficient of fin stabilizer is 2.1, the initial metacentric height is 0.3 m, the inertia $I_x^{\prime }=0.0000176$, the additional inertia $J_x^{\prime }=0.0000034$, and the damping coefficient $A^{\prime }=-1.2552\times {\mathrm{e}}^{-5}$, $B^{\prime }=-4.725\times {\mathrm{e}}^{-8}$.

In addition, the parameters of the proposed controller are selected as $k_1=4$, $k_2=4$, $k_3=3$, ${\rho }_0=0.001$, $M=0.5$, ${\rho }_{\infty }=0.0005$, $\tau =0.1$, $a=0.5$, $b=-7.165$, and $ϵ=2$. The original state of the ship rolling angle is assumed as $\varphi \left(0\right)=0^{°}$. In addition, the initial state of the nonlinear disturbance observer is selected as 0 as well.

In addition, the six-level sea wave momentum that acts on the ship body is gathered from a real environment and depicted in Figure 3. In order to offset the impact caused by the sea wave momentum, the corresponding estimation of the sea wave is demonstrated in Figure 4. It can be noticed that the estimation of the external disturbance, which is also known as sea wave momentum, can fit the real time curve of the sea wave with desired performance at the time point of 10 s.

In order to validate the effectiveness of the proposed prescribed performance control strategy, the time response of the compensated tracking error ${\overline{z}}_1$ is shown in Figure 5. It can be noticed that the amplitude of the compensated tracking error ${\overline{z}}_1$ is bounded by the prescribed performance function $\rho \left(t\right)$. Hence, the dynamic performance and the steady-state of the compensated tracking error ${\overline{z}}_1$ is guaranteed. Consequently, the ship’s rolling angle can provide a desired dynamic process and the steady-state output, which is demonstrated in Figure 6, with respect to the impact caused by the six-level sea wave momentum.

As is shown in Figure 6, Figure 7 and Figure 8, different control strategies are examined through numerical simulations. When the control input is absent, the roll angle cannot be stabilized with respect to the external disturbance within a reasonable amount of time and the amplitude of the rolling angle varies within a relatively large range. The traditional PID controller improves performance significantly compared to the previous situation without control, however, the roll motion response of the ship still changes within an undesirable range. The conventional CBC exhibits better performance than PID with the smaller ship rolling angle. In contrast, the proposed controller in this paper performs better than the PID controller and CBC, and it can be seen that the ship’s roll angle in the proposed controller operation is evidently constrained in the neighborhood of 0 owing to the introduction of prescribed performance. In addition, Figure 7 and Figure 8 indicate that the control input generated by the proposed control strategy is bounded to less than 10${}^{°}$ and 5${}^{°}$/$\mathrm{s}$, which is known as the fin control angle $a_f$ and fin rate, which demonstrates our strategy’s superior performance when compared to the traditional PID controller and CBC.

5. Conclusions

In this paper, a command-filter based backstepping sliding mode controller with prescribed performance is established to realize the ship roll stabilization. First, the impact of external disturbances is eliminated by the formulated nonlinear disturbance observer. Second, the differential expansion problem is avoided through the implementation of a command filter-based backstepping control method. Third, the dynamic performance and the steady-state of the ship rolling angle is guaranteed under our proposed controller by integrating the prescribed performance technique, which ensures the relatively precise tracking performance. The robustness of the proposed control strategy is verified, in that the ship rolling angle exhibits as relatively small with little change when facing the six-level sea wave momentum. Moreover, the favorable control performance of the proposed controller is validated by comparison with the conventional PID and CBC, which indicates that the proposed controller takes effect on the ship roll stabilization.

In future work, the fin stabilizer saturation problem will be addressed through a modified control strategy and applied in experimental cases.