Experimental Study on a Prediction Model of the Shrinkage and Creep of Recycled Aggregate Concrete

Featured Application

The effects of the recycled aggregate replacement rate and water–cement ratio on shrinkage and creep properties were analyzed. The degree of shrinkage and creep of ordinary concrete and recycled aggregate concrete at different ages were compared. A coefficient of increase and a coefficient of contraction increase of the attached mortar were proposed. Based on the old attached mortar, a shrinkage and creep model of recycled aggregate concrete was established.

Abstract

The significant difference between recycled aggregate and natural aggregate is the content of the attached mortar layer. With the increase of the replacement rate of recycled aggregate, the shrinkage and creep of recycled aggregate concrete is significantly increased. In this paper, 180-day shrinkage and creep tests of recycled aggregate concrete with different water–cement ratios were designed in order to analyze the effect of the substitution rate and water–cement ratio on shrinkage and creep properties. The results show that the shrinkage strain of recycled aggregate concrete with a substitution rate of 50% and 100% at 180 days is 26% and 48% higher than that of ordinary concrete, respectively, and the growth of group II is 22% and 47%, respectively. When the load was 180 days old, the creep coefficient of recycled aggregate concrete with a substitution rate of 50% and 100% in group I increased by 19.6% and 39.6%, respectively compared with ordinary concrete, and group II increased by 23.6% and 44.3%, respectively. Based on the difference of adhering mortar content, the creeping increase coefficient and shrinkage increase coefficient of the attached mortar were proposed, and a shrinkage and creep model of recycled aggregate concrete was established. When compared with the experimental results, the model calculation results met the accuracy requirements.

1. Introduction

The recycling of construction waste (RCW) refers to the crushing of construction waste to obtain different types of products and reuse them as resources. An important product of RCW is recycled aggregate, which itself is attached to old mortar that is difficult to peel due to the limitation of crushing technology. Therefore, it can be approximated that recycled aggregate is a two-phase material composed of the old mortar and the natural aggregate wrapped therewith. Recycled aggregate concrete (RAC) refers to recycled aggregate, which is made by crushing and classifying waste concrete and mixing according to a certain proportion, and partially or completely replacing the natural aggregate to make new concrete referred to as RAC [1]. RAC not only digests waste concrete and solves the problem of a serious shortage of natural resources, but also meets the requirements of existing specifications under reasonable design. It is a green building material worthy of promotion. At present, domestic and foreign countries have given eager attention and long-term exploration of RAC, especially towards the shrinkage and creep of the concrete, which can cause structural deterioration and safety problems. Based on a number of research reports on concrete shrinkage and creep [2,3,4], the effects of concrete shrinkage and creep mainly include the increase of beam deflection and the reduction of structural bearing capacity. In addition, the shrinkage and creep of the concrete can also cause prestressing loss of the prestressed members and secondary internal forces that create the structure. In the local area of the concrete, due to the shrinkage of internal stress, it is easy for problems such as cracks on the outer surface of the member to be created. In view of the fact that RAC has properties close to that of ordinary concrete [5,6,7,8,9,10,11,12], the structural adverse effects caused by shrinkage and creep are similar or even more serious than in natural concrete. Therefore, the research on the shrinkage and creep of RAC has an irreplaceable significance.

Many scholars have conducted relevant research on the importance of the shrinkage and creep of RAC. Domingo-Cabo et al. [13] studied the shrinkage and creep tests of RAC with different substitution rates. The results show that with the increase of the replacement rate of recycled aggregates, the shrinkage and creep deformation of RAC increases. However, there is a lack of in-depth exploration of the impact of factors. Geng et al. [14] conducted experimental research on the creep behavior of RAC with different water–cement ratios of base concrete. The results show that the creep properties of recycled base concrete with a low water–cement ratio are significantly affected by recycled coarse aggregate (RCA), and the establishment of a prediction model for the creep of recycled base concrete needs to consider the influence of the water–cement ratio. However, the effects of different recycled aggregate-attached mortars on shrinkage and creep have not been deeply considered. Adam et al. [15] studied the shrinkage and creep of RAC based on three factors: curing condition, loading age, and axial stress level. The experimental results show that the corresponding average ratios of the shrinkage strain of RAC of a 50% and 100% substitution rate are 1.21 and 1.71, compared to ordinary concrete. Guo et al. [16] devoted himself to the study of the effect of old adhesive mortar on the creep of RAC. Based on the experimental data, it is proposed that the RAC with a 100% substitution rate develops more rapidly and the amplitude is 1.6 times larger than that of traditional concrete. Miguel et al. [17] explored the effect of recycled aggregates from Portuguese construction and demolition waste on the shrinkage and creep properties of concrete. The results showed that the creep coefficient of the 12 recycled aggregates tested at 91 days was 0.22 to 1.63. This proves that the shrinkage prediction model of ordinary concrete is not suitable for RAC, so research on a prediction model of the shrinkage and creep of RAC has become the focus of solving the problem of the shrinkage and creep of RAC.

Fathifazl et al. [18] pointed out that the prediction model of RAC creep should consider the influence of mortar attached to the aggregate surface. Based on the MC90 model, the predicted values of the model agree well with the experimental values. Brito et al. [19] studied the Gómez-Soberón test data, and the concrete creep coefficient was corrected considering the difference in apparent density or water absorption between recycled aggregate and natural aggregate. Based on the European standard EC2 model, Brito (D) and Brito (R) obtained two kinds of RAC creep prediction models. The prediction accuracy of the two models is good. Tošic et al. [20] explored the effect of recycled aggregates on the creep of concrete. It was pointed out that when using the creep prediction model of fib Model Code 2010 to predict the creep coefficient of RAC, the creep coefficient of RAC is underestimated relative to the performance of the model on the accompanying natural aggregate concrete (NAC). At the same time, compared with NAC, RAC shows a larger creep coefficient, and the average increase in the coefficient of creep is 39% for RAC at full replacement rate. Silva et al. [21] studied the correction coefficient of the concrete creep of different recycled aggregates and a prediction model suitable for recycled aggregate concrete. Compared with conventional concrete, the use of recycled aggregate to absorb part of the mixed water and cement slurry for coating produces a stronger ITZ (Interface transition zone), which can reduce the creep strain by up to 23%. Liu et al. [22] explored the calculation method of the long-term deformation of recycled concrete beams based on the creep adjustment coefficient. At the same time, the adjustment coefficient of the mortar creep bond was proposed. Three typical ordinary concrete shrinkage and creep prediction models were modified and used for long-term deformation calculation of recycled concrete beams. Luo et al. [23] proposed a model for the shrinkage and creep of RAC that considered the two factors of the regenerated aggregate grade and substitution rate, and the regression coefficient was used to obtain the influence coefficient expression. This can quantitatively calculate the influence coefficient of the shrinkage and creep of recycled aggregates with different quality and different substitution rates. Luo et al. [24] studied the influence coefficient of aggregate pretreatment on the creep behavior of RAC. Xiao et al. [25] corrected the q2 and q4 parameters in the B3 model based on the test results. Considering the influence of the replacement rate of the RCA, the calculated results of the modified model were in good agreement with the experimental results.

However, the existing method of proposing the correction coefficient by a certain influencing factor fails to establish the prediction model of the shrinkage and creep of RAC. In particular, for the effect of recycled aggregate-attached mortar on concrete shrinkage and creep, there is a lack of predictive models with universal significance. In this paper, the key difference between recycled aggregate and natural aggregate-attachment mortar is taken as the entry point, and the coefficient of increase and the coefficient of contraction increase of the attached mortar are proposed. Based on the two increasing factors, the shrinkage and creep model of RAC is established, and the applicability of the model is checked.

2. Shrinkage and Creep Test of Recycled Aggregate Concrete

2.1. Materials

The test materials were selected from PC32.5R ordinary Portland cement, natural coarse aggregate, RCA, natural fine aggregate, ordinary fine sand, and urban tap water. The RCA was provided by Shaanxi Science and Technology Environmental Protection Co., Ltd. (Xi’an, China), and its physical properties are shown in

Table 1. Physical properties of recycled coarse aggregate (RCA) and natural coarse aggregate (NCA).

Aggregate Type	Apparent Density/kg·m−3	Crushing Index/%	Moisture Content/%	Water Absorption Rate/%	Initial Stone/%	Secondary Aggregate/%	Mortar Block/%	Impurity/%
Recycled coarse aggregate	2458	17.0	1.33	3.83	29.5	51.2	16.0	3.3
Natural coarse aggregate	2658	10.6	4.21	0.69	98.7	—		1.3

.

2.2. Mix Proportion Design

According to JGJ55-2011 [26] “Ordinary concrete mix design rules”, the mixing ratio of natural aggregate concrete (NAC) was calculated. The mixing ratio of RAC was replaced by equal mass. The natural coarse aggregate in ordinary concrete was replaced by RCA. Considering that the water absorption of the RCA is higher than that of the natural coarse aggregate, a certain amount of additional water was added, which was 3.83% of the mass of the RCA. The concrete slump of each component during mixing is about 90 mm. The proportions of each group and the compressive strength of the concrete cubes are shown in

Table 2. Mix ratio of recycled aggregate concrete (RAC) and natural aggregate concrete (NAC).

Group Number	r/%	Effective Water–Cement Ratio	Material Consumption/kg·m−3						Compressive Strength/N/mm2
			Cement	Water	Natural Coarse Aggregate	Recycled Coarse Aggregate	Fine Aggregate	Additional Water
NAC-I	0	0.527	370	195	1185	-	660	-	33.3
RAC-50-I	50	0.527	370	195	592.5	592.5	660	22.69	31.6
RAC-100-I	100	0.527	370	195	-	1185	660	45.38	32.4
NAC-II	0	0.40	500	200	1086	-	611	-	35.1
RAC-50-II	50	0.40	500	200	543	543	611	20.8	32.3
RAC-100-II	100	0.40	500	200	-	1086	611	41.6	30.9

Note: Group I was the water–cement ratio (w/c) = 0.527 sample; Group II was the water–cement ratio = 0.4 sample. The additional water was calculated to take 3.83% of the weight of the recycled coarse aggregate under consideration of the water absorption rate of the recycled coarse aggregate.

.

2.3. Specimen Design

The creep test of RAC was carried out in accordance with “Test Method for Long-term Performance and Durability of Ordinary Concrete” [27]. The creep specimen size was 100 mm × 100 mm × 400 mm, the shrinkage specimen size was 100 mm × 100 mm × 515 mm, cubic specimen size was 150 mm × 150 mm × 150 mm, and prismatic specimen size was 150 mm × 150 mm × 300 mm. The specific number of specimens and uses is shown in

Table 3. Number and use of specimens.

Test Piece Number	Specimen Number				Specimen Use
	Cube	Prism	Shrinkage Specimen	Creep Specimen
NAC-I	3	6	3	2	A Cube: Cube used to determine the compressive strength. B Prisms: Three were used to determine the ultimate bearing capacity and three were used to determine the elastic modulus.
RAC-50-I	3	6	3	2
RAC-100-I	3	6	3	2
NAC-II	3	6	3	2
RAC-50-II	3	6	3	2
RAC-100-II	3	6	3	2

.

2.4. Test Loading Process

The creep testing of RAC was carried out using a spring-loaded compression creeper that was loaded with a jack. The load was controlled by a pressure sensor and a digital electronic displacement meter, and the constant value of the load was maintained by the spring reaction force. The creep loading device and shrink test device are shown in Figure 1.

(1)

The creep specimens were maintained for 28 days. The prism compressive strength of the specimens under the same conditions was tested before loading. The electronic displacement meter was checked for zero and the initial reading was recorded.

(2)

After the completion of the alignment, it started loading in time and the creep stress was taken as 60% of the measured prismatic compressive strength.

(3)

The deformation values of the test piece were read at 1 day, 3 days, 7 days, 14 days, 28 days, 45 days, 60 days, 90 days, 120 days, 150 days, and 180 days after loading, and the shrinkage value of the shrinkage test piece in the same environment was recorded.

(4)

The load was checked regularly after loading. If the load changed by more than 2%, the correct load was applied, and the nut on the screw was tightened to make up for it.

3. Test Results and Analysis

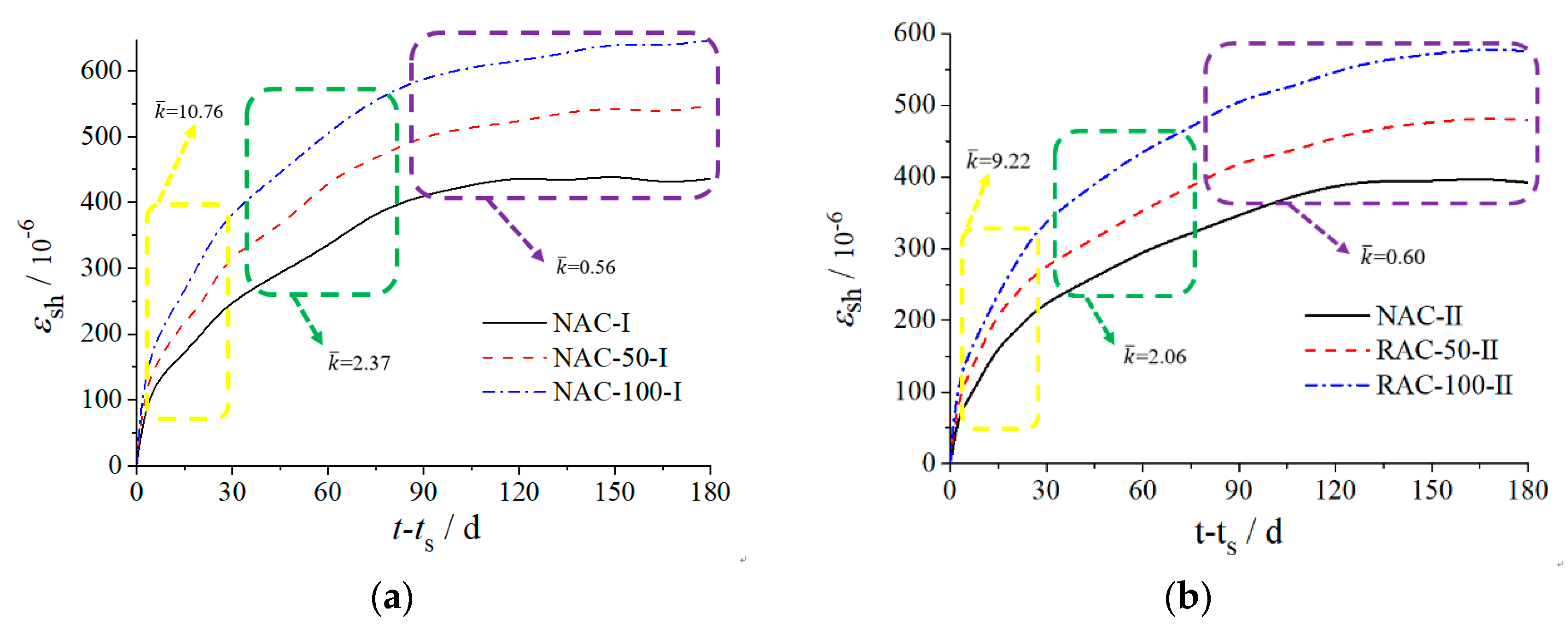
3.1. Analysis of Shrinkage Test Results

The shrinkage of RAC with different substitution rates at 180 days is shown in Figure 2. The shrinkage of RAC is similar to that of normal concrete. At 180 days, the shrinkage of RAC with a 50% and 100% substitution rate in group I increased by 26% and 48%, respectively, compared with that of ordinary concrete, and the shrinkage of RAC with a 50% and 100% substitution rate in group II was increased by 22% % and 47%, respectively, compared with that of ordinary concrete. As the replacement rate of RCA increased, the shrinkage of RAC also increased. In the early stage of shrinkage, the shrinkage of RAC increased faster and shrank faster, and then the rate of shrinkage decreased and slowed down. The shrinkage tended to be gentle until 120 days, and about 95% of the total shrinkage was achieved. It was considered that the shrinkage of RAC tended to be stable at 180 days.

In the early stage of shrinkage, the shrinkage deformation of normal concrete with w/c = 0.4 was close to that of normal concrete with w/c = 0.527, and then the deviation between them gradually increased. Normal concrete shrinkage with w/c = 0.527 at 180 days was 11% higher than normal concrete shrinkage with w/c = 0.4. At 180 days, the shrinkage deformation of RAC with w/c = 0.527 increased by 14% and 12%, respectively, compared with that of RAC with a substitution rate of 50% and 100% with w/c = 0.4. This shows that the water–cement ratio is not the main factor affecting the shrinkage of RAC. As the age increased, the shrinkage of RAC was not affected by the water–cement ratio. In addition, both groups of RAC and ordinary concrete showed an obvious shrinkage development trend in the first 30 days: The average shrinkage slope reached 10.76 and 9.22, respectively; the shrinkage development trend of each group of samples slowed down and contracted from 30 days to 86 days, and the average slope decreased to 2.37 and 2.06, respectively; the shrinkage trend of each group tended to be stable from 90 days to 180 days, and the average shrinkage slopes approached 0.56 and 0.60, respectively. Comparing the changes in the average shrinkage slopes of the two water–cement ratios, it was found that the water–cement ratio had a more obvious influence on the trend of early shrinkage. The average shrinkage slope of the w/c = 0.527 sample increased by 16.7% in the first stage (≤30 days) compared to the w/c = 0.4 sample; the second stage of the increase in value accounted for 17.7% of the first stage; the third stage of the average slope slightly decreased to account for 2.3% of the first stage.

Similarly to ordinary concrete, the main cause of the shrinkage of RAC is cement mortar hardening, internal moisture loss, and deformation caused by volume reduction. However, the shrinkage of RAC is higher than that of ordinary concrete, and as the substitution rate increases, the amount of shrinkage also increases. On the one hand, this is because the micro-cracks inside the RCA cause a decrease in the elastic modulus and strength, resulting in a reduced ability to restrain the shrinkage, a smaller volume loss, and a larger shrinkage deformation. On the other hand, compared with ordinary concrete, due to the presence of the old cement mortar, which is not easily peeled off on the surface of the RCA, the total amount of mortar of the RAC is larger under the same mix ratio, and the shrinkage is mainly caused by the hardening of the cement mortar. Therefore, the shrinkage of RAC in the same environment is stronger than that of ordinary concrete.

3.2. Analysis of Creep Test Results

The creep curve of RAC at 180 days is shown in Figure 3. The creep of RAC is similar to that of ordinary concrete. At 180 days, the creep coefficient of RAC with a 50% and 100% substitution rate in group I increased by 19.6% and 39.6%, respectively, compared with that of ordinary concrete. The creep coefficient of RAC with a 50% and 100% substitution rate in group II was 23.6% and 44.3% higher than that of ordinary concrete, respectively. At the initial stage of loading, the creep of RAC with a 50% and 100% substitution rate increased faster than that of ordinary concrete, and the creep coefficient was always higher than ordinary concrete. The creep growth rate decreased with the passage of time, but the decrease rate of the creep growth rate of ordinary concrete that was close to the creep coefficient of RAC was small. At 120 days, the creep development of all three creeps tended to be flat, and about 90% of the total creep variable was completed, which roughly shows that the creep of the RAC tended to be stable.

At the initial stage of loading, the creep of normal concrete with w/c = 0.4 was faster than that of normal concrete with w/c = 0.527, and the creep coefficient was higher than the latter. After that, the creep growth rate of normal concrete with w/c = 0.4 decreased and that of ordinary concrete with w/c = 0.527 increased rapidly. When loading to 180 days, the creep coefficient of normal concrete with w/c = 0.527 increased by 43.8% compared with that of RAC with w/c = 0.4. For the RAC with w/c = 0.4 and a substitution rate of 50% and 100%, the creep development trend was the same. At 180 days, the creep coefficient of RAC with w/c = 0.527 increased by 40% and 38.7%, respectively, compared with that of RAC with a substitution rate of 50% and 100% with w/c = 0.4. This shows that the water–cement ratio is an important factor affecting the creep of RAC. The high water–cement ratio and the large amount of recycled mortar have a significant effect on creep.

4. Creep and Shrinkage Model of Recycled Aggregate Concrete

At present, there are many models of shrinkage and creep of ordinary concrete at home and abroad. In this paper, five typical models are selected, which are the CEB-FIP 1990 model [28], ACI209R 1992 model [29], GL2000 model [30], B3 model [31], and GB50010 model [32]. Based on the five models, the recycled aggregate attached mortar is taken as the research object, the increasing coefficient of the attached mortar is put forward, and the shrinkage creep model of the RAC is established.

4.1. Creep Increasing Coefficient of Attached Mortar

Fathifazl et al. [18] considered that natural aggregate was replaced by mass or volume percentage when RAC was prepared by traditional methods. Compared with ordinary concrete, a certain amount of cement mortar is wrapped on the surface of the recycled aggregate. The content of natural aggregate in the RAC prepared by the conventional method is decreased and the content of the total mortar is increased. The elastic modulus of the component is decreased, and the shrinkage and the amount of creep are increased. It is assumed that the RCA is a two-phase material composed of residual cement mortar and natural aggregate, and the mortar in the RAC consists of residual cement mortar and new cement mortar on the aggregate surface. Based on the creep test results of RAC, the residual cement mortar content of RCA was taken as the research object to establish the creep prediction model of RAC.

$$C_{\mathrm{AM}}=\frac{C_{\mathrm{RAC}}}{C_{\mathrm{NAC}}}={(\frac{V_{\mathrm{NM}}^{\mathrm{RAC}}+V_{\mathrm{RM}}^{\mathrm{RAC}}}{1-V_{\mathrm{RCA}}^{\mathrm{RAC}}})}^{1.33},$$

(1)

$$V_{\mathrm{NM}}^{\mathrm{RAC}}=1-V_{\mathrm{RCA}}^{\mathrm{RAC}}.$$

(2)

Simultaneous equations:

$$C_{\mathrm{AM}}={(\frac{V_{\mathrm{NM}}^{\mathrm{RAC}}+V_{\mathrm{AM}}^{\mathrm{RAC}}}{1-V_{\mathrm{NCA}}^{\mathrm{NAC}}-V_{\mathrm{RCA}}^{\mathrm{NAC}}})}^{1.33}.$$

(3)

According to the composition of RCA, the following equation holds:

$$v_{\mathrm{RCA}}=v_{\mathrm{AM}}+v_{\mathrm{OVA}},m_{\mathrm{RCA}}=m_{\mathrm{AM}}+m_{\mathrm{OVA}},$$

(4)

$$m_{\mathrm{RCA}}=v_{\mathrm{RCA}}\times {\rho }_{\mathrm{RCA}},m_{\mathrm{AM}}=v_{\mathrm{AM}}\times {\rho }_{\mathrm{AM}},$$

(5)

$$m_{\mathrm{OVA}}=v_{\mathrm{OVA}}\times {\rho }_{\mathrm{OVA}}.$$

(6)

In the equation, V is volume (m³); m is quality (kg); ρ is apparent density (kg/m³).

The parameter $M_{AM}$ is the mass ratio of the attached mortar and the RCA. $M_{AM}=m_{AM}/m_{RCA}$, and the following equation is derived from the above equation:

$${\rho }_{\mathrm{AM}}=\frac{m_{\mathrm{AM}}}{v_{\mathrm{AM}}}=\frac{v_{\mathrm{RCA}}\times {\rho }_{\mathrm{RCA}}\times M_{\mathrm{AM}}}{v_{\mathrm{RCA}}-\frac{(1-M_{\mathrm{AM}})v_{\mathrm{RCA}}\times {\rho }_{\mathrm{RCA}}}{{\rho }_{\mathrm{OVA}}}}=\frac{M_{\mathrm{AM}}}{\frac{1}{{\rho }_{\mathrm{OVA}}}-\frac{1-M_{\mathrm{AM}}}{{\rho }_{\mathrm{OVA}}}},$$

(7)

and $v_{\mathrm{AM}}=v_{\mathrm{RCA}}\times M_{\mathrm{AM}}\times \frac{{\rho }_{\mathrm{RCA}}}{{\rho }_{\mathrm{AM}}}$.

Simultaneous equations:

$$v_{\mathrm{AM}}=v_{\mathrm{RCA}}\times [1-(1-M_{\mathrm{AM}})\frac{{\rho }_{\mathrm{RCA}}}{{\rho }_{\mathrm{OVA}}}],$$

(8)

$$V_{\mathrm{AM}}=V_{\mathrm{RCA}}\times [1-(1-M_{\mathrm{AM}})\frac{{\rho }_{\mathrm{RCA}}}{{\rho }_{\mathrm{OVA}}}].$$

(9)

Generally, the replacement rate of RCA is defined as follows:

$$r=\frac{m_{\mathrm{RCA}}^{\mathrm{RAC}}}{m_{\mathrm{RCA}}^{\mathrm{RAC}}+m_{\mathrm{NCA}}^{\mathrm{RAC}}}.$$

(10)

The volume ratio of natural coarse aggregate and RCA in RAC is R.

$$R=\frac{v_{\mathrm{NCA}}^{\mathrm{RAC}}}{v_{\mathrm{RCA}}^{\mathrm{RAC}}}=\frac{V_{\mathrm{NCA}}^{\mathrm{RAC}}}{V_{\mathrm{RCA}}^{\mathrm{RAC}}}=\frac{(m_{\mathrm{RCA}}^{\mathrm{RAC}}+m_{\mathrm{NCA}}^{\mathrm{RAC}})\times (1-r)/{\rho }_{\mathrm{NCA}}}{(m_{\mathrm{RCA}}^{\mathrm{RAC}}+m_{\mathrm{NCA}}^{\mathrm{RAC}})\times r/{\rho }_{\mathrm{RCA}}}=\frac{1-r}{r}\times \frac{{\rho }_{\mathrm{RCA}}}{{\rho }_{\mathrm{NCA}}}$$

(11)

Equation (3) can be rewritten as

$$C_{\mathrm{AM}}={\left(\frac{1-V_{\mathrm{RCA}}\times [R+(1-M_{\mathrm{AM}})\frac{{\rho }_{\mathrm{RCA}}}{{\rho }_{\mathrm{OVA}}}]}{1-V_{\mathrm{RCA}}^{\mathrm{RAC}}\times (1+R)}\right)}^{1.33}.$$

(12)

In order to simplify the expression, the approximate ${\rho }_{RCA}={\rho }_{OVA}$ is considered, and the relationship between $C_{AM}$ and the RCA replacement rate r is as follows:

$$C_{\mathrm{AM}}={\left(\frac{1-V_{\mathrm{RCA}}^{\mathrm{RAC}}\times [\frac{1-r}{r}\times \frac{{\rho }_{\mathrm{RCA}}}{{\rho }_{\mathrm{NCA}}}+(1-M_{\mathrm{AM}})]}{1-V_{\mathrm{RCA}}^{\mathrm{RAC}}\times (1+\frac{1-r}{r}\times \frac{{\rho }_{\mathrm{RCA}}}{{\rho }_{\mathrm{NCA}}})}\right)}^{1.33}.$$

(13)

When r = 100%, it is all RAC:

$$C_{\mathrm{AM}}={\left(\frac{1-V_{\mathrm{RCA}}^{\mathrm{RAC}}(1-M_{\mathrm{AM}})}{1-V_{\mathrm{RCA}}^{\mathrm{RAC}}}\right)}^{1.33}.$$

(14)

4.2. Shrinkage Increasing Coefficient of Attached Mortar

Concrete is constrained by aggregates, so its dry shrinkage is lower than that of pure grout [33]. The shrinkage of concrete is mainly caused by the hydration of cement mortar. The size of a few coarse aggregates is unstable. However, most of the coarse aggregates have the same size, a large elastic modulus, high crush index, and good restraint on concrete shrinkage. Therefore, the shrinkage of concrete depends on the amount and rigidity of the coarse aggregate in concrete. Considering the combined effect of aggregate content and rigidity, the prediction equation of the shrinkage strain of ordinary concrete is as follows:

$$S_{\mathrm{NAC}}=S_{\mathrm{TP}}^{\mathrm{NAC}}{(V_{\mathrm{TP}}^{\mathrm{NAC}})}^{\alpha }.$$

(15)

In the equation, $S_{NAC}$—the shrinkage strain of ordinary concrete; $S_{TP}$—the shrinkage strain of cement slurry in common concrete under the same conditions; $V_{TP}^{NAC}$—the volume of the total cement slurry in the ordinary concrete; α—empirical coefficient. The change range is 1.2–1.7 and the average is 1.45.

Because of the two-phase nature of RCA, the total mortar content in RAC is composed of attached mortar and fresh mortar. The shrinkage strain of RAC can be expressed as the following equation:

$$S_{\mathrm{RAC}}=S_{\mathrm{TP}}^{\mathrm{RAC}}{(V_{\mathrm{TP}}^{\mathrm{RAC}})}^{\alpha }.$$

(16)

It is assumed that the shrinkage characteristics of cement mortar in RAC are the same as those of ordinary concrete, which simultaneously gives the following equation:

$$\frac{S_{\mathrm{RAC}}}{S_{\mathrm{NAC}}}={(\frac{V_{\mathrm{TP}}^{\mathrm{RAC}}}{V_{\mathrm{TP}}^{\mathrm{NAC}}})}^{\alpha }.$$

(17)

The definition of SAM is the shrinkage increase coefficient of adhesive mortar, $S_{\mathrm{AM}}={(V_{\mathrm{TP}}^{\mathrm{RAC}}/V_{\mathrm{TP}}^{\mathrm{NAC}})}^{\alpha }$. Since the shrinkage of RAC is related to the volume of the total mortar, the volume $V_{\mathrm{TP}}^{\mathrm{RAC}}$ of the total mortar in RAC can be determined according to Equation (9). Then there is the following equation:

$$S_{\mathrm{AM}}={\left(\frac{1-V_{\mathrm{RCA}}^{\mathrm{RAC}}\times [\frac{1-r}{r}\times \frac{{\rho }_{\mathrm{RCA}}}{{\rho }_{\mathrm{NCA}}}+(1-M_{\mathrm{AM}})]}{1-V_{\mathrm{RCA}}^{\mathrm{RAC}}\times (1+\frac{1-r}{r}\times \frac{{\rho }_{\mathrm{RCA}}}{{\rho }_{\mathrm{NCA}}})}\right)}^{1.45}.$$

(18)

When r = 100%, it is all RAC:

$$S_{\mathrm{AM}}={\left(\frac{1-V_{\mathrm{RCA}}^{\mathrm{RAC}}(1-M_{\mathrm{AM}})}{1-V_{\mathrm{RCA}}^{\mathrm{RAC}}}\right)}^{1.45}.$$

(19)

5. Conclusions

(1)

The development law of the shrinkage and creep of RAC is similar to that of ordinary concrete. At 180 days, compared with ordinary concrete, the shrinkage of group I RAC with a substitution rate of 50% and 100% was increased by 26% and 48%, respectively, and the group II RAC was increased by 22% and 47%, respectively. When the load was 180 days old, compared with ordinary concrete, the creep rate of group I RAC with a substitution rate of 50% and 100% was increased by 19.6% and 39.6%, respectively, and group II was increased by 23.6% and 44.3%, respectively. With the increase of the replacement rate of recycled aggregate, the shrinkage and creep of RAC increased significantly, which indicates that the substitution rate is an important factor affecting the shrinkage and creep of RAC, and the water–cement ratio has more significant effects on the creep of RAC.

(2)

The effect of the substitution rate on the shrinkage and creep of RAC is caused by the adhesion of mortar. As the substitution rate increases, the porosity of the attached mortar increases the degree of concrete shrinkage. The increase of the water–cement ratio leads to an increase in the proportion of the attached mortar in the RAC. More adherence of the mortar pores weakens the restraint performance of the RAC, which in turn reduces the resistance of the RAC to creep.

(3)

The key difference between recycled aggregate and natural aggregate is the difference in the content of the attached mortar. In this paper, the contraction point was used to calculate the shrinkage strain and creep coefficient of the RAC shrinkage model, and the attached mortar increase coefficient method was also used. The calculated value of the model takes into account the effect of the recycled mortar itself on the shrinkage and creep of the recycled concrete. The difference between the calculated value and the experimental value is small and can meet the accuracy requirements well.

(4)

Based on the difference of the attached mortar, effective shrinkage and creep of RAC can be established, and the shrinkage and creep of RAC will show a different development trend from ordinary concrete as the age increases. At the same time, according to the same research ideas, a complete prediction model of the shrinkage and creep of RAC with a full-service life cycle can be established, and the calculation method of the long-term deformation of RAC with significant influence on shrinkage and creep can be carried out.