Fixed Grid Numerical Models for Solidification and Melting of Phase Change Materials (PCMs)
Abstract
:1. Introduction
2. PCMs: Basic Characterization
2.1. PCMs Classification
2.2. PCM Applications
3. Phase Change Processes
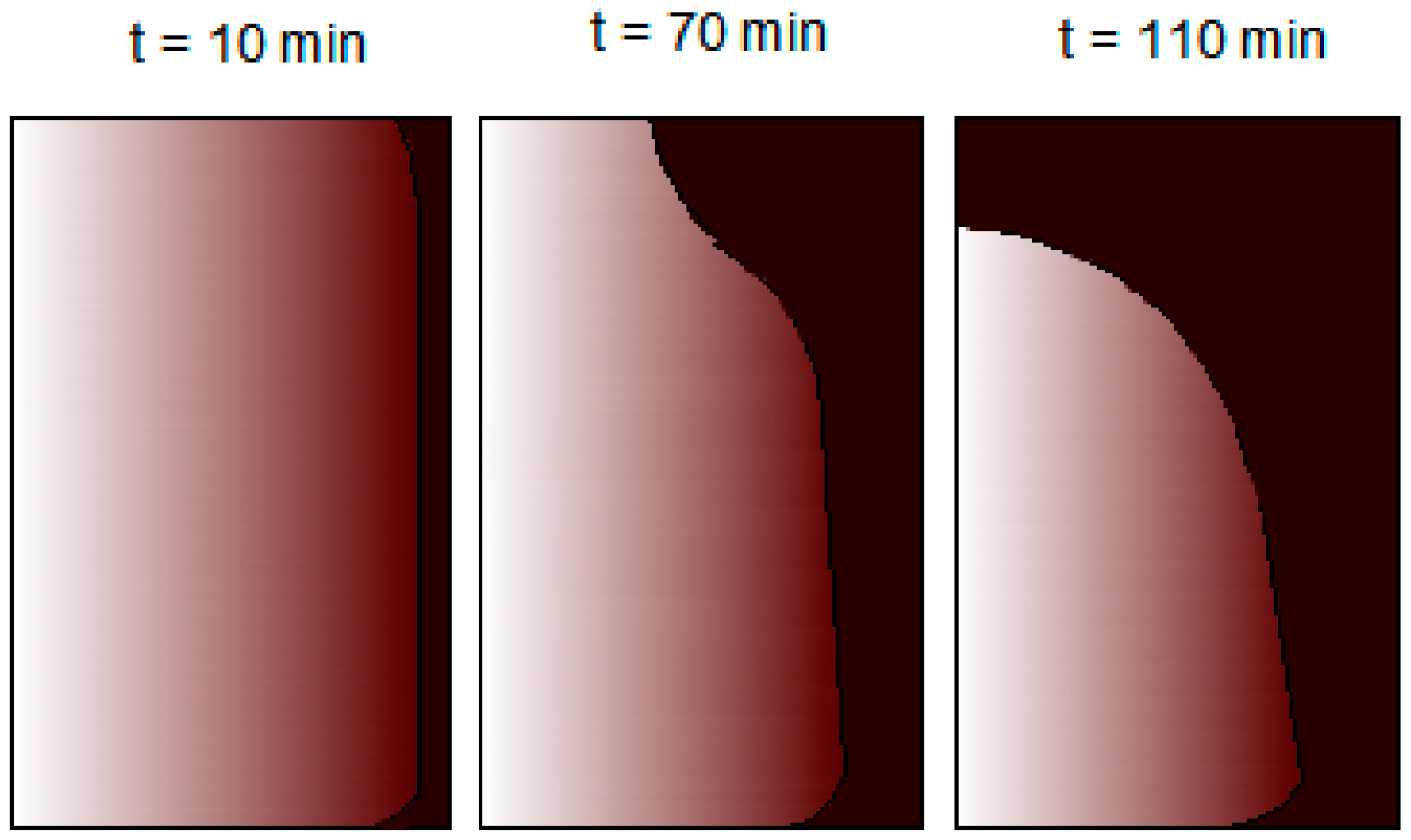
3.1. Solidification Process
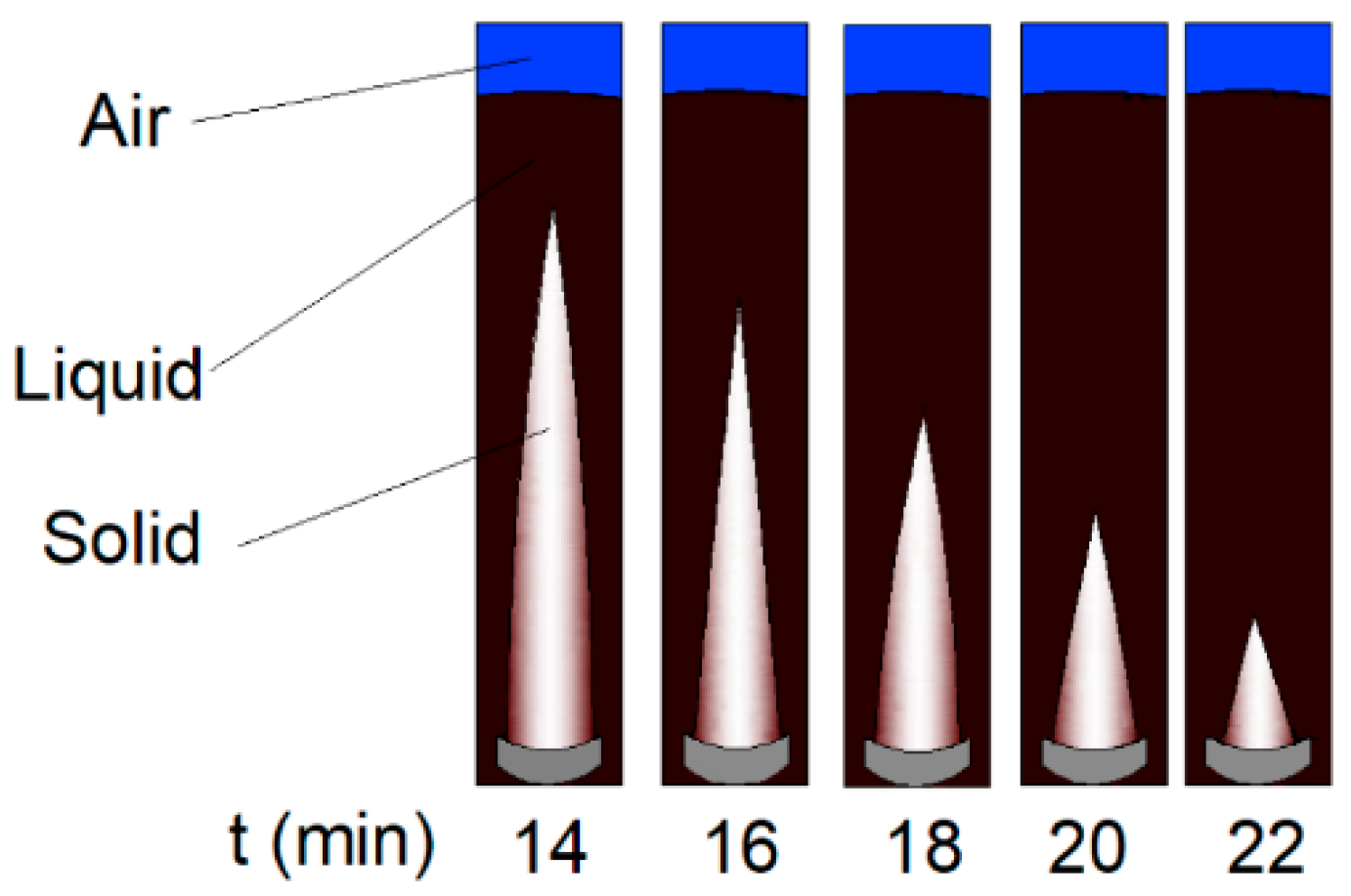
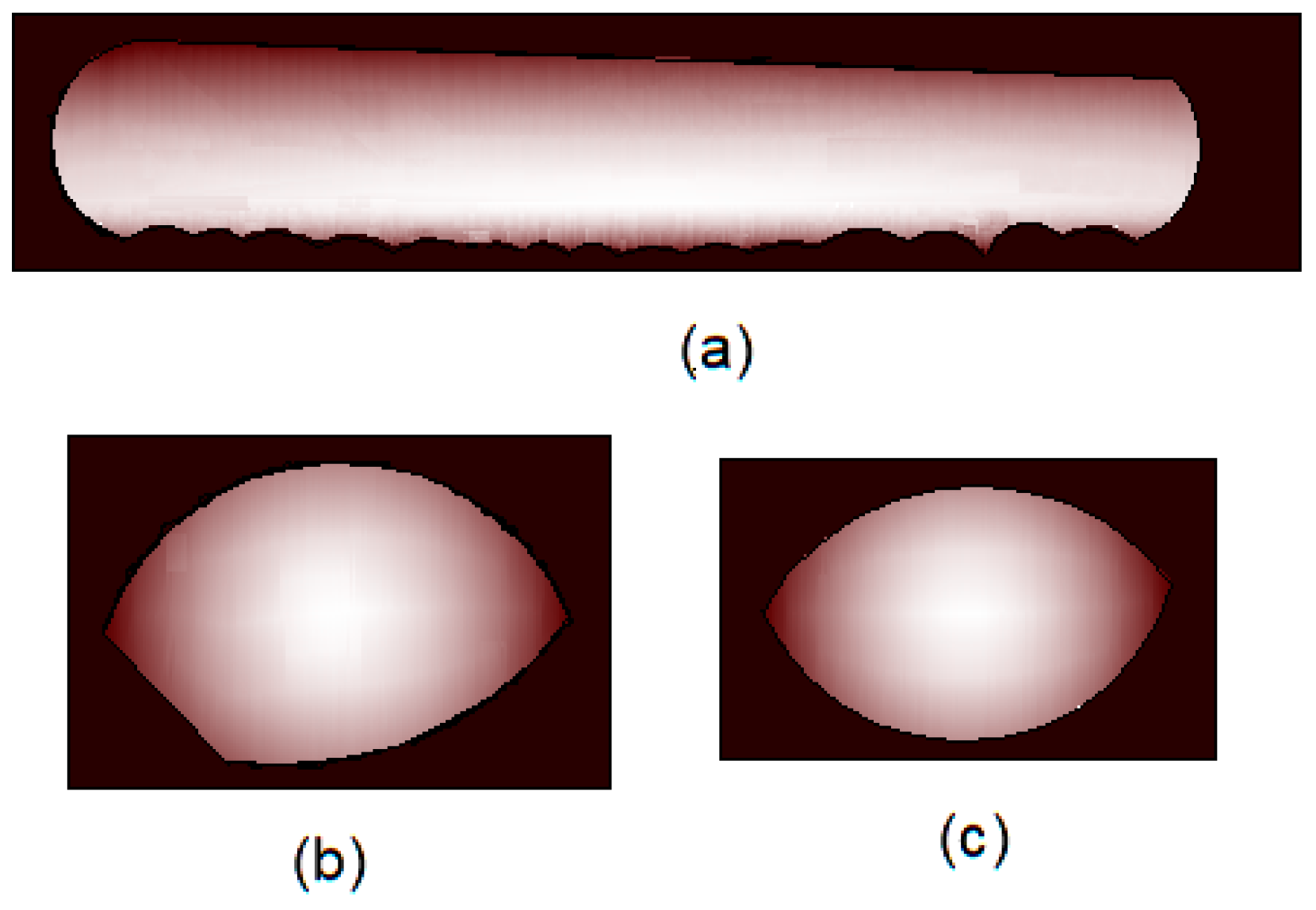
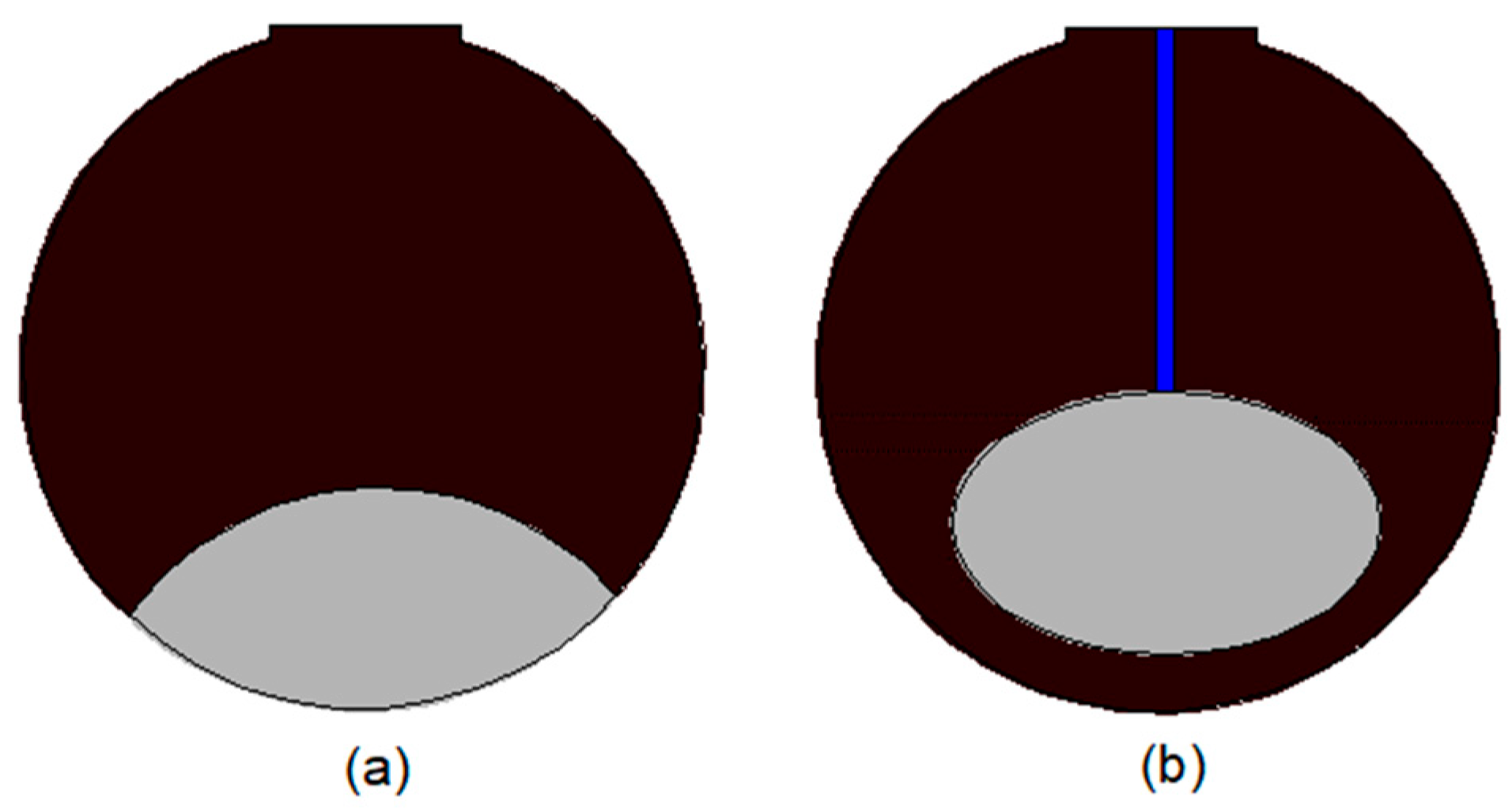
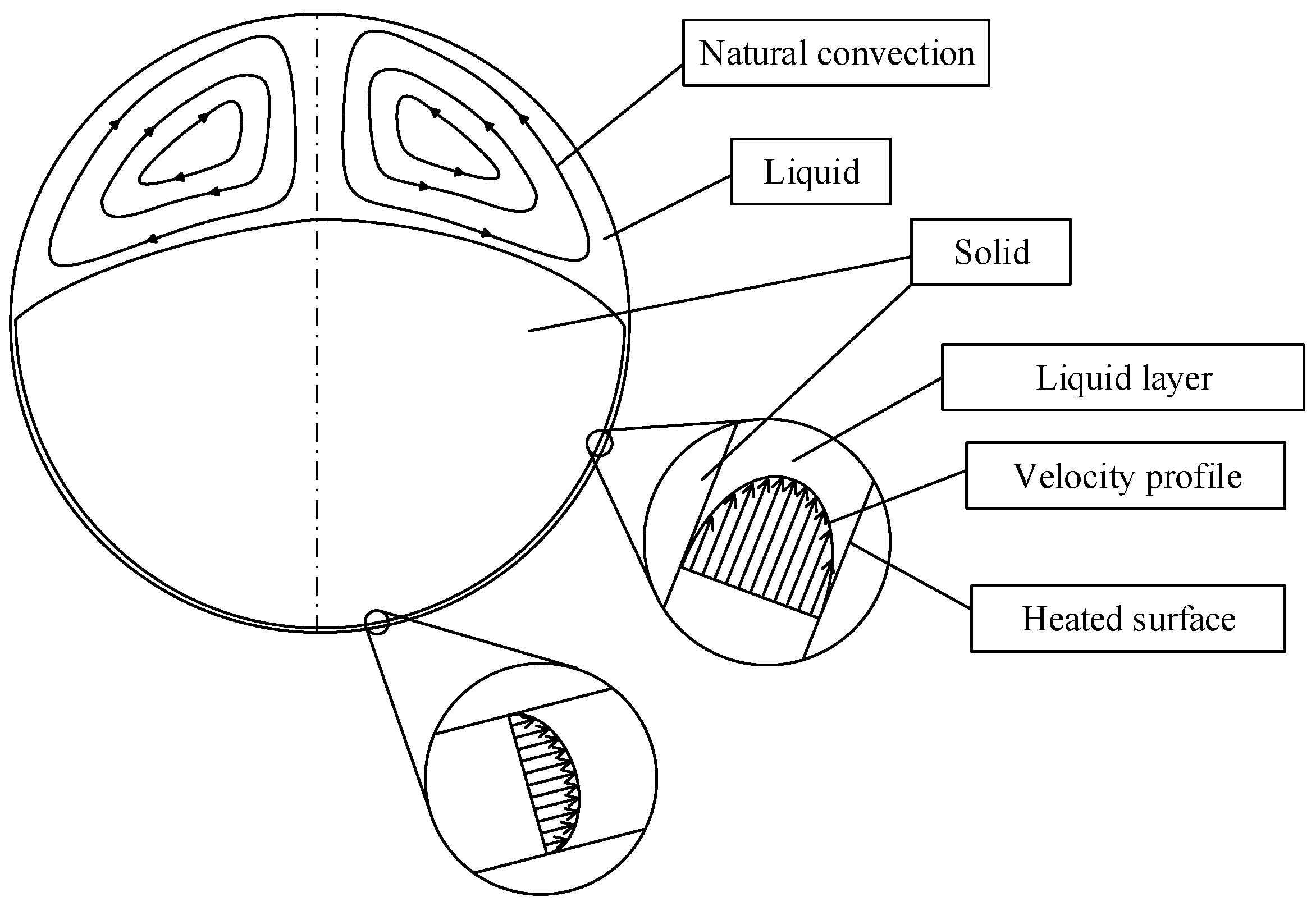
3.2. Melting Process
4. Numerical Models for Phase Change Processes
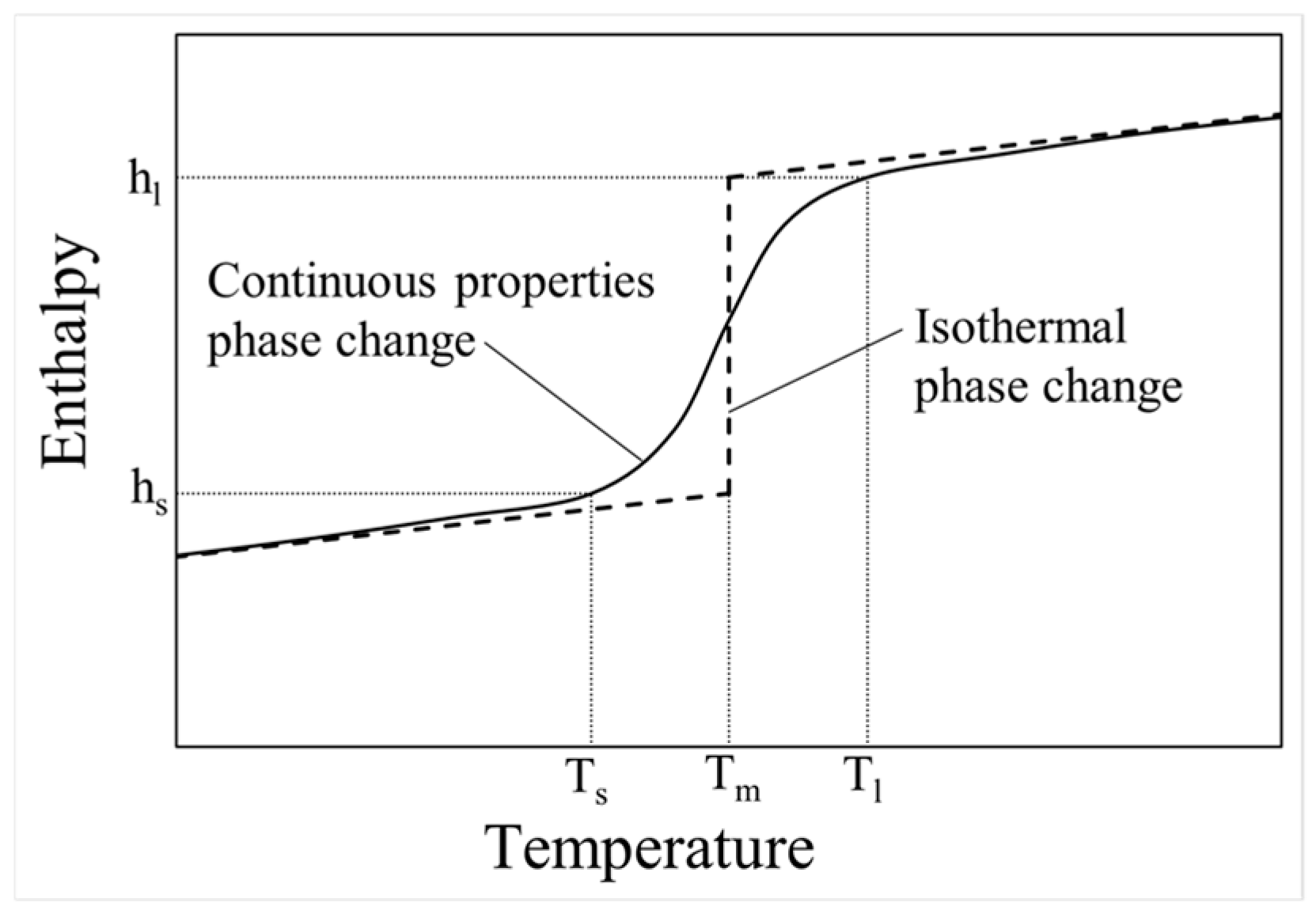
4.1. Latent Heat Modeling
4.1.1. Source Term Method (E-STM)
4.1.2. Temperature Transforming Methods (E-TTM)
4.1.3. Enthalpy-Based Methods
4.2. Velocity Transition Modeling
4.2.1. Switch-Off Methods
4.2.2. Source Term Methods
4.2.3. Variable Viscosity Method
5. Numerical Models Used in Studies Regarding PCMs
5.1. Formulations
5.2. Performance Evaluation of Computers and Numerical Models
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Farid, M.M.; Khudhair, A.M.; Razack, S.A.K.; Al-Hallaj, S. A review on phase change energy storage: Materials and applications. Energy Convers. Manag. 2004, 45, 1597–1615. [Google Scholar] [CrossRef]
- Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Agyenim, F.; Hewitt, N.; Eames, P.; Smyth, M. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS). Renew. Sustain. Energy Rev. 2010, 14, 615–628. [Google Scholar] [CrossRef]
- Abhat, A. Short term thermal energy storage. Rev. Phys. Appl. 1980, 15, 477–501. [Google Scholar] [CrossRef]
- Akeiber, H.; Nejat, P.; Majid, M.Z.A.; Wahid, M.A.; Jomehzadeh, F.; Famileh, I.Z.; Calautit, J.K.; Hughes, B.R.; Zaki, S.A. A review on phase change material (PCM) for sustainable passive cooling in building envelopes. Renew. Sustain. Energy Rev. 2016, 60, 1470–1497. [Google Scholar] [CrossRef]
- Buonomano, A.; Montanaro, U.; Palombo, A.; Santini, S. Dynamic building energy performance analysis: A new adaptive control strategy for stringent thermohygrometric indoor air requirements. Appl. Energy 2016, 163, 361–386. [Google Scholar] [CrossRef]
- Buonomano, A.; De Luca, G.; Montanaro, U.; Palombo, A. Innovative technologies for NZEBs: An energy and economic analysis tool and a case study of a non-residential building for the Mediterranean climate. Energy Build. 2016, 121, 318–343. [Google Scholar] [CrossRef]
- Gil, A.; Medrano, M.; Martorell, I.; Lázaro, A.; Dolado, P.; Zalba, B.; Cabeza, L.F. State of the art on high temperature thermal energy storage for power generation. Part 1—Concepts, materials and modellization. Renew. Sustain. Energy Rev. 2010, 14, 31–55. [Google Scholar] [CrossRef]
- Michels, H.; Pitz-Paal, R. Cascaded latent heat storage for parabolic trough solar power plants. Sol. Energy 2007, 81, 829–837. [Google Scholar] [CrossRef]
- Gong, Z.-X.; Mujumdar, A.S. Thermodynamic optimization of the thermal process in energy storage using multiple phase change materials. Appl. Therm. Eng. 1997, 17, 1067–1083. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Das, M.K.; Rath, P. Application of TCE-PCM based heat sinks for cooling of electronic components: A review. Renew. Sustain. Energy Rev. 2016, 59, 550–582. [Google Scholar] [CrossRef]
- Browne, M.C.; Norton, B.; McCormack, S.J. Heat retention of a photovoltaic/thermal collector with PCM. Sol. Energy 2016, 133, 533–548. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Zhang, D.; Zhang, T.; Wang, T.; Ruan, D.; Xing, D.; Li, H. Study of solid–solid phase change of (n-CnH2n+1NH3) 2MCl4 for thermal energy storage. Thermochim. Acta 1999, 326, 8–11. [Google Scholar] [CrossRef]
- Hasan, A.; McCormack, S.J.; Huang, M.J.; Norton, B. Energy and cost saving of a Photovoltaic-Phase Change Materials (PV-PCM) system through temperature regulation and performance enhancement of photovoltaics. Energies 2014, 7, 1318–1331. [Google Scholar] [CrossRef]
- Abhat, A. Low temperature latent heat thermal energy storage: Heat storage materials. Sol. Energy 1983, 30, 313–332. [Google Scholar] [CrossRef]
- Zalba, B.; Marín, J.M.; Cabeza, L.F.; Mehling, H. Review on thermal energy storage with phase change: Materials, heat transfer analysis and applications. Appl. Therm. Eng. 2003, 23, 251–283. [Google Scholar] [CrossRef]
- Kenisarin, M.M. High-temperature phase change materials for thermal energy storage. Renew. Sustain. Energy Rev. 2010, 14, 955–970. [Google Scholar] [CrossRef]
- Nomura, T.; Okinaka, N.; Akiyama, T. Technology of latent heat storage for high temperature application: A review. ISIJ Int. 2010, 50, 1229–1239. [Google Scholar] [CrossRef]
- Ge, H.; Li, H.; Mei, S.; Liu, J. Low melting point liquid metal as a new class of phase change material: An emerging frontier in energy area. Renew. Sustain. Energy Rev. 2013, 21, 331–346. [Google Scholar] [CrossRef]
- Salunkhe, P.B.; Shembekar, P.S. A review on effect of phase change material encapsulation on the thermal performance of a system. Renew. Sustain. Energy Rev. 2012, 16, 5603–5616. [Google Scholar] [CrossRef]
- Dhaidan, N.S.; Khodadadi, J.M. Melting and convection of phase change materials in different shape containers: A review. Renew. Sustain. Energy Rev. 2015, 43, 449–477. [Google Scholar] [CrossRef] [Green Version]
- Fan, L.; Khodadadi, J.M. Thermal conductivity enhancement of phase change materials for thermal energy storage: A review. Renew. Sustain. Energy Rev. 2011, 15, 24–46. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, Z.; Ghafoor, A. A review of performance enhancement of PCM based latent heat storage system within the context of materials, thermal stability and compatibility. Energy Convers. Manag. 2016, 115, 132–158. [Google Scholar] [CrossRef]
- Verma, P.; Varun; Singal, S.K. Review of mathematical modeling on latent heat thermal energy storage systems using phase-change material. Renew. Sustain. Energy Rev. 2008, 12, 999–1031. [Google Scholar] [CrossRef]
- Dutil, Y.; Rousse, D.R.; Ben Salah, N.; Lassue, S.; Zalewski, L. A review on phase-change materials: Mathematical modeling and simulations. Renew. Sustain. Energy Rev. 2011, 15, 112–130. [Google Scholar] [CrossRef]
- Al-Abidi, A.A.; Bin Mat, S.; Sopian, K.; Sulaiman, M.Y.; Mohammed, A.T. CFD applications for latent heat thermal energy storage: A review. Renew. Sustain. Energy Rev. 2013, 20, 353–363. [Google Scholar] [CrossRef]
- Liu, S.; Li, Y.; Zhang, Y. Mathematical solutions and numerical models employed for the investigations of PCMs’ phase transformations. Renew. Sustain. Energy Rev. 2014, 33, 659–674. [Google Scholar] [CrossRef]
- Ziskind, G. Modelling of Heat Transfer in Phase Change Materials (Pcms) for Thermal Energy Storage Systems in Advances in Thermal Energy Storage Systems: Methods and Applications; Woodhead Publishing Limited: Sawston, Cambridge, UK, 2015; pp. 307–324. [Google Scholar]
- Voller, V.R.; Swaminathan, C.R.; Thomas, B.G. Fixed grid techniques for phase change problems: A review. Int. J. Numer. Methods Eng. 1990, 30, 875–898. [Google Scholar] [CrossRef]
- Samarskii, A.A.; Vabishchevich, P.N.; Iliev, O.P.; Churbanov, A.G. Numerical simulation of convection/diffusion phase change problems—A review. Int. J. Heat Mass Transf. 1993, 36, 4095–4106. [Google Scholar] [CrossRef]
- Hu, H.; Argyropoulos, S.A. Mathematical modelling of solidification and melting: A review. Model. Simul. Mater. Sci. Eng. 1996, 4, 371–396. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, Y. Solid velocity correction schemes for a temperature transforming model for convection phase change. Int. J. Numer. Methods Heat Fluid Flow 2006, 16, 204–225. [Google Scholar] [CrossRef]
- Fallahi, A.; Guldentops, G.; Tao, M.; Granados-Focil, S.; Van Dessel, S. Review on solid-solid phase change materials for thermal energy storage: Molecular structure and thermal properties. Appl. Therm. Eng. 2017, 127, 1427–1441. [Google Scholar] [CrossRef]
- Kenisarin, M.M.; Kenisarina, K.M. Form-stable phase change materials for thermal energy storage. Renew. Sustain. Energy Rev. 2012, 16, 1999–2040. [Google Scholar] [CrossRef]
- Al-Waeli, A.H.A.; Sopian, K.; Kazem, H.A.; Chaichan, M.D. Photovoltaic/Thermal (PV/T) systems: Status and future prospects. Renew. Sustain. Energy Rev. 2017, 77, 109–130. [Google Scholar] [CrossRef]
- Preet, S.; Bhushan, B.; Mahajan, T. Experimental investigation of water based photovoltaic/thermal (PV/T) system with and without phase change material (PCM). Sol. Energy 2017, 155, 1104–1120. [Google Scholar] [CrossRef]
- El-Sebaii, A.A.; Al-Ghamdi, A.A.; Al-Hazmi, F.S.; Faidah, A.S. Thermal performance of a single basin solar still with PCM as a storage medium. Appl. Energy 2009, 86, 1187–1195. [Google Scholar] [CrossRef]
- Chaichan, M.T.; Kazem, H.A. Water solar distiller productivity enhancement using concentrating solar water heater and phase change material (PCM). Case Stud. Therm. Eng. 2015, 5, 151–159. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.K.A.; Al-Abidi, A.A.; Mat, S.; Sopian, K.; Huslan, M.H.; Sulaiman, M.Y.; Rosli, M.A.M. Review of the application of phase change material for heating and domestic hot water systems. Renew. Sustain. Energy Rev. 2015, 42, 557–568. [Google Scholar] [CrossRef]
- Dincer, I.; Rosen, M.A. Thermal Energy Storage Systems and Applications, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hale, D.V.; Hoover, M.J.; O’Neill, M.J. Phase Change Materials Handbook; Technical report No. NASA-CR-61363; NASA: Washington, DC, USA, 1971.
- Saro, O.; Angelis, A.; D’Elia, S.; Lorenzini, G. Utilization of phase change materials (PCM) for energy recovery in the steelmaking industry. J. Eng. Thermophys. 2013, 22, 93–110. [Google Scholar] [CrossRef]
- Yagi, J.; Akiyama, T. Storage of thermal energy for effective use of waste heat from industries. J. Mat. Process. Technol. 1995, 48, 793–804. [Google Scholar] [CrossRef]
- Jaguemont, J.; Omar, N.; Van den Bossche, P.; Mierlo, J. Phase-change materials (PCM) for automotive applications: A review. Appl. Therm. Eng. 2018, 132, 308–320. [Google Scholar] [CrossRef]
- Mondal, S. Phase change materials for smart textiles—An overview. Appl. Therm. Eng. 2008, 28, 1536–1550. [Google Scholar] [CrossRef]
- Shalaby, S.M.; Bek, M.A.; El-Sebaii, A.A. Solar dryers with PCM as energy storage medium: A review. Renew. Sustain. Energy Rev. 2014, 33, 110–116. [Google Scholar] [CrossRef]
- Egolf, P.W.; Manz, H. Theory and modeling of phase change materials with and without mushy regions. Int. J. Heat Mass Transf. 1994, 37, 2917–2924. [Google Scholar] [CrossRef]
- Assis, E.; Katsman, L.; Ziskind, G.; Letan, R. Numerical and experimental study of melting in a spherical shell. Int. J. Heat Mass Transf. 2007, 50, 1790–1804. [Google Scholar] [CrossRef]
- Nazzi Ehms, J.H.; Oliveski, R.D.C.; Oliveira Rocha, L.A.; Biserni, C. Theoretical and numerical analysis on phase change materials (PCM): A case study of the solidification process of erythritol in spheres. Int. J. Heat Mass Transf. 2018, 119, 523–532. [Google Scholar] [CrossRef]
- Shamsundar, N.; Sparrow, E. Effect of density change on multidimensional conduction phase change. J. Heat Transf. 1976, 98, 550–557. [Google Scholar] [CrossRef]
- Voller, V.R.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 709–1719. [Google Scholar] [CrossRef]
- Assis, E.; Ziskind, G.; Letan, R. Numerical and experimental study of solidification in a spherical shell. J. Heat Transf. 2009, 131, 024502. [Google Scholar] [CrossRef]
- Gau, C.; Viskanta, R. Melting and solidification of a pure metal on a vertical wall. J. Heat Transf. 1986, 108, 174–181. [Google Scholar] [CrossRef]
- Ismail, K.A.R.; Lino, F.A.M.; Da Silva, R.C.R.; De Jesus, A.B.; Paixão, L.C. Experimentally validated two dimensional numerical model for the solidification of PCM along a horizontal long tube. Int. J. Therm. Sci. 2014, 75, 184–193. [Google Scholar] [CrossRef]
- Viskanta, R.; Gau, C. Inward solidification of a superheated liquid in a cooled horizontal tube. Wärme Stoffübertrag. 1982, 17, 39–46. [Google Scholar] [CrossRef]
- Dubovsky, V.; Assis, E.; Kochavi, E.; Ziskind, G.; Letan, R. Study of solidification in vertical cylindrical shells. In Proceedings of the 5th European Thermal-Sciences Conference, Eindhoven, Netherlands, 18–22 May 2008. [Google Scholar]
- Al-Abidi, A.A.; Mat, S.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Numerical study of PCM solidification in a triplex tube heat exchanger with internal and external fins. Int. J. Heat Mass Transf. 2013, 61, 684–695. [Google Scholar] [CrossRef]
- Tan, F.L. Constrained and unconstrained melting inside a sphere. Int. Commun. Heat Mass Transf. 2008, 35, 466–475. [Google Scholar] [CrossRef]
- Chan, C.W.; Tan, F.L. Solidification inside a sphere—An experimental study. Int. Commun. Heat Mass Transf. 2006, 33, 335–341. [Google Scholar] [CrossRef]
- Pal, D.; Joshi, Y.K. Melting in a side heated tall enclosure by a uniformly dissipating heat source. Int. J. Heat Mass Transf. 2001, 44, 375–387. [Google Scholar] [CrossRef]
- Shokouhmand, H.; Kamkari, B. Experimental investigation on melting heat transfer characteristics of lauric acid in a rectangular thermal storage unit. Exp. Therm. Fluid Sci. 2013, 50, 201–212. [Google Scholar] [CrossRef]
- Katsman, L.; Dubovsky, V.; Ziskind, G.; Letan, R. Experimental investigation of solid-liquid phase change in cylindrical geometry. In Proceedings of the ASME/JSME 2007 Thermal Engineering Heat Transfer Summer Conference, Vancouver, Canada, 8–12 July 2007; pp. 239–244. [Google Scholar]
- Moallemi, M.K.; Webb, B.W.; Viskanta, R. An experimental and analytical study of close-contact melting. J. Heat Transf. 1986, 108, 894–899. [Google Scholar] [CrossRef]
- Bareiss, M.; Beer, H. An analytical solution of the heat transfer process during melting of an unfixed solid phase change material inside a horizontal tube. Int. J. Heat Mass Transf. 1984, 27, 739–746. [Google Scholar] [CrossRef]
- Hirata, T.; Makino, Y.; Kaneko, Y. Analysis of close-contact melting for octadecane and ice inside isothermally heated horizontal rectangular capsule. Int. J. Heat Mass Transf. 1991, 34, 3097–3106. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Geiger, G.T. Melting in a horizontal tube with the solid either constrained or free to fall under gravity. Int. J. Heat Mass Transf. 1986, 29, 1007–1019. [Google Scholar] [CrossRef]
- Saitoh, T.; Kato, K. Experiment on melting in heat storage capsule with close contact and natural convection. Exp. Therm. Fluid Sci. 1993, 6, 273–281. [Google Scholar] [CrossRef]
- Emerman, S.H.; Turcotte, D.L. Stokes’s problem with melting. Int. J. Heat Mass Transf. 1983, 26, 1625–1630. [Google Scholar] [CrossRef]
- Fomin, S.A.; Saitoh, T.S. Melting of unfixed material in spherical capsule with non-isothermal wall. Int. J. Heat Mass Transf. 1999, 42, 4197–4205. [Google Scholar] [CrossRef]
- Bahrami, P.A.; Wang, T.G. Analysis of gravity and conduction-driven melting in a sphere. J. Heat Transf. 1987, 109, 806–809. [Google Scholar] [CrossRef]
- Bejan, A. Single correlation for theoretical contact melting results in various geometries. Int. Commun. Heat Mass Transf. 1992, 19, 473–483. [Google Scholar] [CrossRef]
- Roy, S.K.; Sengupta, S. Gravity-assisted melting in a spherical enclosure: Effects of natural convection. Int. J. Heat Mass Transf. 1990, 33, 1135–1147. [Google Scholar] [CrossRef]
- Asako, M.; Faghri, Y. Effect of density change on melting of unfixed rectangular phase-change material under low-gravity environment. Numer. Heat Transf. Part. A Appl. 1999, 36, 825–838. [Google Scholar]
- Faden, M.; König-Haagen, A.; Höhlein, S.; Brüggemann, D. An implicit algorithm for melting and settling of phase change material inside macrocapsules. Int. J. Heat Mass Transf. 2018, 117, 757–767. [Google Scholar] [CrossRef]
- Ghasemi, B.; Molki, M. Melting of unfixed solids in square cavities. Int. J. Heat Fluid Flow 1999, 20, 446–452. [Google Scholar] [CrossRef]
- Kasibhatla, R.R.; König-Haagen, A.; Rösler, F.; Brüggemann, D. Numerical modelling of melting and settling of an encapsulated PCM using variable viscosity. Heat Mass Transf. 2017, 53, 1735–1744. [Google Scholar] [CrossRef]
- Stefan, J. Über die Theorie der Eisbildung, insbesondere über die Eisbildung im Polarmeere. Ann. Phys. 1981, 278, 269–286. [Google Scholar] [CrossRef]
- Bennon, W.D.; Incropera, F.P. A continuum model for momentum, heat and species transport binary solid-liquid phase change—I. Model formulation. Int. J. Heat Mass Transf. 1987, 30, 2161–2170. [Google Scholar] [CrossRef]
- Voller, V.R.; Brent, A.D.; Prakash, C. The modelling of heat, mass and solute transport in solidification systems. Int. J. Heat Mass Transf. 1989, 32, 1719–1731. [Google Scholar] [CrossRef]
- Ismail, K.A.R.; Henríquez, J.R. Solidification of pcm inside a spherical capsule. Energy Convers. Manag. 2000, 41, 173–187. [Google Scholar] [CrossRef]
- Gupta, R.S.; Kuma, D. Variable time step methods for one-dimensional Stefan problem with mixed boundary condition. Int. J. Heat Mass Transf. 1981, 24, 251–259. [Google Scholar] [CrossRef]
- Cao, Y.; Faghri, A. A numerical analysis of phase-change problems including natural convection. J. Heat Transf. 1990, 112, 812–816. [Google Scholar] [CrossRef]
- Kozak, Y.; Ziskind, G. Novel enthalpy method for modeling of PCM melting accompanied by sinking of the solid phase. Int. J. Heat Mass Transf. 2017, 112, 568–586. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Li, D.; Ren, Q.; Tong, Z.X.; He, Y.L. Lattice Boltzmann models for axisymmetric solid–liquid phase change. Int. J. Heat Mass Transf. 2017, 112, 795–804. [Google Scholar] [CrossRef]
- Frenkel, D.; Ladd, A.J.C. New Monte Carlo method to compute the free energy of arbitrary solids. Application to the fcc and hcp phases of hard spheres. J. Chem. Phys. 1984, 81, 3188–3193. [Google Scholar] [CrossRef]
- Plapp, M.; Karma, A. Multiscale finite-difference-diffusion-Monte-Carlo method for simulating dendritic solidification. J. Comput. Phys. 2000, 165, 592–619. [Google Scholar] [CrossRef]
- Voller, V.R.; Swaminathan, C.R. General source-based method for solidification phase change. Numer. Heat Transf. Part. B Fundam. 1991, 19, 175–189. [Google Scholar] [CrossRef]
- Morgan, K. A numerical analysis of freezing and melting with convection. Comput. Methods Appl. Mech. Eng. 1981, 28, 275–284. [Google Scholar] [CrossRef]
- Poirier, D.; Salcudean, M. On numerical methods used in mathematical modeling of phase change in liquid metals. J. Heat Transf. 1988, 110, 562–570. [Google Scholar] [CrossRef]
- Swaminathan, C.R.; Voller, V.R. A general enthalpy method for modeling solidification processes. Metall. Trans. B 1992, 23, 651–664. [Google Scholar] [CrossRef]
- Voller, V.R.; Cross, M.; Markatos, N.C. An enthalpy method for convection/diffusion phase change. Int. J. Numer. Methods Eng. 1987, 24, 271–284. [Google Scholar] [CrossRef]
- Gartling, D.K. Finite element analysis of convective heat transfer problems with change of phase. In Proceedings of the Conference on Numerical Methods in Laminar and Turbulent Flow, Swansea, UK, 18–21 July 1978. [Google Scholar]
- Danaila, I.; Moglan, R.; Hecht, F.; Le Masson, S. A Newton method with adaptive finite elements for solving phase-change problems with natural convection. J. Comput. Phys. 2014, 274, 826–840. [Google Scholar] [CrossRef]
- Asako, Y.; Faghri, M.; Charmchi, M.; Bahrami, P.A. Numerical solution for melting of unfixed rectangular phase-change under low-gravity environment. Numer. Heat Transf. Part. A Appl. 1994, 25, 191–208. [Google Scholar] [CrossRef]
- Samara, F.; Groulx, D.; Biwole, P.H. Natural convection driven melting of phase change material: Comparison of two methods. In Proceedings of the COMSOL Conference, Boston, MA, USA, 3–5 October 2012. [Google Scholar]
- Ziaei, S.; Lorente, S.; Bejan, A. Constructal design for convection melting of a phase change body. Int. J. Heat Mass Transf. 2016, 99, 762–769. [Google Scholar] [CrossRef] [Green Version]
- Kasibhatla, R.R.; König-Haagen, A.; Brüggemann, D. Numerical modelling of wetting phenomena during melting of PCM. Procedia Eng. 2016, 157, 139–147. [Google Scholar] [CrossRef]
- Estrázulas, J.J.; Oliveski, R.D.C. Numerical study of PCMs melting process in cylindrical cavity. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2016. [Google Scholar] [CrossRef]
- Raymundo Junior, J.F.; De Cesaro Oliveski, R.; Oliveira Rocha, L.A.; Biserni, C. Numerical investigation on phase change materials (PCM): The melting process of erythritol in spheres under different thermal conditions. Int. J. Mech. Sci. 2018, 148, 20–30. [Google Scholar] [CrossRef]
- Sharifi, N.; Faghri, A.; Bergman, T.L.; Andraka, C.E. Simulation of heat pipe-assisted latent heat thermal energy storage with simultaneous charging and discharging. Int. J. Heat Mass Transf. 2015, 80, 170–179. [Google Scholar] [CrossRef] [Green Version]
- Tay, N.H.S.; Bruno, F.; Belusko, M. Experimental validation of a CFD model for tubes in a phase change thermal energy storage system. Int. J. Heat Mass Transf. 2012, 55, 574–585. [Google Scholar] [CrossRef]
- Brent, A.D.; Voller, V.R.; Reid, K.J. Enthalpy-porosity technique for modeling convection-diffusion phase change: Application to the melting of a pure metal. Numer. Heat Transf. 1988, 13, 297–318. [Google Scholar] [CrossRef]
- Longeon, M.; Soupart, A.; Fourmigué, J.F.; Bruch, A.; Marty, P. Experimental and numerical study of annular PCM storage in the presence of natural convection. Appl. Energy 2013, 112, 175–184. [Google Scholar] [CrossRef]
- Archibold, A.R.; Rahman, M.M.; Gonzalez-Aguilar, J.; Goswami, D.Y.; Stefanakos, E.K.; Romero, M. Phase change and heat transfer numerical analysis during solidification on an encapsulated phase change material. Energy Procedia 2014, 57, 653–661. [Google Scholar] [CrossRef]
- Lee, Y.T.; Hong, S.W.; Chung, J.D. Effects of capsule conduction and capsule outside convection on the thermal storage performance of encapsulated thermal storage tanks. Sol. Energy 2014, 110, 56–63. [Google Scholar] [CrossRef]
- Hosseini, M.J.; Ranjbar, A.A.; Sedighi, K.; Rahimi, M. A combined experimental and computational study on the melting behavior of a medium temperature phase change storage material inside shell and tube heat exchanger. Int. Commun. Heat Mass Transf. 2012, 39, 1416–1424. [Google Scholar] [CrossRef]
- Hosseinizadeh, S.F.; Tan, F.L.; Moosania, S.M. Experimental and numerical studies on performance of PCM-based heat sink with different configurations of internal fins. Appl. Therm. Eng. 2011, 31, 3827–3838. [Google Scholar] [CrossRef]
- Hosseinizadeh, S.F.; Rabienataj Darzi, A.A.; Tan, F.L.; Khodadadi, J.M. Unconstrained melting inside a sphere. Int. J. Therm. Sci. 2013, 63, 55–64. [Google Scholar] [CrossRef]
- Khodadadi, M.; Zhang, Y. Effects of buoyancy-driven convection on melting within spherical containers. Int. J. Heat Mass Transf. 2001, 44, 1605–1618. [Google Scholar] [CrossRef]
- Tan, F.L.; Hosseinizadeh, S.F.; Khodadadi, J.M.; Fan, L. Experimental and computational study of constrained melting of phase change materials (PCM) inside a spherical capsule. Int. J. Heat Mass Transf. 2009, 52, 3464–3472. [Google Scholar] [CrossRef]
- Archibold, A.R.; Rahman, M.M.; Goswami, D.Y.; Stefanakos, E.K. Analysis of heat transfer and fluid flow during melting inside a spherical container for thermal energy storage. Appl. Therm. Eng. 2014, 64, 396–407. [Google Scholar] [CrossRef]
- Archibold, A.R.; Gonzalez-Aguilar, J.; Rahman, M.M.; Yogi Goswami, D.; Romero, M.; Stefanakos, E.K. The melting process of storage materials with relatively high phase change temperatures in partially filled spherical shells. Appl. Energy 2014, 116, 243–252. [Google Scholar] [CrossRef]
- Oliveski, R.D.C.; Del Col, D. Numerical simulation of thermal energy storage with PCM. In Proceedings of the Eurotherm Seminar: Advances in Thermal Energy Storage, Lleida, Spain, 28–30 May 2014. [Google Scholar]
- Faistauer, F.; Rodrigues, P.; Oliveski, R.D.C. Numerical study of phase change of PCM in spherical cavities. Defect Diffus. Forum 2016, 372, 21–30. [Google Scholar] [CrossRef]
- Hosseinizadeh, S.F.; Darzi, A.A.R.; Tan, F.L. Numerical investigations of unconstrained melting of nano-enhanced phase change material (NEPCM) inside a spherical container. Int. J. Therm. Sci. 2012, 51, 77–83. [Google Scholar] [CrossRef]
- Shmueli, H.; Ziskind, G.; Letan, R. Melting in a vertical cylindrical tube: Numerical investigation and comparison with experiments. Int. J. Heat Mass Transf. 2010, 53, 4082–4091. [Google Scholar] [CrossRef]
- Shatikian, V.; Ziskind, G.; Letan, R. Numerical investigation of a PCM-based heat sink with internal fins. Int. J. Heat Mass Transf. 2005, 48, 3689–3706. [Google Scholar] [CrossRef]
- Ye, W.B.; Zhu, D.S.; Wang, N. Fluid flow and heat transfer in a latent thermal energy unit with different phase change material (PCM) cavity volume fractions. Appl. Therm. Eng. 2012, 42, 49–57. [Google Scholar] [CrossRef]
- Solomon, L.; Elmozughi, A.F.; Oztekin, A.; Neti, S. Effect of internal void placement on the heat transfer performance—Encapsulated phase change material for energy storage. Renew. Energy 2015, 78, 438–447. [Google Scholar] [CrossRef]
- Fan, L.-W.; Zhu, Z.-Q.; Xiao, S.-L.; Liu, M.-J.; Lu, H.; Zheng, Y.; Yu, Z.-T.; Cen, K.-F. An experimental and numerical investigation of constrained melting heat transfer of a phase change material in a circumferentially finned spherical capsule for thermal energy storage. Appl. Therm. Eng. 2016, 100, 1063–1075. [Google Scholar] [CrossRef]
- Sattari, H.; Mohebbi, A.; Afsahi, M.M.; Azimi Yancheshme, A. CFD simulation of melting process of phase change materials (PCMs) in a spherical capsule. Int. J. Refrig. 2017, 73, 209–218. [Google Scholar] [CrossRef]
- Li, W.; Li, S.G.; Guan, S.; Wang, Y.; Zhang, X.; Liu, X. Numerical study on melt fraction during melting of phase change material inside a sphere. Int. J. Hydrog. Energy 2017, 42, 18232–18239. [Google Scholar] [CrossRef]
- Darzi, A.A.R.; Afrouzi, H.H.; Khaki, M.; Abbasi, M. Unconstrained melting and solidification inside rectangular enclosure. J. Fundam. Appl. Sci. 2015, 7, 436–451. [Google Scholar] [CrossRef]
- Blanco-Rodríguez, P.; Rodríguez-Aseguinolaza, J.; Gil, A.; Resueno, E.; D’Aguanno, B.; Lorono, I. Martin, Experiments on a lab scale TES unit using eutectic metal alloy as PCM. Energy Procedia 2015, 69, 769–778. [Google Scholar]
- Gui, X.; Qu, W.; Lin, B.; Yuan, X. Two-dimensional transient thermal analysis of a phase-change-material canister of a heat-pipe receiver under gravity. J. Therm. Sci. 2010, 19, 160–166. [Google Scholar] [CrossRef]
- Ye, W.B.; Zhu, D.S.; Wang, N. Numerical simulation on phase-change thermal storage/release in a plate-fin unit. Appl. Therm. Eng. 2011, 31, 3871–3884. [Google Scholar] [CrossRef]
- Elmozughi, A.F.; Solomon, L.; Oztekin, A.; Neti, S. Encapsulated phase change material for high temperature thermal energy storage—Heat transfer analysis. Heat Mass Transf. 2014, 78, 1135–1144. [Google Scholar] [CrossRef]
- Lorente, S.; Bejan, A.; Niu, J.L. Constructal design of latent thermal energy storage with vertical spiral heaters. Int. J. Heat Mass Transf. 2015, 81, 283–288. [Google Scholar] [CrossRef]
- Lorente, S.; Bejan, A.; Niu, J.L. Phase change heat storage in an enclosure with vertical pipe in the center. Int. J. Heat Mass Transf. 2014, 72, 329–335. [Google Scholar] [CrossRef]
- Asako, Y.; Gonçalves, E.; Faghri, M.; Charmchi, M. Numerical solution of melting processes for fixed and unfixed phase change material in the presence of magnetic field—Simulation of low-gravity environment. Numer. Heat Transf. Part. A Appl. 2002, 42, 565–583. [Google Scholar] [CrossRef]
- Erek, A.; Ilken, Z.; Acar, M.A. Experimental and numerical investigation of thermal energy storage with a finned tube. Int. J. Energy Res. 2005, 29, 283–301. [Google Scholar] [CrossRef] [Green Version]
- Bennon, W.D.; Incropera, F.P. A continuum model for momentum, heat and species transport in binary solid-liquid phase change systems—II. Application to solidification in a rectangular cavity. Int. J. Heat Mass Transf. 1987, 30, 2171–2187. [Google Scholar] [CrossRef]
- Lamberg, P.; Lehtiniemi, R.; Henell, A.M. Numerical and experimental investigation of melting and freezing processes in phase change material storage. Int. J. Therm. Sci. 2004, 43, 277–287. [Google Scholar] [CrossRef]
- Neumann, H.; Palomba, V.; Frazzica, A.; Seiler, D.; Wittstadt, U.; Gschwander, S.; Restucia, G. A simplified approach for modelling latent heat storages: Application and validation on two different fin-and-tubes heat exchangers. Appl. Therm. Eng. 2017, 125, 41–52. [Google Scholar] [CrossRef]
- Prieto, M.M.; González, B.; Granado, E. Thermal performance of a heating system working with a PCM plate heat exchanger and comparison with a water tank. Energy Build. 2016, 122, 89–97. [Google Scholar] [CrossRef]
- Zauner, C.; Hengstberger, F.; Etzel, M.; Lager, D.; Hofmann, R.; Walter, H. Experimental characterization and simulation of a fin-tube latent heat storage using high density polyethylene as PCM. Appl. Energy 2016, 179, 237–246. [Google Scholar] [CrossRef]
- Kahwaji, S.; White, M.A. Edible oils as practical phase change materials for thermal energy storage. Appl. Sci. 2019, 9, 1627. [Google Scholar] [CrossRef]
- Mailhe, C.; Duquesne, M.; Palomo del Barrio, E.; Azaiez, M.; Achchaq, F. Phase diagrams of fatty acids as biosourced phase change materials for thermal energy storage. Appl. Sci. 2019, 9, 1067. [Google Scholar] [CrossRef]
- Tomer, D.; Coutu, R.A. A phase change material for reconfigurable circuit applications. Appl. Sci. 2018, 8, 130. [Google Scholar] [CrossRef]



| Reference | Low Temperature | Medium Temperature | High Temperature |
|---|---|---|---|
| Abhat [15] | <120 °C | - | - |
| Zalba et al. [16] | <100 °C | - | - |
| Agyenim et al. [3] | <60 °C | Range 80–120 °C | >150 °C |
| Gil et al. [8] | - | - | >120 °C |
| Nomura et al. [18] | - | - | >100 °C |
| Ge et al. [19] | <30 °C | Range 40–200 °C | >200 °C |
| Reference | Viscosity Function | Viscosity Ratio (μs/μl) |
|---|---|---|
| Bennon and Incropera [78] | ∞ | |
| Voller et al. [92] | 103 | |
| Cao and Faghri [82] | 1010 | |
| Asako et al. [95] | Not specified | ∞ |
| Ma and Zhang [32] | Not specified | 1030 |
| Samara et al. [96] | Not specified | 5.5 × 108–5.5 × 1010 |
| Danaila et al. [94] | Not specified | 108 |
| Ziaei et al. [97] | Not specified | 104 |
| Kasibhatla et al. [98] | Linear | 2.2 × 107 |
| Kasibhatla et al. [76] | Linear | 2.2 × 105–2.2 × 107 |
| Latent Heat Formulations | ||||
|---|---|---|---|---|
| E-STM | E-TTM | E-EM | ||
| Velocity Transition Formulations | SOM/RSOM | [101] | [89] | - |
| STM/RSTM | - | - | [102] | |
| Darcy STM | [51,60,103] | [104] | [42,48,49,52,56,57,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128] | |
| VVM | [75,76,94,98] | [96,97,129,130] | [73,95,131] | |
| Reference | ne | dt [s−1] | η [s−1] |
|---|---|---|---|
| Bennon and Incropera [133]b | 1344 | 90–180 | 44.1–88.2 |
| Brent et al. [103]a | 1764 | 4 | 1.4 |
| Brent et al. [103]b | 1764 | 773 | 288.6 |
| Assis et al. [48]a | 3520 | 4500–6000 | 4400–5866 |
| Hosseinizadeh et al. [109]a | 13565 | 2000 | 7536 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazzi Ehms, J.H.; De Césaro Oliveski, R.; Oliveira Rocha, L.A.; Biserni, C.; Garai, M. Fixed Grid Numerical Models for Solidification and Melting of Phase Change Materials (PCMs). Appl. Sci. 2019, 9, 4334. https://doi.org/10.3390/app9204334
Nazzi Ehms JH, De Césaro Oliveski R, Oliveira Rocha LA, Biserni C, Garai M. Fixed Grid Numerical Models for Solidification and Melting of Phase Change Materials (PCMs). Applied Sciences. 2019; 9(20):4334. https://doi.org/10.3390/app9204334
Chicago/Turabian StyleNazzi Ehms, José Henrique, Rejane De Césaro Oliveski, Luiz Alberto Oliveira Rocha, Cesare Biserni, and Massimo Garai. 2019. "Fixed Grid Numerical Models for Solidification and Melting of Phase Change Materials (PCMs)" Applied Sciences 9, no. 20: 4334. https://doi.org/10.3390/app9204334
APA StyleNazzi Ehms, J. H., De Césaro Oliveski, R., Oliveira Rocha, L. A., Biserni, C., & Garai, M. (2019). Fixed Grid Numerical Models for Solidification and Melting of Phase Change Materials (PCMs). Applied Sciences, 9(20), 4334. https://doi.org/10.3390/app9204334








