Robustness of the Active Rotary Inertia Driver System for Structural Swing Vibration Control Subjected to Multi-Type Hazard Excitations
Abstract
:Featured Application
Abstract
1. Introduction
2. Mathematical Modeling
3. Sensitivity Analysis of the TRID/ARID System
3.1. Parameter Identification
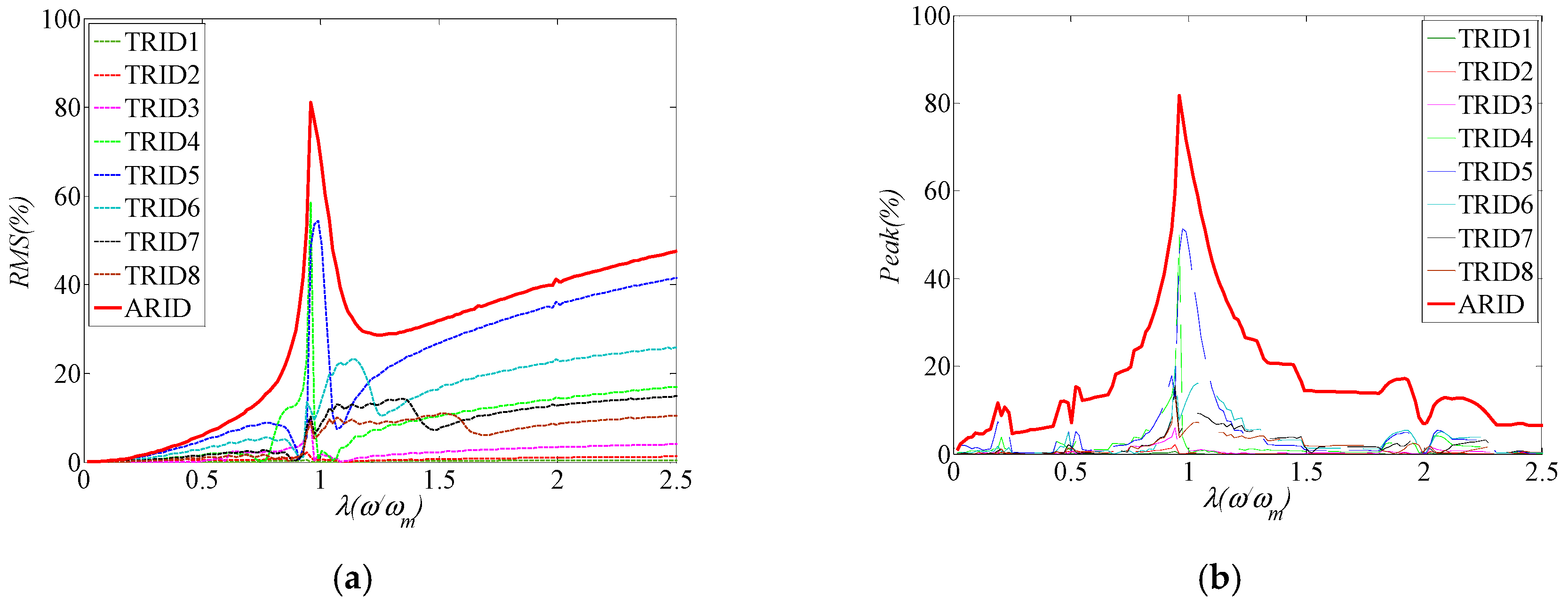
3.2. Control Effectiveness under Different Excitation Frequencies
4. Experimental Design
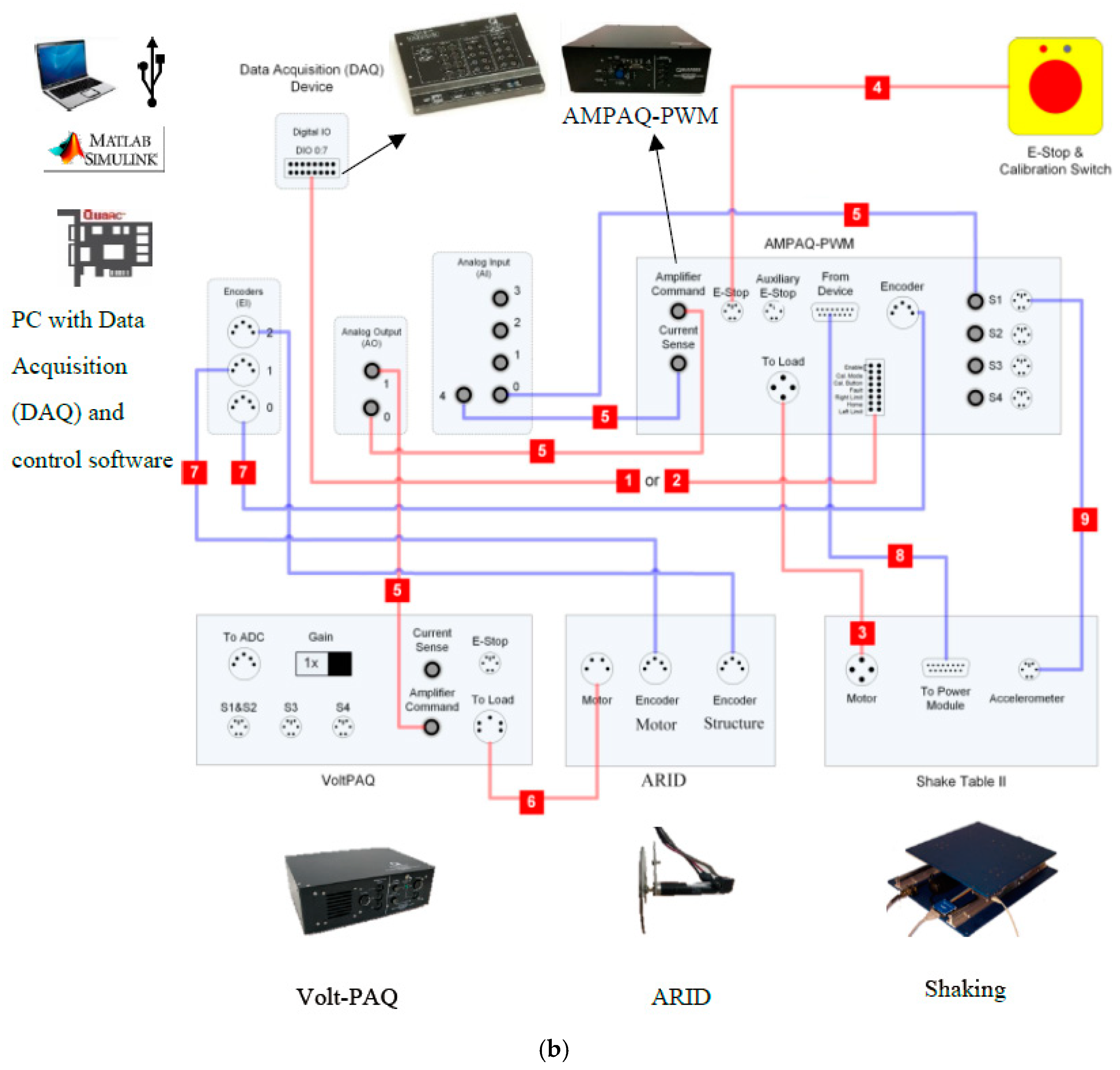
4.1. Experimental System Configuration
4.2. Experimental Setup
5. Control Effectiveness under Multi-Type Hazard Excitation
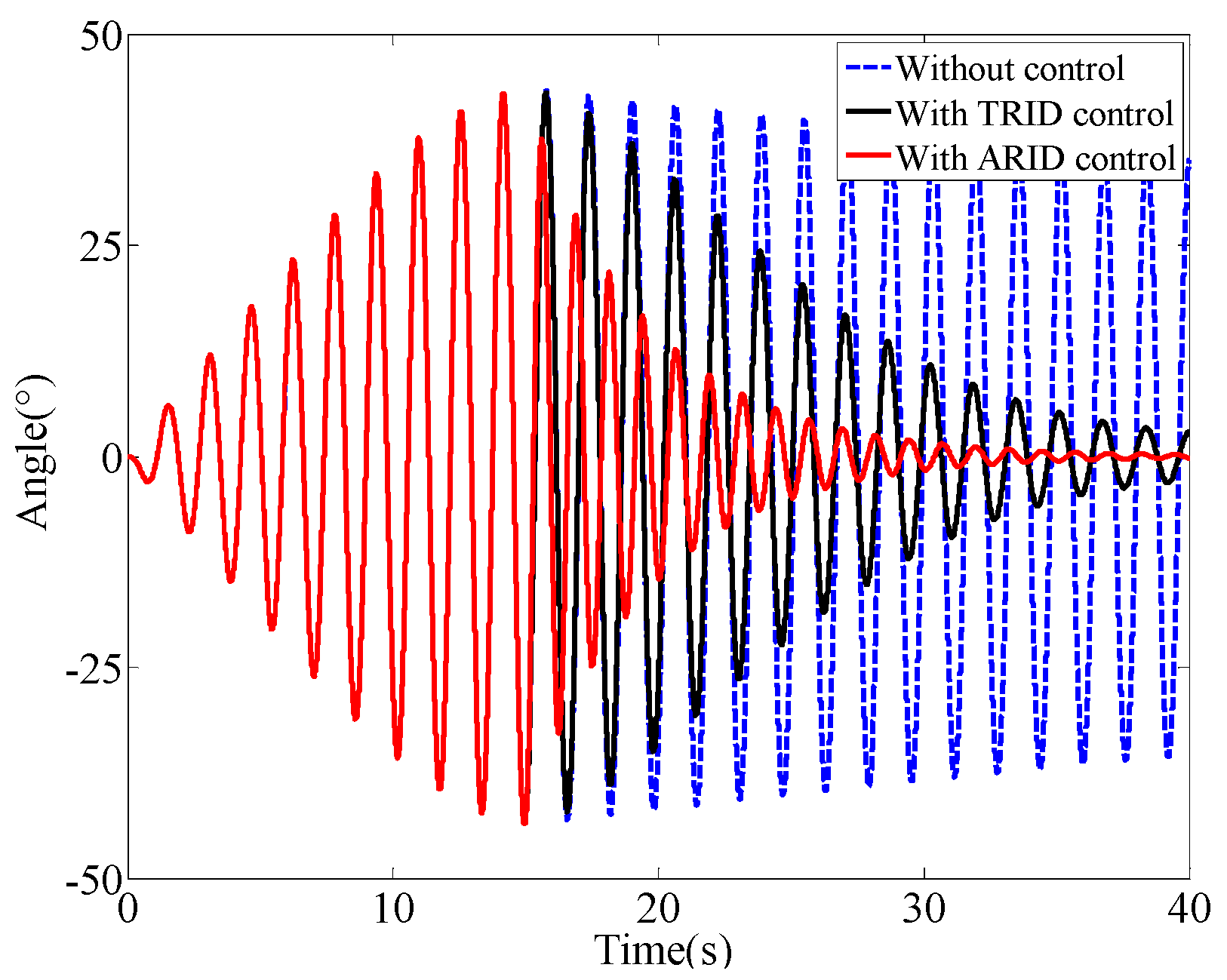
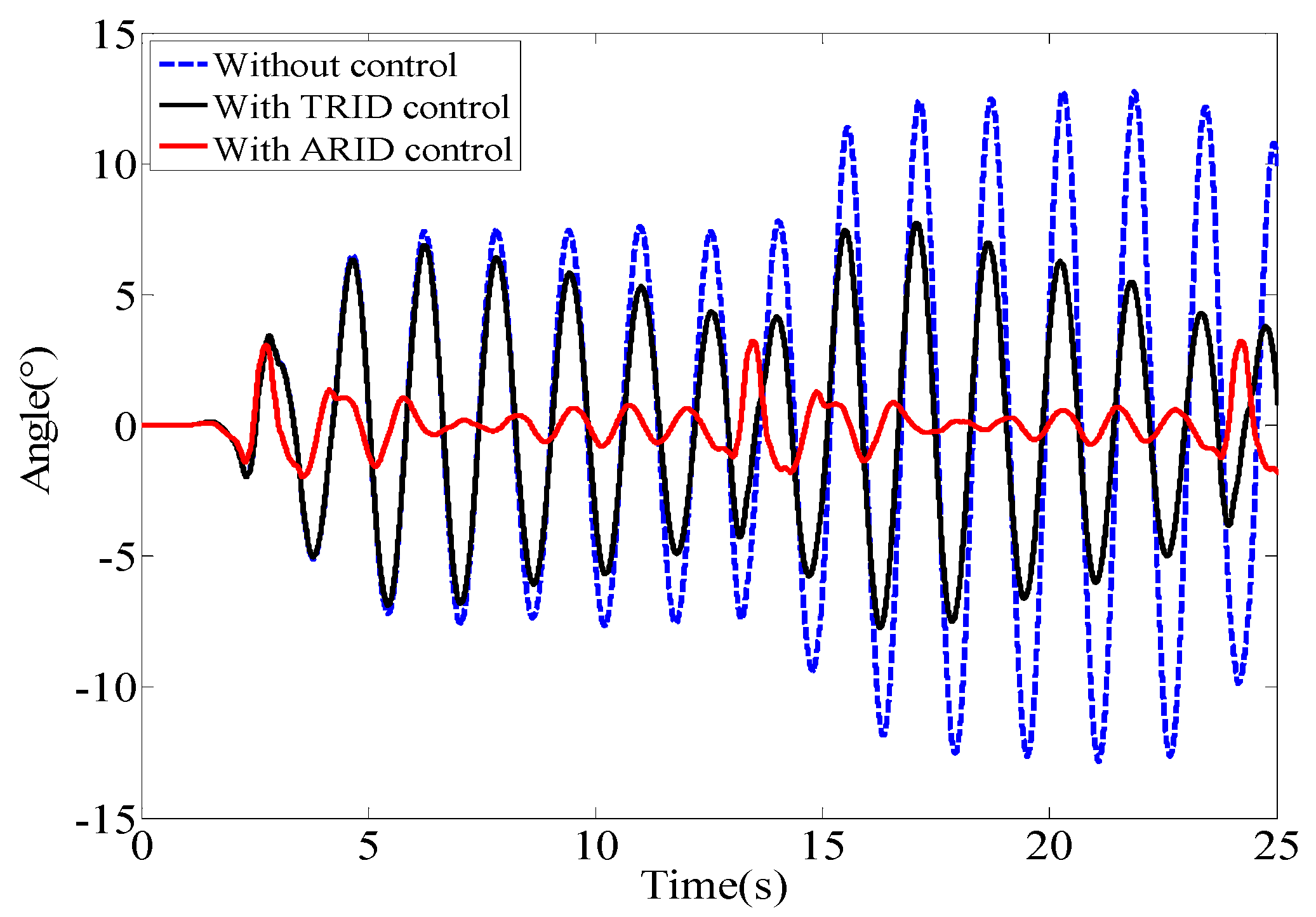
5.1. Free Vibration
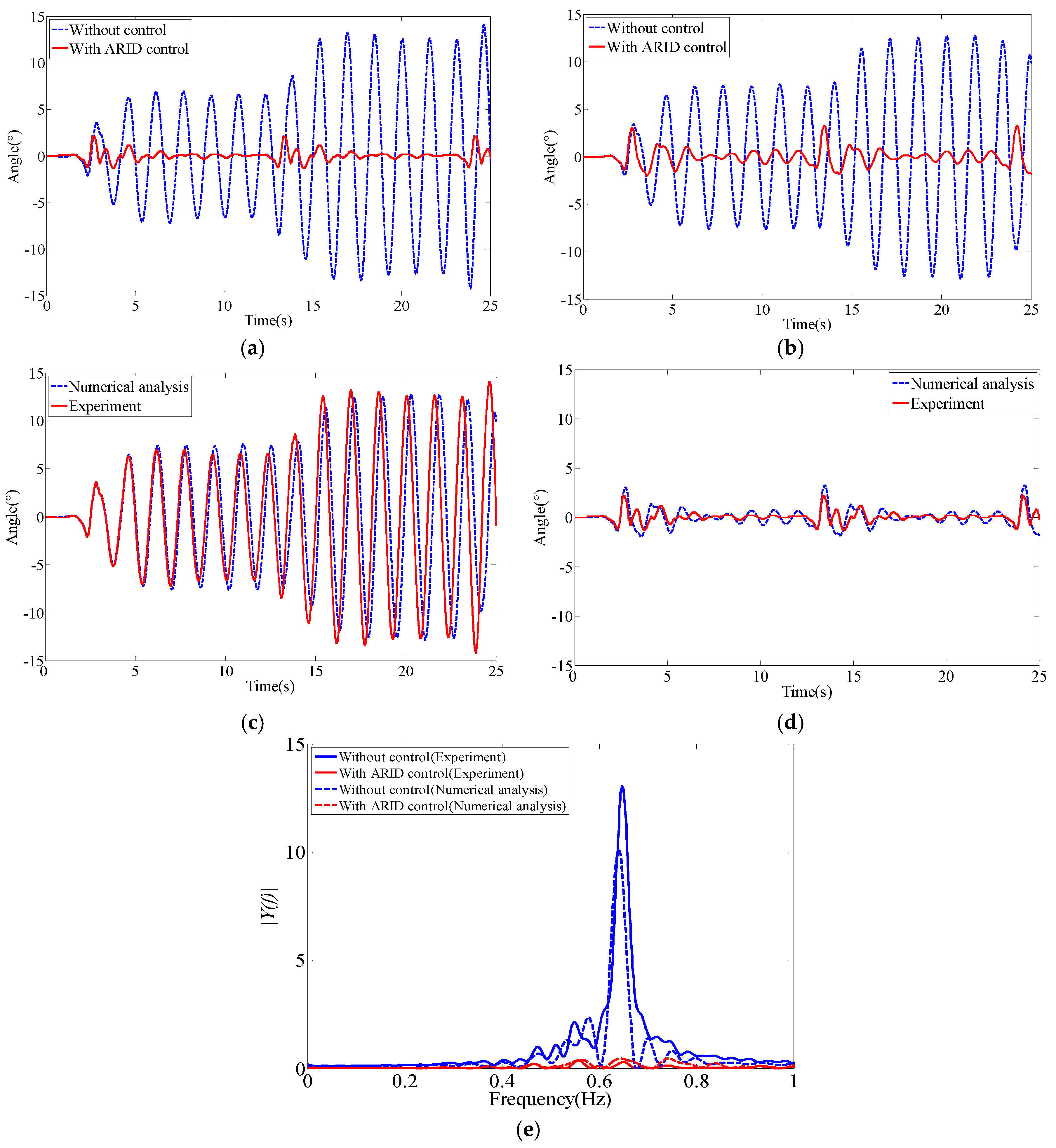
5.2. Forced Vibration
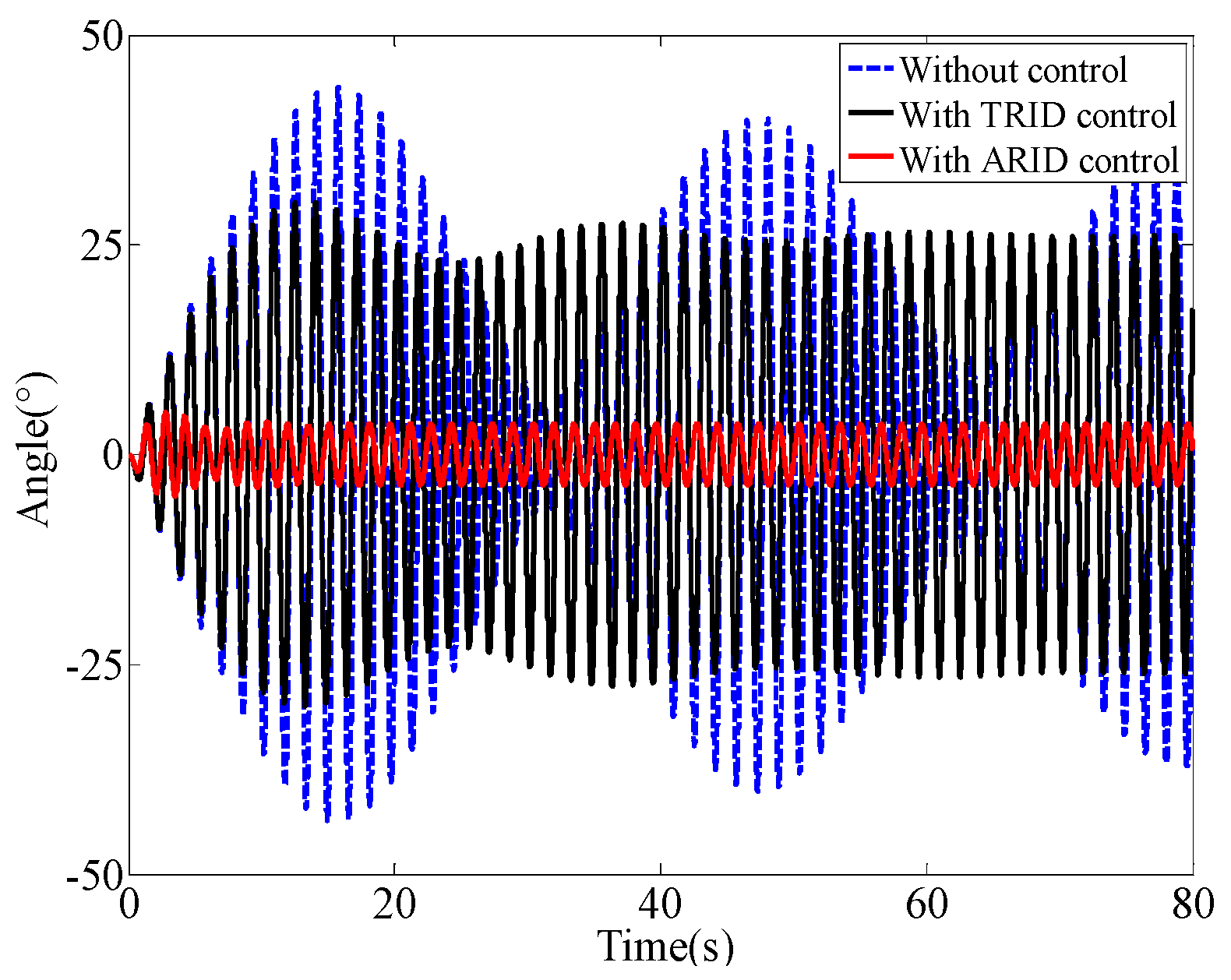
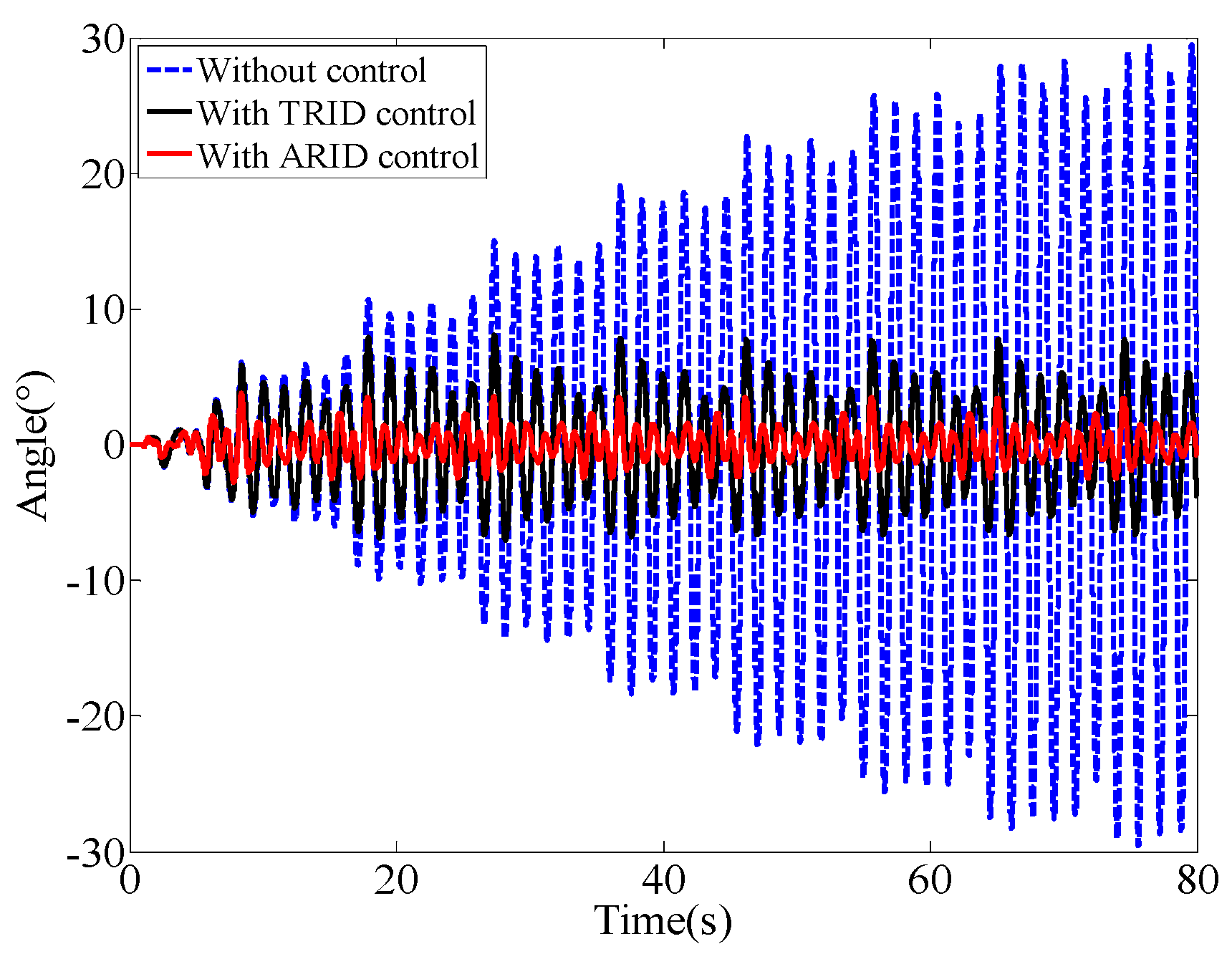
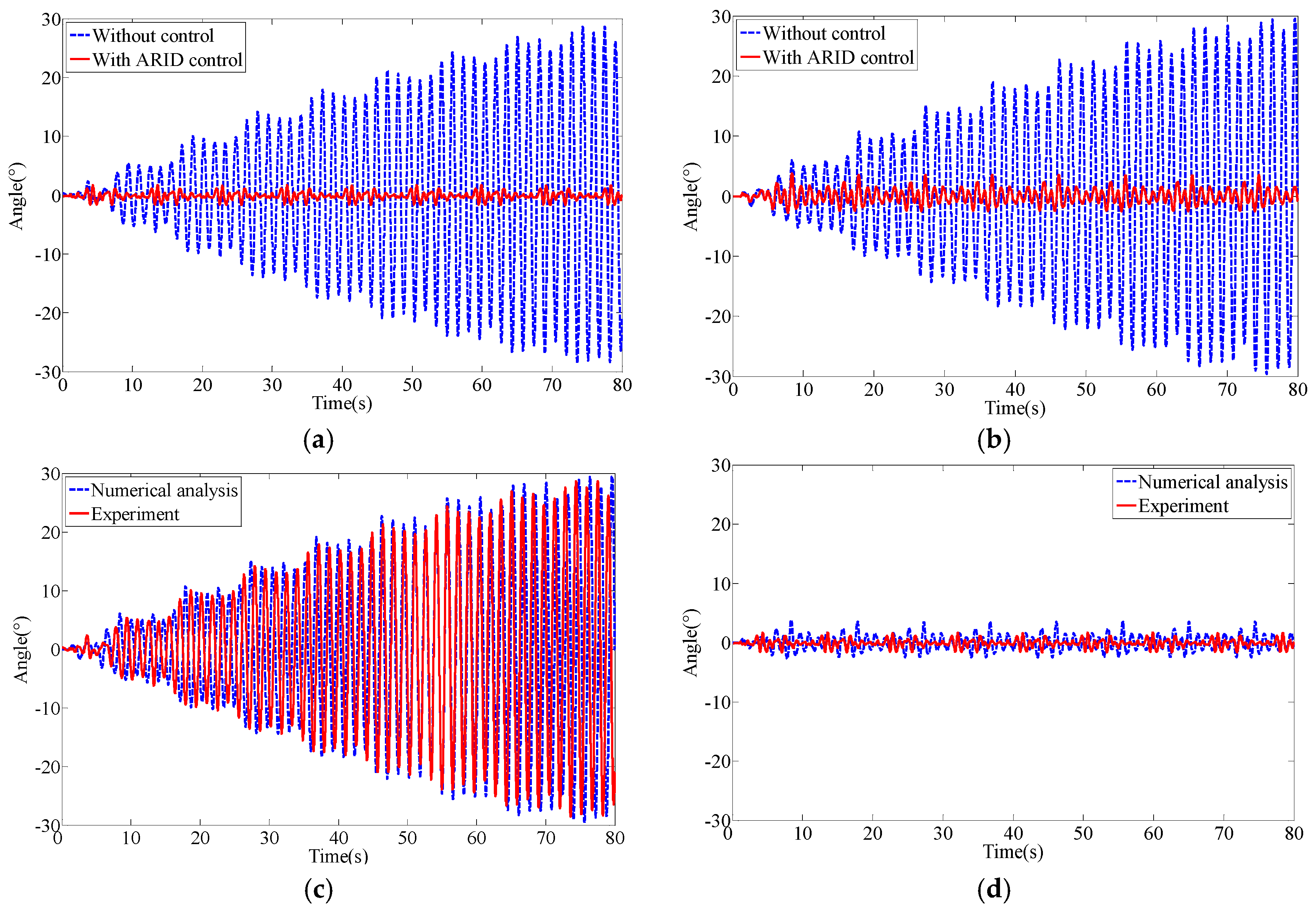
5.3. Sweep Excitation
5.4. Earthquake Excitation
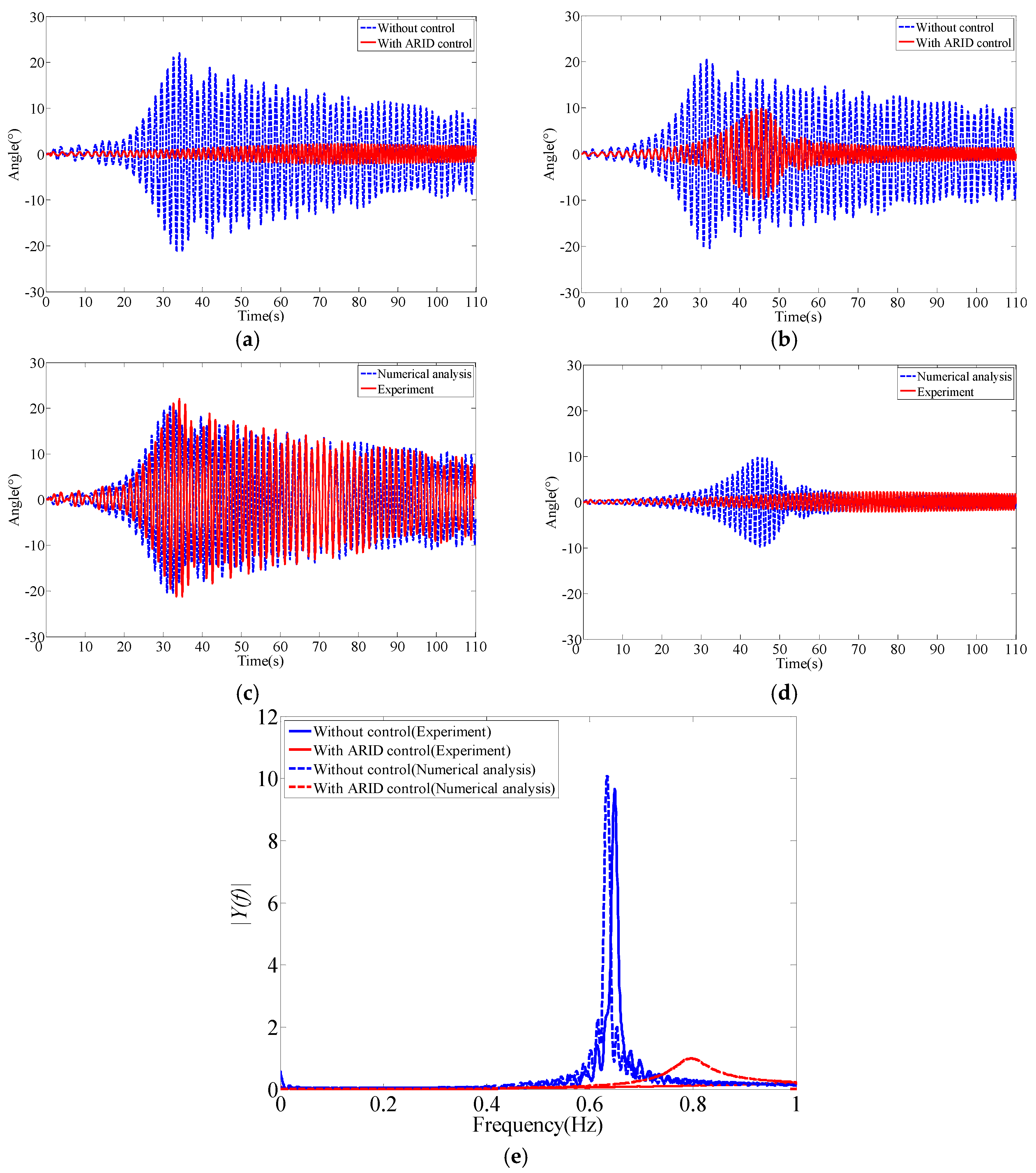
5.5. Sea Wave Excitation
5.6. Control Effectiveness Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Koks, E.E.; Rozenberg, J.; Zorn, C.; Tariverdi, M.; Vousdoukas, M.; Fraser, S.A.; Hall, J.W.; Hallegatte, S. A global multi-hazard risk analysis of road and railway infrastructure assets. Nat. Commun. 2019, 10, 2677. [Google Scholar] [CrossRef] [PubMed]
- Lin, K.; Lu, X.; Li, Y.; Guan, H. Experimental study of a novel multi-hazard resistant prefabricated concrete frame structure. Soil Dyn. Earthq. Eng. 2019, 119, 390–407. [Google Scholar] [CrossRef]
- Zhang, C.; Li, L.; Ou, J. Swinging motion control of suspended structures: Principles and applications. Struct. Control Health 2010, 17, 549–562. [Google Scholar] [CrossRef]
- Chen, S.R.; Cai, C.S. Coupled vibration control with tuned mass damper for long-span bridges. J. Sound Vib. 2004, 278, 449–459. [Google Scholar] [CrossRef]
- Wang, W.; Dalton, D.; Hua, X.; Wang, X.; Chen, Z.; Song, G. Experimental Study on Vibration Control of a Submerged Pipeline Model by Eddy Current Tuned Mass Damper. Appl. Sci. 2017, 7, 987. [Google Scholar] [CrossRef]
- Song, G.; Cai, S.; Li, H.N. Energy Dissipation and Vibration Control: Modeling, Algorithm, and Devices. Appl. Sci. 2017, 7, 801. [Google Scholar] [CrossRef]
- Shi, W.; Wang, L.; Lu, Z. Study on self-adjustable tuned mass damper with variable mass. Struct. Control Health 2018, 25, e2114. [Google Scholar] [CrossRef]
- Zuo, H.; Bi, K.; Hao, H. Using multiple tuned mass dampers to control offshore wind turbine vibrations under multiple hazards. Eng. Struct. 2017, 141, 303–315. [Google Scholar] [CrossRef]
- Matta, E. A novel bidirectional pendulum tuned mass damper using variable homogeneous friction to achieve amplitude-independent control. Earthq. Eng. Struct. Dyn. 2019, 48, 653–667. [Google Scholar] [CrossRef]
- Wang, L.; Shi, W.; Li, X.; Zhang, Q.; Zhou, Y. An adaptive-passive retuning device for a pendulum tuned mass damper considering mass uncertainty and optimum frequency. Struct. Control Health 2019, 26, e2377. [Google Scholar] [CrossRef]
- Ferreira, F.; Moutinho, C.; Cunha, Á.; Caetano, E. Proposal of optimum tuning of semiactive TMDs used to reduce harmonic vibrations based on phase control strategy. Struct. Control Health 2018, 25, e2131. [Google Scholar] [CrossRef]
- Banerji, P.; Murudi, M.; Shah, A.H.; Popplewell, N. Tuned liquid dampers for controlling earthquake response of structures. Earthq. Eng. Struct. Dyn. 2015, 29, 587–602. [Google Scholar] [CrossRef]
- Shum, K.M.; Xu, Y.L. Multiple tuned liquid column dampers for reducing coupled lateral and torsional vibration of structures. Eng. Struct. 2004, 26, 745–758. [Google Scholar] [CrossRef]
- Papalou, A.; Strepelias, E. Effectiveness of particle dampers in reducing monuments’ response under dynamic loads. Mech. Com. Mater. Struct. 2016, 23, 128–135. [Google Scholar] [CrossRef]
- Zhang, P.; Li, L.; Patil, D.; Singla, M.; Li, H.; Mo, Y.L.; Song, G. Parametric study of pounding tuned mass damper for subsea jumpers. Smart Mater. Struct. 2016, 25, 015028. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, P.; Patil, D.; Li, H.; Song, G. Experimental studies on the effectiveness and robustness of a pounding tuned mass damper for vibration suppression of a submerged cylindrical pipe. Struct. Control Health 2017, 24, e2027. [Google Scholar] [CrossRef]
- Tan, J.; Jiang, J.; Liu, M.; Feng, Q.; Zhang, P.; Ho, S.C.M. Implementation of Shape Memory Alloy Sponge as Energy Dissipating Material on Pounding Tuned Mass Damper: An Experimental Investigation. Appl. Sci. 2019, 9, 1079. [Google Scholar] [CrossRef]
- Jiang, J.; Ho, S.C.M.; Markle, N.J.; Wang, N.; Song, G. Design and control performance of a frictional tuned mass damper with bearing-shaft assemblies. J. Vib. Control 2019, 25, 1812–1822. [Google Scholar] [CrossRef]
- Pisal, A.Y.; Jangid, R.S. Vibration control of bridge subjected to multi-axle vehicle using multiple tuned mass friction dampers. Int. J. Adv. Struct. Eng. 2016, 8, 213–227. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Zhang, C.; Li, H.; Tan, P.; Ou, J.; Zhou, F. Active mass driver control system for suppressing wind induced vibration of the Canton Tower structure. Smart Struct. Syst. 2014, 13, 281–303. [Google Scholar] [CrossRef]
- Francisco, P.; Josep, R.; Josep, M.; Hamid, R. Integrated Design of Hybrid Interstory-Interbuilding Multi-Actuation Schemes for Vibration Control of Adjacent Buildings under Seismic Excitations. Appl. Sci. 2017, 7, 323. [Google Scholar] [Green Version]
- Elisabet, S.; Andrés, R.; Antolino, G.; Amadeo, B.C. Entropy Analysis for Damage Quantification of Hysteretic Dampers Used as Seismic Protection of Buildings. Appl. Sci. 2017, 6, 628. [Google Scholar]
- Zhang, C.; Ou, J.; Zhang, J. Parameter Optimization and Analysis of Vehicle Suspension System Controlled by Magnetorheological Fluid Dampers. Struct. Control Health 2006, 13, 885–896. [Google Scholar]
- Preumont, A. Vibration Control of Active Structures: An Introduction; Springer: Berlin/Heidelberg, Germany, 2018; Volume 246. [Google Scholar]
- Li, H.; Song, G.; Kim, J.T.; Li, G. Smart Control Algorithms and Technology in Civil Infrastructures. Math. Probl. Eng. 2014, 2014, 1–2. [Google Scholar] [CrossRef] [Green Version]
- Fitzgerald, B.; Sarkar, S.; Staino, A. Improved reliability of wind turbine towers with active tuned mass dampers (ATMDs). J. Sound Vib. 2018, 419, 103–122. [Google Scholar] [CrossRef]
- Zhang, C. Control Force Characteristics of Different Control Strategies for the Wind-excited 76-story Benchmark Building Structure. Adv. Struct. Eng. 2014, 17, 543–559. [Google Scholar] [CrossRef]
- Venanzi, I.; Ierimonti, L.; Ubertini, F. Effects of control-structure interaction in active mass driver systems with electric torsional servomotor for seismic applications. Bull. Earthq. Eng. 2016, 15, 1543–1557. [Google Scholar] [CrossRef]
- Zhang, C.; Ou, J. Modeling and dynamical performance of the electromagnetic mass driver system for structural vibration control. Eng. Struct. 2015, 82, 93–103. [Google Scholar] [CrossRef]
- Zhang, C.; Ou, J. Control Structure Interaction of Electromagnetic Mass Damper System for Structural Vibration Control. J. Eng. Mech. ASCE 2008, 134, 428–437. [Google Scholar] [CrossRef]
- May, B.S.; Beck, J.L. Probabilistic control for the Active Mass Driver benchmark structural model. Earthq. Eng. Struct. Dyn. 2015, 27, 1331–1346. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, C.; Li, H.; Ou, J. Real-time hybrid simulation approach for performance validation of structural active control systems: A linear motor actuator based active mass driver case study. Struct. Control Health 2014, 21, 574–589. [Google Scholar] [CrossRef]
- Camachogómez, C.; Wang, X.; Pereira, E.; Díaz, I.M.; Salcedo-Sanz, S. Active vibration control design using the Coral Reefs Optimization with Substrate Layer algorithm. Eng. Struct. 2018, 157, 14–26. [Google Scholar] [CrossRef]
- Ho, C.; Zhu, Y.; Lang, Z.Q.; Billings, S.A.; Kohiyama, M.; Wakayama, S. Nonlinear damping based semi-active building isolation system. J. Sound Vib. 2018, 424, 302–317. [Google Scholar] [CrossRef]
- Chey, M.H.; Chase, J.G.; Mander, J.B.; Carr, A.J. Semi-active tuned mass damper building systems, Design. Earthq. Eng. Struct. Dyn. 2010, 39, 119–139. [Google Scholar] [CrossRef]
- Behrooz, M.; Wang, X.; Gordaninejad, F. Modeling of a new semi-active/passive magneto rheological elastomer isolator. Smart Mater. Struct. 2014, 23, 045013. [Google Scholar] [CrossRef]
- Fu, W.; Zhang, C.; Li, M.; Duan, C. Experimental Investigation on Semi-Active Control of Base Isolation System Using Magnetorheological Dampers for Concrete Frame Structure. Appl. Sci. 2019, 9, 3866. [Google Scholar] [CrossRef]
- Pappalardo, C.; Guida, D. Use of the Adjoint Method for Controlling the Mechanical Vibrations of Nonlinear Systems. Mach 2018, 6, 19. [Google Scholar] [CrossRef]
- Bertolazzi, E.; Biral, F.; Da Lio, M. Symbolic–numeric indirect method for solving optimal control problems for large multibody systems. Multibody Syst. Dyn. 2005, 13, 233–252. [Google Scholar] [CrossRef]
- Abdullahi, A.M.; Mohamed, Z.; Selamat, H.; Pota, H.R.; Abidin, M.S.Z.; Ismail, F.S.; Haruna, A. Adaptive output-based command shaping for sway control of a 3D overhead crane with payload hoisting and wind disturbance. Mech. Syst. Signal Process. 2018, 98, 157–172. [Google Scholar] [CrossRef]
- Mori, Y.; Tagawa, Y. Vibration controller for overhead cranes considering limited horizontal acceleration. Control Eng. Pract. 2018, 81, 256–263. [Google Scholar] [CrossRef]
- Mukhtar, F.H.; Hwa, J.Y.; Choudhury, I.A.; Isa, A.I.; Zimit, A.Y.; Kumbasar, T. Current development on using Rotary Inverted Pendulum as a benchmark for testing linear and nonlinear control algorithms. Mech. Syst. Signal Process. 2019, 116, 347–369. [Google Scholar]
- Maghsoudi, M.J.; Mohamed, Z.; Husain, A.R.; Tokhi, M.O. An optimal performance control scheme for a 3D crane. Mech. Syst. Signal Process. 2016, 66–67, 756–768. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, H. Swing Vibration Control of Suspended Structure Using Active Rotary Inertia Driver System: Parametric Analysis and Experimental Verification. Appl. Sci. 2019, 9, 3144. [Google Scholar] [CrossRef]
- He, X.; Li, H. Suppression of random wave-induced vibrations in offshore platform by tuned liquid column damper. J. Vib. Eng. 2008, 21, 71–78. [Google Scholar]
- Chatterjee, T.; Chakraborty, S. Vibration mitigation of structures subjected to random wave forces by liquid column dampers. Ocean Eng. 2014, 87, 151–161. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| Structural length (l)/(m) | 0.65 |
| Suspended particle mass (m)/(kg) | 0.5 |
| Rotary inertia mass (ma)/(kg) | 0.3 |
| Structural damping coefficient (c)/(N·s/m) | 0.005 |
| Rotary inertia (Ja)/(kg·m2) | 0.0015 |
| Radius of rotary inertia mass (r)/(m) | 0.065 |
| Parameters | Value |
|---|---|
| Stroke (Shaking table)/(cm) | ±7.5 |
| The maximum acceleration (Shaking table)/(g) | 2.5 |
| The most frequency (Shaking table)/(Hz) | 10 |
| Rated voltage (Motor)/(V) | 24 |
| No-load speed (Motor)/(rpm) | 8810 |
| Rated speed (Motor)/(rpm) | 8050 |
| Rated torque (Motor)/(mN·m) | 85.6 |
| Moment of inertia (Motor)/(g·mm2) | 3350 |
| Mass (Motor)/(g) | 260 |
| Reduction ratio (Gearbox) | 3.7:1 |
| Moment of inertia (Gearbox)/(g·mm2) | 150 |
| Mass (Gearbox)/(g) | 118 |
| Length (Structure)/(mm) | 650 |
| Radius (Rotary inertia mass)/(mm) | 45 |
| Rotary inertia (Rotary inertia mass)/(g·mm2) | 1,498,413.8 |
| Control Effectiveness | ||||
|---|---|---|---|---|
| Peak Reduction Rate (Peak) | RMS Reduction Rate (RMS) | |||
| Case | TRID | ARID | TRID | ARID |
| Free vibration | - | - | 50% | 82% |
| Forced vibration | 31% | 88% | 28% | 90% |
| Sweep excitation | 25% | 52% | 73% | 80% |
| Earthquake excitation | 45% | 75% | 59% | 93% |
| Sea wave excitation | 73% | 87% | 77% | 94% |
| Experiment | ||||
| Control Effectiveness | Peak Swing Angle (°) | |||
| Case | Peak Reduction Rate (Peak) | Peak Reduction Rate (RMS) | with ARID Control | without Control |
| Free vibration | - | 88% | 47.76 | 47.37 |
| Forced vibration | 97% | 97% | 1.67 | 53.44 |
| Sweep excitation | 90% | 90% | 2.29 | 22.06 |
| Earthquake excitation | 85% | 96% | 2.20 | 14.24 |
| Sea wave excitation | 94% | 97% | 1.67 | 28.65 |
| Numerical Analysis | ||||
| Control Effectiveness | Peak Swing Angle (°) | |||
| Case | Peak Reduction Rate (Peak) | RMS Reduction Rate (RMS) | with ARID Control | without Control |
| Free vibration | - | 82% | 43.58 | 43.58 |
| Forced vibration | 88% | 90% | 5.06 | 43.71 |
| Sweep excitation | 52% | 80% | 9.87 | 20.64 |
| Earthquake excitation | 75% | 93% | 3.24 | 12.85 |
| Sea wave excitation | 87% | 94% | 3.78 | 29.61 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Wang, H. Robustness of the Active Rotary Inertia Driver System for Structural Swing Vibration Control Subjected to Multi-Type Hazard Excitations. Appl. Sci. 2019, 9, 4391. https://doi.org/10.3390/app9204391
Zhang C, Wang H. Robustness of the Active Rotary Inertia Driver System for Structural Swing Vibration Control Subjected to Multi-Type Hazard Excitations. Applied Sciences. 2019; 9(20):4391. https://doi.org/10.3390/app9204391
Chicago/Turabian StyleZhang, Chunwei, and Hao Wang. 2019. "Robustness of the Active Rotary Inertia Driver System for Structural Swing Vibration Control Subjected to Multi-Type Hazard Excitations" Applied Sciences 9, no. 20: 4391. https://doi.org/10.3390/app9204391
APA StyleZhang, C., & Wang, H. (2019). Robustness of the Active Rotary Inertia Driver System for Structural Swing Vibration Control Subjected to Multi-Type Hazard Excitations. Applied Sciences, 9(20), 4391. https://doi.org/10.3390/app9204391






