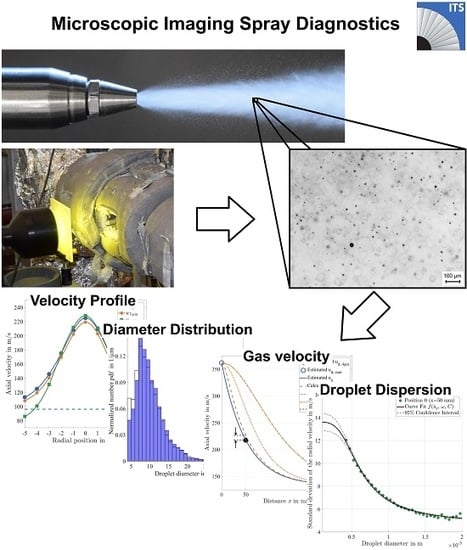
The subsequent discussion of the results is focused on the capabilities of the diagnostics. In this context, the first measurement position downstream of the atomiser (x = 50 mm) is of great importance for the methodology, since the droplet data recorded at this position can be utilised as droplet starting conditions for numerical simulations of spray evaporation. Hence, it must be ensured that sufficient information about the spray is captured in order to avoid inconclusive results.
Furthermore, the accuracy of measuring the gas velocity by using the smallest detectable droplets as seeding particles is assessed by a Stokes number analysis. The resulting gas velocity may yield important information for the analysis of spray systems, since the relative velocity of droplets with regard to the gas phase can be derived. Finally, it will be elucidated that the described methodology will provide experimental validation data, which can be used to study the evaporation characteristics of UWS under technical relevant flow conditions.
3.1. Spray Characteristics
An ambitious goal of numerous spray experiments is the detection of the spray characteristics like droplet diameter distribution or velocity profiles as close as possible to the atomiser. This is in particular important for an insight into the primary atomisation process or if the starting conditions of the droplets are sought for numerical simulations. The first measurement position of this study was placed 50 downstream of the atomiser because secondary atomisation is almost completed at this position. On the other hand, an acceptable droplet concentration is present which facilitates post-processing. The results at this position reveal spray characteristics typical for the twin-fluid atomiser, which will be discussed in detail in the following.
The present diagnostics offer the possibility to vary the position of the measurement volume across the cross section of the pipe by simply moving the camera in the direction of the optical axis as depicted in
Figure 9. In this context, the small depth of field is a significant advantage of the present microscopic imaging setup, since a slim and thus well–defined measurement volume is achieved. Finally, a traversing of ±5
in a radial direction around the centre of the pipe was employed covering 11 measurement positions. At each position, 3000 double frame images are taken with a repetition rate of 10 Hz. The resulting number of evaluated droplets varied from a few thousands at the edge to approximately 120,000 at the centre of the spray.
A typical result is plotted in
Figure 10a in terms of characteristic droplet diameters. Obviously, the profiles are not perfectly symmetric. The reason for this phenomenon is assumed to result from some measurement positions featuring low statistical significance. First of all, it is found that the statistical significance is reduced with increased distance from the centre of the spray due to a lower concentration of droplets. Moreover, the high concentration of droplets at the centre of the spray causes a stronger background noise if the inner spray cone is situated between camera and measurement position. Hence, the outer positions in positive radial direction in
Figure 10a are characterised by a lower signal-to-noise ratio, and therefore a lower quantity of droplets is evaluated. Speaking in numbers, at the extreme positions of +5 mm and −5 mm, approximately 4000 and approximately 19,000 droplets are detected, respectively. Nevertheless, the overall quantity of evaluated droplets is sufficient for a further analysis of the spray characteristics.
In general, the atomiser is capable of producing a very fine spray. The Sauter Mean Diameter stays at a constant level just above 10 over a range of ±2 in a radial direction. In this core zone large droplets, represented by the diameter at 90% volumetric quantile , have a diameter in the range of 20 to 25 . While the arithmetic mean Diameter yields no strong variation in a radial direction, a clear inhomogeneity is revealed by the profiles of and . Both characteristic diameters increase sharply at a distance of 2–3 from the centre of the spray, which gives evidence to an imperfect atomisation process at the outer edge of the spray cone.
In addition to the information about droplet size, the velocity has been determined for each detected droplet. The result is summarised in
Figure 10b by means of three average velocity profiles plotted over the radial direction of the pipe flow. The first profile
represents the average velocity of droplets of 8
diameter, which is calculated for a diameter range of 8 ±
in order to achieve statistical significance. At the centre of the spray, a very high velocity is detected, which is far above the bulk velocity of the gas phase
= 96
. This is caused by the high velocity of the air stream emerging from the nozzle. At the edge of the traverse displacement, the velocity drops down to slightly above the bulk velocity of the gas phase. The reason for this behaviour is given by the slower bulk hot gas flow, which decelerates the air flow from the nozzle. In this context, it should be noted that the outlet bore hole diameter of the atomiser nozzle is 2
.
The velocity
of droplets of 5
diameter was found to be lower than
over the entire profile due to the lower inertia of the smaller droplets. Similarly, the velocity of droplets of a diameter greater than 15
is presumed to feature the fastest velocity over the entire radial dimension. In contrast,
was found to have the fastest velocity only at the centre region of the spray. It shows a strong decrease towards the edges of spray, where the lowest velocity of the three velocity profiles is measured. In this region,
even drops below the bulk velocity of the gas flow. A possible explanation for this effect may be derived from the diameter distribution in
Figure 10a. These results indicate an imperfect atomisation at the outer edge of the spray, which may lead to larger droplets emerging with low initial velocity from the atomiser.
A snapshot of the spray in the near nozzle region was recorded using a relatively long exposure time of approximately
s as shown in
Figure 11. Obviously, the centre of the spray can not be investigated in detail due to motion blur. In contrast to that, droplets at the outer region of the spray as well as liquid structures still connected to the atomiser nozzle are recorded sharply, which implies that they feature a considerably lower velocity in comparison to droplets within the main spray cone. Therefore, the statement of large droplets with low initial velocity is confirmed, which is also in accordance with the general primary atomisation process of an effervescent atomiser as reviewed by Sovani et al. [
39].
The radial position featuring the strongest velocity gradient of all velocity profiles in
Figure 10b, approximately
off the centre, represents the shear layer zone between the jet flow of the atomiser and the surrounding hot gas flow. In this region, the finest spray is recorded as illustrated by the
and in particular by the
. Both characteristic diameters increase sharply at a further distance from the centre of the spray. This behaviour may be caused by the strong velocity gradient in combination with shear layer turbulence. Hence, the atomisation process in this region is dominated by the resulting high relative velocity between the droplets and the hot gas. At this point, it should be emphasised that the evaluation of this correlation between droplet size and velocity is only possible because the diagnostics is capable of detecting the size and velocity of individual droplets.
In conclusion, these initial results of the test section comprise important spray data close to the atomiser. In particular, the possibility to obtain data at different positions in a radial direction in a dense spray region turns out to be a great advantage of the measurement technique. This gives a better understanding of the atomisation process or enables the tuning of the cold gas mass flow of the atomiser in order to achieve desired spray characteristics. Furthermore, the recorded data in the proximity of the atomiser can be utilised as droplet starting conditions for numerical simulations of spray evaporation. In this context, the captured inhomogeneities of the droplet diameter and velocity profiles represent vital input data for numerical predictions.
3.2. Determining the Gas Velocity
The gas velocity is an important parameter for the analysis of spray systems, since the relative velocity of droplets to the gas flow can be derived. This relative velocity, which is also called slip velocity, has a strong influence on droplet kinematics, secondary atomisation, and evaporation [
2]. Hence, the simultaneous measurement of gas and droplet velocity is a great advantage for spray diagnostics. Standard optical techniques for measuring the gas velocity are Laser Doppler Anemometry (LDA) and Particle Image Velocimetry (PIV). Both techniques require seeding the flow with small particles in the order of 1
in diameter. These seeding particles will follow the flow almost perfectly due to their low inertia.
Microscopic imaging has already been demonstrated to be capable to detect such seeding particles if the droplet size is not of interest using Particle Shadow Velocimetry [
40]. In addition to an often simpler optical setup, this technique can be advantageous in comparison to established diagnostics like PIV or LDA for small-scale applications or multiphase flows [
41,
42]. However, the goal of this study is to detect not only the velocity, but also the diameter of individual droplets.
Therefore, one way to realise a simultaneous measurement of gas and droplet velocity is the utilisation of the smallest detectable droplets as seeding particles. Hence, no additional seeding is necessary and the non-intrusive and simultaneous measurement of the gaseous velocity field is possible as long as enough small droplets are present in the flow. This methodology was successfully applied with the PDA for detecting evaporating [
31] and burning droplets [
32]. In these studies, droplets of a size smaller than 3–5
were utilised to derive the gas velocity.
The present microscopic imaging setup also offers the possibility to detect droplets of such small size, which may be utilised as seeding. However, it is mandatory that the droplets of a selected size do follow the flow correctly in order to derive a sensible gas velocity. In this context, it is important to note that the droplet size cannot be specified in advance since it depends on the actual flow field of the gas. Subsequently, the timescales due to the inertia of the droplets will be estimated in order to decide up to which size the droplets are suitable as tracers of the gas flow. This gives a measure of the accuracy of the present diagnostics for determining the gas velocity.
The following estimation will focus on the most critical part of the flow field of the experimental setup in this study: the strong deceleration of the air jet emerging from the atomiser nozzle. First of all, a Stokes flow is assumed for the gas flow around the droplet [
43]. The relevant timescale is the response or relaxation time of a droplet
which is dependent on the density of the droplet
, the droplet diameter
and the dynamic viscosity of the gas
. Considering the relative velocity between droplet and the gas phase
and neglecting gravitation, the equation of motion can be written as
Taking the homogeneous solution of this differential equation, it is obvious that the droplet velocity recovers after a sudden jump according to
The determination of an appropriate timescale of the gaseous phase is not straightforward, since it depends on the actual flow field. As a first approach, the assumption is made that the axial velocity of the droplets of 4
diameter
represents the velocity of the gas phase. The experimental results of the temporal arithmetic mean of
at the centre of the pipe are illustrated in
Figure 12 for the first three measurement positions downstream of the atomiser.
However, the initial velocity of the gas and the droplets at the atomiser exit is not available. Furthermore, the evolution of the velocity directly downstream of the nozzle is governed by gas dynamics and the resulting primary atomisation. In this study, the initial velocity of the droplets and the air is estimated as at the nozzle outlet based on the estimated droplet starting temperature . The present atomiser is operated at supercritical flow conditions in order to achieve a strong pressure drop at the atomiser outlet. Hence, this assumption is reasonable. Furthermore, the assumption is conservative in terms of the estimation of the measurement accuracy, since expected shock waves may lead to a lower effective initial velocity of droplets after primary atomisation in the near nozzle region.
In the next step, a function of the type
is used to fit the estimated and experimental data in order to derive an estimated evolution of the gas velocity
, which is shown in
Figure 12. This function is chosen according to Equation (
5). Hence, a timescale of the gas phase
can be derived and the Stokes number of a droplet with a diameter of 4
can be calculated:
Since the condition,
is not perfectly fulfilled, the derived evolution of the gas velocity is used to solve a more generalised equation of motion of one droplet,
in order to estimate the measurement accuracy. The correlation of Ihme et al. [
44] is used to determine the drag coefficient
This correlation is only valid for perfect spheres, which is a reasonable assumption for the small droplets in this study. Most importantly, Equation (
10) was validated experimentally for droplet Reynolds numbers
Therefore, the main restriction of the Stokes theory (
) is overcome. The resulting spatial evolution of the velocity of a droplet of a diameter of 4
is illustrated in
Figure 12. Obviously, droplets of a diameter of 4
follow the estimated gas velocity very well. Furthermore, this approach yields directly the estimated measurement error at position 0 at a distance of
= 50
downstream of the atomiser:
In view of the strong estimated deceleration at the near-nozzle region, the measurement accuracy is acceptable. Furthermore, an iterative determination of
is possible based on the already obtained results. This way,
can be determined with improved accuracy. In the scope of this paper, however, the gas velocity is simply taken from the velocity of the smallest detectable droplets. Additionally, the response of droplets of 10
and 20
diameter is calculated, which corresponds to the smallest detectable droplet range of non-microscopic imaging techniques. Both results are plotted in
Figure 12 and reveal a drastically greater measurement error than that of the 4
droplets, which emphasizes the specific advantage of the method.
In summary, the use of microscopic imaging seems to be well suited for determining the gas velocity by using the velocity of the smallest detectable droplets. This is advantageous as no additional input is required, neither regarding the experimental setup nor with respect to the processing routine. The additional information about the gas flow field can be utilised to analyse and validate droplet kinematics. In addition, the effect of the slip velocity on secondary atomisation or evaporation can be evaluated.
3.3. Discussion of Velocity Fluctuations
Since the temporal average of the gas velocity can be derived with sufficient accuracy, the discussion is extended to the statistical analysis of velocity fluctuations. This requires the post-processing, as presented in
Section 2.3, to be extended in order to exclude spurious vector assignments, which may compromise the statistical analysis. The universal outlier detection of Westerweel and Scarano [
45] is widely used for Particle Image Velocimetry (PIV) data. This technique is based on a normalised median filter, which considers the neighbour velocity vectors of the vector under concern. Furthermore, this filter was verified for a wide range of Reynolds numbers ranging from
to
. In contrast to PIV data, Particle Tracking Velocimetry (PTV) yields non-equidistant neighbour vectors. Hence, a weighting of neighbour vectors based on the distance from the droplet velocity vector concerned is used as proposed by Duncan et al. [
46]. Finally, this filter is applied using a conservative threshold of 2 to ensure that spurious vectors are effectively removed.
The droplet data at specific spatial positions are split into droplet diameter classes with a constant width of
in order to evaluate the effect of droplet size on velocity fluctuations. The probability distribution of the radial velocity is illustrated exemplarily for two droplet diameter classes at a distance of
x = 50 mm downstream of the atomiser in
Figure 13a. Obviously, this velocity component is normally distributed and the mean value is approximately 0
. Furthermore, the radial velocity of the smaller droplets has a higher standard deviation, which may indicate that those droplets follow the velocity fluctuations of the gas phase considerably better compared to larger ones.
For a more detailed analysis, the standard deviation of the radial velocity is calculated for each droplet diameter class in the range between 4
and 20
. The result reveals a decreasing standard deviation with increasing droplet diameter at all positions downstream of the atomiser as shown in
Figure 13b. The most interesting observation is that, at the position closest to the atomiser nozzle (
x = 50 mm), the standard deviation of the radial velocity is found to be proportional to
. Considering the timescale of droplet relaxation, as indicated by Equation (
3), there is strong evidence that the standard deviation of the droplet velocity is due to the fluctuations of the gas velocity.
Hence, the generally high standard deviation at position 0 obviously results from strong turbulent fluctuations of the gas phase. At this measurement position, a strong shear layer turbulence is generated by the interaction of the rapid cold gas injected by the atomiser with the substantially slower hot gas flow. This result is supported by the strong gradient of the axial droplet velocity as shown in
Figure 10b. The positions further downstream of the atomiser are characterised by a generally lower level of the standard deviation and a considerably weaker dependency on droplet size. This result is sensible, since the influence of the atomiser air flow and the resulting shear layer turbulence decays with increasing distance downstream of the atomiser.
The standard deviation of the radial velocity, as shown in
Figure 13b, represents a valuable result, since it can be directly applied for predicting the turbulent dispersion. Consequently, the droplet trajectories in the test section can be computed dependent on the droplet size. In addition, the standard deviation of the velocity may contain vital information about the turbulent fluctuations of the gas phase. These velocity fluctuations impose an additional relative velocity between droplets and gas, which may affect evaporation or atomisation considerably. In literature, high–spatial–resolution PIV is presented as a promising technique for investigation of turbulent fluctuations in dispersed multiphase flows [
33].
Subsequently, it will be investigated whether an estimation of the turbulent fluctuations of the gas phase or even the turbulent slip velocity is possible based on the present microscopic imaging data. First of all, the theoretical analysis of particle response in an oscillating gas phase presented by Burger et al. [
47] is adapted to turbulent fluctuations. The turbulent gas velocity is simplified by a simple sinusoidal oscillation
which is defined by the amplitude
and the angular frequency
. The mean velocity
is set to 0
. Stokes flow is assumed analogous to the analysis of the mean gas velocity. By inserting Equation (
13) into Equation (
4), the oscillation of the droplet velocity after reaching the steady-state condition can be derived
In this study, only the amplitude of the resulting droplet velocity oscillation is of interest. Hence, the function
is employed for fitting the experimental data. The amplitude is scaled by the factor
in order to enable a direct comparison to the experimentally available standard deviation. Furthermore, the desired dependency of this amplitude function on the droplet diameter is represented by the droplet relaxation time
, which is affected additionally by the density of the droplets
and the dynamic viscosity of the gas phase
. The constant
C was found to be necessary in order to achieve a sensible fit. This offset is supposed to result from fluctuations of the gas velocity, which are characterised by lower frequencies. Hence, all droplets in the presented size range are assumed to follow those low frequency fluctuations almost perfectly.
The fit of
from Equation (
15) is found to be in excellent agreement to the experimental data as shown in
Figure 14. The desired information about the underlying oscillation by means of
and
can be estimated with reasonable accuracy, which is graphically illustrated by 95% confidence intervals for the fitted function. In addition, the resulting parameters of
are summarised in
Table 3.
The cut-off Stokes number
can be determined using the derived frequency of the oscillation
f, as fundamentally introduced in work of Burger et al. [
47] for studying the particle response in oscillating flows. This cut-off Stokes number may be used analogous to the cut-off frequency of a first order low pass filter in order to assign different regimes of droplet motion in a turbulent gas flow. In the case under consideration, the droplet diameter of
is determined using Equation (
16), which is graphically illustrated in
Figure 14. Hence, the droplets in this size range can be used as an indicator for turbulent fluctuations of the gas phase. Subsequently, this will be demonstrated based on a more detailed analysis of the spray characteristics at Position 0 (
x = 50 mm).
In
Figure 15, the Sauter Mean Diameter (
) and the diameter at the 90% volumetric quantile (
) are plotted over the radial position. These results were already discussed in
Section 3.1. In particular, the radial positions featuring the strongest average velocity gradient, ± 2 mm off the centre, were found to correspond to the smallest characteristic diameters. Therefore, shear layer turbulence seems to play a major role during the atomisation process.
For a further in depth analysis, the standard deviation of the radial velocity of very small droplets is discussed. The standard deviation
is plotted in
Figure 15, which is determined using droplets of a diameter between
and
. The distribution of
is found to peak exactly at ± 2 mm off the centre, which confirms the statement that these regions correspond to strong velocity fluctuations caused by shear layer turbulence. Furthermore, the largest droplets of the spray, as represented by the
, are strongly correlated to
. Obviously, the turbulent fluctuations of the hot gas flow induce the dominating slip velocity, which triggers the atomisation process.
In conclusion, the standard deviation of the radial velocity directly yields an estimation of droplet dispersion, which can be utilised to validate the droplet distribution in the pipe flow as a function of the droplet size. Furthermore, information about the underlying turbulent fluctuations can be estimated with reasonable accuracy. Hence, the smallest detectable droplets may be used as an indicator for turbulence intensity.
However, the knowledge of the turbulent fluctuations does not directly yield the turbulent slip velocity of the droplets. Actually, the gradient of the mean velocity in an axial direction needs to be taken into account as well, since a small displacement in a radial direction due to turbulent dispersion may induce a high slip velocity in an axial direction as discussed by Chen et al. [
31]. Hence, turbulent fluctuations may cause a high slip velocity of relatively small droplets, which are characterised by strong dispersion due to their low inertia. This effect needs to be considered in order to estimate an absolute slip velocity caused by turbulent fluctuations. However, a more detailed analysis of this slip velocity is beyond the scope of this paper.
As an outlook, if a high speed camera in combination with a suitable illumination is used, time-dependent droplet data can be recorded, which may give a more detailed insight into the interaction of the spray with turbulent fluctuations of the gas phase.
3.4. Evaporation Characteristics of Urea–Water Solution
The long-term objective of the present methodology is to provide experimental validation data, which can be used to study evaporating urea–water sprays under realistic thermodynamic conditions. In order to pin down the effect of urea on the evaporation process, distilled water is used as an alternative liquid in the measurement campaign. First of all, there is almost no difference in surface tension and viscosity between water and urea–water solution (UWS). Hence, it is presumed that the atomisation process is effectively not affected when using an air assisted nozzle. Therefore, it is expected that the same spray for UWS and water is generated.
However, a recent publication by Kapusta et al. [
26] indicates that replacing UWS with water will influence the spray characteristics considerably. In this study, a pressure driven single fluid nozzle is used and the pressure in the liquid reservoir is preserved. In other words, the pressure difference over the whole injection system is kept constant. Therefore, the liquid volume flow through the atomiser may be affected by the fluid properties, most importantly by the viscosity. Hence, the velocity at the exit of the atomiser nozzle will also be affected, which is one major parameter affecting the primary breakup regime of a cylindrical jet. For the discussion of the effect of the Weber and Ohnesorge number, please refer to the review of Dumouchel [
48]. In conclusion, the study of Kapusta et al. [
26] does not evaluate the influence of different fluid properties on the actual atomisation process but on the performance of a whole injection system.
In contrast, an air assisted nozzle is used in the present study with an identical setting of the air mass flow and velocity, when replacing UWS with pure water. In addition, the liquid volume flow was kept identical. These provisions ensure that the relevant non-dimensional numbers are effectively identical for UWS and pure water. Therefore, the influence of slightly different liquid properties is considerably lower in comparison to simple pressure atomisers.
It should be noted that the density difference between UWS and water of approximately 9% will affect the integral momentum of the spray jet. However, this effect is negligible using a twin-fluid atomiser. Hence, the overall effect of different fluid properties for UWS and water on the atomisation process can definitely be considered as marginal. In summary, the present experimental configuration provides identical droplet initial conditions, since the atomiser produces practically the same spray for UWS and water. By this means, experimental results for water can be used to calibrate numerical simulations in terms of starting conditions and the quality of submodels, since the complex evaporation behaviour of UWS can be excluded. Furthermore, the comparison of droplet diameter distributions of UWS and water further downstream of the atomiser may provide insights in the evaporation behaviour of UWS. Subsequently, it will be evaluated if evaporation characteristics can be retrieved using the present microscopic imaging technique.
The measured droplet size distribution for UWS and water at the centre of the pipe and at a distance of 225
downstream of the atomiser are illustrated in
Figure 16a. At first glance, the normalised number probability density function (PDF) is very similar for both fluids, which confirms the statement that the atomisation process is basically identical. Additionally, the average droplet velocity
of the spray is basically identical. Nevertheless, a detailed comparison reveals a higher probability of small droplets for UWS, whereas most larger diameter classes are characterised by a higher probability of droplets for water. Furthermore, this characteristic effect becomes more prominent with increasing distance from the atomiser as shown in
Figure 16b,c. The reason for this phenomenon can be explained by the effect of urea on the evaporation process.
For a further in depth analysis of the evaporation process, the difference between pure water and UWS will be briefly described. First, it is assumed that the Biot number
resulting in uniform temperature within the droplet. According to a Rapid Mixing evaporation model, uniform urea concentration inside the droplet is additionally assumed. With this assumption, the evaporation of an UWS droplet can be subdivided into two stages: The first stage is characterised by an almost exclusive evaporation of water. This means that there will be no evident difference between the evaporation of pure water and UWS. Once the water of the UWS droplet is consumed by evaporation, the evaporation and thermolysis of urea starts. This is the second stage, which can be described as an evaporation process with a considerably lower evaporation rate in comparison to water. Details of modelling the evaporation of UWS are discussed in the work of Birkhold et al. [
49].
The evaporation process of UWS and water droplets is illustrated in
Figure 17 by means of model results for the present hot gas operating condition. Comparing two droplets after an exemplary residence time (dashed line) in the hot gas environment, the 10
droplet still behaves like a regular water droplet, whereas the 8
features a considerably lower evaporation rate in comparison to water. The important conclusion from the discussion of the evaporation characteristics is that a designated droplet size exists during the lifetime of each UWS droplet, at which the water is completely consumed, and the evaporation rate is drastically reduced.
This knowledge can be transferred to the discussion of the PDFs in
Figure 16a–c. The difference in the PDFs between UWS and water is caused by the sudden change of the evaporation rate. In other words, all droplets smaller than a certain size undergo urea evaporation and the thermolysis process, which explains the higher number of UWS droplets in the small diameter classes in comparison to water. The higher probability of all larger diameter classes for the water spray is a consequence of the normalization of the PDF by the total number of droplets. The discussed difference of the PDFs grows stronger with increasing distance from the atomiser, since the residence time of the droplets in the hot gas increases. This results in a progress of spray evaporation and consequently larger droplets will undergo urea evaporation and thermolysis.
In summary, the analysis of the evaporation characteristics reveals promising results, which can be used to study evaporating urea–water sprays. Therefore, the diagnostics may be used to provide validation data for numerical predictions that focus on the evaporation behaviour of UWS. Most importantly, the reasonable and very detailed differences in the droplet diameter distribution emphasize the accuracy of the present spray diagnostics.