Rolling Bearing Incipient Fault Detection Based on a Multi-Resolution Singular Value Decomposition
Abstract
:1. Introduction
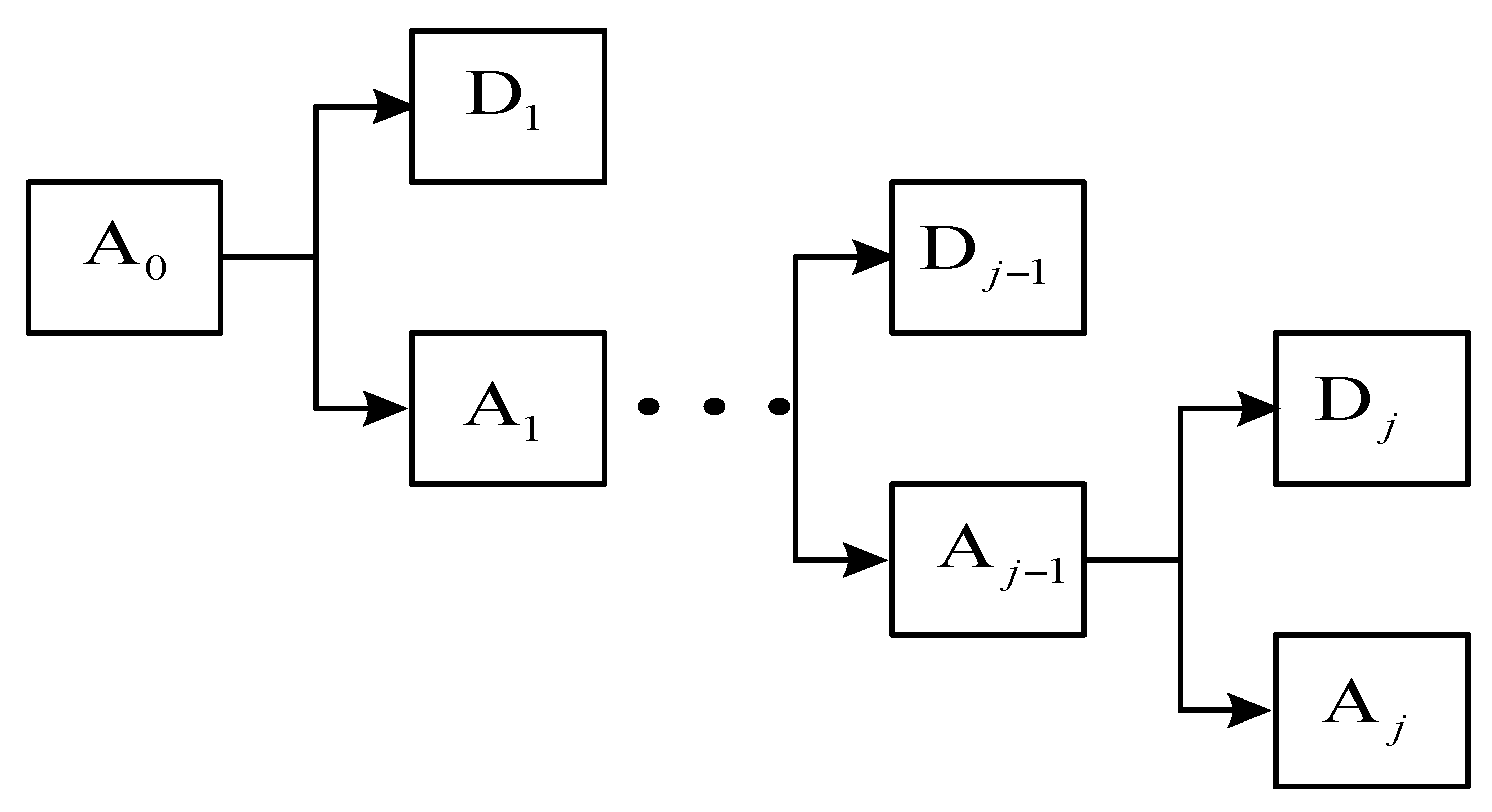
2. Overview of the Method of Multi-Resolution Singular Value Decomposition
2.1. Decomposition Process of MRSVD
2.2. Principle of the SVD Matrix’s Dichotomy Recursive Algorithm
3. Application of the MRSVD Method in the Incipient Fault Detection of the Rolling Bearings
3.1. Study of the Principle of the Noise Cancellation and Anti-Harmonic Interference of the MRSVD Method
3.2. Determination of the Number of Decomposition Layers of MRSVD
4. Simulation Studies
5. Experiment Studies
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics-A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Jaskaran, S.; Ashish, D.; Satinder, P.S. Rolling element bearing fault detection based on Over-Complete rational dilation wavelet transform and auto-correlation of analytic energy operator. Mech. Syst. Signal Process. 2018, 100, 662–693. [Google Scholar]
- Yaqub, M.F.; Gondal, I.; Kamruzzaman, J. Inchoate Fault Detection Framework: Adaptive Selection of Wavelet Nodes and Cumulant Orders. IEEE Trans. Instrum. Meas. 2012, 61, 685–695. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C. Rolling element bearings fault intelligent detection based on convolutional neural networks using raw sensing signal. In Advances in Intelligent Information Hiding and Multimedia Signal Processing; Springer International Publishing: Cham, Germany, 2017. [Google Scholar]
- Jiang, X.; Li, S.; Cheng, C. A novel method for adaptive multiresonance bands detection based on VMD and using MTEO to enhance rolling element bearing fault detection. Shock Vib. 2016, 2016, 7–20. [Google Scholar] [CrossRef]
- Cui, L.; Huang, J.; Zhang, F. Quantitative and localization detection of a defective ball bearing based on Vertical-Horizontal synchronization signal analysis. IEEE Trans. Ind. Electron. 2017, 64, 8695–8705. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, Z.; Wang, M.; Long, J.; Bai, Y.; Li, C. Deep Fuzzy Echo State Networks for Machinery Fault Diagnosis. IEEE Trans. Fuzzy Syst. 2019. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, Z.; Li, C.; Cabrera, D.; Long, J.; Bai, Y. Deep hybrid state network with feature reinforcement for intelligent fault diagnosis of delta 3D printers. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Zi, Y. A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health detection. J. Vib. Acoust. 2010, 132, 613–624. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault detection of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Dong, G. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2014, 48, 103–119. [Google Scholar] [CrossRef]
- Deng, L.; Zhao, R. Fault feature extraction of a rotor system based on local mean decomposition and Teager energy kurtosis. J. Mech. Sci. Technol. 2014, 28, 1161–1169. [Google Scholar] [CrossRef]
- Wang, S.; Chen, X.; Tong, C.; Zhao, Z. Matching synchrosqueezing wavelet transform and application to aeroengine vibration monitoring. IEEE Trans. Instrum. Meas. 2017, 66, 360–372. [Google Scholar] [CrossRef]
- Li, C.; Liang, M. Time-frequency signal analysis for gearbox fault detection using a generalized synchrosqueezing transform. Mech. Syst. Signal Process. 2012, 26, 205–217. [Google Scholar] [CrossRef]
- Osman, S.; Wang, W. A leakage-free resonance sparse decomposition technique for bearing fault detection in gearboxes. Meas. Sci. Technol. 2018, 29, 035004. [Google Scholar] [CrossRef]
- Cui, L.; Gong, X.; Zhang, J.; Wang, H. Double-dictionary matching pursuit for fault extent evaluation of rolling bearing based on the Lempel-Ziv complexity. J. Sound Vib. 2016, 385, 372–388. [Google Scholar] [CrossRef]
- Ding, X.; He, Q. Time-frequency manifold sparse reconstruction: A novel method for bearing fault feature extraction. Mech. Syst. Signal Process. 2016, 80, 392–413. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, Z.; Long, J.; Li, C.; Bai, Y. Dynamic condition monitoring for 3D printers by using error fusion of multiple sparse auto-encoders. Comput. Ind. 2019, 105, 164–176. [Google Scholar] [CrossRef]
- Wang, Y.; Xiang, J.; Markert, R.; Liang, M. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mech. Syst. Signal Process. 2016, 66–67, 679–698. [Google Scholar] [CrossRef]
- Liang, M.; Bozchalooi, I.S. An energy operator approach to joint application of amplitude and frequency-demodulations for bearing fault detection. Mech. Syst. Signal Process. 2010, 24, 1473–1494. [Google Scholar] [CrossRef]
- Rodríguez, P.H.; Alonso, J.B.; Ferrer, M.A. Application of the Teager-Kaiser energy operator in bearing fault detection. ISA Trans. 2013, 52, 278–284. [Google Scholar] [CrossRef]
- Wang, H.; Gao, G.G.; Zeng, X.W. Wind Turbine Gearbox Fault detection Based on Wavelet Theory and Hilbert Demodulation Spectrum. Appl. Mech. Mater. 2015, 703, 390–393. [Google Scholar] [CrossRef]
- Liu, X.; Bo, L.; Peng, C. Application of order cyclostationary demodulation to damage detection in a direct-driven wind turbine bearing. Meas. Sci. Technol. 2014, 25, 25004–25011. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, D.P.; He, Z.C. Research on fault diagnoses of rolling bearing based on the energy operator demodulation approach. Adv. Mater. Res. 2012, 588–589, 134–140. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, J.; Dong, G.M.; Xiao, W.B.; Wang, Z.Y. Application of the horizontal slice of cyclic bispectrum in rolling element bearings detection. Mech. Syst. Signal Process. 2012, 26, 229–243. [Google Scholar] [CrossRef]
- Saidi, L.; Ali, J.B.; Fnaiech, F. Application of higher order spectral features and support vector machines for bearing faults classification. ISA Trans. 2015, 54, 193–206. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K. A comparison of signal processing tools: Higher order spectra versus higher order coherences. J. Vib. Eng. Technol. 2015, 3, 461–472. [Google Scholar]
- Yang, D.M.; Stronach, A.F.; MacConnell, P.; Penman, J. Third-order spectral techniques for the detection of motor bearing condition using artificial neural networks. Mech. Syst. Signal Process. 2002, 16, 391–411. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Nembhard, A.D. Use of composite higher order spectra for faults detection of rotating machines with different foundation flexibilities. Measurement 2015, 70, 47–61. [Google Scholar] [CrossRef]
- Li, F.; Meng, G.; Ye, L.; Chen, P. Wavelet transform-based higher-order statistics for fault detection in rolling element bearings. J. Vib. Control 2008, 14, 1691–1709. [Google Scholar]
- Howard, I.M. Higher-order spectral techniques for machine vibration condition monitoring. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 1997, 211, 211–219. [Google Scholar] [CrossRef]
- Shao, R.; Li, J.; Hu, W.; Dong, F. Multi-fault clustering and detection of gear system mined by spectrum entropy clustering based on higher order cumulants. Rev. Sci. Instrum. 2013, 84, 025107. [Google Scholar] [CrossRef] [PubMed]
- Yunusa-Kaltungo, A.; Sinha, J.K. Sensitivity analysis of higher order coherent spectra in machine faults detection. Struct. Health Monit. 2016, 15, 555–567. [Google Scholar] [CrossRef]
- Sheen, Y.T. On the study of applying Morlet wavelet to the Hilbert transform for the envelope detection of bearing vibrations. Mech. Syst. Signal Process. 2009, 23, 1518–1527. [Google Scholar] [CrossRef]
- Han, G.D.; Wan, S.T.; Lv, Z.J.; Liu, R.H.; Wang, J.; Tang, G.J. The Analysis of Gearbox Fault detection Research Based on the EMD and Hilbert Envelope Demodulation. Adv. Mater. Res. 2014, 926–930, 1800–1805. [Google Scholar] [CrossRef]
- Luo, J.; Yu, D.; Liang, M. A kurtosis-guided adaptive demodulation technique for bearing fault detection based on tunable-Q wavelet transform. Meas. Sci. Technol. 2013, 24, 055009. [Google Scholar] [CrossRef]
- Chibani, A.; Chadli, M.; Ding, S.X.; Braiek, N.B. Design of robust fuzzy fault detection filter for polynomial fuzzy systems with new finite frequency specifications. Automatica 2018, 93, 42–54. [Google Scholar] [CrossRef]
- Chadli, M.; Davoodi, M.; Meskin, N. Distributed state estimation, fault detection and isolation filter design for heterogeneous multi-agent linear parameter-varying systems. IET Control Theory Appl. 2016, 11, 254–262. [Google Scholar] [CrossRef]
- Zhu, X.; Xia, Y.; Chai, S.; Shi, P. Fault detection for vehicle active suspension systems in finite-frequency domain. IET Control Theory Appl. 2019, 13, 387–394. [Google Scholar] [CrossRef]
- Li, L.; Chadli, M.; Ding, S.X.; Qiu, J.; Yang, Y. Diagnostic observer design for t–s fuzzy systems: Application to real-time-weighted fault-detection approach. IEEE Trans. Fuzzy Syst. 2017, 26, 805–816. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, J.; Lu, C.; Wang, Z. Rolling bearing fault detection under variable conditions using LMD-SVD and extreme learning machine. Mech. Mach. Theory 2015, 90, 175–186. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, J.; Dong, G.; Liu, T.; Chen, G. Study on Hankel matrix-based SVD and its application in rolling element bearing fault detection. Mech. Syst. Signal Process. 2015, 52–53, 338–359. [Google Scholar] [CrossRef]
- Shen, F.; Chen, C.; Yan, R.; Gao, R.X. Bearing fault detection based on SVD feature extraction and transfer learning classification. In Proceedings of the Prognostics and System Health Management Conference (PHM), Beijing, China, 21–23 October 2015. [Google Scholar]
- Liao, Z.; Song, L.; Chen, P.; Guan, Z.; Fang, Z.; Li, K. An Effective Singular Value Selection and Bearing Fault Signal Filtering detection Method Based on False Nearest Neighbors and Statistical Information Criteria. Sensors 2018, 18, 2235. [Google Scholar] [CrossRef] [PubMed]
- Qiao, Z.; Pan, Z. SVD principle analysis and fault detection for bearings based on the correlation coefficient. Meas. Sci. Technol. 2015, 26, 085014. [Google Scholar] [CrossRef]
- Zhao, X.; Ye, B.; Chen, T. Theory of multi-resolution singular value decomposition and its application to signal processing and fault detection. J. Mech. Eng. 2010, 46, 64–75. [Google Scholar] [CrossRef]
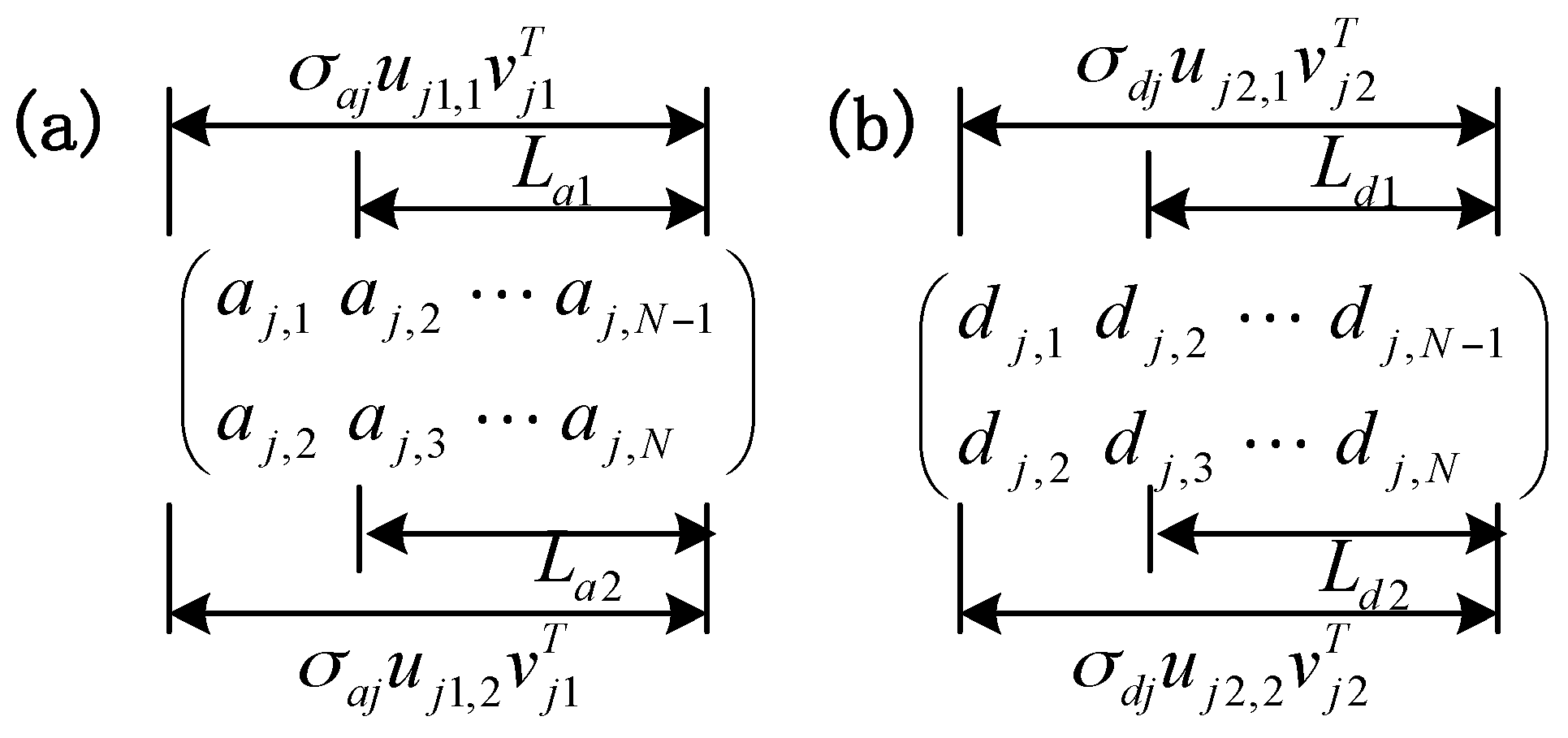


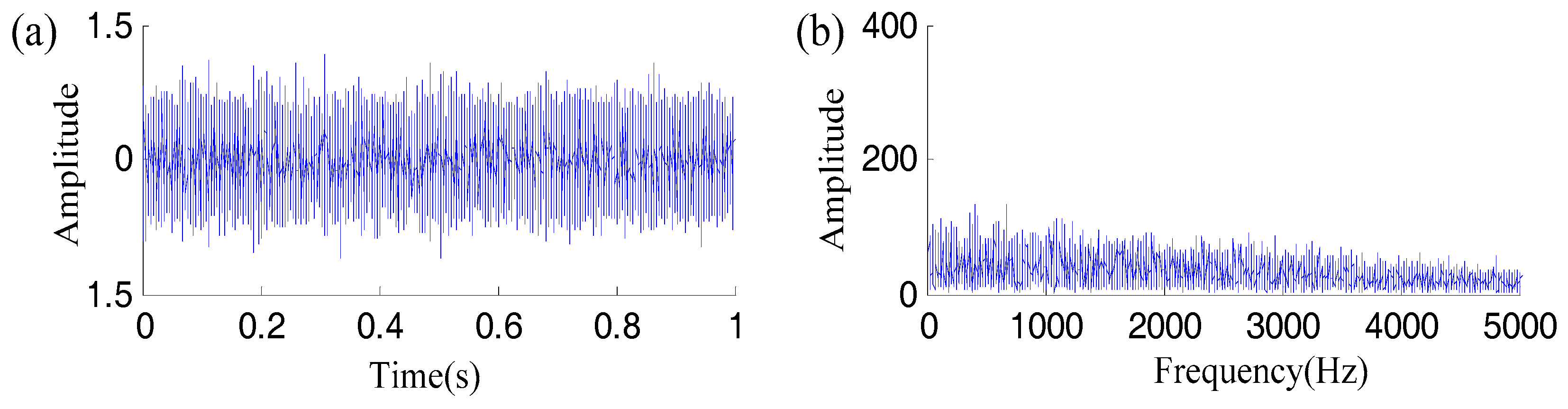

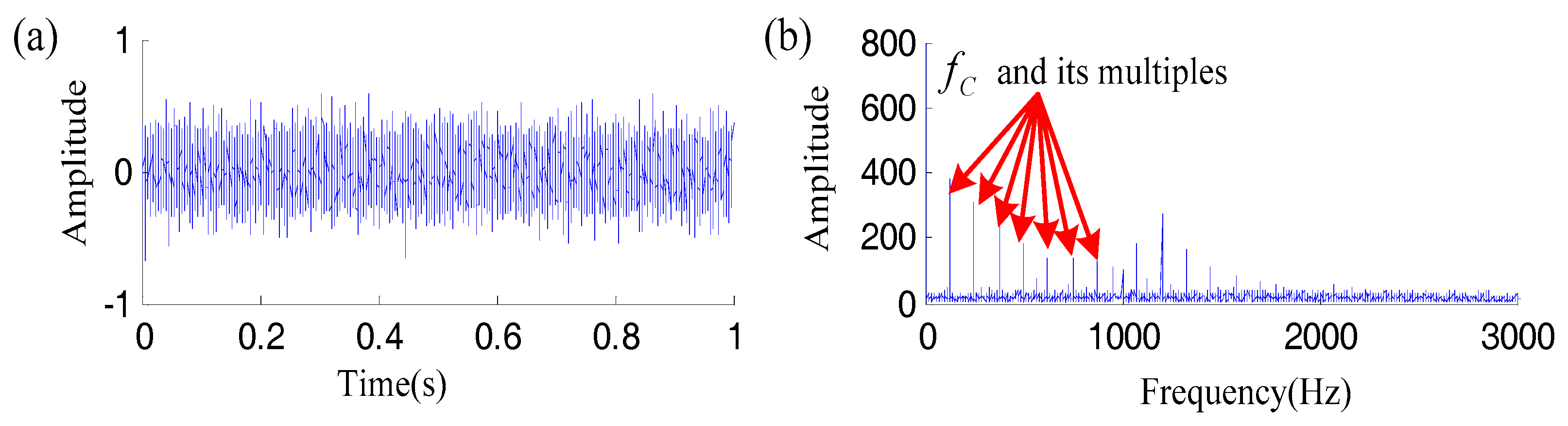


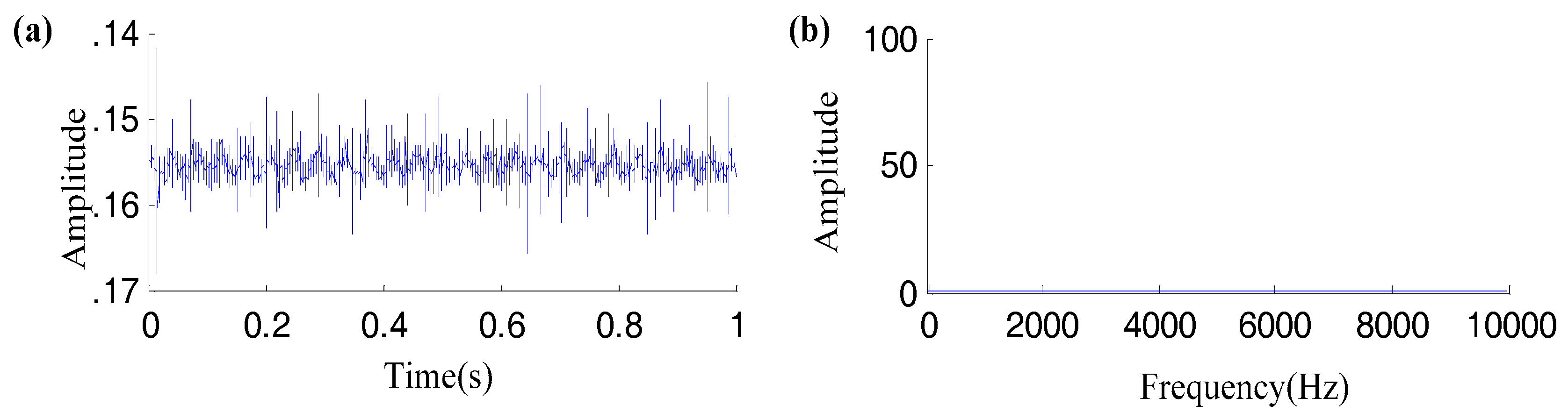
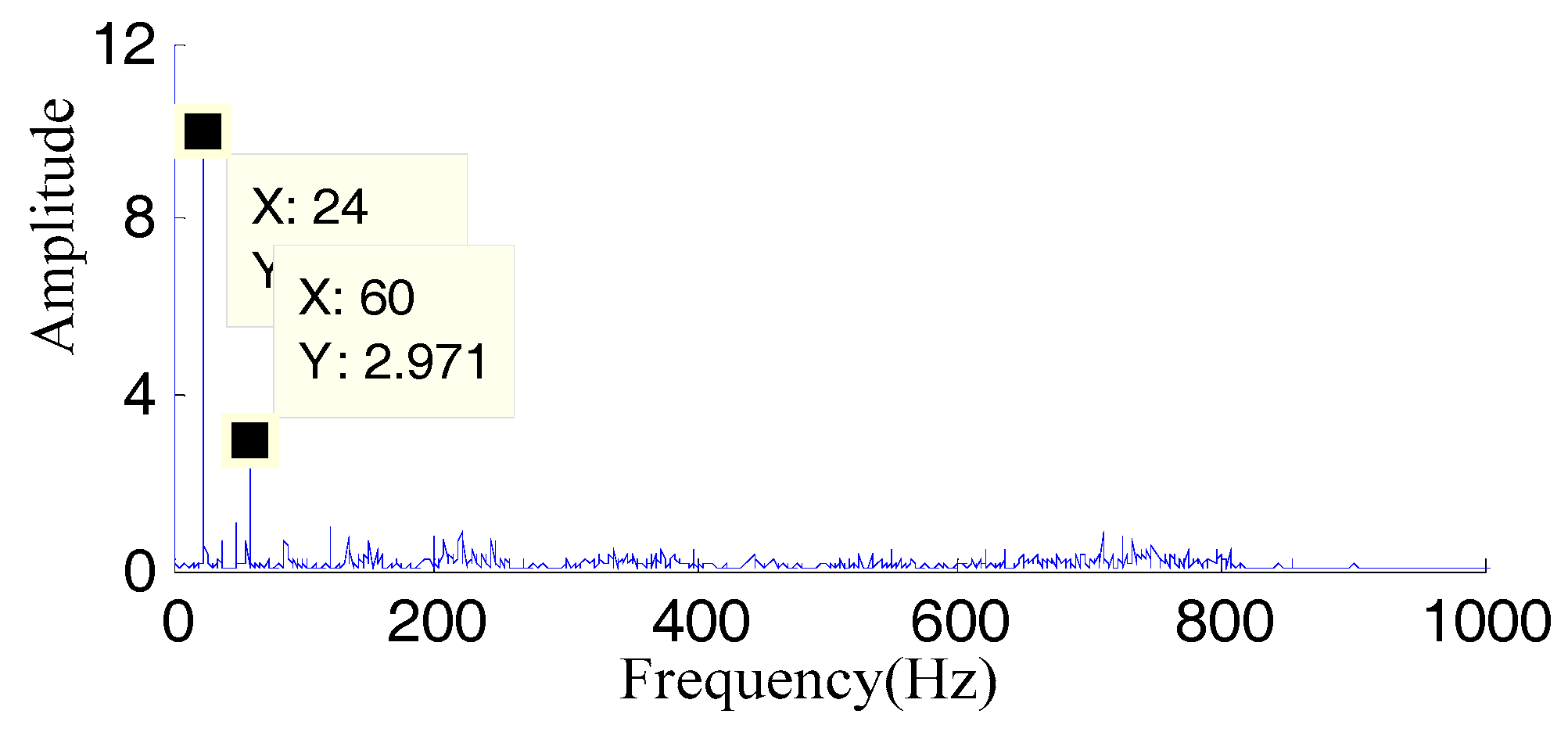
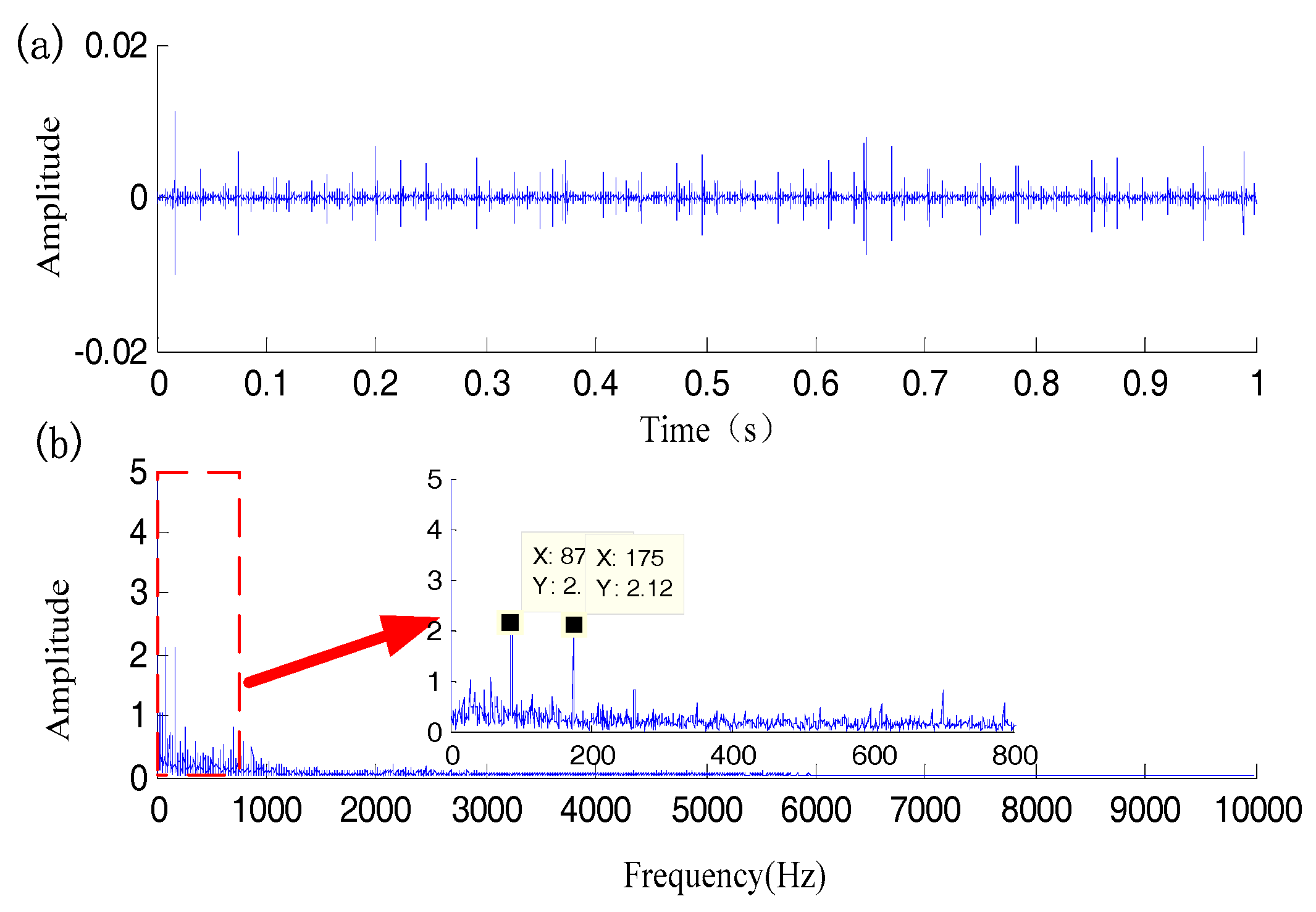
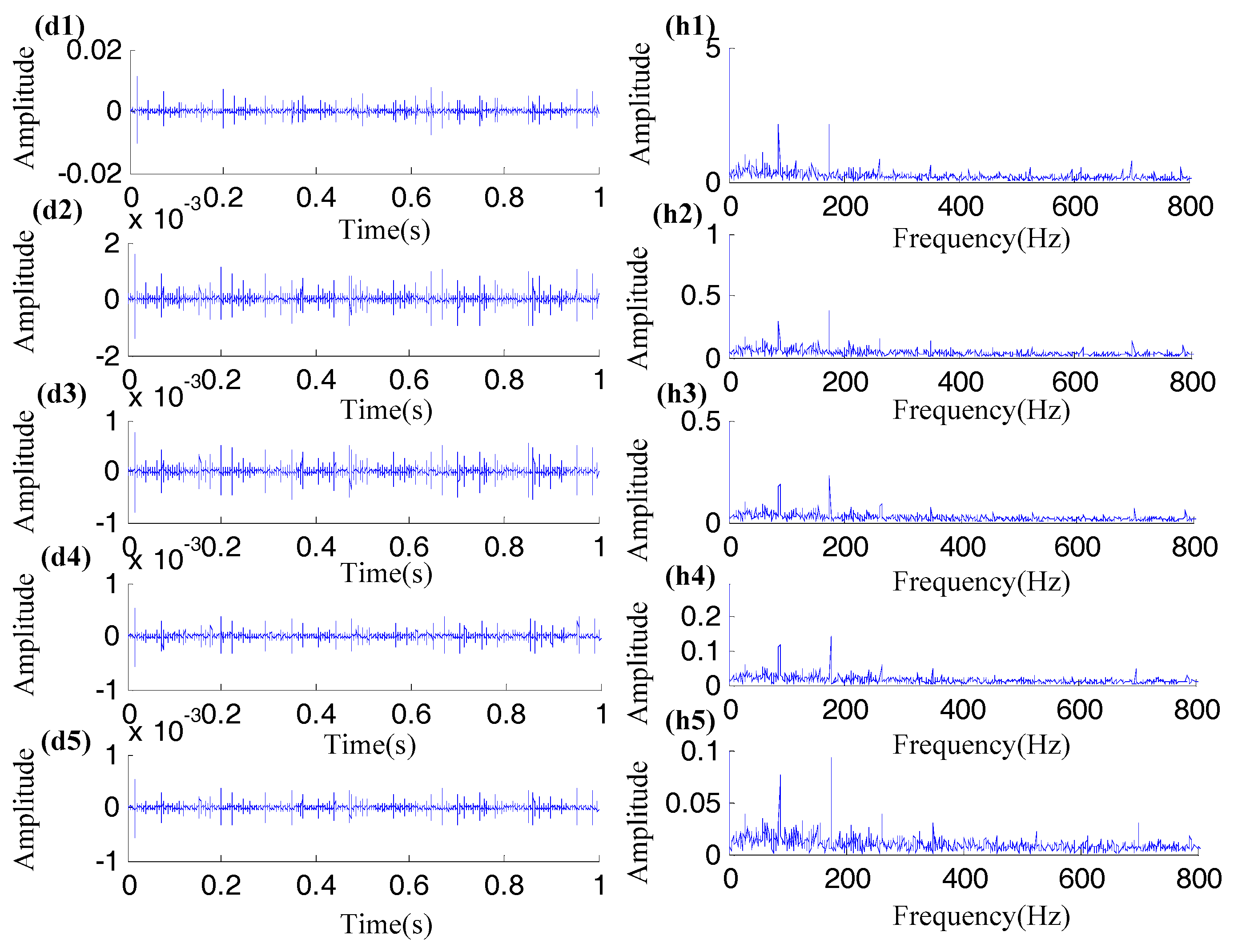
| Am | TP | M | β | ωr | SNR | B1 | f1 | B2 | f2 | B3 | F3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.008s | 250 | 1500 Hz | 2048 Hz | –6 | 1.35 | 60Hz | 1.4 | 230 Hz | 1.5 | 800 Hz |
| Hankerl Matrix | H | Hs | Hn | Hh | |
|---|---|---|---|---|---|
| σ | |||||
| σa | 354.8617 | 44.5982 | 69.4838 | 346.2494 | |
| σd | 73.3264 | 14.2705 | 66.8183 | 17.5887 | |
| Type | Roll diameter | Pitch diameter | Number of rolls | BPFO |
|---|---|---|---|---|
| ER16K | 7.94 mm | 38.52 mm | 9 | 3.572 fr |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Zhang, S. Rolling Bearing Incipient Fault Detection Based on a Multi-Resolution Singular Value Decomposition. Appl. Sci. 2019, 9, 4465. https://doi.org/10.3390/app9204465
Luo J, Zhang S. Rolling Bearing Incipient Fault Detection Based on a Multi-Resolution Singular Value Decomposition. Applied Sciences. 2019; 9(20):4465. https://doi.org/10.3390/app9204465
Chicago/Turabian StyleLuo, Jiesi, and Shaohui Zhang. 2019. "Rolling Bearing Incipient Fault Detection Based on a Multi-Resolution Singular Value Decomposition" Applied Sciences 9, no. 20: 4465. https://doi.org/10.3390/app9204465
APA StyleLuo, J., & Zhang, S. (2019). Rolling Bearing Incipient Fault Detection Based on a Multi-Resolution Singular Value Decomposition. Applied Sciences, 9(20), 4465. https://doi.org/10.3390/app9204465





