Comparisons of Scotopic/Photopic Ratios Using 2- and 10-Degree Spectral Sensitivity Curves

Abstract

Despite the fact that a 2-degree spectral sensitivity curve (SSC) is extensively used in scientific research and relevant applications, the choice between the 10-degree or the 2-degree photopic SSCs in practical applications for the calculation of scotopic/photopic ratios (S/P ratios) depends on actual needs. We examined S/P ratios for more than 300 light sources for correlated colour temperatures (CCTs) from 2000 K to 8000 K and blackbody radiant spectra from 10000 K to 45000 K using 2- and 10-degree SSCs. Results showed that the ratio of the S/P values calculated using the 10-degree and 2-degree SSCs was approximately equal to 0.916. The average mesopic luminance difference increased from 0% to 5.7% at a photopic adaptation luminance from 0.005 to 5 cd/m². For most practical applications, the mesopic luminance values calculated using these two SSCs were different by several percentage units, yet these differences could be neglected. At extremely high CCTs over 10000 K, the mesopic luminance difference may approximate the maximum value of 16%. This work proposes the conversion coefficients for S/P ratios and the transforming mesopic luminance values calculated for 2- and 10-degree SSC systems. These results may help researchers clarify differences between the S/P ratios calculated using different SSCs.

1. Introduction

There are three vision states for human beings, photopic vision with luminance values >5 cd/m², mesopic vision with luminance values from 0.005 to 5 cd/m², and scotopic vision with luminance values <0.005 cd/m² [1]. The luminance of values of several scenes, like roads, tunnels, and dashboard lightings, likely fall in the mesopic vision range. To measure light source performances in mesopic vision states, the scotopic/photopic ratio (S/P ratio) is used [2]. Effectively, this is the ratio of the luminous efficacy of radiation (LER) in scotopic and photopic vision. There are two photopic spectral sensitivity curves (SSCs): one is the Commission Internationale de l´Eclairage (CIE) 1924 2-degree standard observer SSC [3] and the other is the CIE 1964 10-degree standard observer SSC [4]. Some studies claim that the 10-degree SSC constitutes a better representation [5]. Prior research studies on colour differences also show that 10-degree colour matching functions yield smaller colour differences than 2-degree colour matching functions [6]. Another study [7] suggested that there may be problems in the short-wavelength part of the 2-degree SSC. In road lighting, visual tasks sometimes require large visual fields, while peripheral vision is also important [8,9,10]. The rod photoreceptors are mainly distributed in the part of the retina associated with peripheral vision. We may thus conclude that both the 10- and 2-degree systems should be considered for uses in various applications [11].

CIE recommended mesopic vision models for road lighting [2] and published guidelines on how to use the model [12]. However, CIE did not recommend which SSC should be adopted for calculation, implying that either SSC type can be used in applications. In most of the published research studies and practical applications, the 2-degree SSC system has been used. Berman [13] reported S/P ratios of 16 typical light sources in the range from 0.23 to 2.47. Lita et al. [14] reported a light source with an S/P ratio of 2.56 at a correlated colour temperature (CCT) of 5368 K. Nizamoglu et al. [15] reported a white-light emitting diode (WLED) with an S/P ratio of 3.04 at the extremely high CCT of 45000 K. Guo et al. [16] proposed light-emitting diodes (LEDs) for CCTs from 2700 K to 45000 K with S/P ratios in the range from 1.83 to 3.84. Zan et al. [17] reported WLEDs that reached S/P ratios from 1.54 to 3.84, which corresponded to CCTs in the range from 2700 K to 7580 K. Li et al. [18] reported two-hump quantum-dot-based LEDs that reached an S/P ratio value of 2.09 at 4038 K, and a four-hump LED that reached an S/P ratio value of 3.08 at 5015 K. Zhang et al. [19] optimised hybrid white LEDs for high S/P ratios at varying CCTs that reached high colour rendition, and compared their differences. Despite the fact that in some studies it has not been mentioned which SSC was used, we rechecked the spectra in the literature and have confirmed that most studies have used 2-degree SSCs. To date, no study has compared the differences of the calculations of S/P ratios using these two SSCs. In practical applications, there are urgent needs for large-scale assessments of urban lighting [20] and nightscape lighting. However, there are some unsolved technical issues to assure photopic adaptation luminance [21,22], which may cause inaccuracy in assessments.

In this study, we examined the differences of the calculated S/P ratios with two SSCs based on tests with more than 300 light sources [23] with CCTs from 2000 K to 8000 K, and with blackbody radiant (BR) light sources with CCTs from 10000 K to 45000 K. We calculated the mesopic luminance levels at photopic adaptation luminance levels from 0.005 to 5 cd/m² based on the use of the two tested SSCs and compared the differences. Conversion coefficients between the S/P ratio and mesopic luminance calculated using 2- and 10-degree SSCs were proposed. The work may help elucidate the S/P ratios and mesopic luminance differences calculated with these two different SSCs in research studies, and provide convenient conversions in practical applications.

2. S/P Ratio of Monochromatic Spectra

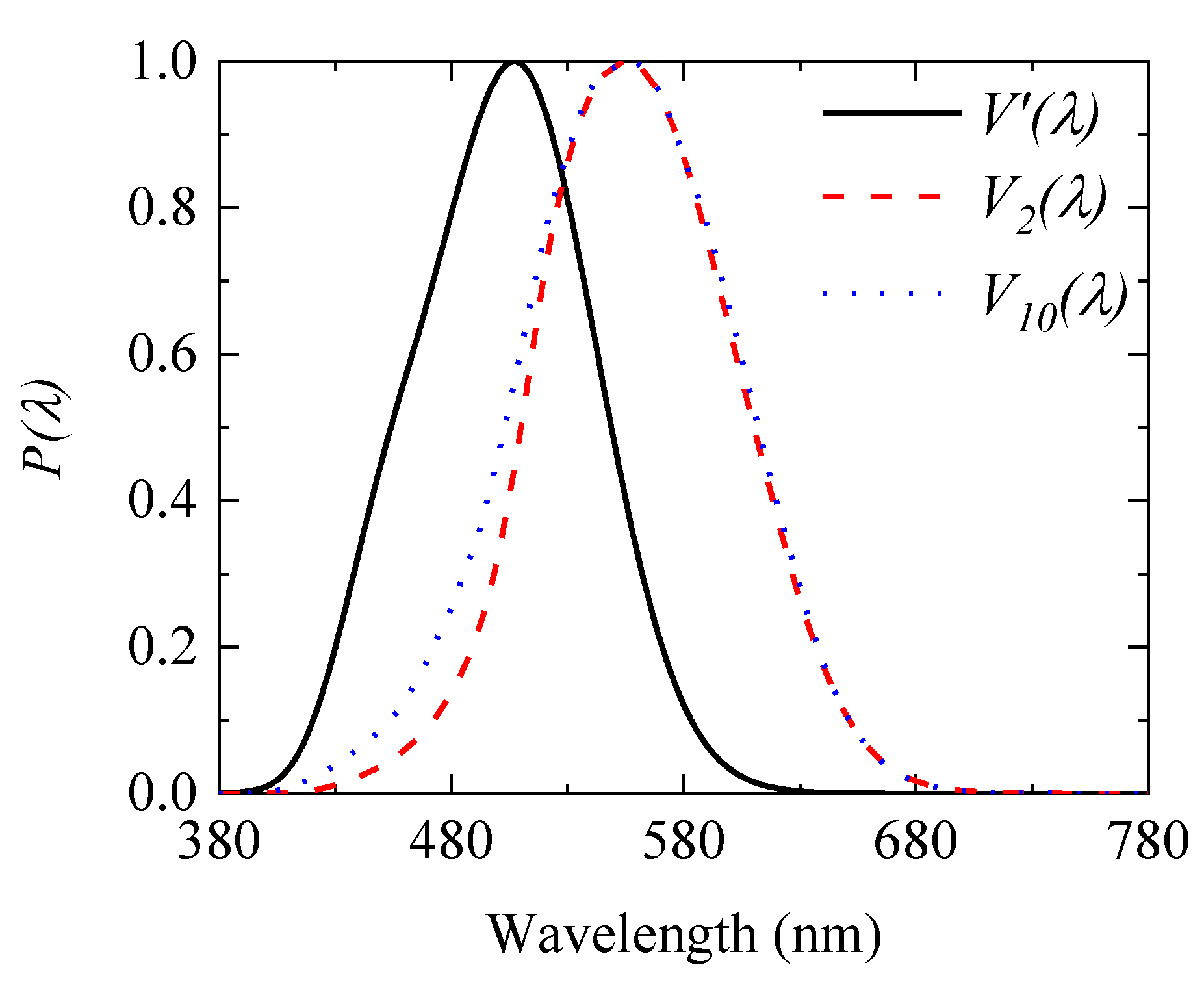
The S/P ratio was calculated by dividing the LER in scotopic vision (LER_s) by that in photopic vision (LER_p). LER_p was defined by Equation (1), LER_s was defined by Equation (2), and the S/P ratio, which can also be expressed as a quotient in the form of Rsp [12], was defined with the use of Equation (3). Herein, P(λ) represents the spectral power distribution (SPD) of the light source, K_m is the maximum photopic luminous efficacy of 683 lm/W at 555 nm, and K_m is the maximum scotopic luminous efficacy of 1700 lm/W at 507 nm. Accordingly, V(λ) is the SSC for photopic vision. Therefore, in the calculations, we used V₂(λ) to denote the 2-degree and V₁₀(λ) to denote the 10-degree systems, respectively. V’(λ) is the SSC for scotopic vision. Both V(λ) and V’(λ) are shown in Figure 1.

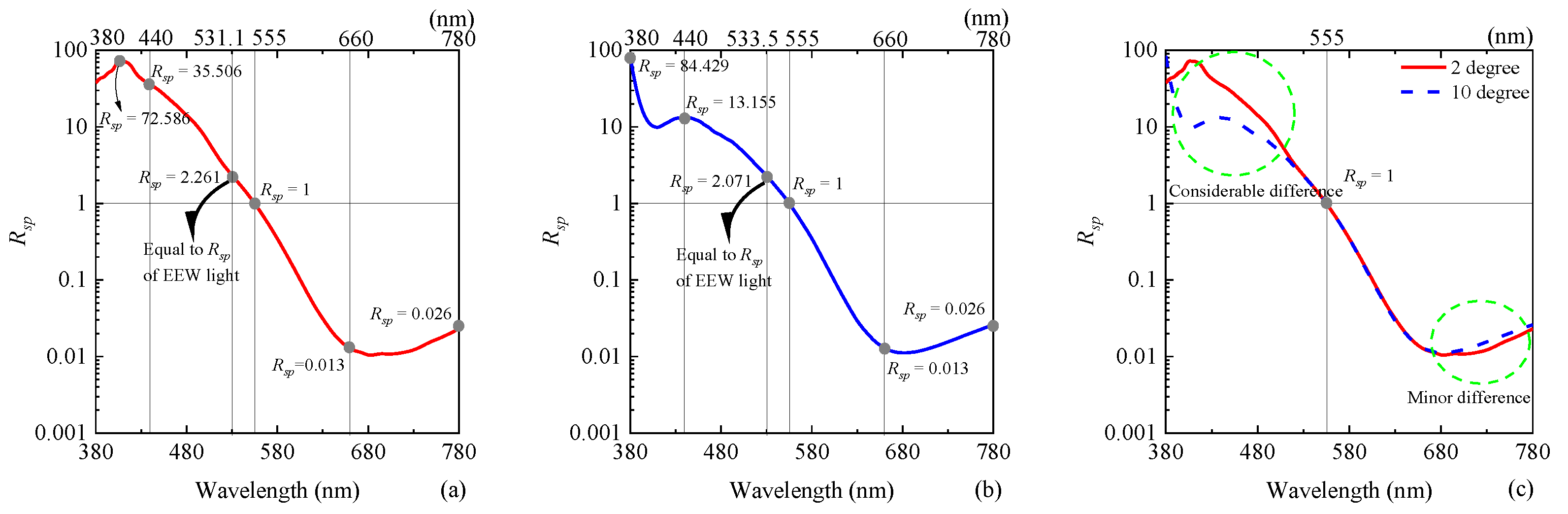
To compare the S/P ratio differences at each wavelength, we calculated the S/P ratios of monochromatic wavelengths for a full width at half maximum (FWHM) distance of 1 nm, from 380 to 780 nm, as shown in Figure 2. The S/P ratio of an equal energy white (EEW) light calculated using 2-degree SSC is 2.261 and 10-degree is 2.071, and the difference is approximately 9%. It is clearly noted that the main differences appear in the short-wavelength range (<500 nm).

$$LE{R}_{\mathrm{p}}=\frac{K_m{\displaystyle {\int }_{380}^{780}P(\lambda )V(\lambda )d\lambda }}{{\displaystyle {\int }_{380}^{780}P(\lambda )d\lambda }}$$

(1)

$$LE{R}_{\mathrm{s}}=\frac{K_m^{\prime }{\displaystyle {\int }_{380}^{780}P(\lambda )V\prime (\lambda )d\lambda }}{{\displaystyle {\int }_{380}^{780}P(\lambda )d\lambda }}$$

(2)

$$S/P\mathrm{ratio}=\frac{K_m^{\prime }{\displaystyle {\int }_{380}^{780}P(\lambda )V\prime (\lambda )d\lambda }}{K_m{\displaystyle {\int }_{380}^{780}P(\lambda )V(\lambda )d\lambda }}.$$

(3)

3. Relation of S/P Ratios of Light Sources Using 2-degree and 10-degree SSCs

Monochromatic spectra calculated for the S/P ratios in Section 2 are considered extreme conditions. In this section, we investigated a set that contained more than 300 light sources. Most of these were commercial light sources. These light source data were presented in the Illuminating Engineering Society of North America (IES-30-15. 2015), including incandescent lamps, fluorescent lamps, high-intensity discharge lamps, and LEDs. The CCTs of these light sources ranged from 2000 to 8000 K. The SPDs were normalised to a maximum intensity of unity. The mean SPD is shown in Figure 3. We calculated S/P ratios of these light sources using both 2- and 10-degree SSCs. Figure 4 shows that the S/P ratio was calculated in the plot of the 10-degree against the 2-degree SSC system. The relation is fitted well by a linear function with a high coefficient of determination, R² = 0.999. The slope of the linear function is approximately equal to the ratio of the EEW light, which is equal to 2.071/2.261 0.916. We can use 0.916 as the conversion coefficient for the transformation of the results calculated with the use of the 2- and the 10-degree SSCs.

Due to the fact that there are no differences in the responses for scotopic vision, the S/P ratio difference is caused by the difference of LER_p. Although considerable differences may exist for S/P ratios, the differences for mesopic luminance values may not be as considerable. We should further examine the mesopic luminance values transformed from photopic adaptation luminance levels in mesopic vision states.

4. Mesopic Luminance Values at Different Photopic Adaptation Luminance Levels

Figure 5 shows the plot of the 10-degree versus the 2-degree luminance values at the photopic adaptation luminance levels of 0.01, 0.03, 0.1, 0.3, 1, and 3 cd/m². These data are well fitted (high R² values) with linear functions. This implies that photopic adaptation luminance is the main factor that influences the results. The slope increases from 1.01 to 2.23 with photopic adaptation luminance values in the range from 0.01 to 3 cd/m². For photopic adaptation luminance values <0.1 cd/m², the differences are very small. When the luminance values >0.3 cd/m², the plotted points are scattered.

Figure 6 shows the mesopic luminance ratio estimated by dividing the mesopic luminance values of the 10-degree SSC by the 2-degree SSC. The mesopic luminance ratio increases as the photopic adaptation luminance increases from 1.000 in scotopic vision to 1.057 in photopic vision. Specifically, the difference of mesopic luminance ranged from 0% to 5.7% based on the calculations with the use of the two SSCs.

5. Examinations of BR Light Sources at Extremely High CCTs

At higher CCTs, the differences of the S/P ratio calculated using two 2-degree and 10-degree SSC systems tend to be greater. We invested BR light sources in the temperature range from 10000 to 45000 K, and results are shown in Figure 7. The differences increase with CCT, and they are over 10%. Figure 8 shows the mesopic luminance ratio as a function of CCT and the photopic adaptation luminance. The mesopic luminance ratio increased as the CCT and photopic adaptation luminance increased. The maximum difference was approximately equal to 16%.

6. Examination of a Real Lighting Scene

We measured luminance distribution of a road in Shenzhen using a typical phosphor converted LED type. The road is 140 m in length and 16 m in width, as shown in Figure 9. We used a spectral image radiance colorimeter EVERFINE SIRC-2000 to measure the luminance distributions and spectral information of light sources. The colorimeter was set at 60 m far away and 1.5 m in height in each measurement. The luminaire was measured at a CCT of 3650 K, and the S/P ratio in the 2- and 10-degree SSCs were 1.33 and 1.28, respectively. The average luminance was approximately 1 cd/m². The referred paradigm was a typical road lighting application at moderate CCT and luminance levels. We transformed the photopic adaptation luminance to mesopic luminance in a point-by-point manner. Figure 10 shows the luminance and the corrected mesopic luminance distributions. There are 810 luminance points in the road, which form the luminance distribution contours. The difference between the corrected mesopic luminance using both the 10- and 2-degree SSCs of these 810 points is approximately 3% on average, as shown in Figure 11.

7. Discussion and Conclusion

In many applications, the 2-degree SSC was used for the calculation of the LER and S/P ratio. However, in some applications, a large visual field was required, and a 10-degree SSC was more reasonable. We analysed the difference between these two SSCs based on an investigation of more than 300 light sources and extremely high CCT BR sources.

Comparison of the S/P ratios calculated using monochromatic light sources yielded considerable differences in the short-wavelength region (<500 nm). Light sources operating at high CCT values will likely cause considerable differences. In the very short-wavelength range (<430 nm), the S/P ratio increased abruptly. However, human eyes are not sensitive to changes in this region, and the precision of SSCs cannot guarantee the precision of the extremely high S/P ratio.

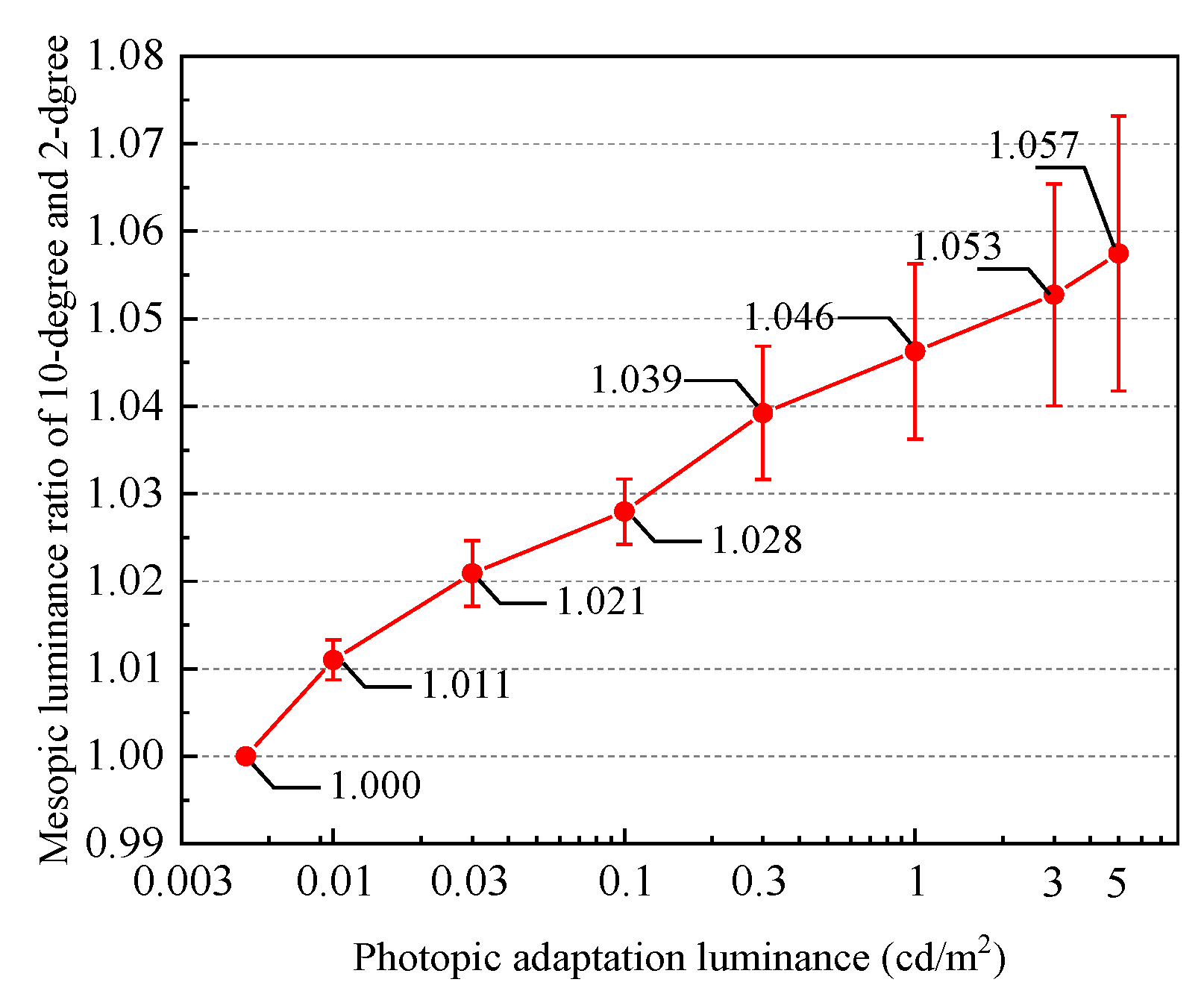
In the mesopic vision range, the differences in the mesopic luminance values of the 300 light sources calculated with the two SSCs increased as the photopic adaptation luminance values increased. In the scotopic vision cases, the same SSC V’(λ) was applied and there were no differences. In photopic vision cases, the average difference reached a value of ~6%. For some practical road lighting applications with luminance values less than 1 cd/m² and with moderate CCTs at approximately 4000 K, the difference of the corrected mesopic luminance values based on the two different SSCs studied herein was approximately 3%. For high CCT values (>6000 K), light sources, and high luminance levels (>1 cd/m²), the difference may reach 5%.

Accordingly, as the differences of the two SSCs increase, the CCTs of the light sources also increased. The differences were relatively small and with values <5% for light sources operating with CCTs in the range from 2000 to 8000 K. For CCTs > 10000 K, the error at some mesopic luminance levels reached values >10%. In some research work, CCT light sources with extremely high S/P ratios have been reported. The S/P ratios for these light sources calculated using the two SSCs are so different that they require further analyses. For some special applications, like dashboard illumination in driving cabins and landscape lightings, blue LEDs might be used. Accordingly, considerable differences may be evoked. However, a few light sources applied in functional lighting operate at extremely high CCTs.

Generally, the average difference of the S/P ratio is approximately 8% for light sources operating at CCTs in the range from 2000 to 8000 K. The mesopic luminance values, which are related to both the photopic adaptation luminance and CCT, do not yield considerable S/P ratio differences. For functional lighting, the photopic adaptation luminance is the main reason for the evoked differences.

In summary, several valuable inferences were drawn based on the findings of this study. Firstly, in most conditions, to transform the S/P ratio calculated using the 2- and 10-degree SSC outcomes, a conversion coefficient equal to 0.916 should be used. Secondly, in most practical applications, the difference of the calculated mesopic luminance using 2- and 10-degree SSCs was approximately in the range of 3%–5%, and the conversion coefficients ranged from 1.03 to 1.05. Thirdly, for applications with CCTs > 10,000 K, and for luminance values >1 cd/m², the differences may be >10%, and mesopic luminance should be calculated using suitable SSCs.

Most urban lighting scenes, such as road lighting and tunnel lighting, are in the mesopic vision range, and in the nightscape lighting. Most of these lighting scenes require large visual field, while others may require small visual fields to observe. Applying the suitable SSC to reach more precise assessments could help improve the lighting design, yield a smaller energy consumption, and reduce the risk of potential light pollutions.

There are some limitations associated with this study. Firstly, it is difficult to determine a very precise photopic adaptation luminance for complex luminance distributions because adaptation luminance may be related to luminance distributions, eye movements, and surrounding luminance effects [21]. Secondly, the adaptation luminance determined from 2-degree and 10-degree visual fields should be different, because the visual angles and adaptation fields [12] are different. The CIE TN 007:2017 recommends the adaptation field to be taken as the design area, and the adaptation luminance as the average luminance of the adaptation field. This is not applicable to designing suitable adaptation fields for each observation point when assessing a large-scale urban lighting scene. There is no feasible way at present to apply a suitable adaptation luminance for the entire road. Therefore, in this work, we only consider the SSC as the factor influencing photopic adaptation luminance and adopt a local photopic adaptation luminance for each observation point.