Optimal Design of Electrothermal Microactuators for Many Criteria by Means of an Immune Game Theory Multiobjective Algorithm

Abstract

The paper presents the application of the IMGAMO (immune game theory multiobective algorithm) in the optimal design of electrothermal microactuators. Several numerical tests on the mathematical benchmark test functions were performed, showing the superiority of the IMGAMO, when a large number of criteria are considered, in comparison to other multiobjective optimizers. A parametric numerical model of an electrothermal microactuaror was developed and verified. Six functionals, which depend on various thermal and mechanical quantities of the microactuator, were proposed, formulated and numerically implemented. These functionals represent real requirements asked of microactuators. The boundary-value problem of an electro-thermo-mechanical field was solved multiple times during the course of optimization by way of the finite element method (FEM). A numerical example of multiobjective optimization of chevron-type electrothermal actuators is included in the paper. Representation of the multi-dimensional Pareto fronts by means of scatter plot matrices, aided by self-organizing maps (SOMs), is presented. The novel method of selecting interesting, compromise-solutions is proposed and described.

1. Introduction

Electrothermal microactuators are mechanical systems where thermally-induced expansion and contraction of materials is responsible for the induction of motion. A temperature change inside the actuator is caused by Joule heating due to the electrical current flow. In the context of microscale and nanoscale engineering, thermal actuators can be used as microelectromechanical systems (MEMS) capable of translating electrical signals into controllable displacements and forces [1]. Electrothermal microactuators have proven to be very useful MEMS structures, which are commonly used in telecommunication, automotive, aviation and medical industries; e.g., microgrippers, switches, filters and modulators. Compared to the other types (e.g., magnetostatic, piezoelectric and electrostatic), the electrothermal actuators have many advantages. They can generate large forces or displacements per unit volume; require low actuation voltages; have linear material characteristics (strain–stress relationship), despite the high temperatures occurring in them; and moreover, they are relatively easy and cheap to fabricate. The disadvantages of microthermal actuators concern comparatively high-power consumptions and relatively slow response times. The Joule heating effect is possible due to the high value of electrical resistance of the material, which is the polycrystalline silicone. Mainly, two types of such microactuators are used in MEMS: U-beam and V-beam ones. U-beam type actuators were originally demonstrated in the early 1990s, whereas V-beam ones were in the late 1990s, and quickly became very popular for the generation of mechanical motion. U-beam microactuators consist of two beams (arms) which have different cross-section areas. They produce different amounts of Joule heating in the presence of the electric currents, which causes the bending of the apexes of the actuators. For the V-beam microactuator, arms are fabricated with a pre-bending angle. The longitudinally extending arms, also due to the Joule heating effect, move the central shaft. The central shaft aggregates the actuation force of the multiple beams, resulting in a total actuation force [2]. The V-beam actuator, called variously—chevron type, bent-beam or symmetric thermal actuator, is considered in the paper. Figure 1a presents an example shape of the chevron microactuator consisting of four pairs of arms, whereas Figure 1b shows the deformation and map of equivalent stress in the structure.

The process of design of such structures has to incorporate many technical aspects and restrictions. Accordingly, optimal design of electrothermal microactuators, requires consideration of many criteria, which depend on the quantities like actuation force, generated displacement, heat or electrical losses, stress concentration, risk of buckling and dynamic characteristics. For such structures, the above criteria strongly depend on the geometry. These criteria are very often contradictory, which leads to the necessity of accepting compromise-solutions. Analytical formulas related to basic electrical, thermal and mechanical quantities have been derived only for the simplified geometry (straight shape arms) of the microactuators. For the arbitrary shape of the geometry in order to calculate objective functions, the quantities derived from numerical simulations of coupled electro-thermo-mechanical analysis have to be used. Functionals expressing assumed criteria, calculated on the basis of multiphysics numerical simulations can be strongly multimodal (have many local minima). It significantly limits the scope of the applicability of classical gradient or non-gradient optimization methods. It can be seen that in order to efficiently optimize such structures, proper multiobjective optimization techniques have to be used [3]. Application of the multiobjective optimization methods leads to a situation where the result is not only a single solution, but a number of optimal solutions. These solutions are called Pareto-optimal solutions.

Very popular approaches to multiobjective optimization are the weighted sum method or taking only one criterion into account, while imposing other criteria as constraints. Such methods are handy to use, because they do not require modification of the optimization algorithm (the single-objective optimization algorithm can be used). Unfortunately, they have significant limitations, which reduce the scope of their application, such as:

• Difficulties in selection of the balance between criteria before optimization, having no knowledge of the considered problem;
• Certain assumptions imposed before optimization can lead to improper or unphysical results;
• Performing a single optimization task gives only one solution;
• The impossibility to obtain solutions for non-convex Pareto fronts.

Population-based approaches, such as metaheuristic algorithms, are free from the disadvantages mentioned above. Moreover, because such algorithms process not one, but a set of solutions, and the result of multicriteria optimization is a set of optimal solutions in the sense of Pareto, they are an ideal tool for these type of tasks.

A group of papers are devoted to the shape optimization of the different types of the thermal actuators: Lee et al., Huang et al. and Ionescu perform optimization of the characteristic dimension of the laterally driven microactuator [4,5,6]. Kwan et al. proposed optimization of the chevron type microactuator, assuming nonuniform cross section of the beams [7]. The process of optimal design can be realized assuming the variant analysis [8,9] or by means of different optimization methods [10]. Some papers are devoted to the topological optimization, which allows finding desired shape of the actuator with respect to applied restriction and criteria. Usually, the optimal shape of the actuator consists of a set of variously shaped arms in a number of geometrical configurations. Sigmund, Giusti et al. and Ansola et al. demonstrated maximizing the output displacement in a given direction of the actuator by means of topology optimization, obtaining quite complicated optimal shapes of the actuator [11,12,13]. Furuta et al. and Xia et al. demonstrated the topological optimization for thermoelectric actuators aided by level-set methods [14,15]. The result of topological optimization can be a good tip for the designer on what the best configuration of the arms is with regard to the considered criterion; however, very complicated shapes (common for topological optimization) can be an obstacle in the design process of practical shapes consisting of repetitive pairs of arms (which is needed for aggregation of the actuation force in the central shaft by multiple arms). Heo and Kim present topological optimization for the rotary thermal actuators [16]. For the majority of cases, a process of finding an optimal design of thermal actuators is dealt with as a single optimization problem. Multiobjective optimization methods are not popular in the design of electrothermal actuators; however, some papers have been devoted to it. Di Barba et al. solved the bi-objective optimization problem of a U-shaped actuator by means of the NSGAII algorithm (non-dominated, sorting genetic algorithm) [17]. It is a well-known fact that NSGAII algorithm (probably the most popular multiobjective optimization algorithm used in diverse engineering disciplines) does not work well for more than three criteria (practically 2). For the other types of the actuators (e.g., piezoelectric and electrostatic) multiobjective optimization problems generally also deal with the simultaneous consideration of at most two criteria.

A review of the literature allows us to claim a lack of research that incorporates many criteria into the optimal design of thermal actuators. Moreover, shape optimization tasks are devoted to the actuators with simplified geometry of the arms. More sophisticated shape of the arms in the optimal design has been considered in the case of topological optimization, but the disadvantages of such an approach have been described above. Furthermore, for the topological optimization, only single objective optimization tasks have been considered.

Bi-objective optimization of the U-beam actuator has been presented in [18], whereas in the present paper, a novel and efficient method of multiobjective optimization for higher number of criteria is proposed. The proposal combines an algorithm based on artificial immune systems (AIS) and elements of game theory (GT); it has been developed and implemented by authors.

Game theory deals with the analysis of conflict situations and can be applied to problems in fields such as economics, psychology and recently, engineering as well. The work which is assumed to be the beginning of game theory is accredited to John von Neumann and Oskar Morgensern [19]. In game theory, the conflict situations are named games. They have several essential features:

• Number of players is known and finite;
• Full game rules are set;
• Payoffs are determined by payoff functions, which depend on strategies chosen by players.

A strategy is a complete description of a player’s activity in all situations. Ideas of multiobjective optimization (MOO) and game theory have several common features. The game theory problems were considered applying multiobjective optimization concepts. MOO solutions which best take into account all criteria (so called non-dominated solutions) are sought, and in game theory, players are looking for best strategies. Finally, in game theory we try to find equilibrium and in MOO we try to find a set of solutions optimal in a Pareto sense. Several papers which considered these approaches were published [20,21,22,23,24].

Artificial immune systems, on the other hand, are one of the systems which belong to a wide range of methods of computational intelligence. The most developed algorithms are: immune networks, clonal selection and negative selection. Clonal selection, used in this present paper, is dedicated to solving optimization problems: fitness functions correspond to the affinities of antibodies to antigens. Solutions in a population are represented by antibodies. Each antibody is cloned several times like in the real immune system. The number of clones is proportional to an antibody’s affinity to antigen (its value of the fitness function) and then the hypermutation is applied. These ideas are extended with the suppression that takes place [25]. Immune systems and algorithms succeed in their application to global and multimodal optimization [26]. There are several adaptations and modifications of the clonal selection algorithm applied to problems with many criteria [27,28,29,30,31].

Artificial immune systems, compared to the population-based metaheuristic algorithms, seem to be predisposed to solve multiobjective problems. The main features of them are directly inspired by the immune system. Diversity of solutions is preserved thanks to a suppression mechanism, which eliminates similar and useless solutions, and as a result, controls the size of population. The elitism mechanism helps preserve the best solutions during the optimization course.

When more than two criteria are considered, the proposed multiobjective optimization algorithm significantly outperforms other metaheuristic multiobjective algorithms (NSGAII, SPEA2) [17,32]. In the present paper, six objective functionals have been proposed, formulated and implemented. The shape optimization method proposed in the paper allows the design of the arms of the chevron type microactuator with the smooth nonuniform cross sectional area and smooth transition between arms and anchors or central shaft. Non uniform, rational B-splines (NURBS) have been applied for the parametrization of the arms [33]. It is obvious that stress concentration is located in sharp corners (see Figure 1b). Increasing the radius between actuator beams and the anchors or central shaft can significantly reduce the stress concentration. Figure 2 shows a comparison of the distribution of the equivalent von Mises stress between a geometric arrangement with a sharp connection of the arms and one with rounded corners (transition radius is twice larger than the width of the arm) in the actuator for the same boundary conditions. This example shows that the maximal value of the equivalent stress is significantly reduced from 982 MPa to 476 MPa. The proposed method of optimal design allows for both, finding the arbitrary shape of the arms and precise selection of the radius at the rounded corners, taking into account the optimal selection of the pre-bending angle as well. As mentioned previously, the result of the multiobjective optimization is expressed in not one, but a set of optimal solutions. When a large number of criteria is considered, the process of selection of a particular compromise-solution could be problematic. The alternative method, compared to the traditional one, concerning the representation and selection-compromise-solutions, is proposed and demonstrated in the paper. The proposed method is aided by self-organizing maps (SOMs), which is one type of artificial neural network (ANN).

The rest of the paper is organized as follows. In Section 2, the model of the chevron type actuator is described, including the governing equations of the problem considered, the numerical model developed, and its verification. Section 3 contains the formulation of the multiobjective optimization problem, including the definition of the formulated criteria and SOMs, whereas in Section 4 the system of optimization build by means of IMGAMO algorithm is presented. Section 5 presents details of the optimization model of the electrothermal microacuator. On the basis of the research carried out, in Section 6, results and discussion are presented. The work is concluded in Section 7 with final remarks. Appendix A shows the details of IMGAMO algorithm, whereas Appendix B illustrates its effectiveness in comparative tests with other algorithms for several benchmarks.

2. Model of the Chevron Type Microactuator

2.1. Governing Equations

As mentioned in the previous paragraph actuation of the thermal microactuator is caused due to the electrical current $I$, which is converted to the heat according to the Joule-Lentz law [34]:

$$Q=R{I}^{2}t,$$

(1)

where $Q$ is internal heat generated, $R$ is electrical resistivity and $t$ is the time.

The thermal strain occurring in the longitudinal arms causes structural deflection. Usually such an actuator is affected by the voltage of the magnitude of a few volts, which causes an increase of temperature, even above 1200 K. Nevertheless, the linear behavior of the microactuator with respect to electric, thermal and mechanical effects is preserved. Such a phenomenon is described by the partial differential equation of electrostatics, Equation (2); heat conduction, Equation (3); and thermoelasticity, Equation (4) [35].

$${\varphi }_{,ii}-\frac{\rho }{{\epsilon }_0}=0,$$

(2)

$$k{T}_{,ii}+Q=0,$$

(3)

$$\mu u_{i,jj}+\left(\mu +\lambda \right)u_{j,ji}-(3\lambda +2\mu ){\alpha }_t{T}_{,i}=0,$$

(4)

where $\varphi$ is electric potential, $T$ is the temperature, $u$ represents the displacement values, $\rho$ is charge flux density, ${\epsilon }_0$ is electric constant, $k$ is thermal conductivity, $Q$ is internal heat source, ${\alpha }_t$ is the linear expansion coefficient, and $\mu$ and $\lambda$ are the Lamé constants, which can be expressed as follows:

$$\begin{gathered} \mu =G=\frac{E}{2\left(1+\nu \right)}, \\ \lambda =\frac{E\nu }{\left(1-2\nu \right)\left(1+\nu \right)}, \end{gathered}$$

(5)

where $\nu$, $E$ and $G$ are Poisson’s ratio, Young’s modulus and the shear modulus, respectively.

The structure considered here is an electro-thermo-elastic body of the domain $\mathsf{\Omega }$, with the boundary area $\mathsf{\Gamma }$ (Figure 3). Partial differential Equations (2)–(4) have to be supplemented by boundary conditions.

• For electrostatics:

$$\begin{array}{l}x\in {\mathsf{\Gamma }}_{\varphi }:\varphi (x)={\varphi }^0(x)\\ x\in {\mathsf{\Gamma }}_{\rho }:\rho (x)={\rho }^0(x)\end{array},$$

(6)

where ${\varphi }^0(x)$ and ${\rho }^0(x)$ denote known electric potential and electric charge flux density on the appropriate parts of the boundary ${\mathsf{\Gamma }}_{\varphi }$ and ${\mathsf{\Gamma }}_{\rho }$;

• For the heat conduction problem, boundary conditions are as follows:

$$\begin{array}{l}x\in {\mathsf{\Gamma }}_T:T(x)=T^0(x)\\ x\in {\mathsf{\Gamma }}_q:q(x)=q^0(x)\\ x\in {\mathsf{\Gamma }}_c:q(x)=\alpha (T(x)-T^{\infty }(x))\end{array},$$

(7)

where $T^0(x)$ and $q^0(x)$ are known temperature and heat flux on the parts ${\mathsf{\Gamma }}_T$ and ${\mathsf{\Gamma }}_q$ of the boundary. The third type of thermal boundary condition (Robin condition) is convection condition, for which $T^{\infty }(x)$ is an ambient temperature, whereas $\alpha$ is a heat convection coefficient.

• For the elasticity problem boundary condition can be defined as:

$$\begin{array}{l}x\in {\mathsf{\Gamma }}_u:u(x)=u^0(x)\\ x\in {\mathsf{\Gamma }}_p:p(x)=p^0(x)\end{array},$$

(8)

where $u^0(x)$ and $p^0(x)$ are known displacement and mechanical loads on the parts ${\mathsf{\Gamma }}_u$ and ${\mathsf{\Gamma }}_p$.

Separate parts of the boundaries where electrical, thermal and mechanical boundary conditions are specified define the boundary of the body. When no electrical, thermal or mechanical boundary conditions are specified on the particular parts of the boundary, it corresponds to the charge flux density free, heat flux free or traction-free conditions respectively. The relationships between separate parts of the boundary $\mathsf{\Gamma }$ can be written as:

$$\mathsf{\Gamma }={\mathsf{\Gamma }}_{\varphi }+{\mathsf{\Gamma }}_{\rho }={\mathsf{\Gamma }}_T+{\mathsf{\Gamma }}_q+{\mathsf{\Gamma }}_c={\mathsf{\Gamma }}_u+{\mathsf{\Gamma }}_p.$$

(9)

The finite element method (FEM) has been used for solving the electro-thermo-mechanical problem [36,37]. The partial differential equation after discretization and after taking into account boundary conditions, can be written as a set of algebraic equations and given in the following matrix form:

$$K_{E}V=I,$$

(10)

$$K_{T}T=Q+Q_E,$$

(11)

$$K_{M}U=F+F_T.$$

(12)

The global electrical conductivity matrix $K_E$, global thermal conductivity matrix $K_T$ and global stiffness matrix $K_M$ are assembled over element matrices. $V$,$I$,$T$,$Q$,$U$ and $F$ are the nodal vector of voltage, electric current, temperatures, heat fluxes, displacements and applied forces, respectively. The problem is weakly coupled, so electrical, thermal and mechanical analyses can be solved separately. Coupling is carried out by transferring loads between the analyses considered and by using staggered procedures. After solving Equation (10), the nodal vector of heat generation due to the current flow $Q_E$ is calculated, whereas after solving Equation (11), the nodal vector of forces due to the thermal strain vector $F_T$ is calculated.

For the buckling analysis, the finite element formulation takes the form:

$$\left[K_{\mathrm{M}}+{\lambda }_i\Delta K_{\mathrm{G}}\right]v_i=0.$$

(13)

Linear buckling analysis is assumed. Equation (13) describes the eigenvalue problem, which is solved by the Lanczos method. Matrix $\Delta K_{\mathrm{G}}$ is a function of the load increment $\Delta P$; ${\lambda }_i$ is the eigenvalue, whereas eigenvector $v_i$ allows for the calculation of post-buckling deformation mode.

As mentioned in the first paragraph, one of the criteria formulated depends on the contact force. Because the movement of the central shaft is almost perfectly vertical, friction between the end of the central shaft and the reaction plane can be neglected. The contact problem is modelled as rigid, deformable and frictionless. The thermal actuator is modelled as a deformable body, whereas the rigid surface is placed with the arbitrarily chosen initial gap between the tip of the central shaft and the rigid surface. For the contact between a deformable body and the rigid surface, the constraint responsible for maintaining the lack of penetration is implemented by transforming the degrees of freedom of the contact node and applying a boundary condition to the normal displacement.

2.2. Verification of the Numerical Model

The optimal design of the chevron type thermal actuator requires building a numerical model of the actuator, which allows one to calculate the values of criteria with the satisfactory level of accuracy. It is possible to analytically calculate electrical, thermal and structural quantities for the actuator with straight arms. This subsection is dedicated to the verification of the numerical model prepared. Simplifying the verification procedure comparison between the numerical and analytical models only for mechanical quantities is shown. Since the thickness perpendicular to the midplane of the actuator (z-axis) and boundary conditions are constant, and thickness is very small compared to other dimensions in the model, only two-dimensional models will be considered.

Consider the fundamental unit of the V-type actuator, a pair of angled beams (Figure 4). The average actuator temperature rise $\Delta T$, caused by the flow of electric current, produces the output displacement $u_y$ and the force $F_y$. An external force $F_i$ may be applied to the central shaft in y direction, affecting the $u_y$ displacement. Analytical modeling of the V-type actuators can be found in [2,5]. The equation below shows relationships between those quantities.

$$u_y=\frac{\alpha \Delta TEA\sin \phi }{\left(\frac{EA}{L}{\sin }^2\phi +\frac{12E{I}_z}{L^3}{\cos }^2\phi \right)}+\frac{-F_i}{\left(\frac{EA}{L}{\sin }^2\phi +\frac{12E{I}_z}{L^3}{\cos }^2\phi \right)}$$

(14)

If the force constraint $F_i$ is equal to zero, Equation (14) expresses the relationship for the free-moving actuator displacement. Taking into account—average temperature rise $\Delta T=450\mathrm{K}$, $\mathrm{E}=158,000\mathrm{MPa}$, length of the beam $L=220\mathsf{\mu }\mathrm{m}$ and the square cross-section area $A=25{\mathsf{\mu }\mathrm{m}}^2$, the FEM numerical model in MSC Mentat/Marc software was prepared and compared with the analytical solution. Plane stress model consisting of four node quad elements was assumed. The density of the mesh was established after some preliminary calculations. The number of 6–8 elements per width of the beam ensures correct results when the actuator bends, and therefore, the model consists of about 6000 elements (Figure 5).

Figure 6 shows the characteristics of the output displacement with respect to the pre-bending angle. The numerical simulation results are in close agreement with the analytical results. The highest discrepancy was obtained for the peak value of the displacement, where relative error was equal to 2.3%.

Analytical Equation (14) may be useful for the straight arms and basic design only; moreover, it underrepresents the interaction between constraint force and displacement when the displacement is close to zero or when a large force is applied [2]. From the practical point of view, actuation force should be modeled as a contact force, as in the model in [38]. Figure 7 shows the relationship between the pre-bending angle and the contact force calculated at the rigid surface, for the same model of the actuator. The gap is understood as a distance from the tip of the central shaft to the rigid surface. A small value of the pre-bending angle actuator cannot generate a high enough value of the force for it to be useful; a higher value of the pre-bending angle actuation force strongly depends on the value of the gap. The peak value of the contact force is decreasing while gap is increasing.

Another important factor, which has to be considered in optimal design of the V-type actuator, is the possibility of buckling. Buckling appears if the internal force in the arms is greater than the critical buckling force. The internal compressing force in a beam is equal to the reaction force in the anchor and can be calculated from [39]:

$$R=\alpha \Delta TEA\frac{{\cos }^2\phi }{\frac{A{L}^2}{12I_z}{\sin }^2\phi +{\cos }^2\phi },$$

(15)

whereas critical force is given by:

$$F_{cr}=\frac{{\pi }^{2}E{I}_{\min }}{{\left(\beta L\right)}^2},$$

(16)

where $I_{\min }$ is minor moment of inertia and $\beta$ is buckling length coefficient

For the verification, buckling analysis of the one actuator beam for the same FEM model was performed. Based on the same geometry, the boundary conditions for the single beam are as follows: the anchor is fixed in all degrees of freedom, while the end of the beam can move in vertical direction but cannot rotate. Critical force calculated for the geometry considered from the Equation (16) gives $F_{cr}=419.5\mathsf{\mu }\mathrm{N}$. While solving buckling analysis by means of FEM (13), the critical load factor (CLF) was calculated. That factor is a ratio between critical and applied load for the first form of stable model equilibrium. Assuming the same numerical data for the FEM-model simulated $CLF=1.058$ indicates a good agreement between numerical and analytical results. Finally, compressive stress in the beam calculated analytically and numerically gives very similar results as well. Note, that the analytical solution incorporates only uniaxial stress and cannot provide information about local stress concentration (see Figure 2).

The calculation performed allows us to state that the numerical FEM model developed has been successfully verified. This model was used to create a parametric model for the optimization task (details in Section 5). It is apparent that the relations between geometrical parameters and the actuation force, displacement generated, buckling factor and internal stresses, are non-obvious. Moreover, for the beams with non-uniform cross-sectional area, analytical formulas cannot be applied, so the relationships between criteria are more complex.

3. Multiobjective Optimization Problem

3.1. General Information

Multiobjective optimization problems are characterized by more than one objective function. Objective functions are usually contradictory, and therefore, cannot be improved simultaneously. The objective functions should be defined in such a way that they correspond to the real demands asked of the system under consideration. In case of electrothermal microactuators it is often desired of them to have low volume, generate high force and generate low stress under working conditions, to name a few demands which can be expressed as objective functions. The determination of objective function values can be done analytically, experimentally or numerically. Analytical methods can only be applied to very simple mechanical systems (which is not the case when considering actuators of an arbitrary shape) and multiple experimental determinations of function values may be too time-consuming or even impossible, as it would require manufacturing multiple microactuators of different shapes and a complex method of measuring values related to objective functions. For those reasons, when optimizing real mechanical systems, the values of objective functions are usually determined numerically using CAE (computer aided engineering) software.

In multi-criteria problems, as opposed to single-criteria problems, where a single solution is sought, the aim is to find a set of solutions rather than a single solution. The set of solutions found should meet the design assumptions defined, as restrictions imposed on the problem and the values of the objective function should be at a level acceptable for the designer; e.g., maximal equivalent stress in the microactuator under working conditions cannot be higher than a value acceptable for a particular material used. Such an approach to the design problem is called Pareto optimization. The aim of multicriteria optimization is to find the vector of design variables describing the system, such as its geometry, material properties or boundary conditions (e.g., width of a microactuator beam, rounding radius between actuator beams and central shaft and pre-bending angle), so that the values of the functions are approaching extremes (e.g., value of vertical deflection and value of force generated). In the general case, the problem of multicriteria optimization can be presented as search of a vector of design variables.

$$x=\left[x_1,x_2,\dots ,x_n\right],$$

(17)

under m equality constraints,

$$\forall i\in \left\{1,2,\dots ,m\right\}:g_i\left(x\right)=0,$$

(18)

and p inequality constraints

$$\forall j\in \left\{1,2,\dots ,p\right\}:h_j\left(x\right)\le 0,$$

(19)

to minimize k objective functions.

$$f_i(x)=\left[f_1(x),f_2(x),\dots ,f_k(x)\right].$$

(20)

The decision domain is, thus, n-dimensional, and the solution domain is k-dimensional. Therefore, a set of non-dominated (or Pareto-optimal) solutions is sought, also called Pareto front. Considering two vectors x and y in the decision domain, vector x strongly dominates y if:

$$\forall i\in \left\{1,2,\dots ,k\right\}:f_i(x)<f_i(y)$$

(21)

solution x weakly dominates y, if:

$$\forall i\in \left\{1,2,\dots ,k\right\}:f_i(x)\le f_i(y)\wedge \exists j\in \left\{1,2,\dots ,k\right\}:f_j(x)<f_j(y)$$

(22)

and solution x is neutral (incomparable) to the y, if:

$$\exists i,j\in \left\{1,2,\dots ,k\right\}:f_i(x)<f_i(y)\wedge f_j(y)>f_j(x)$$

(23)

3.2. Visualisation of the n-Dimensional Pareto Fronts

In case of problems with two objectives, the Pareto front is a curve; in case of three objectives—a surface; and in case of higher orders of solution space—a hypersurface (Figure 8). A large number of objectives may happen to cause problems with representation of results in the graphic form, as the traditional methods may become unclear. Traditional methods of representation of result in the case of four objectives coming down to display the data as a three-dimensional plot, with three objectives shown on the axes of a coordinate system and the fourth objective displayed as a color on data points. For four objectives or more it is even harder to find an efficient way of data visualization. One way of dealing with high-dimensional results’ visualization is utilizing a scatter plot matrix, where objectives are displayed pairwise, resulting in a matrix of (n²−n)/2 scatter plots, where n is the number of objectives. In case of six objectives, as investigated in this paper, this requires the data to be displayed on 15 scatter plots. Such an approach means that the visualization may not carried out in a clear, simple and precise manner. Utilizing self-organizing maps (SOMs) as a visualization tool helps one to overcome some of the flaws of the aforementioned methods.

SOM is an artificial neural network, which has been used, among others, in the visualization of multidimensional data sets. This method was proposed by Kohonen in [40]. In the case of multi-criteria optimization problems with a large number of objectives, which result in multidimensional Pareto fronts, SOM can help to present the results in a graphical form but an alternative way. Multidimensional solution space is transformed into the form of n colorful maps, where n is the number of dimensions of solution space, and the colors of units (nodes) on the map correspond to the approximate values of the objective function. Each unit of SOM is described by a codebook vector of size n. Values of codebook vector elements are determined in an iterative learning process based on input data (Pareto front) presented to the network. The network learning process preserves the topological order of data, so solutions located close to each other on the front of Pareto remain close to each other on the SOM. Such an approach to visualization of results allows for easy determination of tradeoff relationships between objectives of the optimization problem. An effective method of visualizing a set of solutions is a key factor at the stage of information exchange between the person processing the results and the person deciding on the choice of a particular solution. In addition, SOM can be used to group similar solutions into clusters.

3.3. Formulation of the Objectives for the Optimal Design of the Microactuators

For the optimal design of the electro-thermal microactuators, the following six objectives were defined and numerically implemented:

• The minimization of the volume of the structure:

  $$\underset{x}{\min }f1={\displaystyle \underset{\mathsf{\Omega }}{\int }d\mathsf{\Omega }}.$$

  (24)
• The minimization of the maximal value of the equivalent stress:

  $$\underset{x}{\min }f2=\max \left({\sigma }_{eq}\right).$$

  (25)
  To calculate maximal value of the equivalent stress, the Huber–Mises–Hencky hypothesis is used [41]
• The maximization of the vertical deflection of the central shaft:

  $$\underset{x}{\max }f3=\max \left(u_i\right).$$

  (26)
• The minimization of the total heat generated by the actuator:

  $$\underset{x}{\min }f4=\max \left(q_{total}\right).$$

  (27)
• The maximization of the buckling factor:

  $$\underset{x}{\max }f5=\max \left(f_{buck}(P_v)\right).$$

  (28)
  For the calculation of the buckling factor vertical arbitrary force $P_v$ is placed to the top of the central shaft.
• The maximization of the force generated by the actuator:

  $$\underset{x}{\max }f6=\max \left(F_c(d_g)\right).$$

  (29)
  The contact force is calculated with for the arbitrary value of the gap distance $d_g$ between the tip of the central shaft and the rigid surface.

4. Optimal Design System for Electrothermal Microactuators

In order to effectively perform multiobjective optimization of microthermal actuators, it is necessary to use appropriate optimization algorithms, define and implement optimization criteria and use efficient tools for numerical simulation. The system, which combines the immune game theory multiobjective algorithm (IMGAMO) and tools allowing for numerical simulation is proposed in the paper.

IMGAMO is the approach, which take advantages of AIS and game theory and it is used to solve the problems of multiobjective optimization [42,43].

The most important assumptions to the IMGAMO algorithm are as follows:

• Each objective function (payoff function) is assigned to a single player among a group of players, playing a cooperative game, iteratively looking for a Nash equilibrium—a set of optimal solutions;
• Each design variable is assigned to a single player (one player can be assigned more than one design variable);
• The assignment of objective functions to players is constant, but the assignment of design variables to players changes during the course of optimization to provide a diversity of solutions;
• Each player selects their strategy based on the immune algorithm to optimize its assigned objective (each player has its own population);
• Each player can only modify design variables assigned to it, and the rest of design variables are fixed and determined by other players’ strategies, shared between players;
• The result of the algorithm (the determined Pareto frontier) is stored in the population of results.

Each objective in MOO is represented by player’s payoff. Each player has its own objective (a payoff function in the Nash equilibrium). The strategy for a particular player is the optimum solution for this player’s problem, remembering that other players also play their best strategies. The solution of the optimized problem consists of several parameters, each of which is assigned to one of the players. Each player optimizes only its parameters (its strategy), taking the rest of them as constant. The rest of the parameters are set according to information shared by other players. Solutions from all players should establish the solution of the problem. Then, all players use the immune algorithm to optimize their objectives.

In Figure 9, the general idea of algorithm is presented. The multiobjective optimization problem considered in the paper is solved for six criteria and seven design variables. Details of the optimization task are described in Section 5. The IMGAMO algorithm can deal with multiobjective optimization tasks for an arbitrarily chosen number of criteria and design variables. More detailed description of the IMGAMO algorithm is included in Appendix A. In Figure 9, we can see that each player is assigned one criterion and one of the decision variables (DV), which are indicated by different colors. The optimizer (clonal selection) is applied for each criterion (optimizer can change only parameters assigned to this particular player’s objective). In the last step, the results are saved to a secondary population; design variables are assigned anew; and the process is repeated iteratively until the termination condition is met.

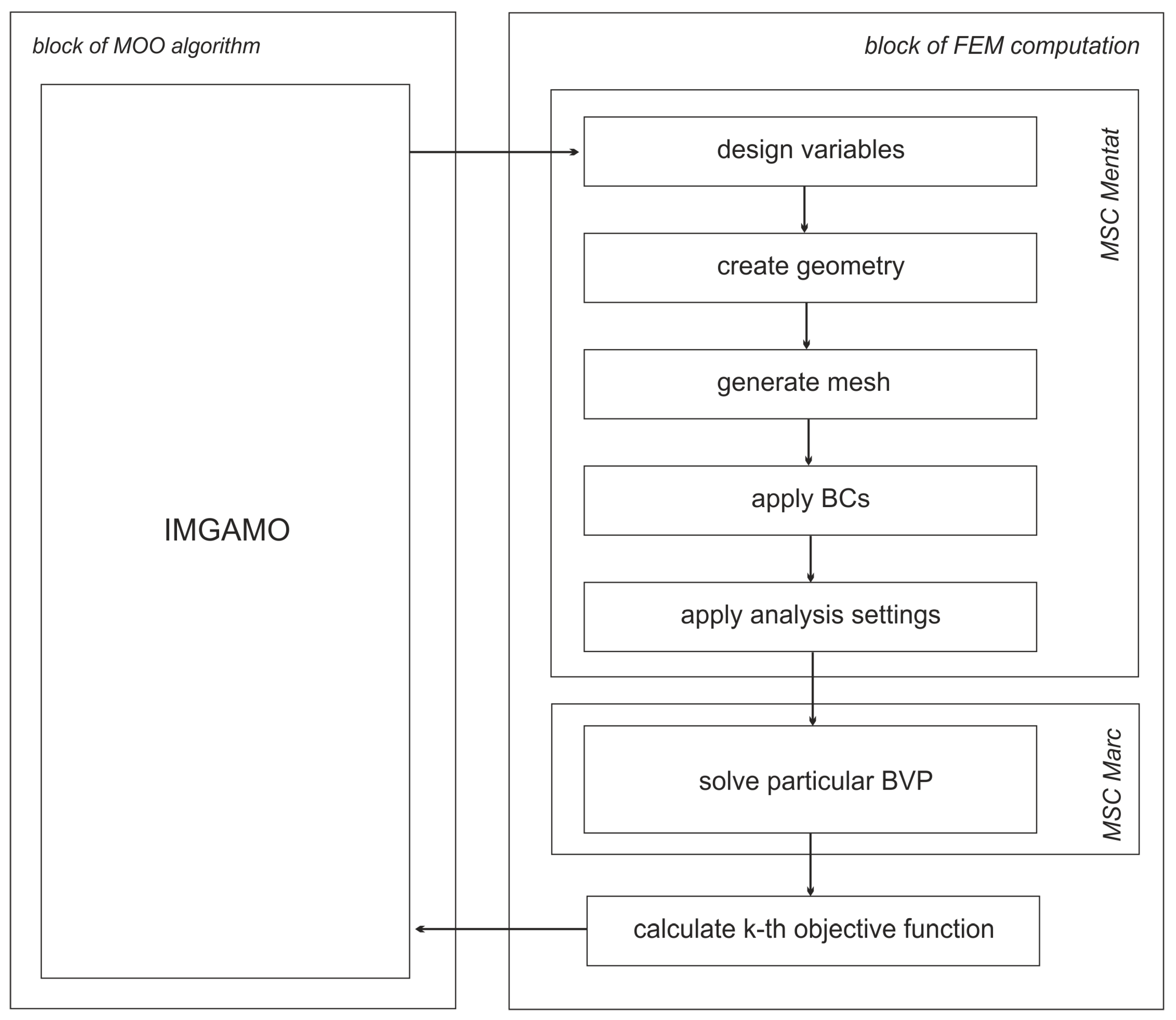
For each internal iteration in IMGAMO algorithm, consecutive evaluation of the proper criteria on the basis of encoded design variables is needed. As mentioned, particular boundary value problems have been solved by mean of FEM. MSC Mentat/Marc commercial software was adopted in order to perform those steps. The whole system of optimization consists of two main blocks: the block of the multiobjective optimization algorithm and the block of the FEM computation. Figure 10 presents the idea of the coupling between IMGAMO algorithm and block of calculation of the consecutive objectives by means of FEM in every internal iteration in IMGAMO.

As mentioned in previous paragraph, B-cells of the AIS, affected by clonal selection and suppression, proliferate and generate new, possibly better solutions. Every memory B-cell contains a set of design variables. On the basis of encoded design variables, the geometry of the optimized model of the actuator is created. Next, for the built geometry, a mesh, boundary conditions, material parameters and analysis settings are established. All these steps are performed by invoking the Mentat preprocessor.

Additional in-house procedures written in C++ and script language implemented in Mentat preprocessor have been developed to facilitate those steps automatically. The procedure allowed us to create an input file for the solving a particular boundary value problem (BVP). Except for one (criterion f1), each problem is solved by means of FEM by invoking MSC Marc software. For the problems considered, the following cases can be distinguished:

• Criterion f1 (Equation (24))—only preprocessor Mentat is invoked to create desired geometry.
• Criterion f2 (Equation (25))—electro-thermo-mechanical analysis is performed (Equations (10)–(12)).
• Criterion f3 (Equation (26))—electro-thermo-mechanical analysis is performed (Equations (10)–12))
• Criterion f4 (Equation (27))—electro-thermal analysis is performed (Equations (10) and (11))
• Criterion f5 (Equation (28))—buckling analysis is performed (Equation (13))
• Criterion f6 (Equation (29))—electro-thermo-mechanical analysis including contact is performed (Equations (10)–(12)).

Calculation of the particular k-th objective is performed on the basis of output file generated by MSC Marc. It should be underlined that solution times for particular analyses differ between each other. As in the proposed method of optimization, each criterion (represented by player’s payoff) is optimized independently; the optimization procedure can be much more efficient compared to the other optimization methods, for which in every iteration all the values of objective functions have to be determined for each solution.

5. Optimization Model

The model of the structure which contains one pair of the arms was considered for the shape optimization. Symmetry along the vertical axis in the center shaft was assumed, which ensured axial movement of the central shaft. The beam was modeled by means of the NURBS curve, which consists of four control points. The knot vector of the NURBS curve is uniformly distributed and has cubic interpolation; the constant value of the control points’ weight being equal to 1.0 is assumed. The shape of the beam is modeled by manipulation of the NURBS control polygon, with symmetry imposed along the centerline of the beam. The first four design variables are distances between a particular control point and the symmetry line. The fifth, sixth and seventh design variables are the pre-bending angle of the beam, radius R1 and radius R2, respectively, so the total number of design variables is seven. Figure 11 presents geometry of the model and the way of parametrization.

The actuator was modeled as plane stress structure fabricated from polycrystalline silicon (Young’s modulus $\mathrm{E}=158\times {10}^3\mathrm{MPa}$, Poisson’s ratio $\nu =0.23$, thermal conductivity $\mathrm{k}=140\times {10}^8\mathrm{pW}/\mathsf{\mu }\mathrm{mK}$, resistivity $\mathrm{R}=3.3\times {10}^{-11}T\mathsf{\Omega }\mathsf{\mu }\mathrm{m}$ and linear expansion coefficient ${\alpha }_t=3\times {10}^{-6}1/\mathrm{K}$). The length of the beam was $220\mathsf{\mu }\mathrm{m}$, whereas the thickness of the in the z-direction was $10\mathsf{\mu }\mathrm{m}$ ($\mu MKS$ system unit is used). The model was supplemented with electrical, thermal and mechanical boundary conditions. Anchors were fixed in all degrees of freedom and the temperature 300 K was assumed. The electric potential difference between anchors was equal to 5 V. For the buckling analysis force $P_v=500\mathsf{\mu }\mathrm{N}$, whereas for the calculation of the contact force, the gap $d_g$ was equal to $2\mathsf{\mu }\mathrm{m}$. Box constraints imposed on the design variables were as follows: for the design variables D1, D2, D3, D4, R1 and R2 within the scope $<1÷20>[\mathsf{\mu }\mathrm{m}]$, whereas the fifth design variable φ was within the scope, $<0.001÷12>[°]$. The multiobjective optimization task concerned determining seven design variables which minimized six defined functionals (Section 3.3) and was performed by means of IMGAMO algorithm. A few runs of IMGAMO algorithm were performed. Due to the simplicity, only two are considered and described in the paper. The following values of IMGAMO parameters were assumed:

• 1st variant (size of the population—5, number of clones—10 and number of iterations—100)
• 2nd variant (size of the population—20, number of clones—20 and number of iterations—100).

6. Results and Discussion

For the first optimization task (variant 1), a six-dimensional Pareto front consisting of 2471 nondominated solutions was found, whereas for the variant 2, there were 3143 solutions. Figure 12 and Figure 13 present scatter plot matrices generated on the basis of set of Pareto optimal solutions, including the distribution of objectives’ values in the form of histograms. To transform maximization problems into minimization problems, some of them were multiplied by −1 so that only minimization tasks were solved.

The size of the set of Pareto optimal solutions is different for both variants; however, shapes of the Pareto fronts in each projection plane are very similar. That shows that it is highly probable, that the solutions obtained are unambiguous and are located close to the optimal front. The differences can only be seen in the filling of the space by the nondominated solutions. It has to be underlined, that the computational effort for the first variant is significantly smaller. A detailed comparison can be found in the

Table 1. Statistics of the objective function evaluations size of the Pareto optimal solutions for the multiobjective optimization tasks performed.

	# eval. f1	# eval. f2	# eval. f3	# eval. f4	# eval. f5	# eval. f6	# Total eval.	Front Size
Variant 1	8291	8242	8265	8266	8178	8322	49,564	2471
Variant 2	21,367	21,189	21,227	21,299	21,112	21,440	12,7634	3143

. Table contains a number of fitness function evaluations for each objective (columns 2–7), the total number of fineness function evaluations (column 8) and the size of the set of Pareto optimal solutions (column 9). Files containing data (values od design variables and values of objective functions) from the set of Pareto-optimal solutions are included in supplementary material.

In order to obtain the scatter plot matrix present, by means of popular bi-objective optimizers, 15 independent runs of optimization tasks were needed. Moreover, for that optimization problem, a multidimensional Pareto front could not be obtained by solving several separate bi-objective tasks, because in this case, structures with no contact force are ignored, and they would not be included in the set of nondominated solutions. Due to this, some comparisons are possible only for the projection plane, which incorporates objective f6. In attempt to compare the results of IMGAMO algorithm with those of a popular and well-known optimization algorithm, a bi-objective NSGAII was chosen as a reference algorithm. A pair of f2 and f6 objectives was selected for the comparison. Figure 14 shows Pareto front obtained by NSGAII, and the projection plane for criteria f2 and f6, obtained by method proposed herein (such projection plane is indicated in Figure 13). The NSGAII algorithm was run for the population size of 50 chromosomes and 100 iterations (File containing data with Pareto optimal solutions in each generation are included in supplementary material). As can be seen, the location of the Pareto front found by both algorithms is comparable; however, IMGAMO found more a widespread one. This comparison also shows the high probability of the correct location of the Pareto front for this problem, found using the method proposed herein.

Extreme solutions for each objective functional are collected in

Table 2. Results of the optimization—values of the objective functions.

	$\mathbf{f}1[{\mathsf{\mu }\mathbf{m}}^3]$	$\mathbf{f}2\left[\mathbf{MPa}\right]$	$\mathbf{f}3\left[\mathsf{\mu }\mathbf{m}\right]$	$\mathbf{f}4\left[\mathsf{\mu }\mathbf{W}\right]$	$\mathbf{f}5[]$	$\mathbf{f}6\left[\mathsf{\mu }\mathbf{N}\right]$
min f1	110,000.50	502.83	−6.09	2.83	−0.09	−28.59
min f2	112,632.01	61.86	−2.37	3.51	−0.72	−483.25
max f3	112,030.51	736.10	−17.76	2.70	−0.04	−166.56
min f4	111,819.23	436.27	−3.68	2.47	−0.12	−9.20
max f5	227,916.45	1216.51	−2.03	32.90	−563.10	−353.35
max f6	211,171.86	1285.59	−3.39	18.79	−165.30	−7548.54
Straight b. 2.5	121,001.05	1737.54	−9.05	5.45	−0.69	−571.85
Straight b. 5.0	142,001.45	2279.89	−3.80	10.48	−8.49	−706.27
Straight b. 10.0	184,000.66	4199.03	−1.34	20.78	−178.30	0.00
compromise-solution	146,834.58	1027.59	−5.88	5.14	−2.09	−1678.99

, whereas Figure 15 presents ghd optimal shape of the actuator for that extremes. Additionally, for comparison, actuators with straight arms (traditional geometry) for different widths of the beam equal to $2.5\mathsf{\mu }\mathrm{m}$, $5.0\mathsf{\mu }\mathrm{m}$ and $10.0\mathsf{\mu }\mathrm{m}$ are included. For such geometry, the pre-bending angle was assumed to $\phi =1.3°$ and a sharp connection between arm and the anchor was assumed. It is natural, that a significantly higher maximal value of the equivalent von Mises stress was observed.

Table 3. Results of the optimization—values of the design variables.

	$\mathbf{D}1\left[\mathsf{\mu }\mathbf{m}\right]$	$\mathbf{D}2\left[\mathsf{\mu }\mathbf{m}\right]$	$\mathbf{D}3\left[\mathsf{\mu }\mathbf{m}\right]$	$\mathbf{D}4\left[\mathsf{\mu }\mathbf{m}\right]$	$\mathsf{\phi }[°]$	$\mathbf{R}1\left[\mathsf{\mu }\mathbf{m}\right]$	$\mathbf{R}2\left[\mathsf{\mu }\mathbf{m}\right]$
min f1	1.06	1.00	1.06	1.76	0.15	2.99	2.10
min f2	1.08	1.14	1.03	1.00	11.69	1.83	19.56
max f3	1.01	1.08	1.03	1.00	0.73	1.76	19.56
min f4	1.03	1.01	1.01	1.13	0.07	1.18	18.97
max f5	9.03	19.54	11.02	19.74	7.92	8.47	15.20
max f6	1.33	19.91	19.84	1.00	8.08	2.02	18.48
compromise-solution	1.00	1.00	3.24	19.24	4.20	18.07	3.09

contains the value of the design variables obtained for the extreme solutions.

Representation of the set of Pareto optimal solutions by means of scatter plot matrix, provides good insight into the nature of the problem. Shapes of the consecutive tradeoffs show dependences between particular objectives. The rapid change at some region of the Pareto front can be very useful information for the designer (small changes in one criterion may cause great changes in the other). However, a higher number of criteria, analyzing too many charts simultaneously, can be a serious obstacle in the effective selection of the interesting solutions. As previously mentioned, utilizing the SOMs as a visualization tool may help to overcome that difficulty and could be very useful for the designer.

On the basis of set of Pareto optimal solutions, colorful grid maps by means of SOM were generated. Figure 16 presents the maps generated for the 2nd variant of optimization. For the 1st variant, the maps generated are comparable, so they are not included in the paper. Each grid in the figure corresponds to a particular optimization criterion, whereas nodes correspond to particular solutions, with the value of each objective depicted as the unit’s color. The general look and the brief analysis of the maps allow us to formulate conclusions:

• Objectives f1 and f4 have quite a similar nature (actuator with a smaller volume generates much smaller amounts of heat);
• Objectives f3 and f5 have contradictory natures, except in the region in the upper right corner of the grid (geometry of the arms resistant to buckle can generate low displacement and vice versa),
• Objectives f4 and f5 have contradictory natures as well.

Deeper insight into the particular regions of the SOM makes it possible to identify more detailed dependencies between the criteria.

Now consider the process of selecting interesting compromise-solutions on the basis the SOM generated. Let us start from the analysis of the criterion f2, by rejecting the solutions with higher values of the maximal equivalent stress (step 1 in Figure 17). The average tensile strength of polysilicon is about 1.45 GPa, so the assumed threshold level was set to 1000 MPa. Then, we got rid of the solution which could buckle. The threshold level was set to the buckling factor about value 2.0. Transmitting such limited region to the criterion f3 (step 2), the two regions with higher value of generated displacement by the actuator can be identified. For the region located in the center (heart shaped curve), smaller values of criteria f1 and f4 were observed, compared to the second region (oval shaped). If we accept the level of the value of actuation force (objective f6), the solution from that region may be chosen (step 3). Figure 18 shows the geometry of the actuator representing that region, whereas values of the objectives and design variables for that solution are included in Table 2 and Table 3.

Note that this compromise-solution is similar to the shape of the actuator proposed by Kwan A. et al., in the work dedicated to improving designs for an electrothermal in-plane microactuator [7]. The actuators with nonuniform beams, for which width increases close to the central shaft, allow for the generation higher of displacement and actuation force compared to the actuator with uniform beams. Other examples of selecting compromise-solutions with respect to the different assumption and restrictions, starting from another arbitrarily chosen criterion, can be found as well.

It should emphasized, that solutions for which the maximal equivalent stress exceeds strength of the material, and solutions for which buckling may occur (factor less than 1.0), are infeasible. That may lead to the conclusion that such criteria should be implemented in optimization as constraints. It is of course possible and can be easily implemented in the method of optimization proposed, and would cause a reduction of the total number of objectives. On the other hand, as previously mentioned, making no assumptions on weights of objectives before optimization, can result in obtaining useful information for the designer concerning trade-off relationships between criteria. Moreover, there are no criteria related to the dynamic characteristic of the actuator considered in this paper. The method of multicriteria optimization proposed allows for the formulation and implementation of more criteria as well.

7. Final Conclusions

A novel method for the multiobjective optimization of an electrothermal microactuator has been presented. A novelty of the proposed method is particularly manifested in effective shape optimization related to the large number of criteria. Six different criteria were formulated and numerically implemented. Multiobjective shape optimization for such criteria was successfully solved. New, additional objectives can be formulated and implemented for the method of optimization proposed. One of the main advantages of the method proposed is the possibility of obtaining a multidimentional set of Pareto-optimal solutions by performing a single optimization task. The IMGAMO algorithm significantly outperforms other popular multiobjective optimization algorithms (NSGAII and SPEA2), when a large number of criteria is considered. Several numerical tests on the mathematical benchmark test functions have been performed. A detailed comparison is included in the paper.

From a practical point of view, solving the problem considered by means of scalarization method, ε-constrained method or performing several separate bi-objective problems, can be inadequate and problematic. The superiority of method proposed here in comparison to the other approach for the problem considered has been presented and discussed. The method proposed for the parametrization of the actuator’s beam allows a reduction in the total number of design parameters and allows for generating shapes with significantly lower stress concentrations. The multidimensional Pareto fronts obtained may consist of thousands of solutions. Selecting the proper solution by browsing such a big data set is very difficult and inefficient. A representation of the multidimentional Pareto fronts by means of scatter plot matrices and aided by SOM has been presented. The method of selecting interesting compromise-solutions has been proposed and described. It can be very helpful as an alternative tool in the optimal design of microthermal actuators. The method proposed for the optimization of a large number of, can be used for solving other multiobjective and multidisciplinary problems related to the different engineering disciplines.

It can be a very time-consuming task, especially for a more complicated geometry, when more design variables or more objectives are considered. Moreover, the solution of the coupled problems is more time-consuming when compared to a single-field problem. Parallel computation should be the next step in order to reduce the time of the optimization.