Influence of Impeller Speed Patterns on Hemodynamic Characteristics and Hemolysis of the Blood Pump
Abstract
:1. Introduction
2. Materials and Methods
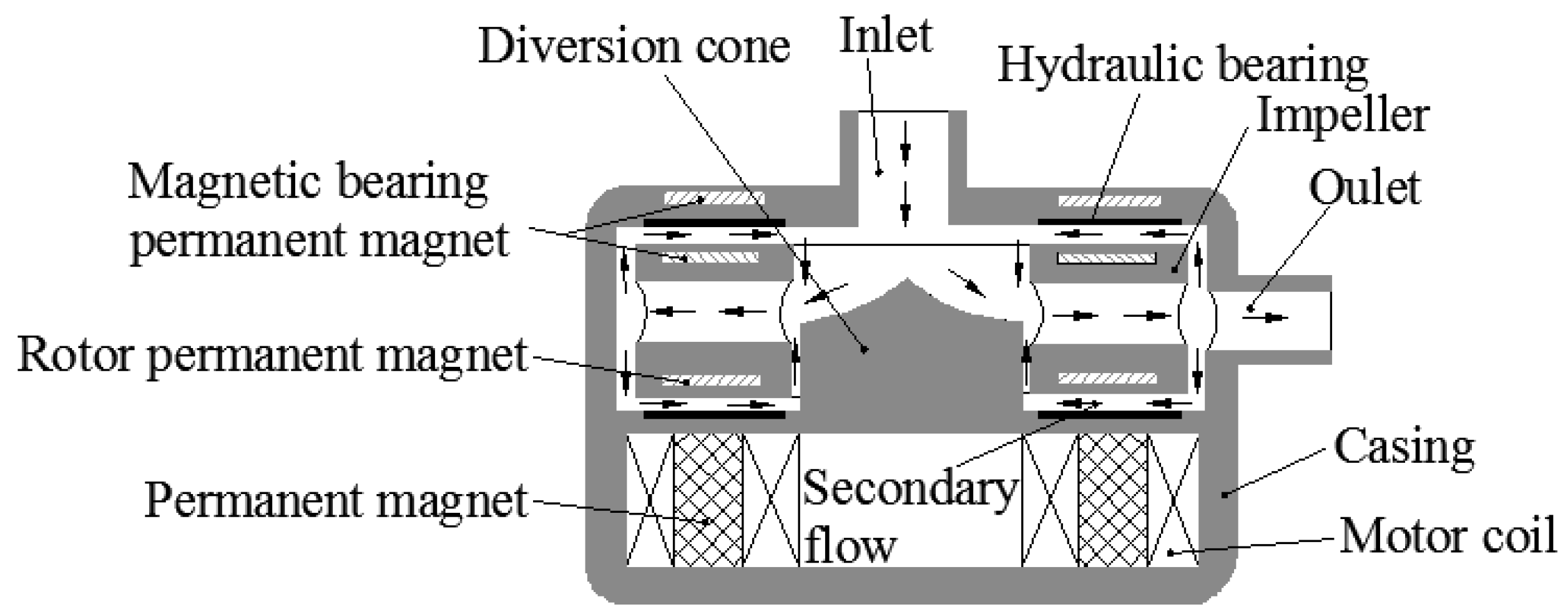
2.1. Structure and Working Principle of the Blood Pump
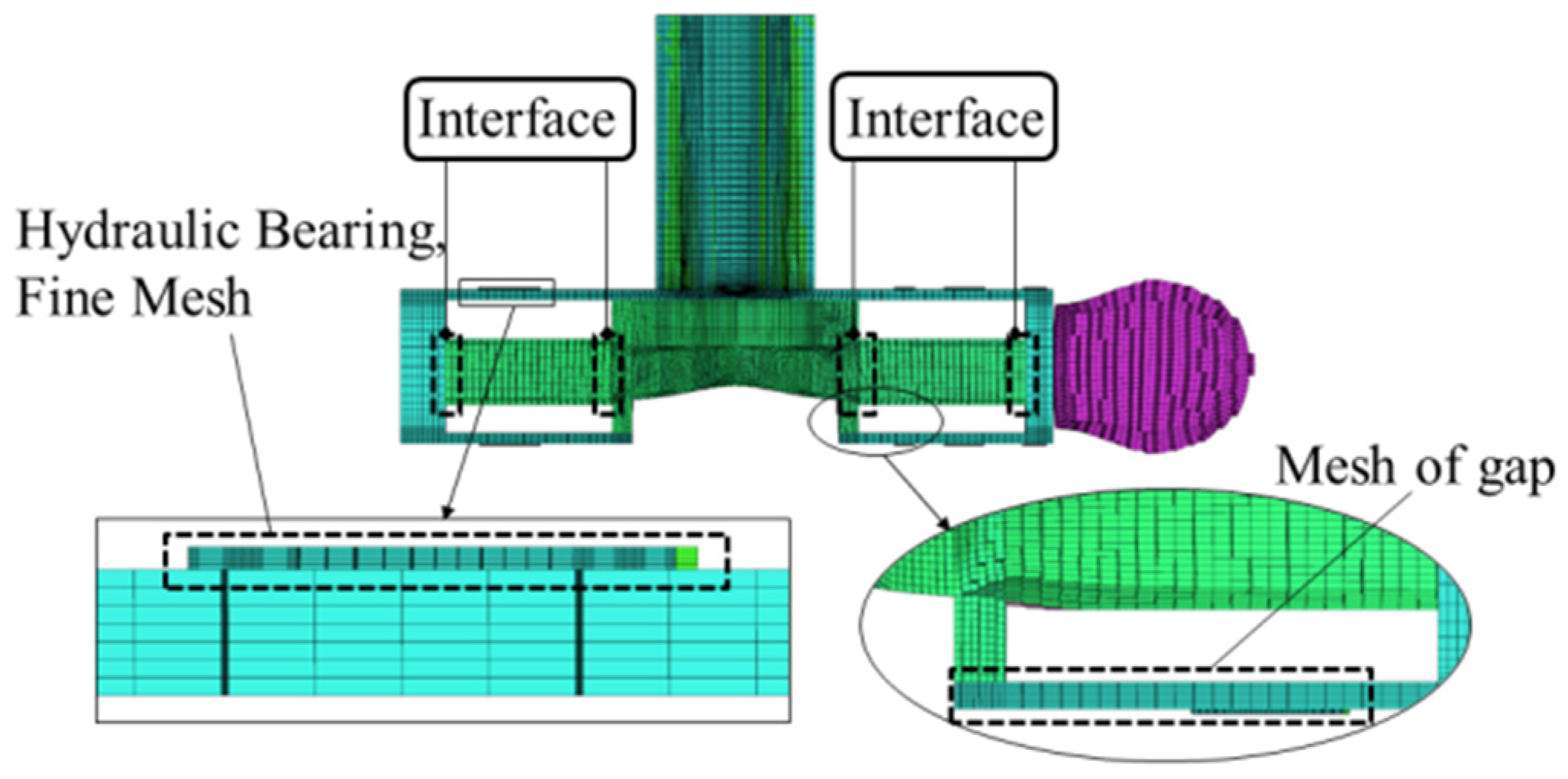
2.2. Modeling and Meshing
2.3. Steady-State Simulation of the Hydrodynamic Characteristics of the Blood Pump
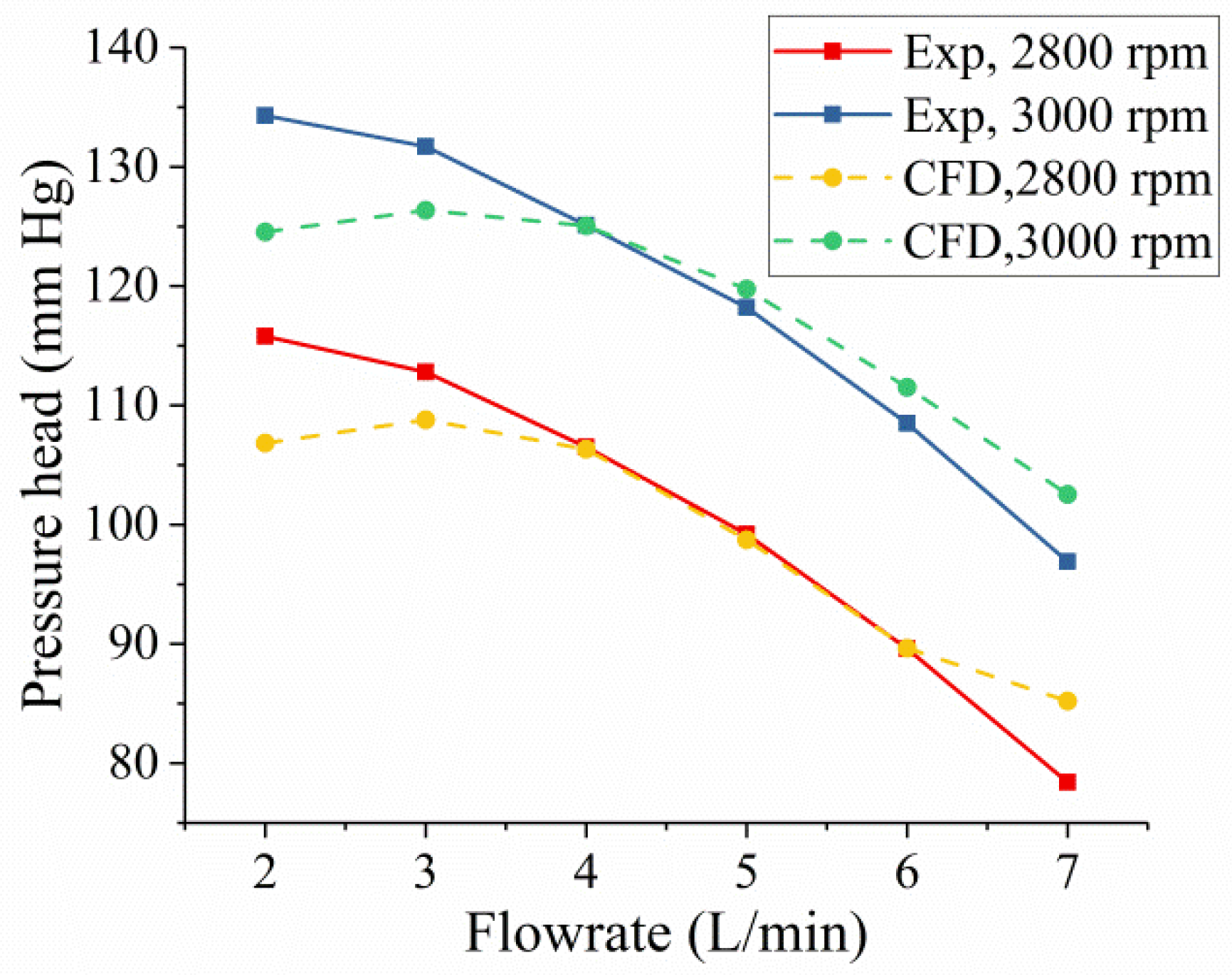
2.4. Hydrodynamic Characteristic Test and Result Analysis
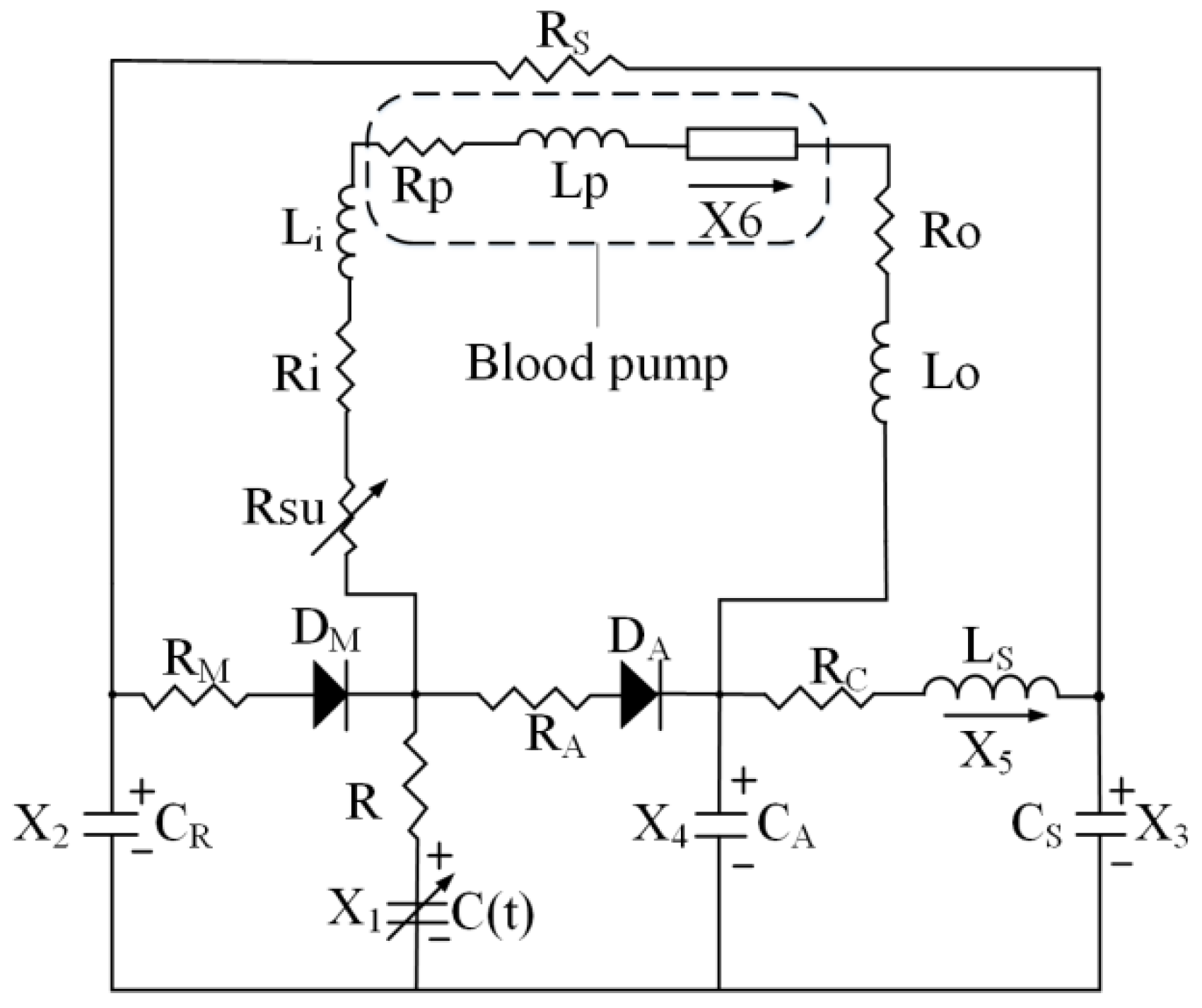
2.5. Cardiovascular System Simulation Model
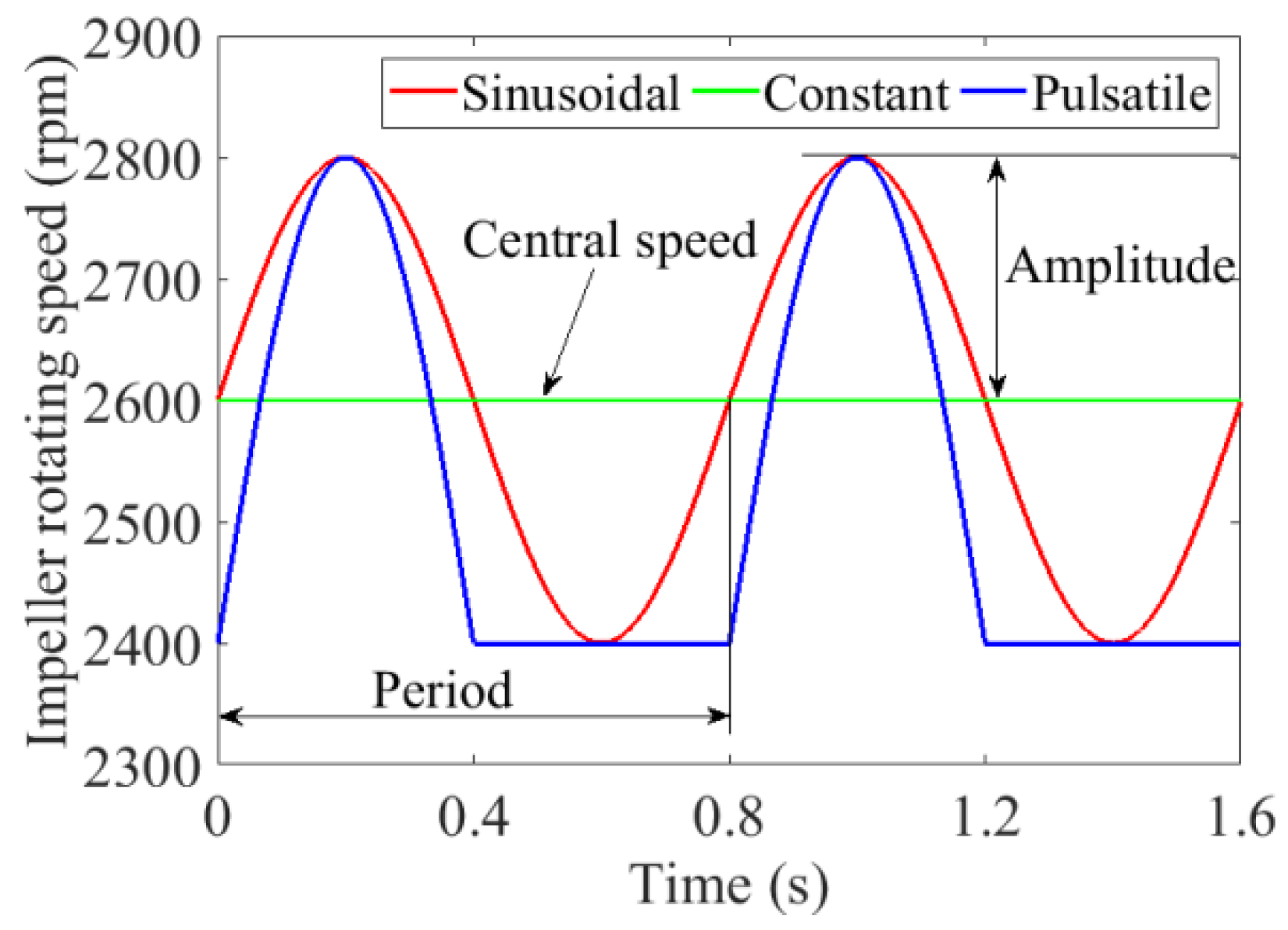
2.6. Speed Modulation of the Blood Pump Impeller
3. Results
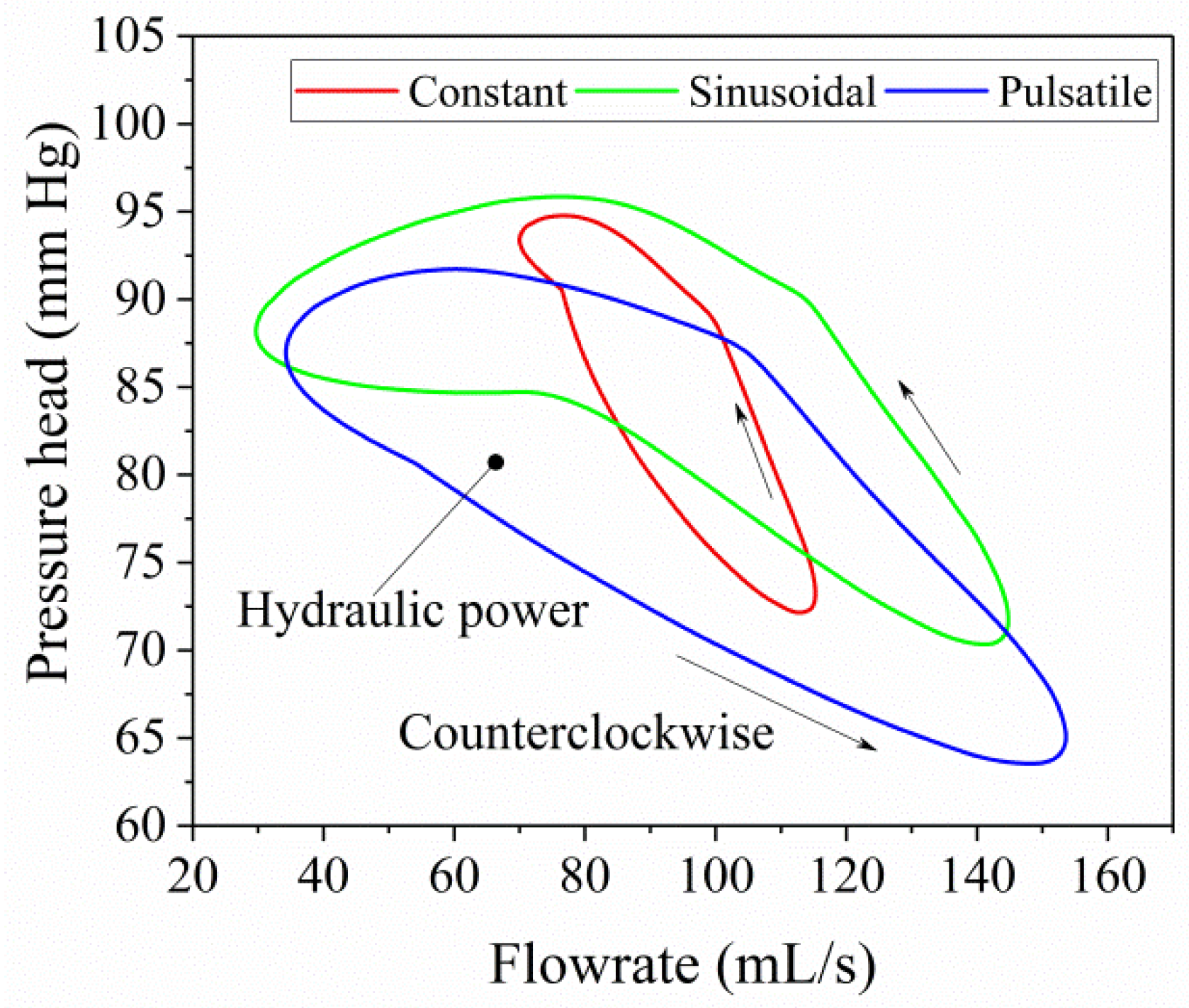
3.1. Analysis of Hemodynamic Characteristics
3.2. Eulerian Hemolysis Model
3.3. Simulation Method of Hemolysis Characteristics of the Impeller with Three Speed Patterns
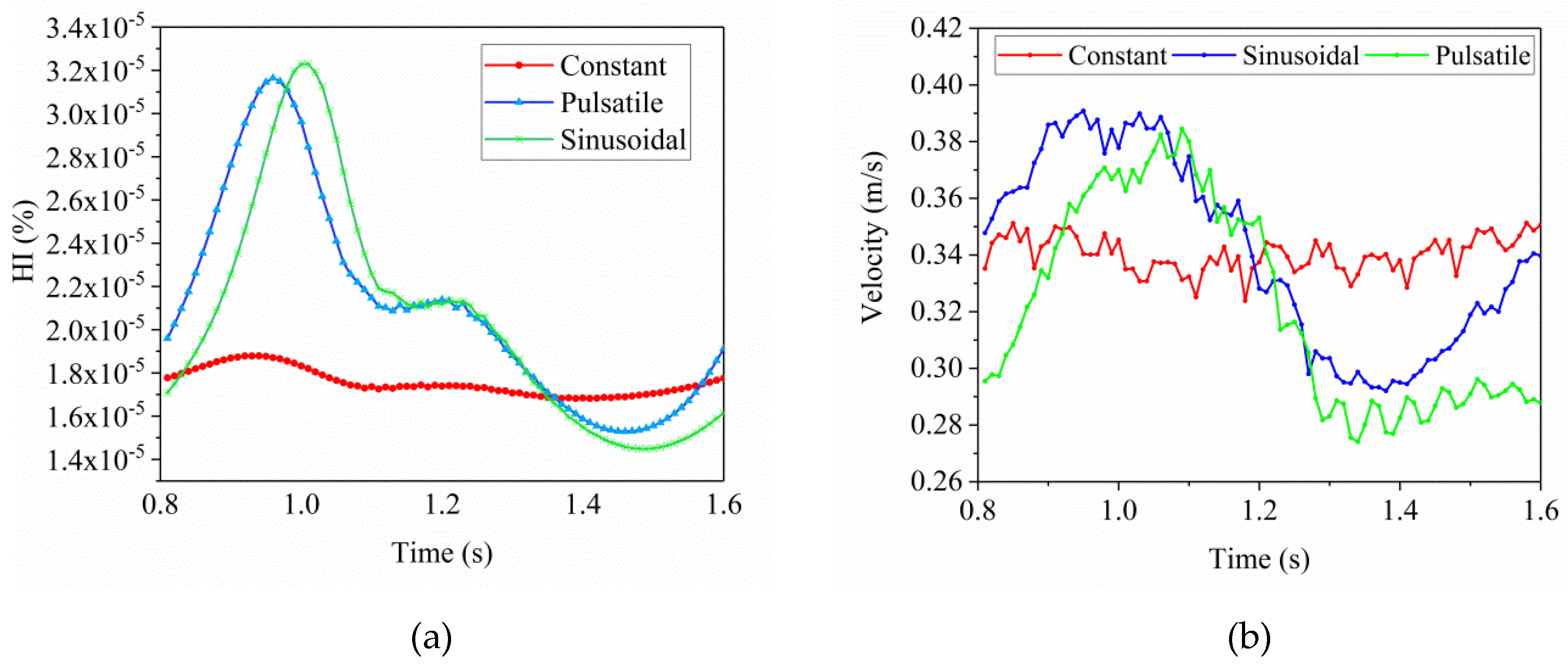
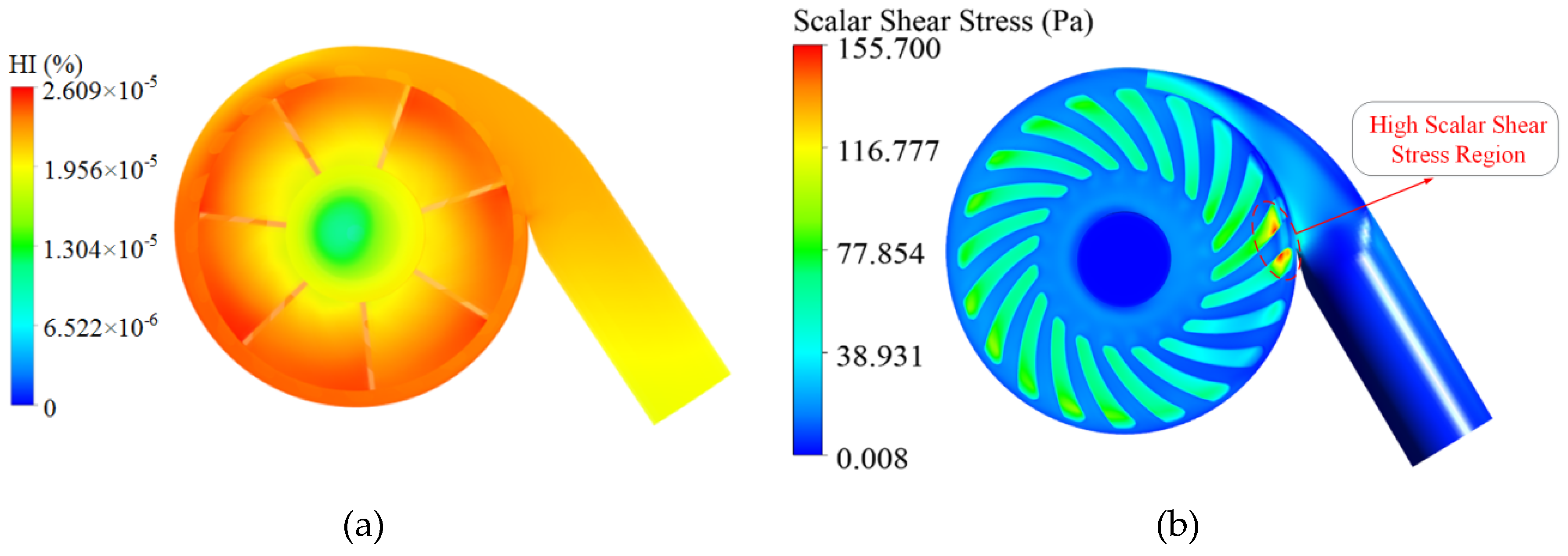
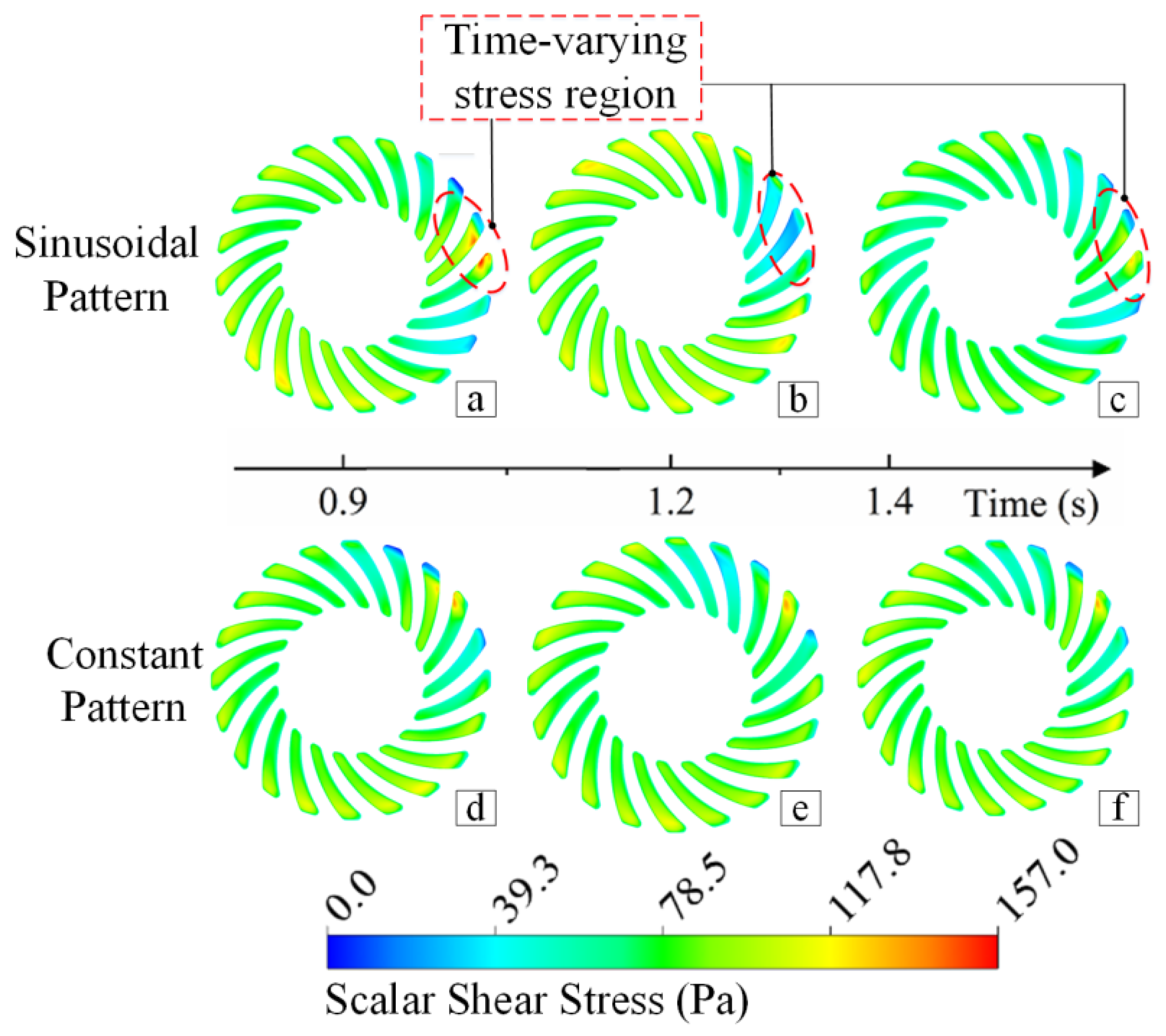
3.4. CFD Results of the Hemodynamic Characteristics and Hemolysis
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Garcia, S.; Kandar, F.; Boyle, A.; Colvin-Adams, M.; Lliao, K.; Joyce, L.; John, R. Effects of Pulsatile- and Continuous-flow Left Ventricular Assist Devices on Left Ventricular Unloading. J. Heart Lung Transplant. 2008, 27, 261–267. [Google Scholar] [CrossRef]
- Bartoli, C.R.; Atluri, P. Do patients with a continuous-flow left ventricular assist device benefit from induced-pulsatility or are we just spinning our wheels. J. Thorac. Cardiovasc. Surg. 2015, 150, 945–946. [Google Scholar] [CrossRef]
- Soucy, K.G.; Koenig, S.C.; Giridharan, G.A.; Sobieski, M.A.; Slaughter, M.S. Defining pulsatility during continuous-flow ventricular assist device support. J. Heart Lung Transplant. 2013, 32, 581–587. [Google Scholar] [CrossRef]
- Bozkurt, S. Physiologic outcome of varying speed rotary blood pump support algorithms: A review study. Australas. Phys. Eng. Sci. Med. 2016, 39, 13–28. [Google Scholar] [CrossRef]
- Naito, N.; Nishimura, T.; Iizuka, K.; Takewa, Y.; Umeki, A.; Ando, M.; Ono, M.; Tatsumi, E. Rotational speed modulation used with continuous-flow left ventricular assist device provides good pulsatility. Interact. Cardiovasc. Thorac. Surg. 2017, 26, 119–123. [Google Scholar] [CrossRef]
- Ising, M.; Warren, S.; Sobieski, M.A.; Slaughter, M.S.; Koenig, S.C.; Giridharan, G.A. Flow Modulation Algorithms for Continuous Flow Left Ventricular Assist Devices to Increase Vascular Pulsatility: A Computer Simulation Study. Cardiovasc. Eng. Technol. 2011, 2, 90–100. [Google Scholar] [CrossRef]
- Qian, K. Design of blood pump impeller with ternary theory. J. Eng. Math. 1987, 4, 99–101. (In Chinese) [Google Scholar]
- Qian, K.; Fei, Q. Pulsatile flow impeller blood pump with low hemolysis. J. Biomed. Eng. China 1990, 9, 113–119. (In Chinese) [Google Scholar]
- Pirbodaghi, T.; Axiak, S.; Weber, A.; Gempp, T.; Vandenberghe, S. Pulsatile control of rotary blood pumps: Does the modulation waveform matter. J. Thorac. Cardiovasc. Surg. 2012, 144, 970–977. [Google Scholar] [CrossRef] [PubMed]
- Cheng, A.; Williamitis, C.A.; Slaughter, M.S. Comparison of continuous-flow and pulsatile-flow left ventricular assist devices: Is there an advantage to pulsatility. Ann. Cardiothorac. Surg. 2014, 3, 573. [Google Scholar]
- Nammakie, E.; Niroomand-Oscuii, H.; Koochaki, M.; Ghalichi, F. Computational fluid dynamics-based study of possibility of generating pulsatile blood flow via a continuous-flow VAD. Med. Biol. Eng. Comput. 2017, 55, 167–178. [Google Scholar] [CrossRef] [PubMed]
- Deepankaew, R.; Plianchaisuk, A.; Naiyanetr, P. Numerical Simulation of aBiventricular Assist Device with Pulsatile Control Operation for Bridge toRecovery. Int. J. Appl. Biomed. Eng. 2015, 8, 10–16. [Google Scholar]
- Shiose, A.; Nowak, K.; Horvath, D.J.; Massiello, A.L.; Golding, L.A.; Fukamachi, K. Speed Modulation of the Continuous-Flow Total Artificial Heart to Simulate a Physiologic Arterial Pressure Waveform. ASAIO J. 2010, 56, 403–409. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ando, M.; Nishimura, T.; Takewa, Y.; Yamazaki, K.; Kyo, S.; Ono, M.; Tsukiya, T.; Mizuno, T.; Taenaka, Y.; Tatsumi, E. Electrocardiogram-Synchronized Rotational Speed Change Mode in Rotary Pumps Could Improve Pulsatility. Artif. Organs 2011, 35, 941–947. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.; Boston, J.R.; Antaki, J.F. Hemodynamic Controller for Left Ventricular Assist Device Based on Pulsatility Ratio. Artif. Organs 2007, 31, 114–125. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Lawford, P.V.; Hose, D.R. Numerical Modeling of Hemodynamics with Pulsatile Impeller Pump Support. Ann. Biomed. Eng. 2010, 38, 2621–2634. [Google Scholar] [CrossRef]
- Alberto, M.B.; Manuel, F.O.J.; Andrés, M.F. Numerical methodology for the CFD simulation of diaphragm volumetric. Int. J. Mech. Sci. 2018, 150, 322–336. [Google Scholar] [CrossRef]
- May-Newman, K.; Vu, V.; Herold, B. Modeling the Link between Left Ventricular Flow and Thromboembolic Risk Using Lagrangian Coherent Structures. Fluids 2016, 1, 38. [Google Scholar] [CrossRef]
- Behbahani, M.; Behr, M.; Hormes, M.; Steinseifer, U.; Arora, D.; Coronado, O.; Pasquali, M. A review of computational fluid dynamics analysis of blood pumps. Eur. J. Appl. Math. 2009, 20, 363–397. [Google Scholar] [CrossRef] [Green Version]
- Moscato, F.; Danieli, G.A.; Schima, H. Dynamic Modeling and Identification of an Axial Flow Ventricular Assist Device. Int. J. Artif. Organs 2009, 32, 336–343. [Google Scholar] [CrossRef]
- Fraser, K.H.; Taskin, M.E.; Griffith, B.P.; Wu, Z.J. The use of computational fluid dynamics in the development of ventricular assist devices. Med. Eng. Phys. 2011, 33, 263–280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferreira, A.; Chen, S.; Simaan, M.A.; Boston, J.R.; Antaki, J.F. A Nonlinear State-Space Model of a Combined Cardiovascular System and a Rotary Pump. In Proceedings of the IEEE Conference on Decision & Control, Seville, Spain, 15 December 2005. [Google Scholar]
- Simaan, M.A. Modeling and control of the heart left ventricle supported with a rotary assist device. In Proceedings of the IEEE Conference on Decision & Control, Cancun, Mexico, 9–11 December 2008. [Google Scholar]
- Noor, M.R.; Ho, C.H.; Parker, K.H.; Simon, A.R.; Banner, N.R.; Bowles, C.T. Investigation of the Characteristics of HeartWare HVAD and Thoratec HeartMate II Under Steady and Pulsatile Flow Conditions. Artif. Organs 2016, 40, 549–560. [Google Scholar] [CrossRef] [PubMed]
- Arvand, A.; Hormes, M.; Reul, H. A Validated Computational Fluid Dynamics Model to Estimate Hemolysis in a Rotary Blood Pump. Artif. Organs 2005, 29, 531–540. [Google Scholar] [CrossRef] [PubMed]
- Ge, L.; Dasi, L.P.; Sotiropoulos, F.; Yoganathan, A.P. Characterization of Hemodynamic Forces Induced by Mechanical Heart Valves: Reynolds vs. Viscous Stresses. Ann. Biomed. Eng. 2008, 36, 276–297. [Google Scholar] [CrossRef]
- Apel, J.; Paul, R.; Klaus, S.; Siess, T.; Reul, H. Assessment of Hemolysis Related Quantities in a Microaxial Blood Pump by Computational Fluid Dynamics. Artif. Organs 2001, 25, 341–347. [Google Scholar] [CrossRef]
- Bludszuweit, C. Three-dimensional numerical prediction of stress loading of blood particles in a centrifugal pump. Artif. Organs 1995, 19, 590–596. [Google Scholar] [CrossRef]
- Giersiepen, M.; Wurzinger, L.J.; Opitz, R.; Reul, H. Estimation of shear stress-related blood damage in heart valve prostheses--in vitro comparison of 25 aortic valves. Int. J. Artif. Organs 1990, 13, 300–306. [Google Scholar] [CrossRef]
- Taskin, M.E.; Fraser, K.H.; Zhang, T.; Wu, C.; Griffith, B.P.; Wu, Z.J. Evaluation of Eulerian and Lagrangian Models for Hemolysis Estimation. ASAIO J. 2012, 58, 363–372. [Google Scholar] [CrossRef]
- Garon, A.; Farinas, M.I. Fast Three-dimensional Numerical Hemolysis Approximation. Artif. Organs 2015, 28, 1016–1025. [Google Scholar] [CrossRef]







| Diversion Zone | Impeller Channel | Inlet Channel and Volute | Outlet Channel | Total |
|---|---|---|---|---|
| 108,000 | 420,600 | 930,500 | 182,900 | 1,642,000 |
(mm Hg/rpm2) | (mm Hg·s/mL) | (mm Hg/(s2·mL)) | (mm Hg·s2/mL) |
|---|---|---|---|
| 1.5674e−5 | −0.1169 | −0.0023 | −0.0034 |
| Variable | Description | Magnitude |
|---|---|---|
| () | Lumped resistance of the arterial system | 1 |
| () | Mitral valve resistance | 0.005 |
| () | Aortic valve resistance value | 0.001 |
| () | Aortic characteristic impedance | 0.0398 |
| () | Myocardial impedance | 0 |
| () | Resistance of inlet cannula | 0.0677 |
| () | Resistance of outlet cannula | 0.0677 |
| () | Lumped compliance of the arterial system | 1.33 |
| () | Aortic compliance | 0.08 |
| () | Left atrial compliance | 4.4 |
| () | Blood flow inertia of the arterial system | 0.0005 |
| () | Inertia of inlet cannula | 0.0127 |
| () | Inertia of outlet cannula | 0.0127 |
| Patterns | CO (L/min) | MAP (mm Hg) | PP (mm Hg) | EEP (mm Hg) | SHE (erg/cm3) |
|---|---|---|---|---|---|
| Constant | 5.2 | 97.2 | 5.0 | 98.2 | 1300.4 |
| Sinusoidal | 5.1 | 94.2 | 11.6 | 97.2 | 4054.9 |
| Pulsatile | 4.9 | 90.8 | 12.7 | 93.8 | 4036.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Shen, P.; Zheng, M.; Fu, P.; Liu, L.; Wang, J.; Yuan, L. Influence of Impeller Speed Patterns on Hemodynamic Characteristics and Hemolysis of the Blood Pump. Appl. Sci. 2019, 9, 4689. https://doi.org/10.3390/app9214689
Wang Y, Shen P, Zheng M, Fu P, Liu L, Wang J, Yuan L. Influence of Impeller Speed Patterns on Hemodynamic Characteristics and Hemolysis of the Blood Pump. Applied Sciences. 2019; 9(21):4689. https://doi.org/10.3390/app9214689
Chicago/Turabian StyleWang, Yiwen, Peng Shen, Minli Zheng, Pengqiang Fu, Lijia Liu, Jingyue Wang, and Lishan Yuan. 2019. "Influence of Impeller Speed Patterns on Hemodynamic Characteristics and Hemolysis of the Blood Pump" Applied Sciences 9, no. 21: 4689. https://doi.org/10.3390/app9214689
APA StyleWang, Y., Shen, P., Zheng, M., Fu, P., Liu, L., Wang, J., & Yuan, L. (2019). Influence of Impeller Speed Patterns on Hemodynamic Characteristics and Hemolysis of the Blood Pump. Applied Sciences, 9(21), 4689. https://doi.org/10.3390/app9214689





