Phase Noise Cancellation in Coherent Communication Systems Using a Radio Frequency Pilot Tone
Abstract
:Featured Application
Abstract
1. Introduction
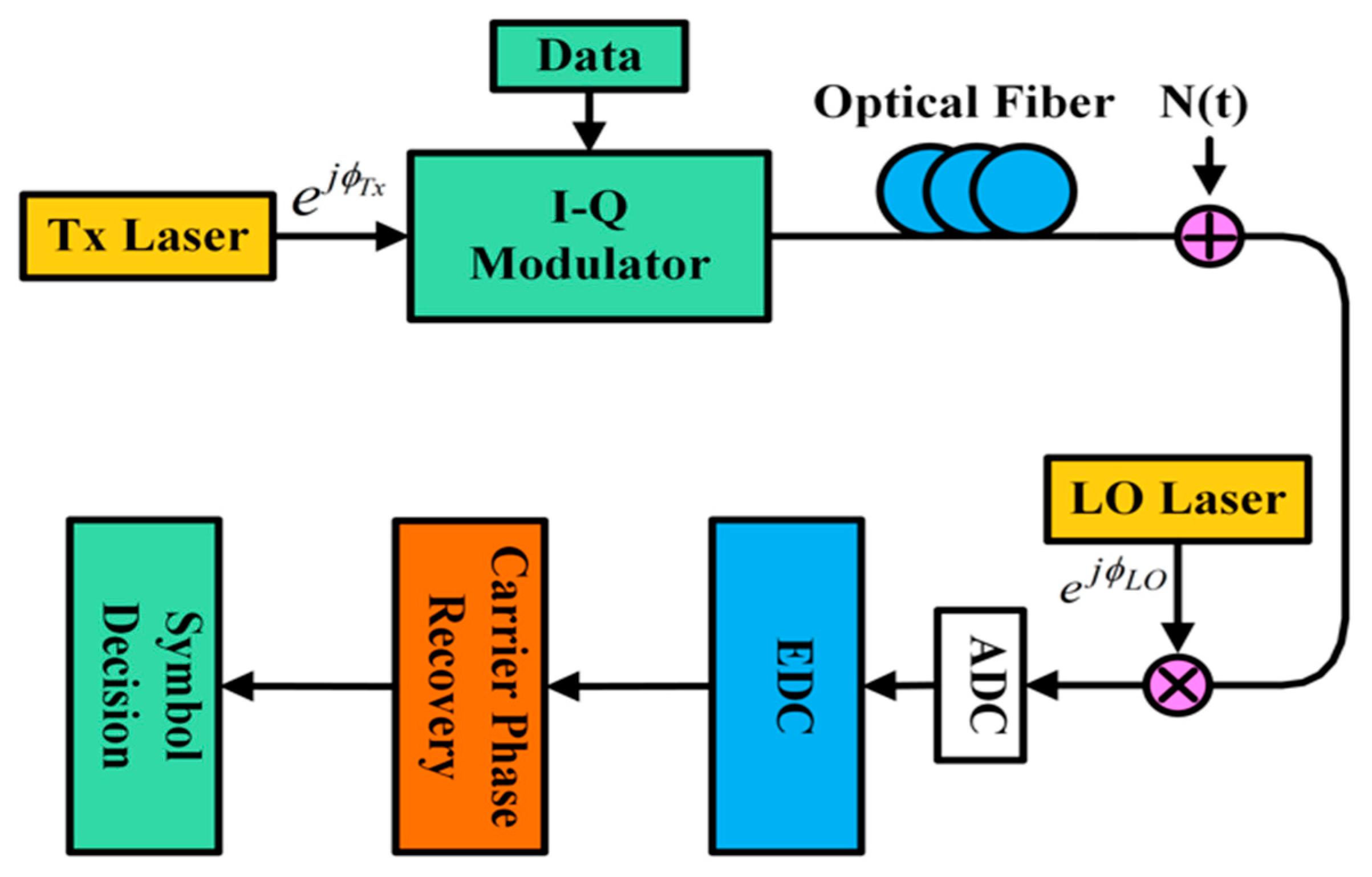
2. EEPN in Optical Communication Systems
3. CPR Using One-Tap NLMS
4. Differential Carrier Phase Recovery
5. Transmission Setup with RF Pilot Tone Scheme
6. Results and Analyses
7. Discussions
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kaminow, I.; Li, T.; Willner, A.E. Optical Fiber Telecommunications VIA: Components and Subsystems, 6th ed.; Academic Press Publisher: Oxford, UK, 2013. [Google Scholar]
- Ip, E.; Lau, A.P.T.; Barros, D.J.F.; Kahn, J.M. Coherent detection in optical fiber systems. Opt. Express 2008, 16, 753–791. [Google Scholar] [CrossRef] [PubMed]
- Winzer, P.J.; Essiambre, R.J. Advanced modulation formats for high-capacity optical transport networks. J. Lightwave Technol. 2006, 24, 4711–4728. [Google Scholar] [CrossRef]
- Savory, S.J. Digital coherent optical receivers: Algorithms and subsystems. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1164–1179. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Xu, T. Advanced DSP for coherent optical fiber communication. App. Sci. 2019, 9, 4192. [Google Scholar] [CrossRef]
- Mori, Y.; Zhang, C.; Igarashi, K.; Katoh, K.; Kikuchi, K. Unrepeated 200 km transmission of 40-Gbit/s 16-QAM signals using digital coherent receiver. Opt. Express 2009, 17, 1435–1441. [Google Scholar] [CrossRef]
- Nakamura, M.; Kamio, Y.; Miyazaki, T. Pilot-carrier based linewidth-tolerant 8PSK self-homodyne using only one modulator. In Proceedings of the 33rd European Conference and Exhibition of Optical Communication, Berlin, Germany, 16–20 September 2007. [Google Scholar]
- Cai, Y.; Gao, X.; Ling, Y.; Xu, B.; Qiu, K. RF pilot tone phase noise cancellation based on DD-MZM SSB modulation for optical heterodyne RoF link. Opt. Commun. 2020, 454, 124502. [Google Scholar] [CrossRef]
- Jacobsen, G.; Xu, T.; Popov, S.; Li, J.; Friberg, A.T.; Zhang, Y. Receiver implemented RF pilot tone phase noise mitigation in coherent optical nPSK and nQAM systems. Opt. Express 2011, 19, 14487–14494. [Google Scholar] [CrossRef]
- Shieh, W.; Ho, K.P. Equalization-enhanced phase noise for coherent detection systems using electronic digital signal processing. Opt. Express 2008, 16, 15718–15727. [Google Scholar] [CrossRef]
- Xie, C. Local oscillator phase noise induced penalties in optical coherent detection systems using electronic chromatic dispersion compensation. In Proceedings of the 2009 Conference on Optical Fiber Communication-Incudes post deadline papers, San Diego, CA, USA, 29 May 2009. [Google Scholar]
- Lau, A.P.T.; Shen, T.S.R.; Shieh, W.; Ho, K.P. Equalization-enhanced phase noise for 100 Gb/s transmission and beyond with coherent detection. Opt. Express 2010, 18, 17239–17251. [Google Scholar] [CrossRef]
- Xu, T.; Liga, G.; Lavery, D.; Thomsen, B.C.; Savory, S.J.; Killey, R.I.; Bayvel, P. Equalization enhanced phase noise in Nyquist-spaced superchannel transmission systems using multi-channel digital back-propagation. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef]
- Zhuge, Q.; Xu, X.; El-Sahn, Z.A.; Mousa-Pasandi, M.E.; Morsy-Osman, M.; Chagnon, M.; Qiu, M.; Plant, D.V. Experimental investigation of the equalization-enhanced phase noise in long haul 56 Gbaud DP-QPSK systems. Opt. Express 2012, 20, 13841–13846. [Google Scholar] [CrossRef] [PubMed]
- Fatadin, I.; Savory, S.J. Impact of phase to amplitude noise conversion in coherent optical systems with digital dispersion compensation. Opt. Express 2010, 18, 16273–16278. [Google Scholar] [CrossRef] [PubMed]
- Kakkar, A.; Navarro, J.R.; Schatz, R.; Louchet, H.; Pang, X.; Ozolins, O.; Jacobsen, G.; Popov, S. Comprehensive study of equalization-enhanced phase noise in coherent optical systems. J. Lightwave Technol. 2015, 33, 4834–4841. [Google Scholar] [CrossRef]
- Xu, T.; Jacobsen, G.; Popov, S.; Li, J.; Friberg, A.T.; Zhang, Y. Carrier phase estimation methods in coherent optical transmission systems influenced by equalization enhanced phase noise. Opt. Commun. 2013, 293, 54–60. [Google Scholar] [CrossRef]
- Colavolpe, G.; Foggi, T.; Forestieri, E.; Secondini, M. Impact of phase noise and compensation techniques in coherent optical systems. J. Lightwave Technol. 2011, 29, 2790–2800. [Google Scholar] [CrossRef]
- Xu, T.; Jacobsen, G.; Popov, S.; Li, J.; Friberg, A.T.; Zhang, Y. Analytical estimation of phase noise influence in coherent transmission system with digital dispersion equalization. Opt. Express 2011, 19, 7756–7768. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Jacobsen, G.; Popov, S.; Li, J.; Wang, K.; Friberg, A.T. Normalized LMS digital filter for chromatic dispersion equalization in 112-Gbit/s PDM-QPSK coherent optical transmission system. Opt. Commun. 2010, 283, 963–967. [Google Scholar] [CrossRef]
- Fatadin, I.; Ives, D.; Savory, S.J. Differential carrier phase recovery for QPSK optical coherent systems with integrated tunable lasers. Opt. Express 2013, 21, 10166–10171. [Google Scholar] [CrossRef]
- Savory, S.J. Digital filters for coherent optical receivers. Opt. Express 2008, 16, 804–817. [Google Scholar] [CrossRef]
- Kudo, R.; Kobayashi, T.; Ishihara, K.; Takatori, Y.; Sano, A.; Miyamoto, Y. Coherent optical single carrier transmission using overlap frequency domain equalization for long-haul optical systems. J. Lightwave Technol. 2009, 27, 3721–3728. [Google Scholar] [CrossRef]
- Jacobsen, G.; Xu, T.; Popov, S.; Sergeyev, S. Study of EEPN mitigation using modified RF pilot and Viterbi-Viterbi based phase noise compensation. Opt. Express 2013, 21, 12351–12362. [Google Scholar] [CrossRef] [PubMed]
- Ly-Gagnon, D.S.; Tsukamoto, S.; Katoh, K.; Kikuchi, K. Coherent detection of optical quadrature phase-shift keying signals with carrier phase estimation. J. Lightwave Technol. 2006, 24, 12–21. [Google Scholar] [CrossRef]
- Viterbi, A.J.; Viterbi, A.M. Nonlinear estimation of PSK-modulated carrier phase with application to burst digital transmission. IEEE Trans. Inf. Theory 1983, 29, 543–551. [Google Scholar] [CrossRef]
- Liga, G.; Xu, T.; Alvarado, A.; Killey, R.I.; Bayvel, P. On the performance of multichannel digital backpropagation in high-capacity long-haul optical transmission. Opt. Express 2014, 22, 30053–30062. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maher, R.; Xu, T.; Galdion, L.; Sato, M. Spectrally shaped DP-16QAM super-channel transmission with multi-channel digital back propagation. Sci. Rep. 2015, 5, 08214. [Google Scholar] [CrossRef] [PubMed]
- Ho, K.P.; Lau, A.P.T.; Shieh, W. Equalization-enhanced phase noise induced timing jitter. Opt. Lett. 2011, 36, 585–587. [Google Scholar] [CrossRef]
- Nakamura, M.; Kamio, Y.; Miyazaki, T. Linewidth-tolerant real-time 40-Gbit⁄s 16-QAM self-homodyne detection using a pilot carrier and ISI suppression based on electronic digital processing. Opt. Lett. 2010, 35, 13–15. [Google Scholar] [CrossRef]
- Nakamura, M.; Kamio, Y.; Miyazaki, T. Linewidth-tolerant real-time 10-Gbit⁄s 16-QAM transmission using a pilot-carrier based phase-noise cancelling technique. Opt. Express 2008, 16, 10611–10616. [Google Scholar] [CrossRef]
- Randel, S.; Adhikari, S.; Jansen, S.L. Analysis of RF-pilot-based phase noise compensation for coherent optical OFDM systems. IEEE Photon. Technol. Lett. 2010, 22, 1288–1290. [Google Scholar] [CrossRef]
- Ip, E.; Kahn, J.M. Digital equalization of chromatic dispersion and polarization mode dispersion. J. Lightwave Technol. 2007, 25, 2033–2043. [Google Scholar] [CrossRef]
- Liga, G.; Czegledi, C.B.; Xu, T.; Agrell, E.; Killey, R.I.; Bayvel, P. Ultra-wideband nonlinearity compensation performance in the presence of PMD. In Proceedings of the 42nd European Conference on Optical Communication, Dusseldorf, Germany, 5 December 2016. [Google Scholar]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, T.; Jin, C.; Zhang, S.; Jacobsen, G.; Popov, S.; Leeson, M.; Liu, T. Phase Noise Cancellation in Coherent Communication Systems Using a Radio Frequency Pilot Tone. Appl. Sci. 2019, 9, 4717. https://doi.org/10.3390/app9214717
Xu T, Jin C, Zhang S, Jacobsen G, Popov S, Leeson M, Liu T. Phase Noise Cancellation in Coherent Communication Systems Using a Radio Frequency Pilot Tone. Applied Sciences. 2019; 9(21):4717. https://doi.org/10.3390/app9214717
Chicago/Turabian StyleXu, Tianhua, Cenqin Jin, Shuqing Zhang, Gunnar Jacobsen, Sergei Popov, Mark Leeson, and Tiegen Liu. 2019. "Phase Noise Cancellation in Coherent Communication Systems Using a Radio Frequency Pilot Tone" Applied Sciences 9, no. 21: 4717. https://doi.org/10.3390/app9214717
APA StyleXu, T., Jin, C., Zhang, S., Jacobsen, G., Popov, S., Leeson, M., & Liu, T. (2019). Phase Noise Cancellation in Coherent Communication Systems Using a Radio Frequency Pilot Tone. Applied Sciences, 9(21), 4717. https://doi.org/10.3390/app9214717






