Validation of a Discrete Element Method (DEM) Model of the Grinding Media Dynamics within an Attritor Mill Using Positron Emission Particle Tracking (PEPT) Measurements
Abstract
:1. Introduction
2. Material and Methods
2.1. Experimental Setup: Attritor Mill HD01 and Positron Emission Particle Tracking (PEPT)
2.2. Positron Emission Particle Tracking (PEPT)
Data Processing: Tracer Location Reconstruction
2.3. DEM and Simulation Conditions
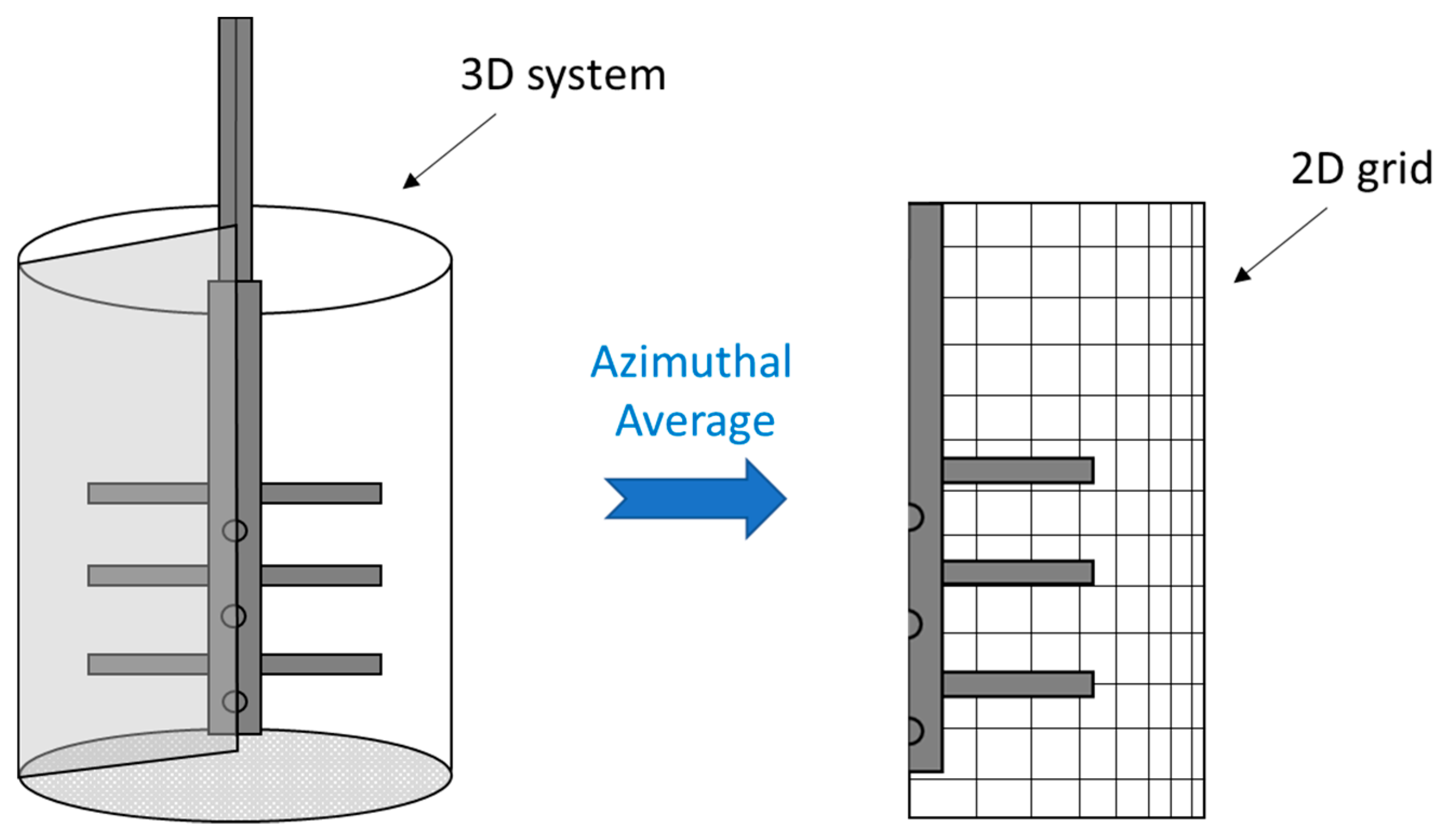
DEM Data Postprocessing Using the Coarse Graining Method
3. Results and Discussion
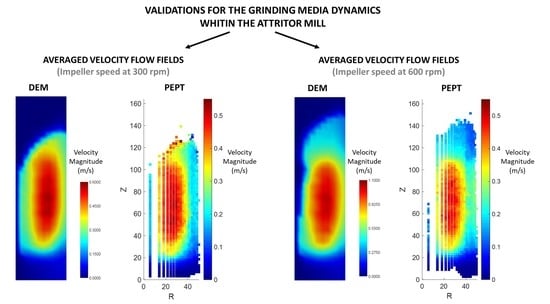
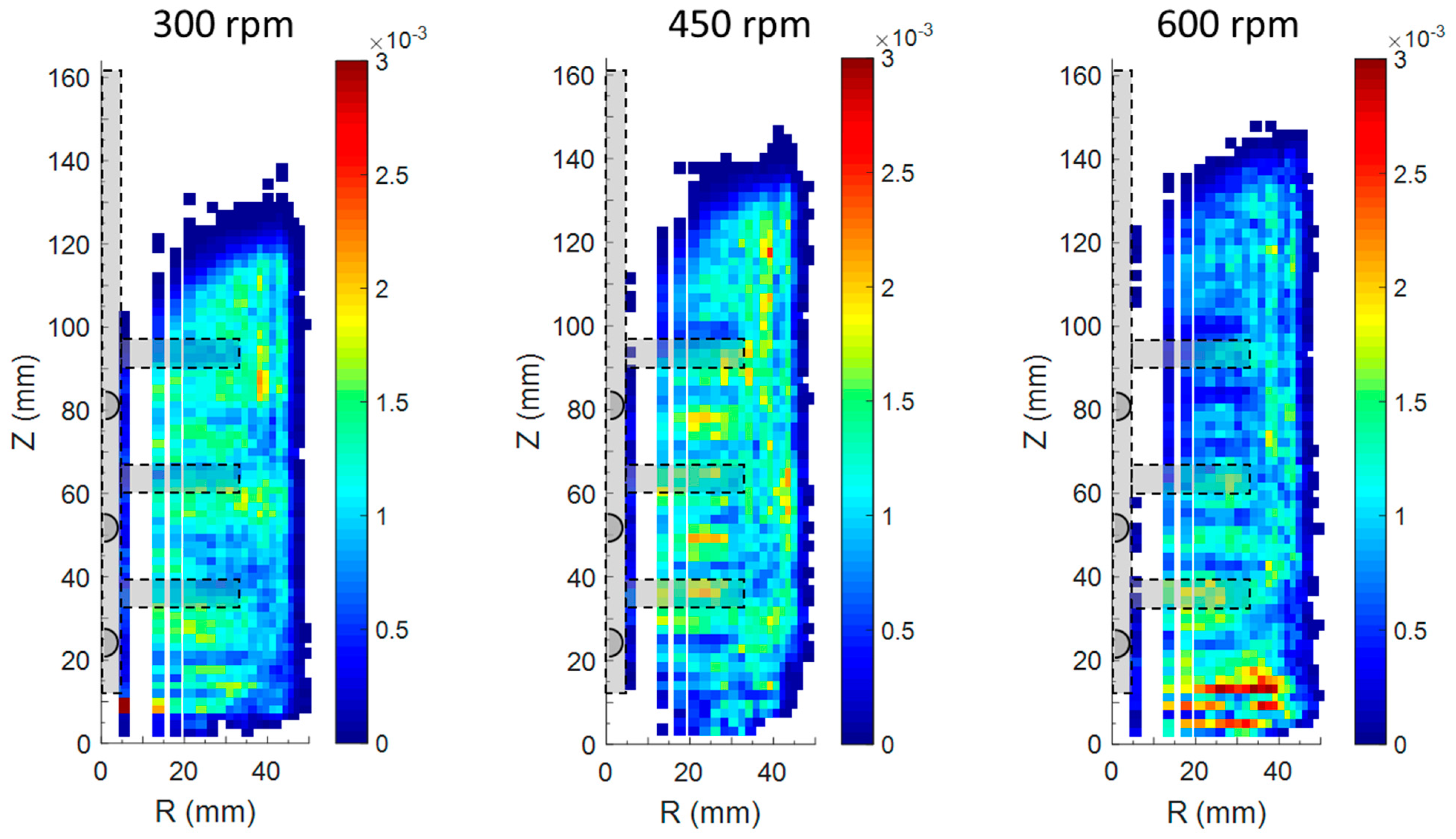
3.1. Effect of Impeller Speed Evaluated from PEPT Experiments
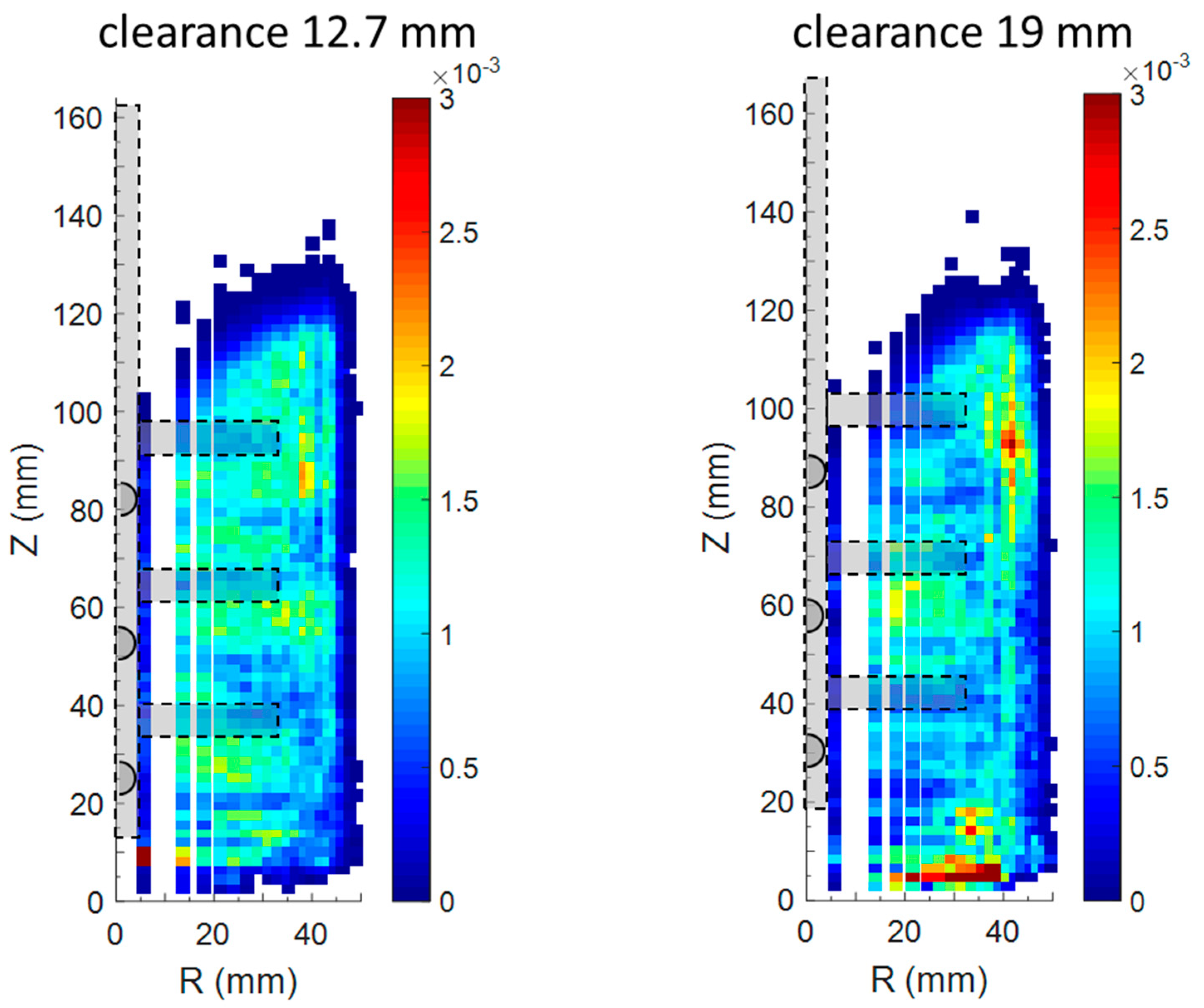
3.2. Effect of the Impeller Clearance Evaluated from PEPT Experiments
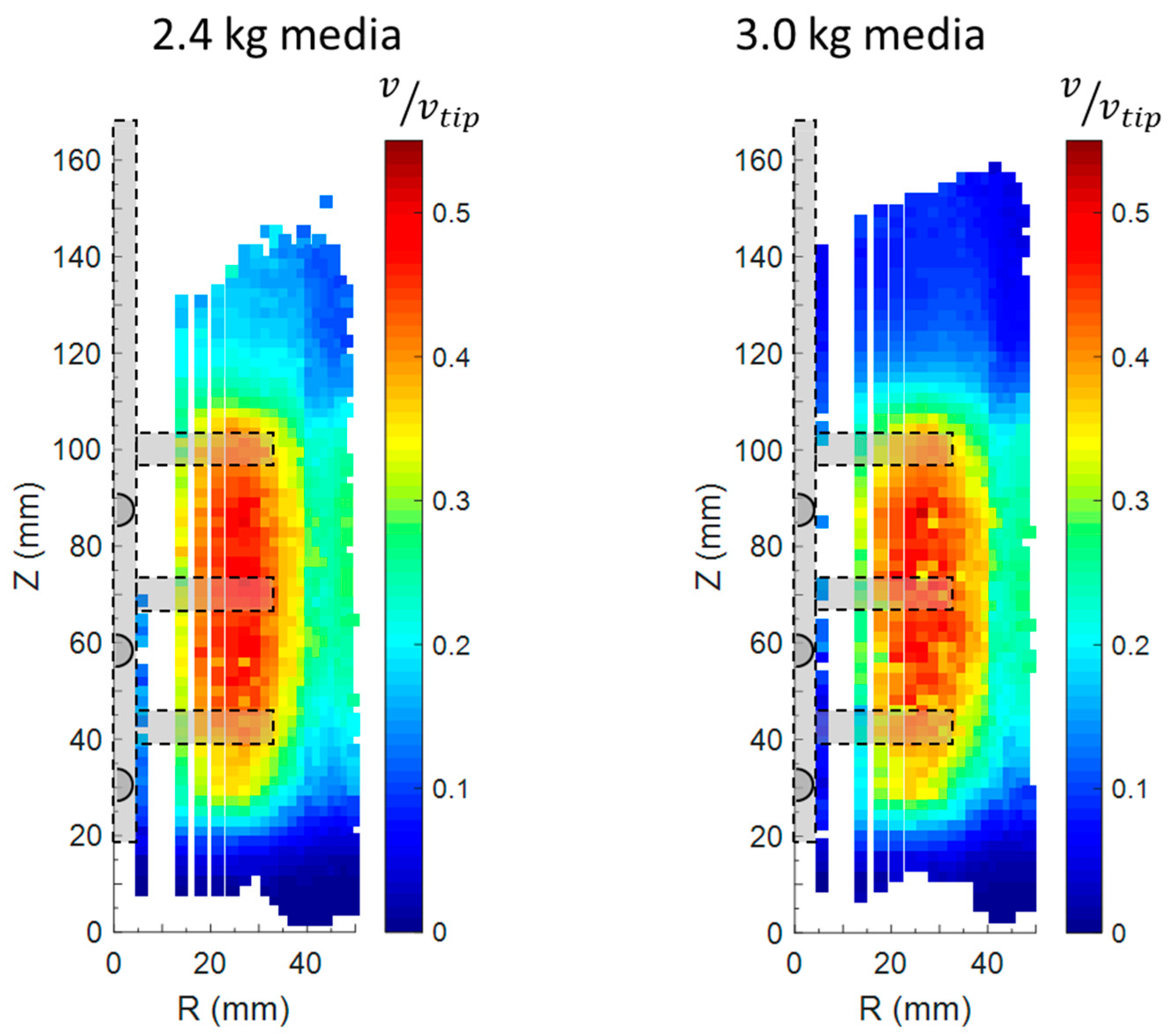
3.3. Effect of the Media Loading Evaluated from PEPT Experiments
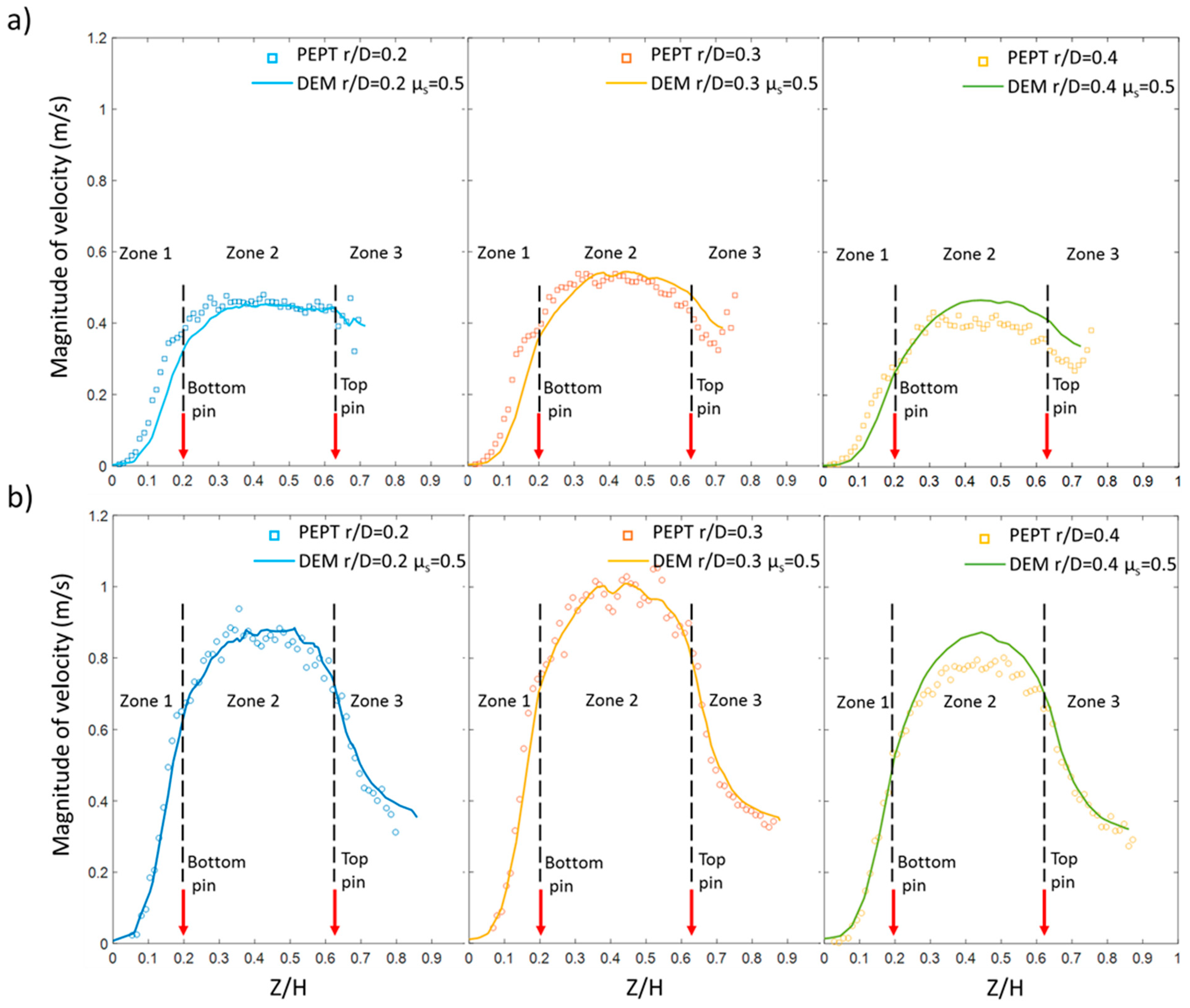
4. Validation of a Static Friction Adjusted-DEM Model by Using Positron Emission Particle Tracking (PEPT) Measurements
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jankovic, A. Variables affecting the fine grinding of minerals using stirred mills. Miner. Eng. 2003, 16, 337–345. [Google Scholar] [CrossRef]
- Shi, F.; Morrison, R.; Cervellin, A.; Burns, F.; Musa, F. Comparison of energy efficiency between ball mills and stirred mills in coarse grinding. Miner. Eng. 2009, 22, 673–680. [Google Scholar] [CrossRef]
- Cleary, P.W.; Sinnott, M.D.; Pereira, G.G. Computational prediction of performance for a full scale Isamill: Part 1—Media motion and energy utilisation in a dry mill. Miner. Eng. 2015, 7, 220–238. [Google Scholar] [CrossRef]
- Altun, O.; Benzer, H.; Enderle, U. Effects of operating parameters on the efficiency of dry stirred milling. Miner. Eng. 2013, 43, 58–66. [Google Scholar] [CrossRef]
- Rydin, R.W.; Maurice, D.; Courtney, T.H. Milling dynamics: Part I. Attritor dynamics: Results of a cinematographic study. Metall. Trans. A 1993, 24, 175–185. [Google Scholar] [CrossRef]
- Govender, I.; Cleary, P.W.; Mainza, A.N. Comparisons of PEPT derived charge features in wet milling environments with a friction-adjusted DEM model. Chem. Eng. Sci. 2013, 97, 162–175. [Google Scholar] [CrossRef]
- Rosenkranz, S.; Breitung-Faes, S.; Kwade, A. Experimental investigations and modelling of the ball motion in planetary ball mills. Powder Technol. 2011, 212, 224–230. [Google Scholar] [CrossRef]
- Hawkesworth, M.R.; Parker, D.J.; Fowles, P.; Crilly, J.F.; Jefferies, N.L.; Jonkers, G. Nonmedical applications of a positron camera, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers. Detect. Assoc. Equip. 1991, 310, 423–434. [Google Scholar] [CrossRef]
- Conway-Baker, J.; Barley, R.W.; Williams, R.A.; Jia, X.; Kostuch, J.; McLoughlin, B.; Parker, D.J. Measurement of the motion of grinding media in a vertically stirred mill using positron emission particle tracking (PEPT). Miner. Eng. 2002, 15, 53–59. [Google Scholar] [CrossRef]
- Barley, R.W.; Conway-Baker, J.; Pascoe, R.D.; Kostuch, J.; McLoughlin, B.; Parker, D.J. Measurement of the motion of grinding media in a vertically stirred mill using positron emission particle tracking (PEPT) Part II. Miner. Eng. 2004, 17, 1179–1187. [Google Scholar] [CrossRef]
- Riley, M.; Pinkney, S.; Blackburn, S.; Rowson, N.A. Spatial distributions of media kinetic energy as measured by positron emission particle tracking in a vertically stirred media mill. Miner. Eng. 2016, 98, 177–186. [Google Scholar] [CrossRef]
- Yang, Y.; Rowson, N.; Tamblyn, R.; Ingram, A. Effect of operating parameters on fine particle grinding in a vertically stirred media mill. Sep. Sci. Technol. 2017, 52. [Google Scholar] [CrossRef]
- Wilkinson, S.K.; Turnbull, S.A.; Yan, Z.; Stitt, E.H.; Marigo, M. A parametric evaluation of powder flowability using a Freeman rheometer through statistical and sensitivity analysis: A discrete element method (DEM) study. Comput. Chem. Eng. 2017, 97, 161–174. [Google Scholar] [CrossRef]
- Yan, Z.; Wilkinson, S.K.; Stitt, E.H.; Marigo, M. Investigating mixing and segregation using discrete element modelling (DEM) in the Freeman FT4 rheometer. Int. J. Pharm. 2016, 513, 38–48. [Google Scholar] [CrossRef]
- Marigo, M.; Davies, M.; Leadbeater, T.; Cairns, D.L.; Ingram, A.; Stitt, E.H. Application of Positron Emission Particle Tracking (PEPT) to validate a Discrete Element Method (DEM) model of granular flow and mixing in the Turbula mixer. Int. J. Pharm. 2013, 446, 46–58. [Google Scholar] [CrossRef]
- Pantaleev, S.; Yordanova, S.; Janda, A.; Marigo, M.; Ooi, J.Y. An experimentally validated DEM study of powder mixing in a paddle blade mixer. Powder Technol. 2017, 311, 287–302. [Google Scholar] [CrossRef]
- Yan, Z.; Wilkinson, S.K.; Stitt, E.H.; Marigo, M. Discrete element modelling (DEM) input parameters: Understanding their impact on model predictions using statistical analysis. Comp. Part. Mech. 2015, 2, 283–299. [Google Scholar] [CrossRef]
- Weerasekara, N.S.; Powell, M.S.; Cleary, P.W.; Tavares, L.M.; Evertsson, M.; Morrison, R.D.; Quist, J.; Carvalho, R.M. The contribution of DEM to the science of comminution. Powder Technol. 2013, 248, 3–24. [Google Scholar] [CrossRef]
- Powell, M.S.; Govender, I.; McBride, A.T. Applying DEM outputs to the unified comminution model. Miner. Eng. 2008, 21, 744–750. [Google Scholar] [CrossRef]
- Yang, R.Y.; Jayasundara, C.T.; Yu, A.B.; Curry, D. DEM simulation of the flow of grinding media in IsaMill. Miner. Eng. 2006, 19, 984–994. [Google Scholar] [CrossRef]
- Cleary, P.W.; Morrison, R.D. Understanding fine ore breakage in a laboratory scale ball mill using DEM. Miner. Eng. 2011, 24, 352–366. [Google Scholar] [CrossRef]
- Sinnott, M.; Cleary, P.W.; Morrison, R. Analysis of stirred mill performance using DEM simulation: Part 1– Media motion, energy consumption and collisional environment. Miner. Eng. 2006, 19, 1537–1550. [Google Scholar] [CrossRef]
- Santhanam, P.R.; Ermoline, A.; Dreizin, E.L. Discrete element model for an attritor mill with impeller responding to interactions with milling balls. Chem. Eng. Sci. 2013, 101, 366–373. [Google Scholar] [CrossRef]
- Daraio, D.; Villoria, J.; Ingram, A.; Stitt, E.H.; Marigo, M. Investigating grinding media dynamics inside a vertical stirred mill using the discrete element method: Effect of impeller arm length. Powder Technol. 2019. [Google Scholar] [CrossRef]
- Santhanam, P.R.; Dreizin, E.L. Predicting conditions for scaled-up manufacturing of materials prepared by ball milling. Powder Technol. 2012, 221, 403–411. [Google Scholar] [CrossRef]
- Cleary, P.W.; Owen, P.J. Using DEM to understand scale-up for a HICOM® mill. Miner. Eng. 2016, 92, 86–109. [Google Scholar] [CrossRef]
- Powell, M.S.; Weerasekara, N.S.; Cole, S.; LaRoche, R.D.; Favier, J. DEM modelling of liner evolution and its influence on grinding rate in ball mills. Miner. Eng. 2011, 24, 341–351. [Google Scholar] [CrossRef]
- Rikio, S.; Junya, K.; Fumio, S. Analysis of Effect of Pin Configuration on Beads Motion in a Stirred Mill by DEM. J. Soc. Powder Technol. Jpn. 2009, 46, 180–186. [Google Scholar]
- Zeng, Y.; Jia, F.; Chen, P.; Qiu, H.; Han, Y.; Meng, X.; Xiao, Y. Effects of convex rib height on spherical particle milling in a lab-scale horizontal rice mill. Powder Technol. 2019, 342, 1–10. [Google Scholar] [CrossRef]
- Jayasundara, C.T.; Yang, R.Y.; Guo, B.Y.; Yu, A.B.; Govender, I.; Mainza, A.; van der Westhuizen, A.; Rubenstein, J. CFD–DEM modelling of particle flow in IsaMills—Comparison between simulations and PEPT measurements. Miner. Eng. 2011, 24, 181–187. [Google Scholar] [CrossRef]
- Ashrafizadeh, H.; Ashrafizaadeh, M. Influence of processing parameters on grinding mechanism in planetary mill by employing discrete element method. Adv. Powder Technol. 2012, 23, 708–716. [Google Scholar] [CrossRef]
- Nakamura, H.; Fujii, H.; Watano, S. Scale-up of high shear mixer-granulator based on discrete element analysis. Powder Technol. 2013, 236, 149–156. [Google Scholar] [CrossRef]
- Hassanpour, A.; Tan, H.; Bayly, A.; Gopalkrishnan, P.; Ng, B.; Ghadiri, M. Analysis of particle motion in a paddle mixer using Discrete Element Method (DEM). Powder Technol. 2011, 206, 189–194. [Google Scholar] [CrossRef]
- Pasha, M.; Hassanpour, A.; Ahmadian, H.; Tan, H.S.; Bayly, A.; Ghadiri, M. A comparative analysis of particle tracking in a mixer by discrete element method and positron emission particle tracking. Powder Technol. 2015, 270, 569–574. [Google Scholar] [CrossRef]
- Fan, X.; Parker, D.J.; Smith, M.D. Labelling a single particle for positron emission particle tracking using direct activation and ion-exchange techniques, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers. Detect. Assoc. Equip. 2006, 562, 345–350. [Google Scholar] [CrossRef]
- Parker, D.J.; Allen, D.A.; Benton, D.M.; Fowles, P.; McNeil, P.A.; Tan, M.; Beynon, T.D. Developments in particle tracking using the Birmingham Positron Camera, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers. Detect. Assoc. Equip. 1997, 392, 421–426. [Google Scholar] [CrossRef]
- Parker, D.J.; Forster, R.N.; Fowles, P.; Takhar, P.S. Positron emission particle tracking using the new Birmingham positron camera, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers. Detect. Assoc. Equip. 2002, 477, 540–545. [Google Scholar] [CrossRef]
- Parker, D.J.; Hawkesworth, M.R.; Broadbent, C.J.; Fowles, P.; Fryer, T.D.; McNeil, P.A. Industrial positron-based imaging: Principles and applications, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers. Detect. Assoc. Equip. 1994, 348, 583–592. [Google Scholar] [CrossRef]
- PEPT Date—University of Birmingham. Available online: https://www.birmingham.ac.uk/research/activity/physics/particle-nuclear/positron-imaging-centre/pept-data/pept-data.aspx (accessed on 7 October 2019).
- Chiti, F.; Bakalis, S.; Bujalski, W.; Barigou, M.; Eaglesham, A.; Nienow, A.W. Using positron emission particle tracking (PEPT) to study the turbulent flow in a baffled vessel agitated by a Rushton turbine: Improving data treatment and validation. Chem. Eng. Res. Des. 2011, 89, 1947–1960. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Jayasundara, C.T.; Yang, R.Y.; Yu, A.B. Effect of the size of media on grinding performance in stirred mills. Miner. Eng. 2012, 33, 66–71. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Wright, B.D.; Yang, R.Y.; Xu, B.H.; Yu, A.B. Rolling friction in the dynamic simulation of sandpile formation. Phys. A Stat. Mech. Appl. 1999, 269, 536–553. [Google Scholar] [CrossRef]
- Yang, R.Y.; Zou, R.P.; Yu, A.B. Microdynamic analysis of particle flow in a horizontal rotating drum. Powder Technol. 2003, 130, 138–146. [Google Scholar] [CrossRef]
- Cleary, P.W. Predicting charge motion, power draw, segregation and wear in ball mills using discrete element methods. Miner. Eng. 1998, 11, 1061–1080. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Soda, R.; Kano, J.; Saito, F. Application of DEM modified with enlarged particle model to simulation of bead motion in a bead mill. Particuology 2014, 14, 103–108. [Google Scholar] [CrossRef]
- Misra, A.; Cheung, J. Particle motion and energy distribution in tumbling ball mills. Powder Technol. 1999, 105, 222–227. [Google Scholar] [CrossRef]
- Weinhart, T.; Labra, C.; Luding, S.; Ooi, J.Y. Influence of coarse-graining parameters on the analysis of DEM simulations of silo flow. Powder Technol. 2016, 293, 138–148. [Google Scholar] [CrossRef]
- Babic, M. Average balance equations for granular materials. Int. J. Eng. Sci. 1997, 35, 523–548. [Google Scholar] [CrossRef]
- Goldhirsch, I. Stress, stress asymmetry and couple stress: From discrete particles to continuous fields. Granul. Matter 2010, 12, 239–252. [Google Scholar] [CrossRef]











| Dimensions (mm) | Material | |
|---|---|---|
| Mill chamber | Yttria-stabilised zirconia | |
| Height | 164 | |
| Diameter | 90 | |
| Impeller arms | Yttria-stabilised zirconia | |
| Diameter | 66 | |
| Grinding media | Yttria-stabilised zirconia | |
| Diameter | 5 |
| N | Impeller Speed (rpm) | Bead Loading (kg) | % Chamber Filling (volumetric) | Bottom Clearance (mm) |
|---|---|---|---|---|
| 1 | 600 | 3.0 | 77 | 12.7 |
| 2 | 300 | 3.0 | 77 | 12.7 |
| 3 | 300 | 3.0 | 77 | 15.9 |
| 4 | 300 | 2.4 | 61 | 19 |
| 5 | 600 | 2.4 | 61 | 19 |
| 6 | 600 | 3.0 | 77 | 19 |
| 7 | 300 | 3.0 | 77 | 19 |
| 8 | 450 | 2.7 | 69 | 19 |
| 9 | 300 | 2.4 | 61 | 12.7 |
| 10 | 450 | 2.4 | 61 | 12.7 |
| 11 | 600 | 2.4 | 61 | 12.7 |
| 12 | 300 | 2.7 | 69 | 15.9 |
| Material Parameters | Symbols | Values |
|---|---|---|
| Media ball radius (mm) | r | 2.5 |
| Media ball density (Kg/m3) | ρ | 5950 |
| Young modulus (Pa) | E | 2.1 × |
| Poisson’s ratio (-) | ν | 0.3 |
| Coefficient of restitution (-) | ε | 0.7 |
| Static friction coefficient (-) | μs | 0.15, 0.35, 0.50 |
| Rolling friction coefficient (-) | μr | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daraio, D.; Villoria, J.; Ingram, A.; Alexiadis, A.; Hugh Stitt, E.; Marigo, M. Validation of a Discrete Element Method (DEM) Model of the Grinding Media Dynamics within an Attritor Mill Using Positron Emission Particle Tracking (PEPT) Measurements. Appl. Sci. 2019, 9, 4816. https://doi.org/10.3390/app9224816
Daraio D, Villoria J, Ingram A, Alexiadis A, Hugh Stitt E, Marigo M. Validation of a Discrete Element Method (DEM) Model of the Grinding Media Dynamics within an Attritor Mill Using Positron Emission Particle Tracking (PEPT) Measurements. Applied Sciences. 2019; 9(22):4816. https://doi.org/10.3390/app9224816
Chicago/Turabian StyleDaraio, Domenico, Jose Villoria, Andrew Ingram, Alessio Alexiadis, E. Hugh Stitt, and Michele Marigo. 2019. "Validation of a Discrete Element Method (DEM) Model of the Grinding Media Dynamics within an Attritor Mill Using Positron Emission Particle Tracking (PEPT) Measurements" Applied Sciences 9, no. 22: 4816. https://doi.org/10.3390/app9224816
APA StyleDaraio, D., Villoria, J., Ingram, A., Alexiadis, A., Hugh Stitt, E., & Marigo, M. (2019). Validation of a Discrete Element Method (DEM) Model of the Grinding Media Dynamics within an Attritor Mill Using Positron Emission Particle Tracking (PEPT) Measurements. Applied Sciences, 9(22), 4816. https://doi.org/10.3390/app9224816