Numerical Simulation of a New Flow Field Design with Rib Grooves for a Proton Exchange Membrane Fuel Cell with a Serpentine Flow Field
Abstract
1. Introduction
2. Model Development
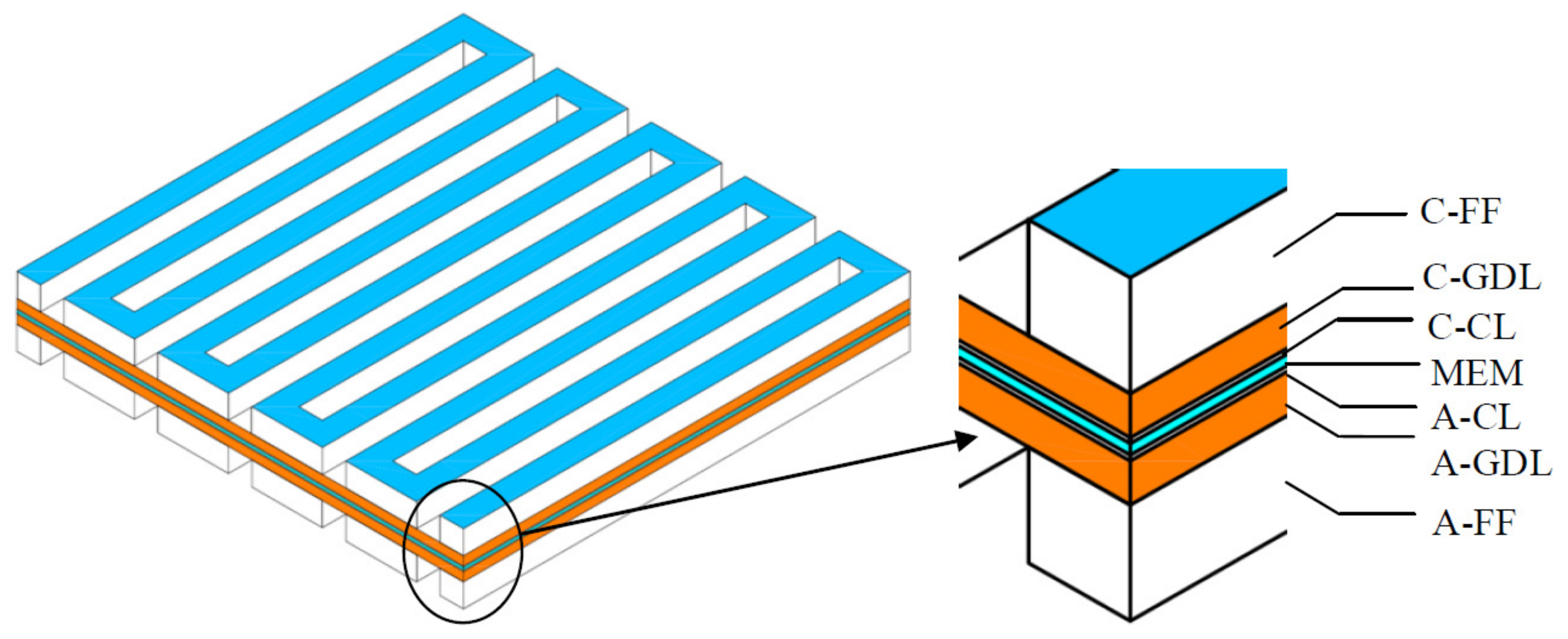
2.1. Model Geometry
2.2. Governing Equations
- (1)
- The porous media was isotropic and continuous;
- (2)
- The flow was assumed to be laminar inside the fuel cell due to the small Reynolds number in the flow field;
- (3)
- The fuel cells were insulated from the environment and worked at steady state conditions;
- (4)
- Reactant gases were ideal, incompressible, and had non-turbulent flow.
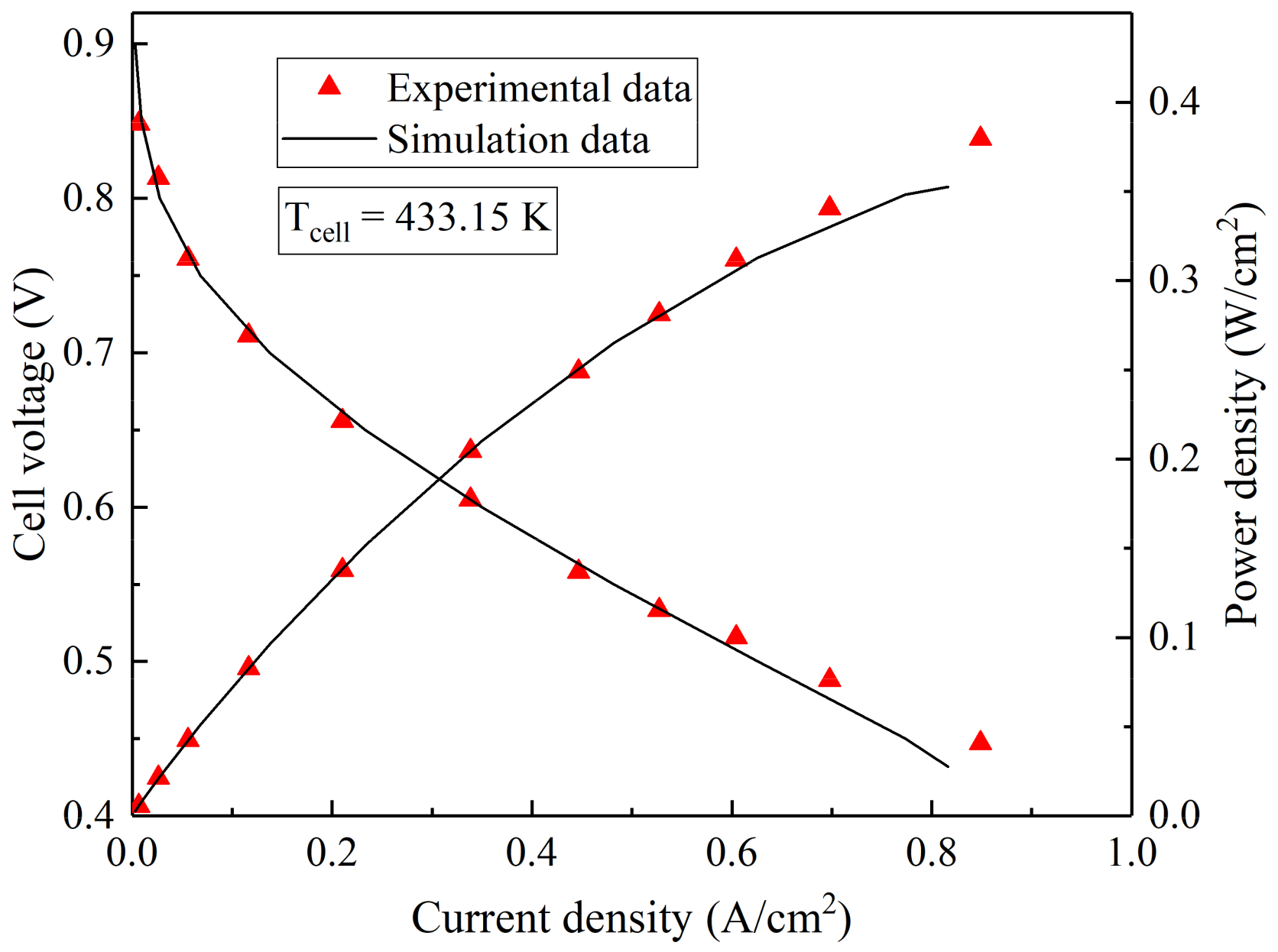
2.3. Model Verification
3. Results and Discussion
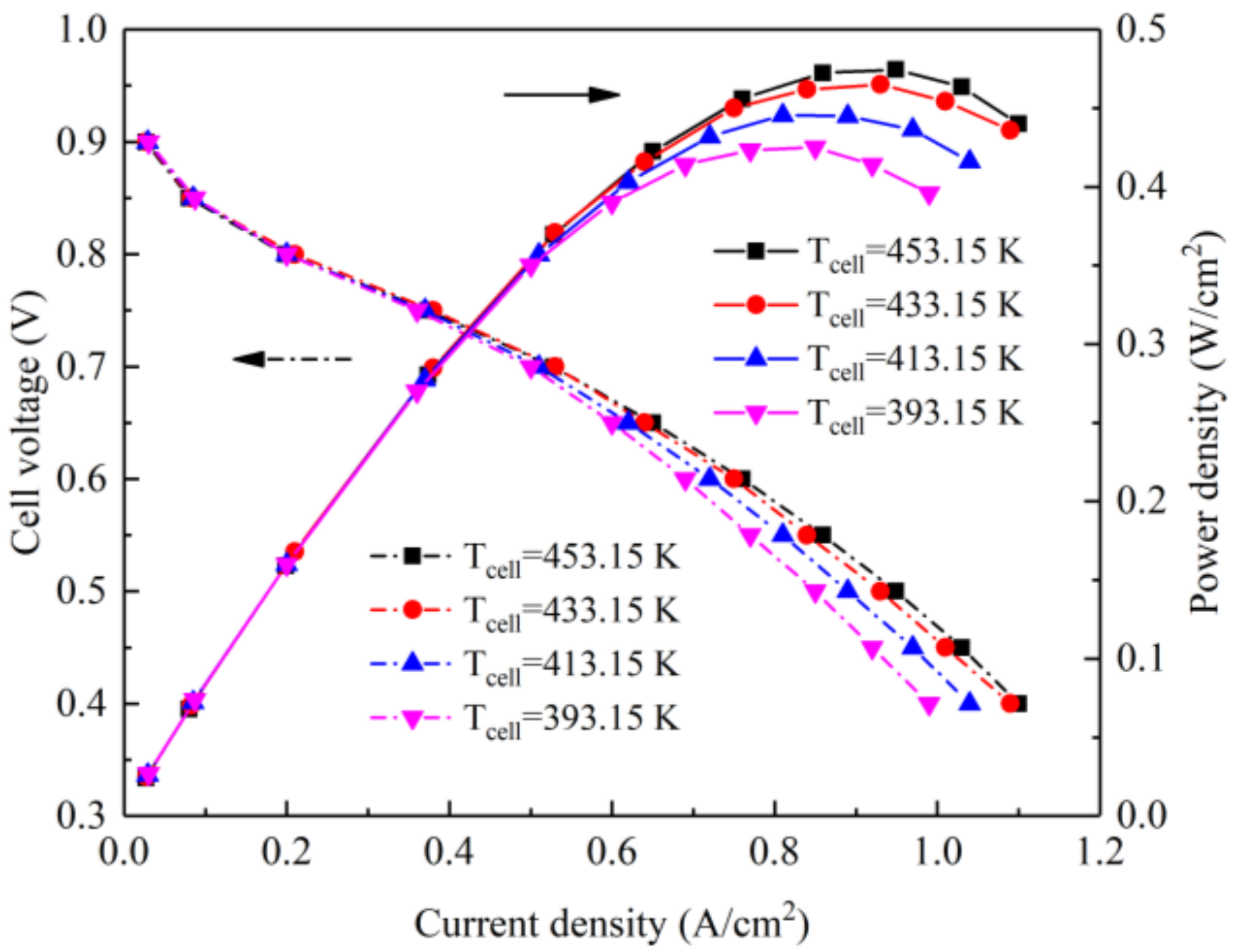
3.1. Effect of Temperature
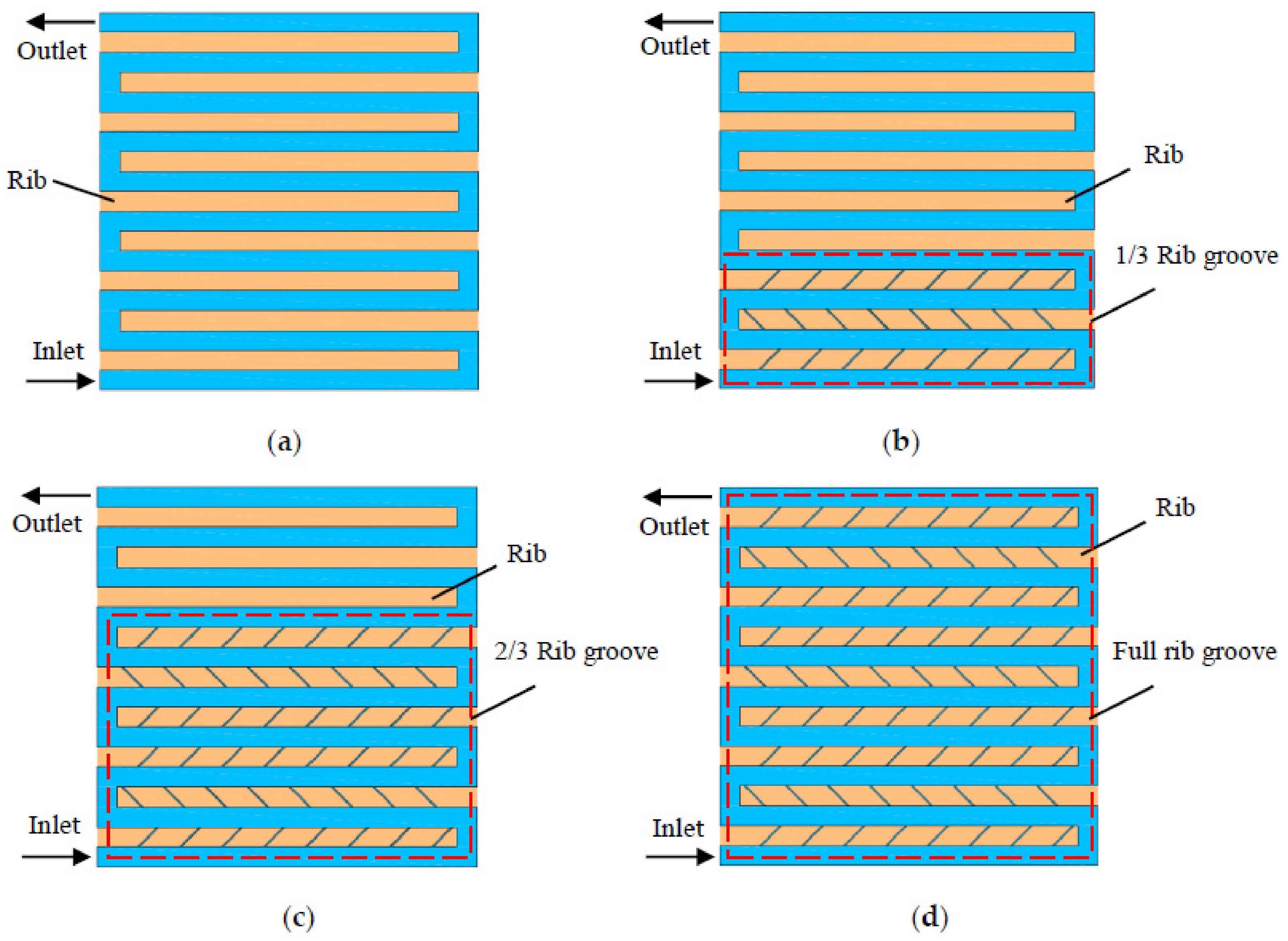
3.2. Effect of Rib Groove Designs
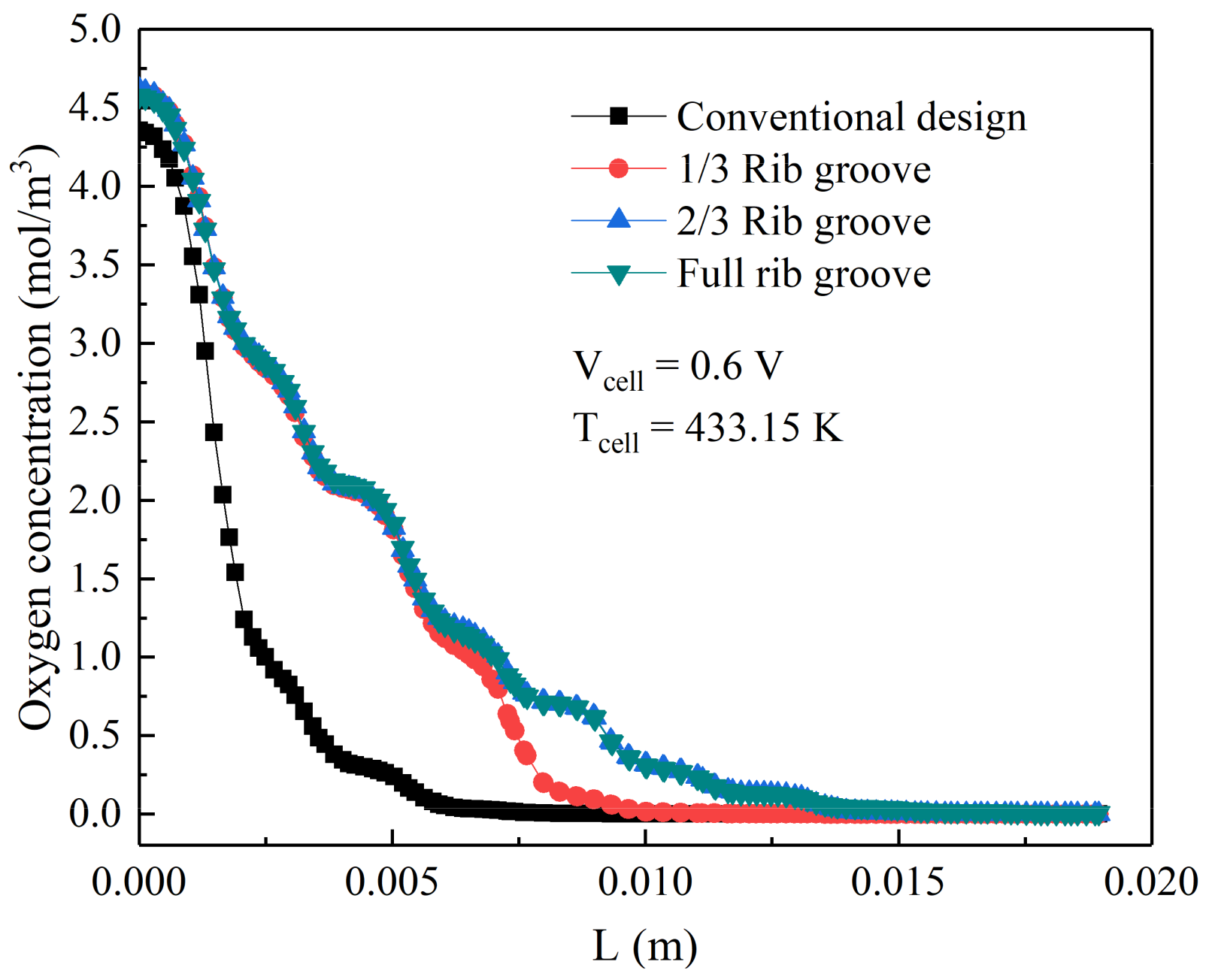
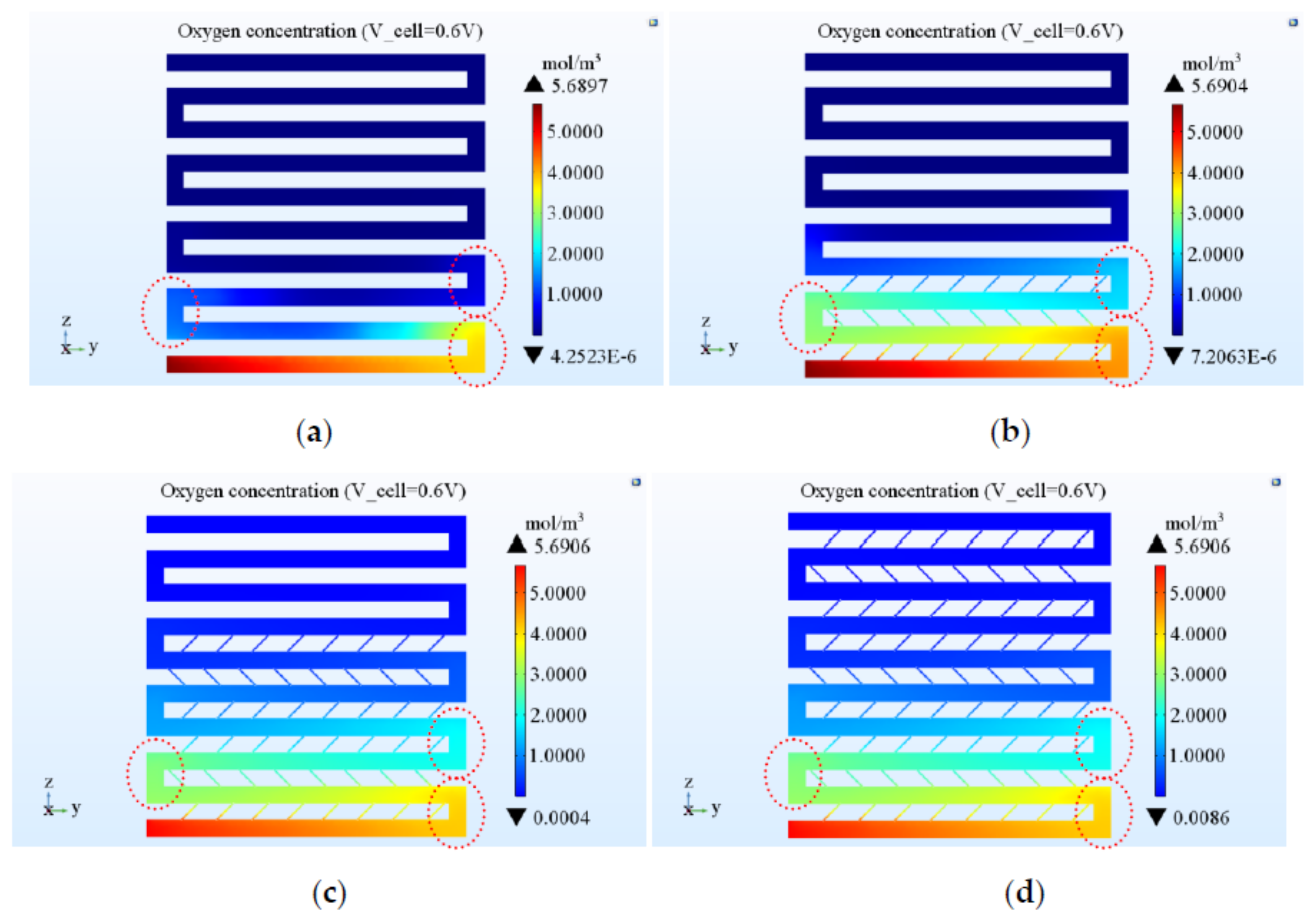
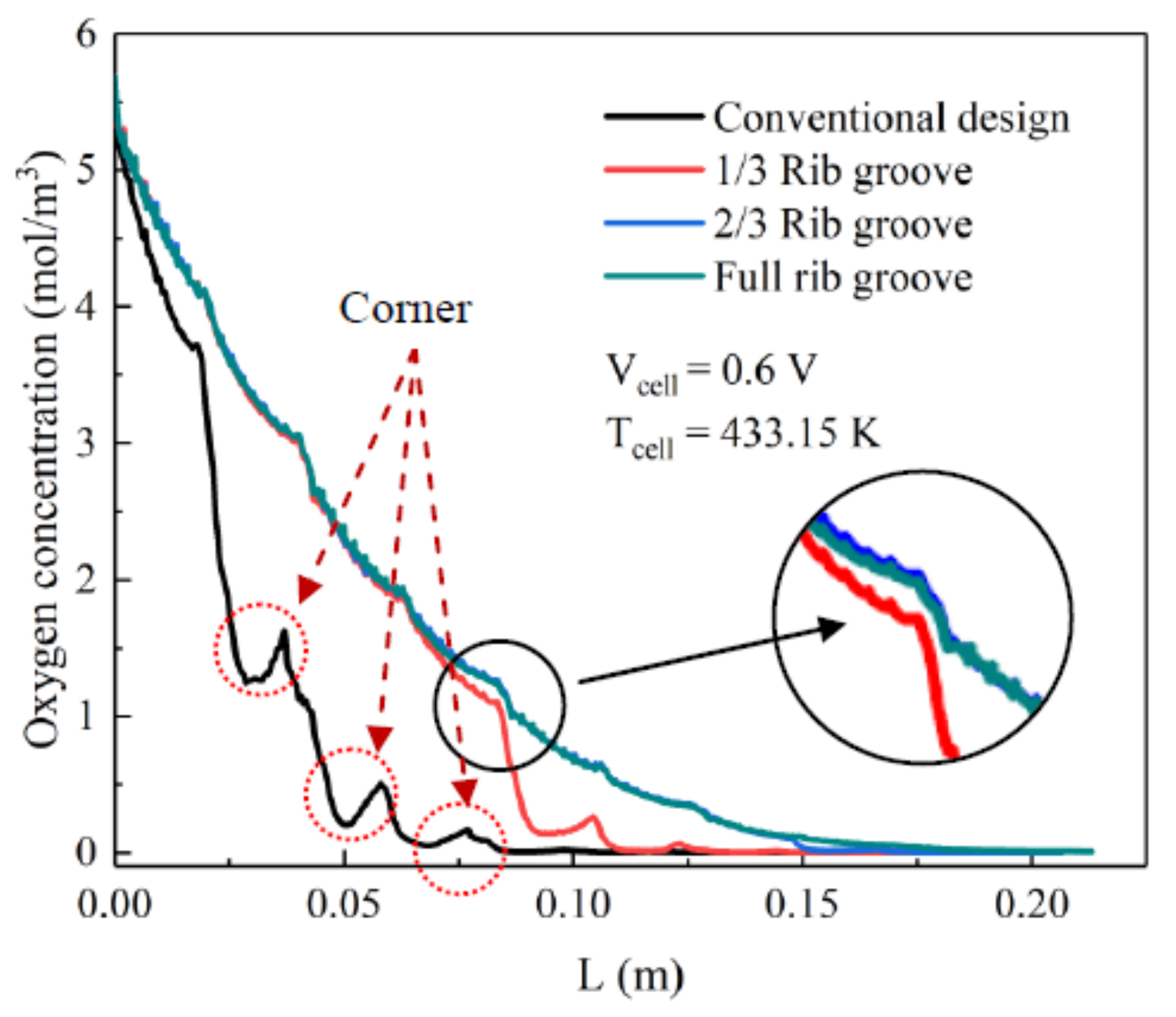
3.3. Distribution of Oxygen Concentration at the Cathode Side
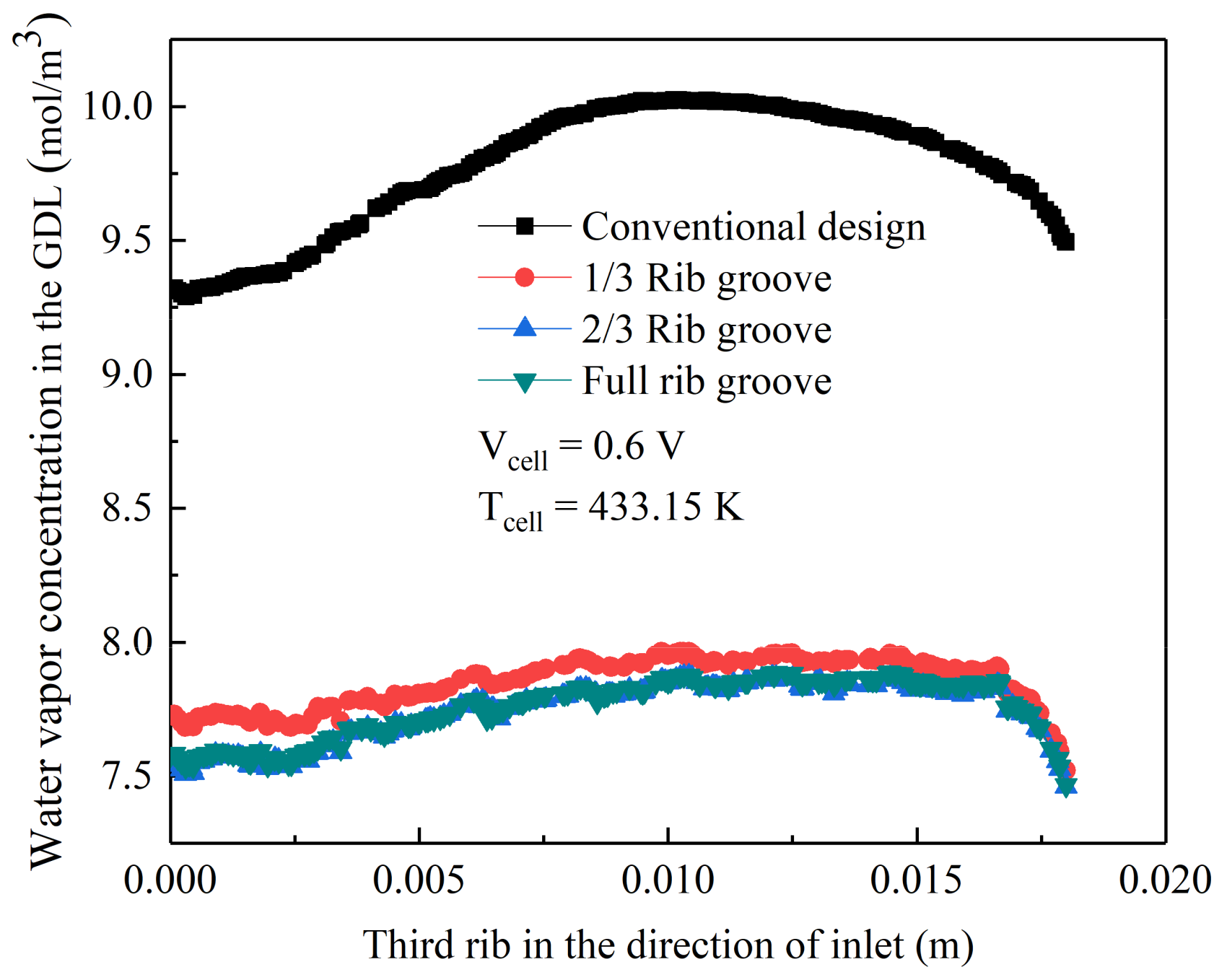
3.4. Distribution of Water Vapor
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| fluid density (kg/m3) | dynamic viscosity (Pa*s) | ||
| fluid velocity in the porous medium (m/s) | porosity of GDL | ||
| Laplace operator | effective permeability of GDL (m2) | ||
| pressure (Pa) | fluid velocity in the flow field (m/s) | ||
| exchange current density (A/m2) | cathode transfer coefficient | ||
| reference exchange current density (A/m2) | activation over-potential (V) | ||
| number of electrons transfer in the reaction | GDL thickness (m) | ||
| absolute temperature (K) | universal gas constant | ||
| reference oxygen concentration (mol/m3) | oxygen concentration (mol/m3) | ||
| open circuit voltage (V) | Faraday constant | ||
| operating voltage of the fuel cell (V) | limiting current density (A/m2) | ||
| lumped resistance (Ω*m2) | effective diffusion coefficient |
References
- Chen, W.; Liu, Y.; Xin, Q. Evaluation of a compression molded composite bipolar plate for direct methanol fuel cell. Int. J. Hydrogen Energy 2010, 35, 3783–3788. [Google Scholar] [CrossRef]
- Tsuchiya, H.; Kobayashi, O. Mass production cost of PEM fuel cell by learning curve. Int. J. Hydrogen Energy 2004, 29, 985–990. [Google Scholar] [CrossRef]
- Li, X.; Sabir, I. Review of bipolar plates in PEM fuel cells: Flow-field designs. Int. J. Hydrogen Energy 2005, 30, 359–371. [Google Scholar] [CrossRef]
- Spernjak, D.; Prasad, A.K.; Advani, S.G. In situ comparison of water content and dynamics in parallel, single-serpentine, and interdigitated flow fields of polymer electrolyte membrane fuel cells. J. Power Sources 2010, 195, 3553–3568. [Google Scholar] [CrossRef]
- Henriques, T.; César, B.; Branco, P.C. Increasing the efficiency of a portable PEM fuel cell by altering the cathode channel geometry: A numerical and experimental study. Appl. Energy 2010, 87, 1400–1409. [Google Scholar] [CrossRef]
- Perng, S.W.; Wu, H.W. Non-isothermal transport phenomenon and cell performance of a cathodic PEM fuel cell with a baffle plate in a tapered channel. Appl. Energy 2011, 88, 52–67. [Google Scholar] [CrossRef]
- Manso, A.P.; Marzo, F.F.; Barranco, J.; Garikano, X.; Mujika, M.G. Influence of geometric parameters of the flow fields on the performance of a PEM fuel cell. A review. Int. J. Hydrogen Energy 2012, 37, 15256–15287. [Google Scholar] [CrossRef]
- Bachman, J.; Santamaria, A.; Tang, H.Y.; Park, J.W. Investigation of polymer electrolyte membrane fuel cell parallel flow field with induced cross flow. J. Power Sources 2012, 198, 143–148. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, T.S. A new flow field design for polymer electrolyte-based fuel cells. Electrochem. Commun. 2007, 9, 497–503. [Google Scholar] [CrossRef]
- Wang, X.D.; Duan, Y.Y.; Yan, W.M. Novel serpentine-baffle flow field design for proton exchange membrane fuel cells. J. Power Sources 2007, 173, 210–221. [Google Scholar] [CrossRef]
- Santamaria, A.D.; Cooper, N.J.; Becton, M.K.; Park, J.W. Effect of channel length on interdigitated flow-field PEMFC performance: A computational and experimental study. Int. J. Hydrogen Energy 2013, 38, 16253–16263. [Google Scholar] [CrossRef]
- Cooper, N.J.; Santamaria, A.D.; Becton, M.K.; Park, J.W. Investigation of the performance improvement in decreasing aspect ratio interdigitated flow field PEMFCs. Energy Convers. Manag. 2017, 136, 307–317. [Google Scholar] [CrossRef]
- Ashorynejad, H.R.; Javaherdeh, K.; Van den Akker, H.E. The effect of pulsating pressure on the performance of a PEM fuel cell with a wavy cathode surface. Int. J. Hydrogen Energy 2016, 41, 14239–14251. [Google Scholar] [CrossRef][Green Version]
- AlRwashdeh, S.S.; Manke, I.; Markötter, H.; Haußmann, J.; Kardjilov, N.; Hilger, A.; Kermani, M.J.; Klages, M.; Al-Falahat, A.; Scholta, J.; et al. Neutron radiographic in operando investigation of water transport in polymer electrolyte membrane fuel cells with channel barriers. Energy Convers. Manag. 2017, 148, 604–610. [Google Scholar] [CrossRef]
- Kim, J.; Luo, G.; Wang, C.Y. Modeling two-phase flow in three-dimensional complex flow-fields of proton exchange membrane fuel cells. J. Power Sources 2017, 365, 419–429. [Google Scholar] [CrossRef]
- Zhang, G.; Fan, L.; Sun, J.; Jiao, K. A 3D model of PEMFC considering detailed multiphase flow and anisotropic transport properties. Int. J. Heat Mass Transf. 2017, 115, 714–724. [Google Scholar] [CrossRef]
- Heidary, H.; Kermani, M.J.; Prasad, A.K.; Advani, S.G.; Dabir, B. Numerical modelling of in-line and staggered blockages in parallel flow field channels of PEM fuel cells. Int. J. Hydrogen Energy 2017, 42, 2265–2277. [Google Scholar] [CrossRef]
- Liu, H.; Li, P.; Wang, K. Optimization of PEM fuel cell flow channel dimensions—Mathematic modeling analysis and experimental verification. Int. J. Hydrogen Energy 2013, 38, 9835–9846. [Google Scholar] [CrossRef]
- Wang, Y.; Yue, L.; Wang, S. New design of a cathode flow-field with a sub-channel to improve the polymer electrolyte membrane fuel cell performance. J. Power Sources 2017, 44, 32–38. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Wang, G.; Yue, L. Numerical study of a new cathode flow-field design with a sub-channel for a parallel flow-field polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energy 2018, 43, 2359–2368. [Google Scholar] [CrossRef]
- Qin, Y.; Li, X.; Jiao, K.; Du, Q.; Yin, Y. Effective removal and transport of water in a PEM fuel cell flow channel having a hydrophilic plate. Appl. Energy 2014, 113, 116–126. [Google Scholar] [CrossRef]
- Caglayan, D.G.; Sezgin, B.; Devrim, Y.; Eroglu, I. Three-dimensional modeling of a high temperature polymer electrolyte membrane fuel cell at different operation temperatures. Int. J. Hydrogen Energy 2016, 41, 10060–10070. [Google Scholar] [CrossRef]
- Santamaria, A.D.; Bachman, J.; Park, J.W. Cold-start of parallel and interdigitated flow-field polymer electrolyte membrane fuel cell. Electrochim. Acta 2013, 107, 327–338. [Google Scholar] [CrossRef]
- Tong, S.; Bachman, J.C.; Santamaria, A.; Park, J.W. Experimental investigation on a polymer electrolyte membrane fuel cell (PEMFC) parallel flow field design with external two-valve regulation on cathode channels. J. Power Sources 2013, 242, 195–201. [Google Scholar] [CrossRef]
- Duy, V.N.; Lee, J.; Kim, K.; Ahn, J.; Park, S.; Kim, T.; Kim, H.M. Dynamic simulations of under-rib convection-driven flow-field configurations and comparison with experiment in polymer electrolyte membrane fuel cells. J. Power Sources 2015, 293, 447–457. [Google Scholar] [CrossRef]
- Sun, H.; Xie, C.; Chen, H.; Almheiri, S. A numerical study on the effects of temperature and mass transfer in high temperature PEM fuel cells with ab-PBI membrane. Appl. Energy 2015, 160, 937–944. [Google Scholar] [CrossRef]
- Cheddie, D.; Munroe, N. Mathematical model of a PEMFC using a PBI membrane. Energy Convers. Manag. 2006, 47, 1490–1504. [Google Scholar] [CrossRef]
- Li, Q.; He, R.; Gao, J.; Jensen, J.; Bjerrum, N. The CO poisoning effect in PEMFCs operational at temperatures up to 200 ℃. J. Electrochem. Soc. 2003, 150, A1599–A1605. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Z.; Zhang, J.; Tang, Y.; Song, C.; Navessin, T.; Shi, Z.; Song, D.; Wang, H.; Wilkinson, D.P.; et al. High temperature PEM fuel cells. J. Power Sources 2006, 160, 872–891. [Google Scholar] [CrossRef]
- Sezgin, B.; Caglayan, D.G.; Devrim, Y.; Steenberg, T.; Eroglu, I. Modeling and sensitivity analysis of high temperature PEM fuel cells by using Comsol Multiphysics. Int. J. Hydrogen Energy 2016, 41, 10001–10009. [Google Scholar] [CrossRef]
- Ubong, E.; Shi, Z.; Wang, X. Three-dimensional modeling and experimental study of a high temperature PBI-based PEM fuel cell. J. Electrochem. Soc. 2009, 156, B1276–B1282. [Google Scholar] [CrossRef]
- Lin, H.; Yu, T.; Chang, W.; Cheng, C.; Hu, C.; Jung, G. Preparation of a low proton resistance PBI/PTFE composite membrane. J. Power Sources 2007, 164, 481–487. [Google Scholar] [CrossRef]
- Yang, J.S.; Cleemann, L.N.; Steenberg, T.; Terkelsen, C.; Li, Q.F.; Jensen, J.O.; Hjuler, H.A.; Bjerrum, N.J.; He, R.H. High molecular weight polybenzimidazole membranes for high temperature PEMFC. Fuel Cells 2014, 14, 7–15. [Google Scholar] [CrossRef]


| Parameter | Value | Units |
|---|---|---|
| Active area | 3.61 | cm2 |
| Length of the flow field | 19 | mm |
| Width of the flow field | 1 | mm |
| Depth of the flow field | 1 | mm |
| Width of the rib | 1 | mm |
| Thickness of the GDL | 0.38 | mm |
| Thickness of the CL | 0.05 | mm |
| Thickness of the membrane | 0.1 | mm |
| Width and depth of the rib grooves | 0.1 | mm |
| Parameter | Value | Units |
|---|---|---|
| GDL porosity | 0.4 | _ |
| GDL electric conductivity | 222 [31] | S/m |
| Inlet O2 mass fraction (cathode) | 0.228 [31] | _ |
| Inlet H2O mass fraction (cathode) | 0.023 [31] | _ |
| Anode inlet flow velocity | 0.2 | m/s |
| Cathode inlet flow velocity | 0.5 | m/s |
| Anode viscosity | 1.19 × 10−5 [31] | Pa*s |
| Cathode viscosity | 2.46 × 10−5 [31] | Pa*s |
| Reference pressure | 1.01 × 105 | Pa |
| Cell temperature | 433.15 | K |
| Hydrogen reference concentration | 40.88 [31] | mol/m3 |
| Oxygen reference concentration | 40.88 [31] | mol/m3 |
| Membrane conductivity | 9.825 [32] | S/m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Chen, S.; Xia, Z.; Zhang, X.; Yuan, W.; Wu, Y. Numerical Simulation of a New Flow Field Design with Rib Grooves for a Proton Exchange Membrane Fuel Cell with a Serpentine Flow Field. Appl. Sci. 2019, 9, 4863. https://doi.org/10.3390/app9224863
Luo X, Chen S, Xia Z, Zhang X, Yuan W, Wu Y. Numerical Simulation of a New Flow Field Design with Rib Grooves for a Proton Exchange Membrane Fuel Cell with a Serpentine Flow Field. Applied Sciences. 2019; 9(22):4863. https://doi.org/10.3390/app9224863
Chicago/Turabian StyleLuo, Xin, Shizhong Chen, Zhongxian Xia, Xuyang Zhang, Wei Yuan, and Yuhou Wu. 2019. "Numerical Simulation of a New Flow Field Design with Rib Grooves for a Proton Exchange Membrane Fuel Cell with a Serpentine Flow Field" Applied Sciences 9, no. 22: 4863. https://doi.org/10.3390/app9224863
APA StyleLuo, X., Chen, S., Xia, Z., Zhang, X., Yuan, W., & Wu, Y. (2019). Numerical Simulation of a New Flow Field Design with Rib Grooves for a Proton Exchange Membrane Fuel Cell with a Serpentine Flow Field. Applied Sciences, 9(22), 4863. https://doi.org/10.3390/app9224863






