Micro-Raman Mapping of the Strain Field in GaAsN/GaAsN:H Planar Heterostructures: A Brief Review and Recent Evolution

Featured Application

Micro-Raman mapping can provide detailed information about the strain distribution in GaAsN/GaASN:H planar heterostructures.

Abstract

Raman scattering is an effective tool for the investigation of the strain state of crystalline solids. In this brief review, we show how the analysis of the GaAs-like longitudinal optical phonon frequency allowed to map the strain behavior across interfaces in planar heterostructures consisting of GaAsN wires embedded in GaAsN:H matrices. Moreover, we recently showed how the evolution of the longitudinal optical frequency with increasing H dose strongly depends on polarization geometry. In a specific geometry, we observed a relaxation of the GaAs selection rules. We also present new results which demonstrate how laser irradiation intensity–even at low levels–may affect the line shape of the GaAs-like spectral features in GaAsN hydrogenated materials.

1. Introduction

It is well known that Raman scattering is an effective tool in detecting the strain state in crystalline solids [1,2] and binary semiconductors, such as GaAs, under stress [3,4]. Besides mechanical stress, other fields may induce strain in a crystal, which in turn can modify the frequency of lattice modes. This is the case of Fe-doped Lithium Niobate. In this crystal, the photorefractive electric field—that can be produced by the Raman probe itself—can induce such a strain via the piezoelectric effect. As a result, a shift in Raman modes can be detected [5]. The phonon deformation potentials (PDP) are the rates of change of long-wavelength optical phonon frequencies with strain. The sensitivity of phonon frequencies to the strain state can be exploited via PDP not only in bulk materials, but also in layers and even heterostructures. An example of special interest is that of the GaAs_1-xN_x alloy [6,7] grown as a pseudomorphic layer on top of GaAs buffer, where the reduced lattice parameter of the alloy results in the development of a biaxial tensile strain in the layer [6,7,8,9]. The incorporation of hydrogen via irradiation makes the lattice parameter increase up to the value of GaAs, or even beyond, eventually leading to the buildup of compressive strain [8,9,10].

In fact, it is now well established that hydrogen almost completely neutralizes the effect of nitrogen on the band structure of the GaAs host matrix via the formation of nitrogen-hydrogen complexes N-nH (with n = 2, 3) [8,9,10,11,12,13,14]. The redshifted band gap E- blueshifts toward the typical energy position in GaAs materials. On the other hand the E+ band disappears after hydrogen irradiation [8,9,10] and the photoreflectance (PR) spectra of the H-treated GaAsN layers closely resemble (broad) GaAs spectra [8,15]. At the same time, after hydrogenation, the GaAs-like Raman features near 292 cm⁻¹ persist. In contrast, the Ga-N local vibrational mode (LVM), near 475 cm⁻¹, disappears [8].

The GaAs-like Raman modes are only weakly perturbed by hydrogenation. Nevertheless, the longitudinal optical (LO) phonon frequency exhibits a blueshift (of the order of 1 cm⁻¹ or less) which is indicative of a reduction of the native biaxial tensile strain of the untreated material [8]. In fact, the frequency shift of the GaAs-like LO mode can be usefully applied for monitoring the strain state of GaAsN layers in planar heterostructures, as reported for GaAsN wires separated by GaAsN:H barriers [16].

This approach may be effective in improving the design of planar heterostructures for light polarization control obtained by selective H-irradiation of dilute nitride semiconductors [11]. In fact, spatially selective hydrogenation [17] can be used to engineer the strain profile and, hence, the mixing of heavy hole and light hole valence-band states. This allows tuning of the optical properties of the material. In particular, by realizing arrays of GaAsN/GaAsN:H wires at different orientations [18], a high degree of linear polarization was achieved for the light emitted by the sample. On the other hand, the same approach can be used to get a deeper insight (on a microscale) on the strain modulation ensuing the formation of N-nH complexes in the patterned GaAsN/GaAsN:H structures. In particular, it was shown that the formation of N-2H complexes (typical of early stage of the hydrogenation process) produces, besides N passivation, near-perfect lattice-matching with the GaAs buffer layer. On the other hand, N-3H centers are related to a sizeable “overshooting” of the lattice parameter of the host material, and consequently induce strain inversion in the H irradiated GaAsN layers [17,18,19,20,21]. If detailed and accurate knowledge of the strain profile derived from Raman map analysis is available, it will reliably compare with results from Finite-Elements calculations, thus serving as a method to check the strain profile in the heterostructure.

As far as other suggested applications are concerned, it is remarkable that one can realize heterostructures in which untreated and hydrogenated GaAsN are characterized by a ~2% refractive index mismatch over a broad spectral interval that comprises the 1.3 and 1.55 µm telecommunications windows [12]. Such mismatch is sufficient to confine light and fabricate optical waveguides [17,22].

In this paper, we firstly recall the main features of the experimental and analytical procedure successfully applied to a previously well-characterized sample for strain field mapping in GaAsN/GaAsN:H planar heterostructures, then we shall discuss the possibility of optically determining the uniaxial strain at the wire-barrier interface by an appropriate data reduction method. Finally, the effects of H dose, experimental polarization geometries, and excitation power on the line shape and frequencies of the Raman structures will be addressed.

2. Experimental and Analytical Procedure

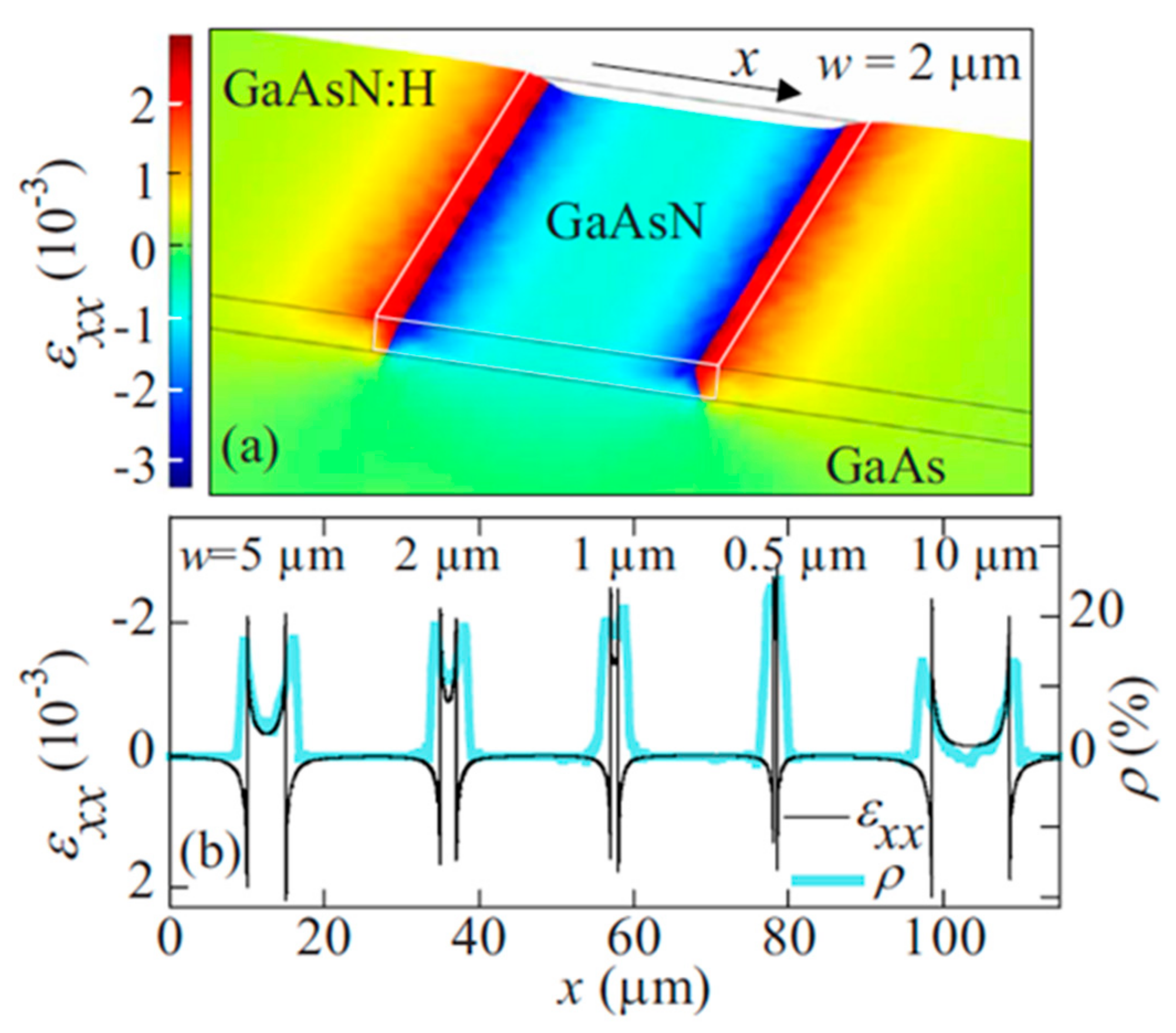
2.1. Optical Mapping

The combination of photoreflectance (PR) spectroscopy and micro-Raman scattering enabled us to perform an all-optical mapping of the strain field in GaAsN/GaAsN:H micro-wires. In fact, by means of PR and Raman scattering, the critical point energies near the energy gap (on a macroscopic scale) and the strain dependence of the longitudinal optical (LO) phonon frequency ω^LO (on a microscopic scale) can be measured [23,24,25,26,27], respectively. As shown in the following, the combined peculiarities of the two experimental approaches allowed to obtain a detailed picture of the strain field resulting from H distribution across the wires. Moreover, the strain field mapping was found to qualitatively agree with simulations based on a system of partial differential equations that reproduce the kinetics of hydrogen in GaAsN [28].

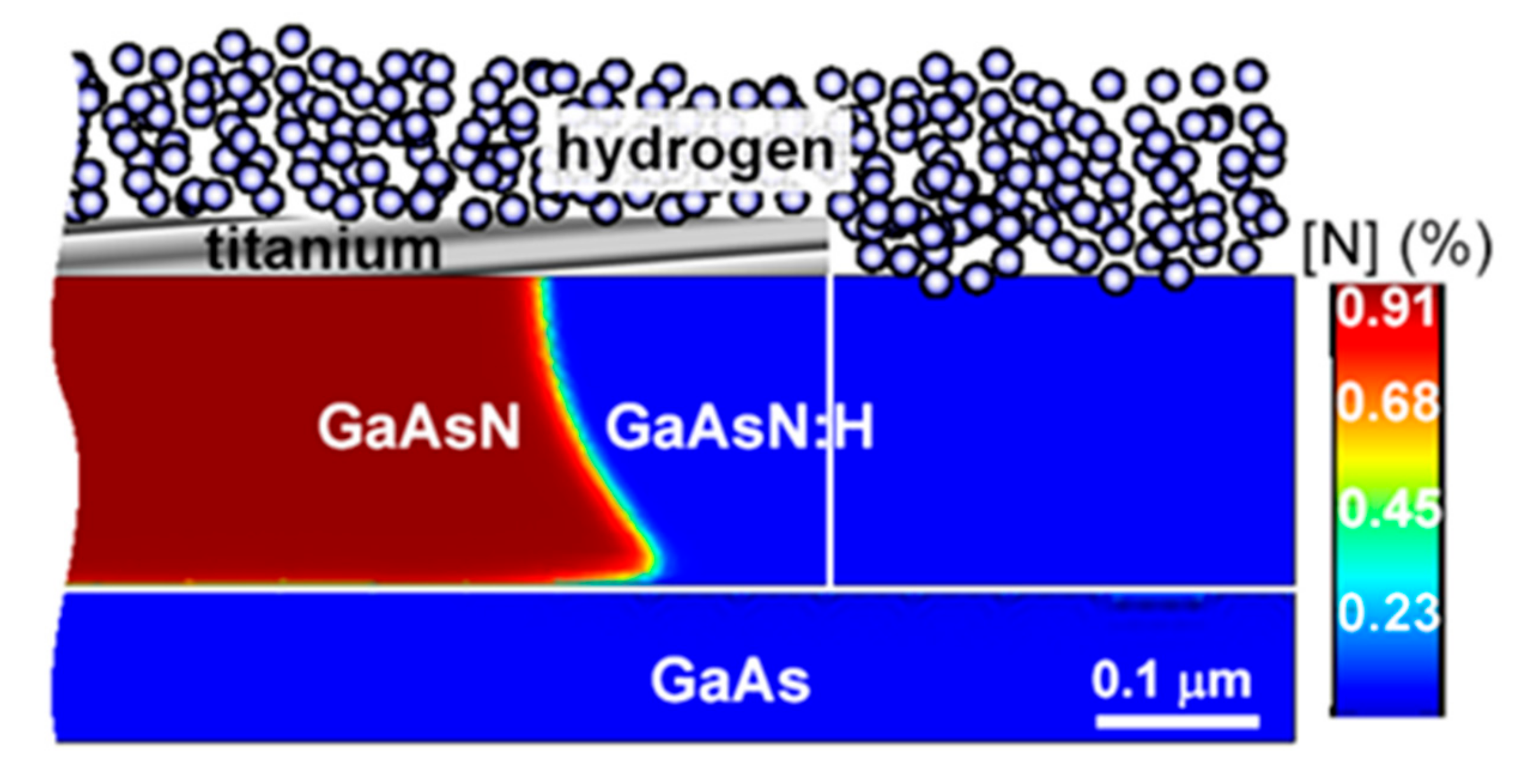
2.2. Samples

As reported in Ref. [16], the samples used to test the strain field mapping were made by growing a GaAs_0.991N_0.009 film on a GaAs buffer. The film was grown by molecular beam epitaxy at 500 °C. Thickness was 200 nm. The buffer was deposited on a [001] GaAs substrate at 600 °C. A radio-frequency plasma source was employed for N₂ cracking. X-ray diffraction measurements allowed the characterization of the film regarding thickness and nitrogen concentration. The GaAsN surface was covered with a 50 nm thick film of titanium, which is not transparent to hydrogen. Electron beam lithography was used to pattern the Ti film. A 100 eV ion beam produced hydrogenation with a H dose ≈ 3 × 10¹⁸ ions/cm². Such dosage allows the full passivation of an unpatterned GaAsN layer of the same thickness. Finally, chemical etching produced the removal of the titanium masks. It must be noted that a sharp GaAsN/GaAsN:H interface can be accomplished between GaAsN wires and the hydrogenated barriers [29], now exhibiting a “GaAs-like” behavior. In fact, hydrogen diffuses In GaAsN with a steep front-line of 10 nm/decade, or less [30].

The hydrogenation process that was used to create the vertical GaAsN/GaAsN:H interfaces defining the wires is illustrated in Figure 1. The figure shows the concentration of electronically active nitrogen atoms following hydrogenation when a 10 µm wide titanium mask is used. In the examined sample of composition GaAs_0.991N_0.009, wires of different width w (w = 0.5, 1, 2, 5, and 10 µm) and parallel to the [110] (or equivalent) direction were interposed with hydrogenated barriers (10–20 µm wide).

2.3. PR Measurements and Average Strain Determination

Near-normal incidence PR measurements were collected in the energy range of interest (here typically 1.1–1.9 eV) with a spectral resolution of 1 meV. The probe beam of the standard experimental apparatus [31] was obtained from a 100 W halogen lamp, while the modulated excitation source was provided by the continuous output of a 20 mW Coherent HeNe laser (λ = 632.8 nm; 1-mm spot diameter) mechanically chopped at a frequency of 220 Hz.

Typical PR spectra, obtained at room-temperature in the energy range of interest, are shown in Figure 2 for the multi-wires sample (panel a) and for the as-grown GaAsN reference sample (panel b). Despite the presence of the articulated and bulky spectral structures (near 1.42 eV), due to signals coming from the buffer/substrate region and related to the GaAs band gap [27], some PR features particularly interesting for determining the strain status of the GaAsN layer can be observed in both spectra.

More in depth:

(i)

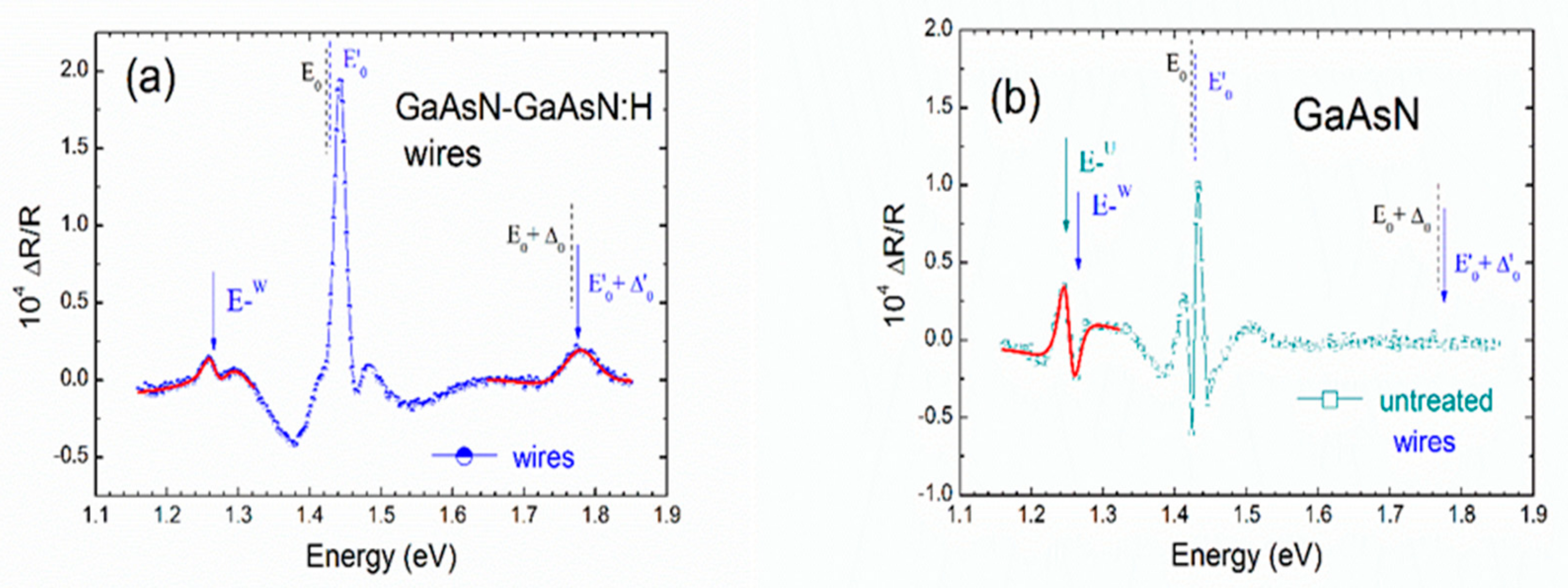
In the multi-wires sample (Figure 1, panel a), the “GaAs-like” spectral structures of the band gap (E₀^′) and of the split-off (SO) band (E₀^′ + ∆₀^′) are due to the optical response of the surface barriers between the GaAsN wires, that hydrogenation has turned into “GaAs-like” sections [9,10,11]. As previously observed [8,10,32], the broadening parameters of these features appear greatly enhanced and their energy position is systematically blueshifted with respect to the corresponding features, E₀ and E₀ + ∆₀, that can be found in the literature of GaAs materials. In particular, the SO blueshift of (9 ± 1) meV [16], obtained by fitting the spectral structure to the appropriate Aspnes line-shape model function [27], must be related to a sizeable expansion of the host lattice resulting from hydrogenation [10,11] and can be used to determine the in-plane strain. An analytical procedure based on the deformation potential theory [25], and thoroughly described elsewhere [10], leads to a value of the average compressive in-plane strain ε_// (in the hydrogenated sections) roughly equal to −1.0 × 10⁻³.

(ii)

In the low energy part of the same spectrum (Figure 1, panel a) one can see the contribution to the PR signal coming from the GaAsN sections (wires). It originates from the presence of the E-band [6,7] at E-^w = 1.265 eV, as determined by a best fit. This value is 11 meV higher than that (E-^u = 1.254 eV) obtained for the same band in the untreated GaAsN sample (see Figure 2, panel b). One should note that the strain field produces shift and splitting of GaAsN valence bands [6,7]. On the other hand, at room temperature, probably due to broadening effects, the doublet is unresolved in the optical response of both samples. For this reason, a single Aspnes model function [27] was used to derive the energy (E-) of the band gap of GaAsN. According to the deformation potential theory [23], the energy gap increases for decreasing tensile stress, and indeed, this is our case. Therefore, the tensile strain in the previously masked wire sections of the hydrogenated multi-wires sample (see Figure 2) is expected to largely decrease, in good agreement with the observation of a compressive strain produced on GaAsN wires by a lattice expansion in the hydrogenated barriers [11].

(iii)

After lowering the temperature of the sample, the improved experimental conditions allowed the doublet in the E- band of the spectra of the untreated GaAsN sample to be resolved (not shown) and to measure a valence band splitting ∆E = (14 ± 2) meV, that corresponds [10,30] to an in-plane tensile strain ε_// ≈ + 1.8 × 10⁻³. It must be pointed out that this value is very close to that expected for the coherent growth of a GaAs_0.991N_0.009 layer on GaAs. We note that, due to the increased broadening parameters, the same procedure could not be applied in the case of the multi-wires sample.

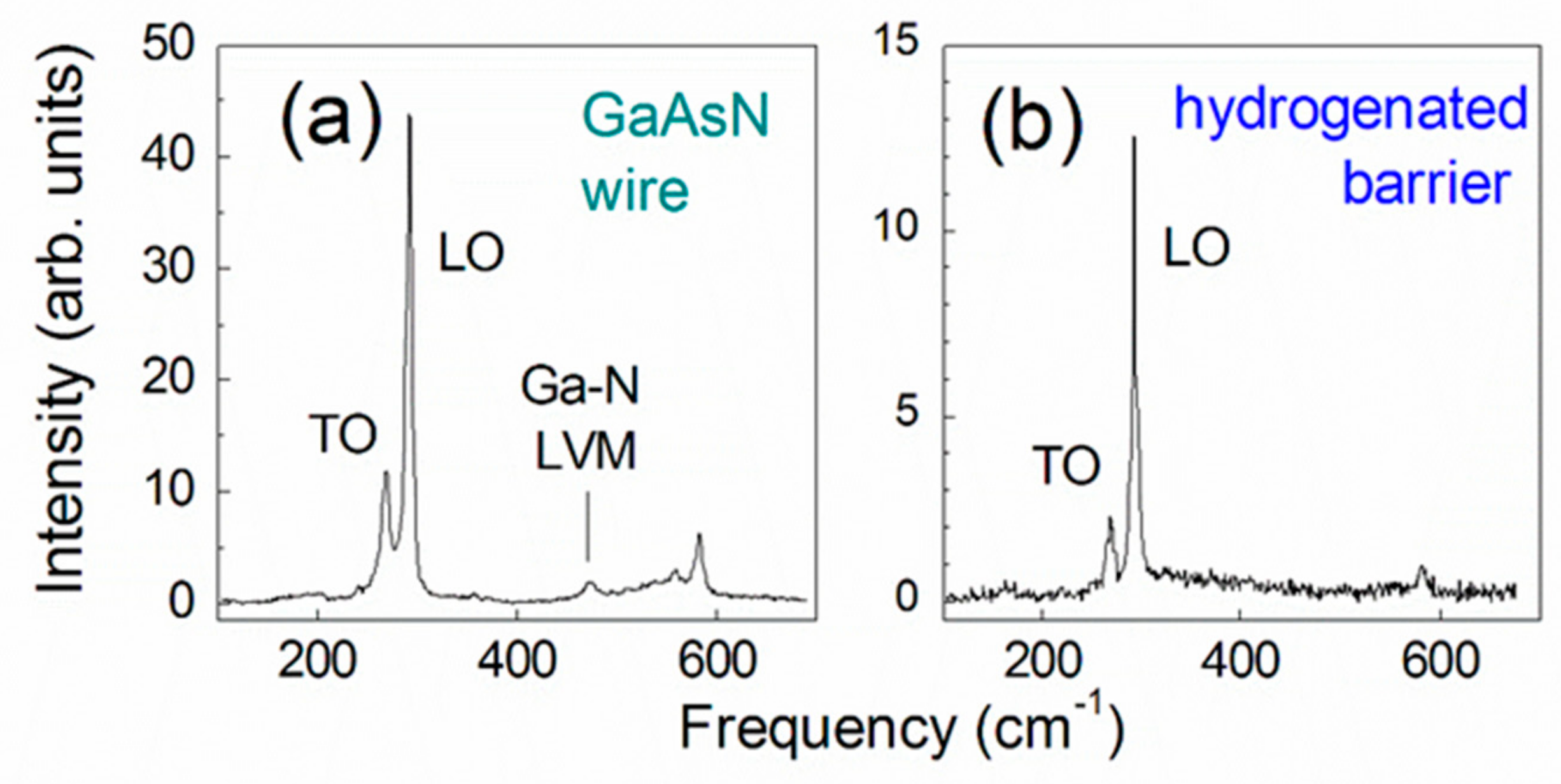
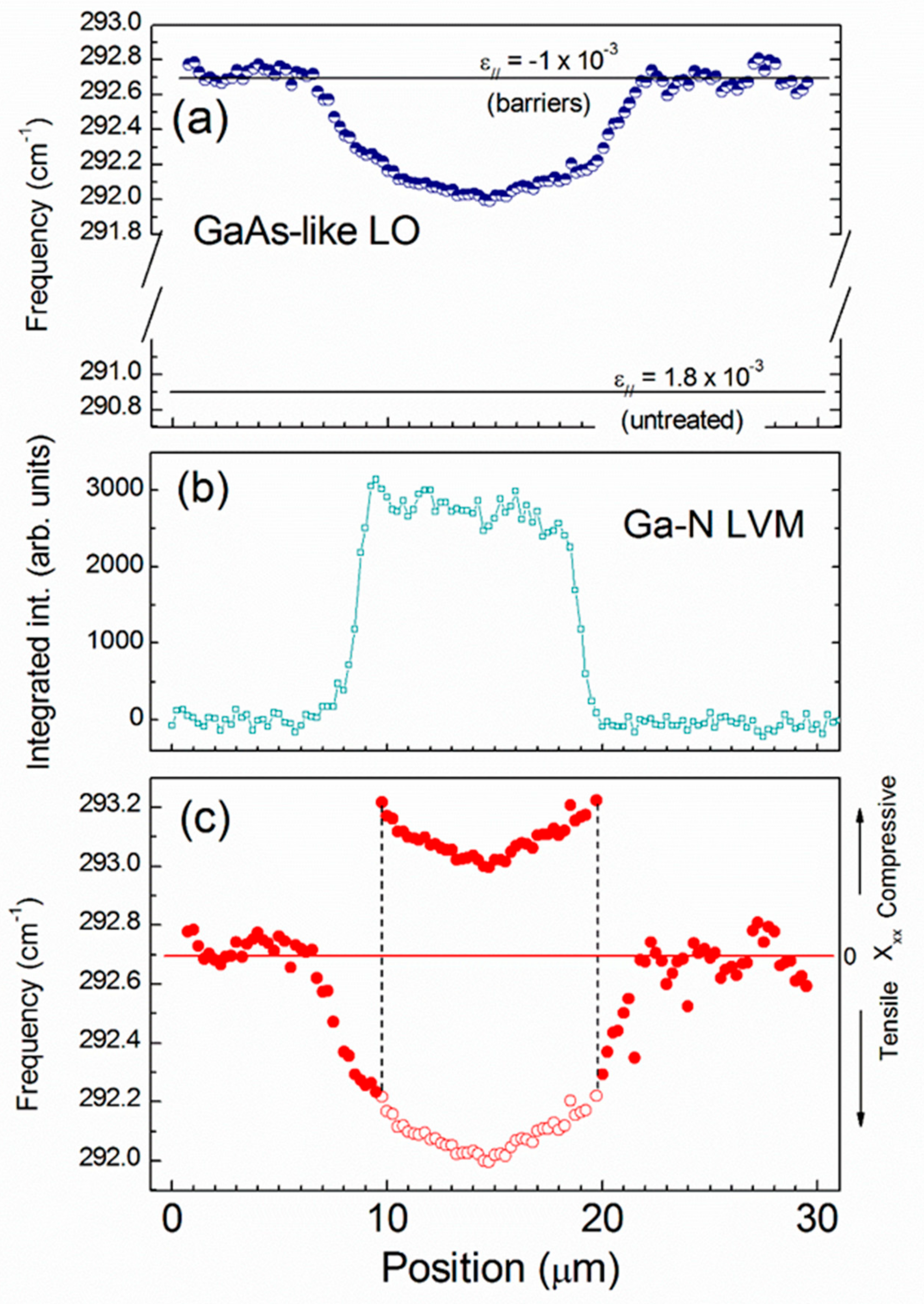
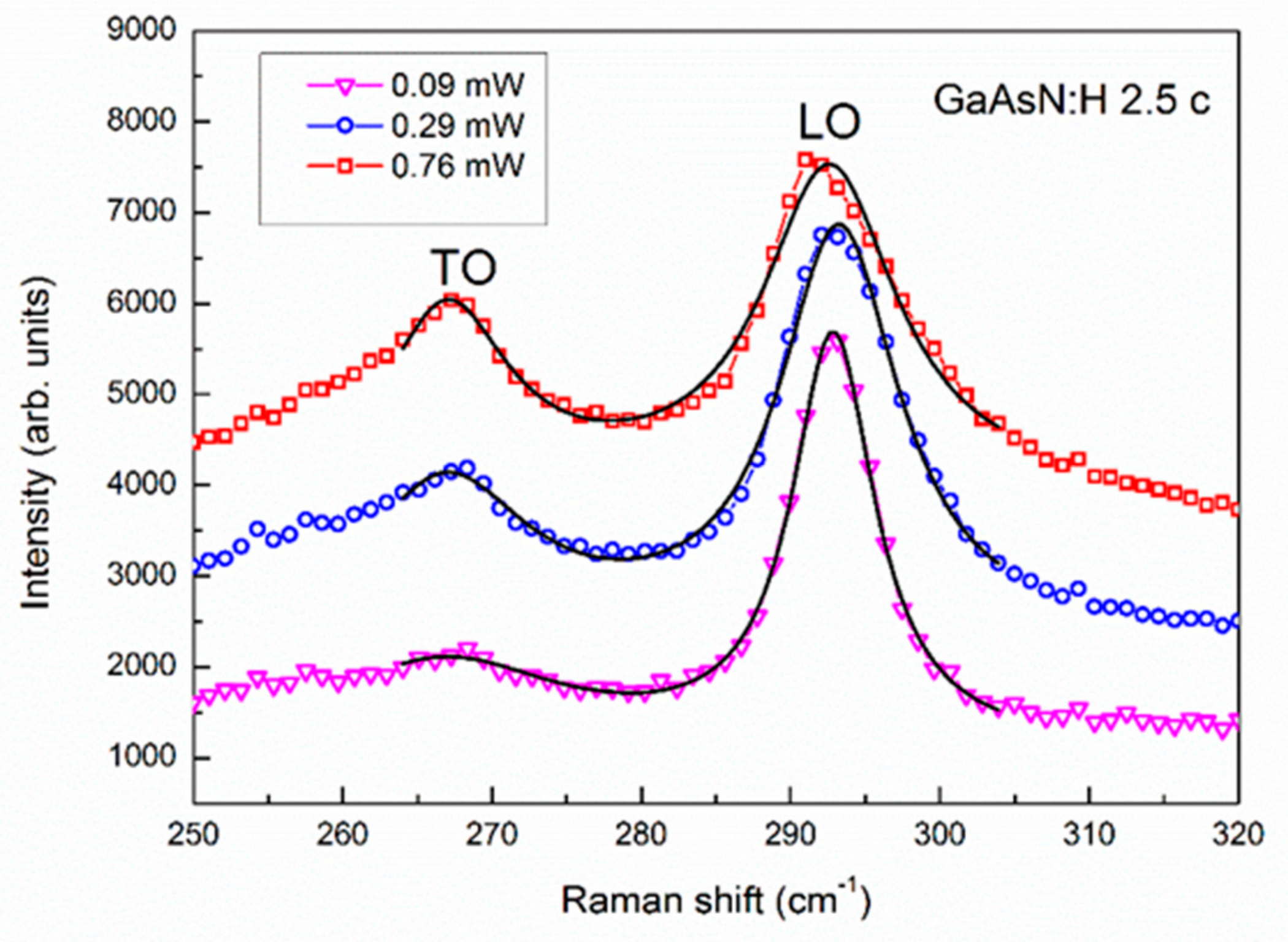
2.4. Raman Scattering Measurements and Micro-Scale Mapping of the Strain Field

All the Raman spectra reported in this paper were obtained using micro-Raman equipment. The light source was a HeNe laser (λ = 632.8 nm). Spectral resolution was 1 cm⁻¹. As reported in Ref. [16], the average in-plane strain can be nicely reproduced by the frequency variation of the longitudinal optical mode (ω^LO) with respect to the unstrained material. The compressive/tensile nature of the strain is marked by increasing/decreasing frequencies, even on a microscopic scale [33,34,35,36,37].

In Figure 3, spectra recorded at the axis of a GaAsN wire (of width w = 10 μm), and in the hydrogenated barrier far from the wire, are reported. One can appreciate how the Ga-N line at 475 cm⁻¹, typical of the untreated alloy, disappears after hydrogenation. The GaAs-like LO and transverse optical (TO) phonons produce a relatively intense line at about 292 cm⁻¹ and a rather weak line at about 270 cm⁻¹, respectively. The LO phonon frequency shifts to higher values in the hydrogenated barrier, in agreement with [8]. This is clearly shown in Figure 4a, whereas Figure 4b evidences the composition profile across the wire resulting from the intensity profile of the Ga-N local mode. Panel 4b reveals that the wire-barrier interface is sharp, actually not resolved as the diffraction-limited laser spot diameter is about 0.7 µm. In contrast, the LO frequency profile reveals that frequency variation at the interface is not steep, but extends over a few microns, which can be neatly resolved by the Raman probe. This can be attributed to uniaxial stress (and strain) extending far beyond the interface thickness.

2.5. Data Reduction

We devised a data reduction method which allows to isolate the LO mode frequency shift produced by strain components other than the biaxial strain [38] associated with the lattice parameter mismatch between the GaAs buffer and the pseudomorphic materials GaAsN and GaAsN:H in the planar heterostructure. To this aim, we assume a linear relation between the isotropic biaxial in-plane strain and the LO phonon frequency. Near the wire-barrier interfaces we also assume a linear relation between the anisotropic components of the strain and the phonon frequency.

These local strain components, in turn, are linearly related to X_xx, the diagonal component of the stress acting perpendicularly to the wire/barrier interfaces. It follows that a linear relationship holds between the phonon frequency and the X_xx stress component. Figure 4, panel (c) illustrates the data reduction method. Inside the wire, the LO phonon frequency data have been incremented by +1.0 cm⁻¹. This amount corresponds to double the shift between the LO frequency in the hydrogenated barrier far from the interface and at the interface. The procedure follows from two assumptions: (i) The elastic constants are equal in the untreated and in the hydrogenated GaAs_0.991N_0.009 alloy, and (ii) they are in accordance with symmetry considerations in the proximity of the interface local uniaxial stress in the wire and in the barrier with equal intensity and the opposite sign. Finite element method (FEM) simulations [11] were made using the same parameters of the sample under experimental investigation. It turns out that the reduced data from Raman experiments favorably compare with the results of simulations, i.e., the uniaxial strain component ε_xx (linearly related to the diagonal X_xx stress component) in wires and barriers oriented in the [110] direction (see Figure 5). Both experiments and simulations, in particular, suggest that nonzero uniaxial stress exists even at wire axis, in accordance with the lack of a frequency plateau within the wire.

3. Raman Line Shape in Dilute Nitrides: Recent Evolution

The effects of the H dose on LO phonon frequencies have been recently investigated in uniformly hydrogenated layers of a GaAsN alloy with N concentration equal to 1% [39]. Measurements were made on samples which received H doses comprised between 1.2 and 3.5 c (1 c = 1.0 × 10¹⁸ ions/cm²), corresponding to the average in-plain biaxial strain ranging from 1.0 × 10⁻³ to −8.0 × 10⁻³, as estimated from PR spectra [39]. The frequency evolution with an increasing H dose strongly depends on the polarization geometry of the Raman scattering experiment

Table 1. Frequencies of GaAs-like LO phonons obtained with different polarization geometries. Reproduced from [39] (E. Giulotto, M. Geddo, M. Patrini, G. Guizzetti, M.S. Sharma, M. Capizzi, A. Polimeni, G. Pettinari, S. Rubini, and M. Felici, J. Appl. Phys. 125, 175701 (2019) https://doi.org/10.1063/1.4905097), with the permission of AIP Publishing.

Incident Light Polarization	Scattered Light Polarization	GaAs Reference	GaAsN	1.2c H Dose	2.5c H Dose	3.5c H Dose
[110]	[110] (allowed)	292.4 cm−1	291.6 cm−1	292.5 cm−1	292.8 cm−1	293.2 cm−1
[110]	[1–10] (forbidden)	-	-	-	-	-
[100]	[010] (allowed)	292.6 cm−1	292.2 cm−1	293.5 cm−1	293.9 cm−1	294.2 cm−1
[100]	[100] (forbidden)	-	290.4 cm−1	290.1 cm−1	289.6 cm−1	289.8 cm−1

.

While in the typically used geometry (incident and scattered light polarization [110]) the linear relationship between strain and frequency is confirmed [39] as supported by the comparison with the PR data for increasing doses (and increasing strain), in other geometries the behavior might be different. The most intriguing case corresponds to incident light polarization along the [100] crystallographic axis and scattered light polarization along the same [100] axis. In this geometry, Raman scattering is forbidden in GaAs, whereas selection rules are known to relax in strained GaAsN [40]. In-plane strain is also the main parameter responsible of the relaxation of selection rules in in GaAsN:H layers. The low scattering intensity in the 1.2 c sample [39] is amenable to the vanishing strain in this particular sample. Scattering intensities in more heavily irradiated samples are larger, in agreement with a larger (compressive) strain, as confirmed by systematic PR measurements [30,39]. In contrast to other geometries, frequencies decrease with an increasing H dose, which is accompanied by an increasing compressive strain. In all micro-Raman experiments on H-irradiated samples, laser power must not exceed the threshold above which dissociation of N-H centers starts to occur [41]. With the instrumental setup typically used in our experiments, such threshold can be prudently set at 1 mW [16]. However, a marked dependence of line shapes (peak position, broadening, symmetry) on power was observed (see Figure 6) starting from about 0.3 mW, especially in more heavily hydrogenated GaAsN samples. It is worth noting that the data reported in Table 1 for GaAsN:H layers were obtained by using an excitation power of 0.1 mW. No comparable effect is observed in GaAs, while it was found negligible in GaAs_1−xN_x (at least for x ≤ 0.01). This effect is completely reversible, so that it is reasonable to believe that it cannot be ascribed to N-nH center dissociation [41,42]. Although further investigation (actually in progress) will be required to fully explain these results, we may notice that the temperature increase due to the laser beam illumination could enhance the free carriers (originating from ionized impurities) activity and locally modify the pre-existing charge density distribution around the N-nH complexes, so adding disorder in the host matrix [20,43]. Since the power effect is completely reversible, we may infer that although the temperature increase is not enough for hydrogen evaporation [20,43,44], nevertheless it favors the introduction of further disorder in the host matrix. This is consistent with the experimentally observed dependence of the redshift of the peak frequency of the Raman LO GaAs-like mode on the power of the laser beam. In fact, the deformation of the line shape of the Raman structures, in particular redshift of the peak frequency, broadening increase and asymmetry of the shape may be accounted for (at least partially) by the laser-beam-induced temporary increase of the lattice disorder. This last is known to produce many of the aforementioned effects on the Raman line shapes in III–V semiconductors [45,46]. Whatever the precise explanation of this “power effect”, it is clear that one must operate very carefully with hydrogenated GaAsN materials and heterostructures to avoid spectral line distortion.

4. Conclusions

In the past few years, Raman scattering has been successfully used to investigate the strain state of GaAsN and GaAsN:H layers. The technique is based on the dependence of GaAs-like phonon frequencies on strain through the phonon deformation potentials. Raman scattering microscopic results compare well with the average in-plane strain determination, independently obtained via PR measurements on a macroscopic scale. In particular, it was possible to relate the GaAs-like LO phonon frequency shift to the H dose received by the sample, hence to the amount of in-plane strain. Checking this linear relation takes advantage of the PR well-established compressive strain dependence on H dose. Remarkably, micro-Raman mapping allowed to gain detailed information about the strain distribution in GaAsN/GaAsN:H heterostructures. A Raman shift in heterostructures depends on both biaxial in-plane strain and uniaxial strain components acting at the interface between, e.g., GaAsN wires and GaAsN:H matrix. It is possible, at least in simple cases, to isolate the strain components other than the biaxial strain. The result of such data reduction is in qualitative agreement with finite element method simulations. The techniques described here can help design devices based on the strain engineering of GaAsN/GaAsN:H heterostructures. Work is in progress concerning wire-barrier heterostructures with different orientations with respect to the crystallographic axes.