Temperature Analysis of Obstacle Lighting Lamp Working under Various Ambient Conditions: Theoretical and Practical Experiments
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
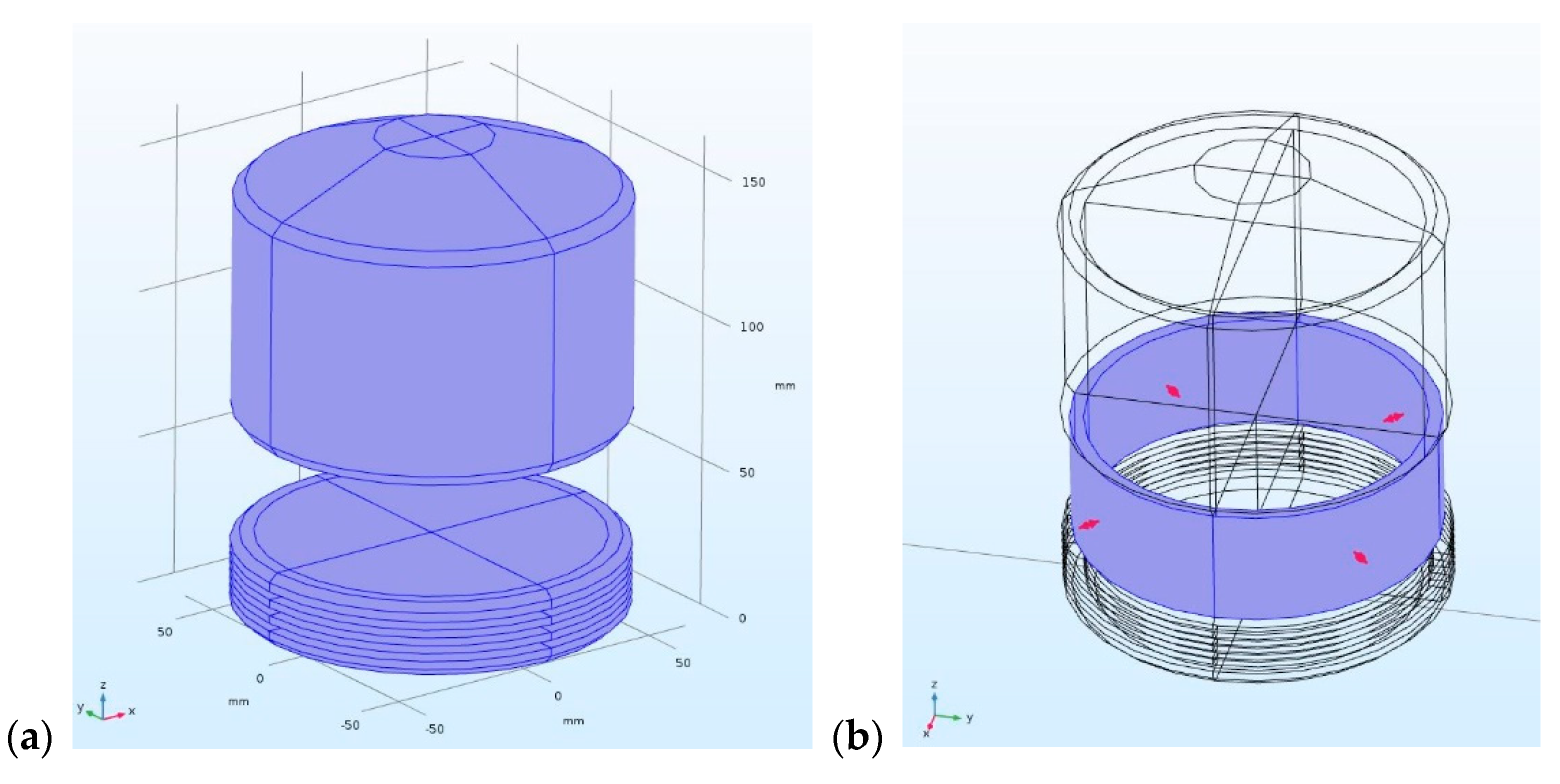
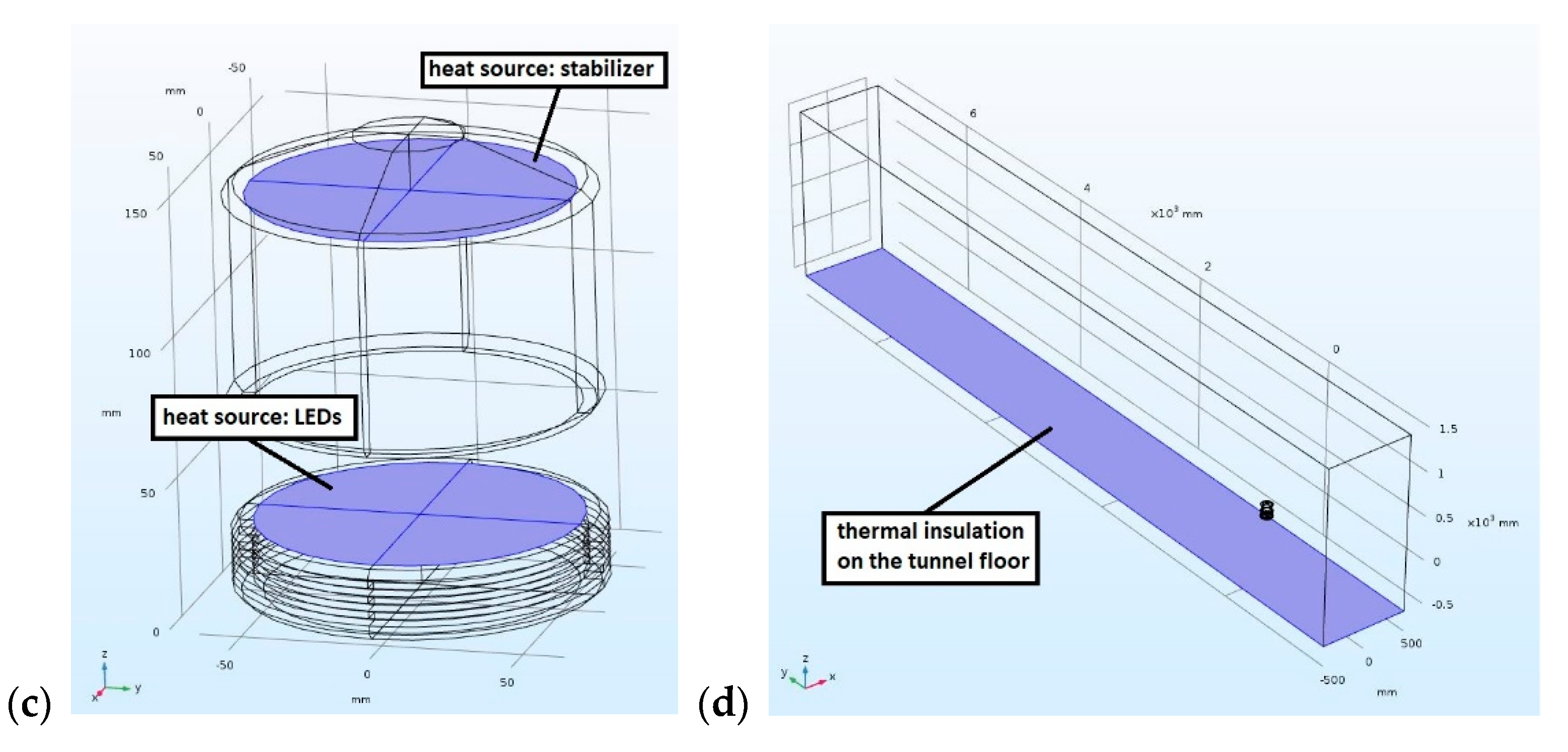
2.1. The Object under Study
2.2. Governing Equations and Model Parameters
2.3. Discretization Mesh
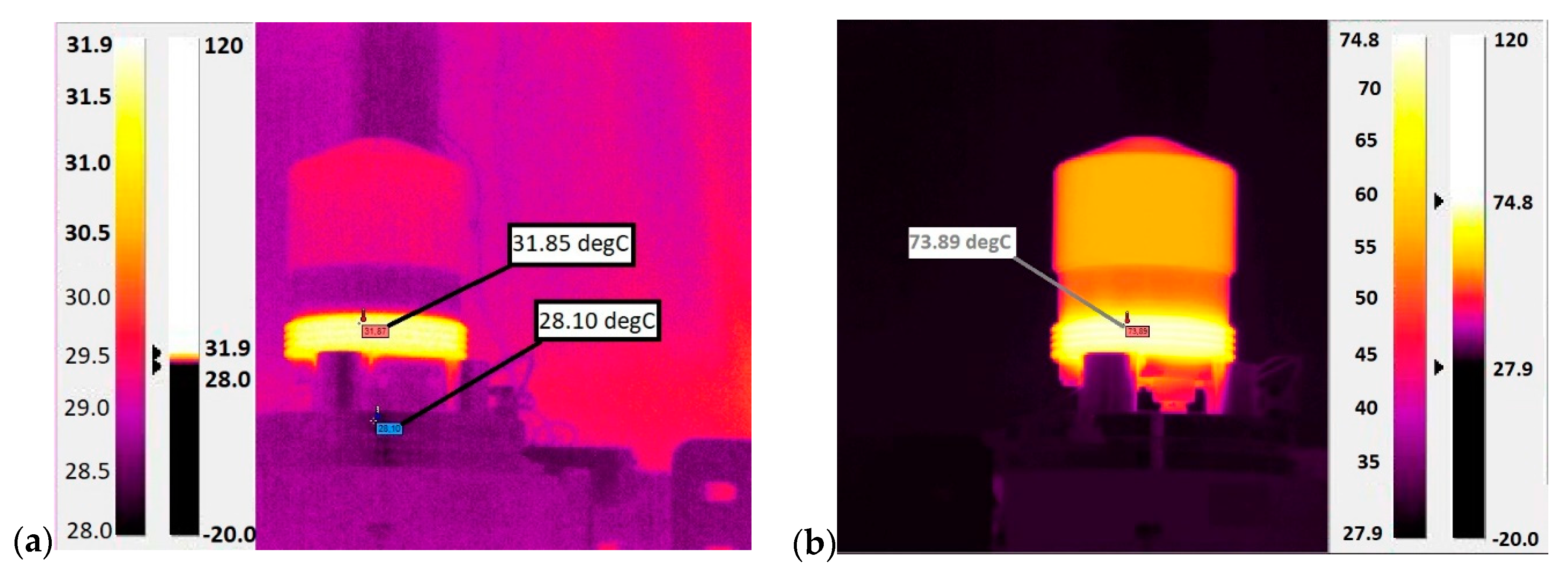
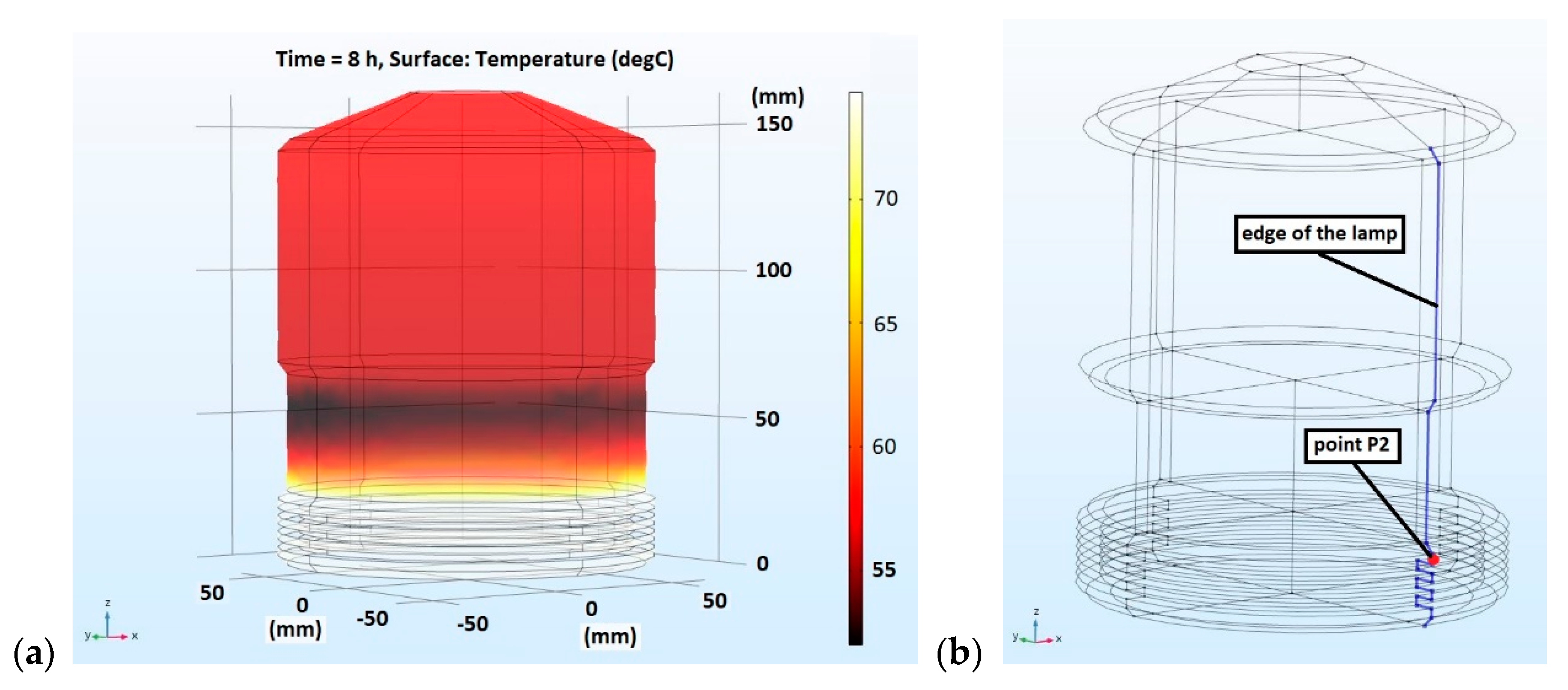
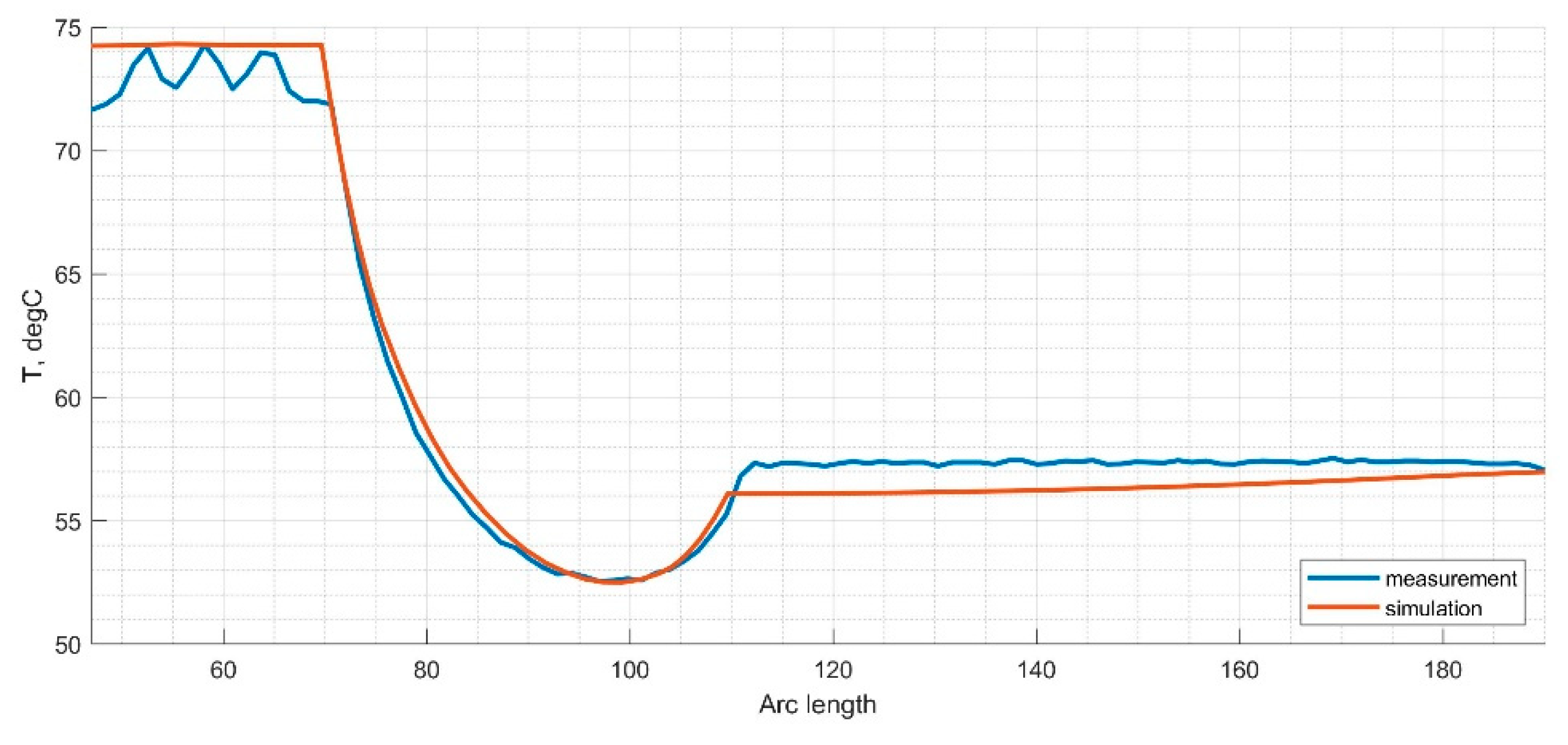
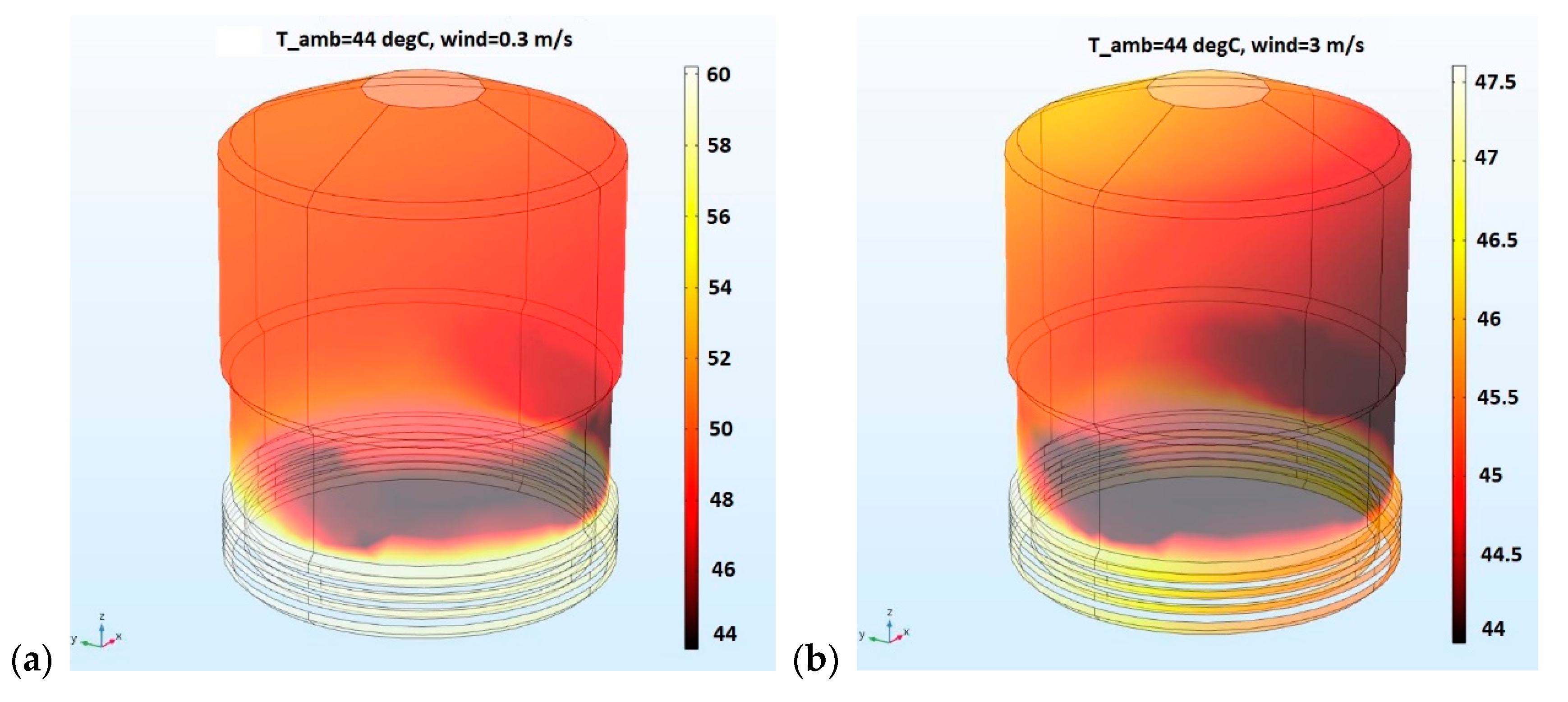
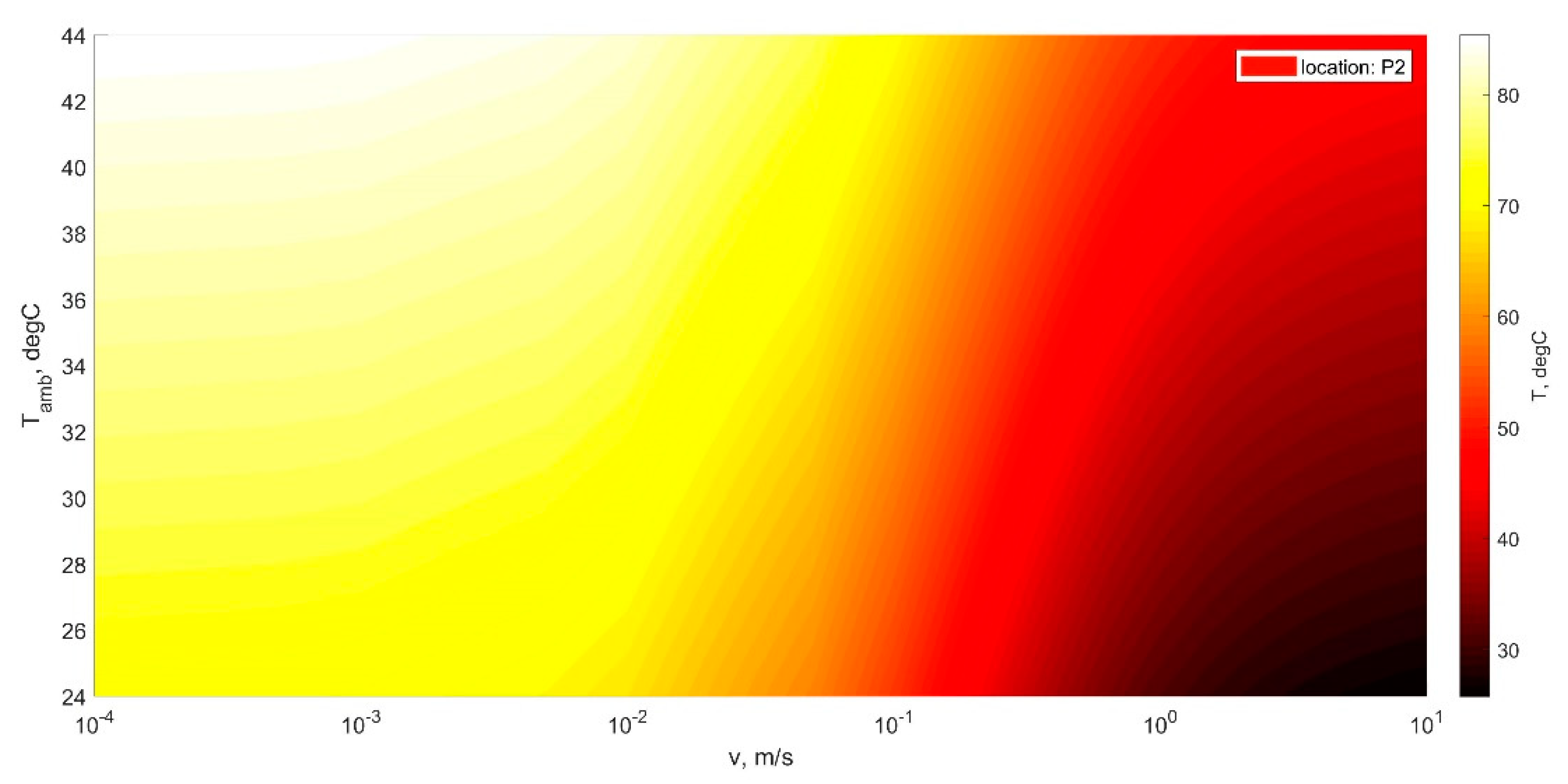
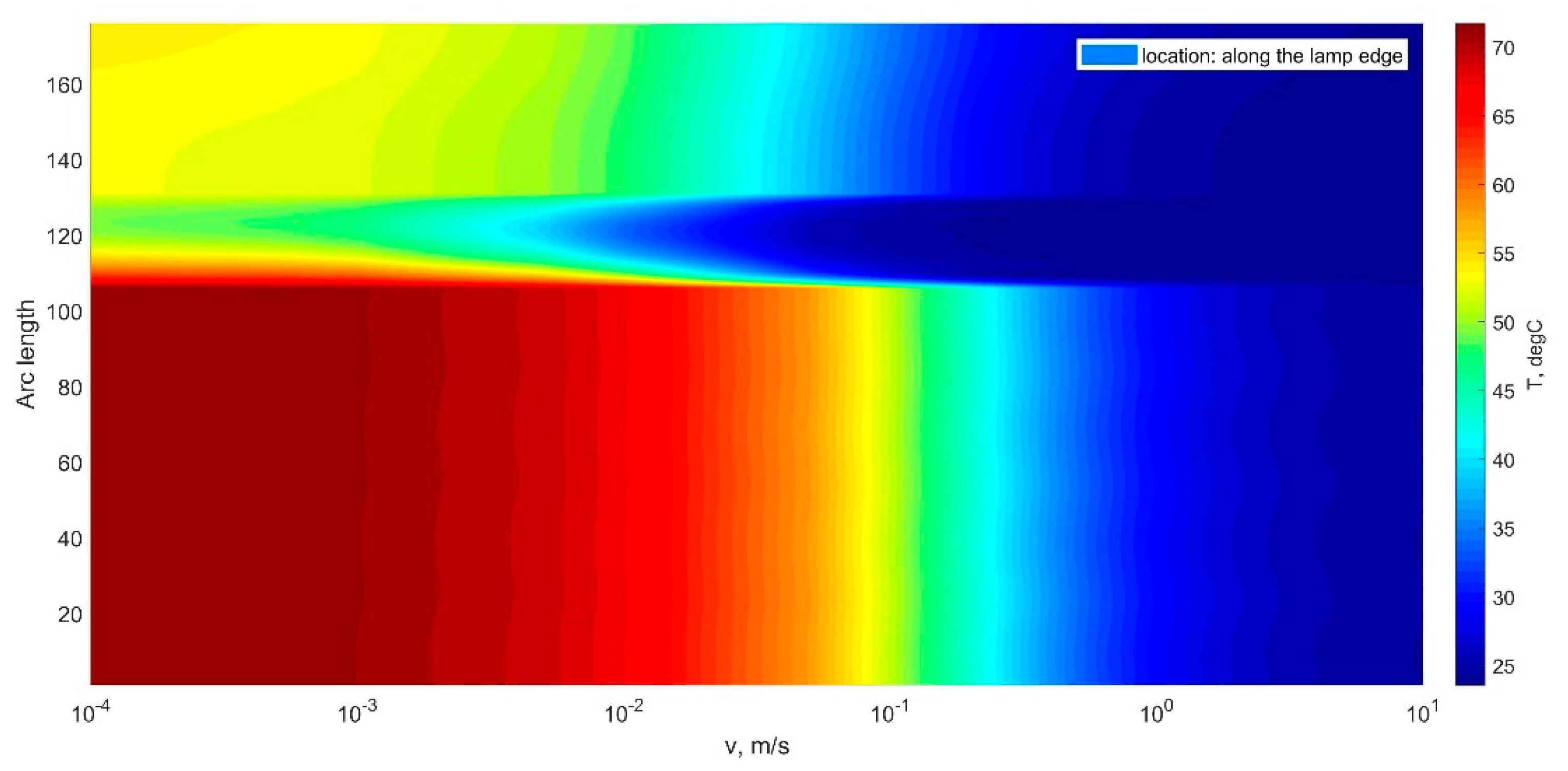
3. Measurement and Analysis Results
4. Discussion, Future Work, and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ochoa, C.E.; Aries, M.B.C.; Hensen, J.L.M. State of the art in lighting simulation for building science: A literature review. J. Build. Perform. Simul. 2012, 5, 209–233. [Google Scholar] [CrossRef]
- International Civil Aviation Organization. Available online: https://www.icao.int/about-icao/Pages/default.aspx (accessed on 27 September 2019).
- Pérez-Ocóna, F.; Pozoa, A.M.; Rabazab, O. New obstruction lighting system for aviation safety. Eng. Struct. 2017, 132, 531–539. [Google Scholar] [CrossRef]
- Jianxin, Z.; Lixia, S. Modelling and Numerical Simulations of Heat Distribution for LED Heat Sink. Discret. Dyn. Nat. Soc. 2016. [Google Scholar] [CrossRef]
- Wu, S.J.; Hsu, H.C.; Fu, S.L.; Yeh, J.N. Numerical simulation of high power LED heat-dissipating system. Electron. Mater. Lett. 2014, 10, 497–502. [Google Scholar] [CrossRef]
- Zhao, X.J.; Cai, Y.X.; Wang, J.; Li, X.H.; Zhang, C. Thermal model design and analysis of the high-power LED automotive head light cooling device. Appl. Therm. Eng. 2015, 75, 248–258. [Google Scholar] [CrossRef]
- Lee, D.W.; Cho, S.W.; Kim, Y.J. Numerical study on the heat dissipation characteristics of high-power LED module. Sci. China Technol. Sci. 2013, 56, 2150–2155. [Google Scholar] [CrossRef]
- Ahmed, H.E.; Salman, B.H.; Kherbeet, A.S.; Ahmed, M.I. Optimization of thermal design of heat sinks: A review. Int. J. Heat Mass Transf. 2018, 118, 129–153. [Google Scholar] [CrossRef]
- Dong, X.D.; Ying, G.L.; Xiao, B.L. Numerical Analysis on temperature field in a LED module. Adv. Mater. Res. 2011, 221, 604–609. [Google Scholar] [CrossRef]
- Luo, X.; Cheng, T.; Xiong, W.; Gan, Z.; Liu, S. Thermal analysis of an 80 W light-emitting diode street lamp. IET Optoelectron. 2007, 1, 191–196. [Google Scholar] [CrossRef]
- Alexandersen, J.; Sigmund, O.; Meyer, K.E.; Lazarov, B.S. Design of passive coolers for light-emitting diode lamps using topology optimization. Int. J. Heat Mass Transf. 2018, 122, 138–149. [Google Scholar] [CrossRef]
- Vinh, Q.; Khanh, T.; Ganev, H.; Wagner, M. LED Lighting: Technology and Perception. Measurement and Modeling of the LED Light Source; Wiley Online Library: Hoboken, NJ, USA, 2014; Chapter 4. [Google Scholar] [CrossRef]
- Stüben, K.A. Review of algebraic multigrid. J. Comp. Appl. Math. 2001, 128, 281–309. [Google Scholar] [CrossRef]
- Schenk, O.; Gärtner, K. Solving unsymmetric sparse systems of linear equations with PARDISO. Future Gener. Comput. Syst. 2004, 20, 475–487. [Google Scholar] [CrossRef]
- Wagner, S. Small-Signal Device and Circuit Simmulation. Ph.D. Thesis, Technische Universität Wien, Vienna, Austria, 2005. Available online: http://www.iue.tuwien.ac.at/phd/wagner/diss.html (accessed on 10 September 2019).


| Description | Aluminum | Air | Acrylic Plastic |
|---|---|---|---|
| Heat capacity at constant pressure [J/(kg·K)] | 900 | Cp(T) | 1470 |
| Thermal conductivity [W/(m·K)] | 238 | k(T) | 0.18 |
| Density [kg/m3] | 2700 | rho(p, T) | 1190 |
| Opacity | Opaque | Transparent | Transparent |
| Surface emissivity | 0.96 (red paint) | - | 0.15 |
| The ratio of specific heats | - | 1.4 | - |
| Diffuse surface-radiation directions | opacity controlled | - | on both sides |
| Description | Value for T | Value for L | Value for V |
|---|---|---|---|
| Maximum element size | 141 [mm] | 308 [mm] | 308 [mm] |
| Minimum element size | 42.4 [mm] | 13.2 [mm] | 13.2 [mm] |
| Curvature factor | 0.7 | 0.3 | 0.3 |
| Resolution of narrow regions | 0.6 | 0.85 | 0.85 |
| Maximum element growth rate | 1.2 | 1.35 | 1.35 |
| Description | Value |
|---|---|
| Minimum element quality | 0.02403 |
| Average element quality | 0.6615 |
| Tetrahedral elements | 169,568 |
| Triangular elements | 13,294 |
| Edge elements | 1760 |
| Vertex elements | 121 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wotzka, D.; Błachowicz, A.; Weisser, P. Temperature Analysis of Obstacle Lighting Lamp Working under Various Ambient Conditions: Theoretical and Practical Experiments. Appl. Sci. 2019, 9, 4951. https://doi.org/10.3390/app9224951
Wotzka D, Błachowicz A, Weisser P. Temperature Analysis of Obstacle Lighting Lamp Working under Various Ambient Conditions: Theoretical and Practical Experiments. Applied Sciences. 2019; 9(22):4951. https://doi.org/10.3390/app9224951
Chicago/Turabian StyleWotzka, Daria, Andrzej Błachowicz, and Patryk Weisser. 2019. "Temperature Analysis of Obstacle Lighting Lamp Working under Various Ambient Conditions: Theoretical and Practical Experiments" Applied Sciences 9, no. 22: 4951. https://doi.org/10.3390/app9224951
APA StyleWotzka, D., Błachowicz, A., & Weisser, P. (2019). Temperature Analysis of Obstacle Lighting Lamp Working under Various Ambient Conditions: Theoretical and Practical Experiments. Applied Sciences, 9(22), 4951. https://doi.org/10.3390/app9224951






