1. Introduction
Carbon fixation by plant biomass units promotes reduction of concentration of greenhouse gases in the atmosphere, thereby lessening global warming [
1,
2,
3,
4,
5,
6]. Therefore, the assessment of the flux and storage of carbon in plant biomass is of great interest. Concomitantly important is the adaptation of methods aimed at non-destructive estimation. For instance, aboveground tree biomass in forest ecosystems has been estimated through remote sensing protocols [
7,
8,
9,
10]. Nevertheless, a number of factors such as sample size, weather, complexity of biophysical settings, study area scale, software, or spatial resolution can induce uncertainty of remote-sensed estimation [
11,
12,
13,
14,
15]. Allometric methods allow implementation of parallel cost-effective non-destructive estimation of plant biomass units [
16,
17,
18,
19,
20,
21,
22,
23,
24]. However, this approach is not also problem-free. Factors like analysis method sample size and data quality can bear significant influences on precision [
25,
26,
27,
28,
29,
30,
31,
32,
33]. Understanding the way procedural factors drive precision of allometric projection of plant biomass units is crucial for assuring reliability. This paper centers on the influences of the analysis method and particularly aims at proposing reliable methods for handling complexity. For clarification it is pertinent reviewing the notions behind interpretation and identification of the allometric paradigm.
As was originally envisioned, the term allometry, also mentioned as biological scaling, refers to the relation between the size of a given organismal trait and overall body size. The notion developed from observations by Otto Snell in 1892 and D’arcy Thompson in 1917. Allometry as a study subject was outlined by Julian Huxley in 1932, in his theory of constant relative growth by two body parts [
34], formulated though the scaling equation:
where
and
are quantifiable traits, the parameter
is nominated as the allometric exponent and
is recognized as the normalization constant. This model also known as the equation of simple allometry has been widely used in research problems in many fields including, biology [
25,
35,
36], biomedical sciences [
37,
38,
39,
40,
41], economics [
42,
43,
44,
45,
46], earth and planetary sciences [
47,
48,
49,
50,
51], resource management and conservation [
52,
53,
54,
55,
56]. The interest for this model lies essentially in its practical utility to produce surrogates of a response
, that is difficult to measure in direct way, by using estimates of the parameters
and
and easily gotten measurements of a covariate
.
Parallel to Equation (1) is the traditional analysis method of allometry (TAMA). This is a widespread protocol that relies in logtransformation in order to transfer Equation (1) into a linear model in geometrical space. Then, the fitted line is back-transformed to yield the original two parameter power function in arithmetical scale. A logtransformation embraces a notion of multiplicative growth. Moreover, in Huxley’s rationale the intercept
of TAMA’s line was of no explicit biological relevance, but the slope
was significant enough as to mean allometry itself. This interpretation maintains nowadays as the only valid theoretical perspective for many practitioners of allometry [
57,
58,
59]. However, in spite of TAMA’s prevalence, there are views asserting this scheme produces biased results [
60,
61,
62,
63,
64]. Also allometrical relationships express as power functions and fit in to a non-linear form in the original scale of data. Thus, keeping the analysis in arithmetical scales is in some way more adequate. Concomitantly for this perspective, direct non-linear regression in arithmetical scales (DNLR) becomes a default standard [
65,
66,
67,
68,
69,
70,
71,
72]. From this slant, the failure of a TAMA fit manly obeys to unsuitable complexity endured by Huxley’s formula of simple allometry. Amendment of this circumstance has encouraged routing further away from Huxley’s perception on covariation among different traits, in order to conceive allometry as centered on covariation between size and shape [
73,
74]. Alongside this it is necessary to consider of multiple-parameter complex allometry (MCA). Related formulations can admit all sorts of nonlinear or discontinuous relationships intended to be fitted in arithmetical scales by means of DNLR protocols [
75,
76,
77,
78].
However, opposing MCA-DNLR slants, defenders of a TAMA approach state that as conceived in the original theoretical standpoint of allometry, a logarithmic transformation is deemed necessary in the analysis [
18,
59,
79,
80,
81,
82,
83,
84,
85,
86,
87]. Thus, embracing MCA-DNLR protocols feeds one of the most central discrepancies among schools of allometric examination. Furthermore, from a traditional stance MCA-DNLR schemes sacrifice appreciation of biological theory in order to privilege statistical correctness [
32,
59,
87]. Besides, a DNLR approach could stand unreliable results, for instance, an inadequate consideration of intrinsic error structure can lead to substantial bias [
88]. In addition, largest values of covariate can be influential of parameter estimates [
18]. From a practical point of view depending on the complexity of MCA to be fitted in direct scales, there could be issues related to initial parameter estimates as well as convergence of non-linear regression algorithms. Therefore, there are also caveats in efficiency of allometric projection of plant biomass units derived from MCA-DNLR arrangements. Then, defenders of traditional allometry assert that overcoming MCA-DNLR inconveniences could be achieved by embracing suitable complexity in geometrical space.
Huxley marked a breakpoint in the log-log plot of chela mass vs. body mass of fiddler crabs (
Uca pugnax). This was endorsed by an abrupt change in relative growth of the chela approximately when crabs reach sexual maturity [
34,
89,
90]. Admittance of a break point for transition to succeeding growth phases readily adapts a notion of curvature in geometrical space. This paradigm is also referred as non-loglinear allometry in Huxley’s original interpretation [
70,
91,
92]. Extension of Huxley’s break point idea allows consideration of polyphasic loglinear allometry (PLA) [
91,
93,
94,
95]. This approach characterizes heterogeneity of the response in geometrical space by composing the range of covariate into sectors separated by break points. Each tract associates to a linear sub model. Therefore, as opposed to examination through MCA-DNLR schemes, endorsing PLA break-point borne curvature offers a way to add complexity while maintaining the essence of traditional allometry. However, curvature as comprehended in the traditional allometric perspective is also controversial. For instance, its manifestation has been associated to distortion produced by the use of a logarithmic transformation itself [
64,
96]. However, Mascaro et al. [
88] emphasizes that the occurrence of curvature has nothing to do with the use of logarithmic transformations since deviations from perfect log-linear allometry can be explained on grounds of methodological factors related to data. In conceiving the aims of the present research we abided by this perspective and offer methods that in our view allow efficient identification of MCA patterns through logtransformation methods. Nevertheless, as we shall explain ahead, present methods could also embrace efficient identification of MCA forms in direct scales.
Following Bervian et al. [
77] and Echavarria-Heras et al. [
92], we can conceive MCA as a generalization of Huxley’s formula of simple allometry, namely,
with
and
belonging to domains
and
one to one, both contained in
, and where
and
are real functions, with
having a range in
. Moreover, as we explain in the methods section, logtransformation of Equation (2) leads to a generalization of a TAMA arrangement that hosts curvature in geometrical space in a direct and intuitive way. Moreover, Mascaro et al. [
88] recommends three ways of addressing this sort of curvilinearity. One adopts a PLA approach by indorsing separation of data in order to contemplate local linear models with the aim of taking into account heterogeneity of effects of the covariate [
97,
98,
99]. A second one is by fitting a polynomial model in geometrical space [
100,
101,
102]. A final one is by fitting a heteroscedastic non-linear regression model in arithmetical scales [
43]. Echavarria Heras et al. [
92] demonstrated that each one of the curvature models suggested by Mascaro et al. [
88] can be derived as logical consequents of suitably chosen forms of the scaling functions
and
in Equation (2). Moreover, allometric proxies of plant biomass units produced by agreeing protocols fitted in geometrical space exhibited high consistency with observed values. This suggests that logarithmic transformation methods could be dependable provided sustaining fitting schemes bear suitable complexity. In this sense, the model of Equation (2) could provide the required approach. Nevertheless, procedures addressed by Echavarria-Heras et al. [
92] only amount to particular characterizations of
and
. Moreover, the problem of identification of these functions in a general set up has not been yet undertaken. The present research is an attempt to address this subject. We advance two general identification procedures for the model of Equation (2). One characterizes
and
one to one by means of independent polynomial forms to be fitted in geometrical space. An alternative approach takes on an operating regime-based modeling slant (ORBM) [
103,
104]. This also allows independent characterizations of
and
from weighted mixtures of linear sub models. It turns out that a PLA perspective can be also hosted by the paradigm of Equation (2) by choosing involved scaling functions in proper forms. Moreover, the ORBM approach undertaken brings about an interpolation device aimed at identifying whatever MCA form renders necessary in direct arithmetical scales. This regardless of complexity of inherent allometric response-covariate linkage in named scales. This construct provides a criterion to test performance of geometrical space methods resulting from the MCA model of Equation (2). Moreover, the present approaches permit adaptation of an index denoted here through the symbol
and aimed at detecting to what extent the complexity of the MCA form in arithmetic space drives curvature in geometrical space. Performance metrics of fits achieved on both real and simulated data suggest that the presently offered geometrical space protocols could entail highly consistent projection of plant biomass units. Beyond providing empirical convenience, the present examination demonstrates that adoption of the MCA paradigm of Equation (2) and the offered identification approaches can overcome controversial views pertaining to suitability of analysis method in allometry.
This paper is organized as follows. In the materials and methods, we specify datasets. Then, we explain formulae and notation conventions behind the considered MCA identification approaches. This specifies both geometrical space as well as direct scales regression protocols. We explain derivation of curvature index formulae and simulation procedures aimed to verify dependability of the MCA approach. The results section analyses the capabilities of the proposed MCA arrangements to produce dependable fits based on real and simulated data. A discussion section highlights the advantages of the present constructs for efficient allometric projection of plant biomass units several Apendices provide details of derived formula and important complementary explanation. A supplementary files section provides data and computational codes backing the results.
4. Discussion
The flux and storage of carbon in overall plant biomass influences global carbon cycle. Traditional approaches to quantification of related carbon fluxes and stocks have essentially relied on allometric methods [
1,
19,
22,
100]. Usually, in this approach, directly obtained measurements of a trait
and the scaling model of Equation (1) allow non-destructive estimation of values of a plant biomass unit
. However, the acquired projections of the response values are markedly sensitive to numerical changes in composing parameters
and
. Moreover, local factors can induce a certain extent of variability on estimates. The influences of analysis method, error structure, sample size, and overall data quality in the study of biological scaling have been widely acknowledged [
25,
26,
27,
131]. Therefore, error propagation of estimates and its influence on overall precision pose important queries, on dependability of allometric surrogates of plant biomass units.
Particularly relevant is the influence of the analysis method. This nourishes a vivid controversy that divides allometric practice into two schools. Views emphasize traditional identification of parameters
and
via logtransformation set biased results, thereby recommending direct non-linear regression analysis. However, defenders of a traditional perspective conceive logtransformation and allometry as inseparable. We have here embraced a view that controversy can be remedied by addressing adequate complexity of an inherent allometric relationship on the direct scales. Alongside this, it becomes necessary choosing a proper form of correction factor for bias of retransformation. In order to validate the present view, we adopted the MCA model of Equation (2), that assimilates necessary complexity through scaling parameters expressed as functions
and
depending on covariate. A particular form of this paradigm was addressed by Bervian et al. [
77] and its generalization into the form offered here was suggested by Echavarria Heras et al. [
132]. A formal exploration established this construct as a source model from which conventional models aimed to address curvature in geometrical space [
88] could be derived. Nevertheless, consideration of MCA there removed the circumscribed general identification problem. This can be conceived as using regression protocols and data pairs
in order to unfold forms of
and
as independent functions granting highest reproducibility. We aimed here to contribute on the subject. This explains present advancement of geometrical space identification methods resulting from Weierstrass approximation theory, essentially epitomized by the
approach, as well as, ORBM alternates represented here by
and
. An ORBM approach also nourished adaptation of the
arrangement aimed to analyse MCA forms in direct scales. The results in
Appendix E explain that a
scheme can automatically adapt complexity as required to identify a pattern conforming to the formula of simple allometry. The extraordinary approximation capabilities of the TSK fuzzy model [
133,
134] endow
interpolation of allometric patterns in direct scales irrespective of intrinsic complexity. Moreover, the
arrangement makes it possible to detect break points for transition among allometric phases which is unattainable by MCA-DNLR methods [
132].
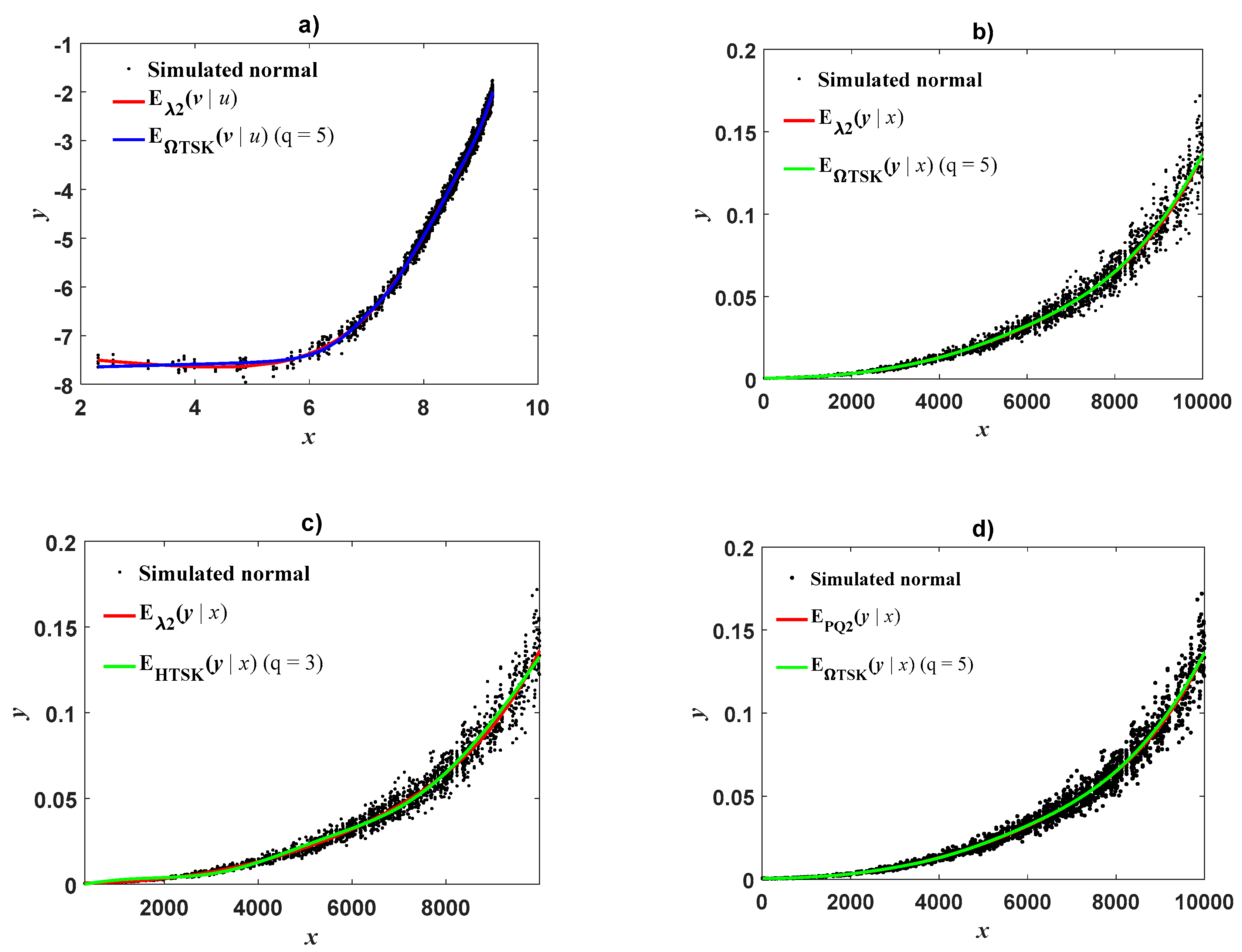
The results of
Appendix E also reveal that a logarithmic transformation itself cannot be blamed for curvature detected in geometrical space. Simulation assays exhibit that geometrical space methods provide reliable proxies on condition that CF is chosen in a suitable form. However, the
scheme could entail steady CF free retransformation to direct scales (
Figure 3d and
Figure 4d). This suggests that a suitable integration of complexity becomes a key factor in driving dependability of allometric projection based on protocols fitted on log-scales. Adoption of an ORBM approach also allowed adaptation of index κ(x) given by Equation (33) that interprets as a measure of curvature in geometrical space implied by the complexity of inherent allometric pattern in direct scales. Moreover,
allows parallel criterion to statistical performance metrics for model selection. Results of simulation runs reveal that information based on
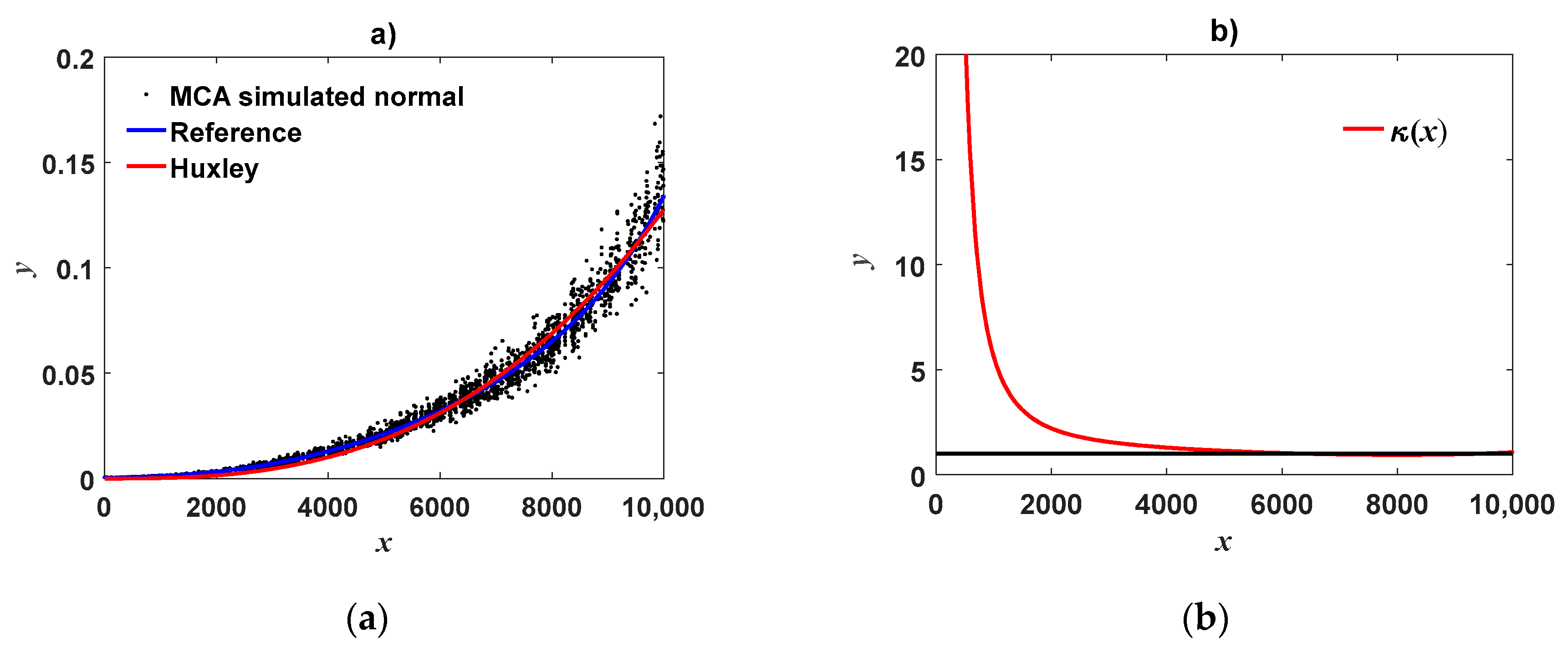
can unravel efficiency of DNLR being only putative. Indeed, visual appraisal of a fit of Huxley’s model of simple allometry to simulated MCA replicates could suggest consistent reproducibility (
Figure 1a). However, a concurrent plot of
index (
Figure 1b) exhibits noticeable deviations from the line
for small values of the covariate. Similarly marked deviations of the
from the line
are shown in the biphasic fit to the Ramirez-Ramirez et al. [
6] data (
Figure 8d). Comparable effects are displayed for small eelgrass leaves (
Figure 12d). This explains manifestation of curvature that was corroborated by dependability of the biphasic forms of the
and
protocols. Therefore, clinging to Huxley’s model, and a non-linear regression protocol in direct scales can at most offer an apparent empirical convenience tied to simplicity, but it may leave behind relevant biological information. This concerns the existence of break points for transition between successive growth phases that are undetected by Huxley’s model of simple allometry and are well recognized by the PLA paradigm [
91,
93,
94,
95]. Likewise, identified break point in
Zostera marina may perhaps be interpreted as a threshold beyond which the plant promotes generation of a relatively greater amount of tissue in leaves to enhance resistance to drag force effects that induce damage and separation from shoots. As a result, allometric scaling parameters among small and large leaves could be different [
30]. Similarly, a break point in the Ramirez-Ramirez [
6] data suggest differential allometric rules depending on tree size. Indeed, resource allocation to different tree attributes like diameter or height could differ during growth as a response to changed environmental-biotic conditions, as well as, to variations in resource availability. In this perception, a risk of suppression by competitors may induce small trees to dispense more resources to increase height. Then, beyond a threshold height at which suppression risk is at a minimum, resources may be assigned to horizontal growth parameters like diameter, crown and root cover [
6,
135]. Thus, since the aim of allometric examination is comprehending the biological processes that bring about covariance among traits, analytical methods entailing break point identification must be preferred. This explains adaptation of the empirical procedure of
Appendix A aiming to extending the
protocol for break point detection. In particular, the contemplated
approach could be a highly biologically meaningful model of allometry, because it can model the break points while keeping the meanings of allometric exponents as Huxley’s original formulation. Moreover, as exemplified by the addressed study cases, the intersection of firing strength factors provides a reliable criterion to break point identification which could be expected to deliver reliable results in the general settings of allometric examination.
5. Conclusions
We aimed here to address the general identification problem of the MCA model of Equation (2). This conceived using regression protocols and data pairs in order to unfold and as independent functions granting highest reproducibility. This task was addressed here in two ways. A first one was through Weierstrass approximation theory that anticipated and as determined by Equation (8) through Equation (10) and that epitomize by the form in geometrical space. A second way to address the general identification problem relied on an ORBM slant. This conceived and in the forms given by Equation (22) and Equation (23) respectively, and that engendered the , and protocols also intended to be fitted in geometrical space. This ORBM approach is also behind the adaptation of the form that takes advantage of the oustanding approximation capabilities of the general output of a first order TSK fuzzy model grants polyphasic interpolation of inherent MCA pattern in arithmetical scales.
A consistent fit of the
arrangement could set up reliable reproducibility by direct retransformation to arithmetical scales. Moreover, this approach can also entail estimation of break point inherent to biphasic patterns. Concomitant broken line
or weighted linear segment mixture
regression could also offer reasonable MCA identification in many instances of allometric examination. Nevertheless, it is opportune to emphasize gains derived from adoption of a
approach. This construct bears a flexible computational assembly that allows intuitive and interactive integration of previous knowledge into the analysis [
132]. This gives
a relative advantage over the conventional protocols addressed here. Moreover, analysis of model performance metrics show that the mean response function
brings about similar reproducibility strength as its
counterpart. Therefore,
could grant efficient identification of allometric proxies indistinctly of inherent complexity. This device also drives direct and intuitive identification of multiple break points for transition among successive growth phases comprising a PLA pattern. It is also worth highlighting that the extraordinary approximation capabilities of a first-order KSK fuzzy model that engenders
grant reliable identification of the scaling functions
and
by retransforming fitted form of
to arithmetical scales. We can then consider that the essential aim of this contribution was fulfilled. The TSK arrangement also allows efficient implementation of the
criterion for curvature assessment. The identification schemes offered can be conveniently implemented on available data by using the codes provided. In summary, the presented MCA paradigm, along with identification schemes plus a suitable CF form could grant efficient projection of plant biomass units. This may well be also extended to the general settings of allometric examination. Nevertheless, we acknowledge that further substantiation is deemed necessary before proposed MCA could be adopted as a comprehensive tool for the analysis of allometric data. Meanwhile, present results endorse the relevance of the excerpt of Kerkhoff and Enquist [
81] on the hopelessness of a divergence between traditional logarithmic transformation and direct non-linear analysis slants in allometry. Surely, the efficiency of the proposed MCA arrangement can elucidate this glowing controversy.