Pseudo-Static Analysis on the Shifting-Girder Process of the Novel Rail-Cable-Shifting-Girder Technique for the Long Span Suspension Bridge
Abstract
:1. Introduction
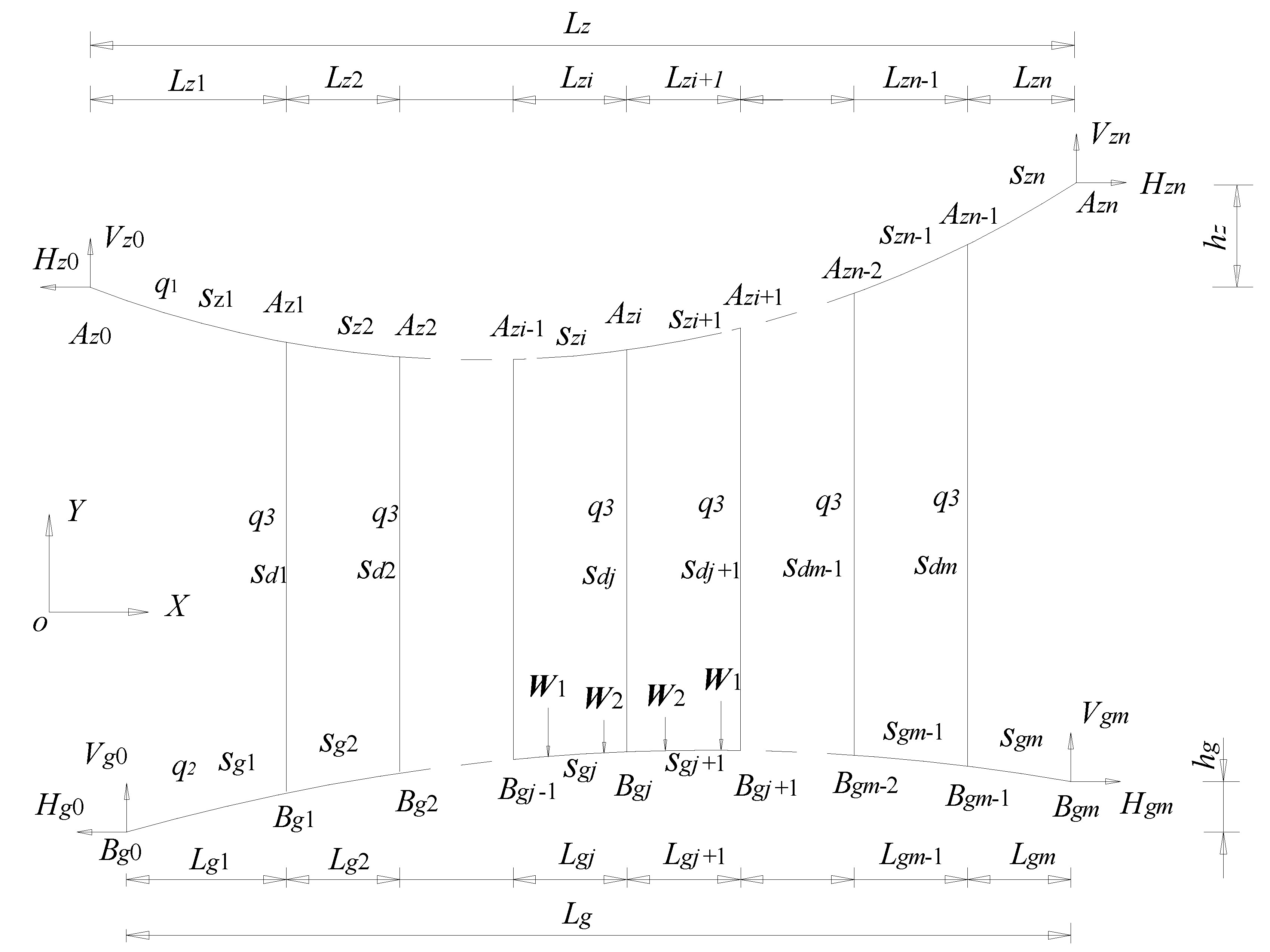
2. Mechanical Model of Shifting-Girder System Undergoing Girder Loads
2.1. Basic Assumptions
- (1)
- The flexible cable can only be tensioned, and compression and bending are not considered.
- (2)
- The stress-strain of the flexible cable satisfies Hooke’s law.
- (3)
- The section area before and after deformation is unchanged to compute the tensile stiffness of the main-cable, rail-cable, and sling.
- (4)
- The main-cable, rail-cable, and sling are uniform in span length with a constant cross-sectional area and elastic modulus.
- (5)
- The friction between the rail-cable and hanging saddle is ignored, due to the fact that the hanging saddle is smooth and their relative deformations are small. The sling has no inclination. The weight of the steel truss girder and the shifting-girder trolley are known.
- (6)
- The contribution of the girder to the systematical stiffness is not considered in the shifting-girder process, i.e., all girder segments are hinged.
2.2. Global Mechanical Model
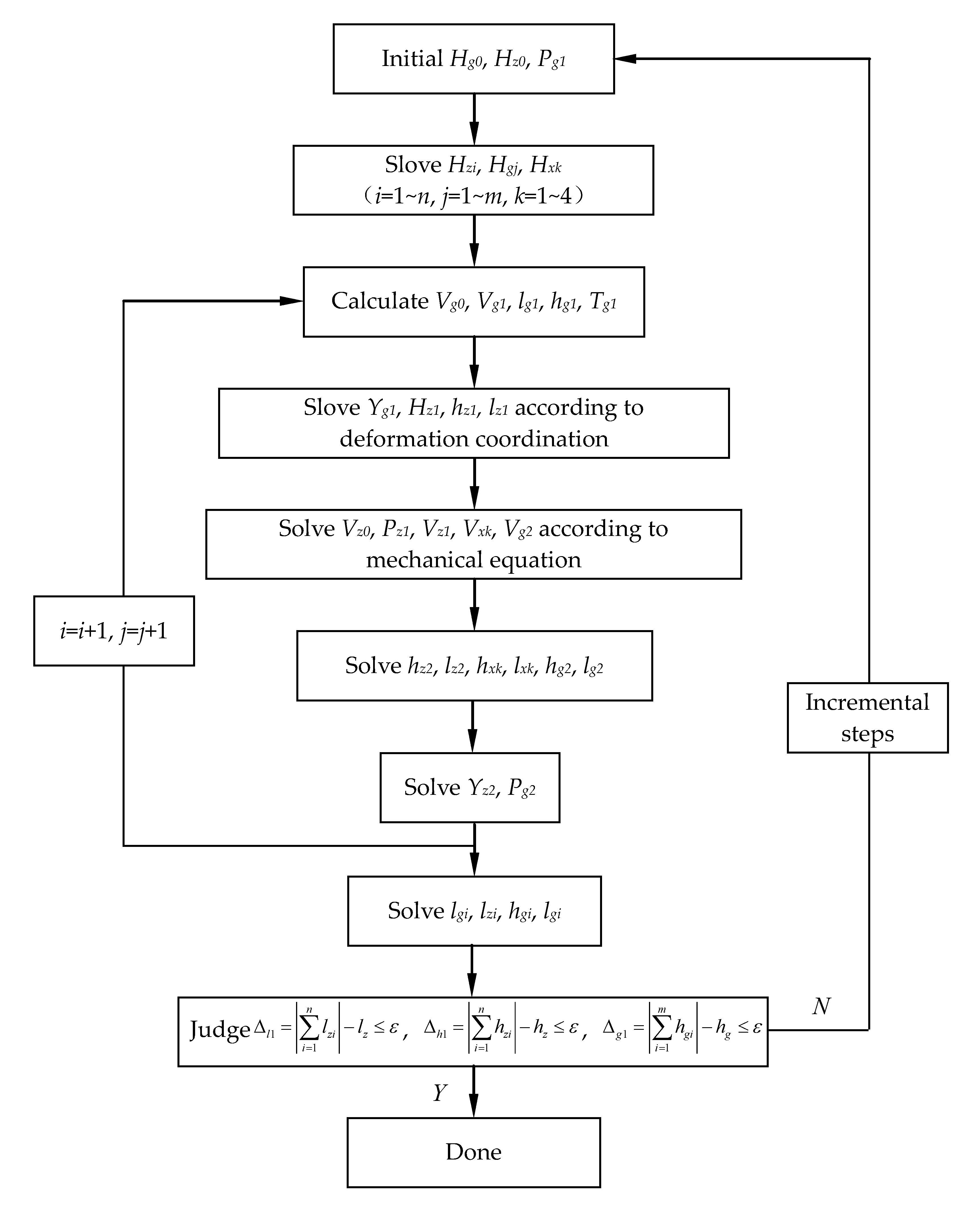
2.3. Solution to the Shifting-Girder System
3. Global Model Test of Shifting-Girder System Undergoing Girder Loads
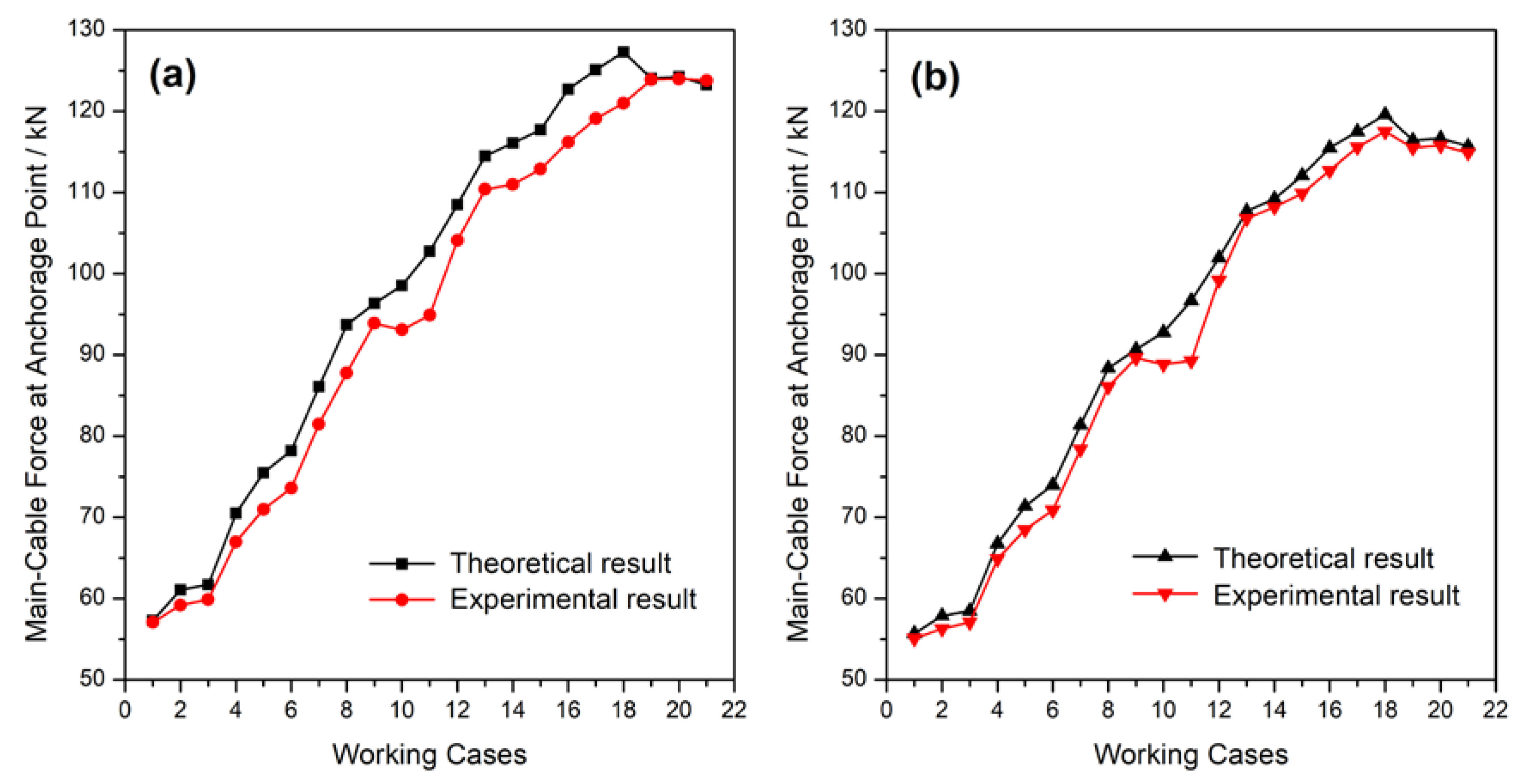
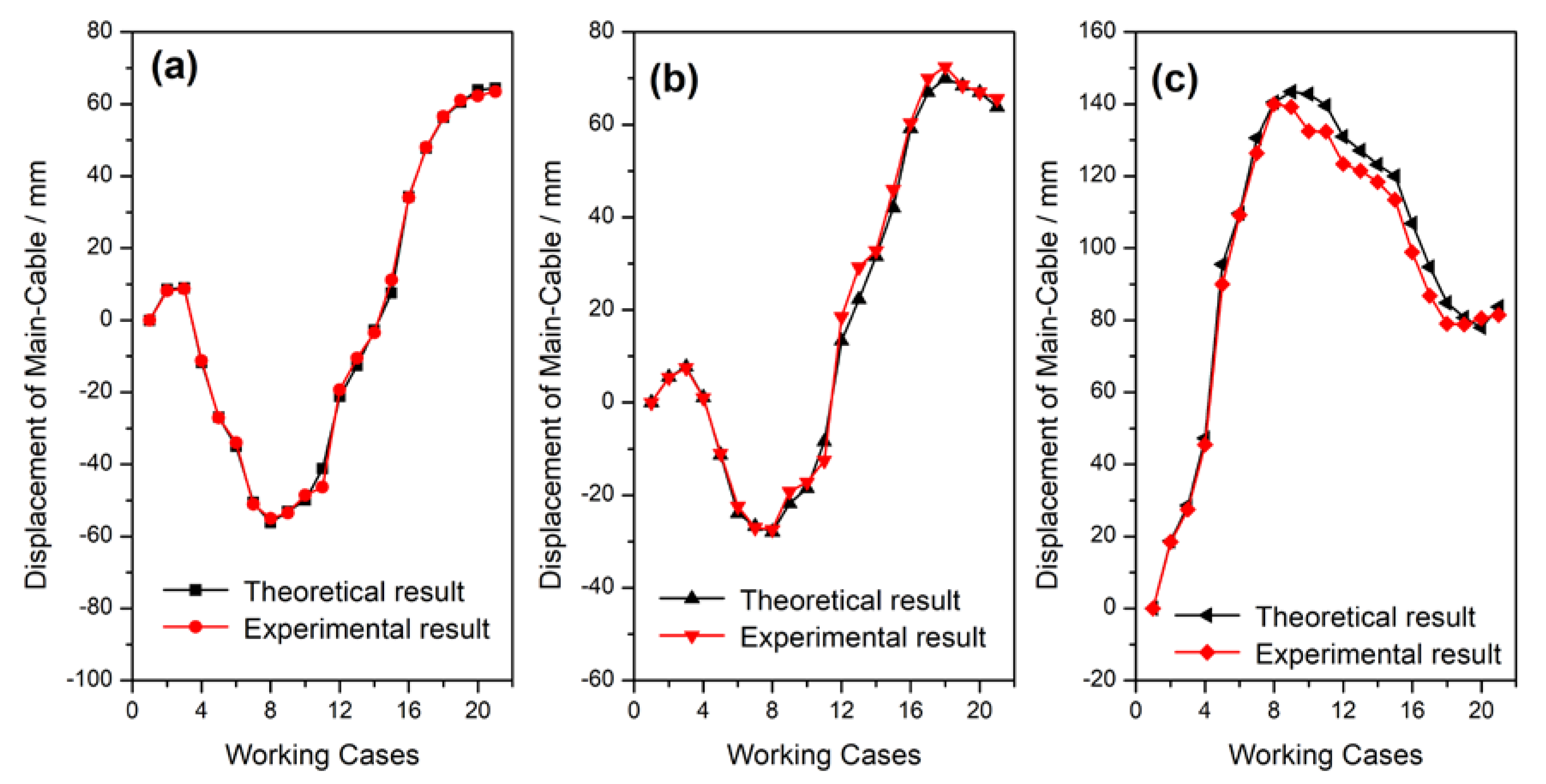
4. Discussion on Results
5. Conclusions
- (1)
- The theoretical results match well with the measured experimental results of the global model test for the 21 working conditions of the shifting-girder system undergoing girder loads. The differences of the forces and deflections from these two methods are small for most of the working conditions, except the maximum deviation of the measured force of rail-cable from the theoretical value reaches 6% in only a few working cases.
- (2)
- The main-cable’s forces at the anchorage points on both sides are increasing in the erecting process of girder segments. The variation of the incremental cable forces is small in the erecting courses of the subsequent girder segments.
- (3)
- The vertical deflections of the main-cable at the locations of both l/4 and 3/4 main span first decrease and then increase in the erecting process, and reach the maximum value when the erections of the girder segments are completed, due to the symmetry of the global structure along the mid-span. The deflection of the main-cable at mid-point first increases and then decreases in the erecting progress, and it reaches the maximum value when 1/4 of girders are completed.
- (4)
- The horizontal deflections of the two towers are increasing at all erecting times, and both point to the mid-span. The variations of these two deflections are small at the erecting stages of the last several girder segments.
- (5)
- The measured rail-cable force of the model test has a slight deviation from the theoretical value, while the variation is basically less than 5% and reaches a maximum of 6% in a few working cases.
- (6)
- The correctness and effectiveness of the presented theoretical method is validated by the experimental results of indoor model test. It is able to obtain the forces and the reflections of the double-layer cable system of the shifting-girder system undergoing girder loads. The accuracy and results satisfy the requirement of practical engineering application, and this simplified method is suitable to solve the RCSG system under load-condition for the long span suspension bridge adopting the RCSG technique for construction. Also, the modeling and studying of the presented theoretical method can supply references for the similar double-layer projects carrying loads.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karoumi, R. Some modeling aspects in the nonlinear finite element analysis of cable supported bridges. Comput. Struct. 1999, 71, 397–412. [Google Scholar] [CrossRef]
- Erdoğan, H.; Gülal, E. The application of time series analysis to describe the dynamic movements of suspension bridges. Nonlinear Anal.-Real. 2009, 10, 910–927. [Google Scholar] [CrossRef]
- Huang, M.H.; Thambiratnam, D.P.; Pererab, N.J. Vibration characteristics of shallow suspension bridge with pre-tensioned cables. Eng. Struct. 2005, 27, 1220–1233. [Google Scholar] [CrossRef]
- Miyata, T.; Matsumoto, K.; Yasuda, M. Circumstances of wind-resistant design examinations for very long suspension bridge. J. Wind Eng. Ind. Aerod. 1992, 42, 1371–1382. [Google Scholar] [CrossRef]
- Cheng, J.; Xu, M.; Xu, H. Mechanical performance analysis and parametric study of double-deck plate-truss composite steel girders of a three-tower four-span suspension bridge. Eng. Struct. 2019, 199. [Google Scholar] [CrossRef]
- Wang, H.; Li, A.; Li, J. Progressive finite element model calibration of a long-span suspension bridge based on ambient vibration and static measurements. Eng. Struct. 2010, 32, 2546–2556. [Google Scholar] [CrossRef]
- An, X.; Gosling, P.D.; Zhou, X. Analytical structural reliability analysis of a suspended cable. Struct. Saf. 2016, 58, 20–30. [Google Scholar] [CrossRef]
- Kim, H.K.; Lee, M.J.; Chang, S.P. Determination of hanger installation procedure for a self-anchored suspension bridge. Eng. Struct. 2006, 28, 959–976. [Google Scholar] [CrossRef]
- Adanur, S.; Günaydin, M.; Altunişik, A.C.; Sevim, B. Construction stage analysis of Humber Suspension Bridge. Appl. Math. Model. 2012, 36, 5492–5505. [Google Scholar] [CrossRef]
- Cho, T.; Kim, T.S. Probabilistic risk assessment for the construction phases of a bridge construction based on finite element analysis. Finite Elem. Anal. Des. 2008, 44, 383–400. [Google Scholar] [CrossRef]
- Ko, J.M.; Xue, S.D.; Xu, Y.L. Modal analysis of suspension bridge deck units in erection stage. Eng. Struct. 1998, 20, 1102–1112. [Google Scholar] [CrossRef]
- Xu, Y.L.; Ko, J.M.; Yu, Z. Modal analysis of tower-cable system of Tsing Ma long suspension bridge. Eng. Struct. 1997, 19, 857–867. [Google Scholar] [CrossRef]
- Bakis, K.N.; Limebeer, D.J.N.; Williams, M.S.; Graham, J.M.R. Passive aeroelastic control of a suspension bridge during erection. J. Fluid. Struct. 2016, 66, 543–570. [Google Scholar] [CrossRef]
- Li, S.; An, Y.; Wang, C.; Wang, D. Experimental and numerical studies on galloping of the flat-topped main-cables for the long span suspension bridge during construction. J. Wind Eng. Ind. Aerod. 2017, 163, 24–32. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, L.; Ding, Q.; Ge, Y. Flutter performance and improvement for a suspension bridge with central-slotted box girder during erection. J. Wind Eng. Ind. Aerod. 2018, 179, 118–124. [Google Scholar] [CrossRef]
- Diana, G.; Yamasaki, Y.; Larsen, A.; Rocchi, D.; Portentoso, M. Construction stages of the long span suspension Izmit Bay Bridge: Wind tunnel test assessment. J. Wind Eng. Ind. Aerod. 2013, 123, 300–310. [Google Scholar] [CrossRef]
- Yi, Z.; Wang, Z.; Zhou, Y.; Stanciulescu, I. Modeling and vibratory characteristics of a mass-carrying cable system with multiple pulley supports in span range. Appl. Math. Model. 2017, 49, 59–68. [Google Scholar] [CrossRef]
- Liu, G.; Peng, Y.; Zhou, P.; Tong, Y.; Pang, S. Research on erection methods of steel stiffening truss girder for Baling River bridge. J. Highway Transp. Res. Dev. 2009, 4, 50–56. [Google Scholar] [CrossRef]
- Pan, Q. Mechanical Analysis and Experimental Research for Rail-Cable Launching Technology about Suspension Bridge with Separated Tower and Stiffening Girder. Ph.D. Thesis, School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha, China, 2015; pp. 14–34. (In Chinese). [Google Scholar]
- Hu, J.H.; Shen, R.L. Technical innovations of the Aizhai Bridge in China. J. Bridge Eng. 2014, 19. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Li, Y.J.; Yu, M.W.; Hu, H.H.; Hu, J.H. Study of the rock foundation stability of the Aizhai suspension bridge over a deep canyon area in China. Eng. Geol. 2015, 198, 65–77. [Google Scholar] [CrossRef]
- Fang, Z.; Zhang, K.Y.; Tu, B. Experimental investigation of a bond-type anchorage system for multiple FRP tendons. Eng. Struct. 2013, 57, 364–373. [Google Scholar] [CrossRef]
- Sun, Y.; Zhu, H.P.; Xu, D. A specific rod model based efficient analysis and design of hanger installation for self-anchored suspension bridges with 3D curved cables. Eng. Struct. 2016, 110, 184–208. [Google Scholar] [CrossRef]
- Huang, Y.H.; Fu, J.Y.; Gan, Q.; Wang, R.H.; Pi, Y.L.; Liu, A.R. New method for identifying internal forces of hangers based on form-finding theory of suspension cable. J. Bridge Eng. 2017, 22, 04017096. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V.; González-Vidosa, F. Life cycle impact assessment of corrosion preventive designs applied to prestressed concrete bridge decks. J. Clean. Prod. 2018, 196, 698–713. [Google Scholar] [CrossRef]
- Yepes, V.; Martí, J.V.; García-Segura, T.; González-Vidosa, F. Heuristics in optimal detailed design of precast road bridges. Arch. Civ. Mech. Eng. 2017, 17, 738–749. [Google Scholar] [CrossRef]
- Pan, Q.; Yan, D.H.; Yi, Z.P. Form-finding analysis on the rail-cable shifting system of the long span suspension bridges. Appl. Sci. 2018, 8, 2033. [Google Scholar] [CrossRef]
- Yi, Z.; Yuan, M.; Tu, G.; Zeng, Y. Modeling of the multi-cable supported arch and a novel technique to investigate the natural vibratory characteristics. Appl. Math. Model. 2019, 75, 640–662. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, J.; Zhao, Y.; Chen, L. Effects of temperature variations on nonlinear planar free and forced oscillations at primary resonances of suspended cables. Nonlinear Dyn. 2017, 89, 2815–2827. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, C.; Chen, L.; Peng, J. Nonlinear vibration behaviors of suspended cables under two-frequency excitation with temperature effects. J. Sound Vib. 2018, 416, 279–294. [Google Scholar] [CrossRef]
- Sun, C.; Zhao, Y.; Wang, Z.; Peng, J. Effects of longitudinal girder vibration on non-linear cable responses in cable-stayed bridges. Eur. J. Environ. Civ. Eng. 2017, 21, 94–107. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, M.; Li, H.; Song, G. Experimental investigations on seismic control of cable-stayed bridges using shape memory alloy self-centering dampers. Struct. Control Health 2018, 25, e2180. [Google Scholar] [CrossRef]
- Liu, M.; Song, G.; Li, H. Non-model-based semi-active vibration suppression of stay cables using Magneto-Rheological fluid dampers. Smart Mater. Struct. 2007, 16, 1447–1452. [Google Scholar] [CrossRef]
- Liu, M.; Sethi, V.; Song, G.; Li, H. Investigation of locking force for stay cable vibration control using magnetorheological fluid damper. J. Vib. Acoust. 2008, 130, 054504. [Google Scholar] [CrossRef]



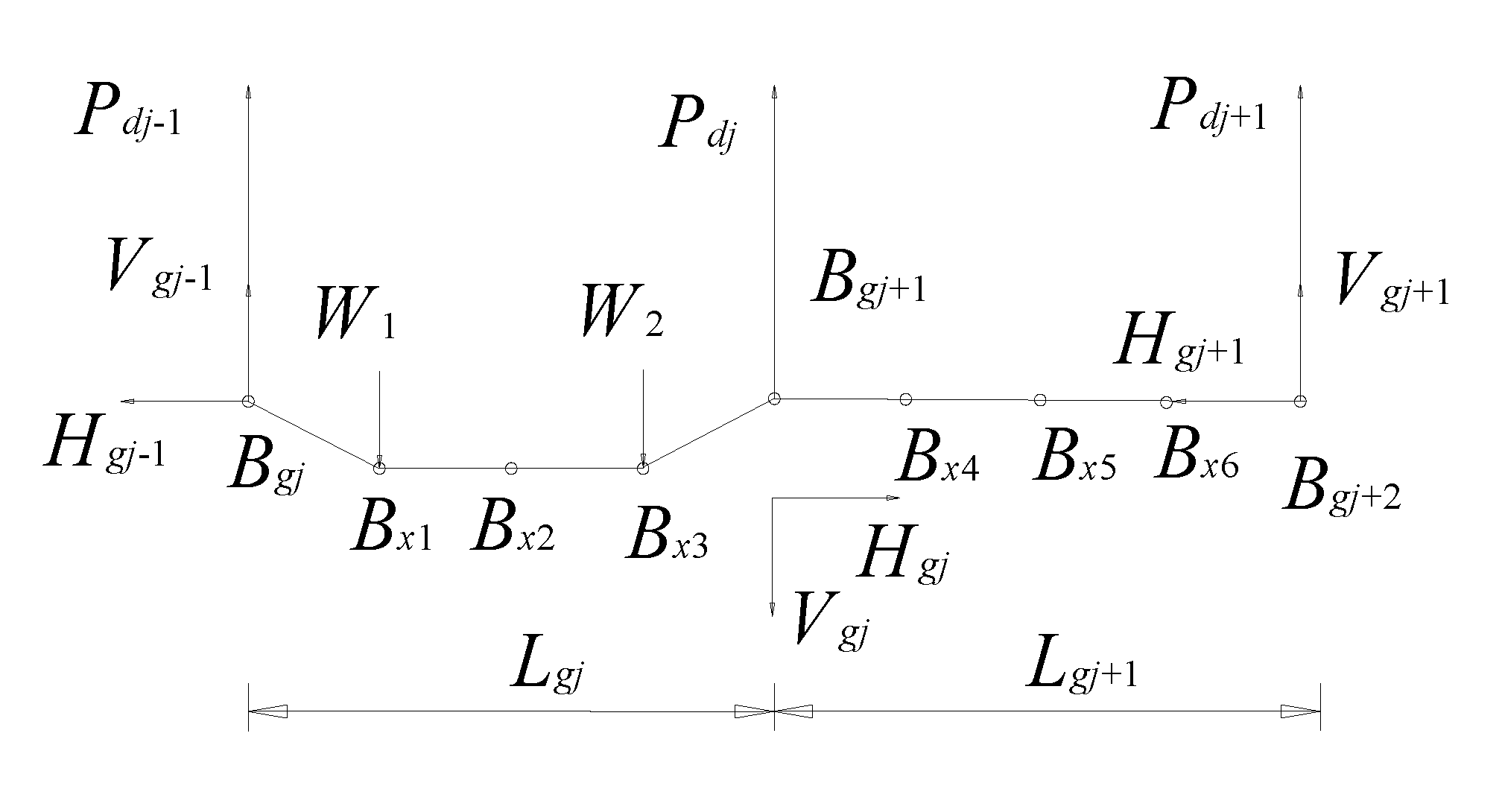
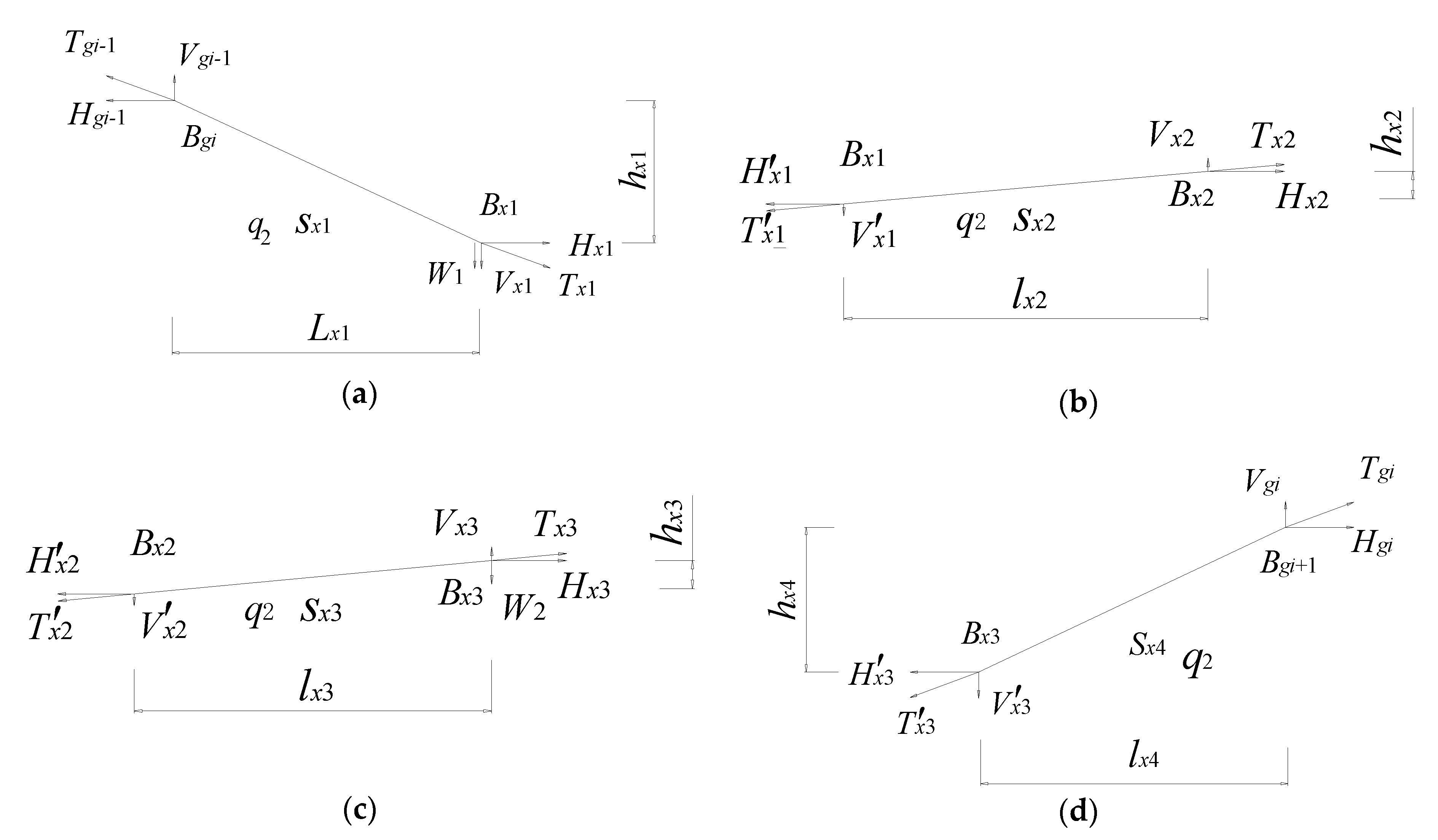



| Working Cases | Contents | Working Cases | Contents |
|---|---|---|---|
| 1 | adjusting empty cables | 12 | erection of girders B19–21, B17’–19’ |
| 2 | tension of rock-anchor cable | 13 | erection of girders B18, B16’ |
| 3 | tension of rail-cable | 14 | erection of girders B17, B15’ |
| 4 | erection of girders B36 | 15 | erection of girders B16, B14’ |
| 5 | erection of girders B35, B33’ | 16 | erection of girders B13–15, B11’–13’ |
| 6 | erection of girders B34, B32’ | 17 | erection of girders B10–12, B8’-10’ |
| 7 | erection of girders B31-33, B29’–31’ | 18 | erection of girders B7–9, B5’–7’ |
| 8 | erection of girders B28-30, B26’–28’ | 19 | erection of girders B4–6, B2’–4’ |
| 9 | erection of girders B25-27, B23’–25’ | 20 | erection of girders B3, B1’ |
| 10 | erection of girders B24, B22’ | 21 | erection of girders B2, B1 |
| 11 | erection of girders B22–23, B20’–21’ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Q.; Yi, Z.; Yan, D.; Xu, H. Pseudo-Static Analysis on the Shifting-Girder Process of the Novel Rail-Cable-Shifting-Girder Technique for the Long Span Suspension Bridge. Appl. Sci. 2019, 9, 5158. https://doi.org/10.3390/app9235158
Pan Q, Yi Z, Yan D, Xu H. Pseudo-Static Analysis on the Shifting-Girder Process of the Novel Rail-Cable-Shifting-Girder Technique for the Long Span Suspension Bridge. Applied Sciences. 2019; 9(23):5158. https://doi.org/10.3390/app9235158
Chicago/Turabian StylePan, Quan, Zhuangpeng Yi, Donghuang Yan, and Hongsheng Xu. 2019. "Pseudo-Static Analysis on the Shifting-Girder Process of the Novel Rail-Cable-Shifting-Girder Technique for the Long Span Suspension Bridge" Applied Sciences 9, no. 23: 5158. https://doi.org/10.3390/app9235158
APA StylePan, Q., Yi, Z., Yan, D., & Xu, H. (2019). Pseudo-Static Analysis on the Shifting-Girder Process of the Novel Rail-Cable-Shifting-Girder Technique for the Long Span Suspension Bridge. Applied Sciences, 9(23), 5158. https://doi.org/10.3390/app9235158




