Abstract
This study paper presents a comprehensive review of virtual inertia (VI)-based inverters in modern power systems. The transition from the synchronous generator (SG)-based conventional power generation to converter-based renewable energy sources (RES) deteriorates the frequency stability of the power system due to the intermittency of wind and photovoltaic (PV) generation. Unlike conventional power generation, the lack of rotational inertia becomes the main challenge to interface RES with the electrical grid via power electronic converters. In the past several years, researchers have addressed this issue by emulating the behavior of SG mathematically via pulse width modulation (PWM) controller linked to conventional inverter systems. These systems are technically known as VI-based inverters, which consist of virtual synchronous machine (VSM), virtual synchronous generator (VSG), and synchronverter. This paper provides an extensive insight into the latest development, application, challenges, and prospect of VI application, which is crucial for the transition to low-carbon power system.
1. Introduction
Over the last decades, global electricity demand has increased significantly [1]. To cater to these demands, many countries are utilizing environmentally friendly power generation such as solar photovoltaic (PV) energy and wind energy. Renewable energy sources (RES) is much preferred because of its merit factors, including cost-effectiveness, energy efficiency, and sustainability [2]. The tremendous growth of RES gravitates modern power grid towards the inverter dominated power system [3], from the conventional synchronous generator (SG) rotational generator dominated power system [4]. Grid-connected or grid-tied RES is beneficial in improving the voltage profile, increasing the reliability of the power system, and controlling the active and reactive power flow [5]. Despite the numerous advantages, studies have shown that high penetration of grid-connected RES introduces critical frequency stability issues [6] and power grid security issues [7], which include the following:
- RES exhibits low or non-existent inertial responses which lead to frequency instability [8].
- In the event of a fault and sudden load change, the system frequency deviates from the nominal frequency [9].
- The frequency nadir and rate of change of frequency (RoCoF) are expected to be higher in the event of a fault or sudden load change, which activates the load-shedding controller to trip frequency relay [10].
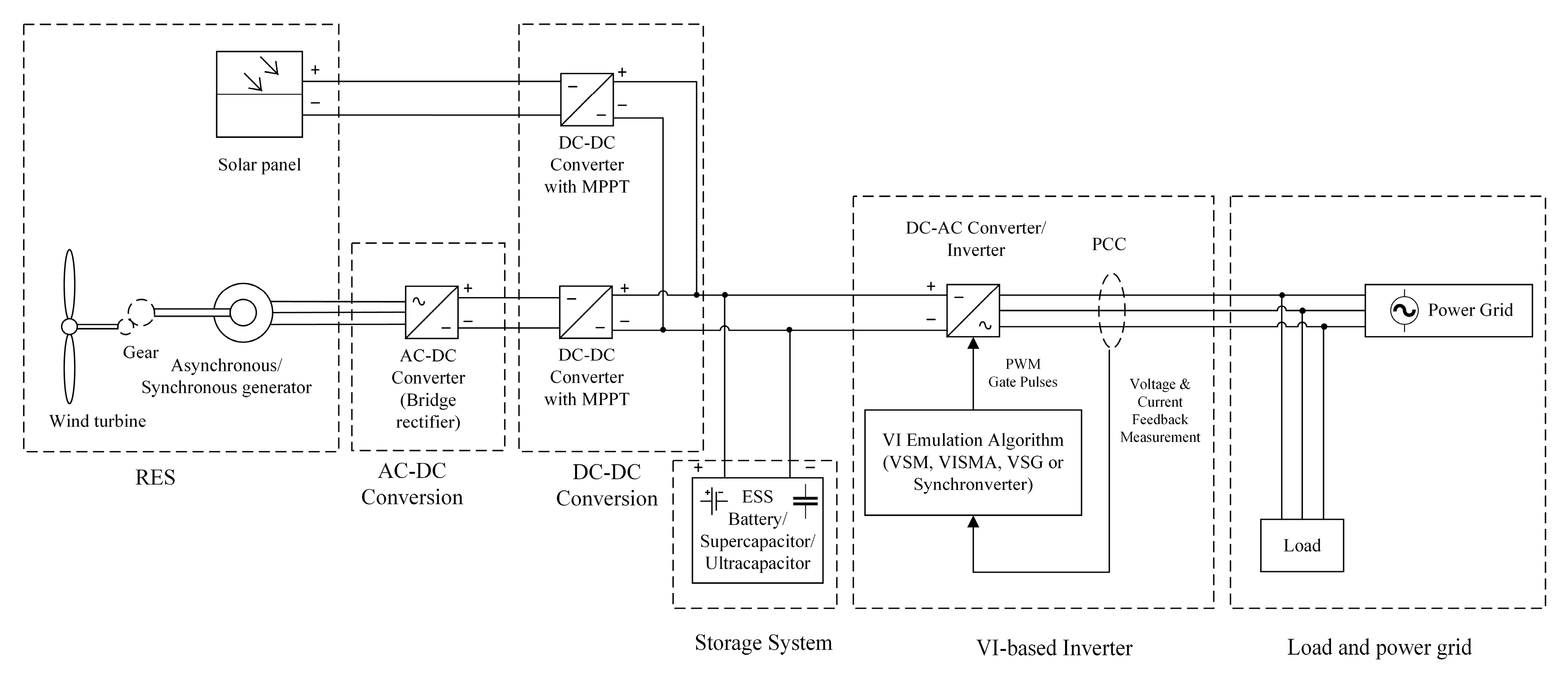
By interfacing RES using a conventional inverter, it degrades the frequency stability due to lack of rotating masses [11]. The RES is intermittent and thus by interfacing RES to the grid via a fast-responding inverter, the RES is presented to grid as a fast-dynamic system [12]. This quick interaction causes frequency, phase angle, and voltage amplitude instability [13]. It causes more significant frequency deviations and transient power exchanges in the event of a power fault. To solve the problems introduced by grid-connected RES, virtual inertia (VI), also known as artificial inertia or synthetic inertia control strategy, has been proposed and researched extensively in conventional inverters. VI emulates the inertia response of a traditional synchronous machine (SM) mathematically via pulse width modulation (PWM). Figure 1 presents the general connection of VI-based inverter in grid-connected solar and wind energy.
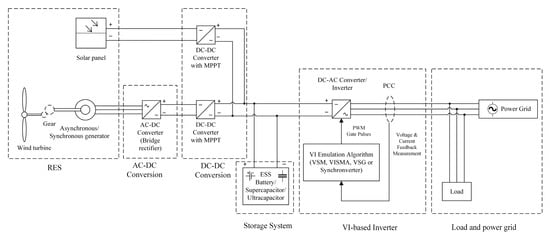
Figure 1.
The general connection of grid-connected solar and wind energy.
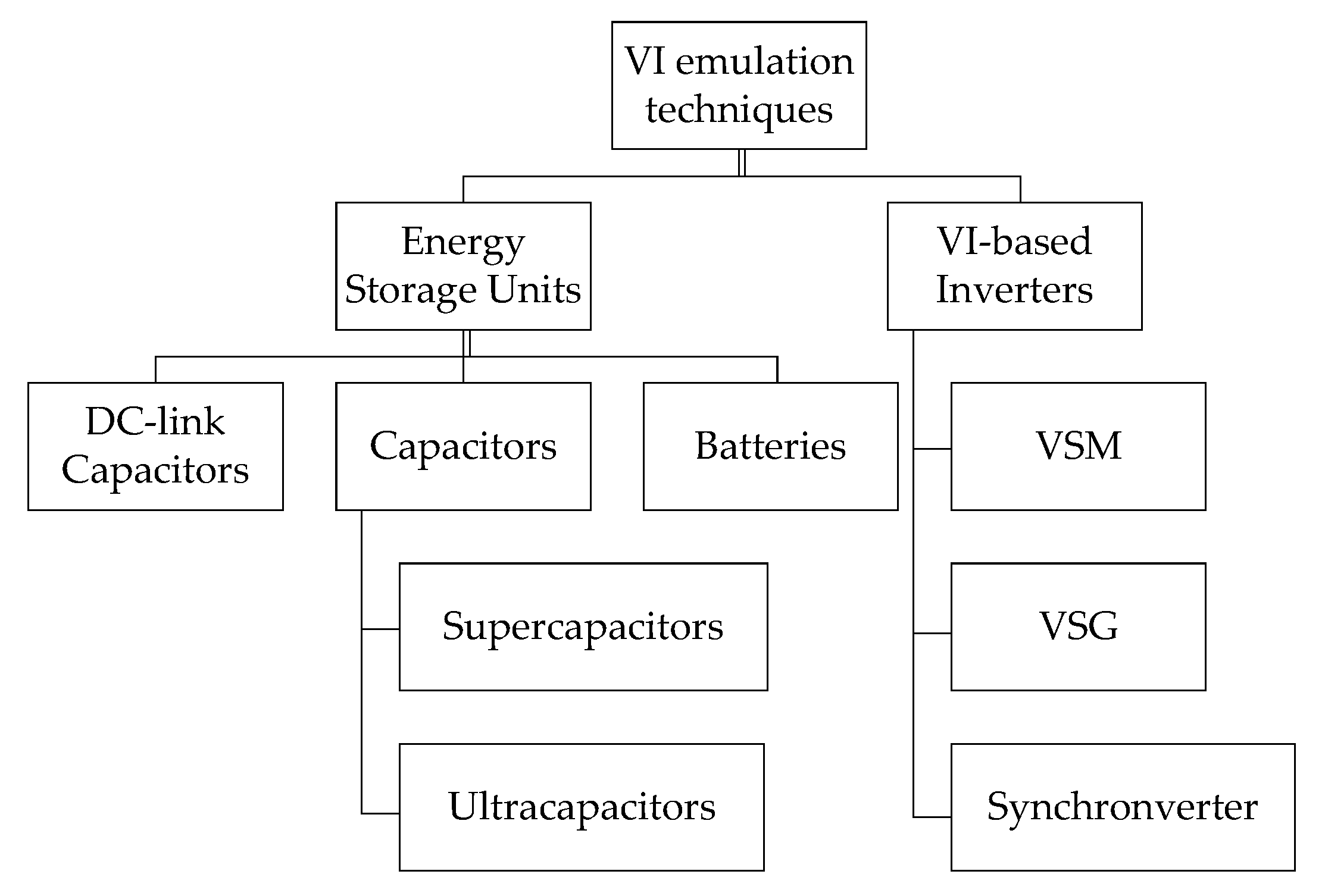
VI-based inverters and their control strategy can be implemented in various applications such as grid-connected wind power [14,15] and solar power plant [16], high voltage direct current (HVDC) transmission [17,18], energy storage system (ESS), microgrid [19], electric vehicle (EV) chargers [20], static synchronous compensator (STATCOM), virtual inertia machine (VIM), modular multilevel converter (MMC)-based direct current (DC) system [21], electronic appliances, and flexible loads to support frequency stability. Figure 2 presents the application and implementation of VI in the modern power system.
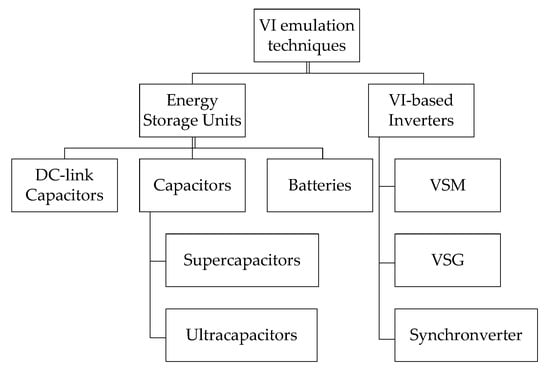
Figure 2.
The implementations of VI emulation technique.
As the amount of solar and wind energy generation increases, grid-connected RES requires VI emulation, and thus VI-related publication and research are increasing [22]. There are limited studies that compare VI-based inverters, namely virtual synchronous generator (VSG), virtual synchronous machine (VSM) and synchronverter, concerning their technical implementations, merits, demerits, and applications. Given the rising demand for inertia to improve frequency regulation [23] as the RES penetration increases, this paper explores and studies the potential of VI for every use in the power grid. The primary objective of this paper is to provide a useful insight into the state-of-the-art VI applicability in RES-dominated power grid quality control and stabilization. This paper presents a comparative review of the various topologies used to implement VI in an inverter. The paper begins with an introductory overview of the RES and VI in Section 1. Following this, VI-based inverters are discussed extensively in Section 2. Section 3 discusses the applications of VI. Section 4 presents the evaluation, comparison, and technical analysis of each VI-based inverter techniques, including VSM, VSG, and synchronverter. The assessment of VI emulation techniques, including the critical analysis, current challenges, and future research on virtual emulation, are presented in Section 5. Section 6 summarizes the recent development of VI emulation in inverters and concludes the overall comparative review.
2. Implementation of VI-Based Inverters
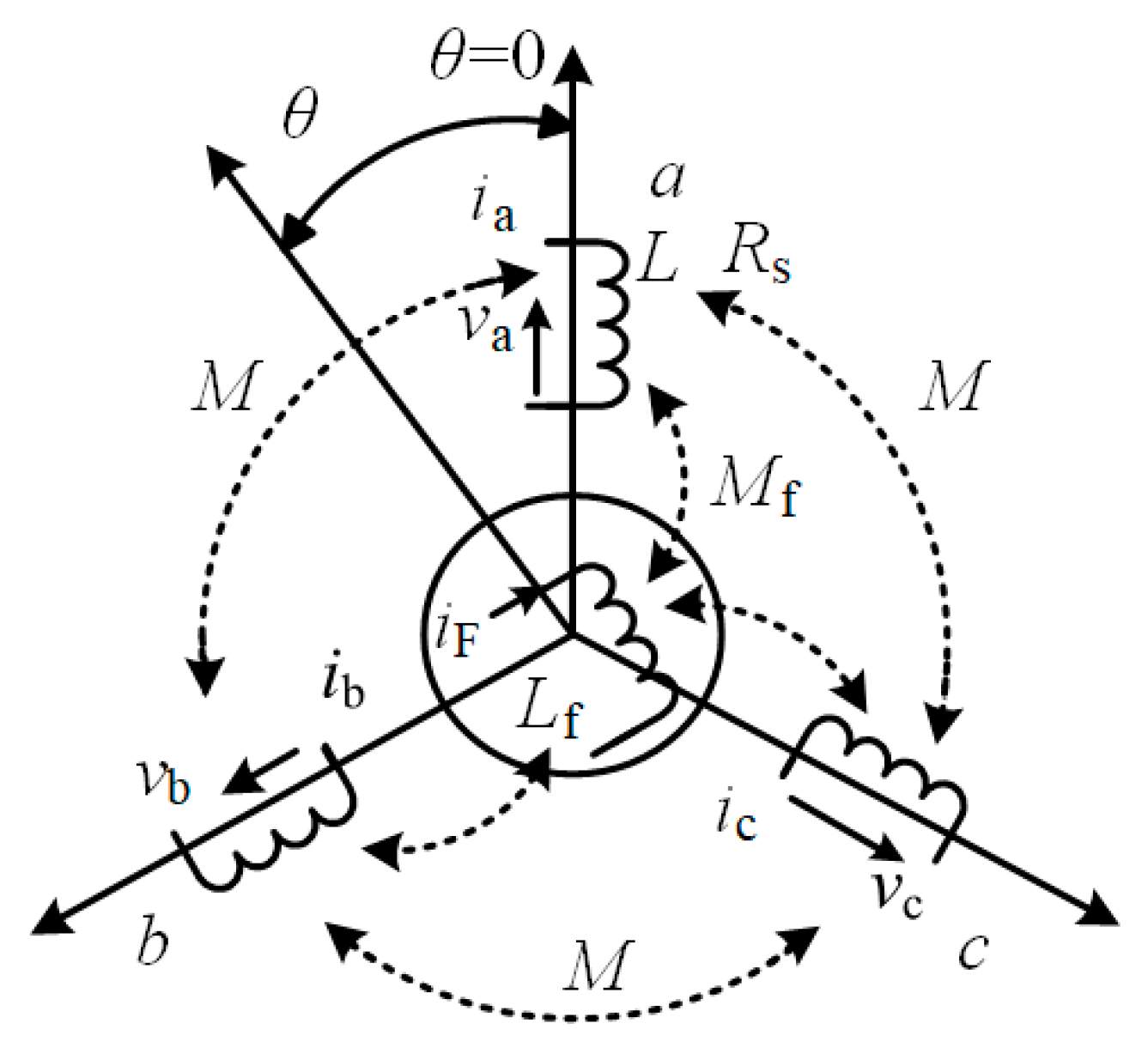
Primarily, all of the VI-based inverters are originated from the structure and mathematic model of SM and SG, which can be found in classic textbooks [24]. SM is a general term that constitutes both synchronous motors and SG. Hence, VSM, VSG, and synchronverter are identical since the modeling of an SG is similar to SM. As illustrated in Figure 3, a round rotor SG is modeled from its first principles and fundamental formulas, by assuming it has one pair of poles per phase and one pair of poles on the rotor (p = 1). The structure is an ideal two-pole SM consist of combining the circuits of a three-phase stator and a rotor that has a spatial displacement in its rotation. All the minimal losses, including magnetic-saturation effects, magnetic reluctance, and losses of the iron core and eddy current, are ignored since the model is assumed as a perfect model without any losses for the simplicity [25].
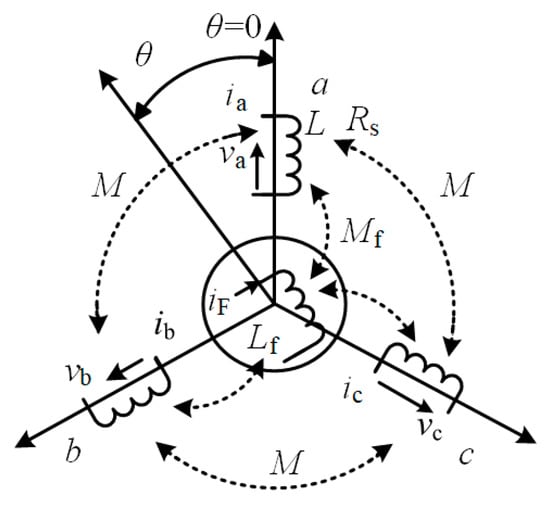
Figure 3.
The mechanical structure of an idealized three-phase round-rotor SG.
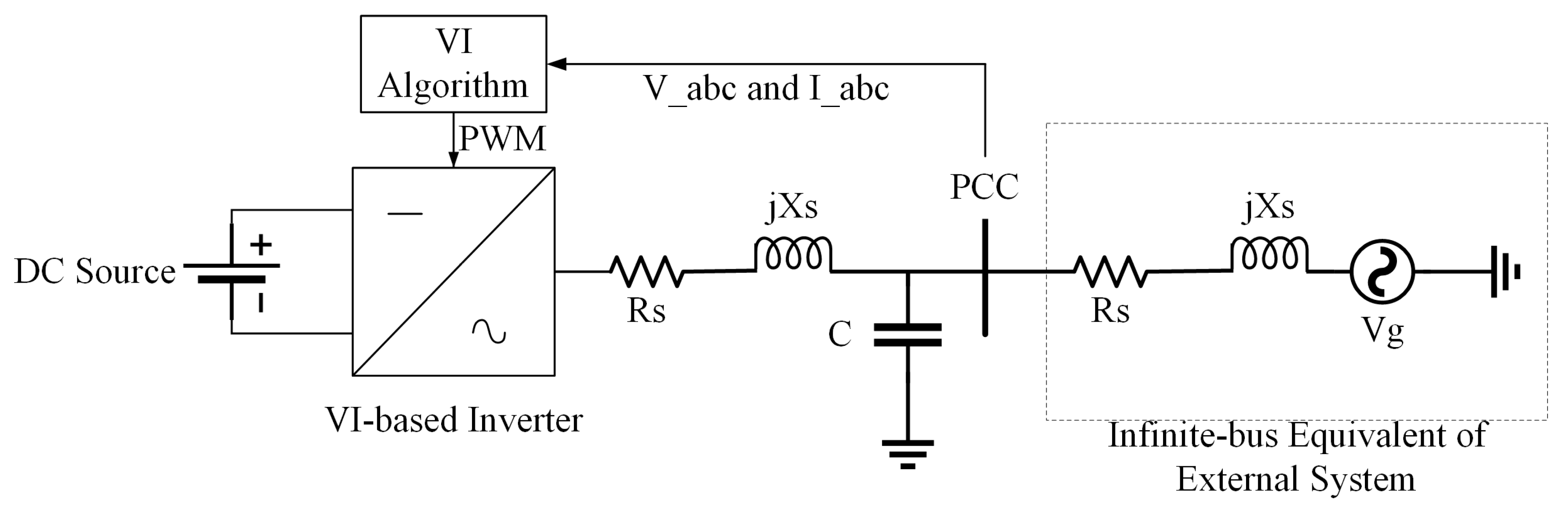
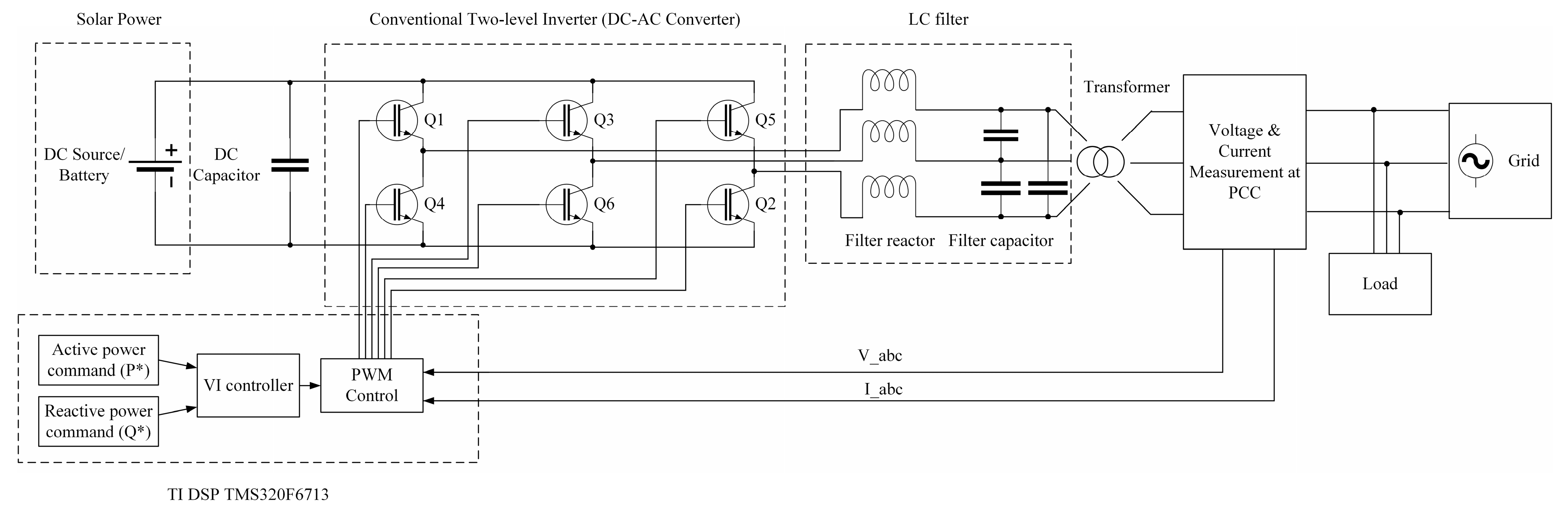
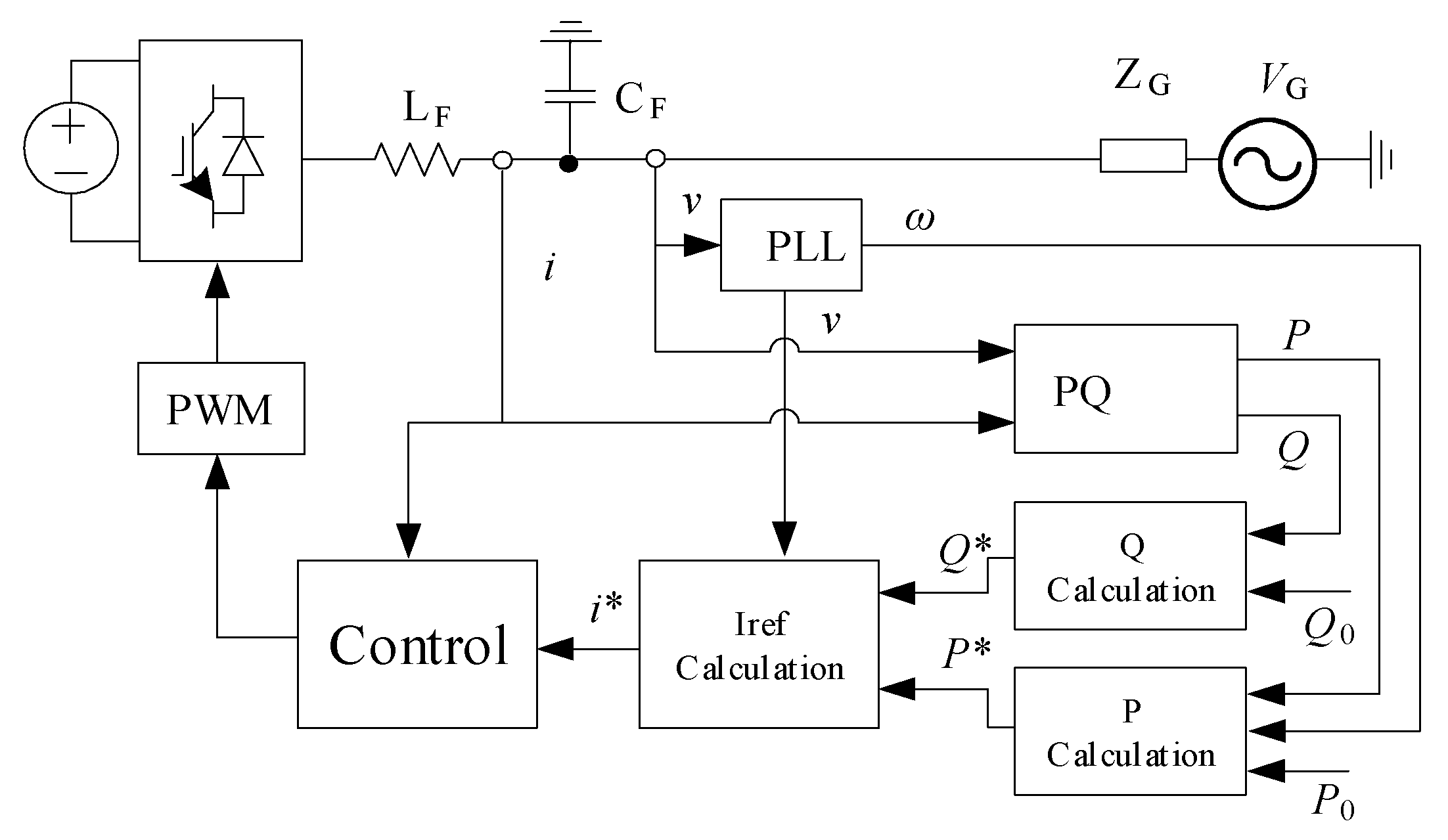
A conventional inverter with VI emulation is referred to as VSM, VSG, and synchronverter. Synchronous voltage source converter (VSC), virtual synchronous control (VSYNC), synchronous inverter (SI), and synchronous converter are the interchangeable terms. Sometimes, it is also known as a photovoltaic virtual synchronous generator (PVSG) or PV-VSG, which consists of solar PV and SG [26]. The general single line diagram of a grid-connected VI-based inverter is illustrated in Figure 4.
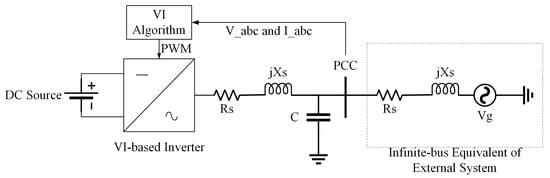
Figure 4.
The general single line diagram.
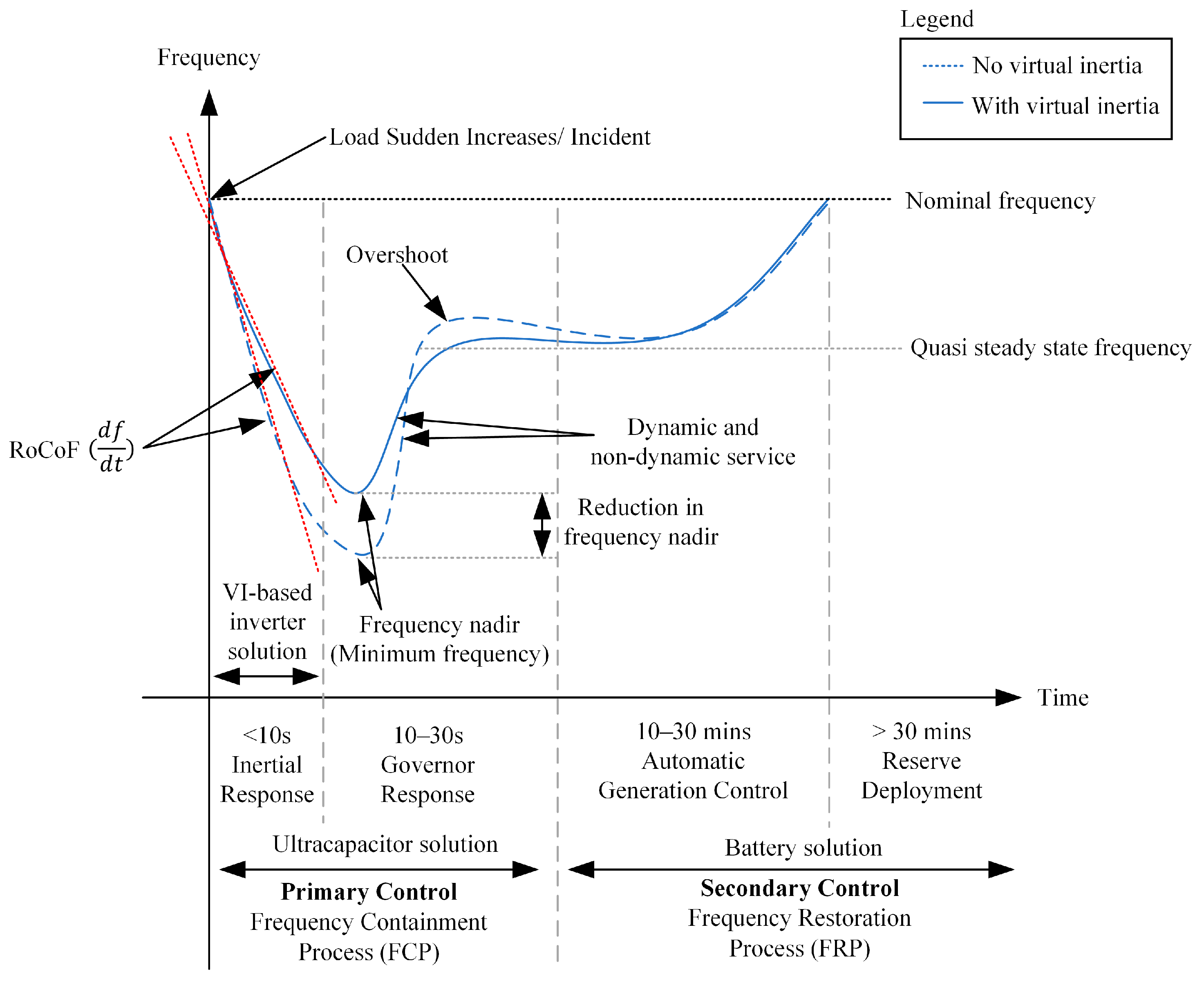
As illustrated in Figure 5, control actions are deployed for a specific time frame to balance the generation and load for frequency control. The figure highlights the main difference between the system with VI and system without VI. The power system with VI has the following advantages:
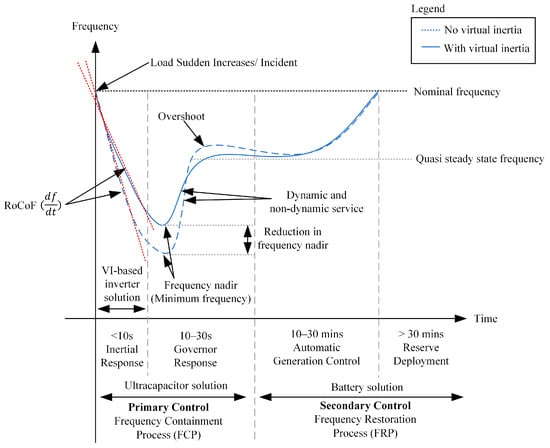
Figure 5.
The effect of VI that reduces sudden frequency drop.
- Reduction in frequency nadir and frequency deviation from nominal frequency (fn)
- Less overshoot and faster transient or respond time
- Less RoCoF and less steep gradient
- Faster recovery time to the nominal frequency
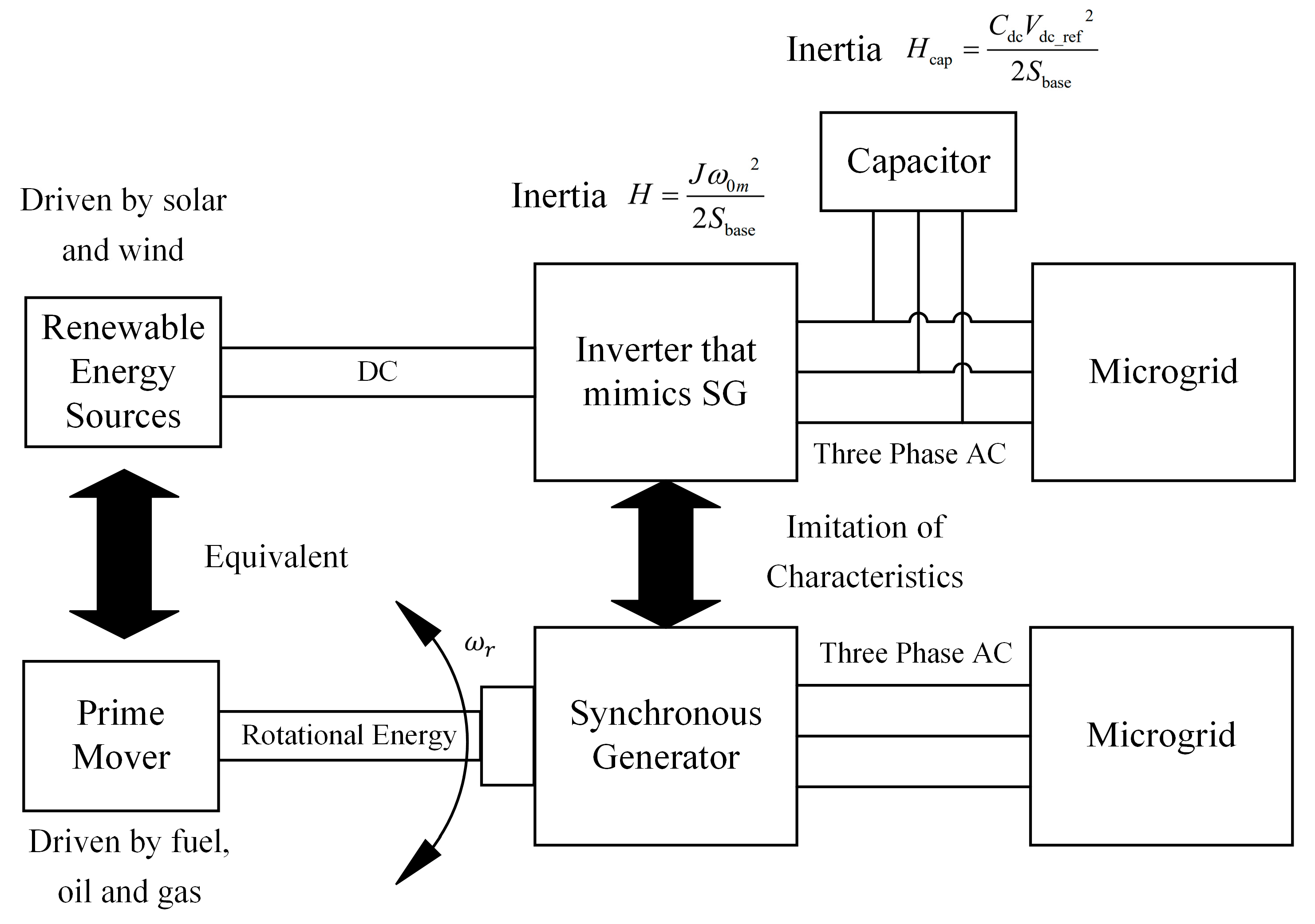
Traditional frequency regulation process and the response of the power system can be divided into three stages, namely primary, secondary, and tertiary frequency response, which is equivalent to inertial response and governor response, automatic generation control (AGC), and reserve deployment, respectively [27]. VI is essential for inertial response in primary control frequency containment process (FCP) to provide dynamic frequency support for the grid with high wind and solar power penetration [28]. Figure 6 illustrates the VI-based inverter is reminiscent of an SG to enable grid-connected RES with the inertial response for stable frequency. Figure 7 presents the general connection of a VI-based inverter in grid-connected RES.
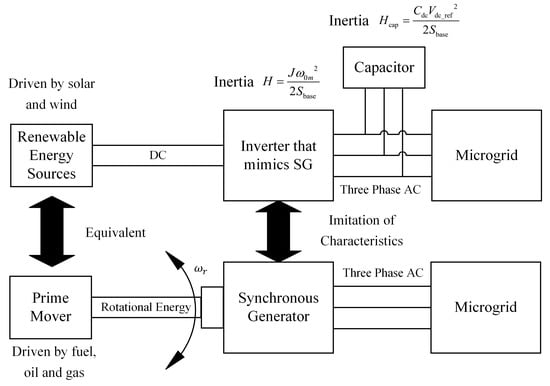
Figure 6.
The VI-based inverter enables the imitation of conventional SG-based power system.
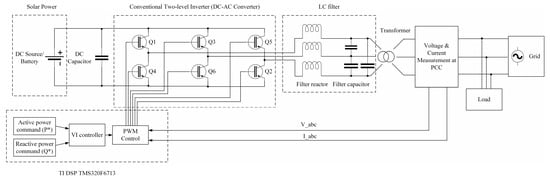
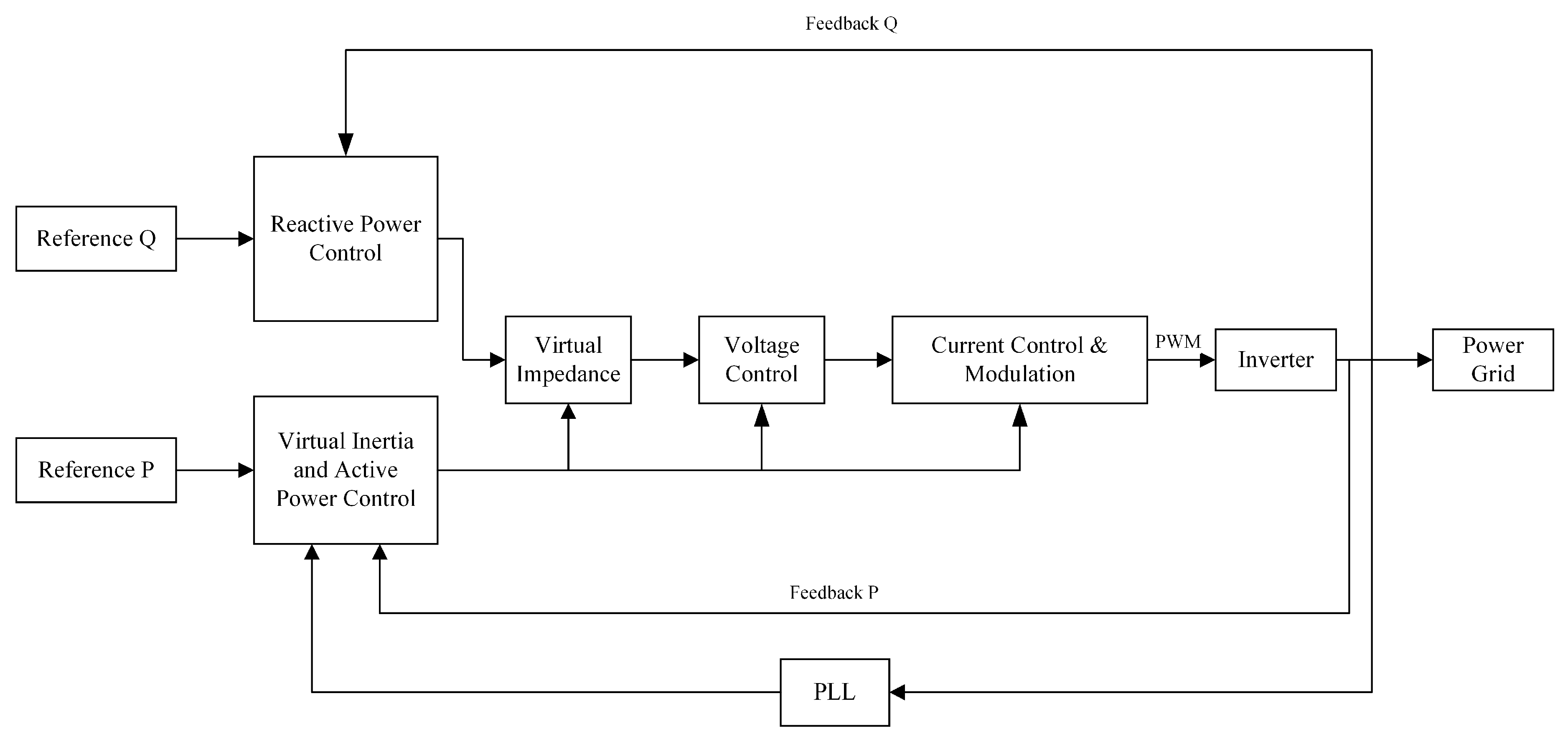
Figure 7.
The typical connection of a generic VI-based inverter.
2.1. VSM
Both VSM and VISMA are abbreviations for the virtual synchronous machine. However, VSM is more commonly used. Both are based on the emulation of SM but with some slightly different implementation topology. Various researchers refer to different abbreviations, but essentially VSM and VISMA are interchangeable terms. Although the terms are different, all of them shares similar VI emulation techniques. The objective of the VSM is to provide grid forming employing frequency droop and VI. A phase lock loop (PLL) is typically used for frequency estimation to calculate the RoCoF in driving the VI loop [29]. The use of PLL is eliminated during regular operation. It is because VSM can synchronize with the grid based on the power balance after initialization by PLL [30].
VSM uses synchronous reference frame or d-q based mathematical model of an SG. The Park transformation of abc to direct-quadrature-zero (dq0) converts three-phase (abc) signal to dq0 rotating reference frame. The inverse Park transformation (dq0 to abc) turns dq0 rotating reference frame back to three-phase (abc) signal. Generally, the Park transformation increases the complexity of the system and total execution time (TET). The measurements of the grid voltage are used to calculate the stator currents. However, VISMA model exhibits numerical instability. The first VSM concept was proposed by Beck and Hesse in 2007 and labeled as VISMA [31]. Virtual synchronous machine zero inertia (VSM0H) is a variant of VSM, which is identical to VSM, but with zero inertia constant (H) as the name suggests. Unlike VSM, it operates without the requirement of PLL. The phase angle of the voltage is derived from an integrator which advances at a rate determined from a conventional droop slope of frequency versus measured active power output.
As shown in Figure 8, the general operations of a generic VSM are the following:
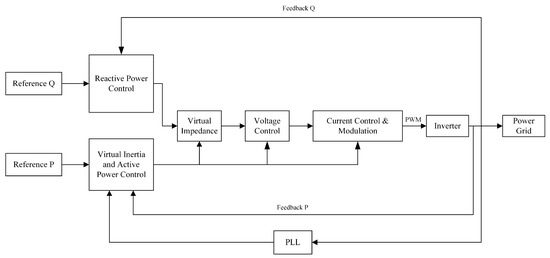
Figure 8.
The block diagram of a generic VSM control strategy to emulate VI.
- Step 1:
- The voltages at point of common coupling (PCC) between the output of VSM and grid are measured to compute the phase currents of the VISMA in real-time.
- Step 2:
- The computed currents are utilized as reference currents for a current-controlled inverter.
- Step 3:
- The pulse width modulation (PWM) modulator drives the inverter.
The active power control loop regulates frequency while the reactive power control loop regulates voltage amplitude. When the current tracking error is small, the inverter behaves as an SM. This behavior fulfills the operation of a proposed VISMA. After the first proposal, there are other topologies that emulate VI for power electronic converters, HVDC, battery storage system (BSS), microgrid, and other applications. The core concept is still the same with different control parameters, approaches, designs, mathematical models, and implementations. The model of an SM has several orders, from first- to seventh-order models. The voltages at the PCC with the grid are measured. In real-time, the measured voltages at PCC are computed to calculate the phase currents of the VISMA. The computed currents values are the reference currents for the inverter to enable the operation of an inverter as a grid-connected current source. The behavior of VISMA depends on the current tracking error. If the error is small, it behaves like a synchronous machine. If the error is large, the behavior changes. VISMA implements a control system to integrate a three-phase inverter with SG characteristics.
VISMA behaves as an SG to imitate the advantages and merits of an SG. VISMA algorithm implements Park’s coordinate reference frame by applying dq transformation to the synchronous machine mathematical model. In general, VISMA and VSM have the same control configuration, which emulates VI by using swing equation. By comparison, the synchronverter has some differences. Enhanced VSM has a larger inertia utilization range, which eliminates the need for having a large DC -link element or battery energy storage system (BESS) [32]. It still provides the same inertia response as a synchronous machine. The damping and governor functions are more flexible to improve its transient responses when compared with conventional VSM. For current references from the SM model, the current reference (iref) is sent to the hysteresis current controller. This implementation has numerical instability, especially in the higher order of the SM model. In contrast, for voltage references, the voltage amplitude and phase angle are directly utilized for the generation of PWM to drive the converter. This method is very similar to synchronverter implementation. The power reference is based on the active and reactive power references generated from active and reactive power controllers to drive the PWM via a voltage reference calculator. Table 1 presents the merits and demerits of a general VSM. Table 2 shows the recent researches and implementations of VSM in various applications, such as RES, microgrid and smart grid.

Table 1.
Current VSM merits and demerits.

Table 2.
Summary of selected VISMA and VSM implementations.
2.2. VSG
VSG is essentially based on conventional inverter hardware with a controller that emulates the inertial response of an SG in response to any frequency changes. VSG control strategy allows the operation of grid-connected inverters to produce VI [39]. The adoption of VSG has attracted significant attention because of its equivalent operating mechanism as an SG to provide a practical scheme for grid-connected RES [40]. The emulation of releasing or absorbing kinetic energy imitates the characteristic of an SG. VSG is different from SG in terms of the ability to modify VI by the microprocessor during frequency variation. Hence, self-tuning algorithms are crucial to vary the VI to minimize frequency variation. Compared to a conventional droop controller that provides frequency regulation only, VSG provides dynamic frequency control based on the derivative of the frequency measurement. This control is similar to the inertial power release or absorption by an SG during a power imbalance. VSG requires pre-synchronization before connecting to the power grid. It is executed by either a conventional PLL or phase angle regulator [41].
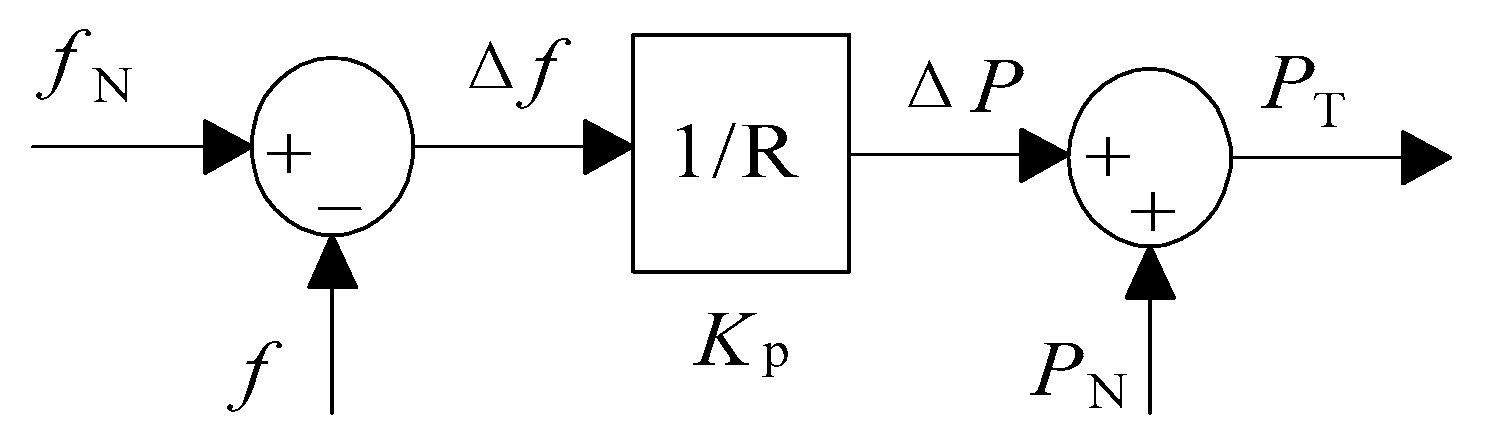
represents the change in angular frequency, and is defined as the rate of change of represents the damping constant while represents the inertial constant. The damping constant is similar and adopted from frequency droop concept. It helps to stabilize frequency and reduce minimum (nadir) frequency. The inertial constant dampens RoCoF by providing fast dynamic frequency response, based on the frequency derivative. This characteristic is crucial for an isolated, islanded, or standalone grid, which exhibits high initial RoCoF. The inertial response acts as a safety measure, which prevents the unnecessary tripping of the protection relay. Since VSG involves d-q transformation, it is based on the d-q current control approach. VSG is based on a current-controlled inverter. Hence, the current references are generated for the current controller based on the reference power from equation (1). The d-axis current reference is computed using Equation (2).
Vd and Vq are defined as the d-axis and q-axis components of the measured grid voltage (v). The q-axis current reference () and the reactive power (Q) is defined as zero, assuming that only the active power is being controlled. This is because the regulation of grid frequency involves the manipulation of active power only. Hence, based on the described terminology, VSG is a current-controlled voltage source inverter, with VI. VSG is popular and used by the European VSYNC research group. It is also widely validated through real-time simulations, field tests, remote microgrid, wind systems, and other applications. The design of VSG control strategies can be categorized into two types, either addressing via output or topology. For the output variant, the VSG can be further sub-divided into the controlled current source and a controlled voltage source. The foundation of VSG is based on SG as the voltage source. Figure 9 illustrates the control strategy of a generic VSG which consists of both active power (P) and reactive power (Q) calculation blocks to generate reference current (Iref) for the PWM control. Figure 10 and Figure 11 show the detailed mathematical modelling of active power loop (APL) and reactive power loop (RPL) respectively.
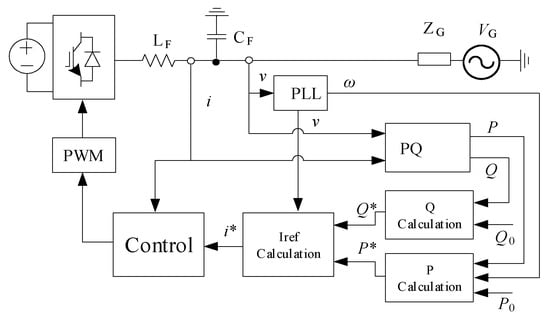
Figure 9.
The general control strategy of a VSG.
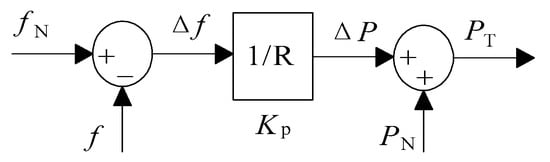
Figure 10.
The active power loop for a VSG.
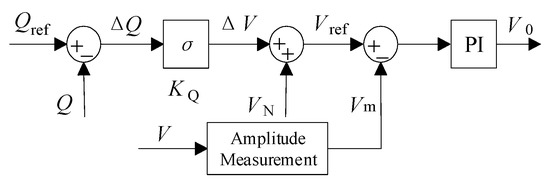
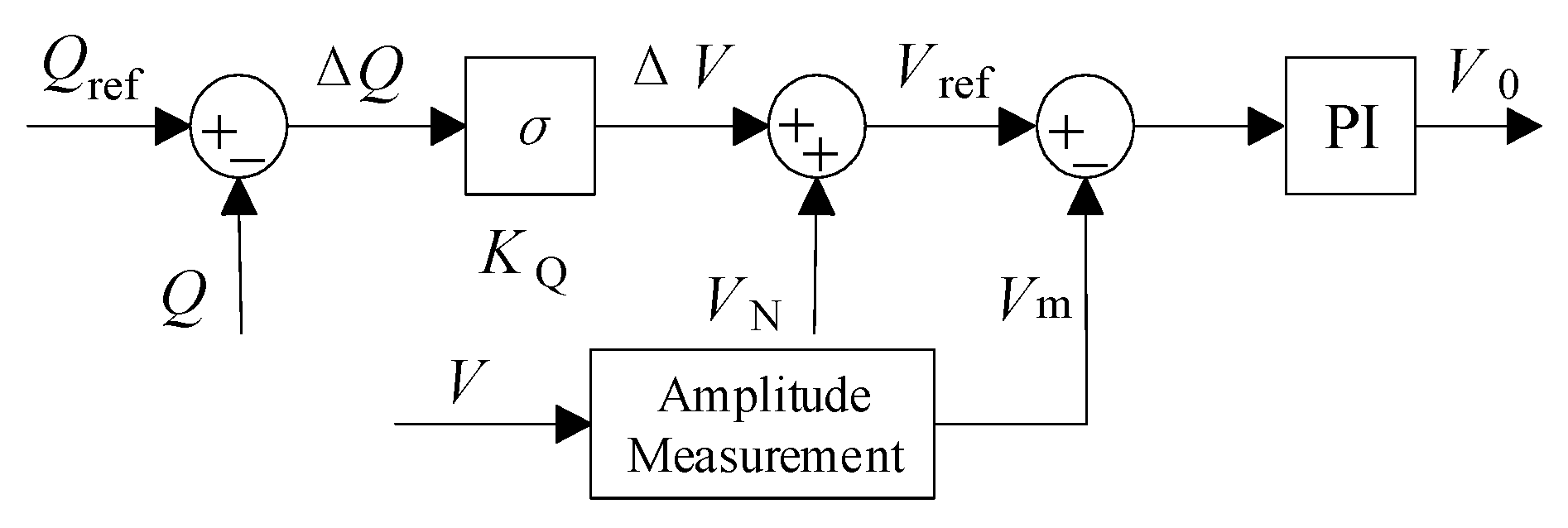
Figure 11.
The reactive power loop for a VSG.
The general operations of a VSG are the following:
- Step 1:
- The grid voltage (V) at PCC between the output of VSG and the grid is measured and sent to the processing unit, which contains the VSG algorithm.
- Step 2:
- The processing unit uses the SM model to compute the stator current of the VSG.
- Step 3:
- Current controller sends the gate signal to inverter based on the calculated reference current (Iref).
Su et al. implemented a VSG algorithm for the interface between solar power generation and the power grid. VSG is designed specifically for grid-connected solar PV plant [42]. The control strategy of a VSG can be implemented by using fuzzy secondary control with better performance compared with conventional droop control and VSG control [43]. The extended VSG controller includes three virtual modules, namely rotor, primary control, and secondary control to further increase the inertia of power electronics-based system and microgrids. The parameters are fine-tuned by using an H-infinity (H∞) robust control method [44]. H∞ is a control strategy to synthesize controllers to acquire stabilization with high performance by expressing the control problem as mathematical optimization. It is an alternative control strategy for VSG other than conventional PI controller parameters tuning. H∞ control is applicable to replace the conventional PI controller [44].
The power and frequency output of a traditional VSG is oscillating when dramatic power fluctuation occurred in the decentralized generation (DG). To overcome oscillation, the control strategy of VSG is modified as adaptive to adjust the rotating inertia and damping coefficient [45]. In general, the VI is designed and emulated for several critical applications, including HVDC, microgrid, DC platforms, etc. The implementational control strategy for VSG includes conventional PI controller, H-infinity control scheme, power decoupling improvement, ESS addition, computational intelligence, and artificial intelligence. The online optimization technique is applicable to self-tune the parameters of VSG, including KI and KD. It minimizes RoCoF and power flow through ESS, neural-network-based controller, and adaptive dynamic programming (ADP), since the ESS injects and absorbs active power (P) and reactive power (Q) actively while AI-based controller enables adaptive moment of inertia (J) and damping factor (D) VSG topology has extended and improved over the years. The frequency nadirs and peaks in the system can be further minimized by utilizing higher energy and power exchange through VI system or vice versa. Active and reactive power dynamic decoupling technique for VSG is vital for medium- and low-voltage microgrids [46]. A self-adaptable reactive power-voltage controller to resolve the sharing problem of reactive power in the parallel VSG. It is executed by using the difference in reactive power to adjust the reactive power-voltage control coefficient [47].
Table 3 summarizes the merits and demerits of a VSG. Despite its rapid development, the major issue of VSG is that it is not applicable for islanded mode since VI-based inverter has to operate as a grid-forming unit in islanded mode. VSG is not a grid-forming inverter because it emulates VI during the variation of frequency instead of the variation of input power. VSG is also unstable and inaccurate because of the PLL measurement. PLL performs undesirably and competes against each other in the weak grid. It exhibits high steady-state error, instability issues, frequency variations, harmonic distortions, and voltage sags or swells. VSG is prone to noise because of the presence of the derivative term which is used to compute RoCoF. The instability issue worsens when a PI-based controller is used to implement inner-current loop of the VSG. The delivered power and frequency of the VSG may prone to oscillation because of the dramatic power fluctuation in RES. The oscillation can be reduced by adjusting the rotating inertia and damping coefficient [45]. Hence, to implement a sophisticated VSG, it requires robust PLL with high stability and measurement accuracy. The output active power of VSG is oscillatory compared to droop control. This problem can be mitigated by tuning the damping factor and the output reactance. VSG control inherits the advantages of droop control. On top of the droop control, VSG also provides inertia support for the system [48]. Table 4 presents the latest VSG implementations in several sectors including wind energy, HVDC and microgrid.

Table 3.
Current VSG merits and demerits.

Table 4.
Summary of selected VSG implementation.
2.3. Synchronverter
Synchronverter, also known as SI, is an inverter with a control algorithm which mimics the operation and behavior of an SM [58]. As the term suggests, it is the combination of “synchronous” and “inverter”, which implies self-synchronizing inverter. The underlying operating mechanism of a synchronverter is based on the dynamic swing equations of an SG, which is under the category of SM. The only difference is the mechanical power exchanged with the prime mover or mechanical load in an SM is replaced with the power exchanged with the DC bus in a synchronverter.
In general, synchronverter consists of a conventional inverter including the filter inductors, capacitors, and associated controller [59]. It is equivalent to an SM with a small capacitor bank connected in parallel to the stator terminals [60]. Hence, a synchronverter carries over the advantages and disadvantages of an SM, which is based on a complex non-linear system. For example, among the undesirable phenomena, loss of stability due to under-excitation as well as oscillations around the synchronous frequency could occur in a synchronverter. The parameters including inertia, friction coefficient, field inductance and mutual inductances can be manipulated in a synchronverter, unlike in SG. It is notable that the energy loss in the virtual mechanical friction is not lost in reality; it is directed back to the DC bus. This kind of inverters with added virtual inertia, called VSG can contribute to the short-term stabilization of the grid frequency. However, the system dynamics seen from the grid side will be different from those of an SM. The concept of synchronverter is identical to VSM. However, synchronverter exhibits simpler logic control compared to VSM. Instead of using a full seventh-order model, the synchronverter is based on the second-order model swing equation of SM. The second-order model enables the massive reduction of complexity to implement the inertial response of an SM. The simplification of the model removes unnecessary calculations including instantaneous internal virtual fluxes into the control algorithm.
The terminology of a synchronverter is to operate the inverter-based DG unit as SG in representing the same dynamic characteristics from the point of view of the grid. It is crucial to allow RES to interface with the power grid without affecting grid frequency and voltage stability. The synchronverter can be modeled with or without the connection of neutral line connected to the grid. In this instance, the synchronverter is modeled without a neutral connection. A conventional DC to AC converter, known as the inverter, is utilized to convert DC power into three-phase AC with certain frequency or vice versa. It typically includes three inverter legs or bridge, which are operated by using PWM in controlling the switching action of IGBT or other switching electronic devices. The LCL filter is used to reduce ripple voltage and current by storing energy in a capacitor and inductor, respectively. A synchronverter is designed to maintain its nominal frequency, maintain its nominal voltage, regulate the generated and consumed real power and regulate the reactive power if it is connected to grid. Synchronverter is modeled by using SG swing equations [61]. Equations (3), (4) and (6) are fundamental equations, used to mathematically describe the dynamic of the SG. Equation (7) defines the vectors of three-phase stator flux (), voltage (v), current (i), , and . The field excitation current is denoted by if while mutual-inductance between stator and field winding is denoted by Mf. Te, e, P, Q, if, and are electromagnetic torque, back electromotive force (EMF) or synchronverter inner generated voltage, active power, reactive power, field current, and Virtual angular speed of the machine, respectively. and are vectors defined as the three-phase angle difference with equal spacing of 120° or in radian.
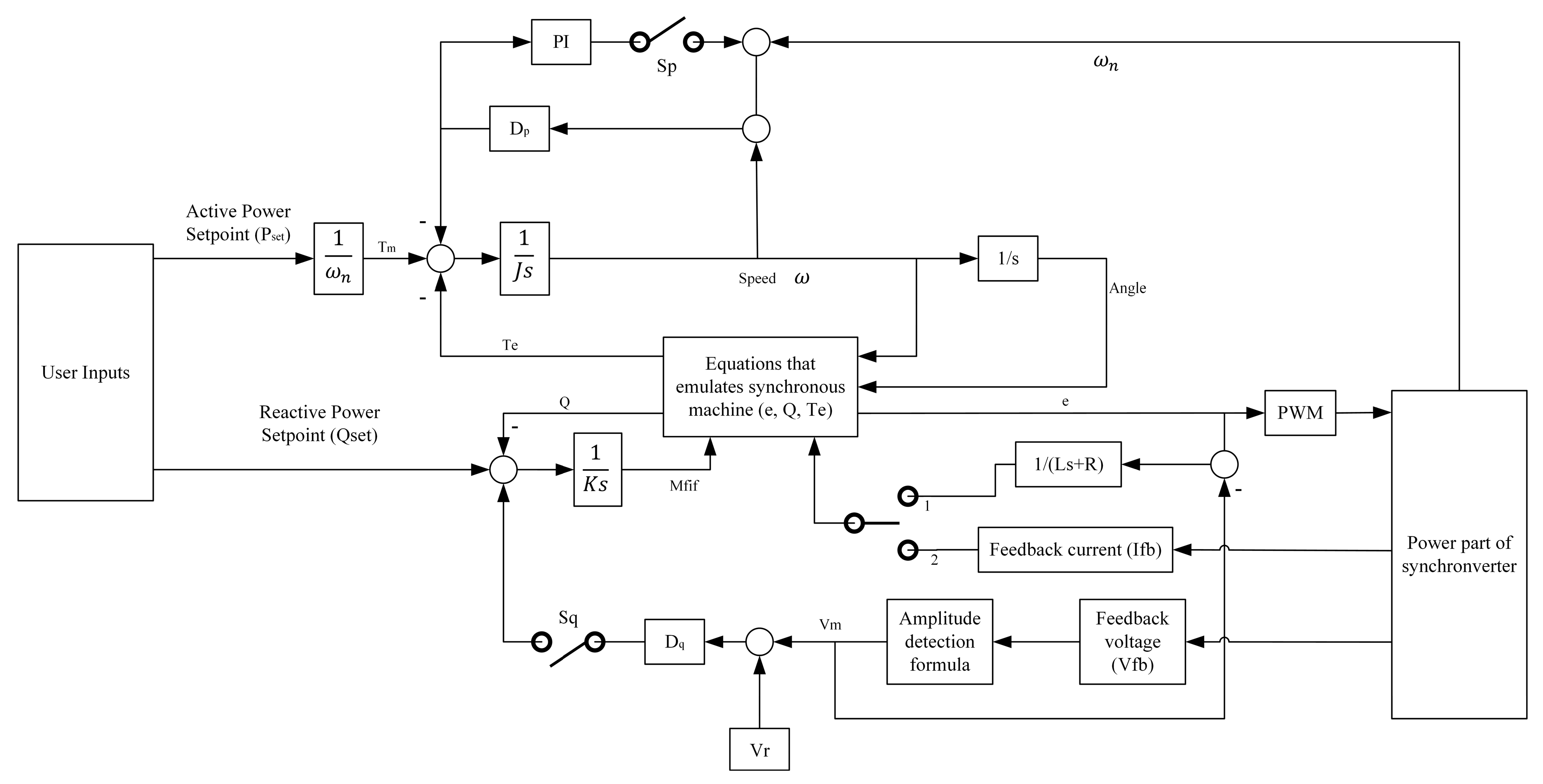
Equations (3), (4) and (6) are discretized and solved in each control cycle in a digital controller, including microcontroller unit (MCU) and digital signal processor (DSP) to generate the gating PWM signals. The inverter output current (i) and grid voltage (v) are the feedback signals to solve the differential equations within the controller. The parameters, including the moment of inertia (J) and damping factor (D), are tunable for desire condition. The selection of these parameters is important for the stability of the system. A PLL, also known as a sinusoid-locked loop, is a control system that maintains the synchronism of inverter with the terminal voltage. The early stage of synchronverter requires PLL for initial synchronization with the power grid. Once the converter is synchronized with the grid, the PLL is no longer required. However, the use of PLL causes instabilities and negative impact on the control performance in a weak grid. In addition, PLL exhibits higher computational complexity, the larger code size of the controller and longer TET. The phase detector or phase comparator is a key element of the PLL to an output voltage signal, which represents the difference in phase between two signal inputs. As illustrated in Figure 12, the general control scheme of a synchronverter is based on the APL and RPL which are derived from the swing equations of a SM.
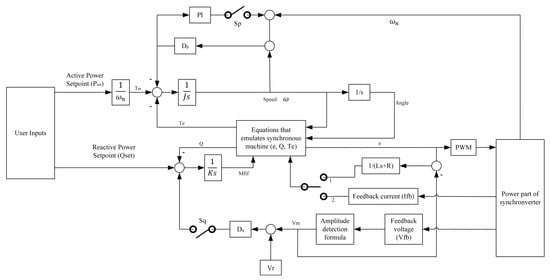
Figure 12.
The general synchronverter control mechanism.
Equations (8) and (9) define the frequency droop and voltage droop, respectively. The mechanical torque (Tm) is a control input while the electromagnetic torque (Te) depends on the i and . Hence, the state variables of the synchronverter are the following: i (the inductor currents), v (the capacitor voltages), θ (virtual angle), and (a virtual angular speed). The moment of inertia is denoted by J, 1/s is the integrator, Dp is the damping factor for active power loop, Dq is the damping factor for reactive power loop, K is the regulator coefficient of reactive power, QSET is the set point of reactive power, r is the reference angular velocity, m is the measured feedback angular velocity, Vr is the reference r.m.s voltage, and Vm is the measured feedback grid voltage.
In case of the absence of a neutral line, only two of the three currents in vector i are independent. Thus, the control inputs of the synchronverter are Tm and Mfif. To operate the synchronverter, the controller is designated to generate the control signals Tm and Mfif in a way that system stability is maintained and the desired values of real and reactive power are obeyed. The synchronverter is controlled by two (dual) channels, similar to the synchronous generator. The two channels are real power and reactive power. The frequency droop control loop controls the real power, while the voltage droop controls the reactive power. The frequency droop compares the with the which normally equals the nominal angular frequency of the grid (). This difference is multiplied with a gain to the active mechanical torque, Tm. The mechanical friction coefficient and the frequency drooping coefficient is denoted as Dp. This frequency loop regulates of the SG and creates the phase angle (θ) for the control signal (e).
The regulation of reactive power flowing out from synchronverter is executed similarly to frequency droop. The voltage droop control is using the voltage droop coefficient (Dq). It regulates the Mfif which is proportional to the amplitude of the voltage generated. In general, a synchronverter has power part and electronic part. The power part is the conventional inverter structure with switching devices (metal–oxide–semiconductor field-effect transistor (MOSFET) or insulated-gate bipolar transistor (IGBT)), gate driver, power sources, inductor-capacitor-inductor (LCL) filter, and other electronic components to convert DC to AC. On the contrary, the electronic part of synchronverter is a control unit comprising of sensors, analogue to digital converter (ADC), and measurement devices, interfaced to a microcontroller, DSP, or any computing devices. The function of the electronic part is to control the gate signal of switching devices in the power part via PWM. The modeling of synchronverter is based on the dynamic characteristic of an SG. The mathematical model ranges from second to seventh order. The higher is the order, the more accurate is the modeling, but with higher complexity and longer calculation time. Hence, the third order is most popular due to its balance between accuracy and complexity.
Among the proposed control strategies, the synchronverter designed by Zhong et al. is the most comprehensive terminology. Their research is the first proposed synchronverter with PLL in 2011 [61]. The original version of synchronverter has been improved since then. The improvements include self-synchronizing synchronverter without PLL [62], digital synchronverter design [63], and bounded frequency and voltage for safety purpose [64]. Zhong et al. improved the original synchronverter by eliminating the need for a dedicated synchronization unit (PLL) for initial synchronization. Instead, a self-synchronizing synchronverter has a PI controller in the frequency droop. PLL is replaced by an active power synchronization loop with virtual impedance. By eliminating PLL, it reduces the development cost, complexity in tuning, and computational time [65]. In general, PLL is complex because of the inclusion of a dq0/abc Park’s transformation block, quadrature signal generation block, non-linear calculation block and a low pass filter. It is time-consuming, complicated, and complex to fine-tune the PLL parameters to achieve satisfactory performance [66]. The performance of PLL degrades with the presence of steady-state error, harmonic distortions, and voltage sags in a weak grid. Another improvement is bounded frequency and voltage, which ensures synchronverter always operates in a stable region [67]. Virtual inductors, capacitors, resistors, and anti-windup have been added to the original synchronverter to get better performance. Overcurrent protection is also added to the original synchronverter for safety purpose since synchronverter is a voltage-controlled controller and does not have inherent current protection. The synchronverter is scalable and available to integrate multiple RES including wind generator and solar photovoltaic system. It consists of angle, frequency, and power control loops [68].
Typically, the design of a synchronverter is based on second- to third-order system models that represent the dynamic characteristics of an SG sufficiently. Although it is a reduced-order model from seventh-order model, second- to third-order systems balance complexity and accuracy for the representation of dynamic characteristics of the SM. The parameter tuning is crucial for stability and performance. Hence, a method to directly compute controller parameter in the synchronverter by using a damping correction loop replaces the iterative method based on small-signal analysis to simplify the tuning process while achieving the desired transient and steady-state performance [69]. M. Blau and G. Weiss designed a synchronverter that improves the damping of inter-area oscillation and the transient stability of a power system based on IEEE benchmark two-area network. Inter-area oscillation is caused by disturbances within interconnected generators through weak transmission lines. The transient stability of a power system is guaranteed by synchronverter, which ensures synchronism even though there is a major disturbance [70]. As presented in Table 5, the synchronverter exhibits merits and demerits that will have to be increasingly addressed in the future by researchers. Table 6 shows the current development of synchronverter in the application of RES, ESS and power system.

Table 5.
Current synchronverter merits and demerits.

Table 6.
Summary of selected synchronverter implementation.
3. Applications of VI-Based Inverters
3.1. Grid-Connected RES
In the future, the power system will be highly decentralized and comprised of massive small-scale RES that has its own generation paces and power quality. This phenomenon results in a different frequency, amplitude, and phase angle AC output. It contributes to AC power instability. Hence, VI-based inverters are crucial to regulate voltage and frequency stability by enabling RES to participate in power quality control [76]. VI control strategy can be adapted to converter integration to interface DC output of RES to the AC power grid. It performs not only grid feeding or following but also provides ancillary services including grid-forming capability, dynamic power support, and harmonics compensation. VI-based inverters are typically utilized and applied for grid-connected RES, specifically in wind turbine and solar PV. The electricity company is expected to utilize VI as an ancillary service. The interface of VI-based inverter for grid-connected RES eliminates the need for an isolating transformer to save cost since VI-based inverter acts as an isolating element. VI is also applicable to the integration of flexible loads. Generally, flexible loads are the loads that are designed according to customer requirements, needs, and production capability. A wind turbine known as a wind energy converter is a device that converts the wind’s kinetic energy into electrical energy. In wind farms, the most commonly used wind turbines are permanent magnet synchronous generator (PMSG) and doubly-fed induction generator (DFIG). By modifying the control strategy and system assembly, a VSG-based wind turbine can deliver VI and power oscillation damping to the grid [77]. It works in a standalone scenario and responds to dispatch orders from the upper-level operator. The wind power system can be transformed into a grid-friendly wind turbine generator by integrating VI-based inverters [78]. It is applicable for both PMSG and DFIG machines to equip them with VI and fault-ride through capabilities.
3.2. HVDC Transmission
HVDC transmission control can be based on synchronverter technology in synchronverter-based HVDC emulation and energy storage. The control of sending end rectifier (AC to DC converters) emulates the characteristics of an SM. The receiving end of inverter controls acts as SG. The combination of these rectifiers and inverter along with a DC link is known as synchronverter-based HVDC transmission [79]. Synchronverter-based HVDC is researched extensively to integrate frequency droop control and voltage regulation [73].
3.3. ESS
ESS is an emerging implementation for VI service. It serves as auxiliary support to inject or compensate active power (P) when required. By providing additional power beyond the rated power of VI-based inverters, ESS enables the smoothening of RES generation profiles and the reliability of the power system. ESS system can be implemented to an existing grid, by interfacing it via a DC-DC converter. VSG-controlled ESS can be implemented as an auxiliary apparatus at the interconnection point to provide frequency support and regulate the power balance. ESS acts as an important buffer for smart grids to dampen frequency variation. Various types of ESS can be operated as VI-based inverter for seamless and friendly integration.
3.4. Microgrid
VI control strategy can be implemented for the microgrid to reduce the voltage fluctuation on the AC and DC bus. A microgrid is defined as a small-scale power grid which operates independently or collaboratively with other small power grid. Various alternating current (AC) loads are connected through converters with varying frequency. Hence, VI-based inverters assist in the regulation of frequency by participating in the inertial response. The rural electrification process requires microgrid, remote standalone power system, and VI plays a crucial role to stabilize the standalone power system. It includes the power extraction from RES, home appliances, uninterruptible power supply (UPS), and other components which require an inverter. Similar topology can be implemented for data center, hospital, and any other place which requires a continuous and stable power supply. Residential microgrid and industrial power systems are the main application for VI-based inverters.
3.5. EV
EV inverter can be implemented with VI services such as VSM [80]. It was shown that the implementation of VIC employing EV might cause oscillations on the EVs current set-point. However, it has also been demonstrated that the presented stabilizer algorithm can reduce oscillations significantly. Similar to vehicles in the distribution network performing vehicle-to-vehicle (V2G) services, a synchronous DG could provide services that include distributed generation to the distribution network. A standard plug-in EV can be charged from mains outlets. VSM control strategy enables the transformation of EV chargers into bi-directional VSM [81]. With the integration of VI, EV charger can take part in grid regulation to achieve V2G with robust control.
4. Comparison of VI-Based Inverters
The technical implementations and control strategies of VI-based inverters consisting of VSM, VSG, and synchronverter are compared and evaluated extensively to discuss their key differences. The comparison highlights the features, merits, and demerits of each VI-based inverter. Droop control is excluded from the study because of its inability to provide an inertial response. Table 7 presents a comprehensive comparison of VI-based inverters, which consist of VSM, VSG, and synchronverter. All VI-based inverters are voltage source inverter (VSI) under the category of VSC, which basically generates AC voltage from a DC voltage. Although VSM, VSG, and synchronverter are based on SM-based VI terminology, there are some slight differences among these VI-based inverters. First, the major difference is that synchronverter is a voltage-controlled inverter (via amplitude and frequency) while VSM and VSG are current-controlled inverters. The voltage-controlled inverter provides grid voltage support while the current-controlled inverter provides high-quality grid current. Second, VSM and VSG are unable to work in the standalone (islanded) mode because they are current-controlled inverters, which exhibit inappropriate sharing of reactive power and stability constraint [82].

Table 7.
Technical comparison between VI-based inverters.
In other words, VSM and VSG only operate in grid-connected mode. On the contrary, synchronverter can work in both standalone (islanded) and grid-connected mode because it is based on a voltage-controlled inverter. Unlike VSM and VSG, synchronverter inherits appropriate sharing of reactive power and high system stability. Third, the topologies of VSM and VSG are very identical to the conventional droop control with larger inertia. Synchronverter has a more comprehensive and universal controller to integrate inverter with VI. In general, current-controlled inverters including VSM and VSG are ideal to drive low impedance loads and feed excess solar energy into the grid. Conversely, synchronverter which is based on a voltage-controlled inverter is suitable to feed isolated loads and supply power to individual appliances since it is applicable for islanded mode. For the denotation, for VSM, is the virtual mechanical input power, P is the active power, Ta is the mechanical time constant, and Pd is the damping power. For VSG, PO is the initial power, PVSG is the output power, is the RoCoF, Kω is the inertia emulation characteristic, and is the damping factor constant. For synchronverter, PSET is the desired active power setpoint, DP is the damping factor, and fref is the reference frequency.
There are two types of VI-based inverters, namely grid-forming and grid-following inverters. It is to differentiate the type of VI-based inverter in term of their participation in the regulation of voltage and frequency. Grid-following inverters are also known as a grid-feeding inverter or P-Q control. Table 8 shows the key differences between grid-forming and grid-following inverter. In general, conventional inverter and VSG are categorized as a grid-following inverter, whereas synchronverter and VSM are the grid-forming inverters. As the name suggests, the grid-following inverter is incapable of regulating voltage and frequency because it interfaces to a utility grid with well-regulated voltage and frequency typically. A grid-following inverter is achieved by current source inverter which is based on a current controller with PPL. The grid-following inverter is also known as a grid-feeding inverter or P-Q control. In contrast, a grid-forming inverter is employed by using voltage source inverter. It is equipped with virtual oscillator control and droop control to control the voltage and frequency of the power grid. The grid-forming inverter is a power conversion system for energy storage applications. It assists and participates in the regulation of both voltage and frequency via active and reactive power control.

Table 8.
Key differences between grid-forming and grid-following inverter.
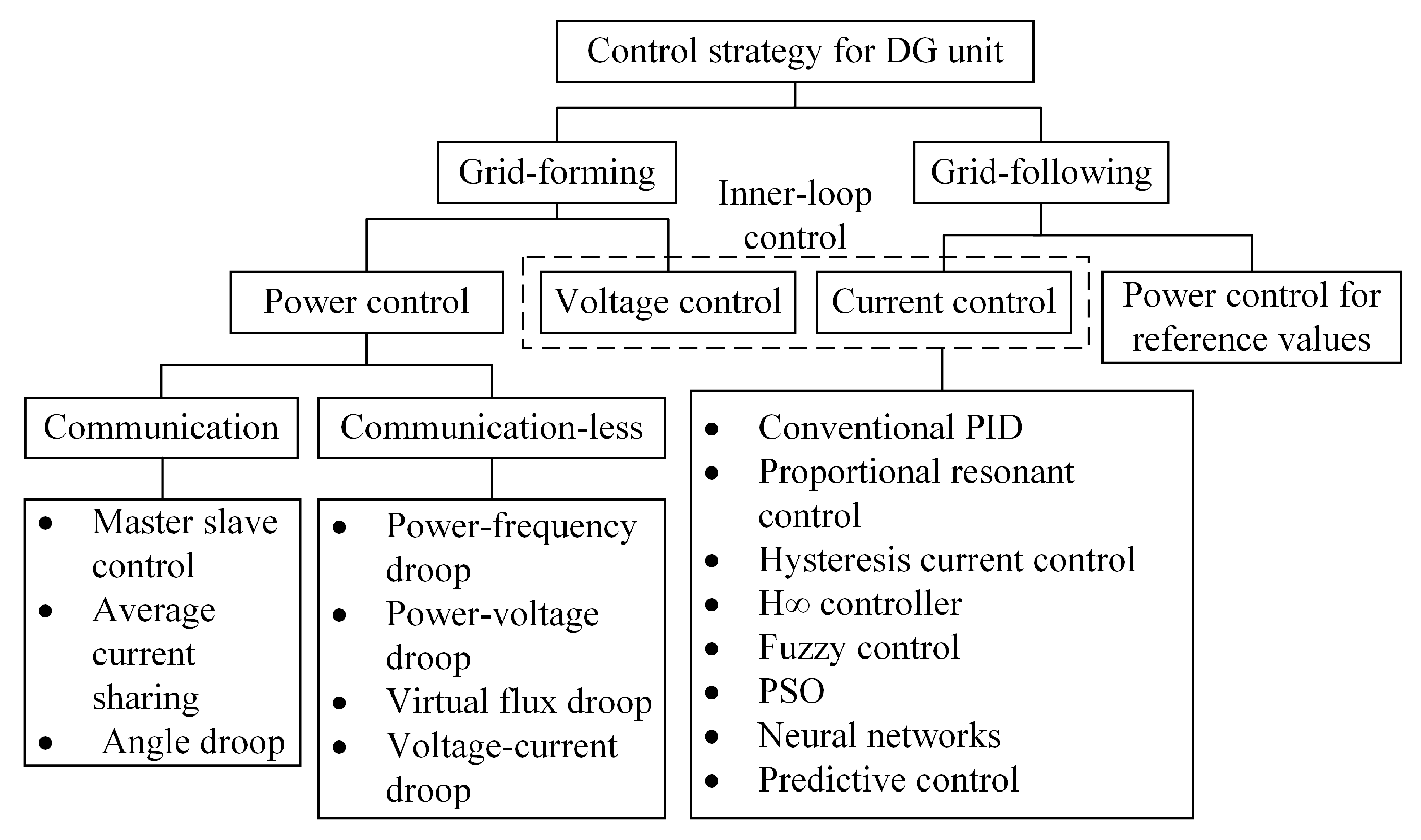
Various control methods of VI-based inverters are developed and designed to improve power quality, disturbance rejection, and voltage or current tracking of the inverter output, as shown in Figure 13. The grid-forming and grid-following inverters can be implemented based on different types of controller. The controller is responsible for optimizing and manipulating voltage or current to generate PWM for an inverter. the inner-loop voltage and current control is the most common control strategy for VI-based inverters. Different developed control strategies are used according to the characteristics of inverter topologies. The control strategies are developed from simple approaches to complex mathematical methods. In general, a conventional proportional integral derivative (PID) is the most commonly used control strategy. However, it exhibits several critical drawbacks including performance degradation during the disturbance.
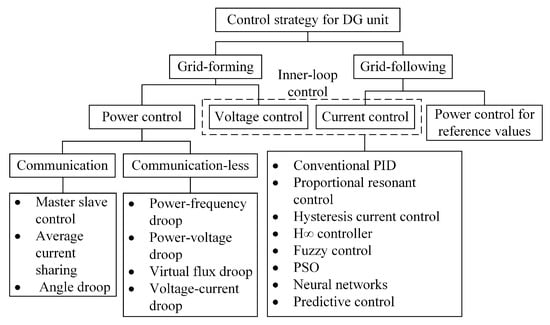
Figure 13.
The controller types of VI-based inverters.
The topology of VI is still a relatively new concept from the year 2007. Its proposed implementations are fragmented and solely depend on the preference and research objectives of the researches. Hence, to defragment and consolidate the overall development of VI in recent years, an extensive comparison and classification are conducted to give useful insight for academic researchers or industrial experts. The technical differences between each implementation are evaluated and discussed. VSM and VSG are not applicable and suitable for islanded and standalone mode because of inappropriate sharing of reactive power and stability constraint. Essentially, VSG and VSM are identical since SG is a sub-category of SM. VI-based inverters exhibit droop characteristics and frequency regulation by the inertial response. It consists of active power loop and reactive power loop. Regarding the topology type of VI-based inverters, their implementation can be divided by order, including full seventh order, full fifth order, reduced fourth order, second order, and first order, as shown in Table 9. The seventh-order model is the full-order model of SM, whereas first- to fifth-order models are reduced models of SM. Among all the models of implementation, the second-order model is simple, stable, and compatible with the control schemes of current converters in traditional power systems. It has a balance between simplicity and accuracy.

Table 9.
Comparison of VSM, VSG, and synchronverter in term of swing equation model order.
5. Future Research
This section points out the outlook for future research directions of VI-based inverters, including main challenges and limitations, ESS for VI emulation, and market trend of VI. Fundamentally, the main idea of VI is to regulate the grid frequency especially for the interface of RES to the power grid. The active power droop from synchronverter shares the same objectives with different implementation and approach. The VI concept enables a static power electronics converter to emulate the dynamic characteristic of an SM or SG. SM is a general category that constitutes both SM and SG. Essentially, VSM, VSG, and synchronverter share similar topologies. VSM is based on SM while VSG and synchronverter are based on SG.
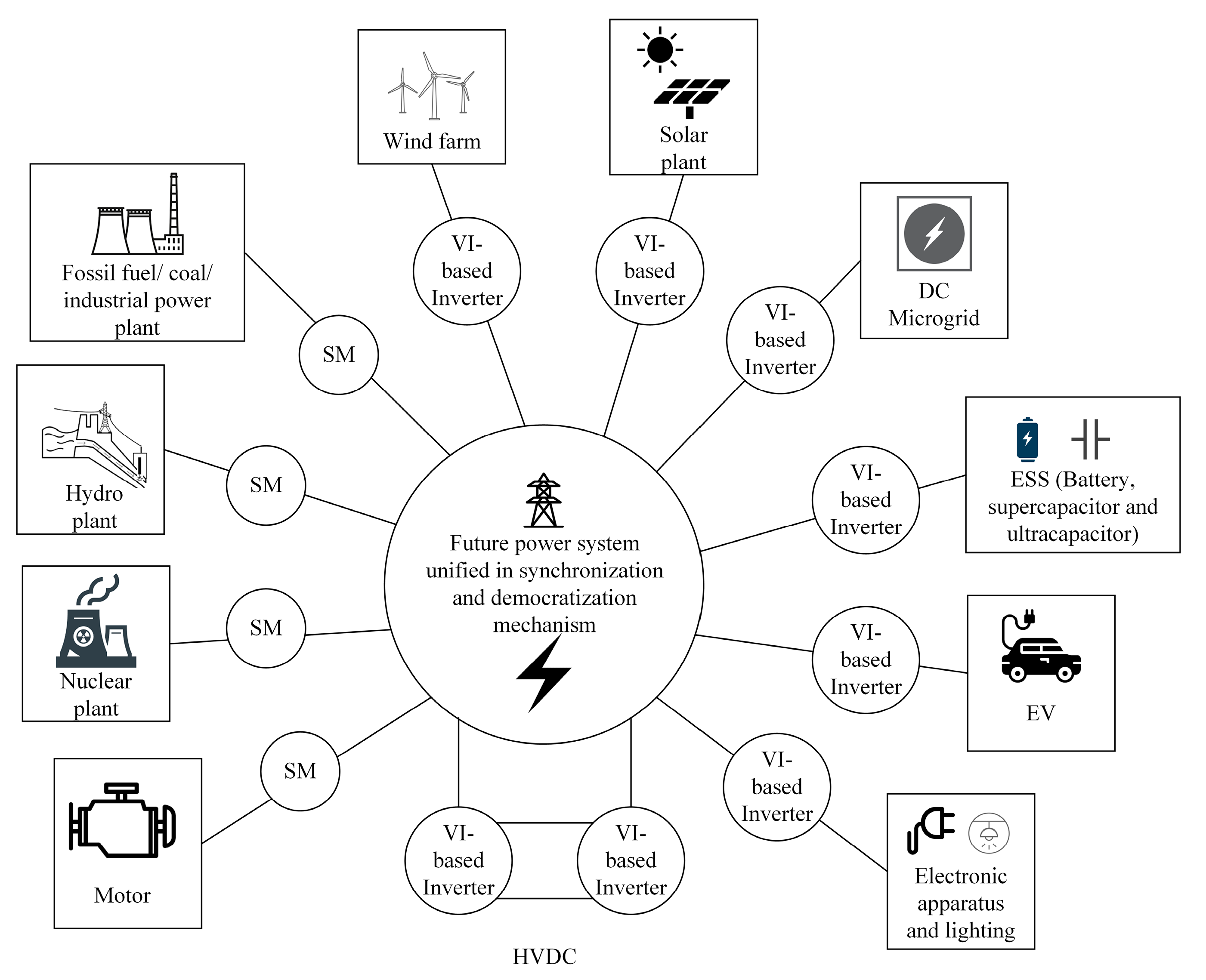
The implementation of VI is flexible and versatile. Various microcontrollers, DSP, or computers including dSpace, Microchip, and Texas Instrument (TI) are applicable to emulate VI with suitable sensors, interface, and configuration. The emulation of VI can be integrated with AI to improve transient response and steady-state error. A fuzzy adaptable logic controller based on a differential evolution algorithm is developed specifically for VI-based frequency regulation [83]. The inertial response of a PV system can be improved by using battery ESS. The combination of droop and inertia emulation [84] is possible to enable the ability to operate at a setpoint of active power and thus guarantee the system frequency stability [85]. VI and conventional active power-frequency droop control are the common approaches to regulate the active power output of the inverter-based generator in maintaining nominal frequency at all time. VI exhibits lower overshoot, better damping, and slower frequency transients compared to the droop [86]. The applications of VI-based inverters are versatile in unifying and synchronizing different sources of energy into modern power system [87]. Figure 14 illustrates the application of VI-based inverters in the modern power system to replace SM.
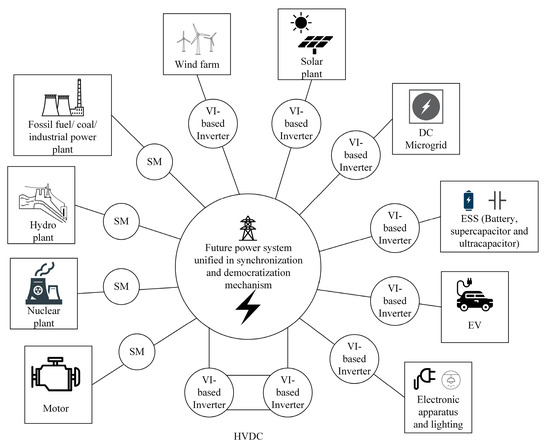
Figure 14.
The applications of conventional SM and VI-based inverters.
Normally, IEEE 9-Bus test system is widely used for the performance assessment of VI-based inverters. The pole-zero plot, Nyquist diagram, and Lyapunov stability [88] are the most common stability assessments for VI-based controller design. VI-based inverters exhibit larger inertia than droop control with better frequency stability and robustness. VSG control and proposed inertial droop control inherit the advantages of droop control, and, in addition, provide inertia support for the system. The amount of inertia is solely dependent on J, whereas the damping ratio depends on the damping factor (D) and output reactance (X). The delay in the governor of VSG reduces the inertia and therefore amplifies oscillation. Hence, the governor delay is unnecessary for VSG control. Contrarily, delay in P droop increases the inertia. VI is gradually becoming an important index and benchmark in microgrids or modern power systems. VI-based inverters have the potential to replace conventional inertia-less droop control [48]. There are multiple research works that have proposed the concept of VI to act as an ancillary service [89,90]. It is utilized for distorted grid condition to ensure the performance of various power converters. The power grid frequency and voltage amplitude are expected to be regulated by VI. The grid support can be improved by designing active power support, reactive power support and VI-based controller into these supporting components.
VI emulation is also applicable to integrate with energy storage units including batteries, flywheels, supercapacitors, and ultracapacitors. The VI is crucial for AC to DC systems to stabilize the conversion of AC to DC. The emulation of any mathematical model-based VI is possible for power electronic system by controlling PWM. The PWM is programmed to emulate any beneficial dynamic and static characteristics of the conventional system. The inducverter and STATCOM are the extended applications of VI. The inducverter is designed to imitate the behavior of the induction generators. It is similar to synchronverter by automatically synchronizing itself without the PLL. STATCOM provides variable reactive in response to voltage variation, similar to reactive power droop control. It serves the same purposes as the VI-based converter, that is supporting the stability of the grid. The Quality of Service (QoS) requirement for smart grid, microgrid, and utility grid is higher, and thus VI is crucial. The open market for power quality control via VI is expected to initiate. The VI-based power converter is designed for the application for electric cars, air conditioners, lighting systems, and electric appliances. The synchronverter is more suitable for an isolated power system because it operates as a grid-forming unit. VSG is applicable for interconnected operation as it acts as a grid-following unit with an inertial response. VI emulation has the capacity to develop into standardized electric power ancillary service by the electricity utility company in the future. It includes power quality conditioning, VI emulation, and harmonic resonance damping to upgrade the existing grid-connected RES [91]. This emerging trend is because of the importance of synchronization for a grid-connected converter. VI is a measurable standard in enhancing power converter’s capability during interrupted operation in abnormal utility voltage conditions. A robust method with advanced features including expert systems has been identified to inject power into the grid with low total harmonic distortion (THD) of the current [92]. To accelerate the penetration of grid-connected RES, several recommendations should be clearly defined as the following:
- The definition of a new grid code and standards: Grid code and standards should enable the integration of large-scale RES into the power grid, by enforcing VI emulation. The frequency regulation should be contributed by RES, and grid-forming inverter should be mandatory.
- The revision of existing reserve policy: Further technical studies and economic analysis are recommended to revise the current policy to adjust proper frequency reserve margin. It is to suit the high penetration of RES in balancing between cost and performance.
- The development of new storage technologies for frequency regulation: Both supercapacitor and ultracapacitor are promising storage technologies that are applicable to VI emulation.
5.1. Current Challenges and Limitations
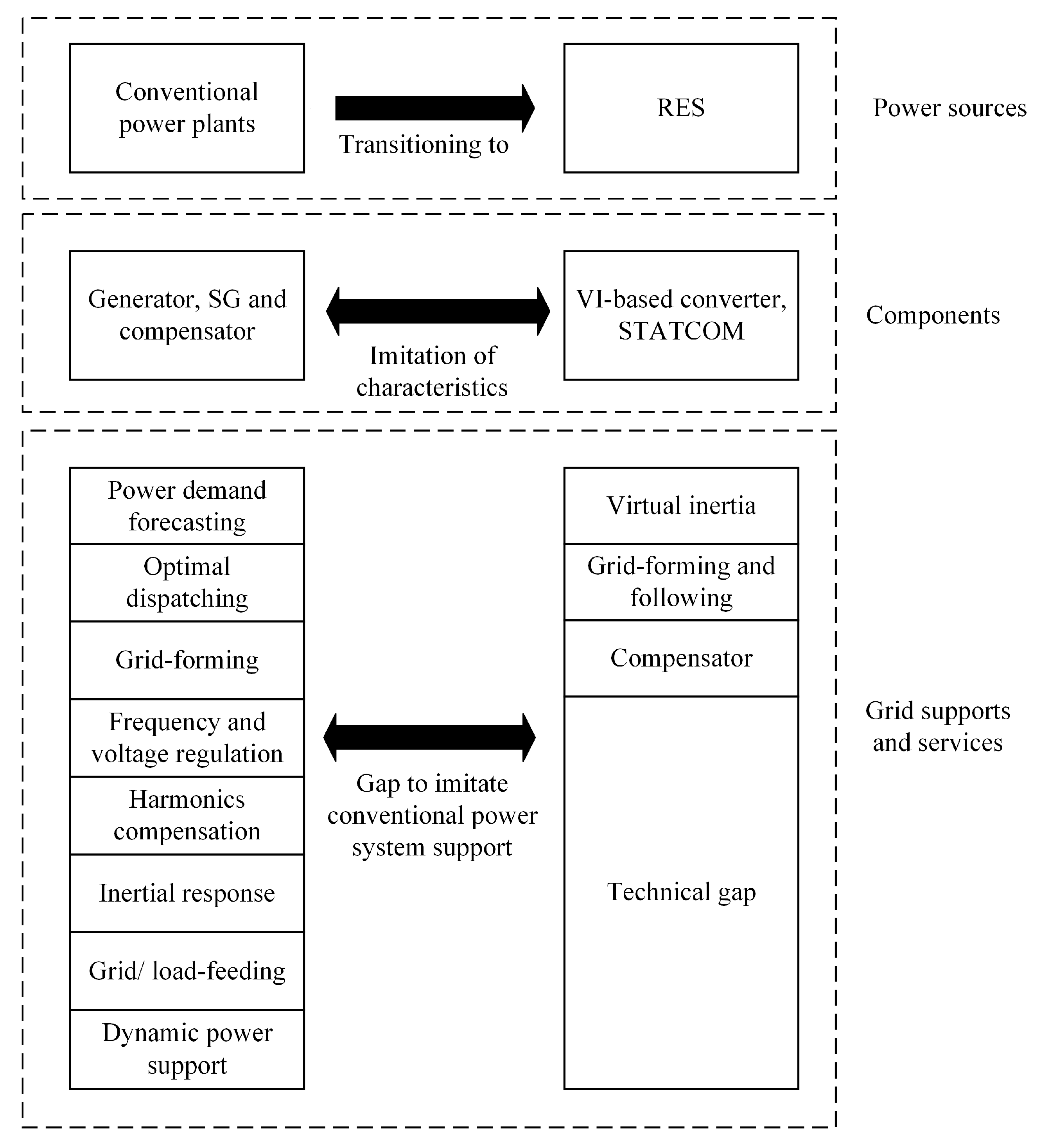
To date, VI-based inverters have several critical issues and limitations. First, the frequency detection and measurement should be accurate, persistent, and consistent for precise control. It is because VI emulation solely depends on frequency variation. It is challenging in term of detailed modeling and complex algorithm development. The cost-effectiveness, algorithm complexity, and computational requirement of VI emulation should be considered as well [93]. Second, the PI systems of VSG, VSM, and synchronverter are analog-based feedback system. The transient response is relatively slow compared with a fully digitalized system. The instability of mathematical modeling and numerical aspect is present. Although the PI system is technologically proven, its scalability, adaptability and lack of self-learning mechanism are the common drawbacks and limitations. The choice to emulate which order of SG is the balance between accuracy and complexity. The higher is the order of SG, the higher is the complexity of the system but with higher accuracy. The most common order of SG is between second and third order. Despite the increasing research on VI-based inverters, there are challenges and technical gaps regarding the integration of RES with the power grid. The existing knowledge of traditional power system operation is unable to replicate completely via VI-based inverters. The present technical gap of VI-based inverters is illustrated in Figure 15.
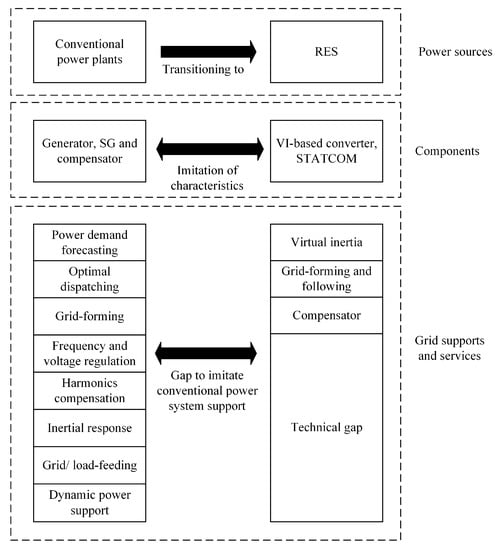
Figure 15.
The technical gap of VI-based inverter.
Most of the proposed implementations are based on conventional PI controller and verified by small-scaled experimental setup only. The tuning of the PI controller parameters is performed by small-signal analysis approaches. It means that the current research works are only valid under certain assumptions. The tuning process of proportional gain (KP) and integral gain (KI) must be robust. It is to ensure that transient response, settling time, overshoots, and oscillations are satisfactory. The robustness of the PI controller is limited because operating environments such as temperature, weather, power surge, sudden load change, and occurrence of faults may affect the performance. The PI controller is not adaptive and does not learn over time. It is required to fine-tune the controllers to ensure the system is stable for every new model. The current limitation of existing VI technique is the requirement of fine-tuning for the frequency droop coefficient, inertia constant, and load frequency controller parameters. The tuning process cannot guarantee the frequency stability of microgrid with low inertia. System reliability should be emphasized to continuously access the robustness of frequency regulation [94]. Generally, VI-based inverter is a relatively new design for a modern power system. Due to its new conceptual design and architecture, there are still many unexplored areas yet to be resolved.
The implementation of VI has its own areas of controversy and conflict. It includes the problems relating to low inertia and consequential loss of generation equipped with RoCoF protection to identify islanding conditions. Various actions have been taken to make protections less sensitive to mal-operation and low inertia. In the future, VI-based inverters are expected to be equipped with advanced capabilities. It should create system voltage without the supply of clean AC power, support power restoration after the blackout, contribute to fault level that supplies fault current in phase with the system without any delay, and be compatible with the existing synchronous plant. VI-based inverters should act as a sink to counter harmonics, inter-harmonics, and unbalance in system voltage.
5.2. ESS for VI System
ESS including capacitors and batteries have been proposed to integrate with VI system. It is to support dynamic frequency control using power electronic converters, in injecting or compensating active power [95]. The supercapacitor or ultracapacitor acts as temporary energy storage to tackle short-term power fluctuation for inertia emulation. It emulates the inertia of a VSG to overcome high-frequency power fluctuations. In contrast, the battery deals with the long-term power fluctuations by emulating the remaining parts of the VSG which consist of droop control and reheat turbine model. The energy storage system reduces the power fluctuations of the battery effectively with the hybrid combination of ultracapacitor and battery. It achieves better system-level frequency stability while improves frequency nadir and RoCoF [96]. ESS is crucial and important for small power network with low inertia [97]. The DC-link capacitor can be replaced by ultracapacitor with larger capacitances and better flexibility for VI emulation [98]. BESS units are well-suited to provide either fast frequency and voltage control reserves or synthetic rotational inertia for power system operation, due to their very fast response behavior. A hybrid ESS consists of a battery and ultracapacitor, where the latter tackles high-frequency power fluctuations and the former resolves low-frequency power fluctuations. It is used to implement a VSG control strategy.
5.3. Current Market and Commercialized VI Service
Currently, the recognition of VI as an electrical ancillary service is still in an early stage. It is considered as an inherent property instead of an ancillary service in most modern power systems. Hence, to design VI as a commercialized service, the inertial requirements including RoCoF, frequency nadir, response time, and other relevant parameters must be technically specified. European VSYNC research group has demonstrated the effectiveness of VSG through real-time simulations only [99]. VI can be commercialized as a standardized service to regulate frequency and voltage amplitude. The microgrid without VI that affects the power grid should be penalized. The QoS metrics should be deployed to continuously access the power quality. The electricity utility providers should emphasize the significance of VI and implement the requirement of VI as standard. For commercialization of VI, a suitable trading unit for VI is inertia in kg·m2 [100]. This SI unit represents the behavior of present SM and suitable for the application of VI. The cost of inertia can be defined as cost per kg m2 to indicate how much the cost will it be for every single unit of kg m2 inertia. VI is also crucial for any power which requires high reliability and stability. This includes modern data centers, hospitals, server centers, and power grids which require an uninterruptible and stable power supply. Any commercial inverter can be improved by emulating VI to become VI-based converter to be power grid ready. The EV requires bidirectional converter (DC to AC) and VI is potential to stabilize the power transfer.
5.4. Industrial Implementation of VI-Based Inverters
From industry aspect, the adoption of VI-based inverter is a promising technology to accelerate the RES grid integration, as compared with a conventional inverter. By 2020, 20% of the global electricity will be generated by RES and fed to the grid. As the RES continues to grow, the microgrid is the key component of the decentralized energy system to support the development of smarter communities. It is a game-changer in a modern power system by shifting to modular, feasible, and scalable alternatives. To ensure the compliance and compatibility of multi-vendor microgrid systems, there is a necessity to emphasize on the standardization of control and communication technologies. It implies that VI-based inverter is the grid enabler in the microgrid to interface RES into a unified power system without sacrificing the system stability.
From the microgrid operator perspective, the high penetration of RES is a welcoming trend due to its cost-effectiveness and environmentally friendly nature. However, the grid stability will be adversely affected by these RES, and thus these concerns limit the utilization of renewable generation in traditional grids or microgrids. The operators do not want to risk instability issues. A blackout might occur in microgrid due to the lack of stabilizing functionality. To make matters worse, the intermittent nature of RES results in large fluctuations in power angle, grid voltage, and power flow. The VI-based inverter has been commercialized as a key project of European Commission Horizon 2020. In a microgrid, with high involvement of RES, alongside with ESS and loads, one of the most important considerations is the control of power converters. As an effort of standardization, most microgrid operators demand the VI emulation via VI-based inverters.
The modularity of the VI-based controller is expected to be commercialized, enabling the easy conversion of the normal inverter via PWM control. Inverter manufacturers such as Schneider Electric, ABB, and FREQCON have included VI response as a key feature in their inverters model lineup, specifically for RES grid integration. For example, ABB microgrid integrates RES by providing VI, grid stabilization, and other ancillary power system services. Another product from ABB—grid stabilizer—is designed to provide VI as an ancillary power system service. It can connect to any point on the network as its versatile ancillary support. It responds to stabilize frequency disturbances, with load shedding minimization. Another product from ABB is the Renewable-to-Grid Connector solution. It reduces the limitations of weak grids from the connection of intermittent renewable generation by improving RES output via VI. This solution provides a standardized and compliant grid connection for any existing form of RES into a weak grid. From the power operator perspective, Hydro-Quebec Transenergie’s (HQT) transmission connection VI requirements are the first power operator to ensure that wind powerplants must be equipped with an inertia emulation system. SYNDEM is another company which focuses on the research of VSM to provide synchronized and democratized power system. From all industrial development, it can be concluded that VI is a crucial element in a commercialized RES grid integration. Thus, more manufacturers, academia researchers and industrial players are involved in the design and advancement of VI application, not limited to RES integration only.
6. Conclusions
This paper presents a comprehensive review of VI-based inverters, including VSM, VSG and, synchronverter. As RES has become increasingly popular over the years, the incompatibility of converter-based non-dispatchable renewable energy generation causes the deterioration of grid frequency stability. Hence, VI-based inverters are designed to regulate the frequency of future converter-dominated power systems by providing an inertial response through the emulation of SM. The grid support by power converters is mandatory under high penetration of RES. The converter-level instability issues due to the grid support, such as the active power support, reactive power support, and virtual inertia control, should be addressed by the VI-based inverters. On the contrary, the system-level stability improvement using the inertia emulated by energy storage units, such as batteries and flywheels, should complement the VI-based inverter to inject more active and reactive power as required during instability transient.
Generally, the suitable VI-based inverter topology can be selected based on the required architecture. The selection criteria are based on the current source or voltage source implementation and desired level of equation order in emulating the exact behavior of SG. To emulate the exact dynamics of SG, synchronverter and VSM are an ideal implementation. In contrast, VSG is focused on the dynamic frequency response without emulating the exact behavior of SG. The VI-based inverter is expected to be evolved into a necessity in a smart grid, modern power system, and RES integration as an ancillary service to improve frequency stability of large power grids. Its development will be accelerated due to the increasing penetration of RES, such as grid-connected solar power and wind power. Apart from grid integrator, similar topology from VI-based inverter can be also applied in the advancement of EV, HVDC, normal inverter, etc.
As the integration of RES grows, more governments, academics, and industrial manufacturers are expected to fund the research and development of VI-based inverters. The power system operator will emphasize of the necessity of VI as a standardized requirement in a microgrid or conventional power grid to avoid electricity blackout, frequency instability, and unnecessary frequency relay tripping, even under high penetration of RES. The ancillary service of VI will be a mandatory requirement and standardized under the International Organization for Standardization (ISO) or other relevant code of practice. These regulations are vital to maintain the power quality of the grid. The control strategy of VI-based inverters is expected to be modernized as digital control, under AI-based topology. There are many funded companies including synchronized and democratized smart grid (SYNDEM) and European Union (EU) Commissioning focusing on the research and development (R&D) of VI-based inverter.
In the next few years, the next generation of VI-inverters with enhanced controller based on the latest technologies such as model predictive control (MPC) and AI are expected to replace the classical proportional integral (PI) controller. The algorithm is evolving into intelligent, adaptive, and MPC algorithm, instead of a conventional PID controller due to its ageing architecture and slower transient response. The emerging strategies including MPC, adaptive VI, enhanced VI by supercapacitors or ESS, AI algorithm, and others are expected to dominate the next generation VI-based inverters. Their aims are to increase the dampening characteristics of VI, decrease the frequency recovery time (transient time), decrease frequency steady-state oscillation error, and improve overall stability as well as algorithm sophistication. Since the VI-inverter is a relatively new technology, there is a lot of room for improvement and enhancement, to match the state-of-the-art SM which has been technologically matured for decades. The tremendous development of EV, HVDC, and electrical appliances are also major factors for developing VI-based inverters. In the future, VI will become an important research direction for the grid interface because of higher RES penetration. VI control strategy provides a feasible way for the transition to the power electronics-based power system from the conventional SM-based one.
Author Contributions
Conceptualization, K.Y.Y., C.R.S. and J.M.-Y.L.; methodology, K.Y.Y.; validation, K.Y.Y., C.R.S. and J.M.-Y.L.; formal analysis, K.Y.Y., C.R.S. and J.M.-Y.L.; investigation, K.Y.Y.; resources, K.Y.Y., C.R.S. and J.M.-Y.L.; data curation, K.Y.Y.; writing—original draft preparation, K.Y.Y.; writing—editing, K.Y.Y.; writing—reviewing & formatting, K.Y.Y., C.R.S. and J.M.-Y.L.; visualization, K.Y.Y.; supervision, C.R.S. and J.M.-Y.L.; project administration, C.R.S. and J.M.-Y.L.; funding acquisition, C.R.S. and J.M.-Y.L.
Acknowledgments
This research was funded by the School of Engineering, Monash University, Malaysia.
Conflicts of Interest
The authors declared that there is no conflict of interest.
References
- Zsiborács, H.; Baranyai, N.H.; Vincze, A.; Zentkó, L.; Birkner, Z.; Máté, K.; Pintér, G. Intermittent Renewable Energy Sources: The Role of Energy Storage in the European Power System of 2040. Electronics 2019, 8, 729. [Google Scholar] [CrossRef]
- Ding, X.; Liu, L.; Huang, G.; Xu, Y.; Guo, J. A Multi-Objective Optimization Model for a Non-Traditional Energy System in Beijing under Climate Change Conditions. Energies 2019, 12, 1692. [Google Scholar] [CrossRef]
- Tamrakar, U.; Shrestha, D.; Malla, N.; Ni, Z.; Hansen, T.M.; Tamrakar, I.; Tonkoski, R. Comparative Analysis of Current Control Techniques to Support Virtual Inertia Applications. Appl. Sci. 2018, 8, 2695. [Google Scholar] [CrossRef]
- Zhang, D.; Wu, Y.; Xiong, L.; Zhao, C. Analysis of Inertia Characteristics of Direct-Drive Permanent-Magnet Synchronous Generator in Micro-Grid. Energies 2019, 12, 3141. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Q.; Wan, D.; Lin, S. A Virtual Inertia-Based Power Feedforward Control Strategy for an Energy Router in a Direct Current Microgrid Application. Energies 2019, 12, 517. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Soltani, H.; Blaabjerg, F.; Calado, M.R.A.; Catalão, J.P.S. Virtual Inertia and Mechanical Power-Based Control Strategy to Provide Stable Grid Operation under High Renewables Penetration. Appl. Sci. 2019, 9, 1043. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, X.; Zhang, B.; Ma, Y.; Wu, M. Research on Distributed PV Storage Virtual Synchronous Generator System and Its Static Frequency Characteristic Analysis. Appl. Sci. 2018, 8, 532. [Google Scholar] [CrossRef]
- Rodriguez, E.; Rodriguez, P. Inertia Emulation in AC/DC Interconnected Power Systems Using Derivative Technique Considering Frequency Measurement Effects. IEEE Trans. Power Syst. 2017, 32, 3338–3351. [Google Scholar]
- Rakhshani, E.; Rouzbehi, K.; Sánchez, A.J.; Tobar, A.C.; Pouresmaeil, E. Integration of Large Scale PV-Based Generation into Power Systems: A Survey. Energies 2019, 12, 1425. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, X. VSG-Based Dynamic Frequency Support Control for Autonomous PV-Diesel Microgrids. Energies 2018, 11, 1814. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y. Virtual Inertia Control Application to Enhance Frequency Stability of Interconnected Power Systems with High Renewable Energy Penetration. Energies 2018, 11, 981. [Google Scholar] [CrossRef]
- Pagola, V.; Peña, R.; Segundo, J.; Ospino, A. Rapid Prototyping of a Hybrid PV-Wind Generation System Implemented in a Real-Time Digital Simulation Platform and Arduino. Electroncis 2019, 8, 102. [Google Scholar] [CrossRef]
- Chen, D.; Xu, Y.; Huang, A.Q. Integration of DC Microgrids as Virtual Synchronous Machines Into the AC Grid. IEEE Trans. Ind. Electron. 2017, 64, 7455–7466. [Google Scholar] [CrossRef]
- Xi, J.; Geng, H.; Ma, S.; Chi, Y.; Yang, G. Inertial response characteristics analysis and optimisation of PMSG-based VSG-controlled WECS. Renew. Power Gener. 2018, 12, 1741–1747. [Google Scholar] [CrossRef]
- Gloe, A.; Jauch, C.; Craciun, B.; Winkelmann, J. Continuous provision of synthetic inertia with wind turbines: Implications for the wind turbine and for the grid. Renew. Power Gener. 2019, 13, 668–675. [Google Scholar] [CrossRef]
- Chandrakar, P.; Saha, S.; Das, P.; Singh, A.; Debbarma, S. Grid Integration of PV System using Synchronverter. In Proceedings of the 2018 International Conference on Computation of Power, Energy, Information and Communication (ICCPEIC), Chennai, India, 28–29 March 2018. [Google Scholar]
- Amin, M.; Molinas, M. Self-synchronisation of Wind Farm in MMC-based HVDC System. IEEE Trans. Energy Convers. 2017, 32, 458–470. [Google Scholar] [CrossRef]
- Zhang, W.; Rouzbehi, K.; Luna, A.; Gharehpetian, G.B.; Rodriguez, P. Multi-terminal HVDC grids with inertia mimicry capability. Renew. Power Gener. 2016, 10, 752–760. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, M.; Li, Y. Self-adaptive inertia control of DC microgrid based on fast predictive converter regulation. Renew. Power Gener. 2017, 11, 1295–1303. [Google Scholar] [CrossRef]
- Dhingra, K.; Singh, M. Frequency support in a micro-grid using virtual synchronous generator based charging station. Renew. Power Gener. 2018, 12, 1034–1044. [Google Scholar] [CrossRef]
- Li, B.; Zhang, W.; He, J. Inertia emulation and dynamic voltage support scheme for MMC-based dc systems. Renew. Power Gener. 2019, 13, 146–154. [Google Scholar] [CrossRef]
- Web of Science Group. Available online: https://mjl.clarivate.com/ (accessed on 10 September 2019).
- Zaman, M.S.U.; Hazazi, K.M.; Haider, Z.M.; Haider, R.; Kim, C.-H. Frequency Response Analysis of a Single-Area Power System with a Modified LFC Model Considering Demand Response and Virtual Inertia. Energies 2018, 11, 787. [Google Scholar] [CrossRef]
- Stephen, J. Electric Machinery Fundamentals; McGraw-Hill Education: New York, NY, USA, 2012. [Google Scholar]
- Zhong, Q.-C.; Weiss, G. Static Synchronous Generators for Distributed Generation and Renewable Energy. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009. [Google Scholar]
- Liu, J.; Yang, D.; Yao, W.; Fang, R.; Zhao, H.; Wang, B. PV-based virtual synchronous generator with variable inertia to enhance power system transient stability utilizing the energy storage system. Prot. Control Mod. Power Syst. 2017, 2, 39. [Google Scholar] [CrossRef]
- Sun, R.; Chen, B.; Lv, Z.H.; Mei, J.; Zang, H.; Wei, Z.; Sun, G. Research on Robust Day-Ahead Dispatch Considering Primary Frequency Response of Wind Turbine. Appl. Sci. 2019, 9, 1784. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, Y.; Zhang, X. Integrated wind turbine controller with virtual inertia and primary frequency responses for grid dynamic frequency support. Renew. Power Gener. 2017, 11, 1129–1137. [Google Scholar] [CrossRef]
- Khan, S.; Bletterie, B.; Anta, A.; Gawlik, W. On Small Signal Frequency Stability under Virtual Inertia and the Role of PLLs. Energies 2018, 11, 2372. [Google Scholar] [CrossRef]
- Miao, H.; Mei, F.; Yang, Y.; Chen, H.; Zheng, J. A Comprehensive VSM Control Strategy Designed for Unbalanced Grids. Energies 2019, 12, 1169. [Google Scholar] [CrossRef]
- Beck, H.-P.; Hesse, R. Virtual Synchronous Machine. In Proceedings of the 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 7 January 2007. [Google Scholar]
- Khajehoddin, S.A.; Karimi-Ghartemani, M.; Ebrahimi, M. Grid-Supporting Inverters With Improved Dynamics. IEEE Trans. Ind. Electron. 2019, 66, 3655–3667. [Google Scholar] [CrossRef]
- Wu, W.; Chen, Y.; Luo, A.; Zhou, L.; Zhou, X.; Yang, L.; Dong, Y.; Guerrero, J.M. A Virtual Inertia Control Strategy for DC Microgrids Analogized With Virtual Synchronous Machines. IEEE Trans. Ind. Electron. 2017, 64, 6005–6016. [Google Scholar] [CrossRef]
- Lv, Z.; Zhong, Q.-C. Control of Modular Multilevel Converters as Virtual Synchronous Machines. In Proceedings of the IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar]
- Bose, U.; Chattopadhyay, S.K.; Chakraborty, C.; Pal, B. A Novel Method of Frequency Regulation in Microgrid. IEEE Trans. Ind. Appl. 2019, 55, 111–121. [Google Scholar] [CrossRef]
- Hu, W.; Wu, Z.; Dou, X.; Hu, M.; Song, H. Dynamic Analysis and Parameters Design of the Load Virtual Synchronous Machine. In Proceedings of the IEEE Power & Energy Society General Meeting, Portland, OR, USA, 24 December 2018. [Google Scholar]
- Ademola-Idowu, A.; Zhang, B. Optimal Design of Virtual Inertia and Damping Coefficients for Virtual Synchronous Machines. arXiv 2018, arXiv:preprint/1806.08488. [Google Scholar]
- D’Arco, S.; Suula, J.A.; Fosso, O.B. A Virtual Synchronous Machine implementation for distributedcontrol of power converters in SmartGrids. Electr. Power Syst. Res. 2015, 122, 180–197. [Google Scholar] [CrossRef]
- Zhang, B.; Yan, X.; Li, D.; Zhang, X.; Han, J.; Xiao, X. Stable Operation and Small-Signal Analysis of Multiple Parallel DG Inverters Based on a Virtual Synchronous Generator Scheme. Energies 2018, 11, 203. [Google Scholar] [CrossRef]
- Ma, Y.; Lin, Z.; Yu, R.; Zhao, S. Research on Improved VSG Control Algorithm Based on Capacity-Limited Energy Storage System. Energies 2018, 11, 677. [Google Scholar] [CrossRef]
- Liu, J.; Hossain, M.; Lu, J.; Raf, F.; Li, H. A hybrid AC/DC microgrid control system based on a virtual synchronous generator for smooth transient performances. Electr. Power Syst. Res. 2018, 162, 169–182. [Google Scholar] [CrossRef]
- Su, J.; Li, W.; Liu, H.; Meng, F.; Wang, L.; Han, X. Application of Virtual Synchronous Generator in Solar Power Generation. J. Phys. Conf. Ser. 2018, 1087. [Google Scholar] [CrossRef]
- Andalib-Bin-Karim, C.; Liang, X.; Zhang, H. Fuzzy-Secondary-Controller-Based Virtual Synchronous Generator Control Scheme for Interfacing Inverters of Renewable Distributed Generation in Microgrids. IEEE Trans. Ind. Appl. 2018, 54, 1047–1061. [Google Scholar] [CrossRef]
- Abdolwahhab, F.; Qobad, S.; Bevrani, H. Robust Frequency Control of Microgrids Using an Extended Virtual Synchronous Generator. IEEE Trans. Ind. Appl. 2018, 33, 6289–6297. [Google Scholar]
- Wang, F.; Zhang, L.; Feng, X.; Guo, H. An Adaptive Control Strategy for Virtual Synchronous Generator. IEEE Trans. Ind. Appl. 2018, 54, 5124–5133. [Google Scholar] [CrossRef]
- Dong, S.; Chen, Y.C. Reducing Transient Active- and Reactive-power Coupling in Virtual Synchronous Generators. In Proceedings of the IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 1090–1095. [Google Scholar]
- Zhang, B.; Li, D.; Wang, Y.; Yan, X. Self-adaptable reactive power-voltage controller for virtual synchronous generators. J. Eng. 2019, 2019, 2969–2973. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Comparison of Dynamic Characteristics Between Virtual Synchronous Generator and Droop Control in Inverter-Based Distributed Generators. IEEE Trans. Power Electron. 2016, 31, 3600–3611. [Google Scholar] [CrossRef]
- Li, B.; Zhou, L.; Yu, X.; Zheng, C.; Liu, J. Improved power decoupling control strategy based on virtual synchronous generator. Power Electron. 2017, 10, 462–470. [Google Scholar] [CrossRef]
- Shi, K.; Ye, H.; Song, W.; Zhou, G. Virtual Inertia Control Strategy in Microgrid Based on Virtual Synchronous Generator Technology. IEEE Access 2018, 6, 27949–27957. [Google Scholar] [CrossRef]
- Ma, Y.; Cao, W.; Yang, L.; Wang, F.; Tolbert, L.M. Virtual Synchronous Generator Control of Full Converter Wind Turbines With Short-Term Energy Storage. IEEE Trans. Ind. Electron. 2017, 64, 8821–8831. [Google Scholar] [CrossRef]
- Yazdi, S.S.H.; Milimonfared, J.; Fathi, S.H.; Rouzbehi, K.; Rakhshani, E. Analytical modeling and inertia estimation of VSG-controlled Type 4 WTGs: Power system frequency response investigation. Electr. Power Energy Syst. 2019, 107, 446–461. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, W.; Li, Y.; Tan, Y.; Chen, C.; He, L.; Hager, U.; Rehtanz, C. A Virtual Synchronous Generator Control Strategy for VSC-MTDC Systems. IEEE Trans. Energy Convers. 2018, 33, 750–761. [Google Scholar] [CrossRef]
- Rahman, F.S.; Kerdphol, T.; Watanabe, M.; Mitani, Y. Optimization of virtual inertia considering system frequency protection scheme. Electr. Power Energy Syst. 2019, 170, 294–302. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y.; Watanabe, M.; Küfeoǧlu, S. Robust Virtual Inertia Control of an Islanded Microgrid Considering High Penetration of Renewable Energy. IEEE Access 2018, 6, 625–636. [Google Scholar] [CrossRef]
- Magdy, G.; Shabib, G.; Elbaset, A.A.; Mitani, Y. Renewable power systems dynamic security using a new coordination of frequency control strategy based on virtual synchronous generator and digital frequency protection. Electr. Power Energy Syst. 2019, 109, 351–368. [Google Scholar] [CrossRef]
- Rathore, B.; Chakrabarti, S.; Anand, S. Frequency response improvement in microgrid using optimized VSG control. In Proceedings of the 2016 National Power Systems Conference, Bhubaneswar, India, 9–21 December 2016. [Google Scholar]
- Sekizaki, S.; Matsuo, K.; Sasaki, Y.; Yorino, N.; Nakamura, Y.; Zoka, Y.; Shimizu, T.; Nishizaki, I. A Development of Single-phase Synchronous Inverter and Integration to Single-phase Microgrid effective for frequency stability enhancement. IFAC-PapersOnLine 2018, 51, 245–250. [Google Scholar] [CrossRef]
- Hu, P.; Chen, H.; Cao, K.; Hu, Y.; Kai, D.; Chen, L.; Wang, Y. Coordinated Control of Multiple Virtual Synchronous Generators in Mitigating Power Oscillation. Energies 2018, 11, 2788. [Google Scholar] [CrossRef]
- Huang, X.; Wang, K.; Li, G.; Zhang, H. Virtual Inertia-Based Control Strategy of Two-Stage Photovoltaic Inverters for Frequency Support in Islanded Micro-Grid. Electronics 2018, 7, 340. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Nguyen, P.-L.; Ma, Z.; Sheng, W. Self-Synchronized Synchronverters: Inverters Without a Dedicated Synchronization Unit. IEEE Trans. Power Electron. 2014, 29, 617–630. [Google Scholar] [CrossRef]
- Reed, J.K.; Zhong, Q.-C.; Saniie, J. Digital Synchronverter Design Flow for Renewable Energy. In Proceedings of the 2017 IEEE International Conference on Electro Information Technology, Lincoln, NE, USA, 14–17 May 2017. [Google Scholar]
- Zhong, Q.-C.; Konstantopoulos, G.C.; Ren, B.; Krstic, M. Improved Synchronverters with Bounded Frequency and Voltage for Smart Grid Integration. IEEE Trans. Smart Grid 2018, 9, 786–796. [Google Scholar] [CrossRef]
- Thomas, A.; Smitha, S.D. A Self-synchronized Synchronverter Technology for Integrating PV Inverters to Grid without Using a Phase Locked Loop. Int. J. Innov. Res. Technol. 2015, 2, 24–29. [Google Scholar]
- Shao, T.; Zheng, T.Q.; Li, H.; Zhang, X. Parameter design and hot seamless transfer of single-phase synchronverter. Electr. Power Energy Syst. 2018, 160, 63–70. [Google Scholar] [CrossRef]
- Younis, T.; Ismeil, M.; Orabi, M.; Hussain, E.K. A Single-phase Self-synchronized Synchronverter with Bounded Droop Characteristics. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018. [Google Scholar]
- Aouini, R.; Nefzi, I.; Kilani, K.B.; Elleuch, M. Exploitation of Synchronverter Control to Improve the Integration of Renewable Sources to the Grid. J. Electr. Syst. 2017, 13, 543–557. [Google Scholar]
- Dong, S.; Chen, Y.C. A Method to Directly Compute Synchronverter Parameters for Desired Dynamic Response. IEEE Trans. Energy Convers. 2018, 33, 814–825. [Google Scholar] [CrossRef]
- Blau, M.; Weiss, G. Synchronverters used for damping inter-area oscillations in two-area power systems. Int. Conf. Renew. Energ. Power Qual. 2018, 1, 45–50. [Google Scholar] [CrossRef]
- Younis, T.; Ismeil, M.; Hussain, E.K.; Orabi, M. An Improved Single-phase Self-synchronized Synchronverter with Enhanced Dynamics and Current Limitation Capability. Res. J. 2018, 12, 337–344. [Google Scholar]
- Wang, X.; Chen, L.; Sun, D.; Zhang, L.; Nian, H. A Modified Self-Synchronized Synchronverter in Unbalanced Power Grids with Balanced Currents and Restrained Power Ripples. Energies 2019, 12, 923. [Google Scholar] [CrossRef]
- Aouini, R.; Marinescu, B.; Kilani, K.B.; Elleuch, M. Synchronverter-Based Emulation and Control of HVDC Transmission. IEEE Trans. Power Syst. 2015, 31, 278–286. [Google Scholar] [CrossRef]
- Zhang, W.; Cantarellas, A.M.; Rocabert, J.; Luna, A.; Rodriguez, P. Synchronous Power Controller With Flexible Droop Characteristics for Renewable Power Generation Systems. IEEE Trans. Sustain. Energy 2016, 7, 1572–1582. [Google Scholar] [CrossRef]
- Barzilai, G.; Marcus, L.; Weiss, G. Energy Storage Systems-Grid Connection Using Synchronverters. In Proceedings of the ISCEE International Conference on the Science of Electrical Engineering, Eilat, Israel, 16–18 November 2016. [Google Scholar]
- Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.P.; Hansen, T.M.; Tonkoski, R. Virtual Inertia: Current Trends and Future Directions. Appl. Sci. 2017, 7, 654. [Google Scholar] [CrossRef]
- Yang, S.; Fang, J.; Tang, Y.; Qiu, H.; Dong, C.; Wang, P. Modular Multilevel Converter Synthetic Inertia-Based Frequency Support for Medium-Voltage Microgrids. IEEE Trans. Ind. Electron. 2019, 66, 8992–9002. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Invernizzi, M.; Labella, A.; Procopio, R. Design and Implementation of a Variable Synthetic Inertia Controller for Wind Turbine Generators. IEEE Trans. Power Syst. 2019, 34, 754–764. [Google Scholar] [CrossRef]
- Rajan, E.; Amrutha, S. Synchronverter based HVDC transmission. In Proceedings of the Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 21–22 April 2017. [Google Scholar]
- Yan, X.; Li, J.; Zhang, B.; Jia, Z.; Tian, Y.; Zeng, H.; Lv, Z. Virtual Synchronous Motor Based-Control of a Three-Phase Electric Vehicle Off-Board Charger for Providing Fast-Charging Service. Appl. Sci. 2018, 8, 856. [Google Scholar] [CrossRef]
- Liu, D. Cluster Control for EVs Participating in Grid Frequency Regulation by Using Virtual Synchronous Machine with Optimized Parameters. Appl. Sci. 2019, 9, 1924. [Google Scholar] [CrossRef]
- Yuan, C.; Xie, P.; Yang, D.; Xiao, X. Transient Stability Analysis of Islanded AC Microgrids with a Significant Share of Virtual Synchronous Generators. Energies 2018, 11, 44. [Google Scholar] [CrossRef]
- Chamorro, H.R.; Riaño, I.; Gerndt, R.; Zelinka, I.; Gonzalez-Longatt, F.; Sood, V.K. Synthetic inertia control based on fuzzy adaptive differential evolution. Electr. Power Energy Syst. 2019, 105, 803–813. [Google Scholar] [CrossRef]
- Beltran, O.; Peña, R.; Segundo, J.; Esparza, A.; Muljadi, E.; Wenzhong, D. Inertia Estimation of Wind Power Plants Based on the Swing Equation and Phasor Measurement Units. Appl. Sci. 2018, 8, 2413. [Google Scholar] [CrossRef]
- Nanou, S.I.; Papakonstantinou, A.G.; Papathanassiou, S.A. A generic model of two-stage grid-connected PV systems with primary frequency response and inertia emulation. Electr. Power Energy Syst. 2015, 127, 186–196. [Google Scholar] [CrossRef]
- Ofir, R.; Markovic, U.; Aristidou, P.; Hug, G. Droop vs. Virtual Inertia: Comparison from the Perspective of Converter Operation Mode. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018. [Google Scholar]
- Yan, X.; Zhang, W. Review of VSG Control-Enabled Universal Compatibility Architecture for Future Power Systems with High-Penetration Renewable Generation. Appl. Sci. 2019, 9, 1484. [Google Scholar] [CrossRef]
- Li, M.; Huang, W.; Tai, N.; Yu, M. Lyapunov-Based Large Signal Stability Assessment for VSG Controlled Inverter-Interfaced Distributed Generators. Energies 2018, 11, 2273. [Google Scholar] [CrossRef]
- Negri, S.; Tironi, E.; Danna, D.S. Integrated Control Strategy for Islanded Operation in Smart Grids: Virtual Inertia and Ancillary Services. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering, Milan, Italy, 6–9 June 2017. [Google Scholar]
- Agranat, Q.; MacGill, I.; Bruce, A. Fast Frequency Markets under High Penetrations of Renewable Energy in the Australian National Electricity Market. In Asia-Pacific Solar Research Conference; UNSW: Sydney, QLD, Australia, 2015. [Google Scholar]
- Zeng, Z.; Li, X.; Shao, W. Multi-functional grid-connected inverter: Upgrading distributed generator with ancillary services. Renew. Power Gener. 2018, 12, 797–805. [Google Scholar] [CrossRef]
- Jaalam, N.; Rahim, N.; Bakar, A.; Tan, C.; Haidar, A.M. A comprehensive review of synchronization methods for grid-connected converters of renewable energy source. Renew. Sustain. Energy Rev. 2016, 59, 1471–1481. [Google Scholar] [CrossRef]
- Jadhav, G.N.; Shaikh, S.J.; Buwa, O.N. Challenges in Implementation of Virtual Synchronous Generator. Compend. Tech. Pap. Springer 2018, 487, 209–221. [Google Scholar]
- Mohammed, O.O.; Otuoze, A.O.; Salisu, S.; Ibrahim, O.; Rufa’i, N.A. Virtual Synchronous Generator: An Overview. Niger. J. Technol. 2019, 38, 153–164. [Google Scholar] [CrossRef]
- Fang, J.; Lin, P.; Li, H.; Yang, Y.; Tang, Y. An Improved Virtual Inertia Control for ThreePhase Voltage Source Converters Connected to a Weak Grid. IEEE Trans. Power Electron. 2018, 34, 8660–8670. [Google Scholar]
- Fang, J.; Tang, Y.; Li, H.; Li, X. A Battery/Ultracapacitor Hybrid Energy Storage System for Implementing the Power Management of Virtual Synchronous Generators. IEEE Trans. Power Electron. 2017, 33, 2820–2824. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 2130–2146. [Google Scholar] [CrossRef]
- Karapanos, V.; de Haan, S.; Zwetsloot, K. Real time simulation of a power system with VSG hardware in the loop. In Proceedings of the 37th Annual Conference of the IEEE Industrial Electronics Society (IECON), Melbourne, Australia, 7–10 November 2011. [Google Scholar]
- Thiesen, H.; Jauch, C.; Gloe, A. Design of a System Substituting Today’s Inherent Inertia in the European Continental Synchronous Area. Energies 2016, 9, 582. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).