Multi-Angle Economic Analysis of Coal-Fired Units with Plasma Ignition and Oil Injection during Deep Peak Shaving in China
Abstract
1. Introduction
- (1)
- A peak-shaving costs function representing the operation characteristics of UPI and UOI in three peak-shaving stages is proposed, and an economic dispatch model is presented to reflect the peak-shaving costs.
- (2)
- An environmental efficiency index is defined to evaluate the environmental benefits; the multi-angle economic analysis of UPI and UOI in deep peak shaving is investigated from perspectives of thermal power plants, wind power plants, and the environment.
2. Three Periods of Peak Shaving
- (1)
- Combustion stability of boiler as the most key factor is closely relevant to the metal fatigue pressure, coal quality, fineness and concentration of coal powder, hot wind speed, and temperature, etc. Generally, when output is lower than Pa, the combustion conditions become worse, which is prone to cause accidents to coal-fired units because of flame failures;
- (2)
- SHWC cannot be ignored when the boiler is running at a low load level. When loads change rapidly, the growing thermal deviation of the circulating pipeline on the water-cooled wall will reduce the circulation flow speed, and further results in boiler circulation stagnation or reversion. The test shows that when the flow speed falls below the critical value at 30% Pn, the SHWC cannot be guaranteed;
- (3)
- Boiler auxiliary machines, such as the coal pulverizing system, water pumps, and fans, are the auxiliary facilities for combustion. On account of boilers’ large inertia, the coal pulverizing system is apt to blocking coals or suspending pulverizations while the boiler is running at low load level. Since the plasma ignition system must operate simultaneously with the coal pulverizing system and the ignition in DPSC is with a high furnace temperature, if there is too much coal powder in the furnace to be ignited timely, the accumulation of coal powder inside the furnace may cause deflagration. The expansion of flue gas from deflagration raises the furnace pressure suddenly and may further lead to the boiler explosion. Since the compressed air supply for the plasma burner contains water and oil, it may induce arcing failure or fire in the barrel of plasma igniter. Meanwhile, the probability of the pump and the fan failure is greatly raised;
- (4)
- During the low-load level operation, the monitoring, protection, and control systems may frequently alert warnings because the boiler with its auxiliary machines is operating near a critical stable point. Operators should timely and agilely deal with alarm signals and ensure the stable combustion of boilers for preventing grievous boiler explosion, which may cause economic losses and casualties.
3. Peak-Shaving Costs and Economic Dispatch Model
3.1. Modeling Peak-Shaving Costs
3.1.1. Coal Consumption Cost
3.1.2. Wear-and-Tear Cost
3.1.3. Combustion Supporting Cost
3.1.4. Environmental Cost
3.2. Prioritized Dispatch Model of Integrated Wind Power
3.3. Environmental Efficiency Index
4. Case Study and Economic Analysis
4.1. Parameters Setting of Case Study
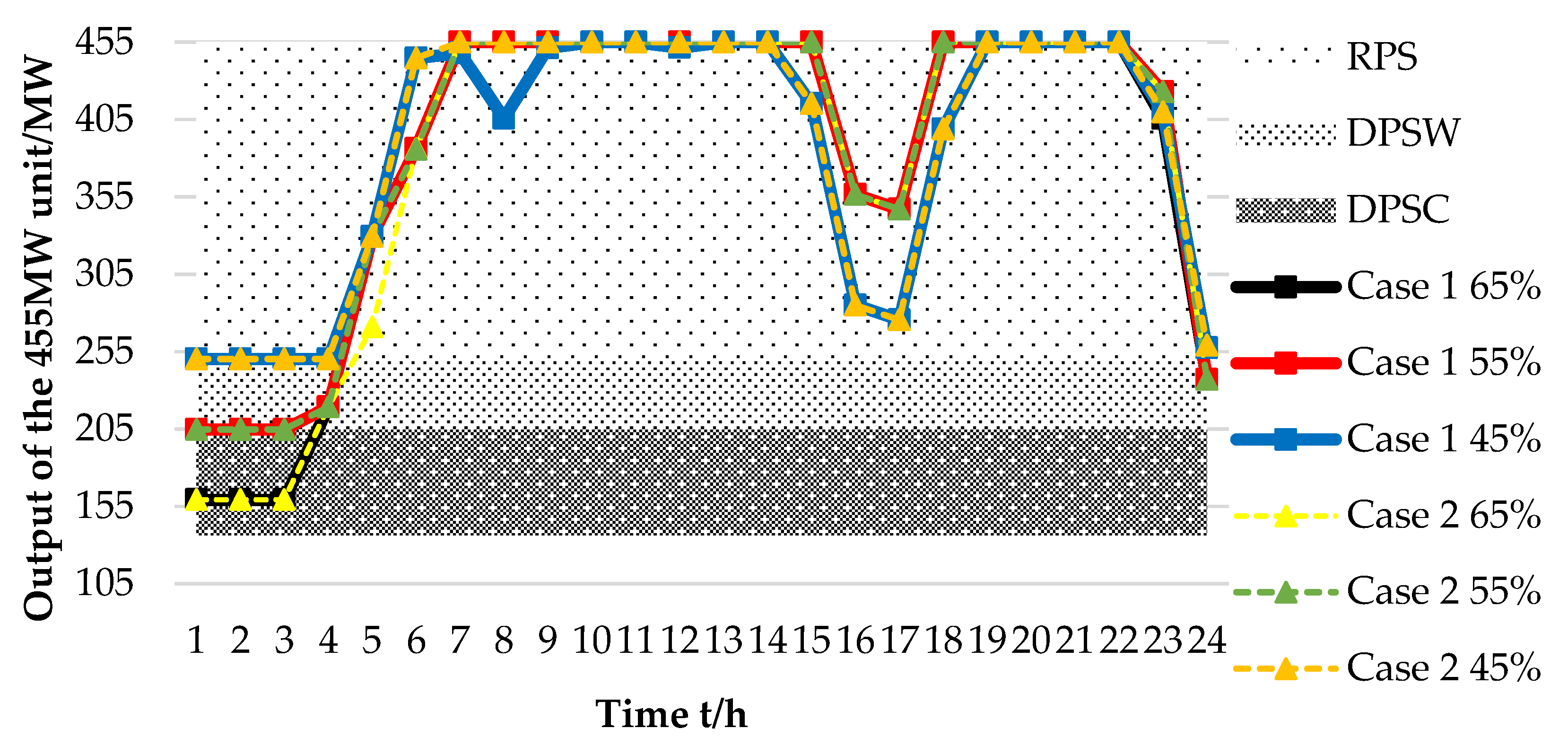
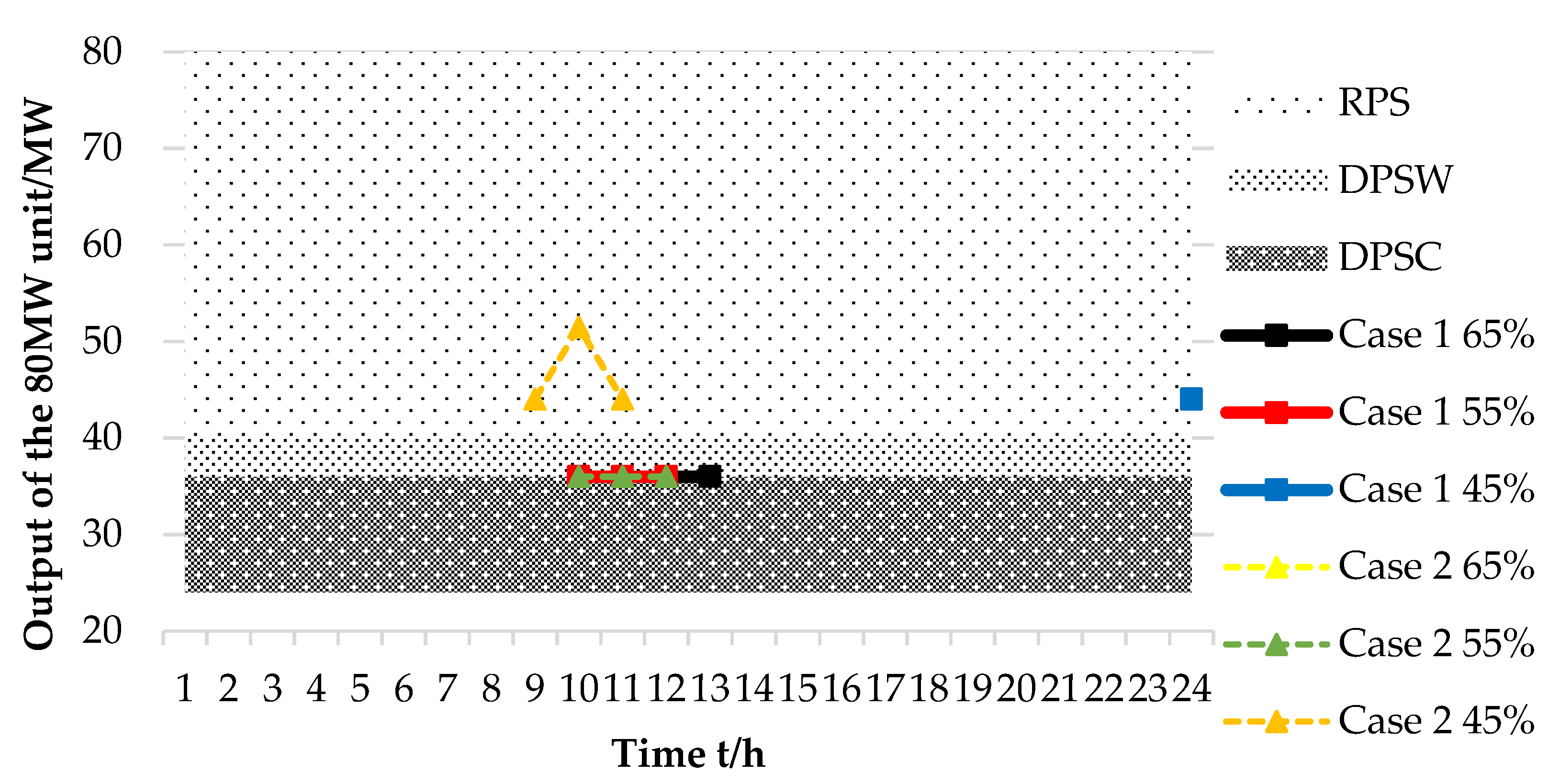
4.2. Results of Economic Dispatch
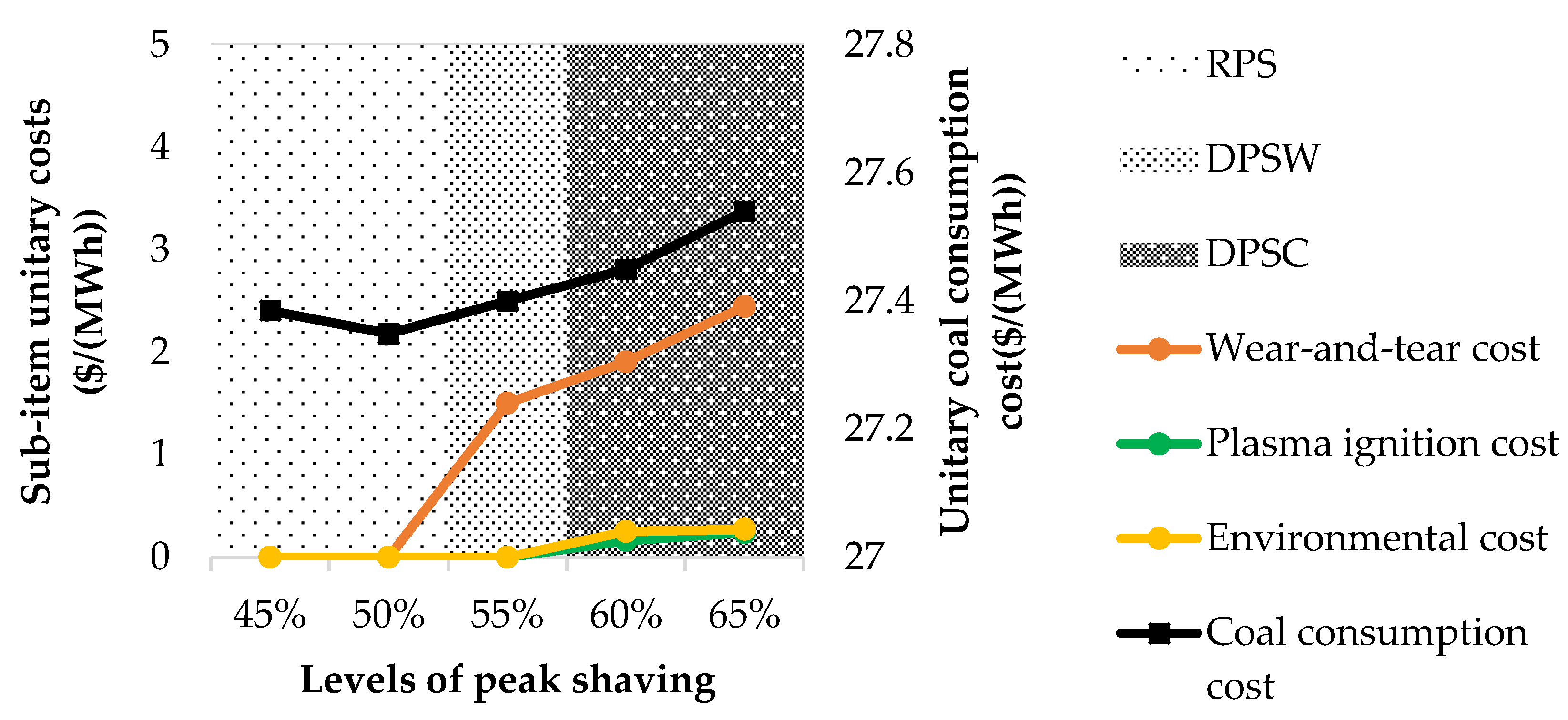
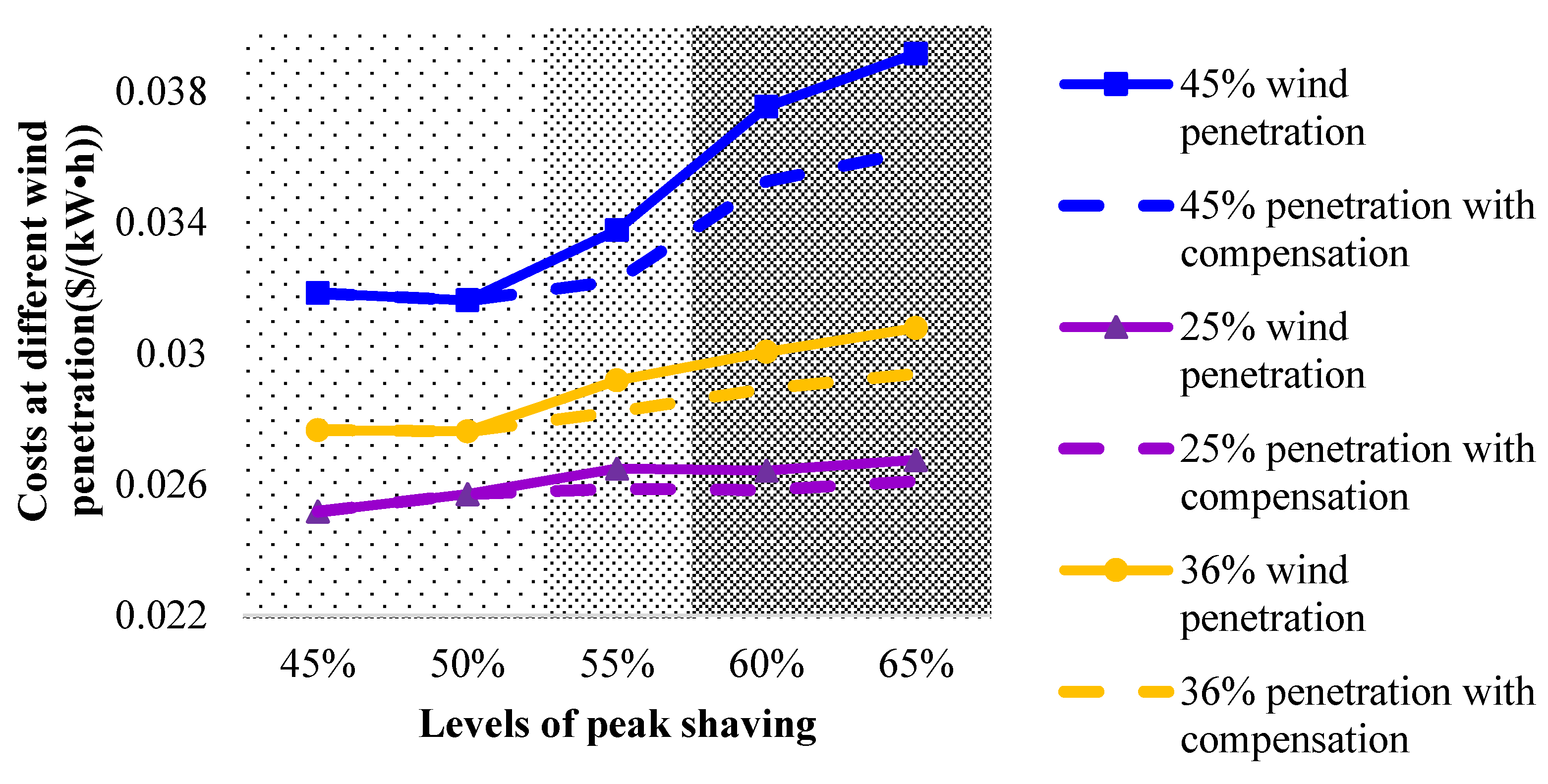
4.3. Multi-Angle Economic Analysis
4.3.1. Economy of Thermal Power Plants in Peak Shaving
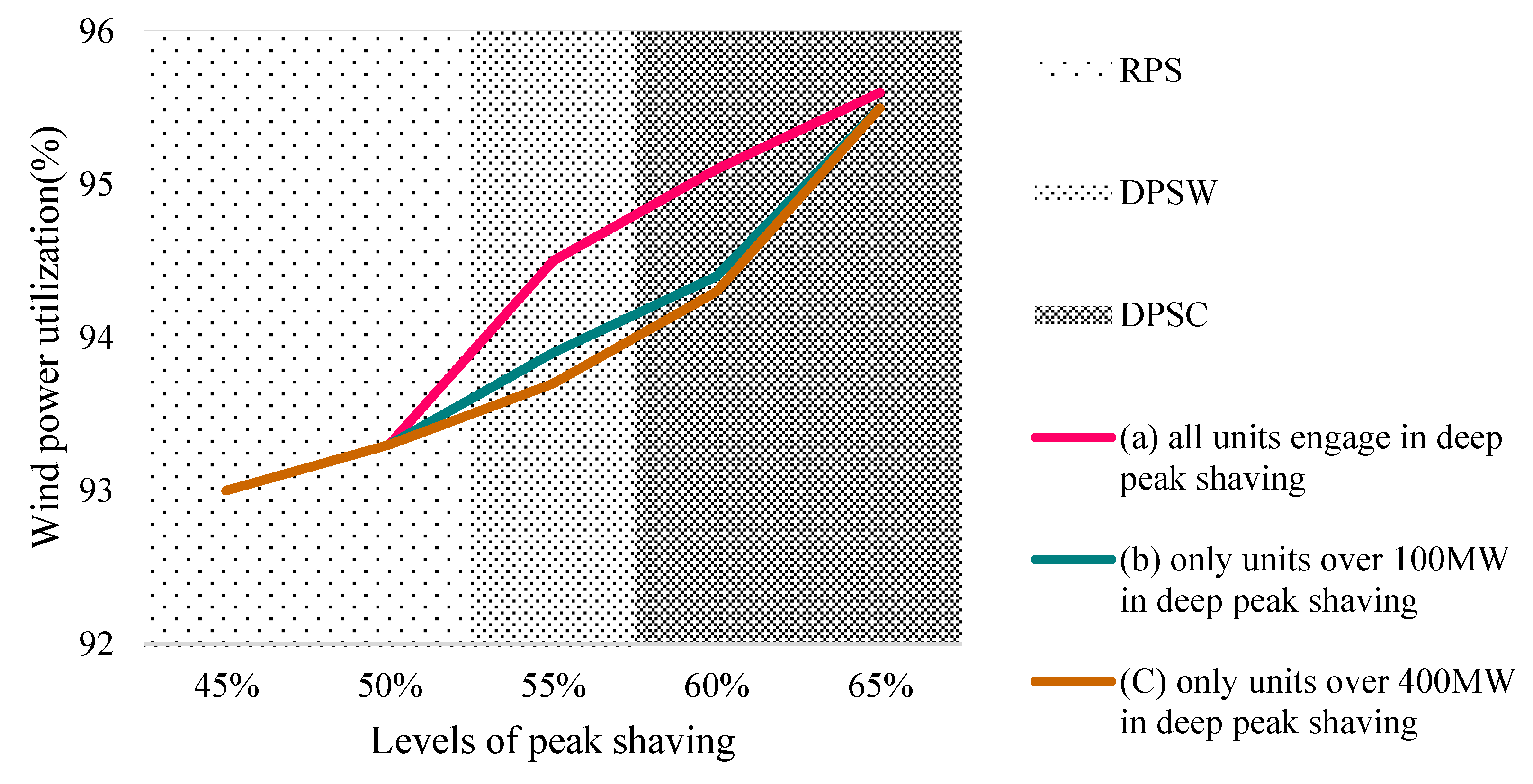
4.3.2. Benefit of Wind Power Plants in Peak Shaving
4.3.3. Environmental Efficiency in Peak Shaving
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A. Acronyms | |
| UPI | Coal-fired Unit with Plasma Ignition |
| UOI | Coal-fired Unit with Oil Injection |
| RPS | Regular Peak Shaving |
| DPSW | Deep Peak Shaving Without combustion supporting |
| DPSC | Deep Peak Shaving with Combustion supporting |
| SHWC | Safety of Hydrodynamic Work Conditions |
| B. Indices and Sets | |
| i, N | Index and total number of coal-fired units |
| j | Index for power-flow interface |
| t, T | Index and total number of time interval |
| k, Ωj | Index and Set of tie line in power-flow interface |
| C. Parameters | |
| , and | Coefficient of coal consumption cost |
| Coefficient of low-cycle fatigue life | |
| Operating power of the burner | |
| Anode- cathode cost of unit i during period | |
| , | Sulfur content and nitrogen content of the coal |
| , | Charge for SO2 and NOX emissions |
| , | Oil-coal conversion coefficient and pollutant-coal conversion coefficient |
| Penalty coefficient of wind power curtailment | |
| , | Oil price and coal price |
| Electricity price of power plants; | |
| , | Shut-up and shut-down cost of unit |
| Predicted wind power output at time period | |
| , | Minimum and maximum output of unit |
| Maximum active power transmitted by interface | |
| , | Minimum continuous ON/ OFF state of unit |
| , | Ramping up and down limits of unit |
| , | Start-up and shut-down power limits of unit |
| , | Maximum and minimum output of unit at time period |
| , | Upper and lower reserve requirements |
| D. Variables | |
| Power output of unit during period | |
| Number of cycles of failure | |
| Oil consumption of unit during period | |
| , | Desulfurization and denitration efficiency |
| Sum of electricity generated by coal-fired units during T time intervals; | |
| ON-OFF state variable of unit during period | |
| Dispatched wind power output at time period | |
| Active power transmitted by tie line in interface | |
| , | The continuously On and OFF hours of unit on time period . |
| D. Functions | |
| Peak shaving cost function of unit |
Appendix A
| Unit Number | ($/MWh2) | ($/MWh) | ($) | (MW) | ($) | ($) | (MW) | (MW) | (MW) |
|---|---|---|---|---|---|---|---|---|---|
| U 1 | 0.00048 | 16.19 | 1000 | 455 | 4500 | 4500 | 227.5 | 204.75 | 136.5 |
| U 2 | 0.00031 | 17.26 | 970 | 455 | 5000 | 5000 | 227.5 | 204.75 | 136.5 |
| U 3 | 0.002 | 16.6 | 700 | 130 | 550 | 550 | 65 | 58.5 | 39 |
| U 4 | 0.00211 | 16.5 | 680 | 130 | 560 | 560 | 65 | 58.5 | 39 |
| U 5 | 0.00398 | 19.7 | 450 | 162 | 900 | 900 | 81 | 72.9 | 48.6 |
| U 6 | 0.00712 | 22.26 | 370 | 80 | 170 | 170 | 40 | 36 | 24 |
| U 7 | 0.00079 | 27.74 | 480 | 85 | 260 | 260 | 42.5 | 38.25 | 25.5 |
| U 8 | 0.00413 | 25.92 | 660 | 55 | 30 | 30 | 27.5 | 24.75 | 16.5 |
| U 9 | 0.00222 | 27.27 | 665 | 55 | 30 | 30 | 27.5 | 24.75 | 16.5 |
| U 10 | 0.00173 | 27.79 | 670 | 55 | 30 | 30 | 27.5 | 24.75 | 16.5 |
| Unit number | U 1 | U 2 | U 3 | U 4 | U 5 | U 6 | U 7 | U 8 | U 9 | U 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Oil consumption (kg/h) | 3800 | 3800 | 2300 | 2300 | 2500 | 1200 | 1500 | 800 | 800 | 800 |
| Type | UPI | ||||
|---|---|---|---|---|---|
| Level of peak shaving | 45% | 50% | 55% | 60% | 65% |
| Electricity by UOI (MWh) | 15,148.1 | 15,084.9 | 14,980.3 | 14,912.3 | 14,841.05 |
| Coal consumption cost ($) | 414,834.29 | 412,561.35 | 410,463.23 | 411,528.41 | 411,943.71 |
| Wear-and-tear cost ($) | 0 | 0 | 22,531.16 | 28,463.56 | 36,338.79 |
| Plasma ignition cost ($) | 0 | 0 | 0 | 2429.20 | 3572.76 |
| Environmental cost ($) | 0 | 0 | 0 | 3777.22 | 4043.96 |
| Type | UOI | ||||
|---|---|---|---|---|---|
| Level of peak shaving | 45% | 50% | 55% | 60% | 65% |
| Electricity by UOI (MWh) | 15,148.1 | 15,057.4 | 14,980.3 | 14,912.3 | 14,841.05 |
| Coal consumption cost ($) | 414,927.87 | 412,558.27 | 410,463.34 | 409,351.93 | 408,229.01 |
| Wear-and-tear cost ($) | 0 | 0 | 22,513.16 | 27,842.38 | 34,180.82 |
| Oil cost ($) | 0 | 0 | 0 | 13,110 | 13,110 |
| Environmental cost ($) | 0 | 0 | 0 | 8713.33 | 9148.67 |
References
- Lin, L.; Cai, X.; Xu, B.; Xia, S. Wind Farm-LA Coordinated Operation Mode and Dispatch Model in Wind Power Accommodation Promotion. Energies 2018, 11, 1227. [Google Scholar] [CrossRef]
- Anastasiadis, A.G.; Vokas, G.A.; Konstantinopoulos, S.A.; Kondylis, G.P.; Khalil, T.; Polyzakis, A.; Tsatsakis, K. Wind Generation and Electric Vehicles coordination in Microgrids for Peak Shaving purposes. Energy Procedia 2017, 119, 407–416. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, B.Z.; Wang, K.Y.; Ai, X. Joint Planning of Energy Storage and Transmission Network Considering Wind Power Accommodation Capability. Power Syst. Technol. 2018, 42, 1480–1489. [Google Scholar]
- Yin, S.; Zhang, S.; Andrews-Speed, P.; Li, W. Economic and environmental effects of peak regulation using coal-fired power for the priority dispatch of wind power in China. J. Clean. Prod. 2017, 162, 361–370. [Google Scholar] [CrossRef]
- Bertsch, J.; Growitsch, C.; Lorenczik, S.; Nagl, S. Flexibility in Europe’s power sector—An additional requirement or an automatic complement? Energy Econ. 2016, 53, 118–131. [Google Scholar] [CrossRef]
- Prasatsap, U.; Kiravittaya, S.; Polprasert, J. Determination of Optimal Energy Storage System for Peak Shaving to Reduce Electricity Cost in a University. Energy Procedia 2017, 138, 967–972. [Google Scholar] [CrossRef]
- Kang, B.O.; Lee, M.; Kim, Y.; Jung, J. Economic analysis of a customer-installed energy storage system for both self-saving operation and demand response program participation in South Korea. Renew. Sustain. Energy Rev. 2018, 94, 69–83. [Google Scholar] [CrossRef]
- Pimm, A.J.; Cockerill, T.T.; Taylor, P.G. The potential for peak shaving on low voltage distribution networks using electricity storage. J. Energy Storage 2018, 16, 231–242. [Google Scholar] [CrossRef]
- NEA. The National Energy Administration of PRC Releases 2018 National Power Industry Statistics; NEA: Beijing, China, 2019. [Google Scholar]
- Xue, Y.; Ge, Z.; Yang, L.; Du, X. Peak shaving performance of coal-fired power generating unit integrated with multi-effect distillation seawater desalination. Appl. Energy 2019, 250, 175–184. [Google Scholar] [CrossRef]
- Simla, T.; Stanek, W.; Czarnowska, L. Thermo-Ecological Cost of Electricity Generated in Wind Turbine Systems. J. Energy Resour. Technol. 2018, 141, 031201. [Google Scholar] [CrossRef]
- Hetzer, J.; Yu, D.C.; Bhattarai, K. An Economic Dispatch Model Incorporating Wind Power. IEEE Trans. Energy Convers. 2008, 23, 603–611. [Google Scholar] [CrossRef]
- Andervazh, M.; Javadi, S. Emission-economic dispatch of thermal power generation units in the presence of hybrid electric vehicles and correlated wind power plants. IET Gener. Transm. Distrib. 2017, 11, 2232–2243. [Google Scholar] [CrossRef]
- Wulandhari, L.A.; Komsiyah, S.; Wicaksono, W. Bat Algorithm Implementation on Economic Dispatch Optimization Problem. Procedia Comput. Sci. 2018, 135, 275–282. [Google Scholar] [CrossRef]
- Yang, Y.; Qin, C.; Zeng, Y.; Wang, C. Interval Optimization-Based Unit Commitment for Deep Peak Regulation of Thermal Units. Energies 2019, 12, 922. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Zhu, Y.; Li, J. Life cycle assessment and environmental cost accounting of coal-fired power generation in China. Energy Policy 2018, 115, 374–384. [Google Scholar] [CrossRef]
- Turconi, R.; O’Dwyer, C.; Flynn, D.; Astrup, T. Emissions from cycling of thermal power plants in electricity systems with high penetration of wind power: Life cycle assessment for Ireland. Appl. Energy 2014, 131, 1–8. [Google Scholar] [CrossRef]
- Oates, D.L.; Jaramillo, P. Production cost and air emissions impacts of coal cycling in power systems with large-scale wind penetration. Environ. Res. Lett. 2013, 8, 024022. [Google Scholar] [CrossRef]
- Arriagada, E.; Lopez, E.; López, M.; Blasco-Gimenez, R.; Roa, C.; Poloujadoff, M. A probabilistic economic dispatch model and methodology considering renewable energy, demand and generator uncertainties. Electr. Power Syst. Res. 2015, 121, 325–332. [Google Scholar] [CrossRef]
- Weng, Z.; Shi, L.; Xu, Z. Power System Dynamic Economic Dispatch Incorporating Wind Power Cost. Proc. CSEE 2014, 34, 514–523. [Google Scholar]
- Plathottam, S.J.; Salehfar, H. Unbiased economic dispatch in control areas with conventional and renewable generation sources. Electr. Power Syst. Res. 2015, 119, 313–321. [Google Scholar] [CrossRef]
- Niu, Y.; Du, M.; Ge, W.; Luo, H.; Zhou, G. A dynamic nonlinear model for a once-through boiler-turbine unit in low load. Appl. Therm. Eng. 2019, 161, 113880. [Google Scholar] [CrossRef]
- Pawlak-Kruczek, H.; Niedźwiecki, Ł.; Ostrycharczyk, M.; Czerep, M.; Plutecki, Z. Potential and methods for increasing the flexibility and efficiency of the lignite fired power unit, using integrated lignite drying. Energy 2019, 181, 1142–1151. [Google Scholar] [CrossRef]
- Prause, J.H.; Hübel, M.; Holtz, D.; Nocke, J.; Hassel, E. Local steam temperature imbalances of coal-fired boilers at very low load. Energy Procedia 2017, 120, 439–446. [Google Scholar] [CrossRef]
- Gherbi, Y.A.; Bouzeboudja, H.; Gherbi, F.Z. The combined economic environmental dispatch using new hybrid metaheuristic. Energy 2016, 115, 468–477. [Google Scholar] [CrossRef]
- Shibli, A.; Ford, J. Damage to Coal Power Plants due to Cyclic Operation. In Coal Power Plant Materials and Life Assessment; Shibli, A., Ed.; Woodhead Publishing: Cambridge, UK, 2014; pp. 333–357. [Google Scholar]
- Bian, S.; Li, W. Calculation of Thermal Stress and Fatigue Life of 1000 MW Steam Turbine Rotor. Energy Power Eng. 2013, 5, 1484. [Google Scholar] [CrossRef]
- Zhang, W.; Hu, Y.-F. Study on Low Cycle Fatigue Loss of Turbine Rotor based on Finite Element Analysis. J. Eng. Therm. Energy Power 2018, 33, 31–38. [Google Scholar]
- Tamura, M.; Abe, F.; Shiba, K.; Sakasegawa, H.; Tanigawa, H. Larson-Miller Constant of Heat-Resistant Steel. Metall. Mater. Trans. A 2013, 44, 2645–2661. [Google Scholar] [CrossRef]
- Hemmecke, R.; Köppe, M.; Lee, J.; Weismantel, R. Nonlinear Integer Programming. In 50 Years of Integer Programming 1958–2008: From the Early Years to the State-of-the-Art; Jünger, M., Liebling, T.M., Naddef, D., Nemhauser, G.L., Pulleyblank, W.R., Reinelt, G., Rinaldi, G., Wolsey, L.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 561–618. [Google Scholar]
- National Development and Reform Commission. General principles for calculation of the comprehensive energy consumption. National Development and Reform Commission: Beijing, China, 2008. [Google Scholar]
- Kazarlis, S.A.; Bakirtzis, A.G.; Petridis, V. A genetic algorithm solution to the unit commitment problem. IEEE Trans. Power Syst. 1996, 11, 83–92. [Google Scholar] [CrossRef]
- Lin, L.; Zou, L.; Zhou, P.; Tian, X. Multi-angle Economic Analysis on Deep Peak Regulation of Thermal Power Units with Large-scale Wind Power Integration. Autom. Electr. Power Syst. 2017, 41, 21–27. [Google Scholar]
- Xia, S.; Jianhua, W.; Dingzhong, H. Benefit evaluation for boiler with application of plasma ignition. J. Shanghai Electr. Power 2003, 3, 270–271. [Google Scholar]
- National Energy Administration. Notice of the North China Energy Regulatory Bureau on Printing and Distributing the “Two Rules” for the Grid-Connected Power Plants in North China (Revised 2019); National Energy Administration: Beijing, China, 2019.








© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, L.; Xu, B.; Xia, S. Multi-Angle Economic Analysis of Coal-Fired Units with Plasma Ignition and Oil Injection during Deep Peak Shaving in China. Appl. Sci. 2019, 9, 5399. https://doi.org/10.3390/app9245399
Lin L, Xu B, Xia S. Multi-Angle Economic Analysis of Coal-Fired Units with Plasma Ignition and Oil Injection during Deep Peak Shaving in China. Applied Sciences. 2019; 9(24):5399. https://doi.org/10.3390/app9245399
Chicago/Turabian StyleLin, Li, Bingqian Xu, and Shiwei Xia. 2019. "Multi-Angle Economic Analysis of Coal-Fired Units with Plasma Ignition and Oil Injection during Deep Peak Shaving in China" Applied Sciences 9, no. 24: 5399. https://doi.org/10.3390/app9245399
APA StyleLin, L., Xu, B., & Xia, S. (2019). Multi-Angle Economic Analysis of Coal-Fired Units with Plasma Ignition and Oil Injection during Deep Peak Shaving in China. Applied Sciences, 9(24), 5399. https://doi.org/10.3390/app9245399






