Numerical Simulation of Polymer Solutions in a Single-Screw Extruder
Abstract
1. Introduction
2. Simulation Methodology
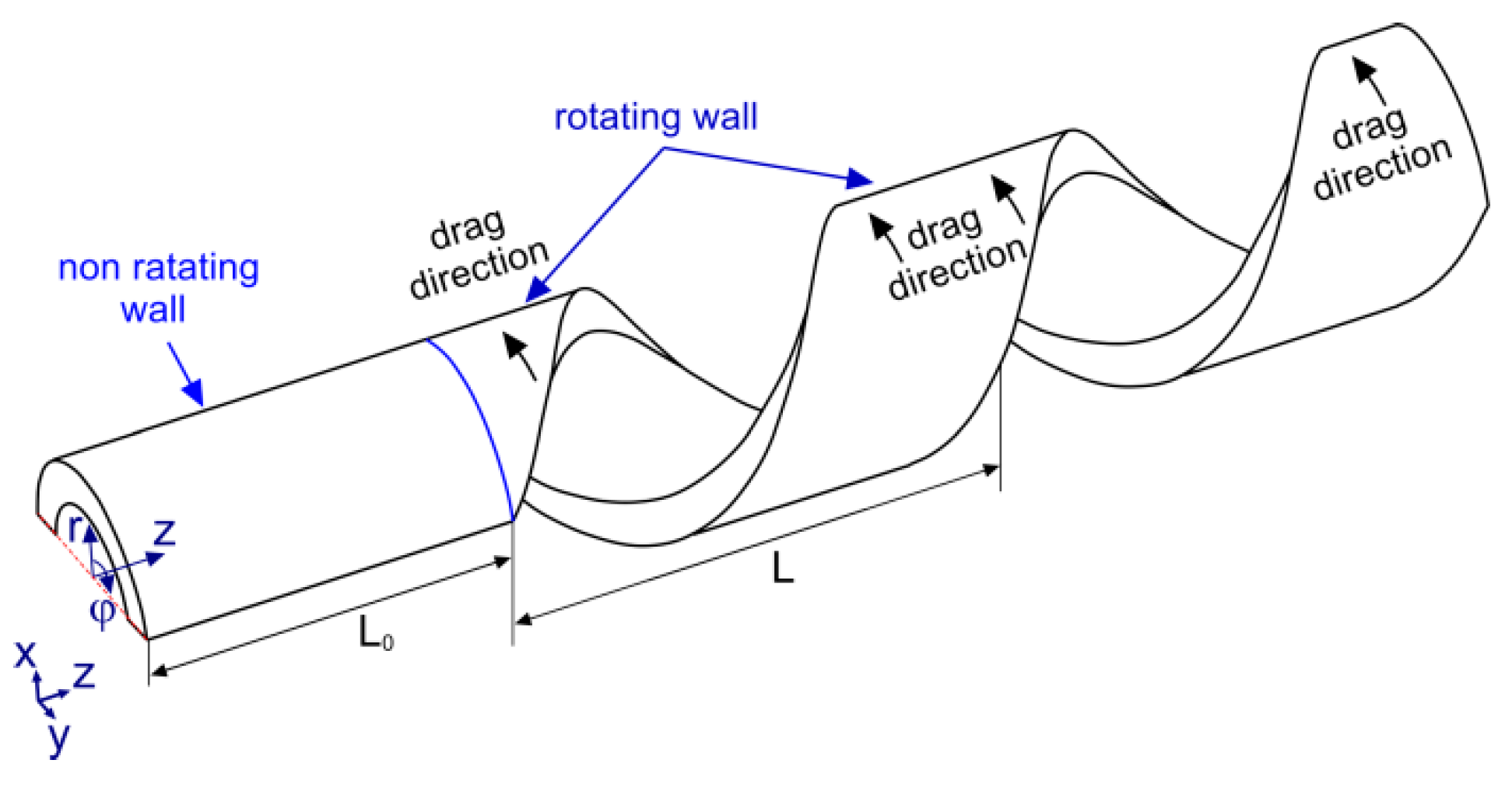
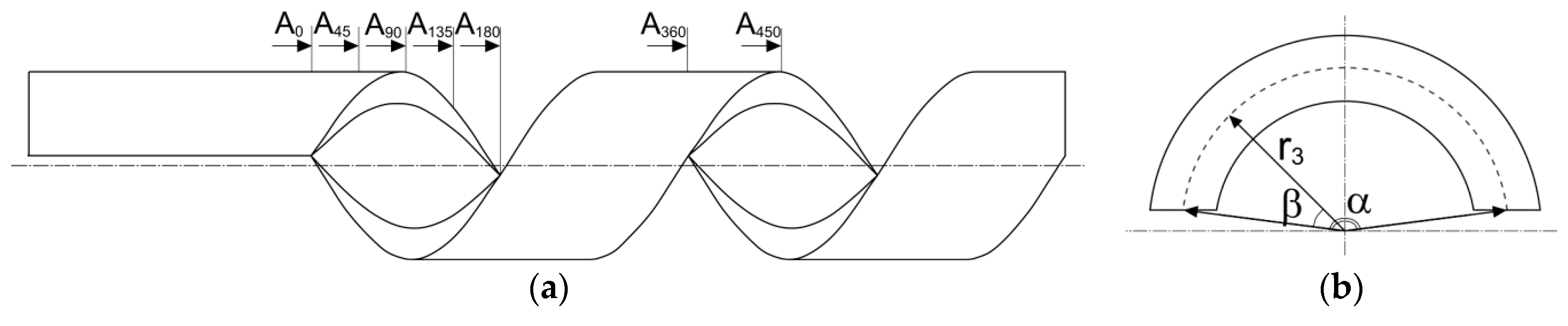
2.1. Geometric Representation, Governing Equations, and Boundary Conditions
2.2. Rheological Properties of Polymer Solutions
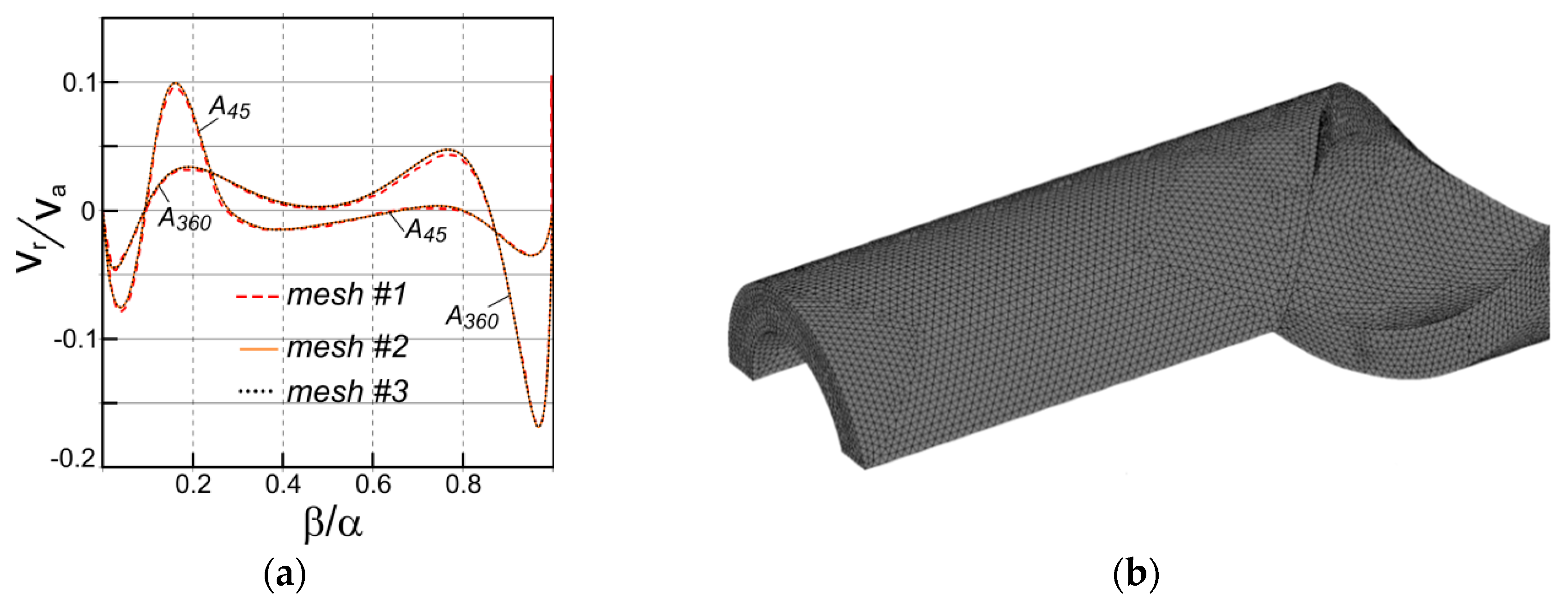
2.3. Mesh Parameters
2.4. Validation
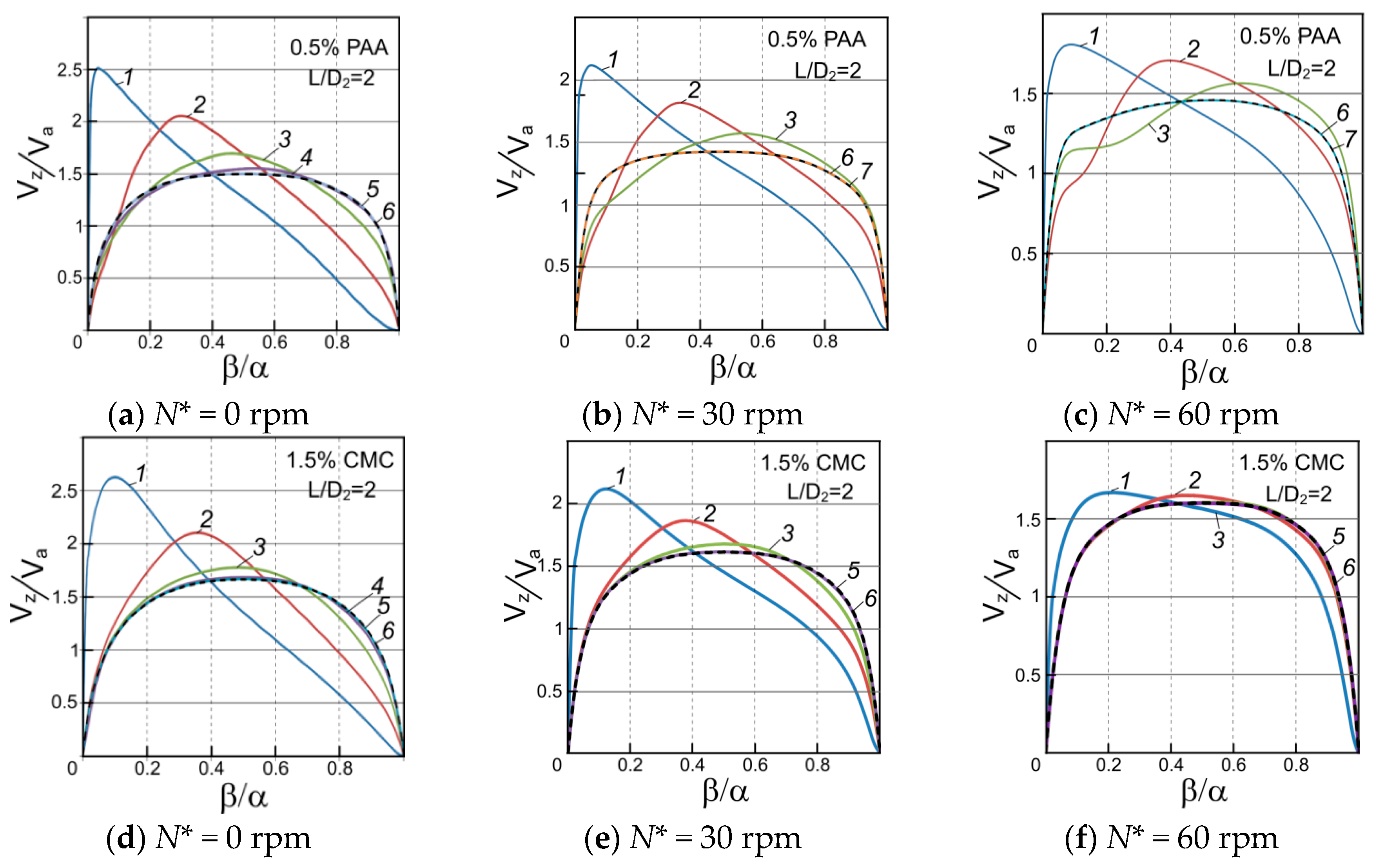
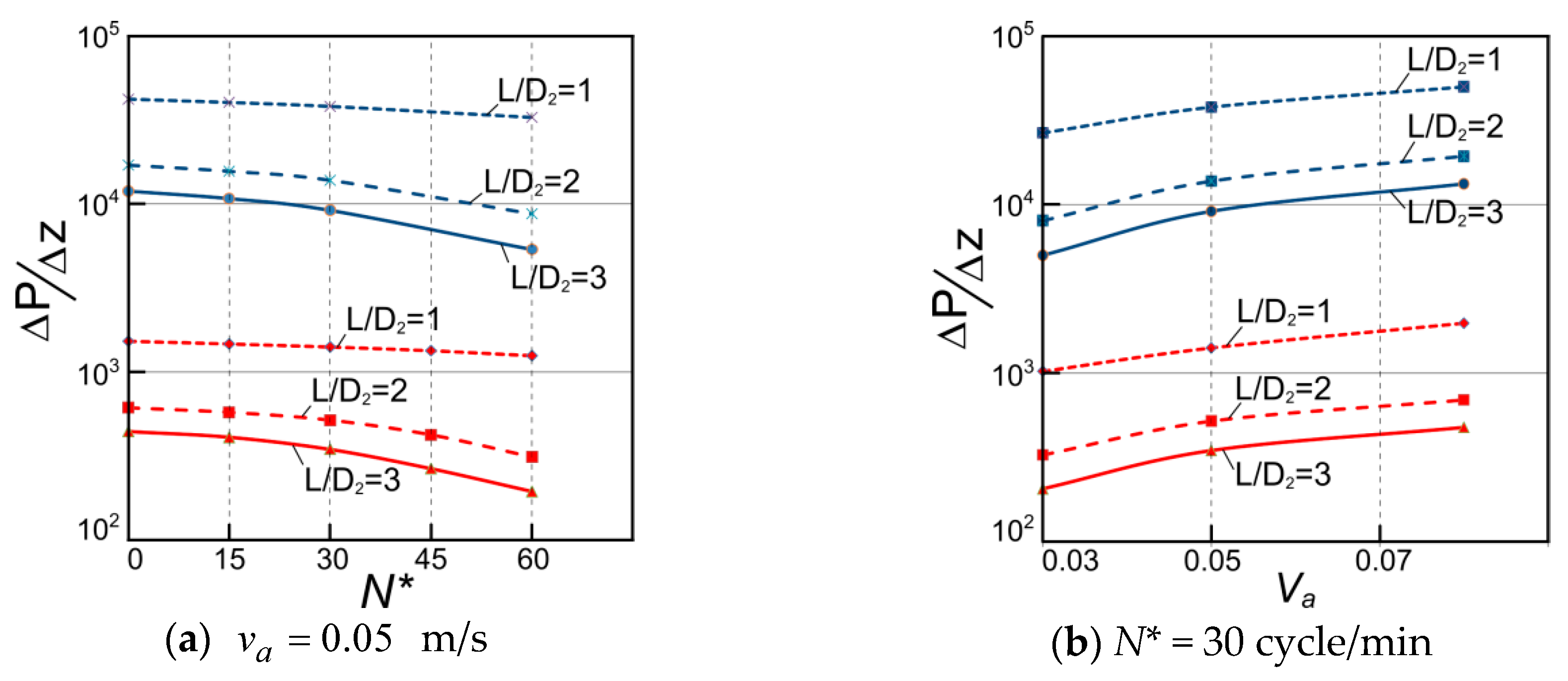
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhu, X.Z.; Tong, Y.; Hu, Y.X. Chaotic Manifold Analysis of Four-Screw Extruders Based on Lagrangian Coherent Structures. Materials 2018, 11, 2272. [Google Scholar] [CrossRef] [PubMed]
- Wilczynski, K.; Buziak, K.; Wilczynski, K.J.; Lewandowski, A.; Nastaj, A. Computer Modeling for Single-Screw Extrusion of Wood-Plastic Composites. Polymers 2018, 10, 295. [Google Scholar] [CrossRef] [PubMed]
- Marschik, C.; Roland, W.; Low-Baselli, B.; Miethlinger, J. A heuristic method for modeling three-dimensional non-Newtonian flows of polymer melts in single-screw extruders. J. Non-Newton. Fluid Mech. 2017, 248, 27–39. [Google Scholar] [CrossRef]
- Bessonova, M.P.; Ponomareva, M.A.; Yakutenok, V.A. Numerical solution of the problem of polymer melt flow in a single screw extruder. Chem. Phys. Mesoscopy 2019, 21, 198–217. [Google Scholar] [CrossRef]
- Li, Y.; Hsieh, F. Modeling of flow in a single screw extruder. J. Food Eng. 1996, 27, 353–375. [Google Scholar] [CrossRef]
- Alves, M.V.C.; Barbosa, J.R.; Prata, A.T. Analytical solution of single screw extrusion applicable to intermediate values of screw channel aspect ratio. J. Food Eng. 2009, 92, 152–156. [Google Scholar] [CrossRef]
- Rauwendaal, C. Polymer Extrusion, 5th ed.; Carl Hanser Verlag GmbH & Company KG: Munich, Germany, 2014. [Google Scholar]
- Krueger, H. Extruder for non-Newtonian melt analysis and performance prediction. Plastics 1963, 53, 711–722. [Google Scholar]
- Rotem, Z.; Shinnar, R. Non-newtonian flow-between parallel boundaries in linear movement. Chem. Eng. Sci. 1961, 15, 130–143. [Google Scholar] [CrossRef]
- Vinogradov, G.V.; Malkin, A.Y. Rheology of Polymers; Khimiya: Moscow, Russia, 1977; pp. 374–399. [Google Scholar]
- Robin, C.; Lorthioir, C.; Amiel, C.; Fall, A.; Ovarlez, G.; Le Coeur, C. Unexpected Rheological Behavior of Concentrated Poly(methacrylic acid) Aqueous Solutions. Macromolecules 2017, 50, 700–710. [Google Scholar] [CrossRef]
- Khan, M.B. Rheological behavior of polyacrylamide solution in the presence of cationic Gemini surfactants/conventional surfactants. Asia-Pac. J. Chem. Eng. 2017, 12, 671–678. [Google Scholar] [CrossRef]
- Merzlikina, D.A. Modeling of Nonlinear Viscoelasticity of Branched Polymer Melts as a Consequence of the Mesoscopic Approach to the Description of Their Dynamics. Ph.D. Thesis, Polzunov Altai State Technical University, Barnaul, Russia, 2018. [Google Scholar]
- Barzic, A.I.; Ioan, S. Viscoelastic Behavior of Liquid-Crystal Polymer in Composite Systems; InTech: Rijeca, Croatia, 2016; pp. 35–52. [Google Scholar]
- Kozitsyna, M.V. Stratified Spatial Flow of Abnormally Viscous Fluids in the Channels of the Forming Tool during Coextrusion. Ph.D. Thesis, Perm National Research Polytechnic University, Perm, Russia, 2019. [Google Scholar]
- Lim, K.H.; Hwang, W.R.; Kim, S.J. A finite-element technique for flows in the single screw extruder using a partial periodic unit. Korea-Aust. Rheol. J. 2019, 31, 59–67. [Google Scholar] [CrossRef]
- Ershov, S.V. Spatial Flow of Polymer Melts in the Channel of the Metering Zone of a Plastic Extruder and a Forming Tool. Ph.D. Thesis, Perm National Research Polytechnic University, Perm, Russia, 2018. [Google Scholar]
- Roland, W.; Kommenda, M.; Marschik, C.; Miethlinger, J. Extended Regression Models for Predicting the Pumping Capability and Viscous Dissipation of Two-Dimensional Flows in Single-Screw Extrusion. Polymers 2019, 11, 334. [Google Scholar] [CrossRef] [PubMed]
- Roland, W.; Miethlinger, J. Heuristic analysis of viscous dissipation in single-screw extrusion. Polym. Eng. Sci. 2018, 58, 2055–2070. [Google Scholar] [CrossRef]
- Cruz, D.O.A.; Pinho, F.T. Analysis of isothermal flow of a Phan-Thien-Tanner fluid in a simplified model of a single-screw extruder. J. Non-Newton. Fluid Mech. 2012, 167, 95–105. [Google Scholar] [CrossRef]
- Roland, W.; Marschik, C.; Krieger, M.; Low-Baselli, B.; Miethlinger, J. Symbolic regression models for predicting viscous dissipation of three-dimensional non-Newtonian flows in single-screw extruders. J. Non-Newton. Fluid Mech. 2019, 268, 12–29. [Google Scholar] [CrossRef]
- Marschik, C.; Roland, W.; Miethlinger, J. A Network-Theory-Based Comparative Study of Melt-Conveying Models in Single-Screw Extrusion: A Isothermal Flow. Polymers 2018, 10, 929. [Google Scholar] [CrossRef]
- Gul, V.E.; Dyakonova, V.P. Physico-Chemical Fundamentals of the Production of Polymer Films: Textbook. Manual for Universities; Higher School: Moscow, Russia, 1978. [Google Scholar]
- Polychronopoulos, N.D.; Vlachopoulos, J. Computer Flow Simulation of Moffatt Eddies in Single Screw Extrusion. Int. Polym. Process. 2018, 33, 662–668. [Google Scholar] [CrossRef]
- Nastaj, A.; Wilczynski, K. Optimization for single screw extrusion of polymeric materials—Experimental studies. Polimery 2018, 63, 38–44. [Google Scholar] [CrossRef]
- Trufanova, N.M.; Ershov, S.V. Numerical analysis of nonisothermal processes of the flow of polymer melts in the dosing zone of the extruder for various spatial mathematical models and rheological laws. Contin. Comput. Mech. 2017, 10, 153–163. [Google Scholar] [CrossRef][Green Version]
- Negi, U. Model of Polymer Melt Flow in Extruder Screw. Master’s Thesis, Czech Technical University, Prague, Czech, 2018. [Google Scholar]
- Ghoreishy, M.H.R.; Razavi-Nouri, M.; Naderi, G. Finite element analysis of a thermoplastic elastomer melt flow in the metering region of a single screw extruder. Comput. Mater. Sci. 2005, 34, 389–396. [Google Scholar] [CrossRef]
- Kim, N.; Kim, H.; Lee, J. Numerical analysis of internal flow and mixing performance in polymer extruder I: Single screw element. Korea-Aust. Rheol. J. 2006, 18, 143–151. [Google Scholar]
- Vempati, B.; Panchagnula, M.V.; Oztekin, A.; Neti, S. Numerical investigation of liquid-liquid coaxial flows. J. Fluids Eng. 2007, 129, 713–719. [Google Scholar] [CrossRef]
- Sun, D.P.; Zhu, X.Z.; Gao, M.G. 3D Numerical Simulation of Reactive Extrusion Processes for Preparing PP/TiO2 Nanocomposites in a Corotating Twin Screw Extruder. Materials 2019, 12, 671. [Google Scholar] [CrossRef] [PubMed]
- Shabaka, I.M.; Abdel Wahab, M.; Hamza, S.E.E.; El-Bakry, M.Y.; Hashem, S. On rheological behavior of aqueous polyacrylamide solution. I—Empirical relation of the viscosity as a function of concentration and shear rate. Int. J. Adv. Res. 2016, 4, 1499–1507. [Google Scholar] [CrossRef]
- Behra, J.S.; Mattsson, J.; Cayre, O.J.; Robles, E.S.J.; Tang, H.Q.; Hunter, T.N. Characterization of Sodium Carboxymethyl Cellulose Aqueous Solutions to Support Complex Product Formulation: A Rheology and Light Scattering Study. ACS Appl. Polym. Mater. 2019, 1, 344–358. [Google Scholar] [CrossRef]
- Sanjabi, F.; Upreti, S.R.; Lohi, A.; Ein-Mozaffari, F. Helical Flow of Polymer Melts in Extruders, Part 1: Model Development. Adv. Polym. Technol. 2010, 29, 249–260. [Google Scholar] [CrossRef]
- Benchabane, A.; Bekkour, K. Rheological properties of carboxymethyl cellulose (CMC) solutions. Colloid Polym. Sci. 2008, 286, 1173–1180. [Google Scholar] [CrossRef]
- Owens, R.G.; Phillips, T.N. Computational Rheology; Imperial College Press: London, UK, 2002. [Google Scholar]
- Shaw, M.T. On Estimating the Zero-Shear-Rate Viscosity: Tests with PIB and PDMS. In Proceedings of the Regional Conference of the Polymer-Processing-Society (PPS), Graz, Austria, 21–25 September 2016. [Google Scholar]
- Xie, J.; Jin, Y.C. Parameter determination for the Cross rheology equation and its application to modeling non-Newtonian flows using the WC-MPS method. Eng. Appl. Comput. Fluid Mech. 2016, 10, 111–129. [Google Scholar] [CrossRef]
- Balan, C.M.; Balan, C. µPIV Measurement and numerical computation of the velocity profiles in microchannels. UPB Sci. Bull. Ser. D Mech. Eng. 2010, 72, 121–128. [Google Scholar]
- Neto, J.L.V.; Martins, A.L.; Ataide, C.H.; Barrozo, M.A.S. The effect of the inner cylinder rotation on the fluid dynamics of non—Newtonian fluids in concentric and eccentric annuli. Braz. J. Chem. Eng. 2014, 31, 829–838. [Google Scholar] [CrossRef]







| Name | Concentration | η0 (Pa·s) | η∞ (Pa·s) | λc (s) | n (-) | ρ (kg/m3) |
|---|---|---|---|---|---|---|
| 1.5% CMC [35] | 1500 ppm | 1.97 | 0.02 | 0.172 | 0.64 | 1025 |
| 0.5% PAA | 500 ppm | 1.08 | 0.0023 | 5 | 0.8 | 999 |
| Parameters | Subdomain | Boundary |
|---|---|---|
| Maximum element size | 0.0013 | 0.0011 |
| Type of elements | Triangle (regular) | Triangle (advancing front) |
| Minimum element quality | 0.3469 | 0.3469 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kadyirov, A.; Gataullin, R.; Karaeva, J. Numerical Simulation of Polymer Solutions in a Single-Screw Extruder. Appl. Sci. 2019, 9, 5423. https://doi.org/10.3390/app9245423
Kadyirov A, Gataullin R, Karaeva J. Numerical Simulation of Polymer Solutions in a Single-Screw Extruder. Applied Sciences. 2019; 9(24):5423. https://doi.org/10.3390/app9245423
Chicago/Turabian StyleKadyirov, Aidar, Rustem Gataullin, and Julia Karaeva. 2019. "Numerical Simulation of Polymer Solutions in a Single-Screw Extruder" Applied Sciences 9, no. 24: 5423. https://doi.org/10.3390/app9245423
APA StyleKadyirov, A., Gataullin, R., & Karaeva, J. (2019). Numerical Simulation of Polymer Solutions in a Single-Screw Extruder. Applied Sciences, 9(24), 5423. https://doi.org/10.3390/app9245423




