Value-Set-Based Approach to Robust Stability Analysis for Ellipsoidal Families of Fractional-Order Polynomials with Complicated Uncertainty Structure
Abstract
:1. Introduction
2. Families of Fractional-Order Polynomials
3. Parametric Uncertainty Structure
- Independent uncertainty structure
- Affine linear uncertainty structure
- Multilinear uncertainty structure
- Polynomic uncertainty structure
- General uncertainty structure
- Single parameter uncertainty
- Retarded quasi-polynomials
4. Uncertainty Bounding Set
5. Robust Stability of Families of Fractional-Order Polynomials with Ellipsoidal Parametric Uncertainty
6. Illustrative Examples
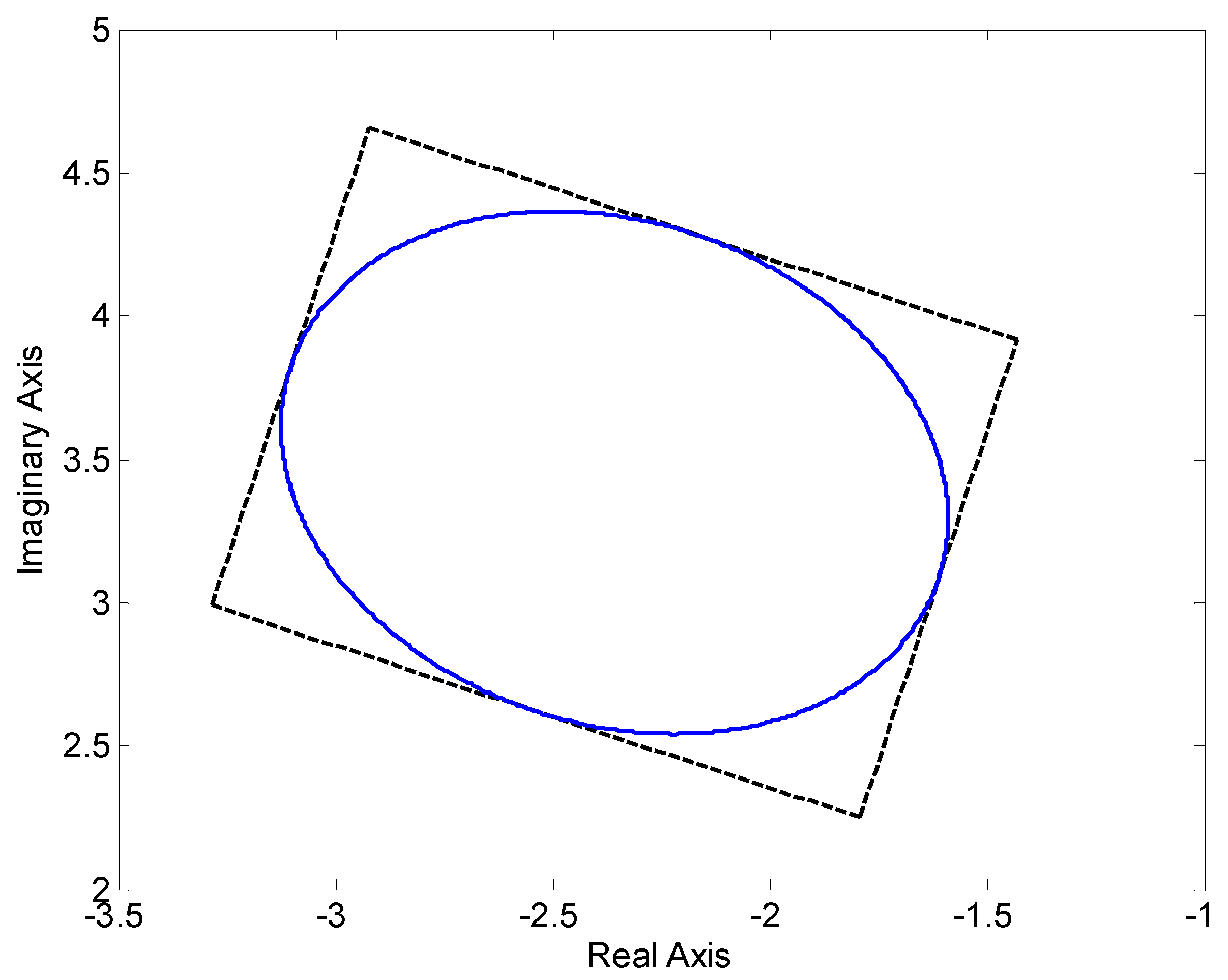
6.1. Example 1—Affine Linear Uncertainty Structure
- Weighted L2 norm (an ellipsoid, or actually an ellipse in this two-dimensional case):that is, equivalently:
- L∞ norm (a box, or actually a rectangle in this two-dimensional case):
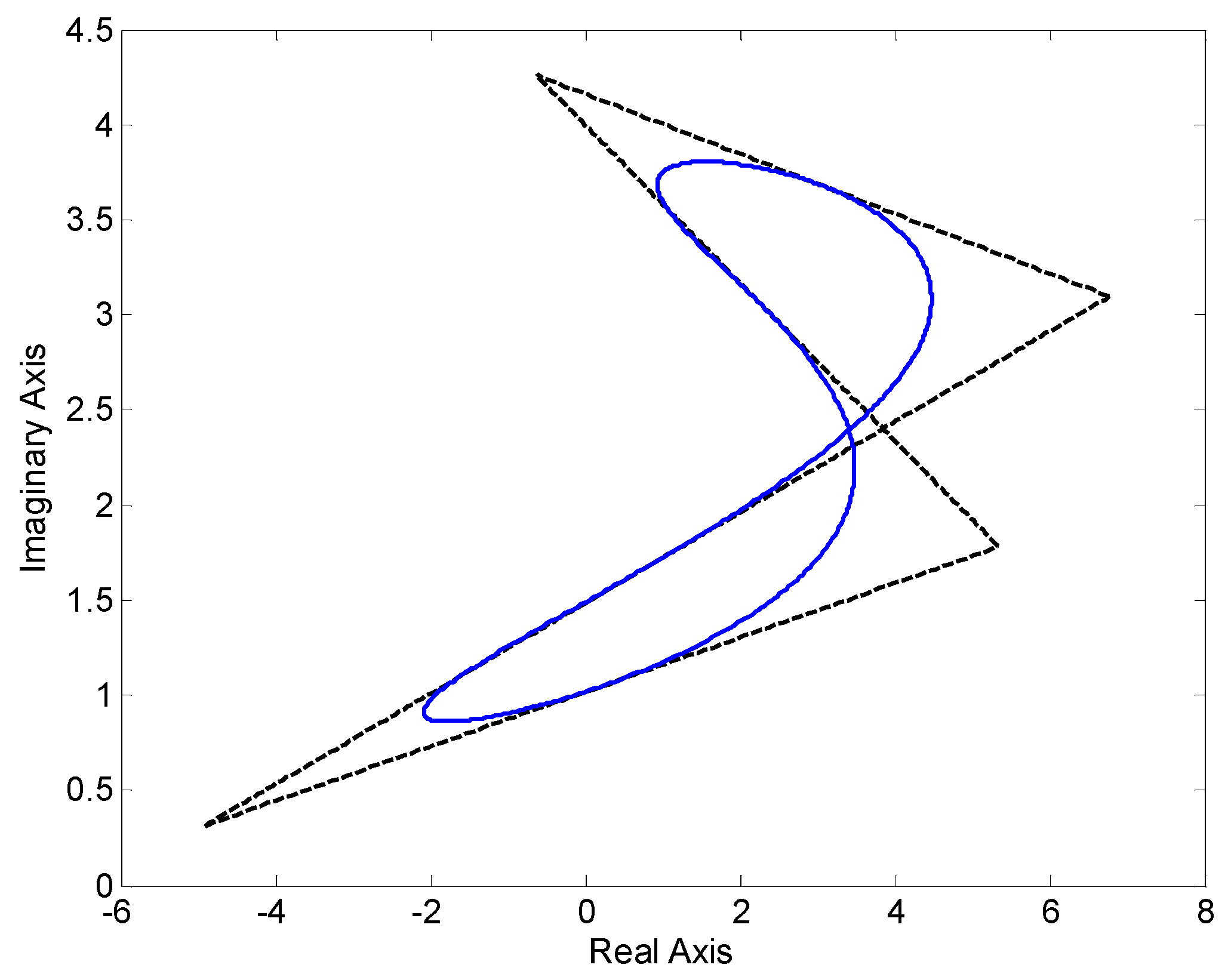
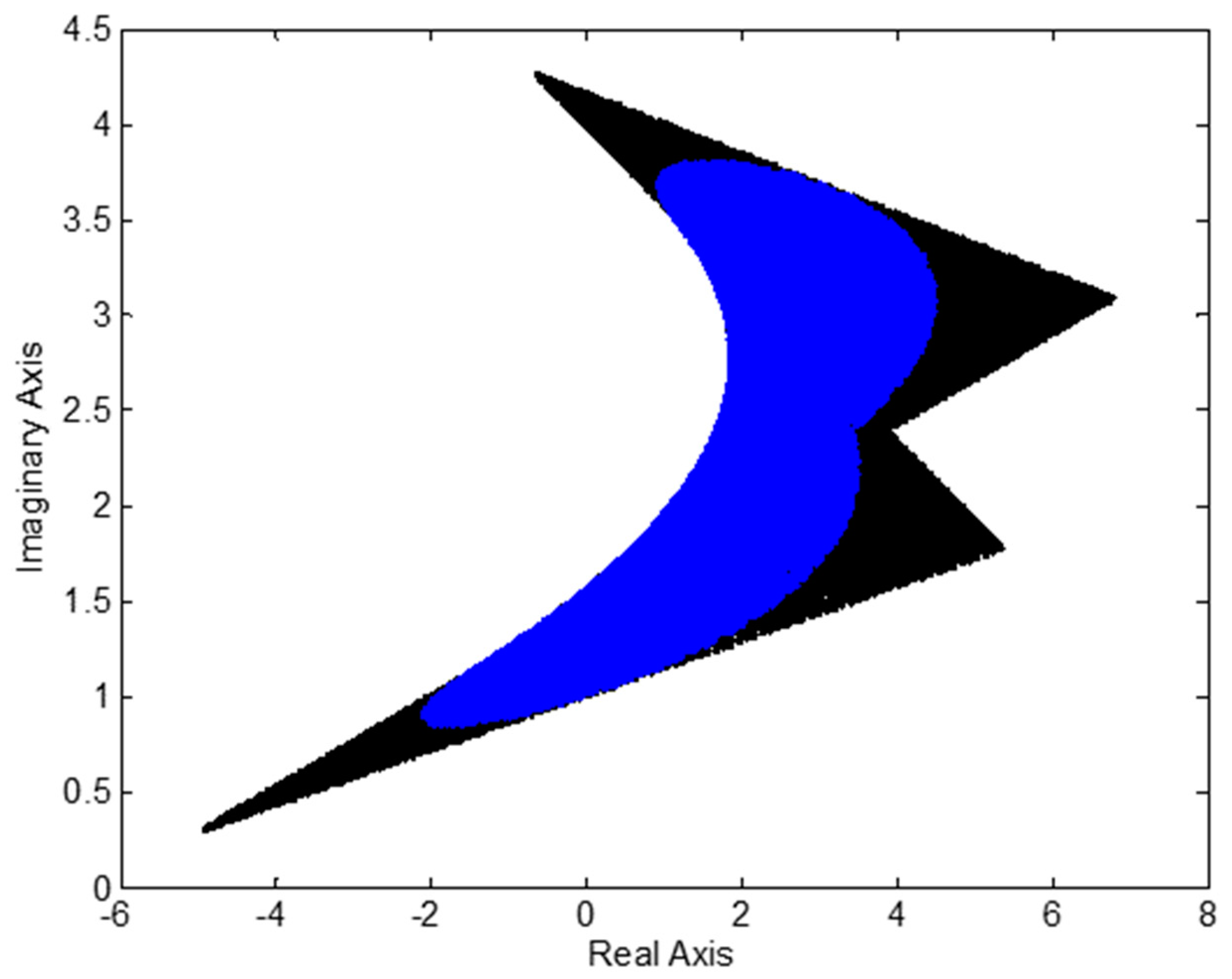
6.2. Example 2—Multilinear Uncertainty Structure
- Weighted L2 norm:i.e.,:
- L∞ norm:
6.3. Example 3—Polynomic Uncertainty Structure
6.4. Example 4—General Uncertainty Structure
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Simani, S.; Castaldi, P. Robust Control Examples Applied to a Wind Turbine Simulated Model. Appl. Sci. 2018, 8, 29. [Google Scholar] [CrossRef] [Green Version]
- Sato, T.; Hayashi, I.; Horibe, Y.; Vilanova, R.; Konishi, Y. Optimal Robust PID Control for First- and Second-Order Plus Dead-Time Processes. Appl. Sci. 2019, 9, 1934. [Google Scholar] [CrossRef] [Green Version]
- Kurokawa, R.; Sato, T.; Vilanova, R.; Konishi, Y. Discrete-Time First-Order Plus Dead-Time Model-Reference Trade-off PID Control Design. Appl. Sci. 2019, 9, 3220. [Google Scholar] [CrossRef] [Green Version]
- Vasičkaninová, A.; Bakošová, M. Robust Controller Design for a Heat Exchanger Using H2, H∞, H2/H∞, and μ-Synthesis Approaches. Acta Chim. Slovaca 2016, 10, 184–193. [Google Scholar] [CrossRef] [Green Version]
- Barmish, B.R. New Tools for Robustness of Linear Systems; Macmillan: New York, NY, USA, 1994. [Google Scholar]
- Bhattacharyya, S.P. Robust control under parametric uncertainty: An overview and recent results. Annu. Rev. Control 2017, 44, 45–77. [Google Scholar] [CrossRef]
- Matušů, R.; Prokop, R. Graphical analysis of robust stability for systems with parametric uncertainty: An overview. Trans. Inst. Meas. Control 2011, 33, 274–290. [Google Scholar] [CrossRef]
- Matušů, R.; Prokop, R. Robust Stability Analysis for Systems with Real Parametric Uncertainty: Implementation of Graphical Tests in Matlab. Int. J. Circuits Syst. Signal Process. 2013, 7, 26–33. [Google Scholar]
- Matušů, R.; Şenol, B.; Pekař, L. Robust stability of fractional order polynomials with complicated uncertainty structure. PLoS ONE 2017, 12, e0180274. [Google Scholar] [CrossRef] [Green Version]
- Matušů, R. Value Sets of Ellipsoidal Polynomial Families with Affine Linear Uncertainty Structure. In Cybernetics and Automation Control Theory Methods in Intelligent Algorithms: Proceedings of the 8th Computer Science On-Line Conference 2019, Volume 3—Advances in Intelligent Systems and Computing (Volume 986); Springer Nature Switzerland AG: Cham, Switzerland, 2019; pp. 255–263. [Google Scholar] [CrossRef]
- Matušů, R.; Şenol, B. Application of Value Set Concept to Ellipsoidal Polynomial Families with Multilinear Uncertainty Structure. In Computational Statistics and Mathematical Modeling Methods in Intelligent Systems: Proceedings of 3rd Computational Methods in Systems and Software 2019, Volume 2—Advances in Intelligent Systems and Computing (Volume 1047); Springer Nature Switzerland AG: Cham, Switzerland, 2019; pp. 81–89. [Google Scholar] [CrossRef]
- Hurák, Z.; Šebek, M. New Tools for Spherical Uncertain Systems in Polynomial Toolbox for Matlab. In Proceedings of the Technical Computing Prague 2000, Prague, Czech Republic, 2000; Available online: https://www.humusoft.cz/archive/events/tcp2000/ (accessed on 24 October 2019).
- Tesi, A.; Vicino, A.; Villoresi, F. Robust Stability of Spherical Plants with Unstructured Uncertainty. In Proceedings of the American Control Conference, Seattle, Washington, WA, USA, 21–23 June 1995. [Google Scholar]
- Polyak, B.T.; Shcherbakov, P.S. Random Spherical Uncertainty in Estimation and Robustness. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 2000. [Google Scholar]
- Matušů, R. Spherical Families of Polynomials: A Graphical Approach to Robust Stability Analysis. Int. J. Circuits Syst. Signal Process. 2016, 10, 326–332. [Google Scholar]
- Matušů, R. Families of spherical polynomials: Description and robust stability analysis. In Proceedings of the 18th International Conference on Systems, Santorini, Greece, 17–21 July 2014; pp. 606–610. [Google Scholar]
- Matušů, R.; Prokop, R. Robust Stability Analysis for Families of Spherical Polynomials. In Intelligent Systems in Cybernetics and Automation Theory: Proceedings of the 4th Computer Science On-line Conference 2015 (CSOC2015), Volume 2—Advances in Intelligent Systems and Computing (Volume 348); Springer International Publishing: Cham, Switzerland, 2015; pp. 57–65. [Google Scholar]
- Kishida, M.; Braatz, R.D. Quality-by-design by skewed spherical structured singular value. IET Control Theory Appl. 2015, 9, 2202–2210. [Google Scholar] [CrossRef] [Green Version]
- Kishida, M.; Braatz, R.D. Ellipsoidal bounds on state trajectories for discrete-time systems with linear fractional uncertainties. Optim. Eng. 2015, 16, 695–711. [Google Scholar] [CrossRef] [Green Version]
- Crisalle, O.D.; Ballamundi, R.K. Robust pole-placement technique for plants with ellipsoidally uncertain parameters. Chem. Eng. Sci. 1996, 51, 3193–3202. [Google Scholar] [CrossRef]
- Raynaud, H.F.; Pronzato, L.; Walter, E. Robust identification and control based on ellipsoidal parametric uncertainty descriptions. Eur. J. Control 2000, 6, 245–255. [Google Scholar] [CrossRef]
- Barenthin, M.; Hjalmarsson, H. Identification and control: Joint input design and H∞ state feedback with ellipsoidal parametric uncertainty via LMIs. Automatica 2008, 44, 543–551. [Google Scholar] [CrossRef]
- Henrion, D.; Šebek, M.; Kučera, V. LMIs for robust stabilization of systems with ellipsoidal uncertainty. In Proceedings of the 13th International Conference on Process Control, Štrbské Pleso, Slovakia, 11–14 June 2001. [Google Scholar]
- Sadeghzadeh, A.; Momeni, H. Fixed-order robust H∞ control and control-oriented uncertainty set shaping for systems with ellipsoidal parametric uncertainty. Int. J. Robust Nonlinear Control 2011, 21, 648–665. [Google Scholar] [CrossRef]
- Sadeghzadeh, A.; Momeni, H.; Karimi, A. Fixed-order H∞ controller design for systems with ellipsoidal parametric uncertainty. Int. J. Control 2011, 84, 57–65. [Google Scholar] [CrossRef] [Green Version]
- Sadeghzadeh, A. Identification and robust control for systems with ellipsoidal parametric uncertainty by convex optimization. Asian J. Control 2012, 14, 1251–1261. [Google Scholar] [CrossRef]
- Sadeghzadeh, A.; Momeni, H. Robust output feedback control for discrete-time systems with ellipsoidal uncertainty. Ima J. Math. Control Inf. 2016, 33, 911–932. [Google Scholar] [CrossRef]
- Soh, C.B.; Berger, C.S.; Dabke, K.P. On the stability properties of polynomials with perturbed coefficients. IEEE Trans. Autom. Control 1985, 30, 1033–1036. [Google Scholar] [CrossRef]
- Biernacki, R.M.; Hwang, H.; Bhattacharyya, S.P. Robust stability with structured real parameter perturbations. IEEE Trans. Autom. Control 1987, 32, 495–506. [Google Scholar] [CrossRef]
- Barmish, B.R.; Tempo, R. On the spectral set for a family of polynomials. IEEE Trans. Autom. Control 1991, 36, 111–115. [Google Scholar] [CrossRef]
- Tsypkin, Y.Z.; Polyak, B.T. Frequency domain criteria for lp-robust stability of continuous linear systems. IEEE Trans. Autom. Control 1991, 36, 1464–1469. [Google Scholar] [CrossRef]
- Matušů, R.; Pekař, L. Robust Stability of Thermal Control Systems with Uncertain Parameters: The Graphical Analysis Examples. Appl. Therm. Eng. 2017, 125, 1157–1163. [Google Scholar] [CrossRef]
- Tan, N.; Özgüven, Ö.F.; Özyetkin, M.M. Robust stability analysis of fractional order interval polynomials. ISA Trans. 2009, 48, 166–172. [Google Scholar] [CrossRef] [PubMed]
- Şenol, B.; Yeroğlu, C. Computation of the Value Set of Fractional Order Uncertain Polynomials: A 2q Convex Parpolygonal Approach. In Proceedings of the 2012 IEEE International Conference on Control Applications, Dubrovnik, Croatia, 3–5 October 2012. [Google Scholar]
- Şenol, B.; Yeroğlu, C. Robust Stability Analysis of Fractional Order Uncertain Polynomials. In Proceedings of the 5th IFAC Workshop on Fractional Differentiation and its Applications, Nanjing, China, 14–17 May 2012. [Google Scholar]
- Yeroğlu, C.; Şenol, B. Investigation of robust stability of fractional order multilinear affine systems: 2q-convex parpolygon approach. Syst. Control Lett. 2013, 62, 845–855. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: New York, NY, USA; London, UK, 1974. [Google Scholar]
- Podlubný, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Machado, J.A.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef] [Green Version]
- Gutiérrez, R.E.; Rosário, J.M.; Machado, J.A.T. Fractional Order Calculus: Basic Concepts and Engineering Applications. Math. Probl. Eng. 2010, 2010. [Google Scholar] [CrossRef]
- Axtell, M.; Bise, M.E. Fractional calculus applications in control systems. In Proceedings of the 1990 National Aerospace and Electronics Conference, Dayton, OH, USA, 21–25 May 1990. [Google Scholar]
- Podlubný, I. Fractional-Order Systems and PIλDμ-Controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Chen, Y.; Petráš, I.; Xue, D. Fractional Order Control—A Tutorial. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009. [Google Scholar]
- Petráš, I. Stability of fractional-order systems with rational orders: A survey. Fract. Calc. Appl. Anal. 2009, 12, 269–298. [Google Scholar]
- Xue, D. Fractional-Order Control Systems: Fundamentals and Numerical Implementations; De Gruyter: Berlin, Germany, 2017. [Google Scholar]
- Altafini, C.; Ticozzi, F. Modeling and Control of Quantum Systems: An Introduction. IEEE Trans. Autom. Control 2012, 57, 1898–1917. [Google Scholar] [CrossRef]
- Dong, D.; Petersen, I.R. Quantum control theory and applications: A survey. IET Control Theory Appl. 2010, 4, 2651–2671. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Wang, L.-C.; Wang, Y. Closed-Loop and Robust Control of Quantum Systems. Sci. World J. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Petersen, I.R.; Ugrinovskii, V.; James, M.R. Robust stability of uncertain linear quantum systems. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 5354–5363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matušů, R.; Şenol, B.; Vašek, V. Robust Stability of Fractional-Order LTI Systems with Independent Structure of Ellipsoidal Parametric Uncertainty. In Proceedings of the 30th DAAAM International Symposium, Zadar, Croatia, 23–26 October 2019. [Google Scholar]
- Lu, J.-G.; Chen, Y. Stability and stabilization of fractional-order linear systems with convex polytopic uncertainties. Fract. Calc. Appl. Anal. 2013, 16, 142–157. [Google Scholar] [CrossRef]
- Šebek, M. Robustní řízení (Robust Control); PDF slides for the course on Robust Control; Czech Technical University in Prague: Prague, Czech Republic, 2002. [Google Scholar]
- Matušů, R.; Prokop, R. Robust Stability of Fractional Order Time-Delay Control Systems: A Graphical Approach. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef] [Green Version]
- Tempo, R.; Calafiore, G.; Dabbene, F. Randomized Algorithms for Analysis and Control of Uncertain Systems: With Applications; Springer: London, UK, 2013. [Google Scholar]
- Barmish, B.R.; Lagoa, C.M. The uniform distribution: A rigorous justification for its use in robustness analysis. Math. ControlSignalsSyst. 1997, 10, 203–222. [Google Scholar] [CrossRef]








© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matušů, R.; Şenol, B.; Pekař, L. Value-Set-Based Approach to Robust Stability Analysis for Ellipsoidal Families of Fractional-Order Polynomials with Complicated Uncertainty Structure. Appl. Sci. 2019, 9, 5451. https://doi.org/10.3390/app9245451
Matušů R, Şenol B, Pekař L. Value-Set-Based Approach to Robust Stability Analysis for Ellipsoidal Families of Fractional-Order Polynomials with Complicated Uncertainty Structure. Applied Sciences. 2019; 9(24):5451. https://doi.org/10.3390/app9245451
Chicago/Turabian StyleMatušů, Radek, Bilal Şenol, and Libor Pekař. 2019. "Value-Set-Based Approach to Robust Stability Analysis for Ellipsoidal Families of Fractional-Order Polynomials with Complicated Uncertainty Structure" Applied Sciences 9, no. 24: 5451. https://doi.org/10.3390/app9245451
APA StyleMatušů, R., Şenol, B., & Pekař, L. (2019). Value-Set-Based Approach to Robust Stability Analysis for Ellipsoidal Families of Fractional-Order Polynomials with Complicated Uncertainty Structure. Applied Sciences, 9(24), 5451. https://doi.org/10.3390/app9245451







