Propagation of Cosh-Airy and Cos-Airy Beams in Parabolic Potential
Abstract
:1. Introduction
2. Propagation of Cosh-Airy and Cos-Airy Beams in Parabolic Potential
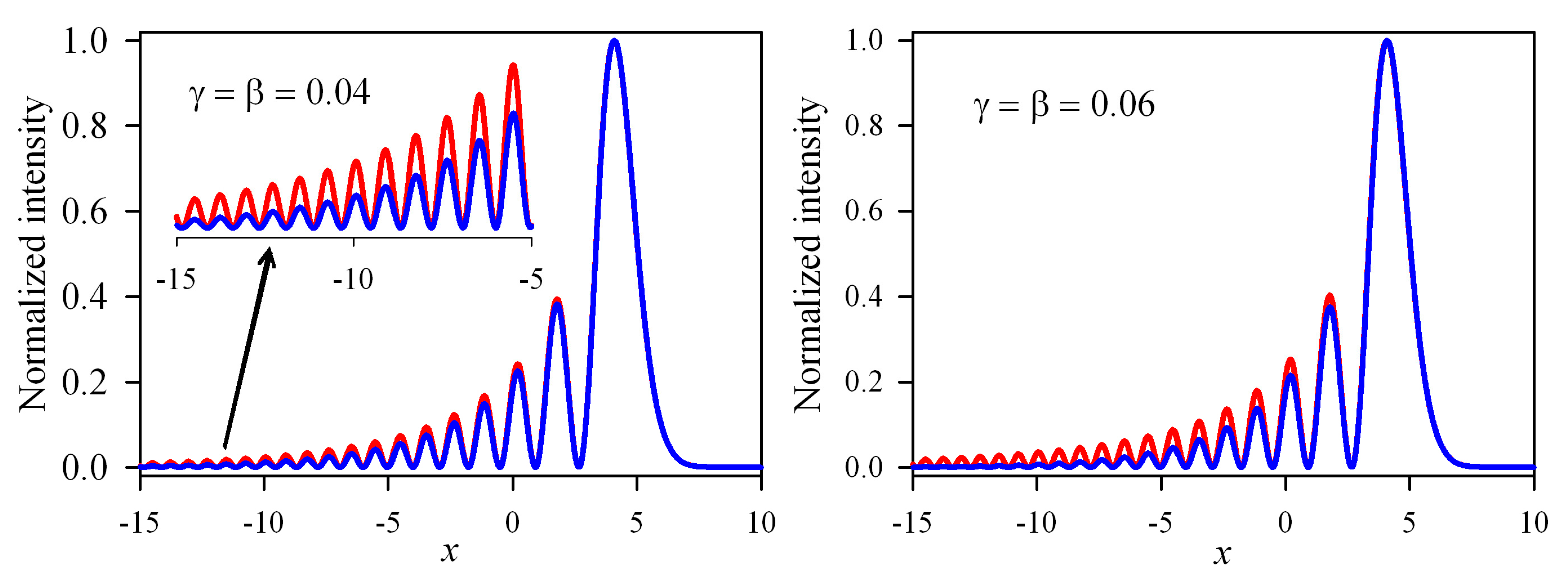
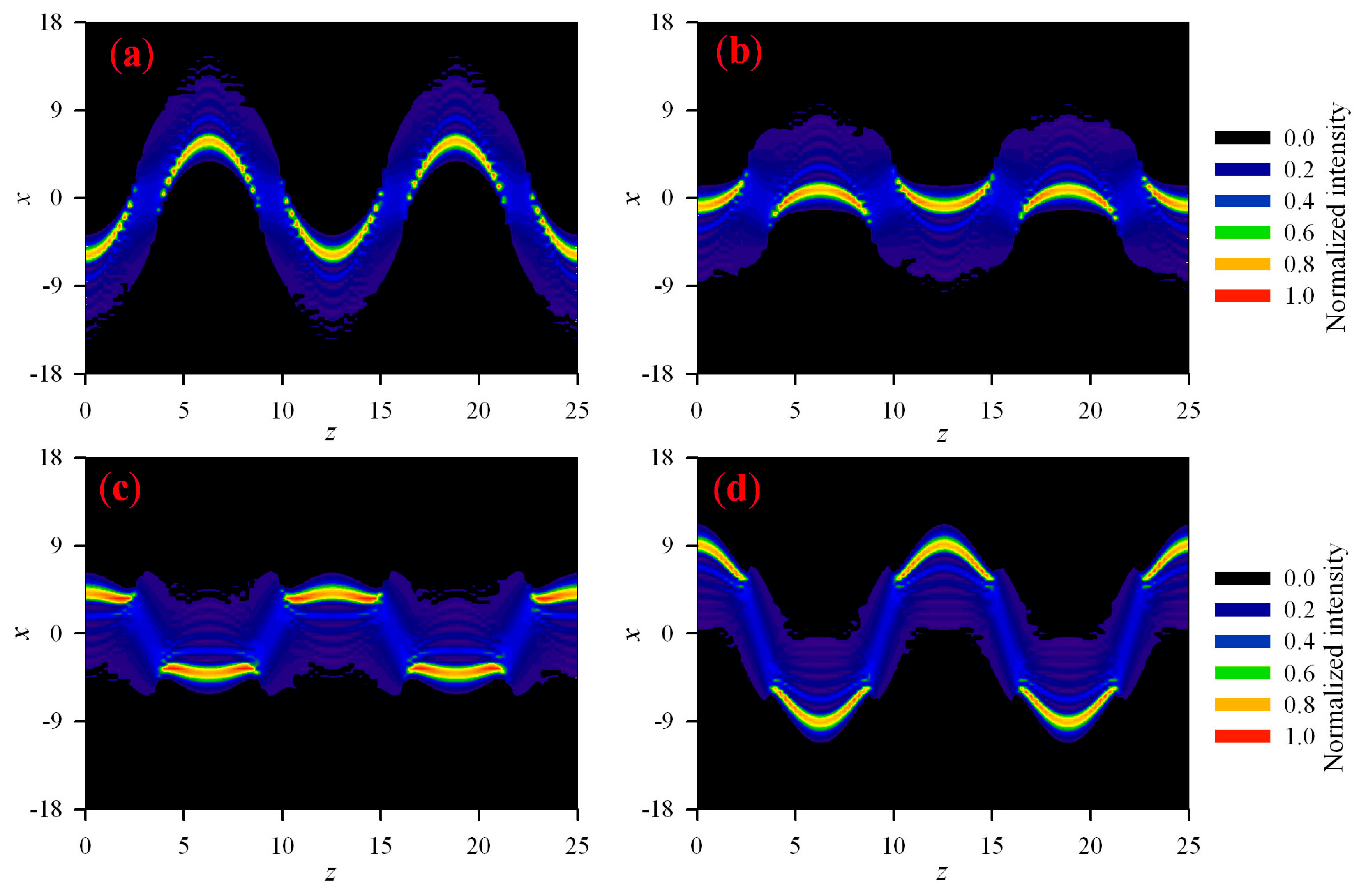
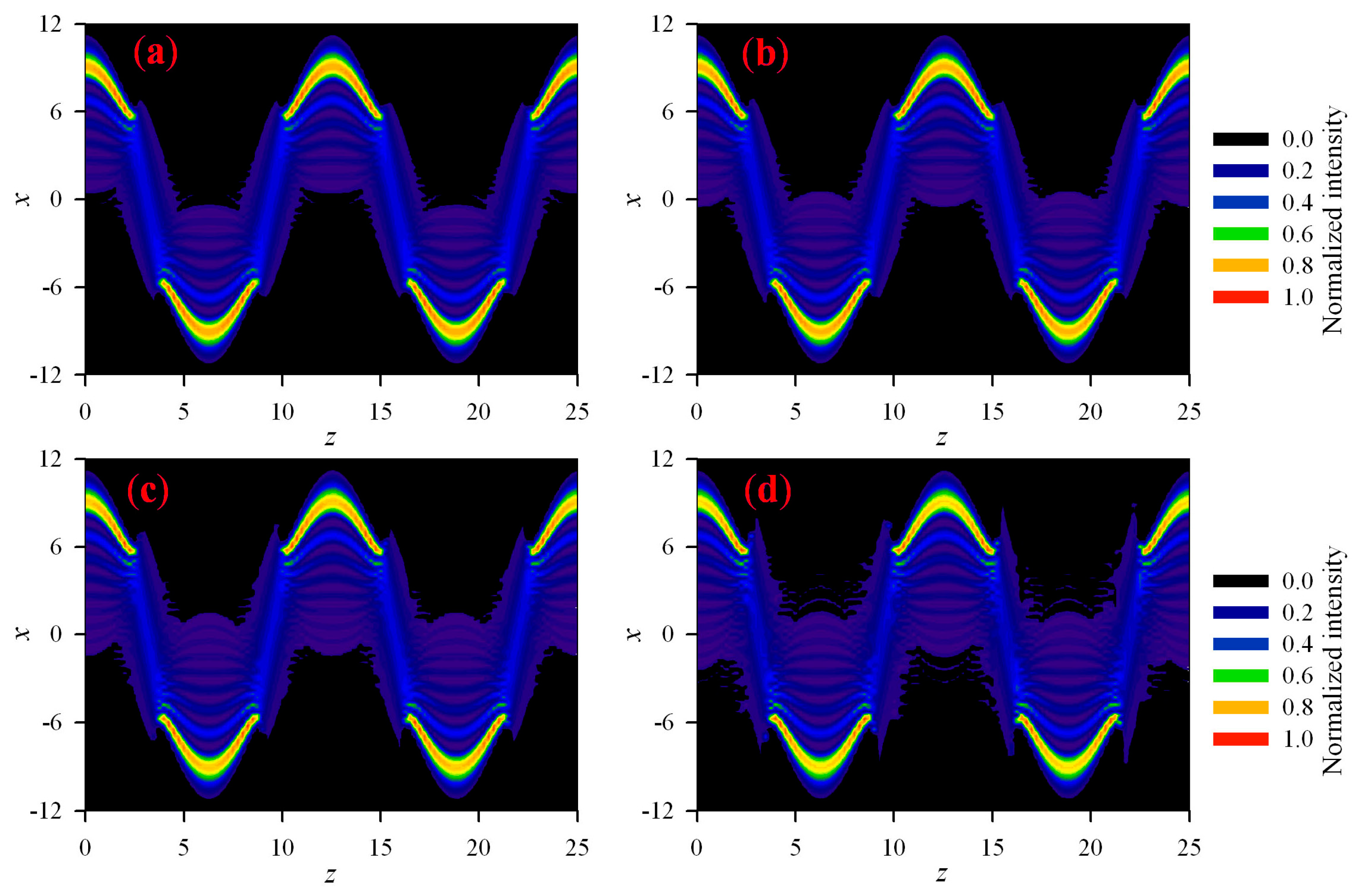
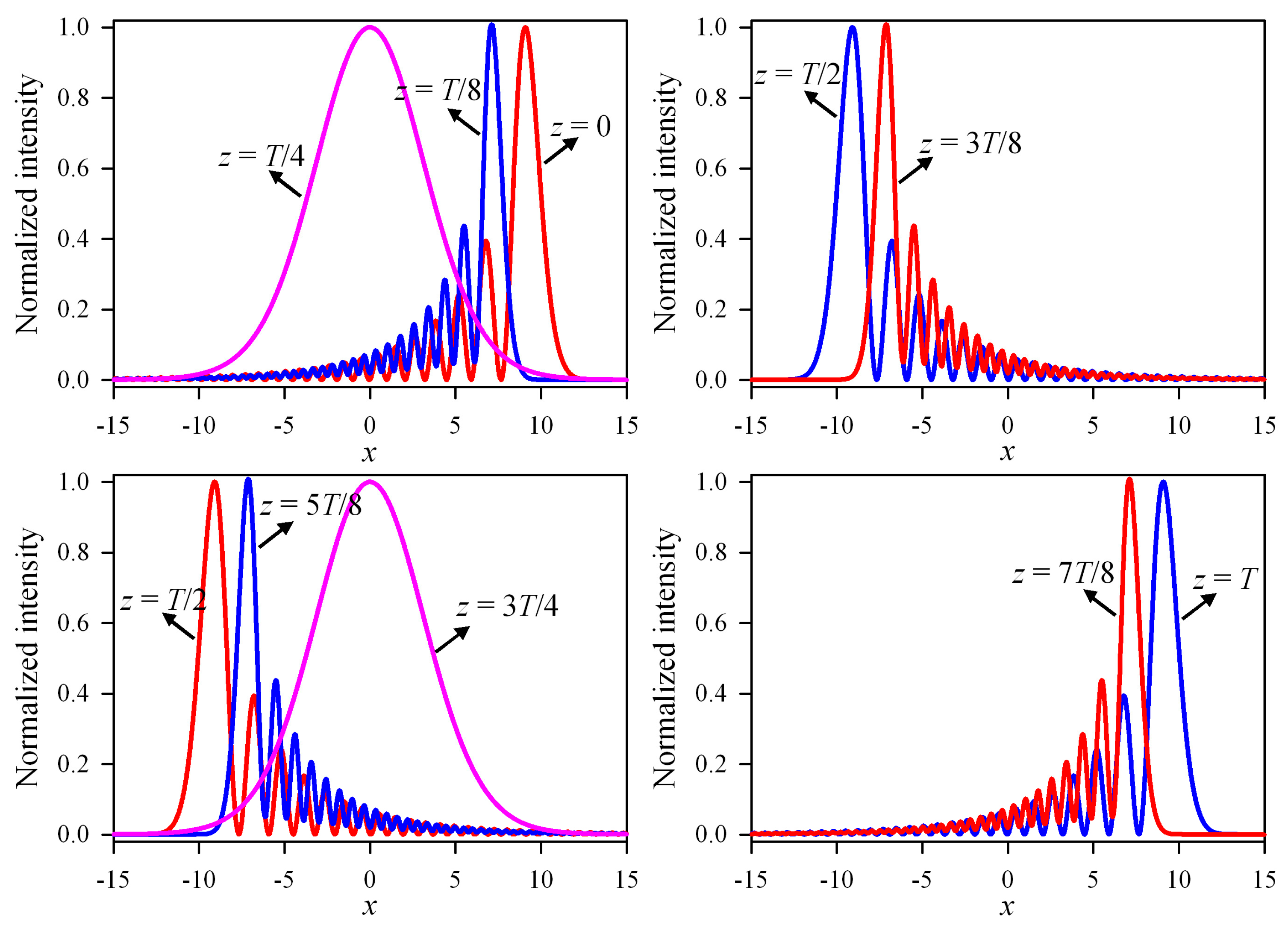
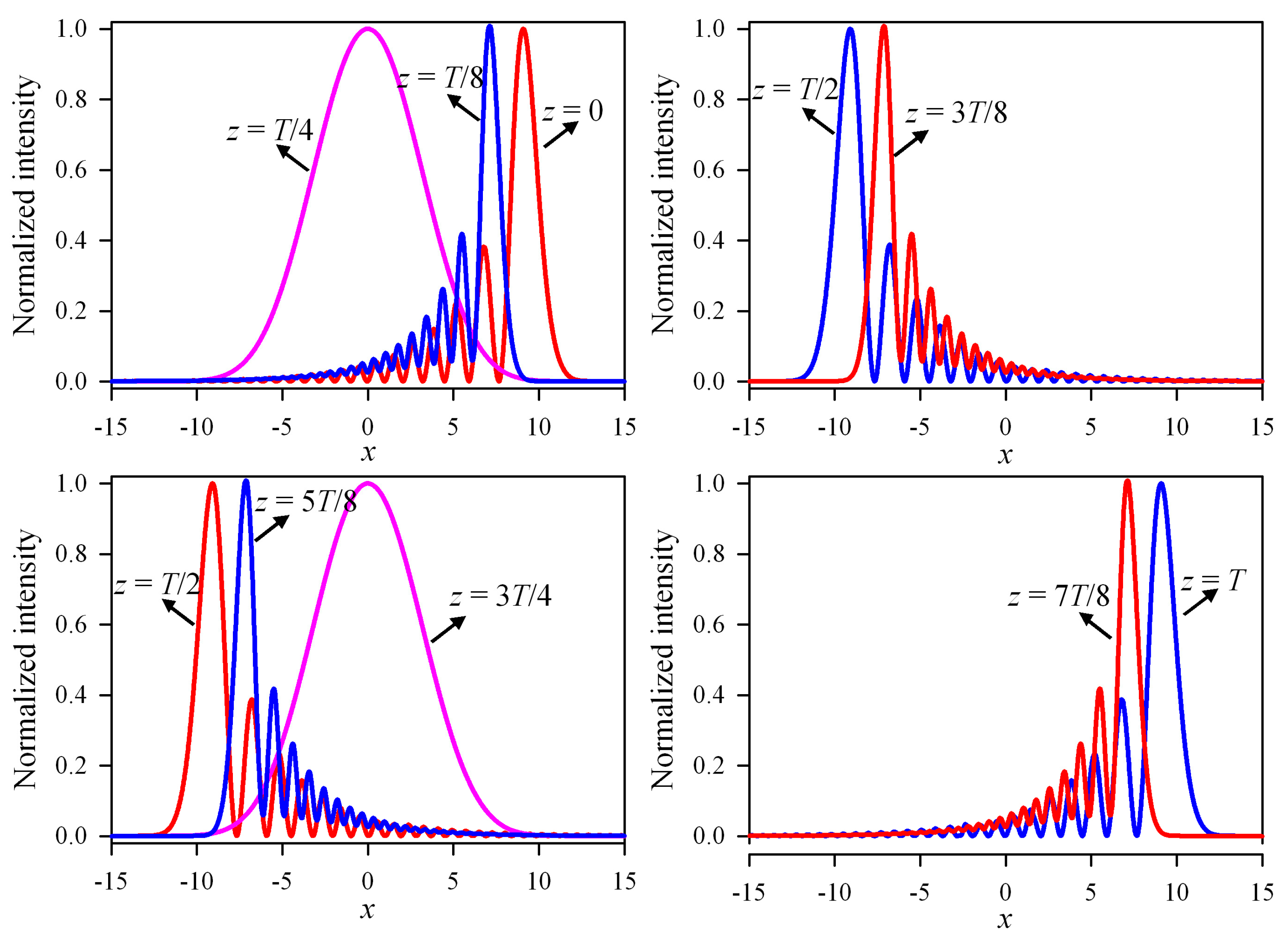
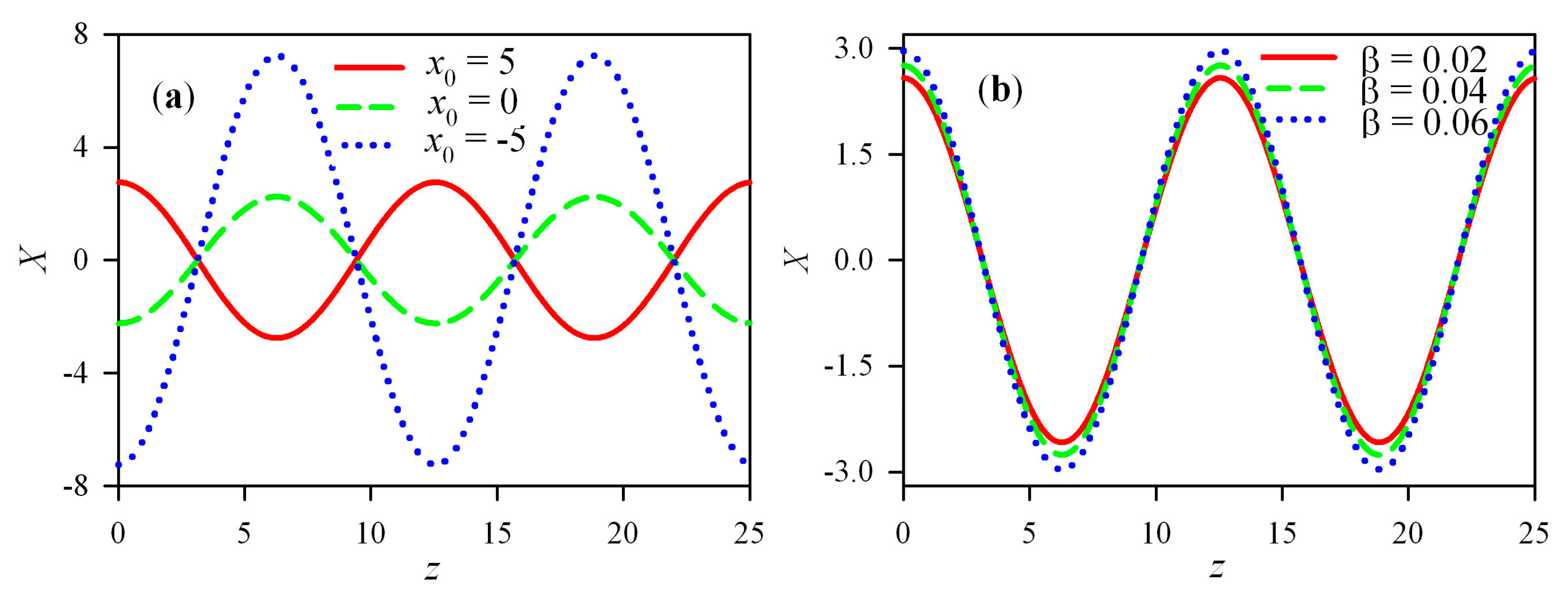
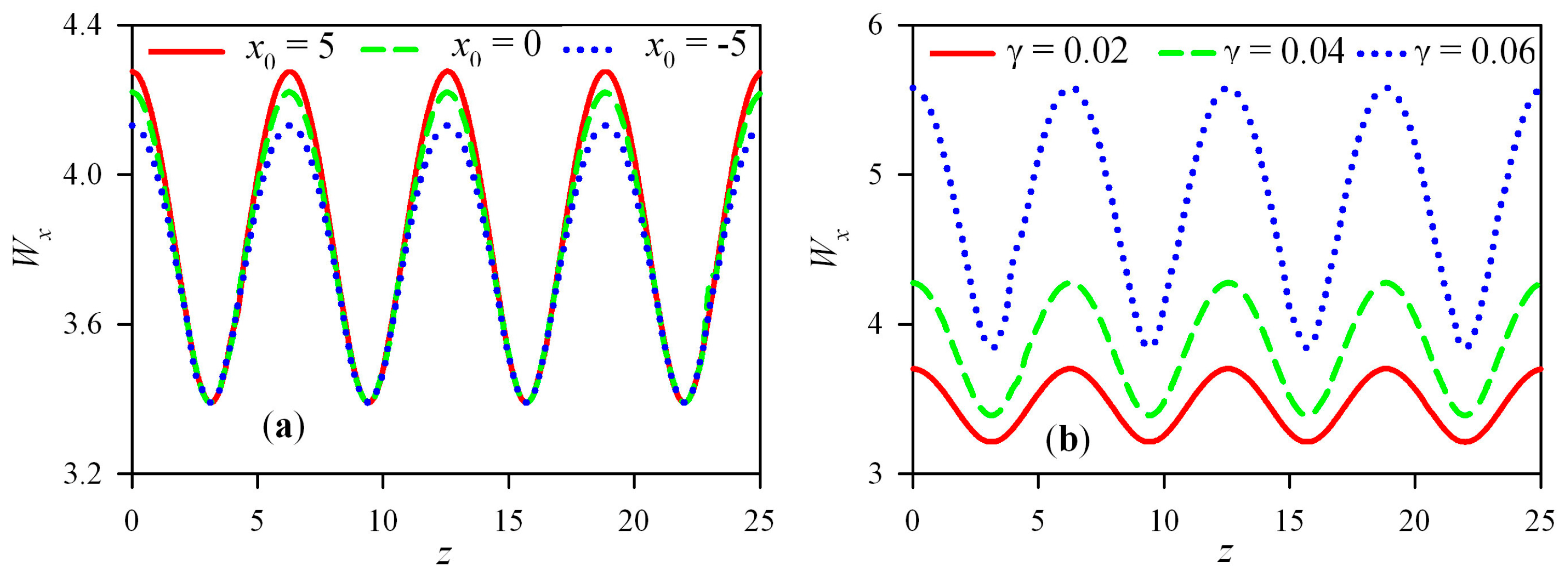
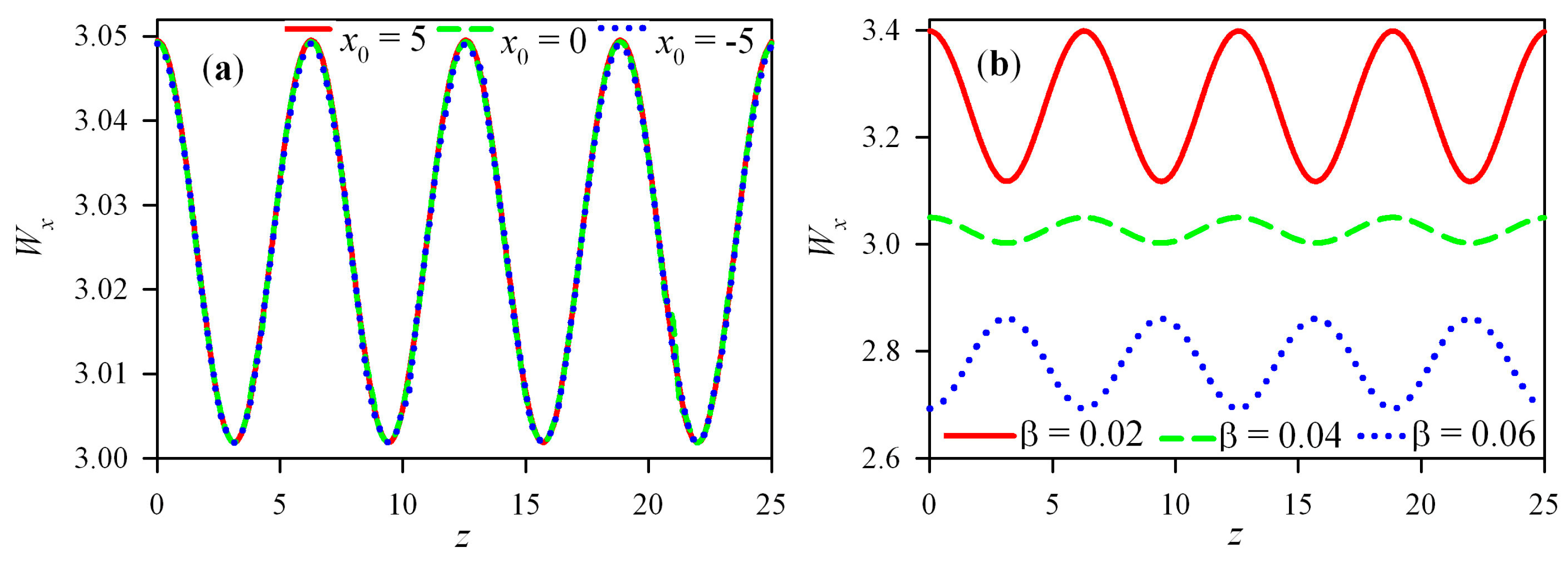
3. Numerical Simulations and Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Berry, M.V.; Balazs, N.L. Nonspreading wave packets. Am. J. Phys. 1979, 47, 264–267. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Brokly, J.; Dogariu, A.; Christodoulides, D.N. Observation of accelerating Airy beam. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
- Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979–981. [Google Scholar] [CrossRef] [PubMed]
- Brokly, J.; Siviloglou, G.A.; Dogariu, A.; Christodoulides, D.N. Self-healing properties of optical Airy beams. Opt. Express 2008, 16, 12880–12891. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sztul, H.I.; Alfano, R.R. The Poynting vector and angular momentum of Airy beams. Opt. Express 2008, 16, 9411–9416. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, G. The far-field divergent properties of an Airy beam. Opt. Laser Technol. 2012, 44, 1318–1323. [Google Scholar] [CrossRef]
- Chen, R.; Ying, C. Beam propagation factor of an Airy beam. J. Opt. 2011, 13, 085704. [Google Scholar] [CrossRef]
- Torre, A. Airy beams and paraxiality. J. Opt. 2014, 16, 035702. [Google Scholar] [CrossRef]
- Kaganovsky, Y.; Heyman, E. Wave analysis of Airy beams. Opt. Express 2010, 18, 8440–8452. [Google Scholar] [CrossRef]
- Chen, R.; Zheng, H.; Dai, C. Wigner distribution function of an Airy beam. J. Opt. Soc. Am. A 2011, 28, 1307–1311. [Google Scholar] [CrossRef]
- Wen, W.; Lu, X.; Zhao, C.; Cai, Y. Propagation of Airy beam passing through the misaligned optical system with hard aperture. Opt. Commun. 2014, 313, 350–355. [Google Scholar] [CrossRef]
- Zhou, G.; Chen, R.; Chu, X. Fractional Fourier transform of Airy beams. Appl. Phys. B 2012, 109, 549–556. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Brokly, J.; Dogariu, A.; Christodoulides, D.N. Ballistic dynamics of Airy beams. Opt. Lett. 2008, 33, 207–209. [Google Scholar] [CrossRef] [PubMed]
- Polynkin, P.; Kolesik, M.; Moloney, J. Filamentation of femtosecond laser Airy beams in water. Phys. Rev. Lett. 2009, 103, 123902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chu, X. Evolution of an Airy beam in turbulence. Opt. Lett. 2011, 36, 2701–2703. [Google Scholar] [CrossRef]
- Tao, R.; Si, L.; Ma, Y.; Zhou, P.; Liu, Z. Average spreading of finite energy Airy beams in non-Kolmogorov turbulence. Opt. Lasers Eng. 2013, 51, 488–492. [Google Scholar] [CrossRef]
- Chen, C.; Yang, H.; Kavehrad, M.; Zhou, Z. Propagation of radial Airy array beams through atmospheric turbulence. Opt. Lasers Eng. 2014, 52, 106–114. [Google Scholar] [CrossRef]
- Jin, Y.; Hu, M.; Luo, M.; Luo, Y.; Mi, X.; Zou, C.; Zhou, L.; Shu, C.; Zhu, X.; He, J.; et al. Beam wander of a partially coherent Airy beam in oceanic turbulence. J. Opt. Soc. Am. A 2018, 35, 1457–1464. [Google Scholar] [CrossRef]
- Zhou, G.; Chen, R.; Chu, X. Propagation of Airy beams in uniaxial crystals orthogonal to the optical axis. Opt. Express 2012, 20, 2196–2205. [Google Scholar] [CrossRef]
- Xiao, F.; Li, B.; Wang, M.; Zhu, W.; Zhang, P.; Liu, S.; Premaratne, M.; Zhao, J. Optical Bloch oscillations of an Airy beam in a photonic lattice with a linear transverse index gradient. Opt. Express 2014, 22, 22763–22770. [Google Scholar] [CrossRef]
- Diebel, F.; Bokic, B.; Boguslawski, M.; Piper, A.; Timotijevic, D.; Jovic, D.; Denz, C. Control of Airy-beam self-acceleration by photonic lattices. Phys. Rev. A 2014, 90, 033802. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.; Chew, K.; Zhao, T.; Li, P.; Li, C. Evolution of an Airy beam in a saturated medium. Laser Phys. 2014, 24, 115402. [Google Scholar] [CrossRef]
- Chen, R.; Yin, C.; Chu, X.; Wang, H. Effect of Kerr nonlinearity on an Airy beam. Phys. Rev. A 2010, 82, 043832. [Google Scholar] [CrossRef]
- Zhou, G.; Chen, R.; Ru, G. Propagation of an Airy beam in a strongly nonlocal nonlinear media. Laser Phys. Lett. 2014, 11, 105001. [Google Scholar] [CrossRef]
- Huang, S.; Shi, X.; Bai, Y.; Fu, X. Multi-solitons shedding from truncated Airy beam in nonlocal nonlinear media. IEEE Photonics Technol. Lett. 2016, 28, 1621–1624. [Google Scholar] [CrossRef]
- Zhang, Y.; Belić, M.R.; Zhang, L.; Zhong, W.; Zhu, D.; Wang, R.; Zhang, Y. Periodic inversion and phase transition of finite energy Airy beams in a medium with parabolic potential. Opt. Express 2015, 23, 10467–10480. [Google Scholar] [CrossRef]
- Lin, H.; Pu, J. Propagation of Airy beams from right-handed material to left-handed material. Chin. Phys. B 2012, 21, 054201. [Google Scholar] [CrossRef]
- Jia, S.; Lee, J.; Fleischer, J.W.; Siviloglou, G.A.; Christodoulides, D.N. Diffusion-trapped Airy beams in photorefractive media. Phys. Rev. Lett. 2010, 104, 253904. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, T.; Huo, G.; Hui, Z.; Duan, Z.; Zha, X. Temporal analysis of Airy beam propagation in photorefractive media. Commun. Nonlinear Sci. 2019, 76, 45–50. [Google Scholar] [CrossRef]
- Li, H.; Tang, M.; Wang, J.; Cao, J.; Li, X. Spin hall effect of Airy beam in inhomogeneous medium. Appl. Phys. B 2019, 125, 51. [Google Scholar] [CrossRef]
- Efremidis, N.K.; Christodoulides, D.N. Abruptly autofocusing waves. Opt. Lett. 2010, 35, 4045–4047. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Khonina, S.N. Generation of azimuthally modulated circular superlinear Airy beams. J. Opt. Soc. Am. B 2017, 34, 2544–2549. [Google Scholar] [CrossRef]
- Belafhal, A.; Ez-Zariy, L.; Hennani, S.; Nebdi, H. Theoretical introduction and generation method of a novel nondiffracting waves: Olver beams. Opt. Photon. J. 2015, 5, 234–246. [Google Scholar] [CrossRef] [Green Version]
- Khonina, S.N.; Ustinov, A.V. Fractional Airy beams. J. Opt. Soc. Am. A 2017, 34, 1991–1999. [Google Scholar] [CrossRef]
- Khonina, S.N. Specular and vortical Airy beams. Opt. Commun. 2011, 284, 4263–4271. [Google Scholar] [CrossRef]
- Vaveliuk, P.; Lencina, A.; Rodrigo, J.A.; Matos, O.M. Symmetric Airy beams. Opt. Lett. 2014, 39, 2370–2373. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Wang, J.; Tang, M.; Li, X. Propagation properties of cosh-Airy beams. J. Mod. Opt. 2018, 65, 314–320. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, Y.; Zhou, G. Beam propagation factor of a cosh-Airy beam. Appl. Sci. 2019, 9, 1817. [Google Scholar] [CrossRef] [Green Version]
- Zhou, G.; Chu, X.; Chen, R.; Zhou, Y. Self-healing properties of cosh-Airy beams. Laser Phys. 2019, 29, 025001. [Google Scholar] [CrossRef]
- Zhou, G.; Chen, R.; Chu, X. Propagation of cosh-Airy beams in uniaxial crystals orthogonal to the optical axis. Opt. Laser Technol. 2019, 116, 72–82. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Tang, M.; Cao, J.; Li, X. Phase transition of cosh-Airy beams in inhomogeneous media. Opt. Commun. 2018, 427, 147–151. [Google Scholar] [CrossRef]
- Feit, M.D.; Fleck, J.A. Light propagation in graded-index optical fibers. Appl. Opt. 1978, 17, 3990–3998. [Google Scholar] [CrossRef] [PubMed]
- Mendlovic, D.; Ozaktas, H.M.; Lohmann, A.W. Graded-index fibers, Wigner-distribution functions, and the fractional Fourier transform. Appl. Opt. 1994, 33, 6188–6193. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dorsch, R.G.; Lohmann, A.W. Fractional Fourier transform used for a lens-design problem. Appl. Opt. 1995, 34, 4111–4112. [Google Scholar] [CrossRef] [PubMed]
- Namias, V. The fractional order Fourier transform and its application to quantum mechanics. IMA J. Appl. Math. 1980, 25, 241–265. [Google Scholar] [CrossRef]
- Mendlovic, D.; Ozaktas, H.M. Fractional Fourier transforms and their optical implementation: I. J. Opt. Soc. Am. A 1993, 10, 1875–1881. [Google Scholar] [CrossRef] [Green Version]
- Kazakov, A.Y. “Separation of variables” in the model problems of the diffraction theory. A formal scheme. J. Math. Sci. 2019, 243, 715–725. [Google Scholar] [CrossRef]
- Agarwal, G.; Simon, R. A simple realization of fractional Fourier transform and relation to harmonic oscillator Green’s function. Opt. Commun. 1994, 110, 23–26. [Google Scholar] [CrossRef]
- Bernardini, C.; Gori, F.; Santarsiero, M. Converting states of a particle under uniform or elastic forces into free particle states. Eur. J. Phys. 1995, 16, 58–62. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Vallée, O.; Manuel, S. Airy Functions and Applications to Physics; Imperial College Press: London, UK, 2010. [Google Scholar]
- Hodgson, N.; Weber, H. Laser Resonators and Beam Propagation; Springer Press: New York, NY, USA, 2005. [Google Scholar]
- Zhou, G. Generalized beam propagation factors of truncated partially coherent cosine-Gaussian and cosh-Gaussian beams. Opt. Laser Technol. 2010, 42, 489–496. [Google Scholar] [CrossRef]
- Zhou, G.; Ji, Z.; Ru, G. Complete analytical expression of Lorentz-Hermite-Gauss laser beams. Lasers Eng. 2018, 40, 127–147. [Google Scholar]
- Nemes, G.; Serna, J. Laser beam characterization with use of second order moments: An overview. OSA TOPS 1998, 17, 200–207. [Google Scholar]
- Zhou, G. Far field structural properties of a Gaussian vortex beam. Lasers Eng. 2013, 26, 1–17. [Google Scholar] [CrossRef]
- Ni, Y.; Ji, Z.; Ru, G.; Zhou, G. Propagation properties of controllable dark hollow laser beams in uniaxial crystals along the optical axis. Lasers Eng. 2017, 38, 283–305. [Google Scholar]
- Khonina, S.N.; Striletz, A.S.; Kovalev, A.A.; Kotlyar, V.V. Propagation of laser vortex beams in a parabolic optical fiber. Proc. SPIE 2010, 7523, 75230B. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Xu, Y.; Chu, X.; Zhou, G. Propagation of Cosh-Airy and Cos-Airy Beams in Parabolic Potential. Appl. Sci. 2019, 9, 5530. https://doi.org/10.3390/app9245530
Zhou Y, Xu Y, Chu X, Zhou G. Propagation of Cosh-Airy and Cos-Airy Beams in Parabolic Potential. Applied Sciences. 2019; 9(24):5530. https://doi.org/10.3390/app9245530
Chicago/Turabian StyleZhou, Yimin, Yiqing Xu, Xiuxiang Chu, and Guoquan Zhou. 2019. "Propagation of Cosh-Airy and Cos-Airy Beams in Parabolic Potential" Applied Sciences 9, no. 24: 5530. https://doi.org/10.3390/app9245530





