Theoretical Study and Application of the Reinforcement of Prestressed Concrete Cylinder Pipes with External Prestressed Steel Strands
Abstract
:1. Introduction
2. Theoretical Derivations
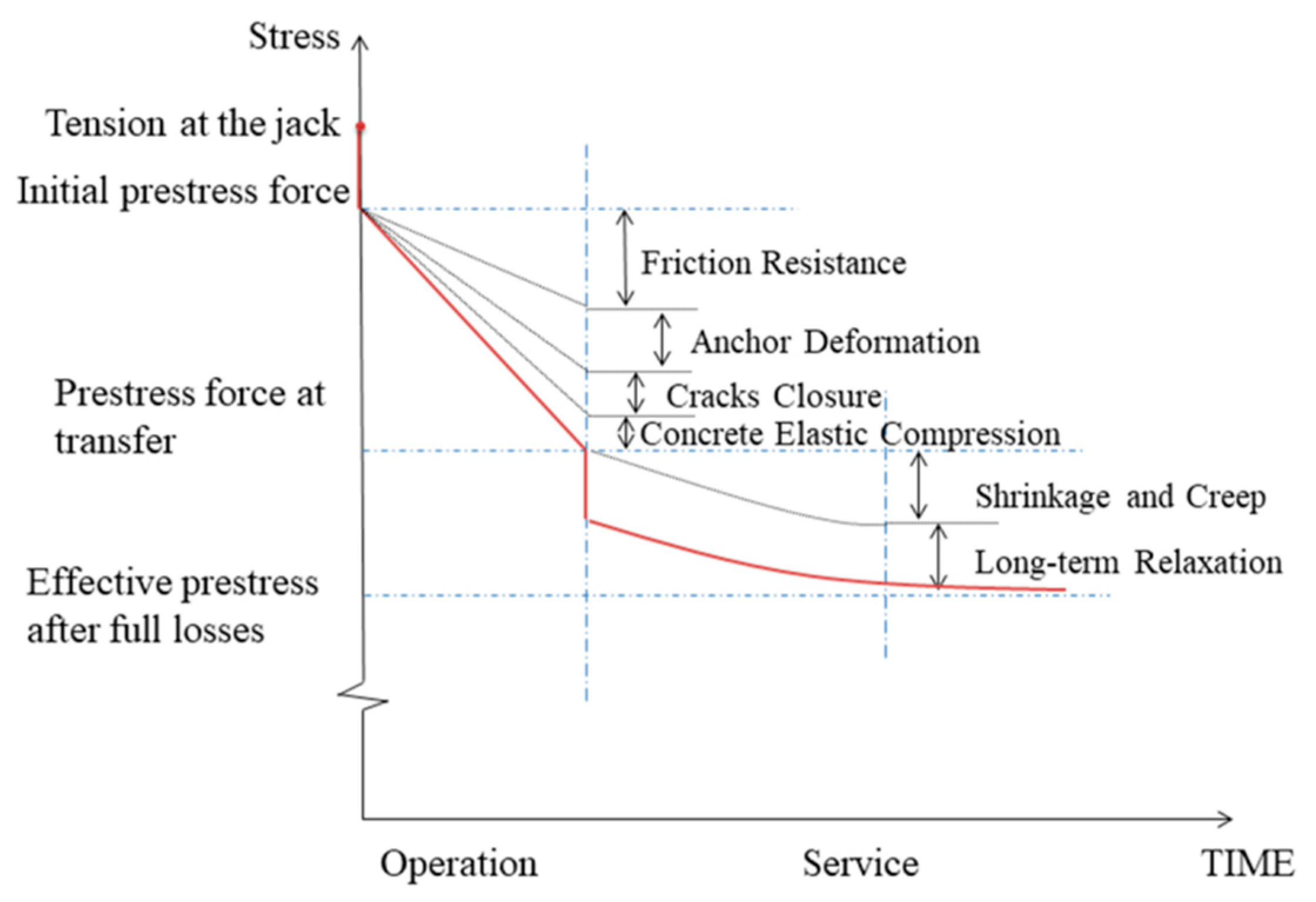
2.1. Calculation of Prestress Loss,
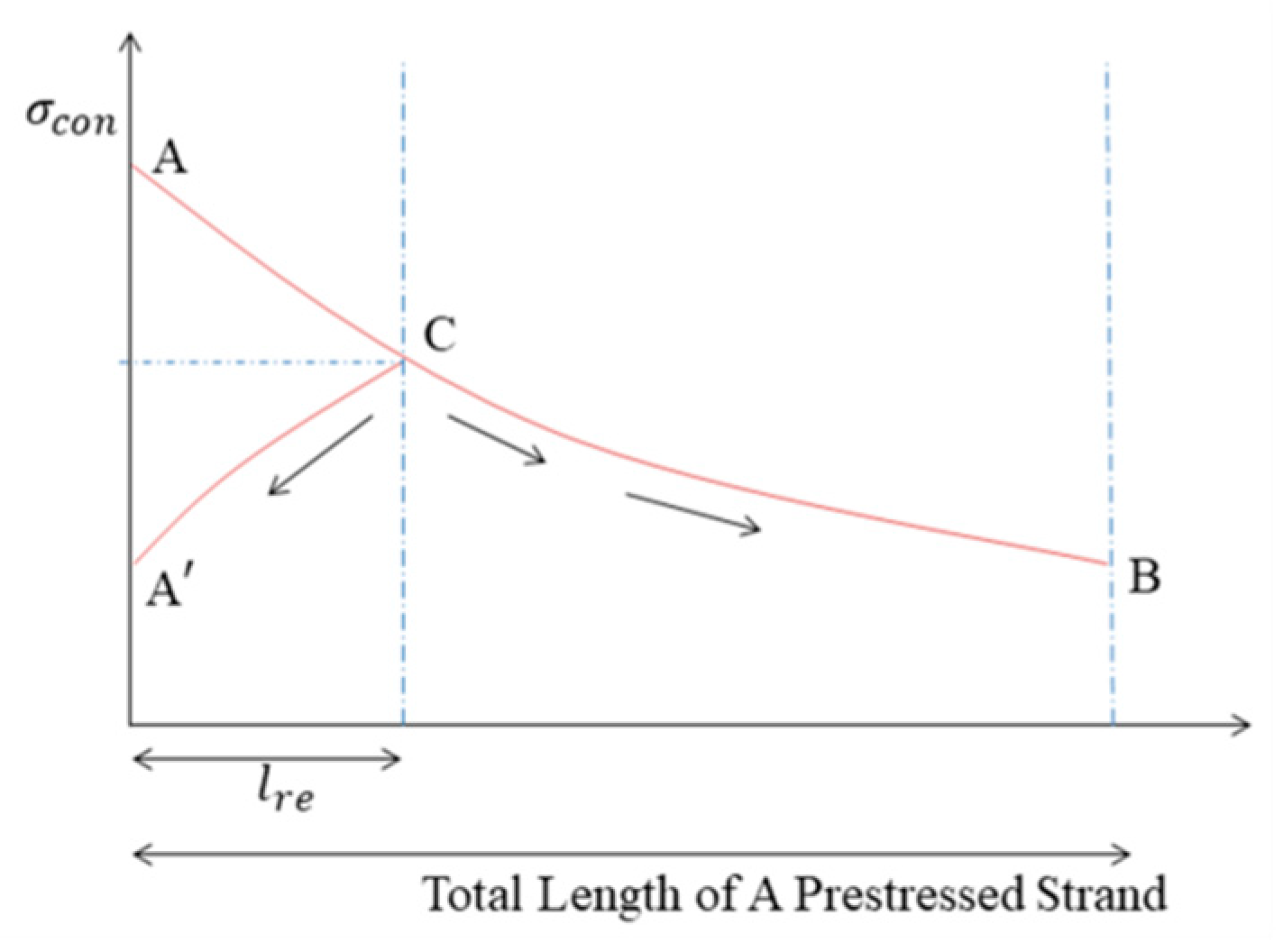
2.1.1. Calculation of Retraction Length, , and Its Corresponding Retraction Angle,
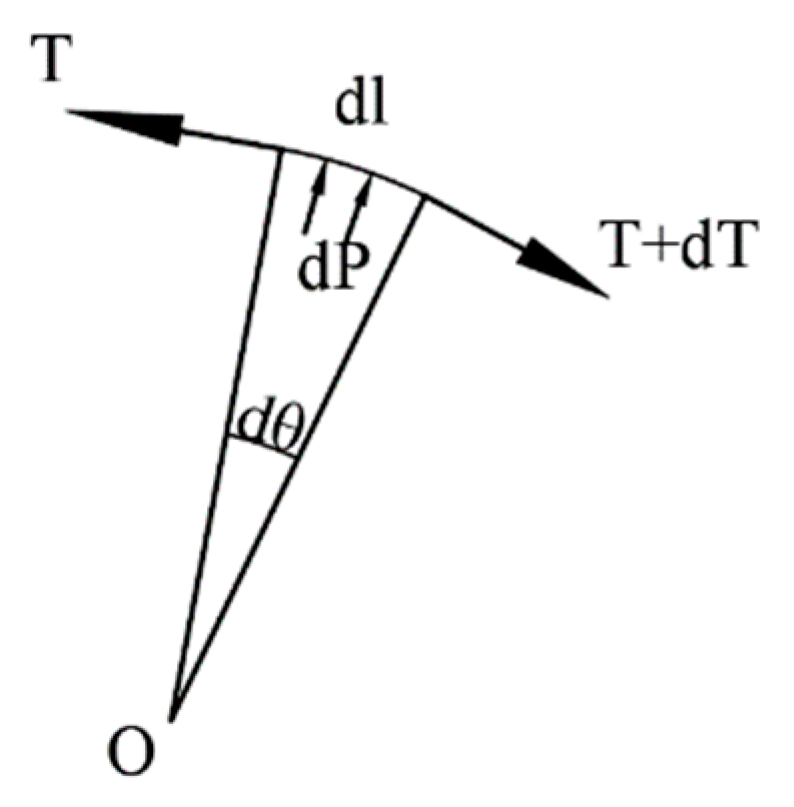
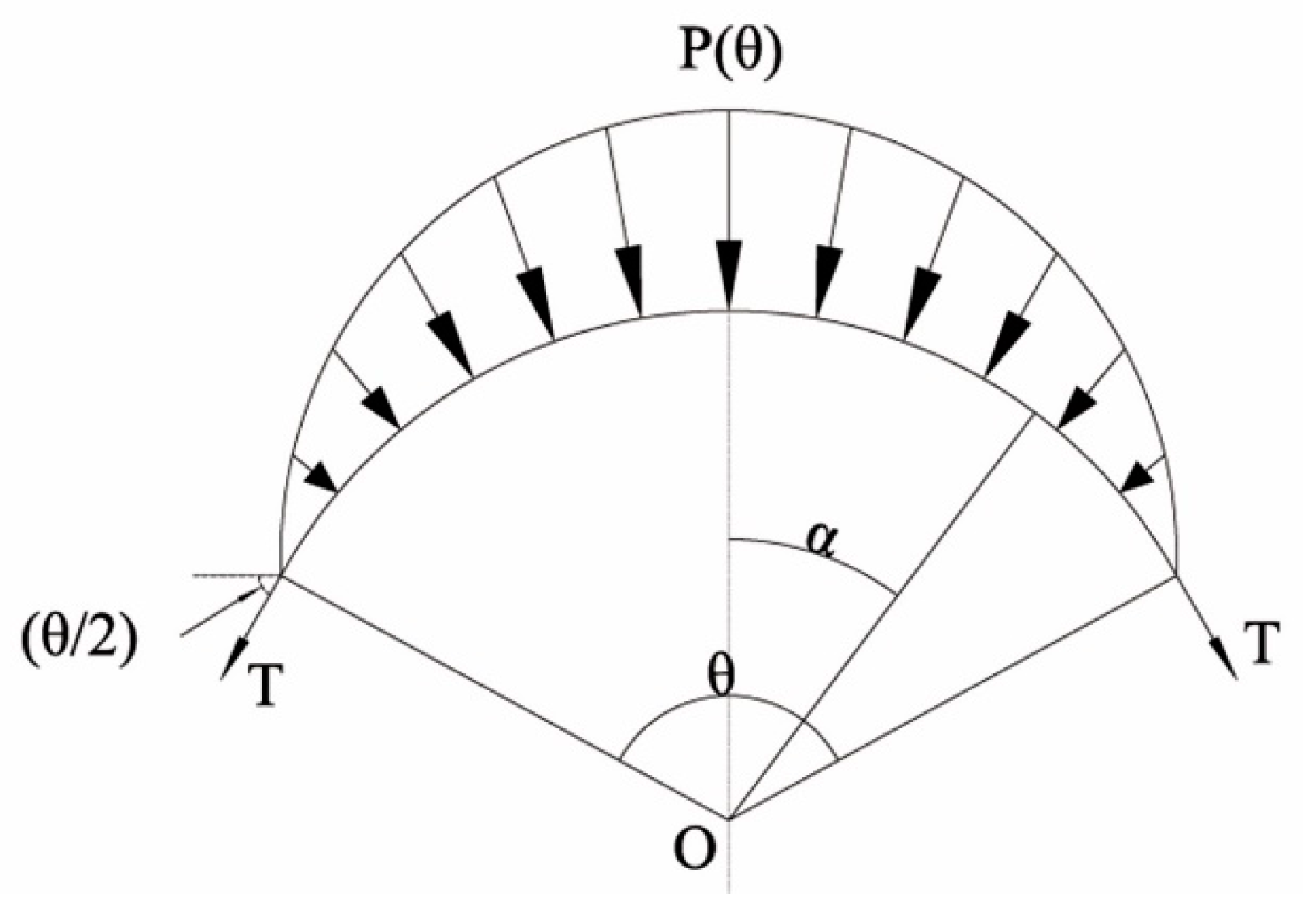
2.1.2. Prestress Loss Caused by Friction Resistance,
2.1.3. Prestress Loss Caused by Anchorage Deformation,
2.1.4. Prestress Loss Caused by the Elastic Compression of Concrete During Batch Tensioning,
2.1.5. Prestress Loss Due to Crack Reduction and Closure,
2.1.6. Prestress Loss Caused by Shrinkage and Creep of Concrete,
2.1.7. Prestress Loss Due to Long-Term Relaxation of the Strand,
2.2. Calculation of Area of Prestressed Steel Strands
2.2.1. Stress of PCCPs under Combined Loads
2.2.2. Calculation of the Area of Prestressed Strands, Considering the Concrete Core Compression of Ultimate Limit States
2.2.3. Checking Calculation of Prestressed Strands Considering the Concrete Core Compression of Serviceability Limit States
2.2.4. Checking Calculation of the Mortar Coating under Serviceability Limit States
2.2.5. Checking Calculation of Mortar Coating under Quasi-Permanent Limit States
3. Applications
3.1. Parameters of the Design and Materials
3.2. Example Calculation
3.2.1. Calculation of Prestress Loss,
3.2.2. Stress of PCCP under Combined Loads
3.3.3. Calculation of Area of Prestressed Strands, Considering the Concrete Core Compression of Ultimate Limit States
3.3.4. Checking Calculation of Prestressed Strands Considering the Concrete Core Compression of Serviceability Limit States
3.3.5. Checking Calculation of Mortar Coating under Serviceability Limit States
3.3.6. Checking Calculation of Mortar Coating under Quasi-Permanent Limit States
3.3. A Prototype Test
4. Conclusions
- (1)
- The calculation formula for the prestress loss of different types of steel strands has been derived and the effective prestress of the prestressed steel strands can be determined.
- (2)
- A stress calculation formula of the concrete core under the ultimate limit states and serviceability limit states was determined and used for calculation. The condition of the mortar coating under the serviceability limit and the quasi-permanent limit states was verified, and the reinforcement area of the steel strand was finally determined. This tentative derivation was applied to the reinforced pipe with broken wires (inner diameter of 2000 mm) to calculate the appropriate area of prestressed steel strands.
- (3)
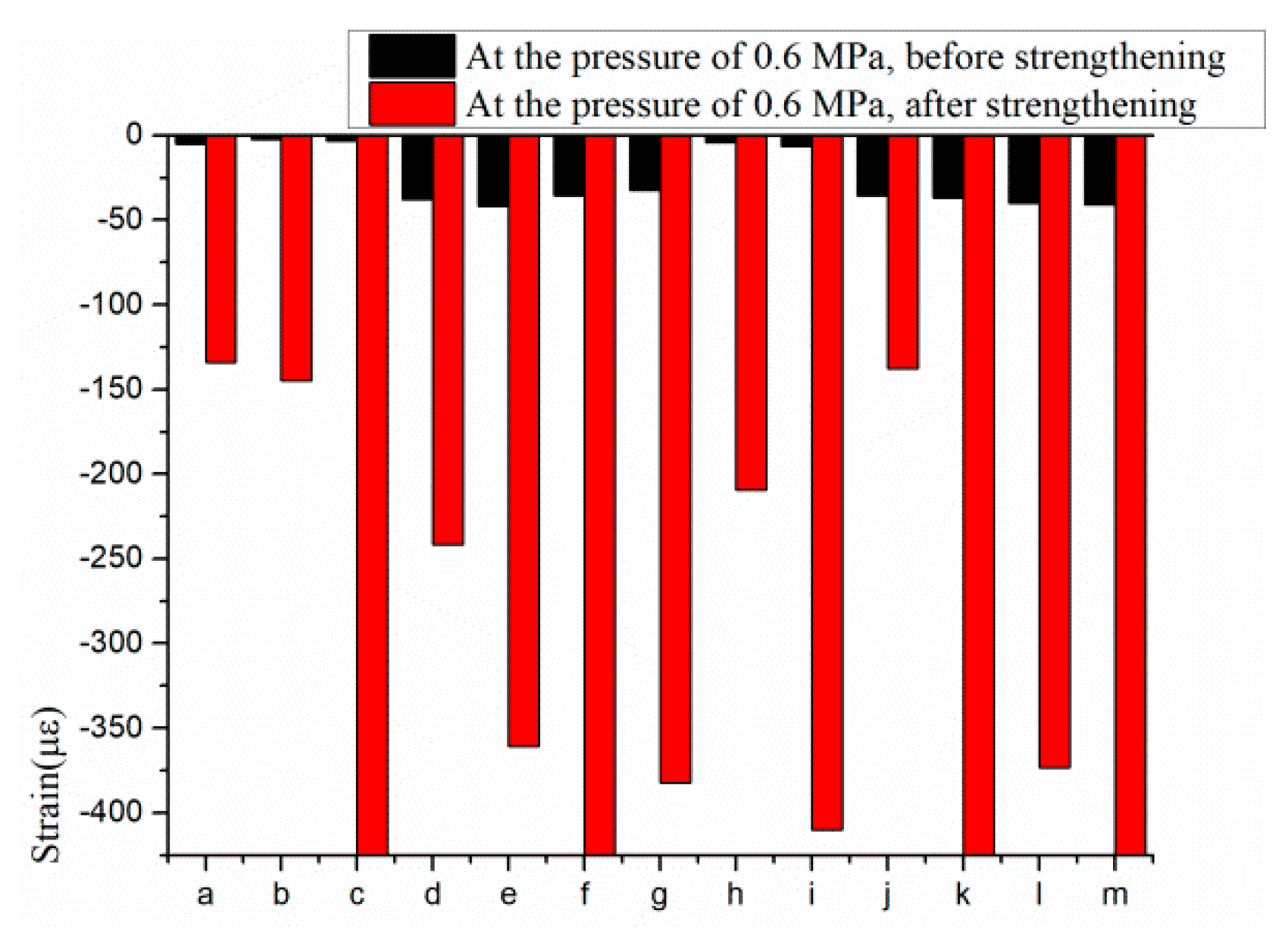
- The crack propagation in the concrete core was constrained by the strands and the test pipe was able to sustain the working pressure after strengthening. In addition, the maximum width of the cracks in the outer concrete core at the spring-line showed some closure because of the contribution of the strands. The bearing capacity of the prototype test was returned to the original design level and the behavior of the pipe was in accordance with the expectation of derivation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Engelmanna, M.; Wellerb, B. Losses of prestress in post-tensioned glass beams. Structures 2019, 19, 248–257. [Google Scholar] [CrossRef]
- Tan, K.H.; Tjandra, R.A. Strengthening of RC Continuous Beams by External Prestressing. J. Struct. Eng. 2007, 133, 195–204. [Google Scholar] [CrossRef]
- Abdel-Jaber, H.; Glisic, B. Monitoring of long-term prestress losses in prestressed concrete structures using fiber optic sensors. Struct. Health Monit. 2019, 18, 254–269. [Google Scholar] [CrossRef]
- Hou, Y.; Cao, S.; Ni, X.; Li, Y. Research on Concrete Columns Reinforced with New Developed High-Strength Steel under Eccentric Loading. Materials 2019, 12, 2139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, S.; Zang, H.; Duan, N.; Jiang, J. Experimental Research and Analysis on Fatigue Life of Carbon Fiber Reinforced Polymer (CFRP) Tendons. Materials 2019, 12, 3383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyamoto, A.; Tei, K.; Nakamura, H.; Bull, J.W. Behavior of prestressed beam strengthened with external tendons. J. Struct. Eng. 2000, 126, 1033–1044. [Google Scholar] [CrossRef]
- Miyamoto, A.; Tei, K.; Gotou, M. Mechanical Behavior and Design Concept of Prestressed Composite Plate Girders with External Tendons; Technology Reports-Yamaguchi University: Yamaguchi, Japan, 1995; pp. 233–258. [Google Scholar]
- Chen, S.; Jia, Y. Numerical investigation of inelastic buckling of steel–concrete composite. Thin Wall Struct. 2010, 48, 233–242. [Google Scholar] [CrossRef]
- Lou, T.; Lopes, S.M.R.; Lopes, A.V. Numerical modeling of externally prestressed steel concrete composite beams. J. Constr. Steel Res. 2016, 121, 229–236. [Google Scholar] [CrossRef]
- Aparicio, A.C.; Ramos, G.; Casas, J.R. Testing of externally prestressed concrete beams. Eng. Struct. 2002, 24, 73–84. [Google Scholar] [CrossRef]
- Park, S.; Kim, T.; Kim, K.; Hong, S.N. Flexural behavior of steel I-beam prestressed with externally unbonded tendons. J. Constr. Steel Res. 2010, 66, 125–132. [Google Scholar] [CrossRef]
- Elnakhat, H.; Raymond, R. Repair of PCCP by Post Tensioning. In Proceedings of the Pipelines 2006, Chicago, IL, USA, 30 July–2 August 2006; pp. 1–5. [Google Scholar]
- Cao, G.; Hu, J.; Kai, Z. Coupling model for calculating prestress loss caused by relaxation loss, shrinkage, and creep of concrete. J. Cent. South Univ. 2016, 23, 470–478. [Google Scholar] [CrossRef]
- Cao, G.; Zhang, W.; Hu, J.; Zhang, K. Experimental study on the long-term behaviour of RBPC T-beams. Int. J. Civ. Eng. 2018, 16, 887–895. [Google Scholar] [CrossRef]
- Baolin, K. The Estimating of the External Prestressing Loss in the Bridge Strengthen System. J. Hebei Inst. Archit. Sci. Technol. 2002, 19, 27–29. [Google Scholar]
- Zhang, J.; Pan, J.; Dong, H. Analysis of Prestressing Loss on Construction of External Prestressed Wooden Buildings: Advanced Materials Research; Trans Tech Publications: Bern, Switzerland, 2012. [Google Scholar]
- GB 50010-2010. Code for Design of Concrete Structures; Industry Press: Beijing, China, 2010. [Google Scholar]
- Kang, Y. Reinforcement Mechanism and Application of External Prestressed Concrete; Hehai University: Nanjing, China, 2006. [Google Scholar]
- Hu, Z. Practical Estimation Method for Prestress Loss of Externally Prestressed Structures. Bridge Constr. 2006, 73–75. [Google Scholar]
- Zhang, S.; Zhang, K.Y.; Xie, B.Y.; Fan, Z.L. Research on the Mechanism of Prestressed Loss for Curving Hole of Prestressed Concrete Structure Caused by Frictional Resistance. In Applied Mechanics and Materials; Trans Tech Publications: Bern, Switzerland, 2013. [Google Scholar]
- Gao, A. Research on Prestress Loss Based on Friction, Retraction and Natural Frequency; Southeast University: Nanjing, China, 2016. [Google Scholar]
- Erbay, O.O.; Zarghamee, M.S.; Ojdrovic, R.P. Failure Risk Analysis of Lined Cylinder Pipes with Broken Wires and Corroded Cylinder. In Pipelines 2007: Advances and Experiences with Trenchless Pipeline Projects; American Society of Civil Engineers: Reston, VA, USA, 2007; pp. 1–10. [Google Scholar]
- Zarghamee, M.S.; Dana, W.R. Step-by-step Integration Procedure for Computing State of Stress in Prestressed concrete pipe. Spec. Publ. 1991, 129, 155–170. [Google Scholar]
- Zarghamee, M.S.; Fok, K.; Sikiotis, E.S. Limit states design of prestressed concrete pipe II: Procedure. J. Struct. Eng. 1990, 116, 2105–2126. [Google Scholar] [CrossRef]
- Zarghamee, M.S.; Fok, K. Analysis of prestressed concrete pipe under combined loads. J. Struct. Eng. 1990, 116, 2022–2039. [Google Scholar] [CrossRef]
- American Water Works Association (Ed.) Concrete Pressure Pipe: M9; American Water Works Association: Denver, CO, USA, 2008. [Google Scholar]
- CECS 140:2011. Specification for Structural Design of Buried Prestressed Concrete Pipeline and Prestressed Concrete Cylinder Pipeline of Water Supply and Sewerage Engineering; Beijing General Municipal Engineering Design& Research Institute Co. Ltd.: Beijing, China, 2011. [Google Scholar]
- GB 50332. Structural Design Code for Pipelines of Water Supply and Waste Water Engineering; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2002.
- Zhao, L.; Dou, T.; Cheng, B.; Xia, S.; Yang, J.; Zhang, Q.; Li, M.; Li, X. Experimental Study on the Reinforcement of Prestressed Concrete Cylinder Pipes with External Prestressed Steel Strands. Appl. Sci. 2019, 9, 149. [Google Scholar] [CrossRef] [Green Version]

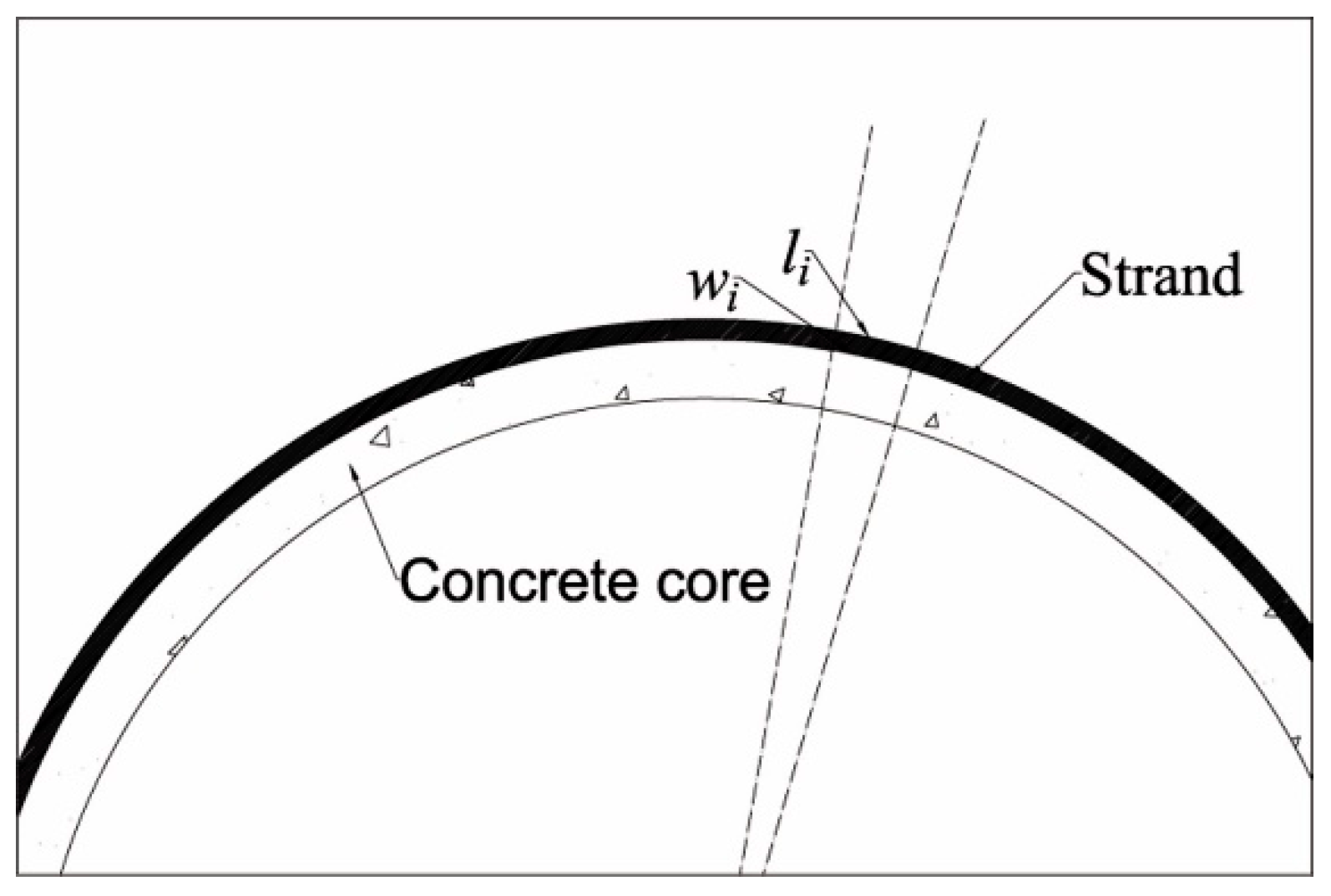


| Geometric Parameter | Value | Geometric Parameter | Value |
|---|---|---|---|
| Inner diameter of PCCP, /mm | 2000 | Net thickness of mortar coating, /mm | 25 |
| Thickness of core concrete, /mm | 140 | Spacing between each wire, /mm | 22.1 |
| Outer diameter of cylinder, /mm | 2103 | Diameter of wires, /mm | 6 |
| Thickness of cylinder, /mm | 1.5 | Number of layers, | 1 |
| Key Parameter | Value | Key Parameter | Value |
|---|---|---|---|
| Designed 28-day compressive strength of the core concrete, /(N/mm2) | 44 | Modulus of concrete, /(N/mm2) | 3.55 × 104 |
| Standard compressive strength of mortar, /(N/mm2) | 45 | Modulus of mortar, /(N/mm2) | 2.416 × 104 |
| Poisson’s ratio of concrete, | 0.167 | Modulus of cylinder, /(N/mm2) | 2.068 × 105 |
| Poisson’s ratio of mortar, | 0.2 | Modulus of wire, /(N/mm2) | 1.93 × 105 |
| Minimum tensile strength of the prestressed wire, /(N/mm2) | 1570 | Designed tensile or compressive yield strength of steel cylinder, /(N/mm2) | |
| Gross wrapping tensile stress in wire, /(N/mm2) | Designed tensile strength of steel cylinder at pipe burst, /(N/mm2) | ||
| Design tensile strength of core concrete, /(N/mm2) | 1.95 | Unit weight of the pipe, | |
| Standard tensile strength of core concrete, /(N/mm2) | Unit weight of mortar, | 23.5 | |
| Unit weight of backfill soil, | 18 | Unit weight of water, |
| Key Parameter | Value | Key Parameter | Value |
|---|---|---|---|
| Nominal diameter without polyethylene /mm | 15.2 | Control coefficient for the tensioning of the steel strands, | 0.63 |
| Nominal section area without PE, | 140 | Tension stress of the prestressed steel strands, /() | 1171.8 |
| Nominal tensile strength, /() | 1860 | Standard tensile yield strength, /() | 1580 |
| Modulus of the strand, /() | 1.95 × 105 | Designed tensile yield strength, /() | 1110 [17] |
| Item | Value |
|---|---|
| Prestress loss related to the bending loss, | 276.099 |
| Correction coefficient accounting for the bending loss and the deviation loss, | 1.01 |
| Prestress loss caused by friction resistance, /() | 278.860 |
| Prestress loss caused by anchorage deformation, /() | 158.802 |
| Prestress loss caused by elastic compression of concrete during batch tensioning, /() | 0 |
| Maximum width of the visible cracks in the concrete core before the reinforcement, | 0.0022 |
| Maximum width of the visible cracks in the concrete core after the reinforcement, | 0.0001 |
| Prestress loss due to the crack reduction and closure, /() | 0.3434 |
| Prestress loss caused by shrinkage and creep of concrete, /() | 0 |
| The relaxation coefficient of the strand, | 0.045 |
| Prestress loss due to long-term relaxation of the strand, /() | 52.731 |
| Total prestress loss of prestressed wires, /() | 490.74 |
| Item | Value |
|---|---|
| Vertical earth pressure at the top of the pipe, | 164.245 |
| Lateral earth pressure, | 25.026 |
| Variable load, | 10 |
| Weight of the pipe, | 29.157 |
| Weight of water in the pipe | 31.416 |
| Item | Value |
|---|---|
| Thickness of the pipe, | 0.171 |
| Calculated radius of the pipe, | 1.0855 |
| Outer diameter of the pipe, | 2.342 |
| Combination coefficient of the variable loads, | 0.9 |
| The factor of importance for two side-by-side pipelines, | 1 |
| Design value of the maximum bending moment of the pipe at the spring-line, | −33.998 |
| Design value of the maximum axial tension of the pipe at the spring-line, | 1111.712 |
| Width of calculated section, | 1 |
| Ratio of modulus of the strand to the concrete, | 5.83 |
| Ratio of modulus of the cylinder to the concrete, | 5.49 |
| Ratio of modulus of the mortar to the concrete, | 0.68 |
| Conversion area of pipe section (including cylinder, steel strands and the mortar coating), | 0.1792 |
| Cross sectional area moment of the cross section of the concrete core, mortar, steel cylinder and prestressed steel strand on the inner surface of the pipe wall, | 0.01496 |
| Cross sectional area of the cylinder for unit pipe length, | 0.0015 |
| Distance from the mandrel to the inner surface of the pipe wall after the conversion, | 0.08347 |
| Distance from the center of the prestressed steel strand to the center of gravity of the pipe wall section, | 0.06412 |
| Comprehensive adjustment factor for ECP whose diameter is larger than 1600 mm, | 0.9 |
| Item | Value |
|---|---|
| Maximum bending moment of the pipe at the bottom, | 36.316 |
| Maximum bending moment of the pipe at the top, | 23.423 |
| Axial tension of the pipe wall, | 879.255 |
| Elastic resistance moment of the unconverted tension edge of the rectangular section of the pipe wall, | 0.00487 |
| Maximum tensile stress at the edge of the pipe at the bottom, | 12.107 |
| Effective prestress of the prestressed steel strands apart from the prestress loss, /() | 681.06 |
| Influence coefficient of concrete in tension area, | 1.2239 |
| Plastic influence coefficient of concrete in tension area, | 1.75 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Dou, T.; Cheng, B.; Xia, S.; Yang, J.; Zhang, Q.; Li, M.; Li, X. Theoretical Study and Application of the Reinforcement of Prestressed Concrete Cylinder Pipes with External Prestressed Steel Strands. Appl. Sci. 2019, 9, 5532. https://doi.org/10.3390/app9245532
Zhao L, Dou T, Cheng B, Xia S, Yang J, Zhang Q, Li M, Li X. Theoretical Study and Application of the Reinforcement of Prestressed Concrete Cylinder Pipes with External Prestressed Steel Strands. Applied Sciences. 2019; 9(24):5532. https://doi.org/10.3390/app9245532
Chicago/Turabian StyleZhao, Lijun, Tiesheng Dou, Bingqing Cheng, Shifa Xia, Jinxin Yang, Qi Zhang, Meng Li, and Xiulin Li. 2019. "Theoretical Study and Application of the Reinforcement of Prestressed Concrete Cylinder Pipes with External Prestressed Steel Strands" Applied Sciences 9, no. 24: 5532. https://doi.org/10.3390/app9245532
APA StyleZhao, L., Dou, T., Cheng, B., Xia, S., Yang, J., Zhang, Q., Li, M., & Li, X. (2019). Theoretical Study and Application of the Reinforcement of Prestressed Concrete Cylinder Pipes with External Prestressed Steel Strands. Applied Sciences, 9(24), 5532. https://doi.org/10.3390/app9245532





