Advanced NDT Methods and Data Processing on Industrial CFRP Components
Abstract
:1. Introduction
2. Materials and Methods
2.1. CFRP Plates and Component
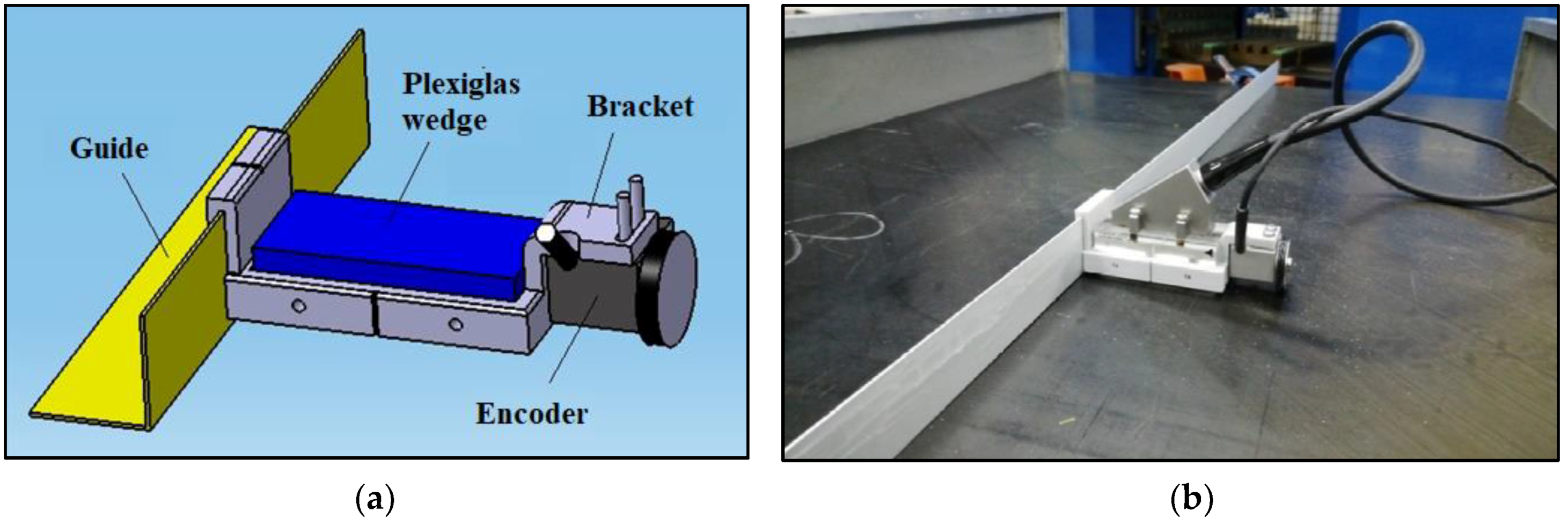
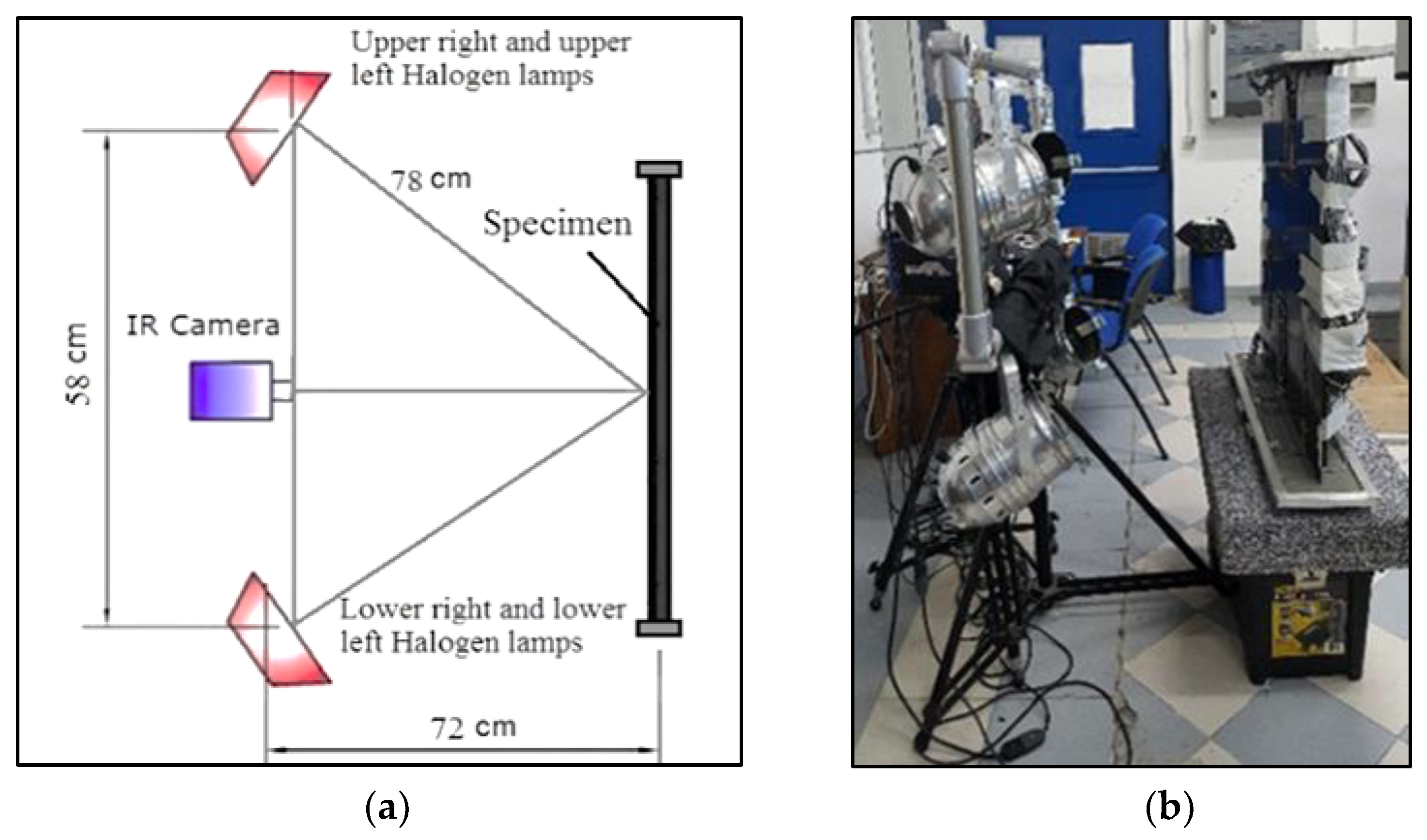
2.2. Experimental Setup and Inspection Methods
3. Data Processing and Image Elaboration Procedures
3.1. Reference Absolute Contrast
3.2. Custom Mapping Optimization in Terms of Thermal Contrast Measurements
4. Defect Mapping on Real Component and Results Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gholizadeh, S. A Review of Nondestructive Testing Methods of Composite Materials. Procedia Struct. Integr. 2016, 1, 50–57. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Venegas, P.; Guerediaga, J.; Vega, L.; Molleda, J.; Bulnes, F.G. Infrared Thermography for Temperature Measurement and Nondestructive Testing. Sensors 2014, 14, 12305–12348. [Google Scholar] [CrossRef]
- Galietti, U.; D’Accardi, E.; Palumbo, D.; Tamborrino, R. A Quantitative Comparison among Different Algorithms for Defects Detection on Aluminum with the Pulsed Thermography Technique. Metals 2018, 8, 859. [Google Scholar] [CrossRef]
- Dattoma, V.; Giancane, S.; Panella, F.W. Fatigue damage in notched GFR composites with thermal and digital image measurements. In Proceedings of the ECCM15—15th European Conference on Composite Materials, Venice, Italy, 24–28 June 2012. [Google Scholar]
- Danesi, S.; Salerno, A.; Wu, D.; Busse, G. Cooling down thermography: Principle and results for NDE. Proc. SPIE 1998, 3361, 266–274. [Google Scholar] [CrossRef]
- Wang, Z.; Tian, G.; Meo, M.; Ciampa, F. Image processing based quantitative damage evaluation in composites with long pulse thermography. NDT E Int. 2018, 99, 93–104. [Google Scholar] [CrossRef]
- Almond, D.P.; Angioni, S.L.; Pickering, S.G. Long pulse excitation thermographic nondestructive evaluation. NDT E Int. 2017, 87, 7–14. [Google Scholar] [CrossRef]
- Usamentiaga, R.; García, D.F.; Molleda, J. Real-time adaptive method for noise filtering of a stream of thermographic line scans based on spatial overlapping and edge detection. J. Electron. Imaging 2008, 17. [Google Scholar] [CrossRef]
- Sun, J. Analysis of data processing methods for pulsed thermal imaging characterization of delaminations. Quant. InfraRed Thermogr. J. 2013, 10, 9–25. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Bendada, A.; Maldague, X. Image and signal processing techniques in pulsed thermography. GESTS Int. Trans. Comput. Sci. Eng. 2005, 22, 89–100. [Google Scholar]
- Balageas, D.L.; Chapuis, B.; Deban, G.; Passilly, F. Improvement of the detection of defects by pulse thermography thanks to the TSR approach in the case of a smart composite repair patch. Quant. InfraRed Thermogr. J. 2010, 7, 167–187. [Google Scholar] [CrossRef]
- Rajic, N. Principal component thermography for flaw contrast enhancement and flaw depth characterization in composite structures. Compos. Struct. 2002, 58, 521–528. [Google Scholar] [CrossRef]
- Bates, D.; Smith, G.; Lu, D.; Hewitt, J. Rapid thermal nondestructive testing of aircraft components. Compos. Part B Eng. 2000, 31, 175–185. [Google Scholar] [CrossRef]
- Scarponi, C.; Briotti, G. Ultrasonic detection of delaminations on composite materials. J. Reinf. Plast. Compos. 1997, 16, 768–790. [Google Scholar] [CrossRef]
- Jeong, H. Effect of void on the mechanical strength and ultrasonic attenuation of laminated composites. J. Compos. Mater. 1997, 31, 277–292. [Google Scholar] [CrossRef]
- Kaczmarek, H. Ultrasonic detection of damage in CFRPs. J. Compos. Mater. 1995, 29, 59–95. [Google Scholar] [CrossRef]
- Scarponi, C.; Briotti, G. Ultrasonic technique for the evaluation of delaminations on CFRP, GFRP, KFRP composite materials. Compos. Part B Eng. 2000, 31, 237–243. [Google Scholar] [CrossRef]
- Dattoma, V.; Carofalo, A.P.; Palano, F.; Panella, F.W. ND Testing Advances on CFRP with Ultrasonic and Thermal Techniques. In Proceedings of the ECCM16—16th European Conference on Composite Materials, Seville, Spain, 22–26 June 2014. scopus Code 109290. [Google Scholar]
- Giorleo, G.; Meola, C. Comparison between pulsed and modulated thermography in glass-epoxy laminates. NDT E Int. 2002, 35, 287–292. [Google Scholar] [CrossRef]
- Dattoma, V.; Nobile, R.; Panella, F.W.; Saponaro, A. NDT Thermographic Techniques on CFRP Structural Components for Aeronautical Application. Procedia Struct. Integr. 2018, 8, 452–461. [Google Scholar] [CrossRef]
- Ruiju, H.; Schmerr, L.W. Characterization of the system functions of ultrasonic linear phased array inspection systems. Ultrasonics 2009, 49, 219–225. [Google Scholar] [CrossRef]
- Xiao, K.; Qiang, W.; Dong, H. Post Signal Processing of Ultrasonic Phased Array Inspection Data for Nondestructive Testing. Procedia Eng. 2012, 43, 419–424. [Google Scholar] [CrossRef]
- Dattoma, V.; Nobile, R.; Panella, F.W.; Pirinu, A.; Saponaro, A. Optimization and comparison of ultrasonic techniques for NDT control of composite material elements. Procedia Struct. Integr. 2018, 12, 9–18. [Google Scholar] [CrossRef]
- Susa, M.; Maldague, X.; Boras, I. Improved Method for Absolute Thermal Contrast Evaluation Using Source Distribution Image (SDI). Infrared Phys. Technol. 2010, 53, 197–203. [Google Scholar] [CrossRef]
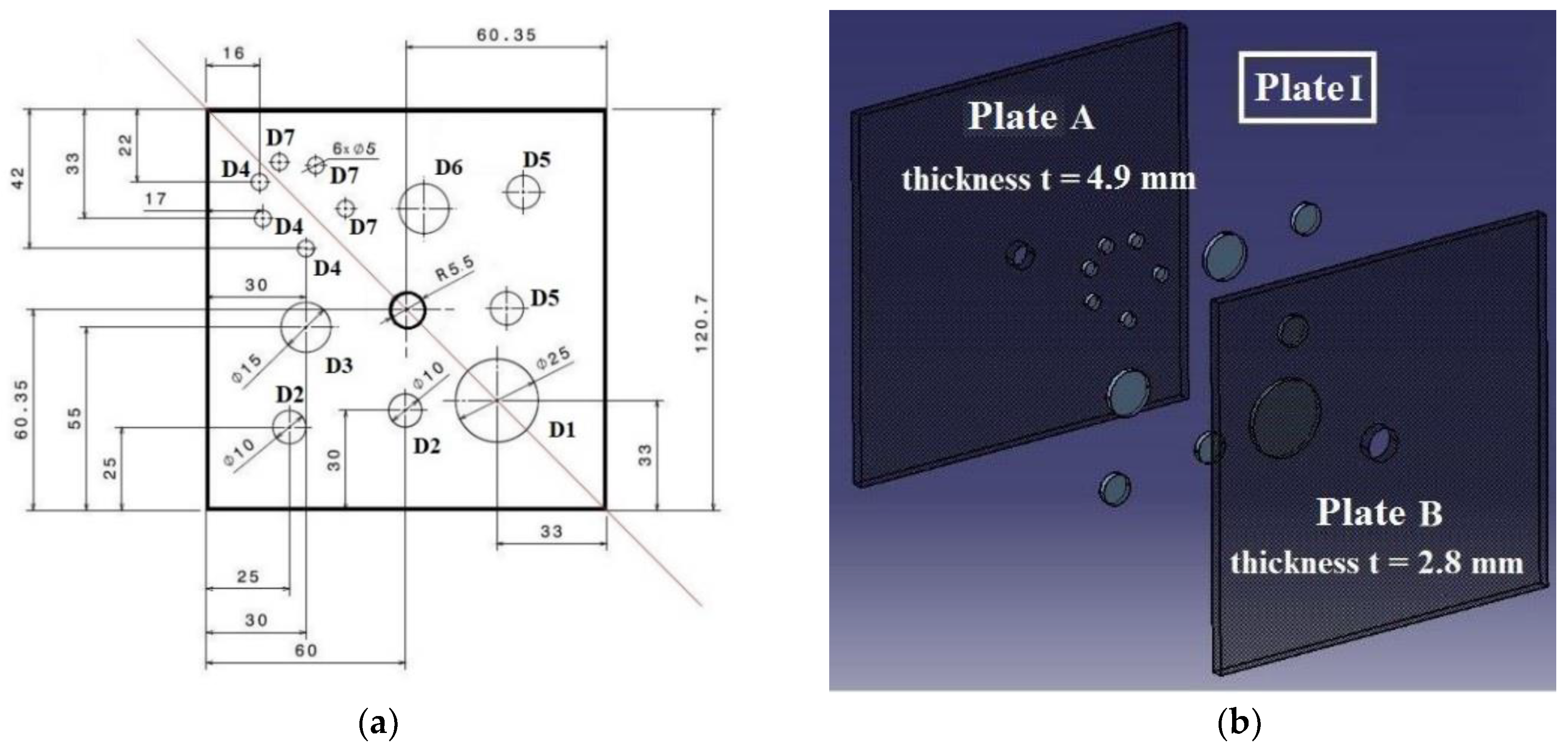
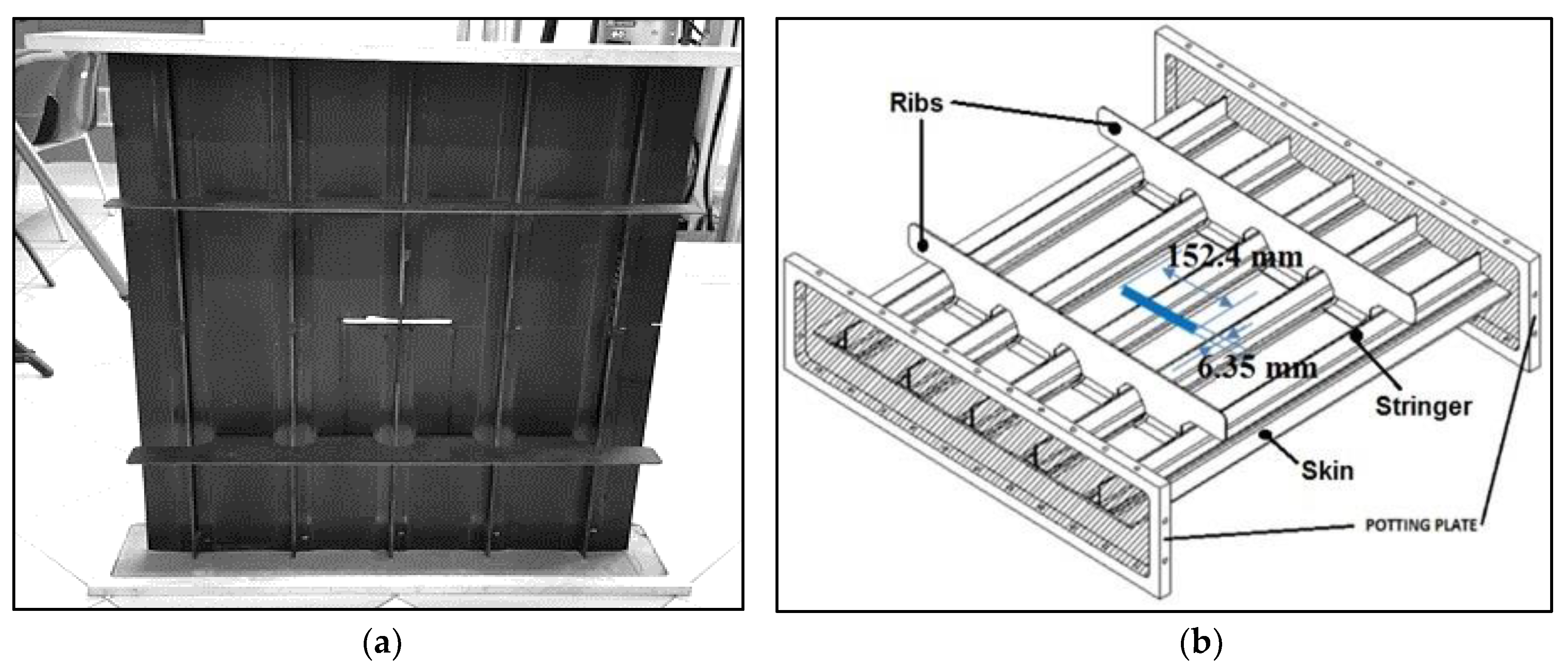

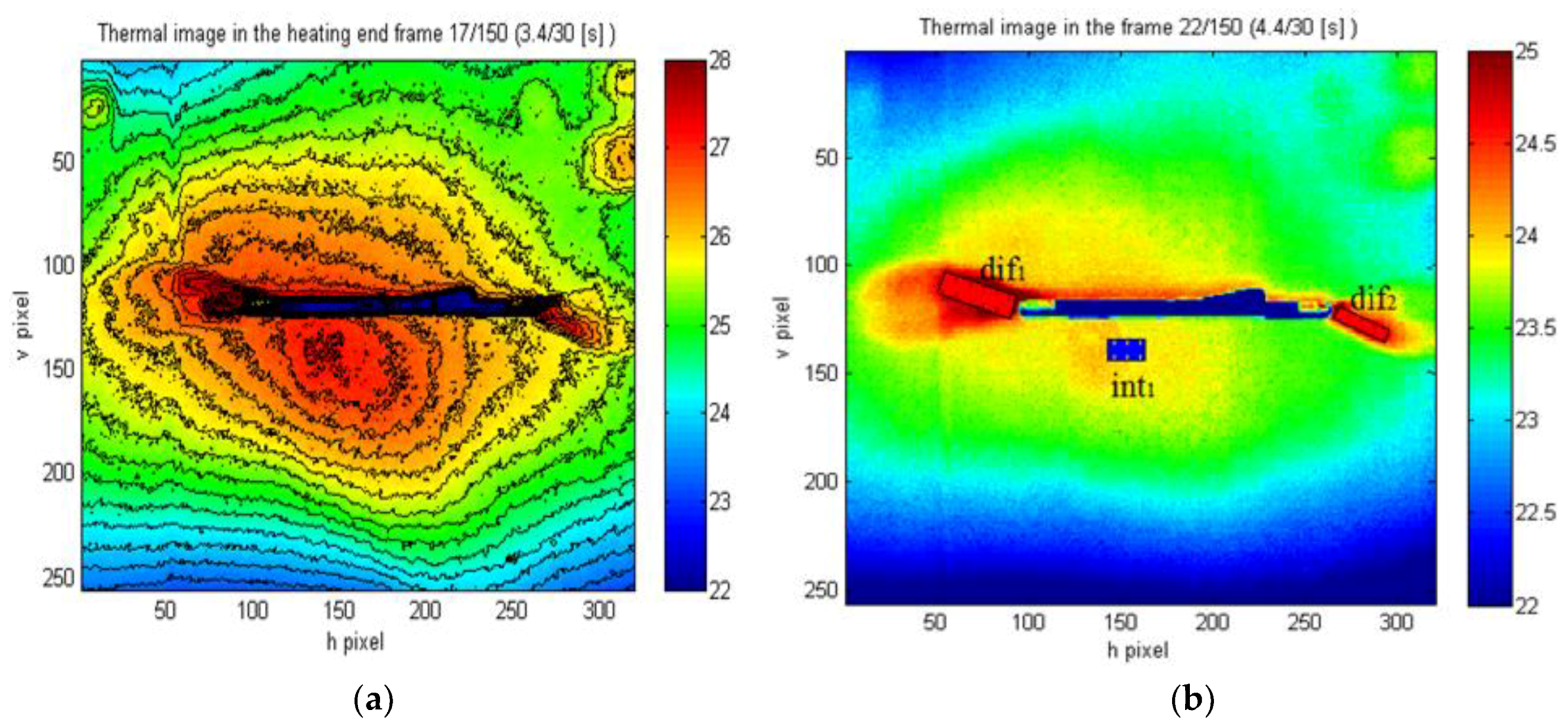
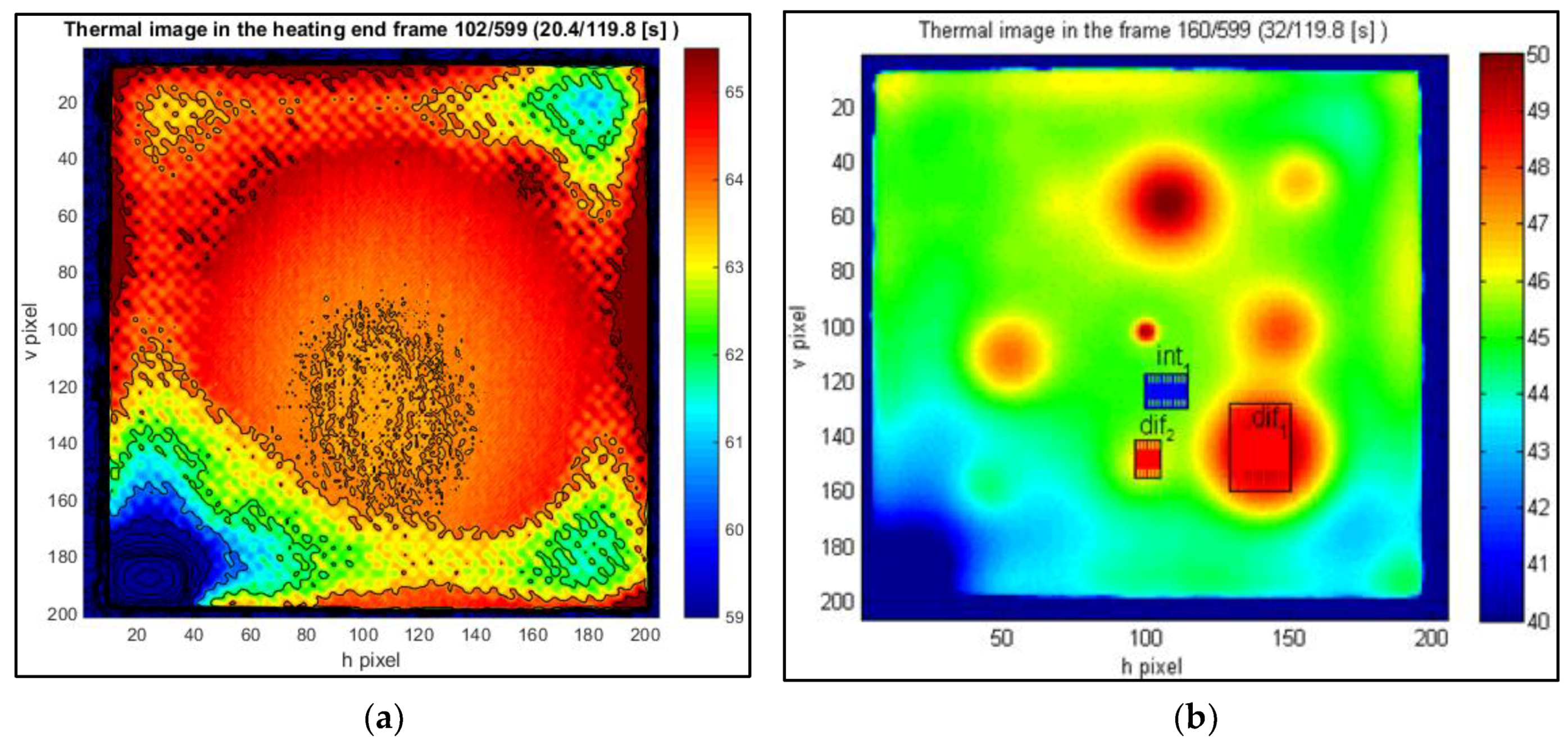
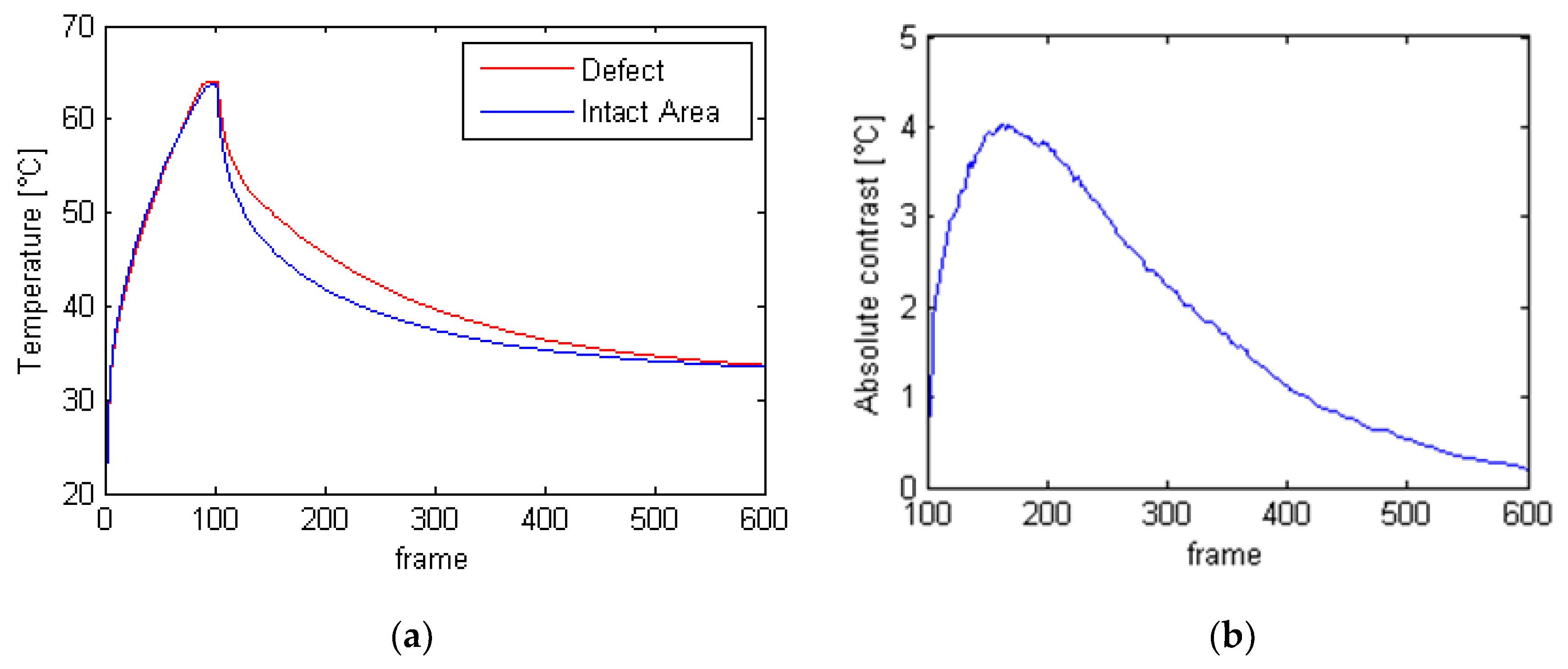

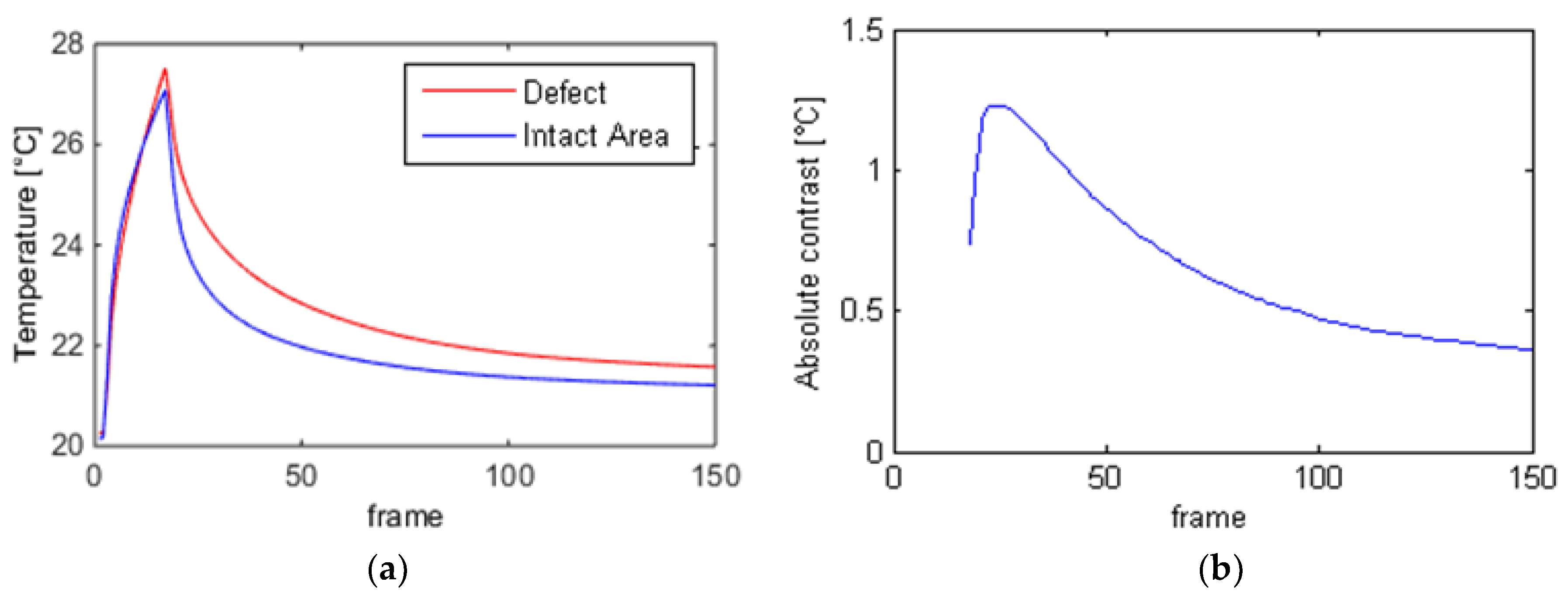
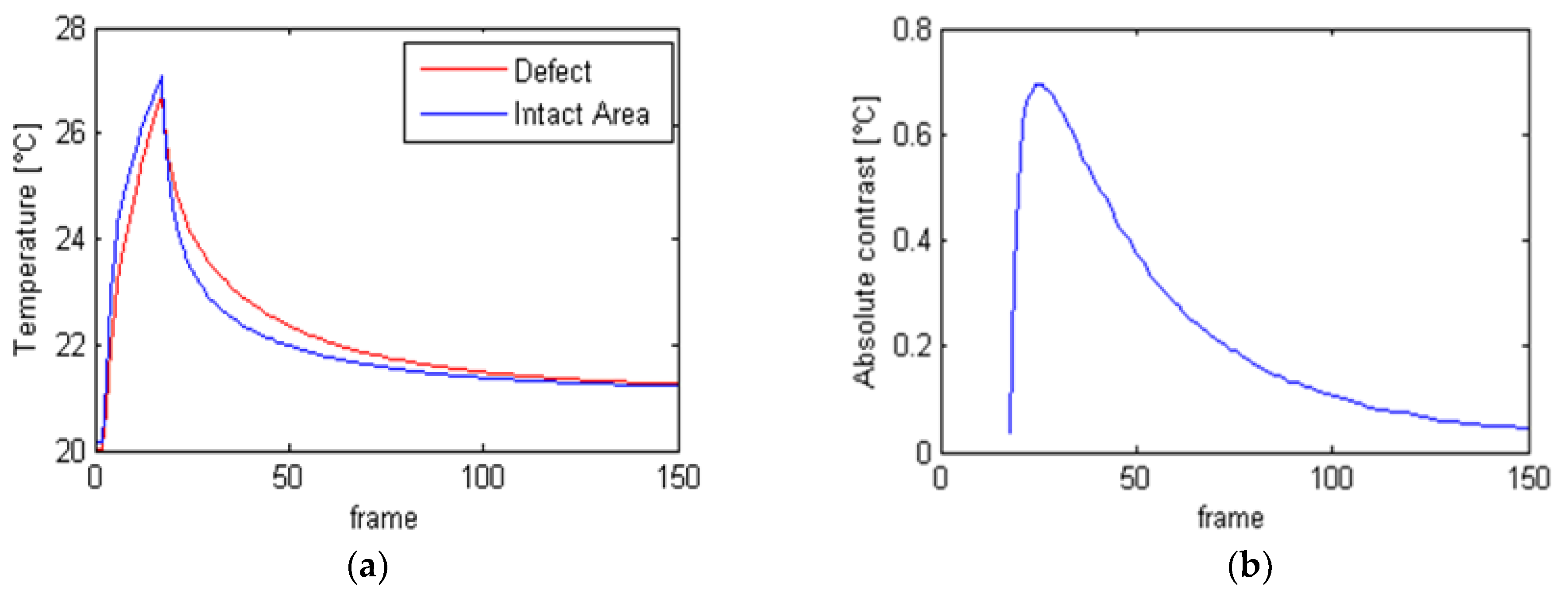
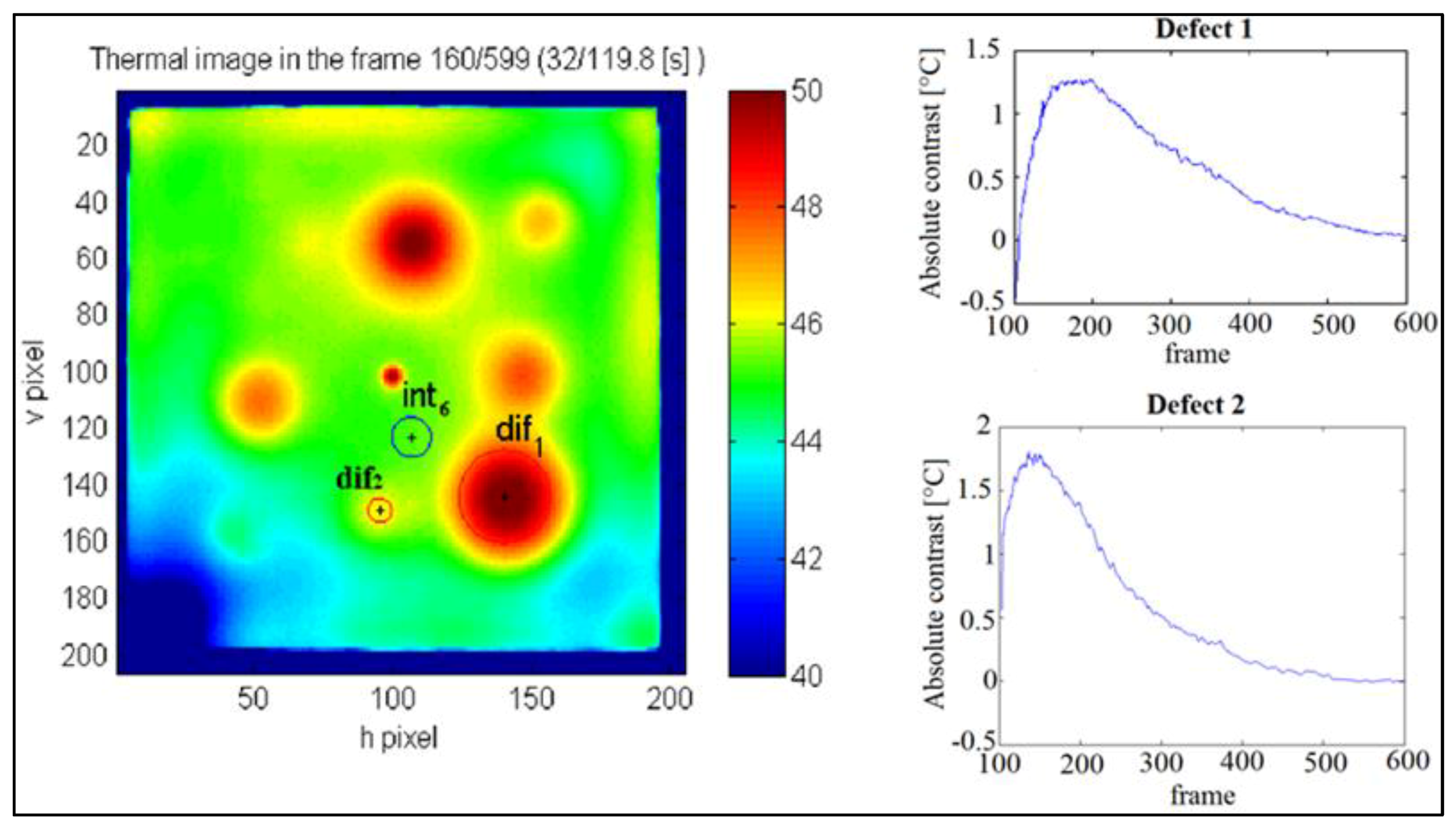
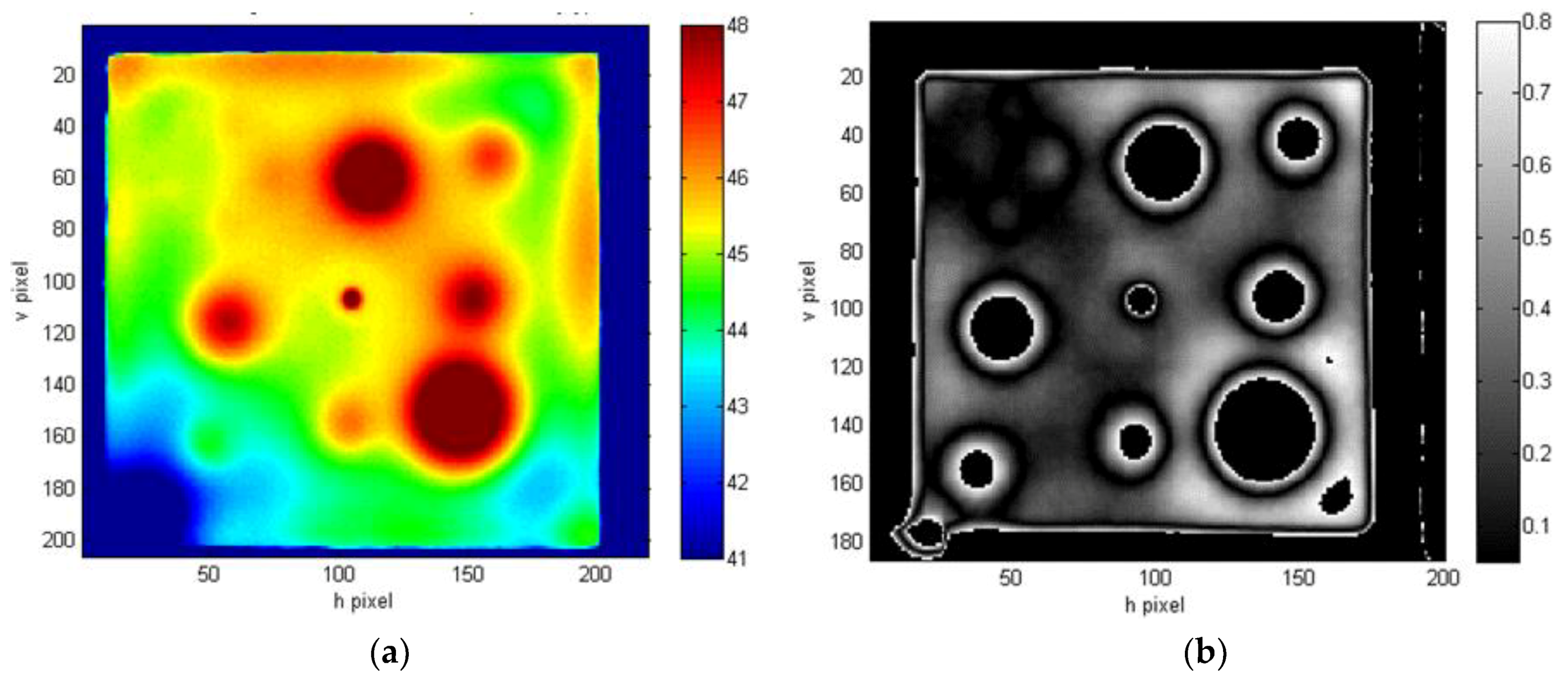
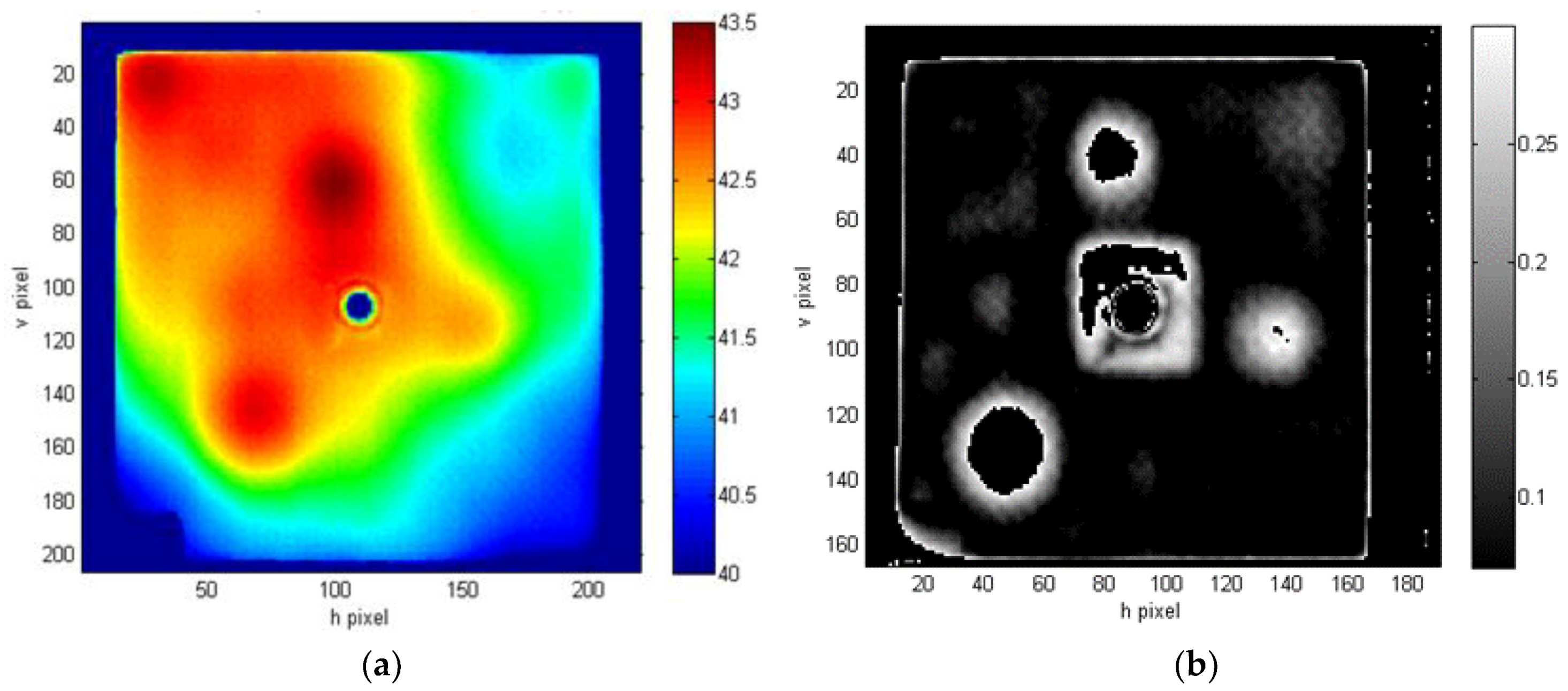
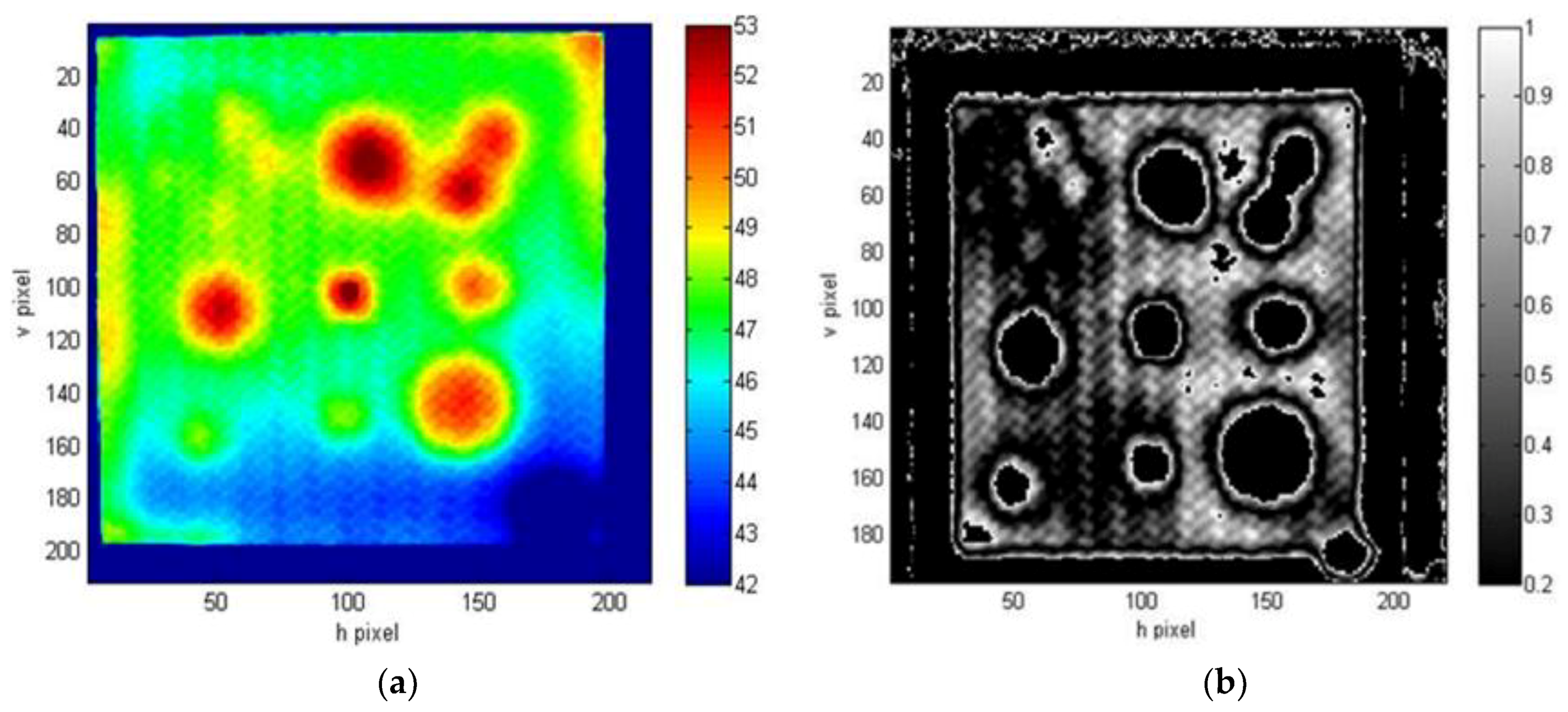
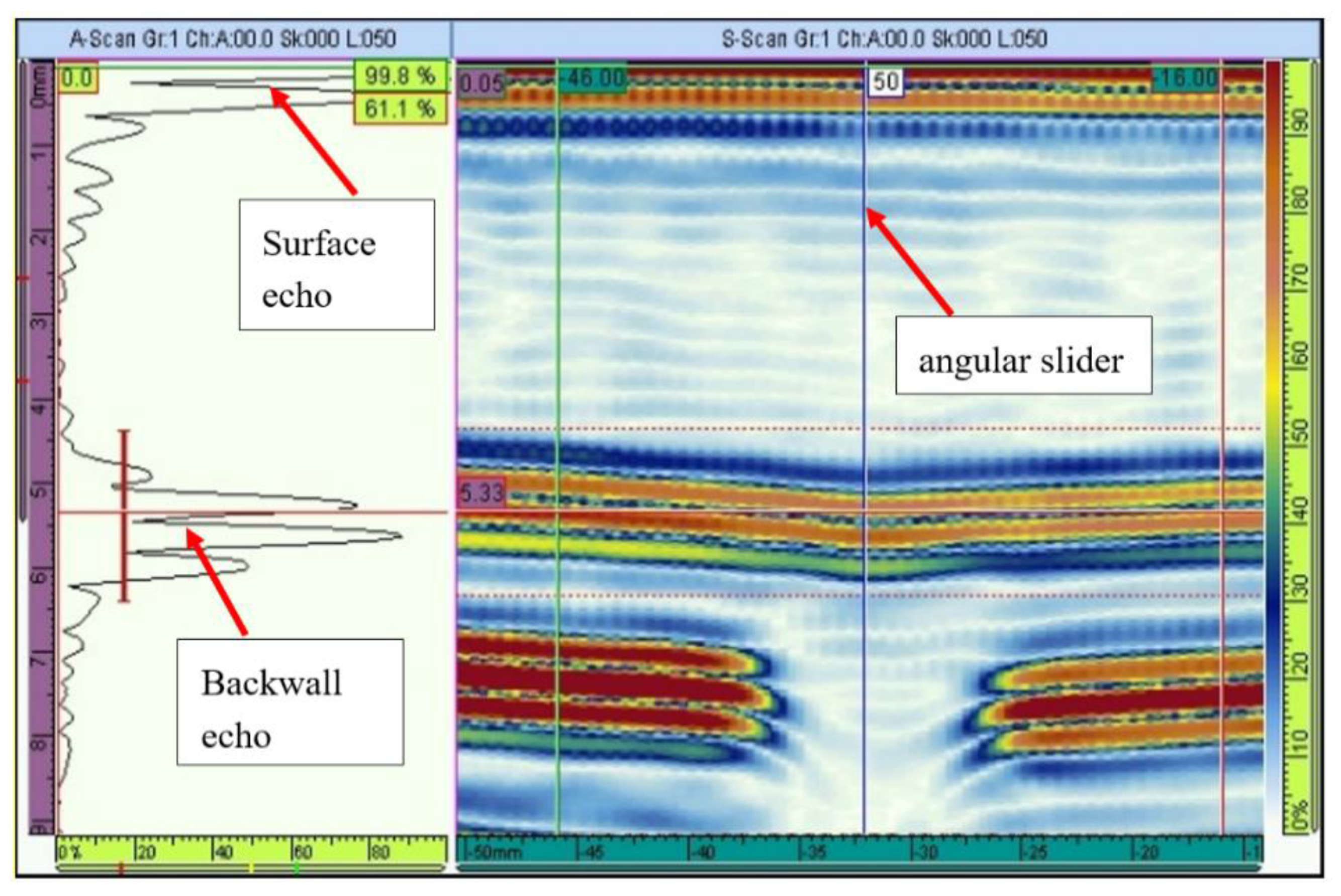
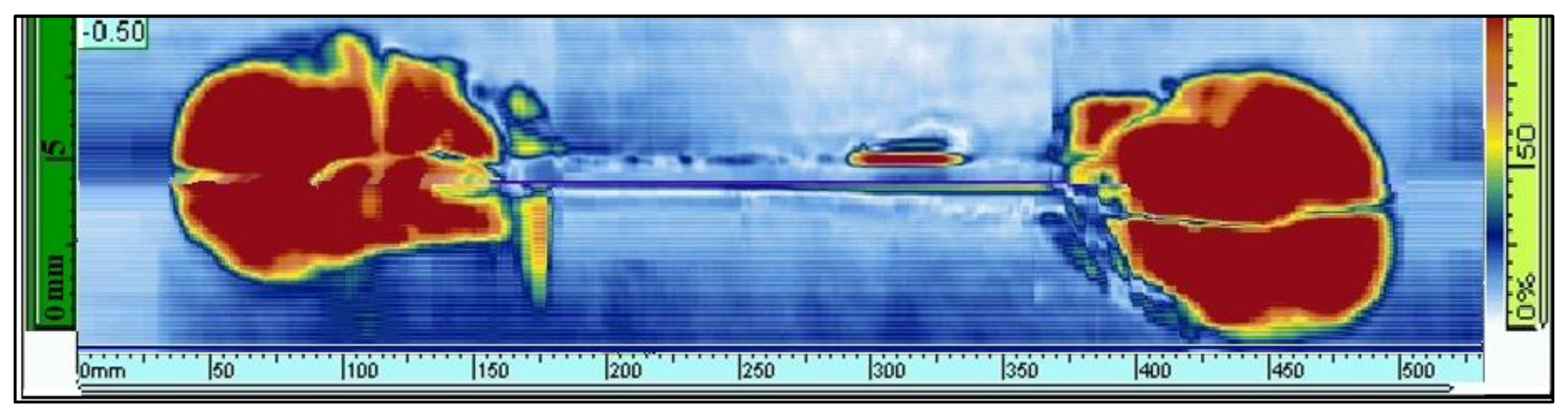
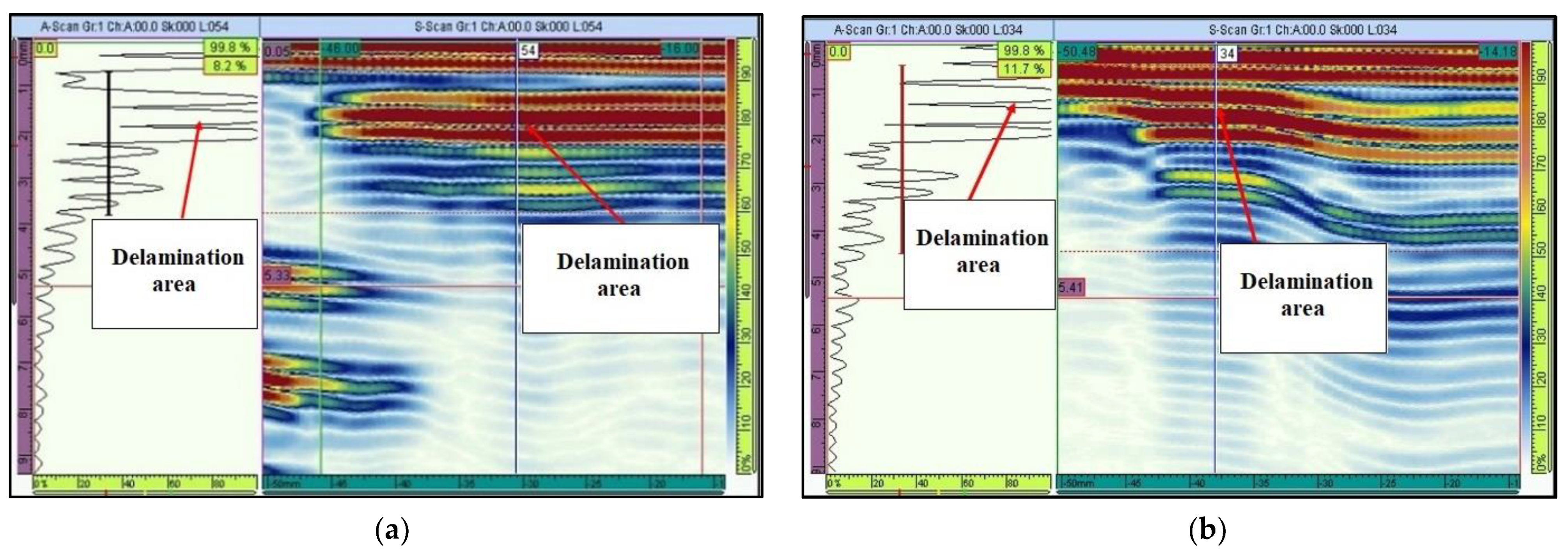


| Defect Nomenclature | D1 | D2 | D3 | D4 | D5 | D6 | D7 |
| N. Defect in Plate I | 1 | 2 | 1 | 3 | 2 | 1 | 3 |
| N. Defect in Plate II | 1 | 2 | 1 | 3 | 2 | 1 | 3 |
| Diameter (mm) | 25 | 10 | 15 | 5 | 10 | 15 | 5 |
| Thickness (mm) | 0.6 | 0.6 | 0.6 | 0.6 | 1.2 | 1.2 | 1.2 |
| Carbon Fiber | |
| Density (g/cm3) | 1.65 |
| Areal weight (g/m2) | 240 |
| Thermal conductivity coefficient (W/mK) | ~ 15 |
| Epoxy Resin | |
| Density (g/ml) | 1.14–1.16 |
| Young Modulus (MPa) | 2900–3100 |
| Ultimate stress (MPa) | 75–80 |
| Ultimate strain (%) | 8.5–9 |
| Thermal conductivity coefficient (W/mK) | ~ 0.22 |
| Part Component | Sub-Part Component | Material | Lamina Thickness (mm) | N° Plies | Stacking Sequence |
|---|---|---|---|---|---|
| Skin | Skin 1 | CFRP | 0.186 | 20 | [45/90/−45/−45/45/90/0/-45/45/0] S |
| Skin 2 | CFRP | 0.186 | 24 | [45/90/0/0/−45/−45/45/90/0/−45/45/0] S | |
| Stringer | CFRP | 0.186 | 12 | [45/90/0/0/−45/0] S | |
| Rib | CFRP | 0.208 | 12 | [45/0/−45/90/45/0] S |
| CFRP Specimen | Side | N° Test | Frame Rate (Hz) | Heating Time (s) | Acquisition Time (s) | Total Frames |
|---|---|---|---|---|---|---|
| 1 | 5 | 20 | 100 | 500 | ||
| A | 2 | 5 | 30 | 100 | 500 | |
| Plate I | 3 | 5 | 40 | 100 | 500 | |
| 4 | 5 | 12 | 200 | 1000 | ||
| B | 5 | 5 | 15 | 200 | 1000 | |
| 6 | 5 | 20 | 250 | 1250 | ||
| 7, 8 | 5 | 12 | 200 | 1000 | ||
| Plate II | A, B | 9, 10 | 5 | 15 | 200 | 1000 |
| 11, 12 | 5 | 20 | 250 | 1250 |
| N° Test | Frame Rate [Hz] | Heating Time [s] | Acquisition Time [s] | Total Frames |
|---|---|---|---|---|
| 1 | 5 | 20 | 100 | 500 |
| 2 | 5 | 30 | 100 | 500 |
| 3 | 5 | 40 | 100 | 500 |
| 4 | 5 | 12 | 200 | 1000 |
| 5 | 5 | 15 | 200 | 1000 |
| CA_MAX of Defect 1 (°C) | CA_MAX of Defect 2 (°C) | ||||
|---|---|---|---|---|---|
| Intact Zones (px2) | Area 20 × 30 | Area 10 × 15 | Area 8 × 14 | Area 5 × 10 | |
| 14 × 12 | 4.02 | 4.72 | 0.9 | 0.99 | |
| 21 × 30 | 4.87 | 5.57 | 1.74 | 1.83 | |
| 14 × 20 | 3.73 | 4.43 | 0.62 | 0.72 | |
| 19 × 20 | 3.41 | 4.11 | 0.37 | 0.46 | |
| 13 × 20 | 3.84 | 4.55 | 0.75 | 0.84 | |
| Mean Value | 3.97 | 4.68 | 0.87 | 2.00 | |
| Standard Deviation | 0.55 | 0.55 | 0.52 | 0.55 | |
| CA_MAX (°C) | |||||
|---|---|---|---|---|---|
| Rectangular Area (px*px) | Circular Area (Ø px) | ||||
| Intact Zone Size | Def. 1 20 × 30 | Def. 2 8 × 14 | Intact Zone Size | Def. 1 Ø 33 | Def. 2 Ø 9 |
| 14 × 12 | 4.02 | 0.9 | 14 | 1.27 | 1.81 |
| 21 × 30 | 4.87 | 1.74 | 30 | 0.91 | 1.49 |
| 14 × 20 | 3.73 | 0.62 | 20 | 1.11 | 1.68 |
| 19 × 20 | 3.41 | 0.37 | 16 | 2.38 | 2.90 |
| 13 × 20 | 3.84 | 0.75 | 18 | 1.69 | 2.12 |
| Mean Value | 3.97 | 0.87 | 1.47 | 2.00 | |
| Standard Deviation | 0.55 | 0.52 | 0.58 | 0.55 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dattoma, V.; Panella, F.W.; Pirinu, A.; Saponaro, A. Advanced NDT Methods and Data Processing on Industrial CFRP Components. Appl. Sci. 2019, 9, 393. https://doi.org/10.3390/app9030393
Dattoma V, Panella FW, Pirinu A, Saponaro A. Advanced NDT Methods and Data Processing on Industrial CFRP Components. Applied Sciences. 2019; 9(3):393. https://doi.org/10.3390/app9030393
Chicago/Turabian StyleDattoma, Vito, Francesco Willem Panella, Alessandra Pirinu, and Andrea Saponaro. 2019. "Advanced NDT Methods and Data Processing on Industrial CFRP Components" Applied Sciences 9, no. 3: 393. https://doi.org/10.3390/app9030393
APA StyleDattoma, V., Panella, F. W., Pirinu, A., & Saponaro, A. (2019). Advanced NDT Methods and Data Processing on Industrial CFRP Components. Applied Sciences, 9(3), 393. https://doi.org/10.3390/app9030393






