Wireless Channel Models for Over-the-Sea Communication: A Comparative Study

Abstract

Over the past few years, the modeling of wireless channels for radio wave propagation over the sea surface has drawn the attention of many researchers. Channel models are designed and implemented for different frequencies and communication scenarios. There are models that emphasize the influence of the height of the evaporation duct in the marine environment, as well as models that deal with different frequencies (2.5, 5, and 10 GHz, etc.) or the impact of various parameters, such as antenna height. Despite the increasing literature on channel modeling for the over-the-sea marine environment, there is no comprehensive study that focuses on key concepts that need to be considered when developing a new channel model, characteristics of channel models, and comparative analysis of existing works along with their possible improvements and future applications. In this paper, channel models are discussed in relation to their operational principles and key features, and they are compared with each other in terms of major characteristics and pros and cons. Some important insights on the design and implementation of a channel model, possible applications and improvements, and challenging issues and research directions are also discussed. The main goal of this paper is to present a comparative study of over-the-sea channel models for radio wave propagation, so that it can help engineers and researchers in this field to choose or design the appropriate channel models based on their applications, classification, features, advantages, and limitations.

1. Introduction

Wireless channels for the radio wave propagation over the sea surface are different from the usual channels used in ground-to-ground wireless communication due to the unique nature of the marine environment. For example, neither the refraction of wave propagation, nor the effect of the evaporation duct is present in the ground-to-ground scenarios. Existing approaches to the modeling of over-the-sea channels vary with frequencies, technology used, and implementation scenario. While some approaches used millimeter waves and wide band technology, others used frequencies such as 1.9, 2, and 10 GHz, etc. Some approaches considered vessel-to-vessel mobile communication on the sea. Ship-to-ship and ship-to-shore wireless communication scenarios were also considered and implemented.

So far, there are two preliminary minor approaches [1,2], that briefly describe a few models of channels for over-the-sea communication; however, with inadequate analysis and limited discussion on various models, applications, future improvements, and research directions. Readers can prompt references [1,2] for further details. Typically, the over-the-sea wave propagation environment can be divided into two types: One is “near the sea surface” and the other is “hundreds of meters above the sea surface or higher.” In the near the sea surface environment, the transceiver platform remains close to the sea surface. For example, communication between a ship and a base station is maintained ashore. Figure 1 shows such a scenario when communication occurs near the sea surface.

Studies conducted in [3] show that for modeling channels in such an environment, special attention is paid to refraction caused by a possible evaporation duct, as well as a direct ray and sea surface-reflected ray. An evaporation duct affects frequencies around 1 GHz and higher. In principle, an evaporation duct is formed due to variation in humidity across the air and sea boundary. This phenomenon is rather dominant in all kinds of seas. For example, the evaporation duct remains prevalent in equatorial and tropical sea regions in 90% of cases. Therefore, to design any channel model for the near-the-sea environment, careful considerations should be given to the effects of the evaporation duct. Moreover, there may be possible communication scenarios where the propagation distance exceeds 3000 m. In this case, a two-ray propagation model of a direct ray and a reflected ray cannot predict the interference zeroes. To deal with this, one should consider a three-ray propagation model consisting of a direct ray, a reflected ray from the sea surface, and a refracted ray caused by the evaporation duct. Two- and three-ray models of wave propagation will be further discussed in the upcoming sections of the paper.

In a scenario where wireless transmission takes place hundreds of meters above the sea surface, the transceiver is deployed on an airborne device or platforms, such as unmanned aerial vehicles (UAVs) or any other aircrafts. It is possible for the elevated duct in the troposphere region to cause an attenuation of the signal and affect air-to-ground communication through the sea wave propagation. The elevated duct is an atmospheric canal that consists of a layer with highly dense air [4]. It starts and remains at high altitudes and mainly affects transmission with a very high frequency. Figure 2 shows a scenario for wireless transmission taking place hundreds of meters above the sea surface.

As shown earlier in Figure 1, in near-the-sea transmission, the signal mainly propagates through the evaporation duct. Compared to such an environment, the airborne propagations must pass through the evaporation duct layer, the air layer (free space layer), and the elevated duct layer, as shown in Figure 2.

In this paper, a comprehensive and comparative study of over-the-sea channel models for radio wave propagation is presented. Our study can help researchers and engineers select an appropriate channel model based on their application. The main contributions of the paper are as follows:

• Theoretical key concepts needed to understand channel models for over-the-sea radio wave propagation are briefly discussed.
• Channel models are examined in relation to their operational principles and key features.
• Channel models are classified based on their propagation type and the mobility of their transceiver platform.
• Channel models are compared with each other in terms of major characteristics, pros, and cons.
• The possibility of unique and novel applications and some possible future improvements of the channel models are addressed.
• Key challenging issues for modeling a wireless channel for over-the-sea communication and the research directions to design a new channel model are discussed.

The rest of the paper is organized as follows. In the following section (Section 2), key concepts related to wireless channel modeling for over-the-sea communication are discussed. In Section 3, existing channel models are classified. In Section 4, existing channel models are reviewed by functional principle, basic operation, and distinctive characteristics. In Section 5, the qualitative comparison of channel models is summarized and discussed. In Section 6, the possibility of unique and novel applications of the channel models is discussed and some possible future improvements of the channel models are presented. In Section 7, we discuss important challenging issues for modeling a wireless channel for over-the-sea communication and the research directions that can be helpful for researchers if they intend to design a new channel model. Finally, the paper is concluded in Section 8.

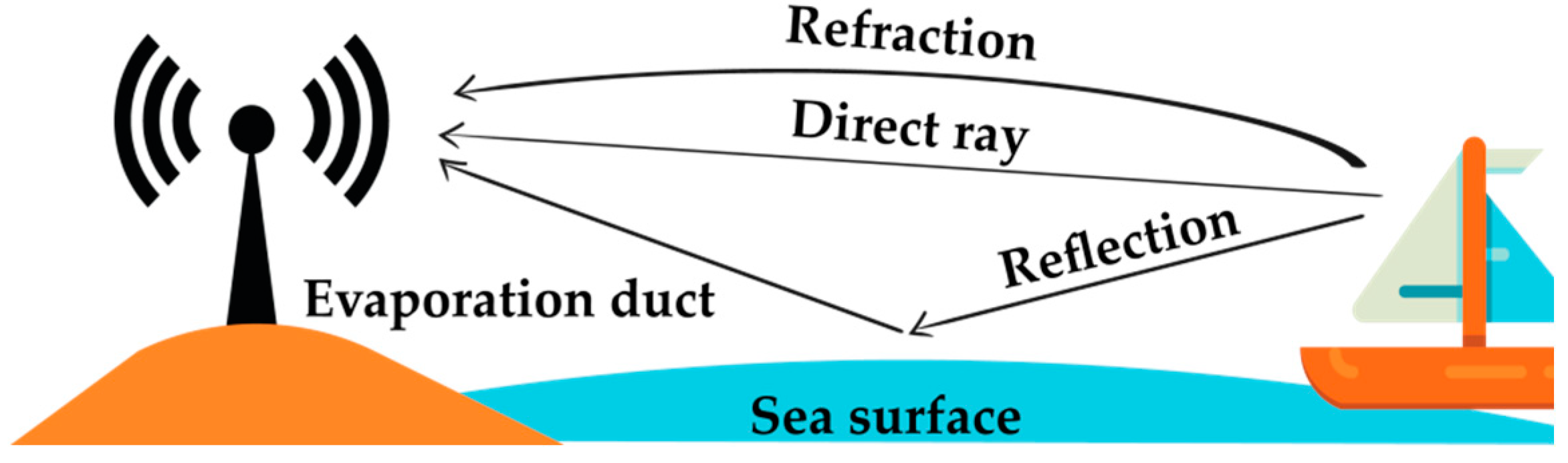
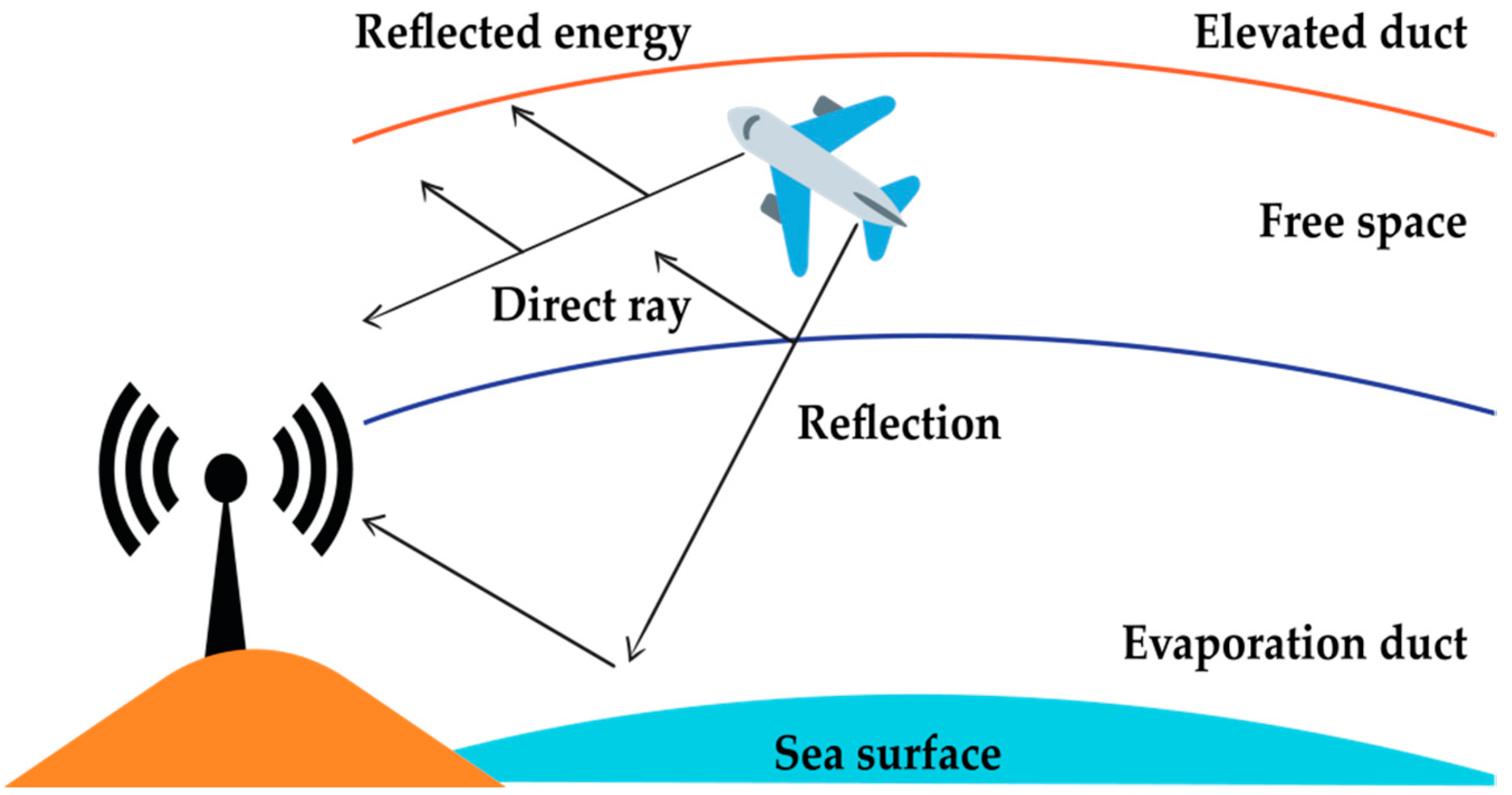
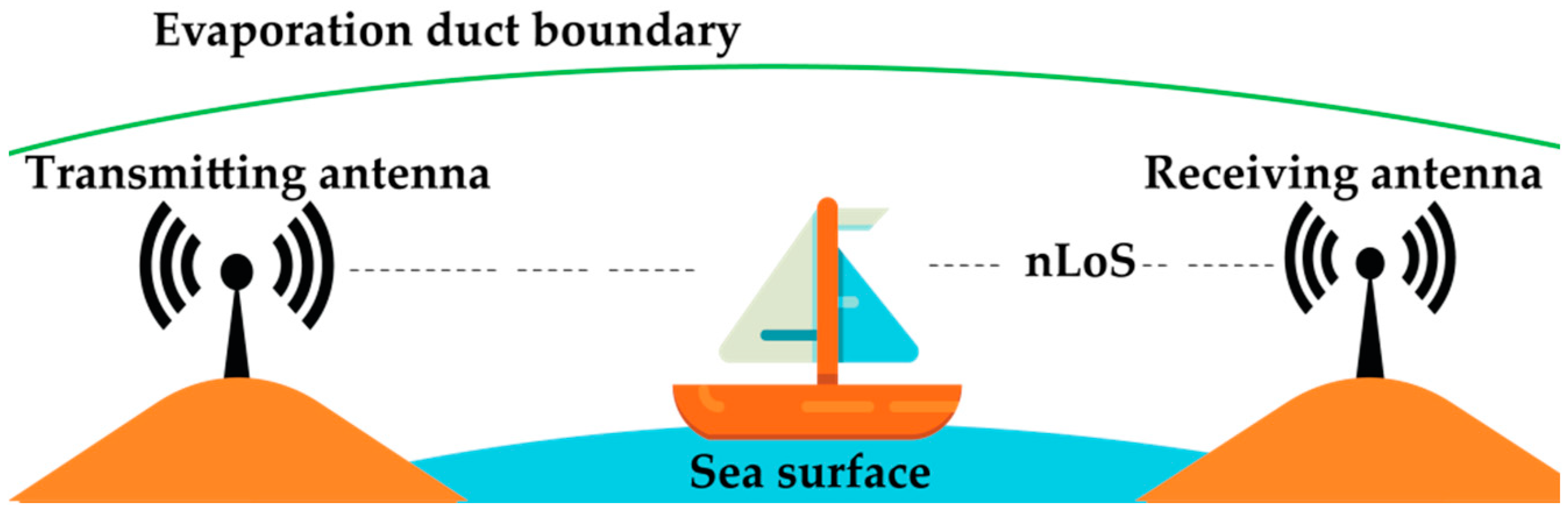
2. Key Concepts in Modeling Over-the-Sea Channels

To design a channel model, a calculation of the propagation loss (PL) is highly important. It is also necessary to derive the correct fading margin. A radio channel designed for over-the-sea wireless communication may experience frequency selective fading, slow fading, and/or fast fading. Small-scale fading is due to the random phases and amplitudes of various multipath components. In addition, inter-symbol interference (ISI) causes signal blurring. Mathematically, it is possible to model multipath propagation using the channel impulse response [5]. Power delay profile (PDP) is also another important term to take care of. It is the intensity of a signal as a function of time delay in the multipath channel. Channel delay spread parameters, such as mean excess delay, maximum excess delay, and root mean-squared delay that can be extracted from PDP, are important features for designing a channel for a wireless transmission system. Moreover, atmospheric ducts play a prime role in influencing existing channel models. Before delving into the channel models, some important terms will be briefly discussed for the convenience of readers.

2.1. Important Definitions and Parameters

Multipath propagation: A propagation that causes radio signals to propagate through two or more paths toward an antenna placed at the receiving end can be regarded as multipath propagation. Multipath can be caused by refraction, reflection, atmospheric ducts, etc. Figure 3 presents a very basic diagram of multipath wave propagation.

Line-of-sight (LoS) propagation: Electromagnetic radiations tend to transmit/travel from a source to a destination along a direct path. This inherent characteristic of electromagnetic (EM) propagation, without any obstacle between the transmitting and receiving antenna, is known as LoS propagation. It is possible that the waves or rays may be refracted, diffracted, and reflected in their path. Figure 4 presents a scenario of LoS propagation.

Non-Line-of-Sight (nLoS) and beyond nLoS: Non-LoS (nLoS) is the transmission of radio signals along a path that has a physical object in its way and is partially obstructed due to this. Signals are partially obstructed in the innermost Fresnel zone. The Fresnel zone is an ellipsoidal region between the transmitting and receiving antennas. The region is widely used to comprehend the strength of the waves transmitted by the sending and receiving antennas. In addition, this zone is useful for estimating whether any obstruction close to the line connecting the transmitter and receiver causes significant interference.

Beyond nLoS (bLoS) is a special case of propagation, where the nLoS propagation confronts links blocked by a huge terrain, an earth bulge, etc., due to transmission over long distances. Figure 5 and Figure 6 show the nLoS and bLoS propagations, respectively.

Slow and fast fading: Slow fading is caused when the delay requirement of the application is relatively less than the coherence time of the channel. In contrast, fast fading occurs when the delay requirement of the application is greater than the coherence time.

Rayleigh and Rician fading: Rayleigh fading is a statistical model that indicates the effect of the propagation environment on radio signals. According to this model, a signal passing through the transmission medium (communication channel) will fade in a random manner. In addition, this fading will occur in accordance with the Rayleigh distribution, which is the radial component of the summation of two uncorrelated Gaussian random variables. A radio propagation anomaly can occur due to partial cancellation of radio signals by themselves. The stochastic model of this phenomenon is regarded as Rician fading.

Frequency selective fading: It is a radio propagation distortion that occurs due to partial cancellation of radio signals. If there is a signal propagating through two different paths, one of them will change. In this kind of fading, the bandwidth of the signal is larger than the coherence bandwidth.

Fade margin: The additional margin in the average received signal power, which is required to achieve a certain level of availability for a given modulation and bit error rate performance in real-time channels, can be considered as a fading margin. Slow fading and fast fading that occur due to changes in the height of the evaporation duct have the safest value that can apply to both. This is considered as a complete fading margin.

Delay spread: It is possible for multipath components to reach their destination at different times. The delay spread can be defined as the difference between the arrival time of the first and last multipath components.

Inter-symbol interference (ISI): Suppose the symbol period is T_s and the delay spread is T_m. If T_s < T_m, then ISI occurs. It is a kind of signal distortion that causes one symbol to interfere with subsequent ones.

Power delay profile (PDP): Using the PDP, we can find out the intensity of a signal received through a multipath channel. It is usually measured as a function of time. PDP can be used to measure some other channel parameters, such as delay spread, etc. It is possible to obtain PDP using the spatial average of the complex baseband channel impulse response.

Mean excess delay: The mean excess delay and root mean square (RMS) delay spread are multipath channel parameters that can be extracted from PDP. The exact first moment of PDP can be denoted as mean excess delay. Mathematical formulation of mean excess delay is as follows:

$$\overline{\tau }= \frac{{\sum }_k{\alpha }_k^2{\tau }_k}{{\sum }_k{\alpha }_k^2},$$

(1)

where α_k is the magnitude of the received signal, and τ_k is the delay between the occurrences of the received multipath waveform after receiving the initial impulse. The RMS delay spread can be defined as the square root of the second central moment of the power delay profile. RMS delay spread (σ_τ) can be formulated as:

$${\sigma }_{\tau }= \sqrt{{\tau }^{\overline{2}}-{(\overline{\tau })}^2}$$

(2)

Atmospheric ducts: Atmospheric ducts are horizontal layers in the lower atmosphere. In atmospheric ducts, radio signals are ducted and they always tend to follow the curvature of the Earth. Waves are bent by atmospheric refraction in such scenarios. The characteristics and formation of such ducts are subject to refractivity of a certain atmosphere. There are four types of atmospheric ducts. They were classified into four types based on their formation process and refractivity profile. These are: (a) evaporation ducts, (b) surface-based ducts, (c) elevated ducts, and (d) surface ducts.

A surface duct mainly occurs due to temperature inversion. The evaporation duct is a special version of the surface duct. The evaporation duct is a refractive layer that results from the rapid decrease in humidity level with altitude. This takes place above water bodies where the atmospheric surface layer exists. Elevated ducts are formed due to a high-density air layer. They commence at a high altitude and continue upwards. These ducts primarily affect very high frequencies. Bending of a ray like this occurs under super-refractive conditions. Surface-based ducts occur when the air in the upper layer is warm and dry compared to the air on/near the surface. Figure 7 shows a transceiver platform in an elevated evaporation duct.

2.2. Measurements and Modeling of Propagation Loss

PL can be defined as the reduction in the power density of an electromagnetic wave, as the propagation takes place through space [6]. From a basic point of view, the channel measurements require a transmitter and a receiver. Figure 8 shows the fundamental setup for radio wave propagation measurements using continuous waves. Amplification of the output from the signal generator is performed before the transmitting antenna sends out a signal. As the signal passes through an over-the-sea channel, the signal is captured by the receiving antenna. After that, the signal is filtered and displayed on a spectrum analyzer. Depending on the application, directional or omni-directional antennas can be used. The PL can be estimated using the following simple equation:

$$PL=P_T+G_{Amp}+G_{AntT}+G_{AntR}-L_f-P_R$$

(3)

where $P_T$ is the output power of the signal generator, $G_{Amp}$ is the gain of the amplifier, $G_{AntT}$ is the gain of the transmitting antenna, $G_{AntR}$ is the gain of the receiving antenna, $L_f$ is the loss of filter, and $P_R$ is the power indicated in the spectrum analyzer.

For free space and clear air conditions, the PL can be modeled using the free space loss (FSL) model [6] using the following equation, where $L_{FSL}$ is the free space loss in dB, d is the propagation distance, and f is the frequency:

$$L_{FSL}= -27.56+ lo{g}_{10}\left(f\right)+ 20lo{g}_{10}\left(d\right)$$

(4)

The reflection of the sea surface is very important to design a channel for the ocean environment. When it exists alongside with the LoS (direct ray) component, the PL can be measured using the two-ray model [6] as follows:

$$L_{2-ray}=-10lo{g}_{10}\{{\left(\frac{\lambda }{4\pi d}\right)}^2[2\sin \left(\frac{2\pi h_t{h}_r}{\lambda d}\right){]}^2\},$$

(5)

where $L_{2-ray}$ is the two-ray path loss in dB, $h_t$ is the height of the transmitter, $h_r$ is the height of the receiver, and $\lambda$ is the wavelength.

A simplified three-ray model [7] with an assumption that a horizontally homogeneous evaporation duct layer exists can be expressed as a simplified three-dimensional model [7]:

$$L_{3-ray}= -10lo{g}_{10} \{{\left(\frac{\lambda }{4\pi d}\right)}^2{[2\left(1+\Delta \right)]}^2\}$$

(6)

with

$$\Delta =2\sin \left(\frac{2\pi h_t{h}_r}{\lambda d}\right) \sin \left[\frac{2\pi \left(h_e-h_t\right)\left(h_e-h_r\right)}{\lambda d}\right]$$

(7)

where $h_t$ and $h_r$ are the heights of transmitter and receiver in meters, respectively, $h_e$ is the effective duct height, $\lambda$ is the wavelength in meters, and d is the propagation distance in meters.

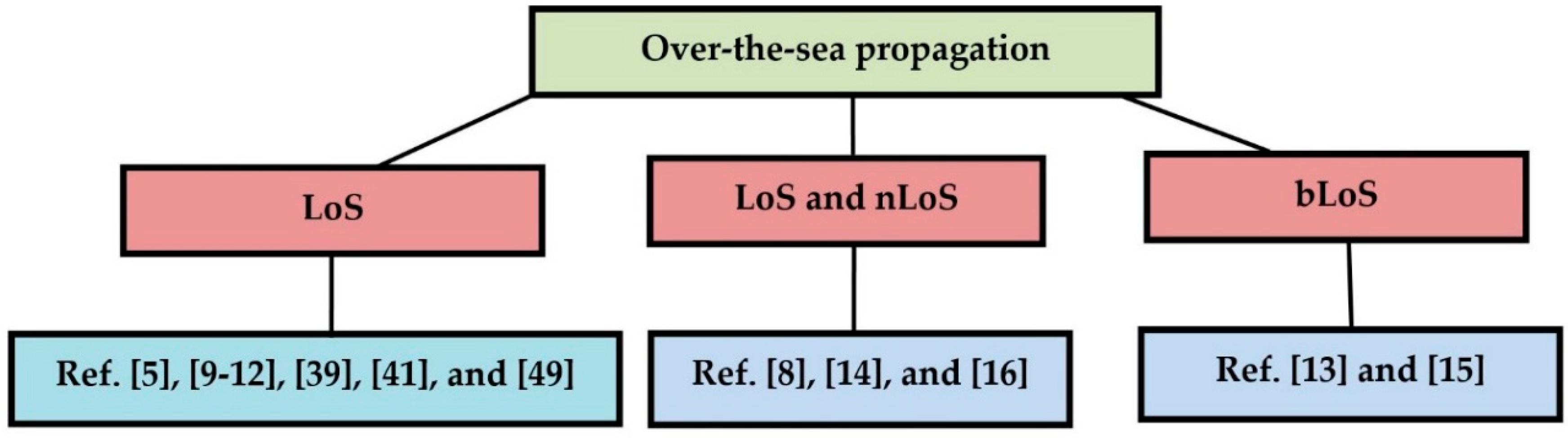
3. Classification of Over-the-Sea Channel Models

In this section, we will classify the existing over-the-sea wave propagation channel models reported so far in the literature. First, we will discuss the existing works briefly, and the channel models will be classified on the basis of the wireless LoS, nLoS, and bLoS wave propagations. Then, the channel models will be classified by considering the mobility of the transmitter and/or receiver.

In [8], an approach was adopted to characterize a wideband channel for over-the-sea wave propagation. It presents a statistical representation and measurements of wideband mobile radio channels at 1.9 GHz. In [9], the focus was to evaluate the effects of sea surface shadowing conditions on the marine communication channel, modeled by the finite difference time domain (FDTD) method, for UAVs deployed for maritime surveillance operations. The results of measurements that characterize radio channels at 2 GHz in the open sea were presented in [10]. The results were obtained using a mobile single-antenna ship-borne transmitter and a fixed dual antenna terrestrial receiver. In [11], by means of narrowband measurements, the propagation of radio waves was analyzed at 5 GHz, taking into account the LoS near the sea surface. The work presented in [12] presents an analysis of the propagation of millimeter waves for the over-the-sea environment. In [5], a multipath channel model for radio wave propagation over the sea surface was designed for ship-to-ship and ship-to-shore wireless communication. An analytical expression for the effective width of the trapping beam of a transmitter for over-the-sea transmission was derived in [13]. Reference [14], published this year, adopts mathematical formulations to calculate the complete fading margin of the South China Sea. References [15,16] placed an effort into finding the optimal frequency and antenna height for radio wave propagation in the evaporation duct. In [17], Mehrima et al. presented a LoS ship-to-ship wireless channel model for over-the-sea communication. Wu et al. collected and analyzed the three-dimensional contour data of Diaoyu islands to generate a sea surface scenario, by using MATLAB, in order to design a channel model in that area [18]. Lee et al. presented measurement results for land-to-ship offshore wireless channel [19]. The frequency used in this channel model was 2.4 GHz. The model was investigated through the implementation of a narrowband channel measurement system between the quay and a sailing patrol boat. Cao et al. presented a channel model using a Ka-band [20]. In [21], Shi et al. used wideband technology to develop a channel model for UAVs to surface vessels.

There are also other works on channel modeling for the over-the-sea environment with a focus on the effect of the evaporation duct height in the marine environment [22,23], and different frequencies taking into account such parameters as signal strength or antenna height [24,25,26,27]. Among all the works that have been published so far to develop wireless channel models for the ocean environment, we decided to discuss and comparatively analyze [5,8,9,10,11,12,13,14,15,16,17,18,19,20,21], because the implementation scenario and frequency used in each of these works are different. In addition, they considered a wide range of channel option parameters (fading margin, delay spread, etc.). To the best of our knowledge, no such review paper exists that has yet discussed and comparatively analyzed the existing channel models for the over-the-sea marine environment.

In Section 2.1, LoS, nLoS, and bLoS wave propagations are briefly introduced with their example scenarios. One of the basic and crucial factors of wireless channel modeling is how the radio links propagate between the transmitter and receiver. A LoS between the transmitting and receiving antennas is desirable, but it is not possible to have a clear LoS always in the sea environment. It can be crowded with ships, affected by unique seasonal and weather effects, and affected by huge barriers like islands, rocks, etc. These may cause reflections of the propagated radio waves. This is where multipath wave propagation techniques play an important role by exploiting nLoS and bLoS wave propagation methods. As mentioned earlier, nLoS wave propagation describes a radio link that does not have a clear LoS and that have obstructions in the way. The effect of an obstruction can be negligible to a complete barrier.

If the obstruction is smaller than the incident wavelength, it is negligible. Obstructions having the same size of the incident wave length cause diffraction and go to the other end with minor attenuation. If an obstruction is larger than the incident wavelength, the signal is obstructed in varying degrees depending on the materials of the obstructions and their characteristics. Similar scenarios are taken into account in the channel models exploiting nLoS wave propagation techniques. bLoS wave propagation is an especial case of nLoS propagation and is suitable for the applications where very long-distance communication is necessary, and where communication links may get obstructed by huge terrains, rocks, islands, etc. Modeling channels for bLoS propagation over the sea is a great challenge and very few works have been reported to work upon bLoS propagation. Most of the channel models in the literature fall under the classification of LoS propagation. References [5,9,10,11,12,17,19,21] are the channel models that support LoS propagation only. There are channel models that support both LoS and nLoS propagations. Channel models presented in [8,14,16] are such kind of models. Channel models presented in [13,15] support bLoS propagation. The fifteen channel models discussed in this paper are classified based on the LoS, nLoS, and bLoS propagations in Figure 9.

Classifying the channel models based on the mobility of the transmitter and receiver is very important because of the Doppler effect. It refers to the apparent shifts in the frequency of the signals due to the motion of the transmitter or receiver or both. This may result in channel fading. Many of the existing channel models dealt with the issues and calculated fade margin for the fading caused by the Doppler effect. They are classified on the basis of the three scenarios found in the literature:

(a)

Both the transmitter and receiver are mobile ([10,11,14,15,17,18,21]);

(b)

Both the transmitter and receiver are fixed ([16]); and

(c)

The receiver is fixed but the transmitter is mobile ([5,8,9,12,19]).

4. Channel Models for Over-the-Sea Wave Propagation

As discussed earlier, approaches for over-the-sea channel modeling differ mainly in frequency, technology used, and implementation scenario. In this section, some existing channel models will be extensively reviewed.

4.1. Wideband Channel Modeling for Over-the-Sea Wave Propagation

The channel model was developed for use in the Aegean Sea, Greece, for a mobile vessel-to-vessel communication system. The frequency used in this channel model [8] is 1.9 GHz. The focus of the present study lies in the delay profile that is nothing more than a normalized plot of received power against delay, if the pulse is transmitted and faces erosion. The large-scale characterization of the measured environments was carried out using the long-distance path loss model [6]. The path loss equation for the channel model [8] is:

$$PL\left(d\right)=PL\left(d_0\right)+10n\log (\frac{d}{d_0})\left(dB\right)$$

(8)

where n is the attenuation factor, $PL\left(d_o\right)$ is the measurement of path loss at a particular location at a distance of $d_o$ from the transmitter (TX), where d is used to denote the distance of interest. For small-scale characterization, a time dispersion analysis along with a time and space domain analysis were performed. Figure 10 shows a mobile vessel-to-vessel communication scenario for the channel model.

The outstanding part of the work in [8] is that it presents authentic real-time data, based on real life implementations. The main problem of this model was the consideration of multipath effects, which arise only because of coastline hills. Multipath effects caused by fluctuating sea waves were ignored. It has a high delay for the nLoS propagation links and the system is much too dependent on the global positioning system (GPS).

4.2. Marine Communication Channel Modeling Based on the Finite Difference Time Domain (FDTD)

The work presented in [9] aims to gain a more complete understanding of the communication channels in which UAVs are deployed for low-level maritime operations. The channel modeling scheme was also presented using the FDTD method [28]. It also made a great effort to assess the effects of shadowing conditions on the sea surface on marine communication channels. The authors developed a 2-D EM simulator using a modified Pierson–Moscowitz (PM) spectral model [29]. The simulator was used to produce multipath scattering by generating a random sea surface in a deep water location. After analyzing the data retrieved from the simulation results, it was found that the simulation results gave a generalized path loss exponent, standard deviation, mean excess delay, and RMS delay as the functions of the frequency and the observable sea surface height for the stationary transmitter and receiver locations. Figure 11 presents a simple case scenario in which a UAV is communicating with a mobile vessel at a low-altitude, above-sea location.

It is inevitable to lose the aircraft in the sea or have vehicular collision due to the loss of communication [30]. To establish a safe operation protocol for airborne maritime surveillance operations, path loss and multipath effects [31,32] of the communication channels are key concerns. In the study presented in [9], the FDTD method is introduced to quantify the relevant parameters of maritime communication channels, through the simulation of the electromagnetic phenomena that contribute to the received waveform envelope in shadowing conditions. The work is mainly aimed at proposing a novel approach to the choice of a maritime communication channel. However, the authors claimed that the obtained research result is applicable to any sea-surface vehicle or sensor that uses wireless communications in the range of very high frequency (VHF) to 3 GHz. There are two reasons why the authors chose to apply the FDTD method for propagation analysis. One of them is the high accuracy of the method, and the other is the direct transient solution of Maxwell’s equations [33]. Using this method, Maxwell’s equations were solved through transient recursive calculations for EM analysis.

The EM simulation engine developed by the authors in this paper contained three segments. These are random generation of the sea surface, implementation of the FDTD algorithm for analyzing EM propagation, and channel modeling based on the transient simulation results. The channel was simulated as a 2-D cross section [9]. The sea surface in the simulation was implemented as a perfectly conducting boundary condition. The transient impulse response for a random sea surface was numerically estimated using FDTD simulation, Next, this process was repeatedly used for multiple sea surfaces with different heights. These repetitive processes were undertaken to produce a significant set of population data.

Friis’ free space path loss equation [34] was used as a foundation for signal attenuation for wireless transmission. It can be described as:

$$L_s\left(d\right)={\left(4\pi d/\lambda \right)}^2$$

(9)

where d is the physical distance between the TX and receiver (RX), and λ is the wavelength. A critical parameter for modeling wireless channels over the sea surface area is the path loss exponent. This parameter is critical in the system design process. The basic path loss calculation [9] can be formulated as:

$$L_p\left(d\right)=L_s\left(d_o\right)+10nlog\left(\frac{d}{d_o}\right)+X_f,$$

(10)

where $L_s\left(d_o\right)$ is the measurement of the path loss at a particular location, which is at a distance of $d_o$ from TX [35]. Here d is used to denote the distance of interest, and n is the path loss exponent. $X_f$ denotes fast fading effects, which are also Gaussian random contributors. The attenuation of typical transmission confronts was characterized by the perfection and accuracy of knowledge about the path loss exponent. This knowledge provided a universal means of characterizing such attenuation, regardless of the specific features of physical communication channels.

The multipath characteristics of the wireless communication channel over the sea surface are also of interest in [9]. Signals at TX and RX locations with variable physical pathways experience different propagation delays. Regardless of the carrier frequency of a wireless communication channel, ISI is a key consideration in the realistic bandwidth that the channel can support. Therefore, characterizing a wireless communication channel required particular attention to the mean excess delay. The loss exponent, standard deviation, mean excess delay, and RMS delay were calculated for the development of the simulation engine to implement a new wireless channel model for UAVs to be deployed over the sea surface using equations (1–3) and (4) from [9]. For propagation analysis, it was necessary to generate a random sea surface, as the channel modeling was based on the sea surface environment. In [9], wireless channel simulation was performed using a PM spectra model representing a North Atlantic area with a deep sea. The authors chose this area because the fading effects are high and severe there. They chose the Frosen’s formulation [36] to represent the spectral content of the North Atlantic sea region as follows:

$$S_m \left(\omega \right)[4·{\pi }^3·H_s^2/T_z^4·{\omega }^5]·\exp \left(-16·{\pi }^3/T_z^4·{\omega }^4\right)$$

(11)

where $\omega$ is the frequency, $T_z$ is the wave period, and $H_s$ is the wave height. The wave period $T_z$ can be formulated as:

$$T_z= 2\pi \sqrt{m_0/m_1}$$

(12)

where $m_0 \mathrm{and} m_1$ are the spectrum moments, which are formulated as:

$$m_0=\frac{A}{4·B}$$

(13)

and

$$m_1=0.306·A / B^{3/4}$$

(14)

where A and B are constants that can be represented by equations (15) and (16), respectively, in which $g$ is the gravitational acceleration and V is the wind speed.

$$A=8.1· {10}^{-3}{g}^2$$

(15)

$$B= 0.74· {\left(g/V\right)}^4$$

(16)

The wave height $H_s$ can be represented by:

$$H_s=0.21· \frac{V^2}{g}$$

(17)

After determining the spectral content of the waves with their certain desired height, the authors in [9] derived a transient displacement using Fourier analysis. Using the study and formulation, conducted in [37], the physical wavelength L_d, based on the period (T_p) of a single wave, can be formulated as:

$$L_d=\left(\frac{g}{2\pi }\right)· T_p$$

(18)

The channel modeling in [9] is highly suitable for creating UAVs for ocean surface area-based communications, but it has some limitations. The entire modeling process was carried out using the 2-D approximation, but it would be more realistic if the 3-D approximation was used. In addition, the simulations of channels were conducted taking into account the sea surface up to 12 m. Simulations could be performed with a wider range. It was also claimed in [9] that the channel modeling is well suited for other marine surface vessel communication systems. However, they do not indicate what kind of communication systems are suitable, other than the deployment of UAVs, especially when UAVs have high mobility and there are other types of communication systems where the nodes are stationary.

4.3. Experimental Multipath Delay Profile of Mobile Radio Channels Over the Sea at 2 GHz

The path loss model and measurement results for over-the-sea wave propagation were already studied at short distances in [8], which we have described in Section 4.1. However, the work [10] showed two campaigns and well extended the work presented in [8]. These two campaigns have a short-distance over-the-sea wave propagation (ranging up to 15 km) and a long-distance over-the-sea wave propagation (ranging up to 45 km). Channel properties such as probability density function (PDF), cumulative distribution function (CDF), RMS delay spread, and mean excess delay were presented for both of the campaigns. The measured PDFs were characterized by using a three-term Gaussian model. For a short-range campaign, a fixed dual-antenna channel sounder receiver was positioned in the harbor area. A high-speed craft contained a mobile single-antenna transmitter. For the long-range campaign, a fixed dual-antenna channel sounder receiver was placed on the coastline area close to the shore in an open sea. A research vessel contained a mobile single-antenna transmitter in this case. A simple channel model scenario, where the receiving antenna is fixed on shore, and the mobile transmitter is in the vessel is presented in Figure 12.

After analyzing all the experimental results, it was found that the PDF of the mean excess delay and RMS delay in short-range measurements, adopted from the harbor area via an omni-directional transmitting antenna, are Gaussian-like or contain a peak that allowed the authors of [10] to model these channel parameters using the three-term Gaussian model. It was found that the reflection from the environment is too weak and very close to the LoS in the delay domain, when considering the long-range measurements taken from the coastline with a directional transmitting antenna. The main drawback of this paper is the lack of specific measurements for the specular and diffuse components of multipath propagation. Moreover, no specific path loss model has been elaborated in the measurement techniques.

4.4. Modeling of Near-the-Sea Mobile Radio Wave Propagation at 5 GHz

The paper presented in [11] investigated near-sea-surface LoS radio wave propagation at 5 GHz. The investigation was conducted using narrowband measurements. The results obtained for the received signal strength were compared with the FSL model [6] and the two-ray path loss model [6]. The results and analysis carried out in [7] show that in the maritime environment considered in [11] there is an evaporation duct layer. For this reason, a three-ray path loss model could predict the trend of the LoS signal strength variations at a larger propagation distance, by taking into account both the reflection from the sea surface and the refraction caused by the evaporation duct.

The measurement system in [11] used 5.15 GHz for continuous wave transmission with no interfering signal. At an approximate height of 3.5m above sea level, an omni-directional antenna was set up in a speedboat. The antenna was connected to a high-power amplifier and a signal generator. The base station was on shore. The LoS condition between the transmitter and the receiver was ensured because the receiver consisted of an identical omni-directional antenna. The measurements in [11] were carried out in the open sea area, located at the southeast coast of Singapore.

As discussed earlier, the results of the received signal strength, having a transmission distance of up to 10 km, were analyzed using the FSL model and the two-ray model in [11]. The PL can be predicted by the FSL model for radio wave propagation using equation (2). In addition, the two-ray path loss model can be obtained in equation (3). Both of these models (FSL and two-ray) were used in [11] for predicting the received signal strength in ideal conditions for the near-sea-surface radio wave propagation at 5.15 GHz. The results obtained from these two models were compared with the three-ray path loss model [7]. The authors in [11] assumed that the evaporation duct layer was horizontally homogeneous in their three-ray path loss model. The three-ray path loss model can be summarized by equations (4) and (5) in this paper.

In [11], a three-ray path loss model was implemented in a realistic maritime environment, with real-time experimental results obtained that show superiority over the two-ray and FSL models, especially when the propagation distance exceeds 2000 or 3000 m. The only parameter authors have taken into account is the signal strength. The error rate of the received signal could have been considered as another parameter.

4.5. Novel Maritime Channel Model Using Millimeter Radio Waves

A channel characterization technique was presented in [12] by implementing an approach based on ray tracing using 5G frequencies (35 and 94 GHz). The path loss, received power, RMS delay spread, and power delay profile were considered as key parameters for evaluating channel quality. A significant improvement in channel quality is observed because the mentioned frequency bands have the least attenuation for oxygen and water. Because the two-ray model [6] works only in short ranges and the FSL model cannot properly detect the behavior of a channel model designed especially for over-the-sea wave propagation, a new propagation model was designed.

The study authors have conducted is based on a tool called “Wireless InSite.” Readers can prompt [38] for further information on this tool. The tool was mainly used for ray tracing to make it easy to have a meticulous elaboration and description of the interaction of the rays in the marine environment. The results obtained on this simulator were later imported into MATLAB for further processing in order to develop a channel model that includes parameters such as path loss, received power, PDP, and RMS delay spread. The simulation was carried out for both frequency bands: 35 and 94 GHz.

The modified two-ray model that was presented in [12] can be represented as:

$$L_{m2-ray}=-20lo{g}_{10}\left\{\left(\frac{\lambda }{4\pi d}\right)\left|1+R exp\left(j\frac{\alpha 2\pi \Delta d}{\lambda }\right)\right|\right\}$$

(19)

where λ is the wavelength, d is the distance between the transmitter and the receiver, $\Delta d$ is the distance between two ray paths, and R is the reflection coefficient equal to –1, because the roughness considered is zero.

The best part in [12] is the introduction of a new model that could predict the last peak of path loss better than the existing two-ray model [6], without showing any extra peak. Therefore, the channel model developed in this study can be used to deploy 5G systems over the sea surface. The biggest flaw of the work in [12] is that the value of R (reflection coefficient) is considered to be –1, because the sea roughness is assumed to be zero, which is impractical.

4.6. Multipath Channel Model for Propagation of Radio Waves Over the Sea Surface

This paper presents an analytical approach to the development of a multipath channel model for the propagation of radio waves above the sea surface. A modeling approach can be applied to establish a channel impulse response consisting of a specular multipath, produced by a smooth sea surface, and a diffuse multipath, produced by a rough sea surface. The authors in [5] showed that a diffuse multipath can be obtained by gathering diffuse scattering energy together from the glistening surface. Methods for formulating impulse response curves for specular and diffuse multipath propagations were also discussed in detail in [5]. The introduced channel model in [5] is actually a modification of [39]. However, the modeling approach in [39] did not lead to their findings for over-the-sea radio wave propagation. Therefore, the authors in [5] modified the channel model in [39] using the Fresnel reflection coefficient of the sea, dipole antenna pattern at the transmitter and receiver, and parameters of sea states. Finally, the developed channel model was tested using various sea states, carrier frequencies, and transmission distances.

In [5], the ratio of the specular multipath and direct path can be expressed as:

$$\frac{Specular path Voltage}{Direct Path Voltage}= {\rho }_s\sqrt{G_{ant}}\left|{\mathrm{\Gamma }}_v\right|$$

(20)

where ${\rho }_s$ is the reflection coefficient of the specular point, $G_{ant}$ is the relative antenna gain, and ${\mathrm{\Gamma }}_v$ denotes the Fresnel reflection coefficient. What part of the incident angle is absorbed by the surface depends on this coefficient. The scattering of the rough sea surface causes diffuse reflection of the transmitted radio waves. The strength of diffuse reflection depends on the strength of the direct path signal. It can be calculated as:

$$\frac{Diffuse Voltage}{Direct Path Voltage}= \sqrt{\frac{1}{4\pi }{(\frac{R}{R_1{R}_{2 }})}^2\left(\frac{1}{{\beta }_0^2}\right)Fig\exp \left(\frac{{\beta }^2}{{\beta }_0^2}\right) dA·}{\rho }_{roughness}·\sqrt{G_{ant}}·\left|{\mathrm{\Gamma }}_v\right|·\sqrt{S_f}$$

(21)

where R is the direct path length to the receiver, $R_1$ is the path length from the transmitter to the differential path, and $R_2$ is the path length from the differential patch to the receiver. β is the surface tilt, β₀ is the mean square value of the surface of the region of interest, ${\rho }_{roughness}$ is the roughness factor, and $S_f$ is the shadowing factor.

The main problem of previous studies on modeling a multipath channel in an oceanic environment is that the models are based only on measured data and; therefore, are applicable to particular frequencies and geographical situations. The approach in [5] overcomes this problem, because it presented a theoretical multipath wireless channel modeling approach applicable to different carrier frequencies, transmission conditions, sea states, and transmission distances. The only drawback of this work is that the measurement results are not validated by any real-time implementation.

4.7. Channel Model for Surface Ducts

Effects of signal trapping by evaporation ducts can be utilized for bLoS links. To address this issue, Dine et al. developed a channel model representing a large-scale path loss model for surface ducts based on parabolic equation methods. In addition, the authors of [13] analyzed the delay spread and the angle of arrival of the duct using the method of ray optics (RO) [40]. The developed RO method allowed one to successfully deduce an expression for the trapped bandwidth of the transmitter to estimate the range of the beam width. The focused operating frequency was 5–15 GHz.

Authors of [13] developed a large-scale path loss model. This model was utilized for the prediction of slow fading and communication ranges, and can be expressed by the following equation:

$$PL=20\log \left(\frac{4\pi }{\left|u\left(x,z\right)\right|}\right)+10\log \left(r\right)-30\log \left(\lambda \right)$$

(22)

where λ is the wavelength, r is the range, u(x, z) is the reduced function, and x and z represent the horizontal and vertical axes, respectively. Additionally, the calculation of ray trajectories in ducts using the RO method was presented in [13]. This allowed for analyzing the delay spreads to find out the fading behavior of the channel. The ray paths were calculated using the following equation:

$$z=\frac{1}{2}\left(\frac{1}{n\left(0\right)}· \frac{dn}{dz}-\frac{1}{R_o}\right) x^2+ \theta x+h_t$$

(23)

where $\theta$ is the angle of the ray relative to the ground at the transmitter, $R_o$ is the radius of the Earth, n(0) is 1.005, and z is the vertical axis height. Finally, an analytical formula was presented for the trapped bandwidth (${\theta }_{max,min}^T$) within the duct as follows:

$${\theta }_{max,min}^T= \pm \sqrt{2\left(\frac{1}{n\left(0\right)}· \frac{dn}{dz}-\frac{1}{R_o}\right)\left(h_t-\mathsf{\delta }\right)}$$

(24)

It actually represents the range of the beam width that can be trapped depending on the channel conditions.

No calculation regarding the complete fading margin is presented in [13]. Again, not describing the mobility of the transceiver platform is the major drawback of the paper. The biggest advantage of the presented channel model is the consideration of bLoS links that none of the channel models in the literature have taken into account.

4.8. Channel Fading Margin for a Wireless Link

Radio waves can easily get trapped within evaporation ducts and the sea surface. The propagation of signals and the estimation of refractivity are well studied in many existing models of the ocean surface channel. The fading characteristics of the evaporation ducts are a relatively newer topic in this area and should be analyzed and studied well to find the appropriate fading margin required for reliable wireless communication. To solve this problem, Zaidi et al. presented a method for calculating the complete fading margin for a wireless link over the surface of the South China Sea [14].

Based on the recent reports on the evaporation duct measurements, the authors of [14] calculated the statistical distribution of path loss at different distances in the South China Sea. The calculated path loss distributions vary from time to time and depend on the weather. They also suffer due to the slow and fast fading characteristics. After determining the fading characteristics, a complete fading margin was deduced. For 100 km, it was found that approximately 99% availability can be achieved with an 88-dB fading margin. For a shorter distance of 50 km, the necessary value of fading margin for 99% availability is only 50 dB.

To calculate the fading margin, the first refractivity profile data is produced as follows:

$$M\left(z\right)= M_0+0.125z-0.125\mathsf{\delta }\ln \left(\frac{z+z_0}{z_0}\right)$$

(25)

where M is the modified refractivity, z is the height in meters, $z_0$ is the aerodynamic roughness in length, and $\mathsf{\delta }$ is the evaporation duct height. The PE tool [41] analyzed the data, including other parameters, to calculate the path loss. The antenna height for both the receiver and the sender was 4 m, which helped them continue transmission within the evaporation duct at 10.5 GHz. Since we know that the average signal-to-noise ratio is highly necessary for finding the fading margin, the mean path loss at a given distance must first be obtained. It was calculated using the following equation:

$$\overline{PL\left(d\right)}= \gamma \left(d\right)+ E\left(x_{dB}^{\prime }\right), d\ge 0$$

(26)

where $\gamma \left(d\right)$ is the location parameter that varies with distance d, and $E\left(x_{dB}^{\prime }\right)$ is the expectation of path loss in dB. The fading margin for slow fading and fast fading can be calculated by the formulae:

$$f_{m,slow}= X_0\left(P_{avail}\right)- E\left(x_{dB}^{\prime }\right)$$

(27)

$$f_{m,fast}= -10 log \left[-ln \left(1-P_{out}\right)\right]$$

(28)

where $P_{avail}$ is the probability of availability of slow fading for a given threshold value of $X_0$, and $P_{out}$ is the outage probability. Finally, the fading margin was calculated by summing up the slow and fast fading.

The work presented in [14] is unique because no one has critically analyzed the calculation of the fading margin for over-the-sea wireless communication in the evaporation duct layer. The contribution is high, but there are a few areas for improvement that could be considered. However, it is not clearly mentioned whether the transmitter or receiver is mobile or static. This is important because, mostly, the transmitter is mobile in such a scenario and mobility can be a big concern. In addition, calculating the fading margin for other types of ducts can be performed in the future together with an implementation scenario.

4.9. Over-the Sea Radio Links of Malaysian Shore Using the Evaporation Duct

Malaysia has a lot of islands in the South China Sea surrounded by large water bodies. Discovering energy resources, hydrocarbon exploration, and oil reserves in the deep sea requires high-speed over-the-sea communication between ships, vessels, and islands. To deal with this issue, the study undertaken in [15] presents the feasibility study of the bLoS radio links in the evaporation duct over the sea near Malaysian shores.

The main objective of [15] was to analyze if it is possible to design a channel model for bLoS links in the Malaysian sea region. To do this, investigations were made to find the radio link propagation characteristics in the evaporation duct to find the optimum frequency and antenna height. Propagation path loss was calculated using 1.9–2.5 GHz frequency, 5 m of antenna height, and 1 degree of vertical beam width. The highest applied frequency of the channel model was 24.125 GHz. It was found that the use of 10.5 GHz frequency with an antenna height of 4 m is suitable for bLoS wave propagation channel in the sea environment close to the Malaysian shore.

The study in [15] is simple but also the first trial considering the sea region. It is helpful as a preliminary study for the choice of frequency and antenna height in the mentioned sea scenario. However, the authors did not mention the specific path loss model they have used. Crucial channel evaluation parameters like mean excess delay, fade margin, RMS delay spread, etc. were ignored while doing the feasibility study.

4.10. High-Capacity and Long Range Microwave Over-the-Sea Link Propagation Using the Evaporation Duct

The paper presented in [16] is the first ever study of the propagation of a high-capacity radio-link over-ocean evaporation duct from the Australian mainland to the Great Barrier Reef (GBR). GBR is the largest marine park of the world. Monitoring GBR is a great challenge since it involves a complex ecological system. Real-time monitoring of different environmental parameters is highly necessary. Using ad hoc sensor networks to perform this monitoring task can be helpful for the researchers. The major problem of this kind of ad hoc system is relaying on gathered information of the sensor nodes over the sea surface, to the mainland, from GBR. To overcome this problem, authors in [16] proposed to use the evaporation duct by appropriately selecting the antenna height and operating frequency for an extended range. A 78 km link that operates at a frequency of 10.6 GHz with a data rate of 10 Mb/s was used to verify the technique.

The refractive index depending on atmospheric pressure, temperature, and humidity is calculated by the following equation:

$$N= \frac{A_N}{T}+\frac{B_{N}e}{T^2}$$

(29)

where $A_N$ = 77.6, and $B_N$ = 3.73 × ${10}^5$, T is the temperature in Kelvin, p is atmospheric pressure in Pascal, and e is humidity. The path loss is calculated using the following equation:

$$P{r}_{\left(dB\right)}=P{t}_{dB}+G{t}_{dB}-pathlos{s}_{\left(dB\right)}+G{r}_{dB}$$

(30)

where Pt is the transmitted power, Gt and Gr are the antenna gains of transmitting and receiving antennas, respectively, and pathloss is the attenuation between the transmitter and receiver antennas.

For the purpose of studying the feasibility of using the evaporation duct to transmit signals from the mainland to the GBR, a computer simulation was undertaken using the Advanced Refractive Effects Prediction System (AREPS) program [42]. The propagation path loss is calculated using this software. Link budget calculation is done for the test link sent from the mainland to GBR. Parameters used in the link budget calculation are:

• Path loss = 141 dB
• Transmitted power = 27 dBm
• Antenna gain of the transmitter and receiver = 40 dB
• Bandwidth = 14 MHz

The path loss used in this calculation is based on 10.6 GHz frequency, with antennas located 7 m above the mean sea level separated by a 78 km range.

This work [16] is the first real-time implementation of wireless radio link propagation over the sea surface. Authors were successful in sending a video captured in GBR back to the mainland using their model and calculations. The received signal in the receiving antenna; however, experiences a 34 dB lower signal level than expected. Authors did not mention the reason behind this in the paper. Additionally, an effort to find out the fade margin and PDP could have made the work presented in [16] more reliable.

4.11. Multipath Delay Profile and Doppler Spread of Millimeter Radio Waves Over the Sea Surface

Millimeter waves usually have high bandwidth and capacity. In [17], Mehrima et al. presented an LoS ship-to-ship wireless channel model for over-the-sea communication. They considered the small-scale behaviors of a channel model like Doppler spread, RMS delay spread, and coherence bandwidth. Thirty-five GHz and 94 GHz were the frequencies used in [17].

The proposed channel model was based on a ray-tracing channel simulator named Wireless Insite [38]. Geometry of the sea surface environment, objects within the terrain dimension, transmitter and receiver specifications (such as heights and locations), types of antenna, carrier frequency, and specification of the sea water were designed using the mentioned tool. Next, the software was used to calculate the time of arrival, angle of arrival, and received power of each signal path. Finally, the data were processed to compute the Doppler spread, PDP, RMS delay spread, and coherence bandwidth.

For considering reduction in the reflected energy in specular direction, the reflection coefficient R was formulated as:

$$R=R_0\exp [-8(\frac{\pi (\Delta h)\cos {\theta }_i}{{\lambda }_0}{)}^2]$$

(31)

where $R_0$ is the smooth surface coefficient, ${\theta }_i$ is the angle of incidence, $\Delta h$ is the standard deviation in the surface height, and ${\lambda }_0$ is the wavelength. Statistical properties of mean excess delay and RMS delay spread were obtained from the average PDPs using Equations (1) and (2) in Section 2 of this paper. Authors of [17] showed the effect of receiver speed over the sea surface, which caused a shift in the Doppler frequency. For i-th propagation path, the Doppler Effect was given by:

$$\Delta f_i=f_0[\frac{d_i{V}_T}{c}+\frac{a_i{V}_R}{c}]$$

(32)

where $V_R$ and $V_T$ are velocities of the receiver and transmitter, $a_i$ and $d_i$ are the directions of arrival and departure of the i-th ray, $f_0$ is the carrier frequency, and c is the speed of light. When the time correlation of the impulse response is 50%, the coherence time is formulated as:

$$T_c=\frac{9}{16\pi f_m}$$

(33)

where $T_c$ is the coherence time. As another small-scale parameter, coherence distance is extracted from the angle of arrival. This parameter refers to the amount of separation in space where a fading channel does not confront any change. It was formulated as:

$$D_c=\frac{\lambda \sqrt{ln2}}{A\sqrt{23(1-\gamma \cos [2\left(\theta -{\theta }_{max}\right)}])}$$

(34)

where $D_c$ is the coherence distance, $A$ is the angular speed, $\gamma$ is the angular constriction, ${\theta }_{max}$ is the maximum fading in the azimuth direction, $\lambda$ is the wavelength, and θ is the direction of arrival.

Even though the proposed channel model had a high capacity and data rate, only LoS propagations were considered. Authors of [17] did not consider nLoS and bLoS propagation links. In [17], the effects of atmospheric ducts were overcome but they failed to analyze the refractive profile of the rough sea surface.

4.12. Ray-Tracing-Based Wireless Channel Modeling for Over-the-Sea Communication Near Diaoyu Islands

The Diaoyu archipelago is one of the main islands of its kind located in East China Sea. It is quite challenging and critical to design and implement a channel model considering this area due to the extremely uncertain sea waves and islands that work as propagation barriers. Wu et al. collected and analyzed the three-dimensional contour data of Diaoyu islands to generate a sea surface scenario, using MATLAB, in order to design a channel model in that area [18]. The ray tracing technique was used to model the wireless channel.

Authors of [18] obtained calculations for both the reflected and diffracted rays. Propagation path loss was calculated as the ratio of the effective transmitting power and the received power. It was formulated as:

$$PL\left(dB\right)=20log\frac{E_r}{E_t}$$

(35)

where $E_t$ and $E_r$ are electric field intensities of transmitting and receiving rays, subsequently.

The proposed channel model is incomplete and incompetent for real time deployment because it did not consider the atmospheric duct effects. Furthermore, there was no consideration for the refractive rays while designing the channel model. Refraction caused due to evaporation ducts plays a prime role in maritime wave propagation. Nevertheless, it has a very small range.

4.13. Measurement and Analysis on a Land-to-Ship Offshore Wireless Channel in 2.4 GHz

Many of the existing wireless channel modes designed for over-the-sea communication use VHF radios or satellite communication systems. These channel models do not support a very high data rate because of the lack of bandwidth and the high cost incurred due to expensive satellite services. To address this issue, Lee et al. presented measurement results for land-to-ship offshore wireless channels [19]. The frequency used in this channel model was 2.4 GHz. The model was investigated through an implementation of a narrowband channel measurement system between the quay and a sailing patrol boat. For large-scale fading, different existing path loss models were compared with the empirical path loss data. The free space path loss model, two-ray path loss model, and ITU-R P.1546 model [43] were taken into consideration for comparative analysis. Destructive and constructive interferences around distances ranging from 200 to 500 m were observed from empirical path loss data, which led the authors of [19] to conclude that the two-ray path loss model was the best fit for their scenario. The Kolmogorov–Smirinov (K-S) test [44] was conducted to verify the goodness of the fit. The received field intensities of direct and reflected rays were formulated using the following two equations in the channel model as follows:

$$E_{LOS}=\frac{E_0}{d_1}\exp \left(-\frac{j2\pi f{d}_1}{c}\right)$$

(36)

and

$$E_R=\mathrm{\Gamma }\frac{E_0}{d_2}\exp \left(-\frac{j2\pi f{d}_2}{c}\right)$$

(37)

where $d_1$ and $d_1$ are the distances between the transmitter and receiver for direct path and reflected path, subsequently, $E_{LOS}$ is the field intensity of the direct rays, $E_R$ is the field intensity of the reflected ray, $E_0$ is the free space electric field, f is the carrier frequency, and $\Gamma$ is the reflection coefficient. The total electric field intensity was the summation of Equations (36) and (37), as represented below:

$$E_{tot}=E_{LOS}+E_R$$

(38)

The measurements for the channel model were conducted in the Incheon Maritime Police Port, located on the Yellow Sea in South Korea. Experiments were conducted for the cases when the ship was in static mode and moving with high speed. Propagation loss data was obtained in real time using received signal strength. For small scale fading, authors of [19] considered multipath propagation, speed of the mobile vehicle, changes of surrounding objects, and transmission bandwidth of the signal. Rayleigh distributions are widely known to model the functions of small-scale fading. In [19]; however, it was found suitable to use the Rician distribution.

This is the only channel model that analyzes different propagation loss models comparatively, with the practical data obtained manually. Additionally, the channel model was designed to consider both small- and large-scale fading. Unfortunately, the fade margin calculation was not done in [19].

4.14. Research on Sea-Surface Ka-Band Stochastic Multipath Modeling

Cao et al. presented a channel model using the Ka-band [20]. It also used the stochastic bridge process [45] to design the sea-surface multipath propagation channel. The Ka-band ranges from 26.5–40 GHz. This band features high system capacity, small size terminal antenna, narrow beam, etc. Therefore, it can play a significant role in wireless channel modeling for over-the-sea communication by overcoming the serious interference caused by multipath components. Stochastic bridge channel modeling denotes the emission of electromagnetic waves as rays, and it considers propagation multiple paths as stochastic process samples. The starting and ending points of the stochastic bridge process were the transmitter and receiver. Waves emitted from the transmitter were assumed to be random rays. Apart from these rays, the random rays can reach the receiver through multiple reflections getting spread on the sea surface. The probability density function for the effective random rays at the receiving end was expressed as:

$$Q\left(x,y,z\right)=\frac{27}{4{\pi }^2{D}_k^3}\exp \left(-\frac{3r}{D_k}\right)$$

(39)

where $D_k$ is related to the number of reflection and sea conditions and r is the distance between the transmitter and receiver. Energy attenuation of the horizontally polarized waves is huge when they fall upon the sea surface obliquely. That is why incident signals used in this channel model were vertically polarized waves. Reflection coefficient of vertical polarization was calculated using the following equation:

$$\mathrm{\Gamma }=\frac{{\epsilon }_c{\sin \theta }_i-\sqrt{{\epsilon }_c-{\cos }^2{\theta }_i}}{{\epsilon }_c{\sin \theta }_i+\sqrt{{\epsilon }_c-{\cos }^2{\theta }_i}}$$

(40)

where ${\theta }_i$ is the angle of incidence of radio waves and ${\epsilon }_c$ is the complex permittivity. Time delay, phase delay, and amplitude gain of each effective path were calculated using the approaches presented in [46,47,48], subsequently.

The authors of [20] presented a channel model that had high data rate and used small terminal antennas. They did not specify, formulate, or assume any kind of propagation loss model. In addition, only the vertical polarization was used for the incident rays.

4.15. Modeling of a Channel Using the FDTD Method between UAVs and Sea Surface Vehicles

Shi et al. used wideband technology, in [21], to develop a channel model for communication between UAVs and surface vessels using the FDTD method [28]. They developed a random sea surface based on a spectral model. Implementation of the channel model was done in a two-dimensional cross section, where sea surface was assumed to be a perfectly conducting boundary. Using FDTD simulation, the transient impulse response for a random sea surface was numerically evaluated. On the basis of the resulting transient pulse, parameters were calculated. This process was repeatedly executed for multiple sea surface heights to generate a good amount of population data.

In [21], authors used the JONSWAP (Joint North Sea Wave Project) spectral model, which was first proposed in [49]. The spectral content of the sea surface proposed in this channel model was formulated as:

$$S\left(\omega \right)=\alpha \frac{g^2}{{\omega }^5}\exp [-1.25(\frac{{\omega }_0}{\omega }{)}^4{\gamma }^{\exp [-(\omega -{\omega }_0{)}^2/2{\sigma }^2{\omega }_0^2] }]$$

(41)

where g is the acceleration due to gravity, $\omega$ is the frequency, ${\omega }_0$ is the spectral peak frequency, $\gamma$ and $\sigma$ are peak enhancement coefficients, and $\alpha$ is the scale coefficient. The FDTD method was used to solve Maxwell’s equations [33] in this channel model. Readers can see Section 4.2 for the details. After getting the received signal wave from the FDTD simulation, it was found that the obtained results were not accurate for the channel properties. The channel impulse response was used to find the total information of the channel.

This wireless channel model is incomplete because important channel parameters like mean excess delay, RMS delay spread, etc. were ignored. Apart from this, it was necessary that authors of [21] mention what kind of model was used to calculate the path losses. Besides, due to refraction in the duct layers, it was also necessary to explore the atmospheric duct effects in the channel model.

5. Comparison of the Channel Models

Wireless channel models for over-the-sea wave propagation vary mainly in their allowed frequencies. Except for one channel model, presented in [5], the works covered in this study can be divided based on frequency values. We have chosen different works [5,8,9,10,11,12,13,14,15,16] to present here, in such a way that a wide range of frequencies (from 1.9 to 94 GHz) are covered. The channel models covered are based on real-time measurements, except [5], representing a universal scheme applicable to any frequency and sea state. The eight channel models covered have both advantages and limitations. For example, the measured data in [8] is highly accurate, because they have been collected in a real-life implementation. On the contrary, reliability is low, because the effect of multipath due to fluctuations of the sea waves is not considered. In [11], we can find that the channel model is applicable for long-distance transmission, even beyond 3000 m, but the only channel parameter considered was signal strength. To validate their propositions, the authors of [11] should have conducted more experiments on different parameters. Again, the paper presented in [5] applied a channel model under different carrier frequencies, transmission distances, and sea states, which is a great advantage for understanding and deploying the protocol, but the measured data are not verified using experiments. The paper presented in [10] works for both mobile and fixed antennas, but measurements of specular and diffuse multipath propagation were not carried out. The wireless channel model presented in [21] is incomplete because important channel parameters like mean excess delay, RMS delay spread, etc. were ignored. Apart from this, it was necessary that authors of [21] mention what kind of model was used to calculate the path losses. The authors of [20] presented a channel model that had a high data rate and used small terminal antennas. However, they did not specify, formulate, or assume any kind of propagation loss model. Additionally, only the vertical polarization was used for the incident rays. The proposed channel model in [18] did not consider the atmospheric duct effects. In addition, there was no consideration for the refractive rays while designing the channel model.

Table 1. Comparison of channel models for over-the-sea wave propagation.

Channel Model	Used Frequency	Outstanding Features	Advantages	Limitations
Measurements and wideband channel characterization for over-the-sea propagation [8]	1.9 GHz	• Supports mobile wireless vessel-to-vessel communication. • Implements a wideband radio channel.	• Measured data are authentic real-time data based on practical implementation. • Propagation environment includes both the sea and the land.	• Highly dependent on global positioning system (GPS). • Increased delay under non-line-of-sight (nLoS) propagation. • Multipath effect caused by fluctuating sea waves is ignored.
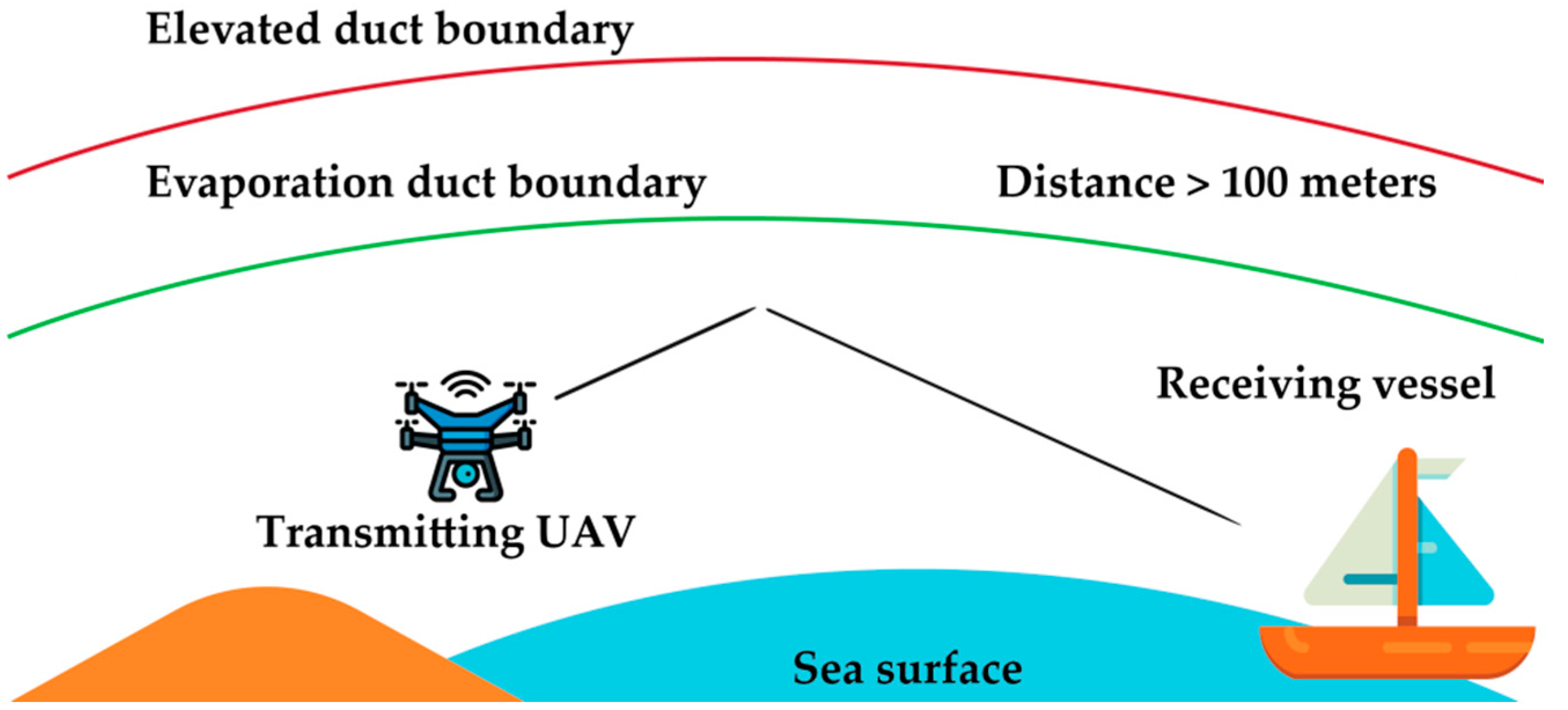
Marine communication channel modeling using the finite-difference time domain method [9]	Very high frequency (VHF) to 3 GHz	• Specially designed channel model for unmanned aerial vehicles (UAVs) to be deployed in an oceanic environment. • Applicable for very high frequencies up to 3 GHz.	• High channel accuracy due to finite difference time domain (FDTD) method. • Applicable to any sea-surface vehicle or sensor. • Prevents communication loss and reduces the probability of a collision.	• No particular deployment scenario has been elaborated. • Modeling process is performed through two-dimensional (2-D) approximation, which could have been better if it was performed using three-dimensional (3-D) approximation.
Experimental multipath delay profile of mobile radio channels over the sea [10]	2 GHz	• Channel model is applicable for both short-range and long-range communication.	• Channel model is applicable for both mobile and fixed antennas.	• No measurements were undertaken for specular and diffuse multipath propagation.
Near-sea-surface mobile radio wave propagation at 5 GHz: measurements and modeling [11]	5 GHz	• The only channel model in the literature so far to implement and compare three path loss models (two-ray, three-ray, and free space loss model (FSL)). • Both reflection and refraction are taken into account when modeling the channel.	• Works at very long distances, greater than 3000 m. • Measurement data are based on real-time application.	• The only channel parameter considered is the signal strength. • No consideration of the error rate.
Novel maritime channel models for millimeter radio waves [12]	34 and 95 GHz	• Uses 5G candidate frequencies (35 and 94 GHz). • Modifies the two-ray model for the better prediction of path loss.	• Comparison results are shown for two different frequency bands. • Can predict the last peak of the path loss without showing any extra peak.	• Considers the sea surface as flat, without roughness. • The incident angles of the rays are not at all considered to be small.
Multipath channel model for radio wave propagation over the sea surface [5]	Applicable for multiple frequencies	• Applicable for ship-to-ship and ship-to-shore wireless communication over the sea. • Applied channel model under different carrier frequencies, transmission distances, and sea states.	• A global channel model applicable to all frequencies and geographic situations. • Considers both the reflection and refraction of rays.	• Coastline hills and the surrounding ships are not involved in channel modeling, thus making the channel model applicable only to the open sea. • Measured data are not based on real-time implementation.
Channel model for surface ducts [13]	5–15 GHz	• Independent of polarization. • Channel model is symmetric.	• Reliable use of the RO method because the frequency used is more than 3 GHz. • Considers beyond non-line-of-sight (bLoS) links.	• No calculation presented of the complete fading margin. • Mobility of the transmitter and receiver is not mentioned.
Channel fading margin for a wireless link in the South China Sea [14]	10.5 GHz	• Detailed analysis of the effects of both slow fading and fast fading. • Introducing the concept of complete fading margin, where both types of fading were incorporated.	• Consideration of both line-of-sight (LoS) and nLoS. • Fading margin is calculated both for short (50 km) and long distances (100 km).	• Fading margin is calculated only on the basis of the evaporation duct. Other types of atmospheric ducts are not considered. • No specification of the transmitter and receiver mobility.
Over-the-sea radio links of Malaysian shore using evaporation duct [15]	1.7–25 GHz	• Supports over-the- sea bLoS communication links. • Supports mobility of the transceiver platforms.	• Experimental results were obtained for a wide range of frequencies (2.4, 5.8, 10.5, and 24.125).	• No elaborate discussion on path loss model. • Important parameters like mean excess delay, RMS delay spread, and channel fade margin are ignored.
High-capacity and long-range microwave over-the-sea link propagation using evaporation duct [16]	10.6 GHz	• Supports ad hoc sensor network applications. • Antennas operate at optimal height for evaporation duct.	• Real life implementation of wave propagation mechanism using evaporation duct from sea to mainland. • Transmission of heavy multimedia (image and video) data is possible.	• Good amount of signal attenuation at the receiver end. • No consideration for channel fading. • Delay spread is not considered as a channel evaluation parameter.
Multipath delay profile and Doppler spread of millimeter radio waves [17]	35 and 94 GHz	• Supports the data rate requirements for 5G. • Uses millimeter wave. • Implementable with multi-input multi-output (MIMO) systems.	•High rate for data transmission. • Tolerant to the effects of Doppler frequency. • Handled signal distortion caused by the mobility of the transceiver platform.	• Propagation loss equation was not assumed or formulated. • Considered LoS propagation only.
Ray-tracing-based wireless channel modeling for over-the-sea communication near Diaoyu islands [18]	2.5 GHz	• Applies the ray tracing method. • The transceiver platforms can be set into hot air balloons.	• 3-D simulation of the sea environment. • Computation of the electric field intensity for both receiving and transmitting rays.	• Islands are huge barriers of wave propagation. No consideration of bLoS links to overcome those barriers. • Atmospheric duct height effects were ignored. • Fading characteristics of the channel were not explored.
Measurement and analysis of the land-to-ship offshore wireless channel in 2.4 GHz [19]	2.4 GHz	• Comparison among the path loss models. • Use of empirical data to test the path loss models.	• Real-time implementation with the authentic author-collected data. • Considered both small- and large-scale fading.	• No experiments and calculations were conducted for fade margin.
Research on sea-surface Ka-band stochastic multipath modeling [20]	26.5–40 GHz	• Used Ka-band for wave propagation.	•High data rate. • Small size terminal antenna. • Narrow beam.	• No specified path loss model. • Considered vertical polarization only for the incident rays.
Modeling of a channel using the FDTD method between UAV to sea surface vehicle [21]	Not specified	• Supports UAV to surface vessel communication links.	• Use of the FDTD method.	• Sea surface was assumed to be a perfectly conducting boundary, which is not realistic. • No specific carrier frequency was used.

discusses, in detail, the comparison of channel models based on outstanding features, routing metrics, advantages, and disadvantages.

As mentioned earlier, the channel models presented in this paper can be distinguished in terms of the propagation scenario (LoS, bLoS, nLoS) and the mobility of the transmitter and receiver. In addition, different models considered different types of ducts.

Table 2. Comparison of propagation environment and parameters.

Channel Model	Type of Propagation	Mobility of Transmitter	Mobility of Receiver	Considered Atmospheric Duct	Channel Parameters	Propagation Loss Model
Ref. [8]	Line-of-sight (LoS) and non-line-of-sight (nLoS)	Yes	No	Not considered	Propagation loss, RMS delay spread, and mean excess delay	Long-distance path loss model (eqn. (1))
Ref. [9]	LoS	Yes	No	Not considered	Propagation loss, mean excess delay, and RMS delay spread	Basic path loss model (eqn. (8))
Ref. [10]	LoS	Yes	Yes	Not considered	Mean excess delay, and RMS delay spread	Not mentioned
Ref. [11]	LoS	Yes	Yes	Evaporation duct	Propagation loss, transmitted power, transmitter height, and receiver height	three-ray path loss model (eqn. (4))
Ref. [12]	LoS	Yes	No	Evaporation duct	Propagation loss, RMS delay spread, path loss, and received power	Modified two-ray path loss model (eqn. (19))
Ref. [5]	LoS	Yes	No	Not considered	Propagation loss, power delay profile, and inter-symbol interference	Not mentioned
Ref. [13]	Beyond non-line-of-sight (bLoS)	Not mentioned	Not mentioned	Surface duct	Propagation loss, delay spread, and angle of arrival	Custom path loss model using (eqn. (22))
Ref. [14]	LoS and nLoS	Not mentioned	Not mentioned	Evaporation duct	Propagation loss, channel fade margin, slow fading, and fast fading	Log normal path loss distribution
Ref. [15]	bLoS	Yes	Yes	Evaporation duct	Propagation loss	Not mentioned
Ref. [16]	nLoS and LoS	No	No	Evaporation duct	Propagation loss	Parabolic equation method
Ref. [17]	LoS	Yes	Yes	Not considered	Power delay profile, coherence time, bandwidth, and distance	Not mentioned
Ref. [18]	Not mentioned	Yes	Yes	Not considered	Propagation loss, time delay, and angle of arrival	Custom path loss model using (eqn. (35))
Ref. [19]	LoS	Yes	No	Not considered	Propagation loss, and large- and small-scale fading	two-ray path loss model (eqn. (5))
Ref. [20]	Not mentioned	Not mentioned	Not mentioned	Not considered	Time delay, phase delay, and amplitude gain	Not mentioned
Ref. [21]	LoS	Yes	Yes	Not considered	Propagation loss	Not mentioned

shows a comparison of channel models based on these parameters.

Existing channel models can be also compared with each other based on some other parameters, like antenna type, range, bandwidth, height of the transmitter, and transmission power.

Table 3. Comparison of antenna specification and performance.

Channel Model	Antenna Type	Range	Bandwidth	Antenna Height	Transmitting Power
Ref. [8]	Omni-directional	30 km	Not specified	21.5 m	30 dBm
Ref. [9]	Not specified	100 m	Not specified	Not specified	Not specified
Ref. [10]	Omni-directional	Short range: 15 km Long range: 45 km	Not specified	For short range Transmitter: 6.4 m Receiver: 21 m For long range Transmitter: 9.5 m Receiver: 11.2 m	27.2 dBm
Ref. [11]	Omni-directional	18.52 km	Not specified	Transmitter: 3.5 m Receiver: 20 m	23 dBm
Ref. [12]	Omni-directional	2 km	200 MHz	Transmitter: 5 m Receiver: 9.7m	23 dBm
Ref. [5]	Dipole antenna	Not specified	Not specified	Not specified	Not specified
Ref. [13]	Not specified	500 km	20 MHz	Transmitter: 27 m Receiver: 27 m	30 dBm
Ref. [14]	Gaussian	100 km	Not specified	Transmitter: 4 m Receiver: 4 m	Not specified
Ref. [15]	Sin(x)/x	100 km	Not specified	5 m	30 dBm
Ref. [16]	Parabolic dish antenna	78 km	14 MHz	Transmitter: 7 m Receiver: 7 m	27 dBm
Ref. [17]	Omni-directional	10 km	200 MHz	Transmitter: 5.63 m Receiver: 20 m	23 dBm
Ref. [18]	Omni-directional	Not specified	Not specified	Transmitter: 5 m Receiver: 100 m	Not specified
Ref. [19]	Omni-directional	2 km	Not specified	Transmitter: 3 m Receiver: 4.5 m	25 dBm
Ref. [20]	Not specified	Not specified	0.95 MHz	Not specified	Not specified
Ref. [21]	Not specified	10 m	Not specified	Transmitter: 40 m	Not specified

shows the comparison results of the discussed channel models based on the mentioned parameters. It can be observed that omni-directional antennas have been widely used as antenna type. The height of the transmitters and receivers varied based on the sea environment, technology used, and applications. The highest range has been covered by [13]. It covered 500 km. The lowest range of the analyzed channel models was found to be 2 km ([12,41]). Additionally, it can be observed that the transmitting power level of the antenna lies between 23 to 30 dBm.

6. Possible Applications and Improvements

In this section, we first address the applications of the discussed channel models. We then discuss the possibility of unique and novel applications of the channel models in our point of view. After that, some possible future improvements of the channel models are presented. Finally, we discuss some critical issues, prospects, and phenomena in order to give our insights to readers.

6.1. Applications of the Channel Models

The channel models reported in the literature can be applied for various purposes and scenarios. For example, the channel model in [9] is applicable for UAVs that want to carry out ocean surveillance and report to the ship using the duct layer communication principles. The channel model in [10] is applicable for high-speed water vehicles. The channel model in [12] can support the 5G network architecture and is; thereby, applicable in such a scenario where the 5G network is deployed. The channel model presented in [8] can be used to support highly mobile water vehicles. Sea surfaces are assumed to be smooth in most of the channel models in the literature. However, the channel model presented in [5] went beyond the paradigm of the smooth sea surface and worked upon the rough sea surface. In [13], authors designed a channel model applicable for a scenario where bLoS propagation is needed. It has also been noticed that there are channel models that are only applicable for specific sea regions, as the environment and parameters vary a lot in different places. References [14,15,18] have been subsequently designed for wireless wave propagation in the South China Sea, the sea region encompassing Malaysian shores, and Diaoyu islands in China, respectively. The channel model proposed in [16] is especially applicable for transmitting the data gathered from the ad hoc sensor nodes for environmental monitoring purposes. A mathematical model for calculating the fading margin applicable only for the South China Sea was designed in [14]. The probable applications of channel models discussed in this paper are listed in

Table 4. Applications of the channel models.

Channel Model	Application
Ref. [8]	Applicable to vessel-to-vessel communication system where both the transmitter and receiver are mobile.
Ref. [9]	UAV to surface vessel based communication.
Ref. [10]	Applicable to high-speed watercraft transmitter or receiver.
Ref. [11]	Channel model can be applied to a mobile vessel to sea shore based communication.
Ref. [12]	Applicable to the 5G network architecture.
Ref. [5]	Applicable for vessels in both smooth and rough sea surfaces.
Ref. [13]	Applicable to a scenario in which the transmitter and receiver have bLoS propagation.
Ref. [14]	A mathematical model for calculating the fading margin is applicable only for the South China Sea.
Ref. [15]	Applicable for over-the-sea communication in the deep sea.
Ref. [16]	Especially applicable for transmitting the data gathered from the ad hoc sensor nodes for environmental monitoring purposes.
Ref. [17]	Applicable for highly mobile water vehicles with high speed.
Ref. [18]	Applicable for airborne devices to sea vehicles.
Ref. [19]	Applicable for ship-to-shore communication.
Ref. [20]	Designed for applications requiring high data rate.
Ref. [21]	UAV to surface vessel based ocean surveillance.

.

6.2. Possibility of Unique and Novel Applications of the Channel Models

In this subsection, the possibilities of unique and novel applications of the channel models are exploited and discussed.

Ocean surveillance for military applications: Applications of UAVs have increased a lot these days. They can be applied to monitor the sea surface in different regions. After data acquisition, it is necessary for them to transmit the data to the nearby sea vessels, ships, etc. To do that, it is mandatory to use an efficient channel model that is robust enough to support the communication between UAVs and sea surface vessels by considering atmospheric duct effects, path loss, fading caused by Doppler effects, etc. It is also possible to support a high data rate by using appropriate frequencies. Channel models proposed in [9,21] are suitable for this purpose. With the loss of communication, it is inevitable to lose the aircraft in the sea or have vehicular collision, but such kind of phenomenon is not acceptable in military operations. In [9], a great effort was put to avoid the aircraft loss and it is highly suitable for military applications requiring ocean surveillance through UAVs.

Resource expedition in deep sea: Expeditions are undertaken often in the deep sea for resource exploration. This requires reliable long-range communication supporting bLoS links. bLoS links are necessary in this case because it is quite impossible to predict the obstructions that the transmitted signals may face. The channel model proposed in [13] considered bLoS of propagation and it has a huge range of 500 km. Therefore, this channel model is highly applicable for resource expedition in deep sea regions. Furthermore, using the channel model proposed in [15], transmitters and receivers can communicate even if there are obstructions such as big as islands. It can also be applied for deep sea expedition.

Marine forecast and warning system: Marine activities are often threatened by frequently changing climate and potential natural disasters. Channel models that are capable of providing reliable communication, with a fair amount of fading and attenuation in an adverse natural situation, can be used to design ship-to-shore marine forecast warning systems. The channel model presented in [5] is suitable for this kind of application.

Marine protection: We all know that seas all around the world are full of natural resources. They need continuous monitoring. Under water sensor networks or typical wireless sensor networks can be deployed for ocean monitoring for marine protection to the natural resources. The channel model proposed in [16] can be used to integrate sensor networks with the transceiver platforms.

Integrating wireless multimedia sensor nodes: Sensor nodes capable of capturing and processing multimedia data, such as image, audio, or video, are considered as multimedia sensor nodes. Ocean surveillance and environment monitoring may require capturing multimedia data, whereby these nodes can play a crucial role. But wireless multimedia sensor nodes have high chunks of data that require a high data rate. In [21], a channel model was designed that can support a high data rate. Wireless multimedia sensor networks can be integrated with the channel model proposed in [21].

Over-the-sea communication in the arctic sea: Wireless communication in the arctic sea is quite challenging due to the icebergs. The channel models proposed in [13,15] can be used in that kind of scenario.

6.3. Possible Future Improvements of the Channel Models

Existing channel models can be improved in many aspects. The channel model in [8] can be improved by considering the multipath effect caused by fluctuations of sea waves. In [8], multipath effects of the sea surface may be incorporated into the channel model in the future to make it more reliable. The channel model proposed in [9] can be improved by integrating elevated duct-based measurements. The channel model in [10] does not have a deployment scenario and does not take into account the elevated duct, even though the UAVs were involved in the channel model. Roughness of the sea was ignored while designing the channel model proposed in [12]. For further improvement, sea-roughness can be included as a parameter. The channel model proposed in [5] does not have a path loss model. This can be included for further improvement of the channel model. In [13], only the surface duct is considered as an atmospheric channel. To make it robust, other types of ducting effects must also be considered. The channel model proposed in [15] ignored many of the important channel evaluation parameters, such as mean excess delay, fade margin, etc. They can be considered in the future design of the channel model. Again, the channel model proposed in [17] can be integrated to support nLoS and bLoS propagation. Both the channel models proposed in [19,20] can be improved by incorporating the fade margin calculation. Lastly, the channel model proposed in [21] can be improvised by changing the sea surface design from two-dimensions to three-dimensions. Possible future improvements of all discussed channels are summarized in

Table 5. Possible future improvements of the channel models.

Channel Model	Possible Future Improvements
Ref. [8]	Multipath effects of the sea surface may be incorporated into the channel model in the future to make it more reliable.
Ref. [9]	Elevated duct-based channel measurements may be included.
Ref. [10]	Diffuse and specular multipath propagations may be introduced in this channel model in the future.
Ref. [11]	The channel model can be improved by taking into account the error rate along with the signal strength as a parameter.
Ref. [12]	Sea roughness can be included as a channel modeling parameter.
Ref. [5]	A propagation loss model can be introduced.
Ref. [13]	A complete fading margin calculation may be introduced, consisting of slow and fast fading.
Ref. [14]	Technical validation of the mathematical idea should be introduced in the future.
Ref. [15]	Channel evaluation parameters, such as mean excess delay, fade margin, etc., can be introduced for a reliable design.
Ref. [16]	Channel evaluation parameters, such as mean excess delay, fade margin, etc., can be introduced for a reliable design.
Ref. [17]	Channel model can be integrated to support nLoS or bLoS propagations.
Ref. [18]	Channel model should be integrated with complex real time path loss model and duct effects.
Ref. [19]	Fade margin determination can be introduced in the model.
Ref. [20]	Fade margin determination can be introduced in the model.
Ref. [21]	Sea surface can be designed in a 3-D cross section.

.

6.4. Insights on Modeling the Over-the-Sea Wireless Channels

In this subsection, some critical issues, prospects, and phenomena are addressed and discussed in order to share our insights with readers.

Scattering of the sea waves: Scattering of electromagnetic waves is a key factor in wireless channel modeling for over-the-sea communication. It puts a great impact on the multipath fading of a channel. Obstructions are not frequent and dense in the sea. Sparse scattering holds most of the channel links including the air-to-sea, ship-to-ship, or land-to-ship channels. Because Rayleigh fading is very commonly used for terrestrial channel modeling, it is not suitable for sea surface channel modeling. The scattering model proposed in [50,51] can be used.

Suitability of the two-ray model: In Section 2 of this paper, we introduced a two-ray path loss model [6]. Two paths are highly important for designing a wireless channel model. One ray is the LoS path and the other is the reflected path. The two-ray model is a good approximation when we have a bigger antenna height. If the antenna height is low, scattering of rays will display more randomness in the channel. For this kind of scenario, more paths are necessary to be taken into consideration.

Impact of Tx–Rx distance: Widely distributed transmitters (Tx) and receivers (Rx) have an impact on the angle domain. It is possible that the LoS path and the sea surface reflection path have identical angular directions. When the distance between the Tx and Rx increases, the angle difference between these two paths decreases. If multiple antenna arrays are set either in the transmitting end or in the receiving end, it may cause high correlation between the antenna elements. This may result in a rank-deficient MIMO channel matrix.

When the Tx–Rx distance is short, the channel can be modeled by using the classic two-ray model [6]. As the distance increases, a three-ray model [7] becomes more suitable. When the receiver continuously moves far away, LoS and surface reflection paths vanish due to the curvature of the Earth. It is still possible that the receiver can hear from the transmitter in the presence of the duct layer.

Effects of the sea wave movement: Sea wave movement has a great impact on radio wave propagation. It is especially dominant for surface reflection paths. Sea wave height, average sea wave length, and sea wave period are important parameters for characterizing sea wave movement. For highly rough sea wave movement, the incoming wave fronts confront more scattering and reflections. The two-ray model in this type of scenario is not suitable. Change in the sea surface height while calculating the amplitude of the main reflection path, and the components scattered in the irregular sea surface, should be considered. Karasawa’s model [52] can be highly suitable because it accounts for these parameters. Unfortunately, none of the channel models in the literature exploited this model to develop channel models for over-the-sea communication.

Three-ray model reduced to Rician fading: A three-ray model consists of one LoS path and two other reflection paths [7]. The relative amplitude of these two reflection paths can get affected by the unstable maritime propagation environment. For a calm sea surface, a stronger reflection path is dominant. For a rough sea surface, it is usual that the strength of all the reflection paths will decrease. A single reflection path is denoted as the superposition of the multiple weak reflections. If the number of weak reflection paths is large, the three-ray model will reduce to Rician fading for narrowband transmission.

Incoherent super position of the diffuse scattered radio waves: It is possible to determine the path length between the specular and direct paths. Phase relationships among the reflections across the sea surface are tough to predict due to the roughness of the sea surface. It is necessary to address the time dispersion of the diffused paths in the statistical sense because of the uncertainly of the diffuse points in a glistening surface. The channel model presented in [5] takes this issue under consideration. Not considering this in a multipath channel model will lead to an incoherent super position of diffused scattered radio waves.

7. Challenging Issues and Research Directions

Modeling wireless channels for over-the-sea wave propagation is a relatively new research topic. In this section, important challenging issues for modeling a wireless channel for over-the-sea communication are presented. We also elaborately discuss the research directions that can be helpful for researchers if they intend to design a new channel model.

7.1. Challenging Issues

Due to the fluctuant and uncertain nature of the marine environment, it is quite challenging to develop a robust wireless channel model for over-the-sea wave propagation. Challenges that need to be addressed in the study of this area are briefly discussed in this subsection.

Path loss model: Path loss can be caused by reflection, diffraction, scattering, refraction, etc. As the sea surface is an unrest surface, scattering of waves is large, and when developing a path loss model, refraction phenomena should be carefully considered. Popular models are two-ray, FSL, and three-ray path loss models. Researchers have to carefully select a model. For example, if someone intends to design a wireless channel that will serve for long-distance wave propagation, a three-ray path loss model may be the best option. On the contrary, the two-ray path loss model works fine for short-distance wave propagation. It is also possible to develop a new path loss model by modifying some parameters in the existing ones.

Real-life implementation: The ongoing trend of research in this area is to opt for real-life implementation of the developed channel models. For example, the work presented in [8] was implemented in the Aegean Sea, Greece. This requires a good amount of hardware and deployment costs, which is a great challenge for researchers. There are works, such as [13,14], that do not present real-life implementation scenarios and; therefore, are not reliable regarding how mathematical models will perform in real life.

Lack of simulation tool: There is no simulator specifically designed for the wave propagation in the sea surface environment. If someone wants to conduct research in this field using simulation, they must either make a custom simulator or use any traditional one with a custom implementation.

Barriers to the wave propagation: Coastline hills and the surrounding ships are great barriers to the propagation of waves over the sea surface, which causes significant signal attenuation. Considering this fact while developing a channel model is difficult.

Fluctuating sea environment: The marine environment varies greatly. Atmospheric pressure, humidity, air temperature, surface pressure, etc. change at different times of the day in the same sea surface area. In addition, different oceans (e.g., Pacific, Atlantic, etc.) have different environments, and important parameters change for each of the mentioned ocean surfaces. For example, the height of the evaporation duct on different sea surfaces varies greatly. Therefore, it is almost impossible to develop a universal channel model with common parameters.

Lack of statistical data: To develop a channel model for the surface of the ocean, a huge amount of sea state statistics is needed, such as temperature, pressure, and evaporation duct heights. This kind of data acquisition is often voluntary and not available for different oceans in the world. Therefore, this type of channel model is very difficult to develop due to the lack of data. In [14], a fading margin calculation scheme was introduced based on the years of statistical data gathered on evaporation duct heights in the South China Sea. However, it was possible to propose such mathematical formulations only because the data were available.

Frequently changing weather: Spontaneous changes in the weather are very frequent on the sea surface. Any disaster can drastically affect the propagation of waves.

7.2. Furture Research Directions

In this subsection, we shed some light on the future research directions of the wireless channel models for over-the-sea communication.

Antenna height: Antenna height can be really crucial for over-the-sea wave propagation, due to different kinds of surface ducts. Usually, a vertical distance more than 100 m is thought to fall under the elevated duct region, not in the evaporation duct region. Channel models vary in different kinds of surface ducts. Therefore, a channel model meant to facilitate an elevated duct can have a height more than 100 m. On the other hand, the ideal height for wave propagation in an evaporation duct starts from 7 m. Therefore, while designing a new channel model, careful consideration should be given to choose the optimal antenna height.

Sea-surface smoothness: A sea surface can be considered as a smooth and perfect reflector. A channel model based on this assumption is quite different from the assumption that the sea surface is rough and cannot act as a perfect reflector. A perfect channel model should consider the roughness of the sea surface. In the existing works, very few channel models consider the sea surface roughness. They avoided it because of the complex calculations needed to find the refractive profile for a rough sea surface. A future channel model can address this issue.

Type of links: This is a very important issue to be taken care of in future researches. Channels can be modeled based on LoS, nLoS, or bLoS propagation links. Propagation loss models and channel evaluation parameters (such as mean excess delay, RMS delay spread, etc.) vary based on the type of links considered in the channel model. Therefore, a thorough study is needed regarding the region of interest in the sea. For example, if anyone wants to design a channel model for over-the-sea communication that involves a lot of islands and rocks, which may work as obstructions to links, bLoS links should be considered with higher frequencies (35–94 GHz). For short range communication, bLoS propagation links are not necessary. Considering LoS and nLoS propagation is enough.

Selecting channel evaluation parameters: Different channel evaluation parameters can be considered depending on the design and application of the channel models. Usually, mean excess delay, RMS delay spread, channel fade margin, etc. are the common parameters. A future channel model should consider as many channel evaluation parameters as possible to prove the robustness of the design.

Appropriate frequency: Selecting a perfect frequency based on the application, range, and sea type is an important design issue. Long- and short-range transmissions require selecting different frequencies while designing the channel.

Comparative study: The existing channel models did not compare the performance of the designed channel models with the other existing ones. Such kind of comparison helps the readers understand the superiority and robustness of the channel models. It is absent in the current works and can be considered in the future works.

8. Conclusions

This work focuses on the key concepts and a comparative study of existing models of channels that have been developed so far for over-the-sea wave propagation. Key concepts include basic definitions and a brief elaboration of the parameters required to understand channel models. The comparative study extensively discusses the advantages, limitations, and unique features of channel models that will be helpful for researchers and engineers to select any model from the discussed ones, based on the needs of their applications. In addition, if someone intends to improve existing channel models, a table is also presented regarding possible improvements that can be made. To the best of our knowledge, this is going to be the first comprehensive study of ocean channel models that can help interested researchers in this field by providing guidance on current trends.