Modified Nonlocal Strain Gradient Elasticity for Nano-Rods and Application to Carbon Nanotubes
Abstract
:1. Introduction
2. Modified Nonlocal Strain Gradient Law for Rods
3. Elastic Equilibrium Problem
- Step 1: Solve the equilibrium Equation (22) to get the expression of the axial force
- Step 2: Solve the second-order differential Equation (6) in the formobtaining the expression of the elastic axial strain of the nano-rod in terms of three integration constants (, , and ) to be determined.
- Step 3: Solve the first-order differential in Equation (23) in terms of the axial displacement u of the nano-rod to get the expression of u in terms of four integration constants (, , , and ) to be determined.
- Step 4: Determine the four integration constants (, , , and ) by imposing the two CBC given by Equation (7) in terms of the axial displacement uand the two classical boundary conditions at the nano-rod end points and by specifying
4. Closed-Form Solutions for FG Nano-Rods
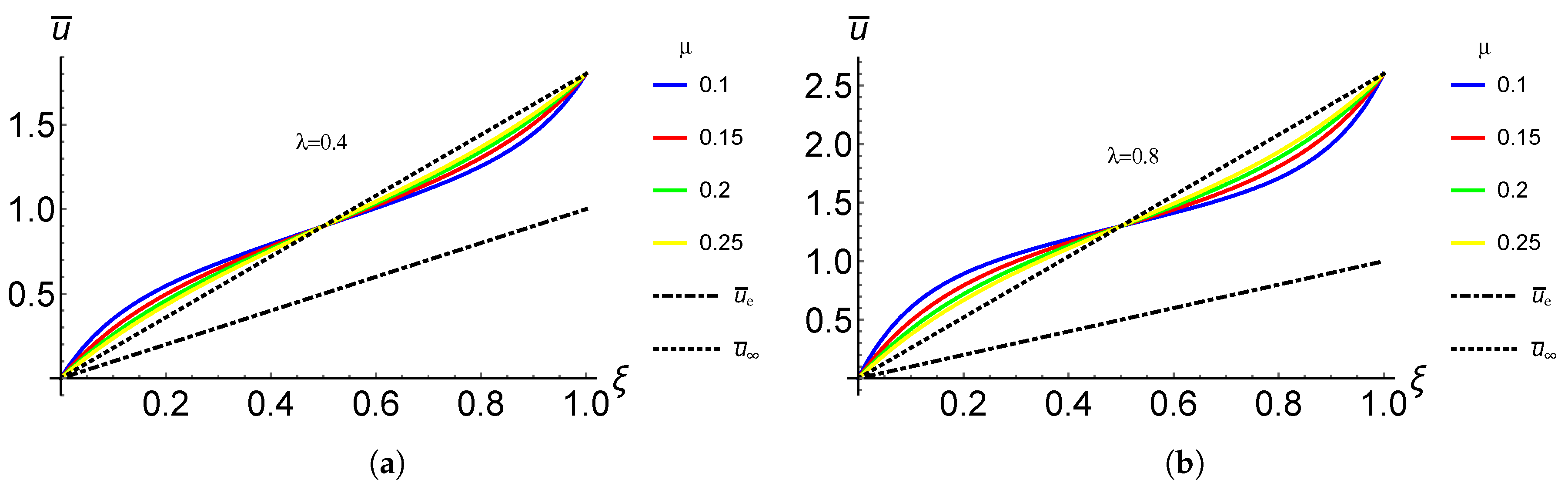
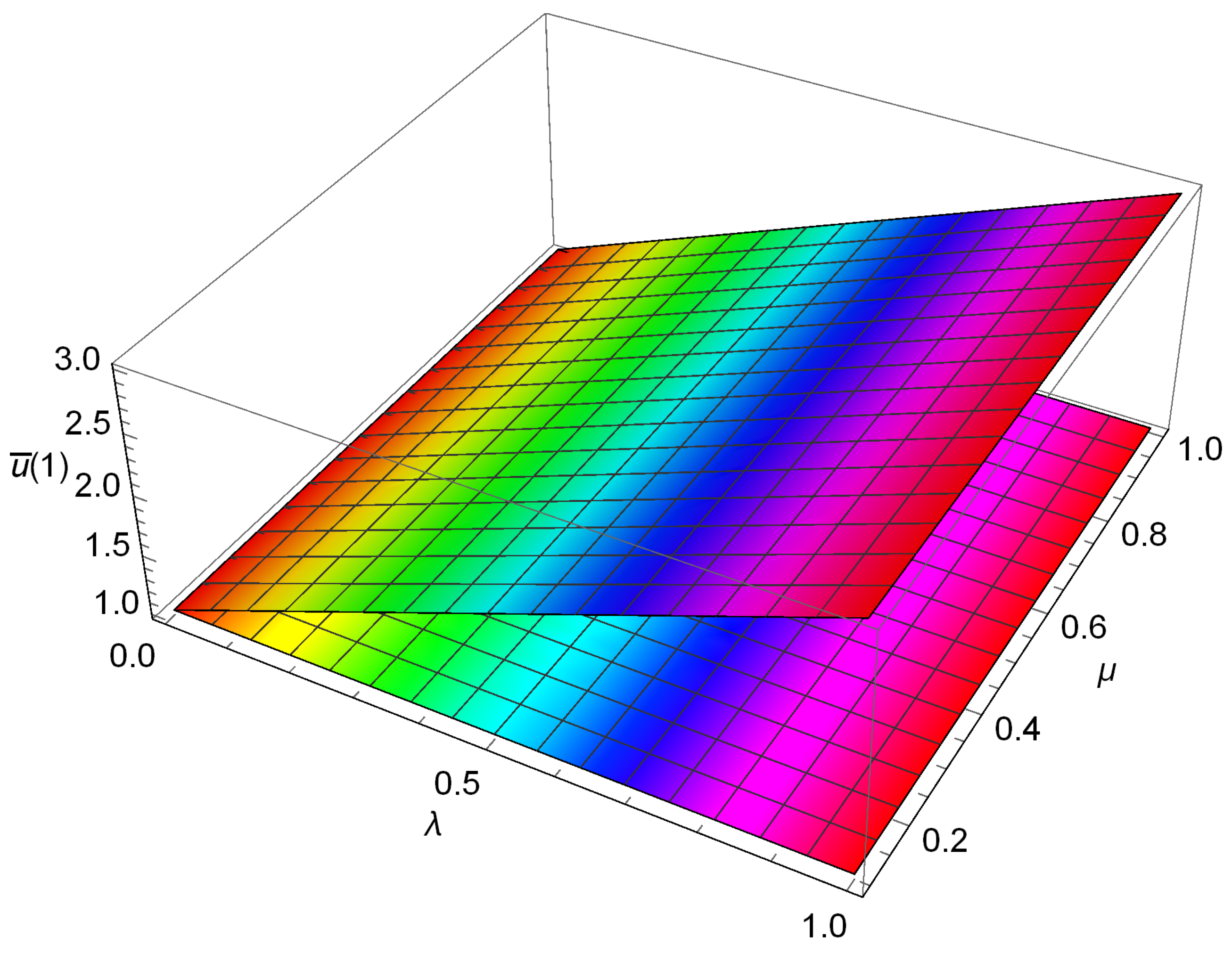
4.1. Case I: CF FG Nano-Rod with a Concentrated Load at the Free End
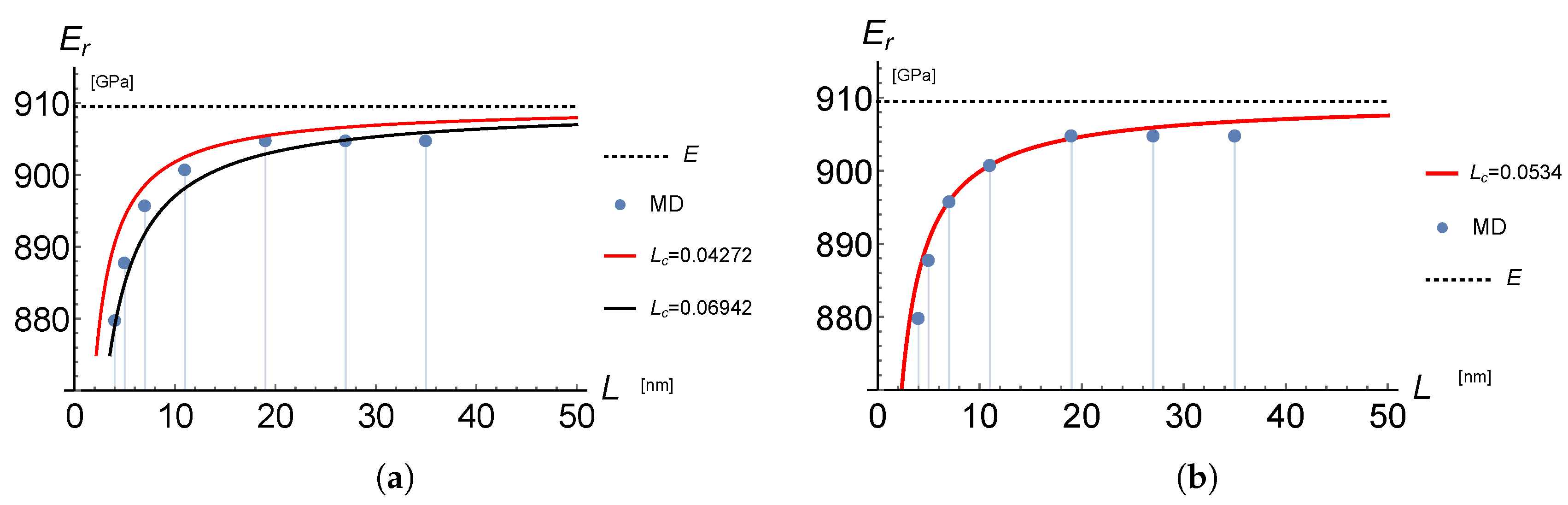
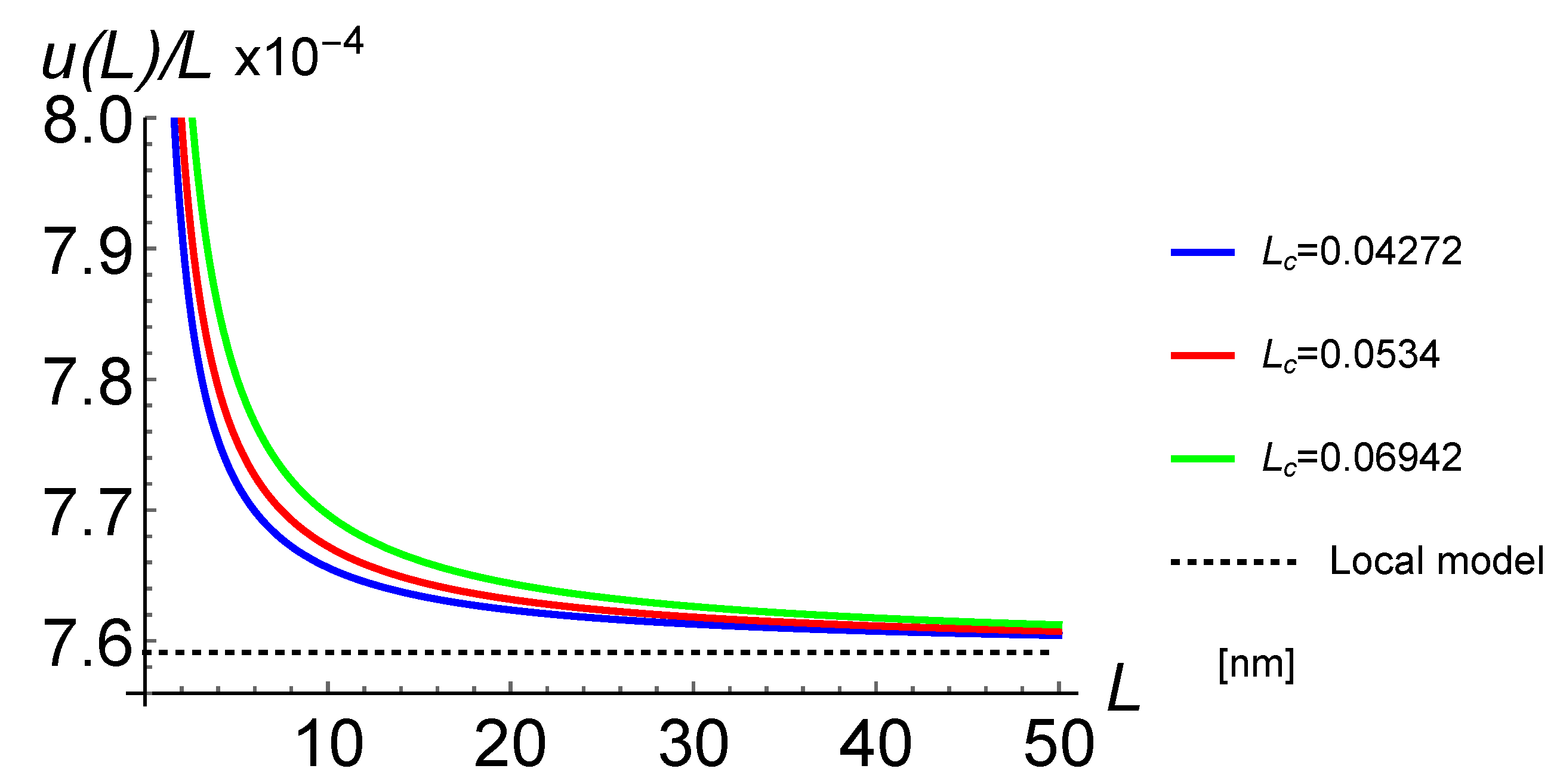
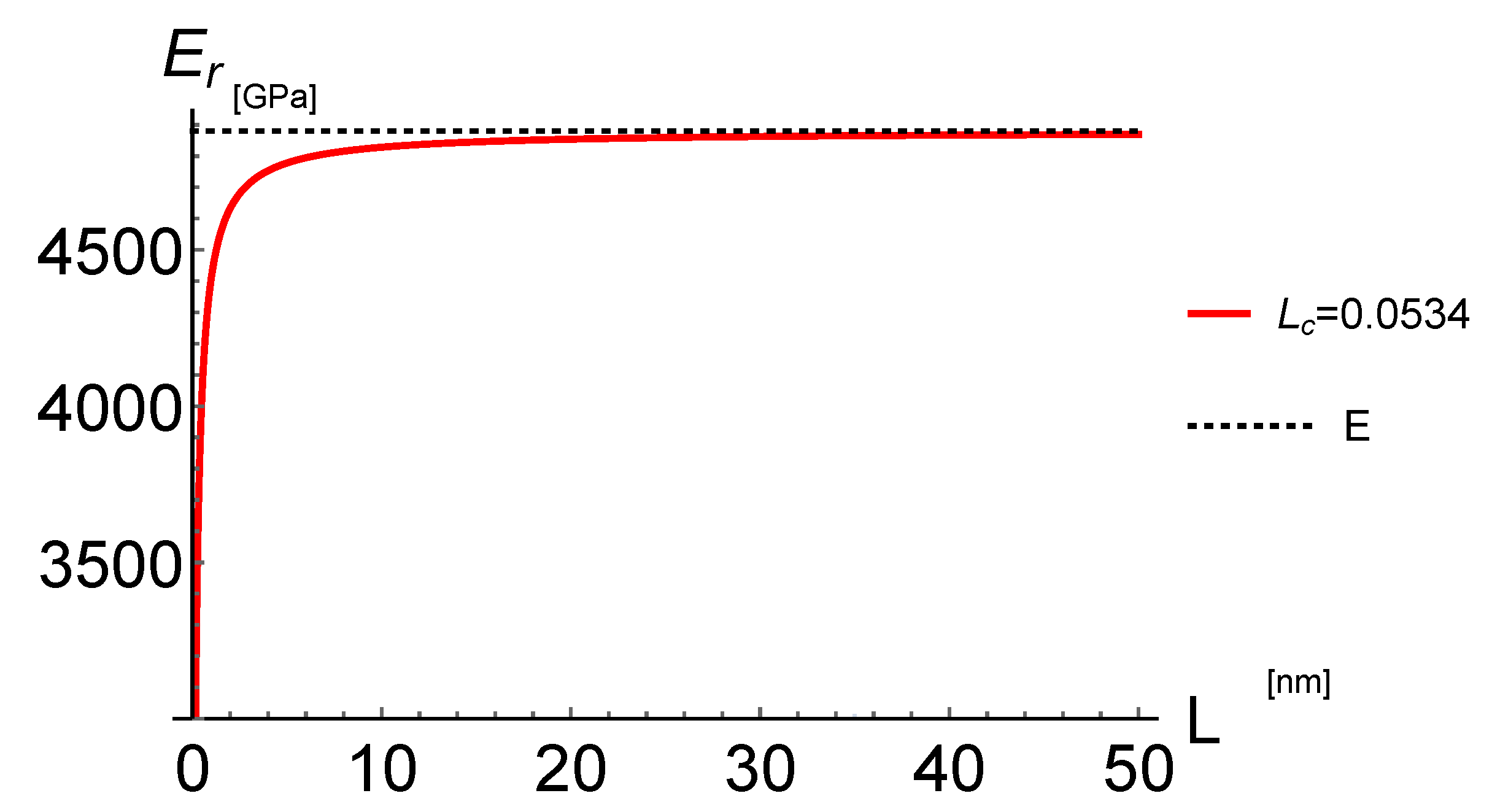
4.2. Reduced Young’s Modulus
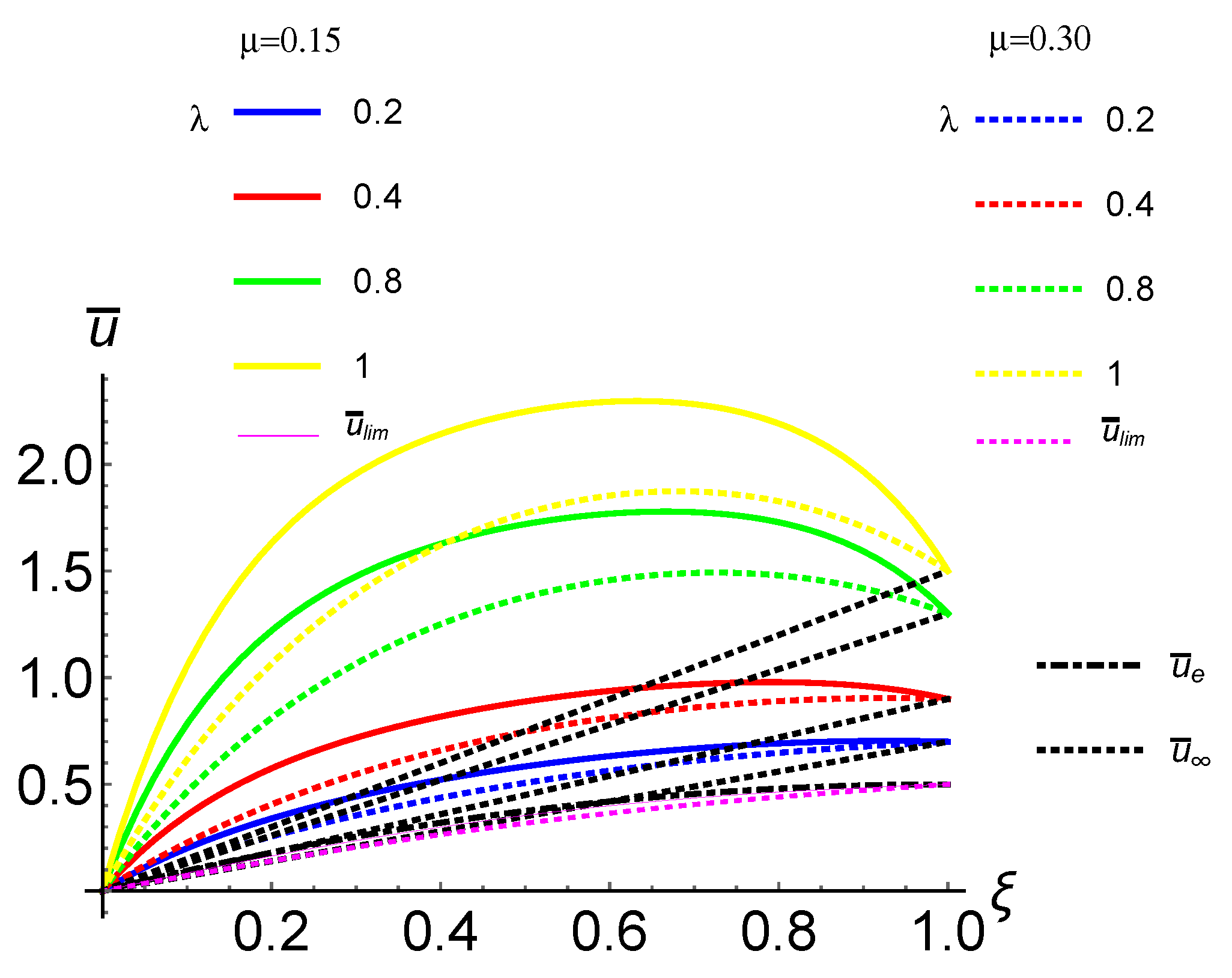
4.3. Case II: CF FG Nano-Rod Subject to a Uniformly Distributed Axial Load
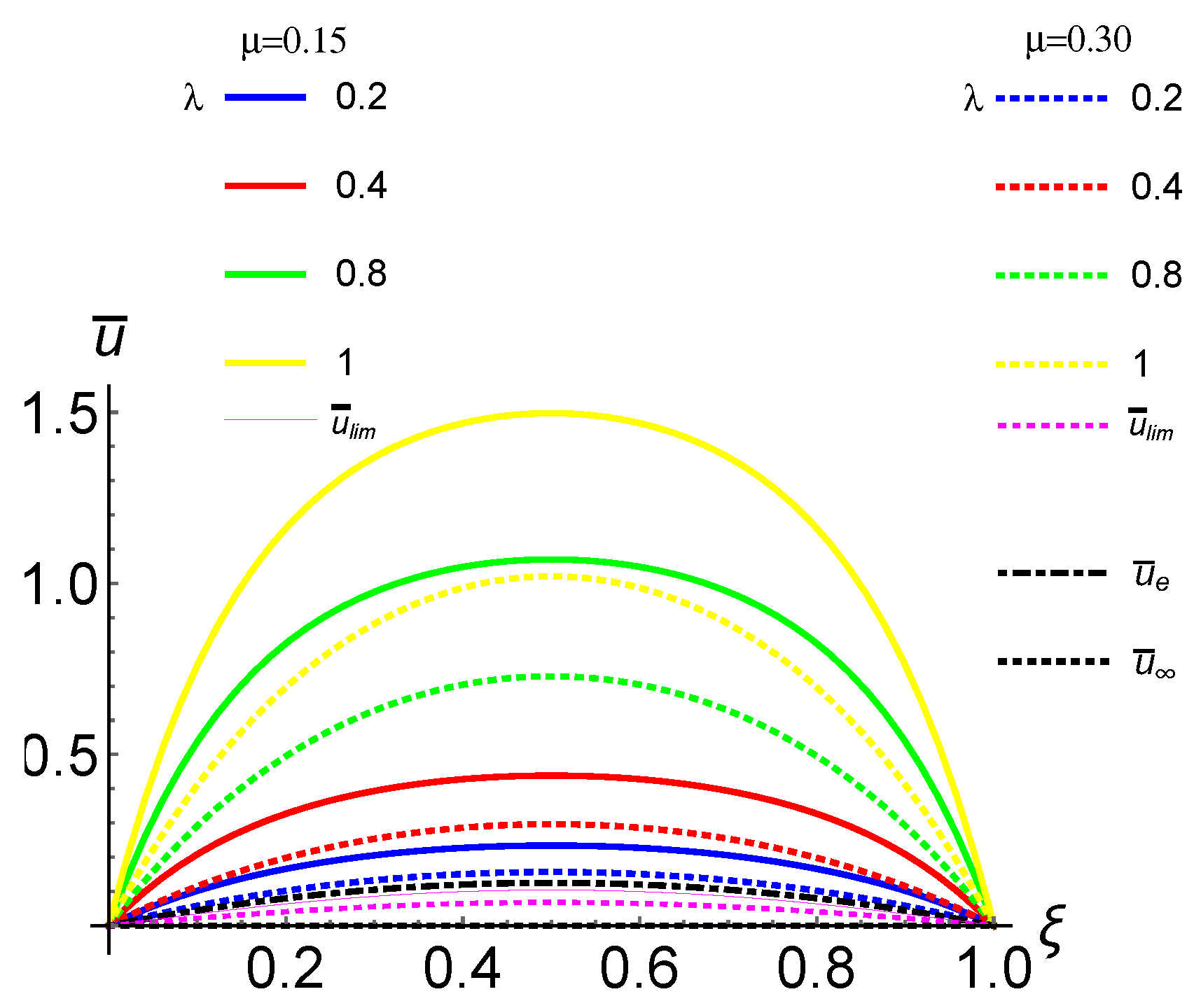
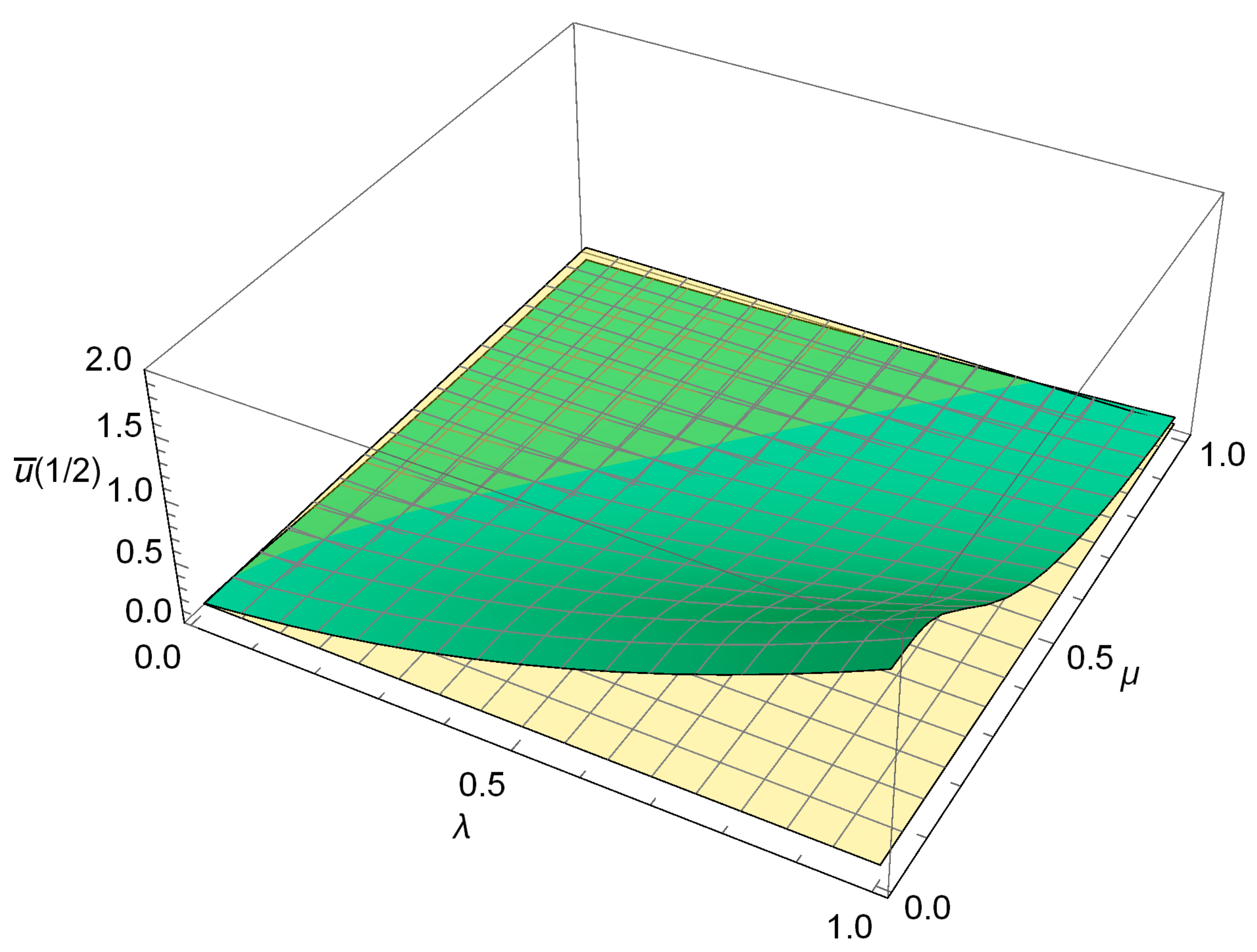
4.4. Case III: CC FG Nano-Rod Subject to a Uniformly Distributed Axial Load
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Peerlings, R.H.J.; Geers, M.G.D.; de Borst, R.; Brekelmans, W.A.M. A critical comparison of nonlocal and gradient-enhanced softening continua. Int. J. Solids Struct. 2001, 38, 7723–7746. [Google Scholar] [CrossRef]
- Marotti de Sciarra, F.; Barretta, R. A new nonlocal bending model for Euler-Bernoulli nanobeams. Mech. Res. Commun. 2014, 62, 25–30. [Google Scholar] [CrossRef]
- Askes, H.; Aifantis, E.C. Gradient elasticity in statics and dynamics: an overview of formulations, length scale identification procedures, finite element implementations and new results. Int. J. Solids Struct. 2011, 48, 1962–1990. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Barretta, R.; Marotti de Sciarra, F. Analogies between nonlocal and local Bernoulli–Euler nanobeams. Arch. Appl. Mech. 2015, 85, 89–99. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Nonlocal elasticity in nanobeams: the stress-driven integral model. Int. J. Eng. Sci. 2017, 115, 14–27. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M.; Marotti de Sciarra, F. Constitutive boundary conditions and paradoxes in nonlocal elastic nano-beams. Int. J. Mech. Sci. 2017, 121, 151–156. [Google Scholar] [CrossRef]
- Barretta, R.; Diaco, M.; Feo, L.; Luciano, R.; Marotti de Sciarra, F.; Penna, R. Stress-driven integral elastic theory for torsion of nano-beams. Mech. Res. Commun. 2018, 87, 35–41. [Google Scholar] [CrossRef]
- Barretta, R.; Čanadija, M.; Luciano, R.; Marotti de Sciarra, F. Stress-driven modeling of nonlocal thermoelastic behaviour of nanobeams. Int. J. Eng. Sci. 2018, 126, 53–67. [Google Scholar] [CrossRef]
- Barretta, R.; Čanadija, M.; Feo, L.; Luciano, R.; Marotti de Sciarra, F.; Penna, R. Exact solutions of inflected functionally graded nano-beams in integral elasticity. Compos. Part B 2018, 142, 273–286. [Google Scholar] [CrossRef]
- Barati, M.R. On wave propagation in nanoporous materials. Int. J. Eng. Sci. 2017, 116, 1–11. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R. Vibrations of Bernoulli-Euler beams using the two-phase nonlocal elasticity theory. Int. J. Eng. Sci. 2017, 119, 232–248. [Google Scholar] [CrossRef]
- Vila, J.; Fernández-Sáez, J.; Zaera, R. Nonlinear continuum models for the dynamic behavior of 1D microstructured solids. Int. J. Solids Struct. 2017, 117, 111–122. [Google Scholar] [CrossRef]
- Xu, X.-J.; Zheng, M.-L.; Wang, X.-C. On vibrations of nonlocal rods: Boundary conditions, exact solutions and their asymptotics. Int. J. Eng. Sci. 2017, 119, 217–231. [Google Scholar] [CrossRef]
- Faghidian, S.A. On non-linear flexure of beams based on nonlocal elasticity theory. Int. J. Eng. Sci. 2018, 124, 49–63. [Google Scholar] [CrossRef]
- Faghidian, S.A. Integro-differential nonlocal theory of elasticity. Int. J. Eng. Sci. 2018, 129, 96–110. [Google Scholar] [CrossRef]
- Sahmani, S.; Bahrami, M.; Ansari, R. Nonlinear free vibration analysis of functionally graded third-order shear deformable microbeams based on the modified strain gradient elasticity theory. Compos. Struct. 2014, 110, 219–230. [Google Scholar] [CrossRef]
- Polizzotto, C.; Fuschi, P.; Pisano, A.A. A nonhomogeneous nonlocal elasticity model. Eur. J. Mech. A/Solids 2006, 25, 308–333. [Google Scholar] [CrossRef]
- Fuschi, P.; Pisano, A.A.; Polizzotto, C. Size effects of small-scale beams in bending addressed with a straindifference based nonlocal elasticity theory. Int. J. Mech. Sci. 2019, 151, 661–671. [Google Scholar] [CrossRef]
- Mindlin, R.D. Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 1964, 16, 51–78. [Google Scholar] [CrossRef] [Green Version]
- Akgöz, B.; Civalek, Ö. Longitudinal vibration analysis of strain gradient bars made of functionally graded materials (FGM). Compos. Part B 2013, 55, 263–268. [Google Scholar] [CrossRef]
- Rahaeifard, M. Size-dependent torsion of functionally graded bars. Compos. Part B 2015, 82, 205–211. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. Strain gradient elasticity and modified couple stress models for buckling analysis of axially loaded micro-scaled beams. Int. J. Eng. Sci. 2011, 49, 1268–1280. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Alici, G. Size-dependent performance of microgyroscopes. Int. J. Eng. Sci. 2016, 100, 99–111. [Google Scholar] [CrossRef]
- Guo, J.; Chen, J.; Pan, E. Static deformation of anisotropic layered magnetoelectroelastic plates based on modified couple-stress theory. Compos. Part B 2016, 107, 84–96. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Fernandes, R.; El-Borgi, S.; Mousavi, S.; Reddy, J.; Mechmoum, A. Nonlinear size-dependent longitudinal vibration of carbon nanotubes embedded in an elastic medium. Physica E 2017, 88, 18–25. [Google Scholar] [CrossRef]
- Guo, S.; He, Y.; Liu, D.; Lei, J.; Shen, L.; Li, Z. Torsional vibration of carbon nanotube with axial velocity and velocity gradient effect. Int. J. Mech. Sci. 2016, 119, 88–96. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Li, X. Longitudinal vibration of size-dependent rods via nonlocal strain gradient theory. Int. J. Mech. Sci. 2016, 115, 135–144. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Ling, L. Flexural wave propagation in small-scaled functionally graded beams via a nonlocal strain gradient theory. Compos. Struct. 2015, 133, 1079–1092. [Google Scholar] [CrossRef]
- Simsek, M. Nonlinear free vibration of a functionally graded nanobeam using nonlocal strain gradient theory and a novel hamiltonian approach. Int. J. Eng. Sci. 2016, 105, 12–27. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, Y.; Li, L. Torsion of a functionally graded material. Int. J. Eng. Sci. 2016, 109, 14–28. [Google Scholar] [CrossRef]
- Barati, M.R.; Zenkour, A. A general bi-helmholtz nonlocal strain-gradient elasticity for wave propagation in nanoporous graded double-nanobeam systems on elastic substrate. Compos. Struct. 2017, 168, 885–892. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 107, 77–97. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Dabbagh, A. Wave dispersion characteristics of orthotropic double-nanoplatesystem subjected to a longitudinal magnetic field. Microsyst. Technol. 2018, 24, 2929–2939. [Google Scholar] [CrossRef]
- Mirkalantari, S.A.; Hashemian, M.; Eftekhari, S.A.; Toghraie, D. Pull-in instability analysis of rectangular nanoplate based on strain gradient theory considering surface stress effects. Physica B 2017, 519, 1–14. [Google Scholar] [CrossRef]
- Li, L.; Li, X.; Hu, Y. Free vibration analysis of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 102, 77–92. [Google Scholar] [CrossRef]
- Xu, X.J.; Wang, X.C.; Zheng, M.L.; Ma, Z. Bending and buckling of nonlocal strain gradient elastic beams. Compos. Struct. 2017, 160, 366–377. [Google Scholar] [CrossRef]
- Zhu, X.; Li, L. Closed form solution for a nonlocal strain gradient rod in tension. Int. J. Eng. Sci. 2017, 119, 16–28. [Google Scholar] [CrossRef]
- Xu, X.-J.; Zhou, B.; Zheng, M.-L. Comment on “Free vibration analysis of nonlocal strain gradient beams made of functionally graded material” [Int. J. Eng. Sci. 2016, 102, 77–92]. Int. J. Eng. Sci. 2017, 119, 189–191. [Google Scholar] [CrossRef]
- Barretta, R.; Marotti de Sciarra, F. Constitutive boundary conditions for nonlocal strain gradient elastic nano-beams. Int. J. Eng. Sci. 2018, 130, 187–198. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Faghidian, S.A.; Luciano, R.; Marotti de Sciarra, F. Free vibrations of elastic beams by modified nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 133, 99–108. [Google Scholar] [CrossRef]
- Duan, K.; Li, L.; Hu, Y.; Wang, X. Enhanced interfacial strength of carbon nanotube/copper nanocomposites via Ni-coating: Molecular-dynamics insights. Physica E 2017, 88, 259–264. [Google Scholar] [CrossRef]
- Vodenitcharova, T.; Zhang, L.C. Effective wall thickness of a single-walled carbon nanotube. Phys. Rev. B 2003, 68, 165401. [Google Scholar] [CrossRef]
- De Domenico, D.; Askes, H. Stress gradient, strain gradient and inertia gradient beam theories for the simulation of flexural wave dispersion in carbon nanotubes. Compos. Part B 2018, 153, 285–294. [Google Scholar] [CrossRef]
- De Domenico, D.; Askes, H. Nano-scale wave dispersion beyond the First Brillouin Zone simulated with inertia gradient continua. J. Appl. Phys. 2018, 124, 205107. [Google Scholar] [CrossRef]



| FG Nano-Rod Constraints—Applied Load | Boundary Conditions | |
|---|---|---|
| Classical | Constitutive | |
| Non-Dimensional Axial Displacement | Applied Load |
|---|---|
| Uniform axial load | |
| Axial force at | |
| Uniform axial load at |
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| 0.1 | 0.1743260 | 0.1417390 | 0.1059420 | 0.0779542 | 0.0581303 |
| 0.2 | 0.2532480 | 0.2086930 | 0.1567630 | 0.1155910 | 0.0862860 |
| 0.3 | 0.3519010 | 0.2923860 | 0.2202890 | 0.1626370 | 0.1214810 |
| 0.4 | 0.4702840 | 0.3928170 | 0.2965200 | 0.2190920 | 0.1637140 |
| 0.5 | 0.6083970 | 0.5099870 | 0.3854570 | 0.2849560 | 0.2129860 |
| 0.6 | 0.7662410 | 0.6438960 | 0.4870980 | 0.3602290 | 0.2692980 |
| 0.7 | 0.9438160 | 0.7945430 | 0.6014450 | 0.4449110 | 0.3326480 |
| 0.8 | 1.1411200 | 0.9619290 | 0.7284970 | 0.5390030 | 0.4030370 |
| 0.9 | 1.3581600 | 1.1460500 | 0.8682550 | 0.6425040 | 0.4804650 |
| 1.0 | 1.5949200 | 1.3469200 | 1.0207200 | 0.7554140 | 0.5649320 |
| 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
| 0.1 | 0.0443324 | 0.0346164 | 0.0276280 | 0.0224832 | 0.0186098 |
| 0.2 | 0.0658438 | 0.0514320 | 0.0410586 | 0.0334183 | 0.0276642 |
| 0.3 | 0.0927330 | 0.0724514 | 0.0578469 | 0.0470872 | 0.0389824 |
| 0.4 | 0.1250000 | 0.0976747 | 0.0779928 | 0.0634899 | 0.0525641 |
| 0.5 | 0.1626450 | 0.1271020 | 0.1014960 | 0.0826264 | 0.0684094 |
| 0.6 | 0.2056680 | 0.1607330 | 0.1283580 | 0.1044970 | 0.0865184 |
| 0.7 | 0.2540680 | 0.1985680 | 0.1585770 | 0.1291010 | 0.1068910 |
| 0.8 | 0.3078470 | 0.2406070 | 0.1921530 | 0.1564380 | 0.1295270 |
| 0.9 | 0.3670030 | 0.2868500 | 0.2290870 | 0.1865100 | 0.1544270 |
| 1.0 | 0.4315370 | 0.3372960 | 0.2693790 | 0.2193150 | 0.1815910 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barretta, R.; Čanadija, M.; Marotti de Sciarra, F. Modified Nonlocal Strain Gradient Elasticity for Nano-Rods and Application to Carbon Nanotubes. Appl. Sci. 2019, 9, 514. https://doi.org/10.3390/app9030514
Barretta R, Čanadija M, Marotti de Sciarra F. Modified Nonlocal Strain Gradient Elasticity for Nano-Rods and Application to Carbon Nanotubes. Applied Sciences. 2019; 9(3):514. https://doi.org/10.3390/app9030514
Chicago/Turabian StyleBarretta, Raffaele, Marko Čanadija, and Francesco Marotti de Sciarra. 2019. "Modified Nonlocal Strain Gradient Elasticity for Nano-Rods and Application to Carbon Nanotubes" Applied Sciences 9, no. 3: 514. https://doi.org/10.3390/app9030514
APA StyleBarretta, R., Čanadija, M., & Marotti de Sciarra, F. (2019). Modified Nonlocal Strain Gradient Elasticity for Nano-Rods and Application to Carbon Nanotubes. Applied Sciences, 9(3), 514. https://doi.org/10.3390/app9030514







