Sensitivity Analysis of a Numerical Model for Percutaneous Auricular Vagus Nerve Stimulation
Abstract
:1. Introduction
2. Materials and Methods
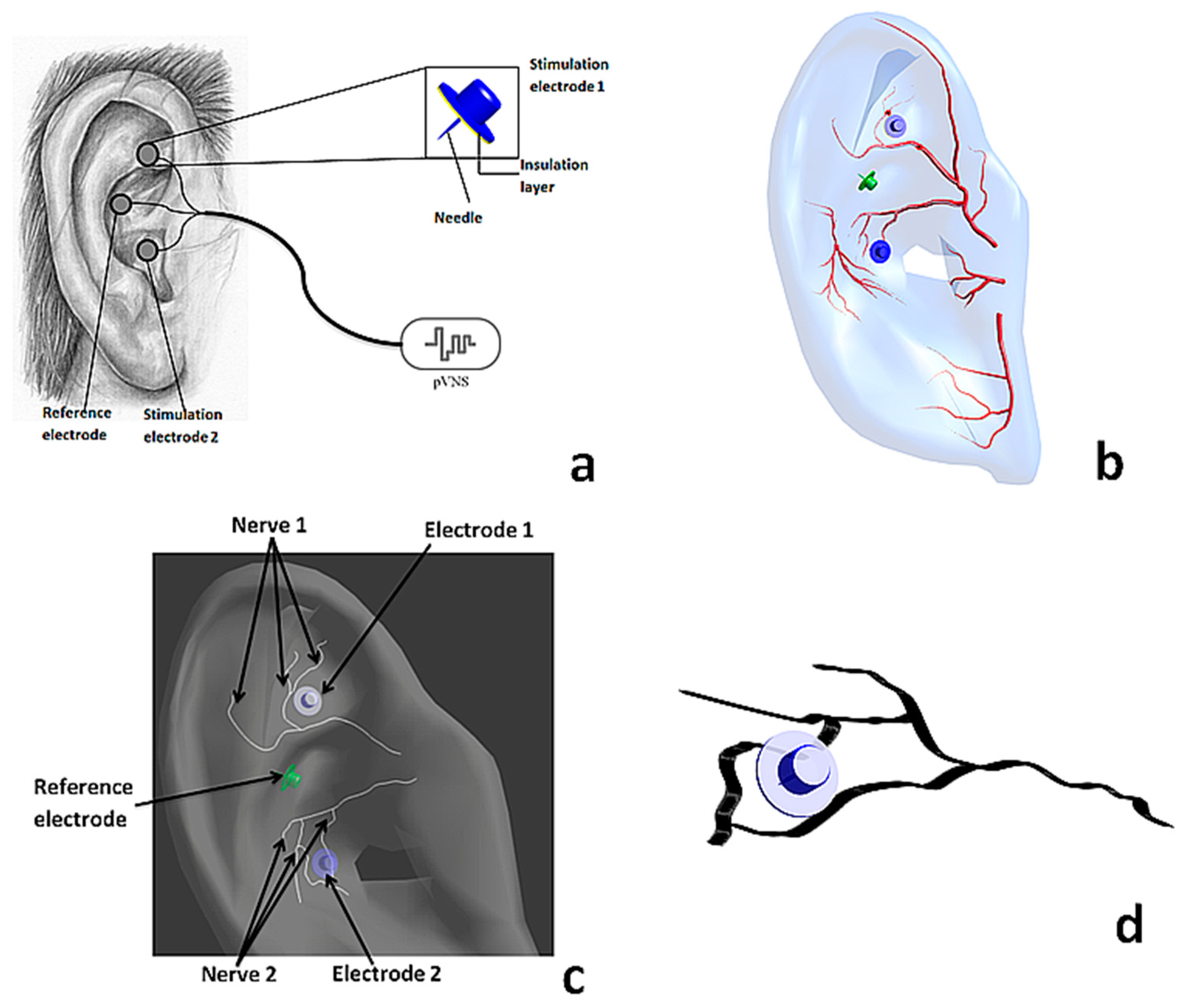
2.1. Simulation Platform
- and are the internal and external nodal voltages, respectively;
- is the nodal capacitance;
- is the axial internodal conductance;
- is the nodal membrane conductance;
- is time;
- is the axon diameter;
- is the internodal distance;
- is the membrane conductivity (30.4 mS/);
- is the nodal gap (2.5 μm);
- is the axoplasm resistivity (110 Ω·cm); and
2.2. Numerical Model
2.3. Sensitivity Assessment of the Numerical Model
- The model temperature was changed based on recent investigations of the variation in normal ear temperature measured in 2006 individuals [26].
3. Results
3.1. Electric Field Distribution
3.2. Sensitivity of the Stimulation Thresholds for Single Nerves
3.2.1. Effect of the Fiber Diameter
3.2.2. Effect of the Temperature
3.2.3. Effect of the Tissue Conductivity
3.3. Sensitivity of the Percentage of Stimulated Axons
3.3.1. Effect of the Fiber Diameter
3.3.2. Effect of the Axons Number
3.3.3. Effect of the Model Temperature
3.3.4. Effect of the Electrodes’ Position and Depth on the Percentage of Activated Axons
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Berthoud, H.; Neuhuber, W. Functional and chemical anatomy of the afferent vagal system. Auton. Neurosci. 2000, 85, 1–17. [Google Scholar] [CrossRef]
- Sator-Katzenschlager, S.M.; Michalek-Sauberer, A. P-Stim auricular electroacupuncture stimulation device for pain relief. Expert Rev. Med. Devices 2007, 4, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Payrits, T.; Ernst, A.; Ladits, E.; Pokorny, H.; Viragos, I.; Längle, F. Vagal stimulation—A new possibility for conservative treatment of peripheral arterial occlusion disease. Zentralblatt für Chirurgie 2011, 136, 431–435. [Google Scholar] [CrossRef] [PubMed]
- Széles, J.; Litscher, G. Objectivation of cerebral effects with a new continuous electrical auricular stimulation technique for pain management. Neurol. Res. 2004, 26, 797–800. [Google Scholar] [CrossRef] [PubMed]
- Tracey, K. Reflex control of immunity. Nat. Rev. Immunol. 2009, 9, 418–428. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Y.; He, W.; Jing, X.; Liu, J.L.; Rong, P.J.; Ben, H.; Liu, K.; Zhu, B. Transcutaneous Auricular Vagus Nerve Stimulation Protects Endotoxemic Rat from Lipopolysaccharide-Induced Inflammation. Evid.-Based Complement. Altern. Med. 2012, 2012, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Groves, D.; Brown, V. Vagal nerve stimulation: A review of its applications and potential mechanisms that mediate its clinical effects. Neurosci. Biobehav. Rev. 2005, 29, 493–500. [Google Scholar] [CrossRef] [PubMed]
- De Ferrari, G.; Crijns, H.; Borggrefe, M.; Milasinovic, G.; Smid, J.; Zabel, M.; Gavazzi, A.; Sanzo, A.; Dennert, R.; Kuschyk, J.; et al. Chronic vagus nerve stimulation: A new and promising therapeutic approach for chronic heart failure. Eur. Heart J. 2011, 32, 847–855. [Google Scholar] [CrossRef]
- Ellrich, J. Transcutaneous Vagus Nerve Stimulation. Eur. Neurol. Rev. 2011, 6, 254. [Google Scholar] [CrossRef]
- Kampusch, S.; Kaniusas, E.; Széles, J. New Approaches in Multi-Punctual Percutaneous Stimulation of the Auricular Vagus Nerve. In Proceedings of the 6th International IEEE EMBS Conference on Neural Engineering, San Diego, CA, USA, 6–8 November 2013; pp. 263–266. [Google Scholar]
- Peuker, E.; Filler, T. The nerve supply of the human auricle. Clin. Anat. 2002, 15, 35–37. [Google Scholar] [CrossRef]
- Samoudi, A.M.; Kampusch, S.; Tanghe, E.; Széles, J.C.; Martens, L.; Kaniusas, E.; Joseph, W. Numerical modeling of percutaneous auricular vagus nerve stimulation: A realistic 3D model to evaluate sensitivity of neural activation to electrode position. Med. Biol. Eng. Comput. 2017. [Google Scholar] [CrossRef] [PubMed]
- Saltelli, A.; Chan, K.; Scott, E.M. Sensitivity Analysis; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iooss, B.; Lemaitre, P. A review on global sensitivity analysis methods. Uncertainty Management in Simulation-Optimization of Complex Systems: Algorithms and Applications. In Uncertainty Management in Simulation-Optimization of Complex Systems; Springer: Berlin, Germany, 2015. [Google Scholar]
- Cacuci, D.G. Sensitivity theory for nonlinear systems. I. Nonlinear functional analysis approach. J. Math. Phys. 1981, 22, 2794. [Google Scholar] [CrossRef]
- Sim4Life, Zurich Med Tech. Available online: www.zurichmedtech.com/sim4life/ (accessed on 3 January 2019).
- Reilly, J.; Freeman, V.; Larkin, W. Sensory Effects of Transient Electrical Stimulation—Evaluation with a Neuroelectric Model. IEEE Trans. Biomed. Eng. 1985, 32, 1001–1011. [Google Scholar] [CrossRef] [PubMed]
- McNeal, D. Analysis of a Model for Excitation of Myelinated Nerve. IEEE Trans. Biomed. Eng. 1976, 23, 329–337. [Google Scholar] [CrossRef] [PubMed]
- Frankenhaeuser, B.; Huxley, A.F. The action potential in the myelinated nerve fiber of Xenopus Laevis as computed on the basis of voltage clamp data. J. Physiol. 1964, 171, 302. [Google Scholar] [CrossRef] [PubMed]
- Tilotta, F.; Lazaroo, B.; Laujac, M.; Gaudy, J. A study of the vascularization of the auricle by dissection and diaphanization. Surg. Radiol. Anat. 2009, 31, 259–265. [Google Scholar] [CrossRef]
- Alvord, L.; Farmer, B. Anatomy and orientation of the human external ear. J. Am. Acad. Audiol. 1997, 8, 383–390. [Google Scholar]
- Chaturvedi, A.; Foutz, T.; McIntyre, C. Current steering to activate targeted neural pathways during deep brain stimulation of the subthalamic region. Brain Stimul. 2012, 5, 369–377. [Google Scholar] [CrossRef] [Green Version]
- Safi, S.; Ellrich, J.; Neuhuber, W. Myelinated Axons in the Auricular Branch of the Human Vagus Nerve. Anat. Rec. 2016, 299, 1184–1191. [Google Scholar] [CrossRef] [Green Version]
- Erlanger, J.; Gasser, H.S. Electrical Signs and Nervous Activity; Univ of Pennsylvania Press: Philadelphia, PA, USA, 1938. [Google Scholar]
- Levander, M.S.; Grodzinsky, E. Variation in Normal Ear Temperature. Am. J Med. Sci. 2017, 354, 370–378. [Google Scholar] [CrossRef] [PubMed]
- Santis, V.; Chen, X.; Laakso, I.; Hirata, A. An equivalent skin conductivity model for low-frequency magnetic field dosimetry. Biomed. Phys. Eng. Express 2015, 1, 015201. [Google Scholar] [CrossRef]
- Schmid, G.; Cecil, S.; Überbacher, R. The role of skin conductivity in a low frequency exposure assessment for peripheral nerve tissue according to the ICNIRP 2010 guidelines. Phys. Med. Biol. 2013, 58, 4703–4715. [Google Scholar] [CrossRef] [PubMed]
- Samoudi, A.M.; Vermeeren, G.; Tanghe, E.; Van Holen, R.; Martens, L.; Josephs, W. Numerically simulated exposure of children and adults to pulsed gradient fields in MRI. J. Magn. Reson. Imaging 2016, 44, 1360–1367. [Google Scholar] [CrossRef] [PubMed] [Green Version]









| Parameter | Range | AV | Step | Reference |
|---|---|---|---|---|
| Number of axons (1) | 21–133 | 68 | 18 | [24] |
| Axon fiber diameter (μm) | 7–12 | 8 | 0.5 | [24] |
| Model temperature (°C) | 35.6–37 | 36.3 | 0.2 | [26] |
| Ear conductivity (S/m) | 0.1–0.7 | 0.4 | 0.1 | [27] |
| Electrode penetration depth (mm) | 0.8–1.5 | - * | 0.1 | [12] |
| Electrode position (mm) | (±0.1, ±0.1) | 0 | 0.1 | [12] |
| Parameter | SI (%) |
|---|---|
| Diameter of axon (N1, single axon) | 13 |
| Diameter of axon (N2, single axon) | 17 |
| Temperature (N1, single axon) | 0.9 |
| Temperature (N2, single axon) | 0.7 |
| Ear conductivity (single axons) | 0.1 |
| Diameter (nerve population, monophasic) | 14 |
| Diameter (nerve population, biphasic) | 13 |
| Number of axons | 18 |
| Temperature (nerve population) | 0.7 |
| Electrode penetration depth (nerve population) * | 22.3 |
| Electrode position (nerve population) * | 6.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samoudi, A.M.; Kampusch, S.; Tanghe, E.; Széles, J.C.; Martens, L.; Kaniusas, E.; Joseph, W. Sensitivity Analysis of a Numerical Model for Percutaneous Auricular Vagus Nerve Stimulation. Appl. Sci. 2019, 9, 540. https://doi.org/10.3390/app9030540
Samoudi AM, Kampusch S, Tanghe E, Széles JC, Martens L, Kaniusas E, Joseph W. Sensitivity Analysis of a Numerical Model for Percutaneous Auricular Vagus Nerve Stimulation. Applied Sciences. 2019; 9(3):540. https://doi.org/10.3390/app9030540
Chicago/Turabian StyleSamoudi, Amine M., Stefan Kampusch, Emmeric Tanghe, Jozsef C. Széles, Luc Martens, Eugenijus Kaniusas, and Wout Joseph. 2019. "Sensitivity Analysis of a Numerical Model for Percutaneous Auricular Vagus Nerve Stimulation" Applied Sciences 9, no. 3: 540. https://doi.org/10.3390/app9030540
APA StyleSamoudi, A. M., Kampusch, S., Tanghe, E., Széles, J. C., Martens, L., Kaniusas, E., & Joseph, W. (2019). Sensitivity Analysis of a Numerical Model for Percutaneous Auricular Vagus Nerve Stimulation. Applied Sciences, 9(3), 540. https://doi.org/10.3390/app9030540







