Topological Qubits as Carriers of Quantum Information in Optics

Abstract

Winding number is a topologically significant quantity that has found valuable applications in various areas of mathematical physics. Here, topological qubits are shown capable of formation from winding number superpositions and so of being used in the communication of quantum information in linear optical systems, the most common realm for quantum communication. In particular, it is shown that winding number qubits appear in several aspects of such systems, including quantum electromagnetic states of spin, momentum, orbital angular momentum, polarization of beams of particles propagating in free-space, optical fiber, beam splitters, and optical multiports.

1. Introduction

Topological quantities, such as winding numbers, Chern numbers, and Euler characteristics [1,2], depend on global properties of a system and are unchanged by smooth, local deformations of the space on which they are defined. They have become prominent in areas of physics ranging from particle physics and condensed matter physics to quantum communications and optics. Part of the reason for this surge of interest is their stability against disturbances: since they are integer-valued, rather than continuous functions of the system parameters, small continuous deformations of those parameters often leave them unchanged. In particular, the idea of information processing using quantum bits (qubits) that are encoded into topologically stable quantities has become an active research area, due to the possibilty of constructing quantum computing systems with reduced need for error correction. The most prominent candidate for such topological qubits are anyons [3,4], which are unfortunately challenging to produce and manipulate experimentally. Here we point out that topologically-based qubits appear naturally in optical systems and that these optical topological qubits are often relatively easy to produce, manipulate, and detect, allowing the possibility of their use in topological quantum information processing.

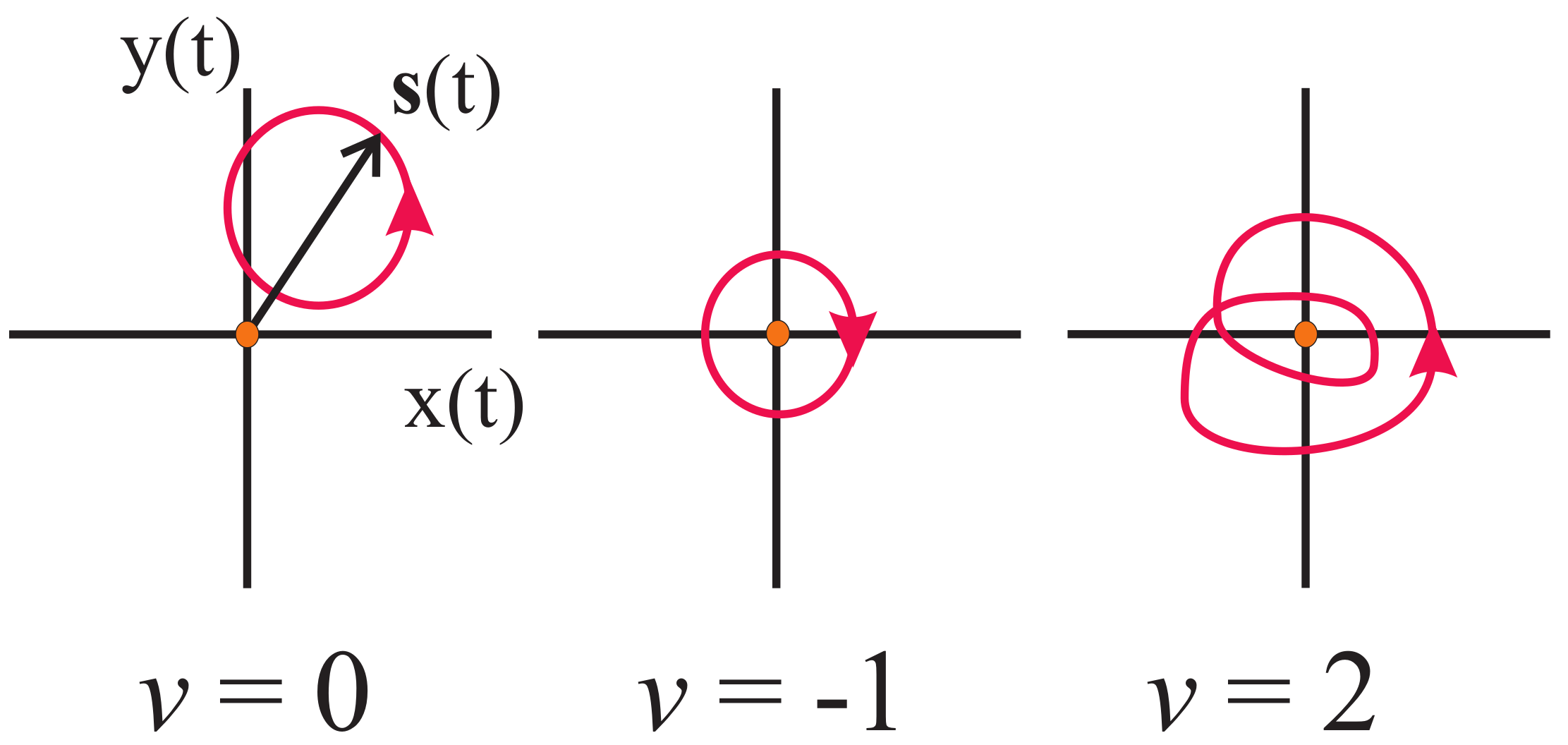
Consider a continuous closed curve $\mathit{s}\left(t\right)$ confined to a plane. This plane could be in position or momentum space, for example, or in an abstract Hilbert space. Most simply considered, the winding number $\nu$ [5] of $\mathit{s}\left(t\right)$ is the net number of counterclockwise turns traced out about the origin as parameter t runs from 0 to 1. The winding number is therefore well described using the polar coordinates $\mathit{s}\left(t\right)=\left\{r\left(t\right),\varphi \left(t\right)\right\}$ in the plane. The winding number $\nu \in \mathbb{Z}$, can be given as

$$\nu =\frac{\varphi \left(1\right)-\varphi \left(0\right)}{2\pi }.$$

(1)

In optical contexts, the winding number might count the number of rotations of a polarization vector, the amount of orbital angular momentum present, or the number of times a phase rotates as the photon momentum circles the Brillioun zone of a spatially periodic system.

Although this characterization can be generalized to include the winding number relative to any point p in the plane, the winding number about the origin is considered here without loss of generality; see Figure 1. Winding number is a topologically significant quantity, in that it is invariant under smooth deformations of the curve which don’t involve crossing the origin. When the origin is crossed, $\nu$ changes by a discrete integer amount. A wide range of physical systems whose descriptions have interesting topological aspects have been considered in optics, solid state physics, elementary particle physics, and elsewhere in the study of nature; a number of these can be considered via the winding number or its various generalizations, such as the Chern number [6]. In the quantum theoretical context in particular, quantum states with various values of winding number can be identified. Among the quantum applications is the characterization of distinct topological phases of materials and the topologically protected edge or boundary states between them [7,8,9,10,11,12]. Long known in momentum space in solid state systems, such topological states have recently been studied in photonic quantum walk systems as well [13,14,15,16].

In applications, the fact that the homotopy class of a curve does not depend on the the radial part of the parametrized curve $\mathit{s}\left(t\right)$ is of great value; for example, it means that physical quantities depending only on the winding number are very stable against the effects of small perturbations to the system. As a consequence of the lack of radial dependence, one can simply consider homotopy classes of maps from the circle to itself: any such curve is continuously deformable to one of maps of the circle, $S^1\to S^1:S\mapsto S^n$ with multiplication being that on the complex unit circle. (Recall that the i-th homotopy group $\pi \left(S^n\right)$ captures the continuous mapping of the i-dimensional sphere $S^i$ into the n-dimensional sphere $S^n$.) This does not distinguish two maps that can be continuously deformed from one to the other; only equivalence classes of mappings are pertinent. The homotopy groups of spheres algebraically describe the spheres as topological spaces with an operation of addition defined on their equivalence classes, giving rise to an Abelian group structure. The homotopy classes of maps from a circle to a topological space form the first homotopy group, which is some subgroup of the group of integers $\mathbb{Z}$ under addition; the winding number of a curve in the complex plane $\mathbb{C}$ (the set of points $x+iy$) labels its homotopy class [1,17].

Here, we provide a unified overview of the appearance of topological qubits arising in several areas of linear quantum optics, including quantum electromagnetic states (EM) of polarization, spin, momentum, orbital angular momentum (OAM) [18,19,20]. In particular, we show how winding number qubits, the natural description of which is in the so-called Bloch sphere $S^2$ (cf., e.g., [21], Section 1.2), appear in a sequence of three progressively more useful examples.

2. Quantum Momentum-Space Winding Number

Consider a complex-valued electromagnetic field, representing an optical beam. Recall that the winding number $\nu$ indicates the different equivalence classes in the homotopy group. Each equivalence class consists of the set of closed curves in space for which a point with the parametrized phase circles the origin in the complex plane $\nu$ times, as the angle in physical space circles the beam axis once. From the quantum perspective, the EM field can be viewed as possessing excited states, corresponding to discrete numbers of particles, called photons. The spin angular momentum of the photons gives rise to linear polarization states, which can become correlated with a winding number. Superpositions of polarization states then lead to superposition of winding number, or in other words, to winding number qubits.

One context in which such polarization-based winding number qubits can be formed was demonstrated already in the 1980’s [22]. For example, consider light traveling along an optical fibre wound helically into a coil characterized by a helix pitch angle $\theta$ relative to the local axis of the fiber (Figure 2). The photons propagate with momentum $\overrightarrow{k}\left(\tau \right)$ parallel to the fiber axis along an optical path parametrized by arclength $\tau$ along the fiber. These photons have a general spin state $|\overrightarrow{k},\sigma \rangle$ such that

$$\overrightarrow{s}·\overrightarrow{k}|\overrightarrow{k}\left(\tau \right),\sigma \rangle =\sigma |\overrightarrow{k}\left(\tau \right),\sigma \rangle ,$$

(2)

where eigenvalue $\sigma$ characterizes the photon helicity. Superpositions of photon helicity states lead to linearly polarized light. This polarized light can then be sent, for instance, into a single-mode isotropic fiber that is helically wound; cf., [23]. The momentum $\overrightarrow{k}$ is of fixed magnitude, but its direction rotates as the fiber is traversed; accordingly $\overrightarrow{k}$ takes a path on the intersection of a plane with the momentum 3-sphere, or in other words, on a circle in momentum space (Figure 3a). In this case the number of windings about the axis in momentum space also corresponds to the windings in physical space.

One can consider a non-trivial geometrical phase known as the Berry phase [24,25,26,27], which arises as a system is taken around a closed loop in parameter space. In his original paper on the subject [24], Berry showed that this phase takes the form

$$\gamma \left(C\right)=-\sigma \mathsf{\Omega }\left(C\right),$$

(3)

where C is the closed path traced out on the Bloch sphere by the quantum state of the photon as it winds along the curve, and where $\mathsf{\Omega }\left(C\right)$ is the solid angle subtended by the curve C relative to the origin of a relevant Hilbert space. This proportionality between geometric phase and areas or solid angles is generic behavior for geometric phases. In the case of interest here, the parameter being varied adiabatically is the direction of the momentum vector as the light winds around the helix, and the polarization state will trace out a curve C on the Bloch sphere as in Figure 3b. The Bloch sphere is often used to describe qubit states in a two-state system. In the current case, the basis qubits $|0\rangle$ and $|1\rangle$ are represented by vertically and horizontally polarized optical states, respectively. These lie at the poles of the Bloch sphere (which is often called the Poincaré sphere in the optical context), with diagonal linear polarizations, circular polarizations, and other equal superpositions of the horizontal and vertical states all lying on the equator.

If C is a circle subtending a cone with the origin as apex, and $\theta$ is the helix pitch angle relative to the local axis of the fiber, then geometric arguments [22] show that the solid angle subtended by C is given by

$$\mathsf{\Omega }\left(C\right)=2\pi \nu (1-cos\theta ).$$

(4)

The geometric phase, Equation (3), is therefore proportional to the winding number.

Consider a physical situation in which laser photons enter a non-birefringingent material in such a uniformly helically-wound fiber in the linear polarization superposition state

$$|\psi \rangle =\frac{1}{\sqrt{2}}\left(|\uparrow \rangle +|\to \rangle \right).$$

(5)

Ignoring any overall dynamical phase factors, the kinetics of the situation dictate that the exit polarization state of the photons leaving the fiber at the other end will be

$$|{\psi }^{\prime }\rangle =\frac{1}{\sqrt{2}}\left(exp\left(i\gamma \right)|\uparrow \rangle +exp(-i\gamma )|\to \rangle \right),$$

(6)

where $exp\left(\pm i\gamma \right)$ are the phases picked up during parallel transport of the optical state along the fiber. The physical interpretation of the Berry phase is that it measures the rotation of the linear polarization direction [23]. Using a fixed reference beam for comparison, $\gamma$ can be measured interferometrically, so that one can find the winding number for fixed pitch angle $\theta$:

$$\nu =\frac{\gamma }{2\pi (1-cos\theta )}.$$

(7)

Accordingly, for example, for $\gamma =\pi$ and a pitch angle of $\theta =\frac{\pi }{3}$, one has achieved winding number $\nu =1$. A coherent superposition can then be constructed via an optical-fiber Mach-Zehnder interferometer (cf., e.g., [21], Section 1.6) with an entry beamsplitter of variable transmittance that provides one path with such a twisted fiber and the other with an untwisted but otherwise identical fiber and an exit beamsplitter on which the two paths are recombined after an appropriate corresponding relative phase shift between the two arms to produce superpositions of the state of Equation (5), which has winding number 0, and that of Equation (6), that is, a variable-amplitude ${\alpha }_i$ ($\alpha \in \mathcal{C}$, $i\in \{0,1\}$, $|{\alpha }_0{|}^2+{|{\alpha }_1|}^2=1$) superposition of winding number 0 and winding number 1:

$$|\psi \rangle =\frac{1}{\sqrt{2}}\left({\alpha }_0|0;\nu =0\rangle +{\alpha }_1|{\gamma }_{+};\nu =1\rangle \right),$$

(8)

that is, a generic winding number qubit state on the surface of the Bloch sphere.

The topological aspects of this qubit are in some sense trivial; although it is produced by different windings in the coils, the state that leaves the coil is simply a superposition of two computational basis states with a relative phase shift. There is in no sense any topological protection of the output, despite the topological nature of its generation. In the next section, we consider a second example that partially remedies this deficiency.

3. Winding Number and Quantum OAM

In the study of quantum electromagnetic states of nonzero orbital angular momentum, it is most common to consider those arising in paraxial laser light beams, that is, beams propagating nearly parallel to a given axis. It is convenient to consider these states in the basis formed by the Laguerre–Gauss (LG) mode functions [28] of the field; these can be seen to depend on the winding number associated with the angle about the propagation axis $\varphi$; see Figure 4. In this context, the wave has a phase proportional to the azimuthal angle, $\psi \sim e^{il\varphi }$. The wavefunction is required to be single–valued, which forces parameter l to be integer–valued. It is in fact a conserved quantum number for the system: it characterizes the orbital angular momentum (OAM) eigenvalue of the corresponding field eigenstate and plays the role of winding number, $l\equiv \nu$ (see below).

Recall that, in general, the EM field possesses energy, momentum, and angular momentum, the last being associated with either spin or spatial degrees of freedom [29]. To see directly the connection to winding number, first note that, in free space, the Poynting vector $\overrightarrow{S}=c^2\overrightarrow{P}$ of the EM field, indicating the direction and magnitude of the field momentum $\overrightarrow{P}$ is

$$\overrightarrow{P}=\overrightarrow{E}\times \overrightarrow{B},$$

(9)

the vector cross-product of the electric ($\overrightarrow{E}$) and magnetic ($\overrightarrow{B}$) field intensities. It has been theoretically demonstrated [30] and experimentally observed [31] that LG modes of a laser beam carry an OAM for quantum states of linearly polarized light that are (in the paraxial case) independent of the corresponding spin-angular momentum (polarization) of the beam photons. Whereas the polarization is a result of the intrinsic spin-1 nature of the light, the OAM is a result of spatial structure imposed on the shape of its wavefronts. It has also been shown experimentally that the OAM carried by LG modes is conserved in spontaneous parametric down conversion (SPDC), with the OAM of the incoming pump beam determining the combined OAM of the two outgoing daughter modes [32].

In general, fields of laser beams can be described by the product of a Hermite polynomial and a spatial Gaussian, that is, they are described via the Hermite–Gaussian (HG) basis. However, it is convenient and most common to consider the states under consideration in this case in the basis formed by the Laguerre–Gauss (LG) mode functions $L_p^{\alpha }\left(x\right)$ of the field. If the phase front of the propagating field is helical, the Poynting vector of the beam possesses a non-trivial azimuthal component corresponding to the OAM circulating about the beam axis (along the z direction), tracing out a continuous closed curve in the x-y plane and forming an optical vortex on the axis with annular intensity profiles with radii increasing with the magnitude $|l|$ of the winding number, the modes being describable in that plane.

For the EM field in the paraxial case, only the region close to the propagation axis need be considered [33,34,35,36,37,38,39]; the LG laser mode functions of a paraxial cylindrical beam have the helical phase factor

$$exp(-il\varphi ).$$

(10)

This phase becomes undefined on the beam axis, so the axis corresponds to a singular vortex line. Applying the angular momentum operator about the propagation axis, ${\widehat{L}}_z=i\hslash \frac{\partial }{\partial \varphi }$, it is clear that the discrete integer value l, often called the topological charge, determines the quantized angular momentum eigenvalue

$$L_z=l\hslash ,$$

(11)

where $l\in \mathbb{Z}$ with the phase front turning counter-clockwise for $l>0$ and clockwise for $l<0$. From Equation (10), the phase $l\varphi$ winds around the origin l times each time the spatial azimuthal angle $\varphi$ circles the axis once; thus, l is the winding number of the phase function about the phase singularity on the beam axis. Such OAM states are described as solutions of the paraxial Helmholtz equation—i.e., in the approximation of a slowly varying envelope $A\left(r\right)$ of the wave $U\left(\overrightarrow{r}\right)=A\left(\overrightarrow{r}\right)exp\left(ikz\right)$ in the z direction, where $\frac{\partial A}{\partial z}\ll kA$ and $\frac{{\partial }^{2}A}{{\partial z}^2}\ll k^{2}A$ and slow means the variation of $A\left(\overrightarrow{r}\right)$ is slow within the distance $\lambda =2\pi /k$ of one wavelength along z; cf. e.g., [40], p. 51. As a specific example of such a field, the Laguerre–Gauss (LG) mode functions of the EM field ${\mathrm{LG}}_p^l$ have winding number l associated with the azimuthal dependence of the phase $\varphi$ as in Equation (10); the linear increase of phase tilts the wavefronts, producing a corkscrew-shaped wavefront that rotates about the axis like a screw as it propagates (Figure 4). The value of l determines how often the phase completes a full cycle of $2\pi$ as one winds around the spatial axis once (Figure 5).

The LG beam field state with orbital angular momentum $l\hslash$ with winding number l and with p radial nodes can be written explicitly as [41]

$$\begin{array}{cc}\hfill E_{lp}(r,z,\varphi )& =\frac{E_0}{w\left(z\right)}{\left(\frac{\sqrt{2}r}{w\left(z\right)}\right)}^{|l|}{e}^{-r^2/w^2\left(r\right)}{L}_p^{|l|}\left(\frac{2r^2}{w^2\left(r\right)}\right)\hfill \\ & \times e^{-ik{r}^{2}z/\left(2(z^2+z_R^2)\right)}{e}^{-i\varphi l+i(2p+|l|+1)arctan(z/z_R)},\hfill \end{array}$$

(12)

where $E_0$ is a constant and $w\left(z\right)=w_0\sqrt{1+\frac{z}{z_R}}$ is the beam radius at distance z; $z_R=\frac{\pi w_0^2}{\lambda }$ is called Rayleigh range. The $arctan(z/z_R)$ term is the well-known Gouy phase that routinely appears in beam optics. Integer p indexes the radial properties of the mode, with a central dark spot, $u_{lp}$ surrounded by p dark nodal rings; see Figure 6.

Creation and annihilation operators can be defined that connect quantum states with different p values, and a differential operator may be defined for which these states serve as eigenstates [42,43,44]. Examples of the intensity and phase of these beams are given in Figure 5 at $p=0$ for different values of l; plots of intensity for different p at fixed l are shown in Figure 6. Making use of orbital angular momentum beamsplitters [45], one can form qubit states of angular momentum and thereby of winding number [46]. In particular, one can make use of devices (analogous to polarization beam splitters) that select the optical path based on OAM, with one path for each of the distinguishable OAM states [45].

A coherent superposition of two OAM states can be constructed via an OAM analog of the Mach-Zehnder interferometer (cf., e.g., [21], Section 1.6) with an entry OAM beamsplitter of variable transmittance on which the two paths are recombined after an appropriate corresponding relative phase shift between the two arms to produce superpositions of the state of Equation (5), which has winding number 0, and that of Equation (6), that is, a variable-amplitude ${\alpha }_i$ ($\alpha \in \mathcal{C}$, $i\in \{0,1\}$, $|{\alpha }_0{|}^2+{|{\alpha }_1|}^2=1$) superposition of winding number 0 and winding number 1:

$$|\psi \rangle =\frac{1}{\sqrt{2}}\left({\alpha }_0|l=0\rangle +{\alpha }_1|l=1\rangle \right)=\frac{1}{\sqrt{2}}\left({\alpha }_0|\nu =0\rangle +{\alpha }_1|\nu =1\rangle \right)$$

(13)

that is, again, a generic qubit state on the surface of the Bloch sphere.

This OAM-based qubit avoids the main deficiency of the helical fiber example of the previous section. Each term in the outgoing superposition state has a well-defined winding number about a central vortex singularity. This winding number can be easily measured by standard methods, and the total winding number exhibits robust topological protection. There is still one drawback, however: in free space propagation, turbulence can cause the central vortex to break up into a set of daughter vortices, each of lower winding number. Although the total topological charge of all of the vortices together is conserved, the daughter vortices can become widely separated under propagation, so that any finite-size detector will register a reduced winding number [47,48]. Thus, the effective winding number can be reduced by external disturbances. In the next section, we consider another physical implementation of optical topological qubits that does not suffer from this problem

4. Multiports and Winding Number

Recall that quantum optical beams of photons can be divided by beam splitters (BS)—producing superposition states of paths for photons in ordinary space—and by their polarized versions (PBS), which selectively direct them in beams according to polarization characteristics. Ordinary beam splitters can be combined and/or modified to form more complex linear optical systems which elicit specific additional beam properties including winding number.

Standard beam splitters produce two output beams from one input beam, with no backward propagation back out to the input direction. Basic multiport generalizations of standard beamsplitters allow for more than two output beams, but only allow uni-directional net movement of photons—i.e., these quantum systems preclude reversals of beam direction inside themselves. Recently, a generalized multiport (MBS) has been proposed [49] and experimentally demonstrated [50] that allows a reversal of beam direction. These directionally unbiased multiports can be viewed as optical scattering vertices and thus can be combined into networks that give rise to scattering-based quantum walks on graph structures [51,52,53].

In such unbiased multiports, the beamsplitter input/output ports can be attached at their internal vertices, as shown in the inset of Figure 7 left. Adding a phase shifter allows the output of the multiport to be altered, so that different phase shifts at the vertices influence the interference between photon paths; when sufficiently small (see [49]), such a unit is described by an $n\times n$ unitary transition matrix $\widehat{U}$ whose rows and columns correspond to the input and output states at the ports—rows and columns correspond to the ports A, B, C.

When the internal phase shifts at all three mirror units are the same, one has

$$\widehat{U}\left(\theta \right)=\frac{e^{i\theta }}{2+i{e}^{i\theta }}\left(\begin{array}{ccc}1& i{e}^{-i\theta }-1& i{e}^{-i\theta }-1\\ i{e}^{-i\theta }-1& 1& i{e}^{-i\theta }-1\\ i{e}^{-i\theta }-1& i{e}^{-i\theta }-1& 1\end{array}\right),$$

(14)

where $\theta$ is the total phase shift at each mirror unit (comprising the mirror and phase plate).

Consider the optical units shown on the left in Figure 8 [51,52,53] each of which corresponds to an implementation of the abstract diamond graph on the right. Each diamond graph unit consists of a pair of three-point scattering vertices connected at two edges, with an additional phase shift on one connecting edge. Each of the optical units contains a pair of three-ports; each graph edge corresponds to an optical path and each multiport provides a physical implementation of an abstract three-point scattering vertex. Let the multiports be very small relative to the distance between them, so they can be treated as approximately pointlike in scale; each unit cell contains four multiports and two phase shifters. The phase shifts ${\varphi }_a$ and ${\varphi }_b$ in the two diamonds may be different from each other. In the configuration of units shown in Figure 9, the phase plates rotate the polarization by ${90}^{\circ }$. A time unit T is defined as the time to go from one diamond graph to the next. Photons present in the areas labeled a and b, bounded by the phase plates, represent two substates at each lattice site. When ${\varphi }_a\ne {\varphi }_b$, the two triangle graphs inside each cell will have different transmittance; take the transmission probabilities corresponding to the two graphs $T_a={|t_a|}^2$ and $T_b={|t_b|}^2$ then. The polarization state flips upon each passage through a phase plate allows the a and b states to be easily distinguished. Photons can be introduced to and released from this system via optical switches and circulators [18].

This system is directly analogous to a one-dimensional lattices of atoms, such as a polyacetylene molecule, in which topological effects are well-known. In such systems, there is an alternation of two distinct types of unit cells, leading to a periodic modulation of hopping amplitudes for electrons moving through the structure. As a result of this periodic modulation in space, the energy levels wrap around the Brillouin zone in a topologically nontrivial manner, leading to a nonzero winding number as the quasi-momentum traverses a full Brillouin zone. Here, similar effects occur in an optical system by having unit cells (pairs of diamond graphs) whose internal phase shifts alternate periodically. The transition amplitudes for photons hopping through the system then become periodically modulated in space. As in the condensed matter case, this leads to energy bands that wind nontrivially around the Brillouin zone. The transition amplitudes depend on the phase shifts in the diamond graphs, which can be arranged to be easily controlled (by varying path lengths or by using electro-optically controlled phase plates); as a result, the topological behavior of the system can also be readily controlled by the experimenter, in contrast to the situation in condensed matter systems.

Consider a discrete-time view of such a system. Its behavior can be described by a quantum Hamiltonian $\widehat{H}$ and the corresponding discrete-time evolution matrix $\widehat{U}=e^{-i\widehat{H}T}$ that takes the system forward one time-step T. (Here, the units are chosen such that $\hslash =1$.) There is then one photon collision with a diamond graph per unit time. For initial photon quantum state $|\psi (0)\rangle$, the state at time $t=nT$ is

$$|\psi \left(nT\right)\rangle ={\widehat{U}}^n|\psi \left(0\right)\rangle .$$

(15)

One can then define a quasi-momentum k on a one-dimensional periodic lattice made from a sequence of repeating unit cells, labeled by an integer, m; the quasi-momentum k and the position variable m is dimensionless and discrete. A quantum Hamiltonian expression for a system behaving in this way is

$$\begin{array}{cc}\hfill \widehat{H}=& |t_a|\sum _{m=1}^N\left(|m,b\rangle \langle m,a|+|m,a\rangle \langle m,b|\right)\hfill \\ & +|t_b|\sum _{m=1}^{N-1}\left(|m+1,a\rangle \langle m,b|+|m,b\rangle \langle m+1,a|\right),\hfill \end{array}$$

(16)

where the diamond graph transmission amplitudes for phase shifts are [51,52,53]:

$$t_j\left(k\right)=\frac{4(1+e^{-i{\varphi }_j})(1-e^{-i({\varphi }_j+4k)})}{e^{-4ik}{(1+e^{-i{\varphi }_j})}^2-{(3e^{-i({\varphi }_j+4k)}-1)}^2},$$

(17)

where $j=a,b$.

At each fixed lattice site m or each fixed k, this Hamiltonian can be written in terms of the identity matrix and the Pauli matrices [21].

$$\widehat{H}\left(k\right)=d_0\left(k\right)I+\overrightarrow{d\left(k\right)}·\overrightarrow{\sigma },$$

(18)

describing the dynamics in a two dimensional “internal” subspace labeled by the two substates present at each lattice site. The two energy levels are then separated by a momentum-dependent gap. Without loss of generality, an appropriate redefinition of states allows the quantum state amplitudes to be made real:

$$\begin{array}{c}\hfill \langle m,a|m,b\rangle =|t_a|\end{array}$$

(19)

$$\begin{array}{c}\hfill \langle m+1,a|m,b\rangle =\langle m,b|m+1,a\rangle =|t_b|.\end{array}$$

(20)

Transitions in which the photon “reflects off” the diamond graph, returning to the same subcell add a constant background term to the Hamiltonian and can be ignored for current purposes. The remaining terms are those that take a photon from one subcell to an adjacent subcell in a single time step of the corresponding quantum walk.

The nonvanishing coefficients of the Pauli matrices in Equation (18) are now

$$\begin{array}{ccc}\hfill d_x\left(k\right)& =& |t_a\left(k\right)|+|t_b\left(k\right)|cosk\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill d_y\left(k\right)& =& |t_b\left(k\right)|sink.\hfill \end{array}$$

(22)

As k goes from 0 to $2\pi$, $\overrightarrow{d}$ then traces out paths labeled by their winding numbers $\nu$ about the origin. These winding numbers are functions of photon hopping amplitudes: $\nu (v,w)=\nu (|t_a|,|t_b|)$. Because $t_a$ and $t_b$ vary only weakly with k, the path traced out by $\overrightarrow{d\left(k\right)}$ encloses the origin and, so, has nonzero winding number if $|t_b|>|t_a|$. Different values of the phase shifts allow solutions with both zero and nonzero winding numbers to occur: Evaluation of Equations (17), (21) and (22) for a range of ${\varphi }_a$ and ${\varphi }_b$ values readily shows that varying these phases causes the path traced out by $\overrightarrow{d}$ to shift horizontally and change radius, leading to transitions between winding numbers 0 and 1 due to the lack of enclosure to enclosure of the origin in this space as shown in Figure 10. This system is topologically equivalent to the well-known Su-Schreiffer-Heeger (SSH) system [54] and reduces exactly to the pure SSH model when the transmission amplitudes are independent of k.

Different phase values in the two diamond graphs therefore lead to different topological phases, distinguished by their distinct winding numbers. By attaching two chains of these graphs with different winding numbers on each chain there arise localized, topologically-protected states at their mutual boundaries [7,8,9,18]. With appropriate choices of phase shifts ${\varphi }_a$ and ${\varphi }_b$, a persistent probability of finding the photon at the boundary between the two path topologies appearing in the complex system described in Section 4 can be achieved; a localized quantum optical state protected from noise influences by winding-number [8,9,18] arises when two chains of directionally unbiased three-ports, the two chains having different winding numbers [18,20].

In addition, it has been shown [55,56] that at the boundaries between regions of different winding number there is strong reflection of the wave function. By appropriate choice of parameters transmission between regions can be made arbitrarily small; thus winding-number bit flip errors can be made negligible. Furthermore, by entangling the winding number with a more easily measured variable, such as polarization, the value of the winding number bit can be read in a straightforward manner by measurement of the variable entangled to it [20].

Such winding number-polarization entangled states can be achieved in practice by making the phase shifts in the diamond graphs polarization-dependent [20]. In this way, if a photon is prepared in a polarization superposition state

$$|{\psi }_0\rangle ={\alpha }_0|\uparrow \rangle +{\alpha }_1|\to \rangle$$

(23)

and placed into the chain, it will give rise to the winding number superposition state

$$|\psi \rangle ={\alpha }_0|\nu =0,\uparrow \rangle +{\alpha }_1|\nu =1,\to \rangle ,$$

(24)

where the 0 and 1 represent winding number values [20]. Interpreting these winding numbers as bit values, the photons now form a winding number qubit, directly analogous to those of Equations (8) and (13), and spanning the full set of quantum states in a two-dimensional complex Hilbert space. The topological stability of the winding number state suppresses bit flips, but since each winding number is unambiguously associated with a given value of a more easily measured variable (polarization), the bit value can easily be read out by polarization measurements.

The multiport system produces winding number without the disadvantages of the previous examples: the qubits can be readily produced, manipulated, and detected. Examining Figure 7, it can be seen that there are no ports open to the vacuum at any of the beam splitters; as a result, no vacuum noise is introduced, in contrast to other quantum optical approaches. Further, since the qubit values in this system depend only on the discrete topological class of the energy band, small perturbations of any kind generally introduce no errors; thus normal levels of noise in the system have little effect, with robust topological protection of the qubits.

5. Conclusions

It has been shown that winding number, a topologically significant quantity, can be used as a coding parameter for the carrying of quantum information in linear optical systems, the most common realm for quantum communication. In particular, it was shown that winding number can be coded in several physical quantities of such systems, including quantum electromagnetic states of spin, momentum, orbital angular momentum, polarization of beams of particles propagating in free-space, optical fiber, beam splitters, and optical multiports. By taking two winding number values as bit values, the photons considered are seen as carriers of winding number qubits, because bit pairs have become qubit pairs by being encoded into a pair of superposable quantum states in a two-dimensional complex Hilbert space. Making use of the topologically-induced robustness of winding number qubits opens new possibilities for building error-protection into information processing systems.