Influence of Stress and Crack Patterns on the Sensitive Characteristics of Fissure Sandstone Permeability under Hydromechanical Coupling
Abstract
:1. Introduction
2. Materials and Methods
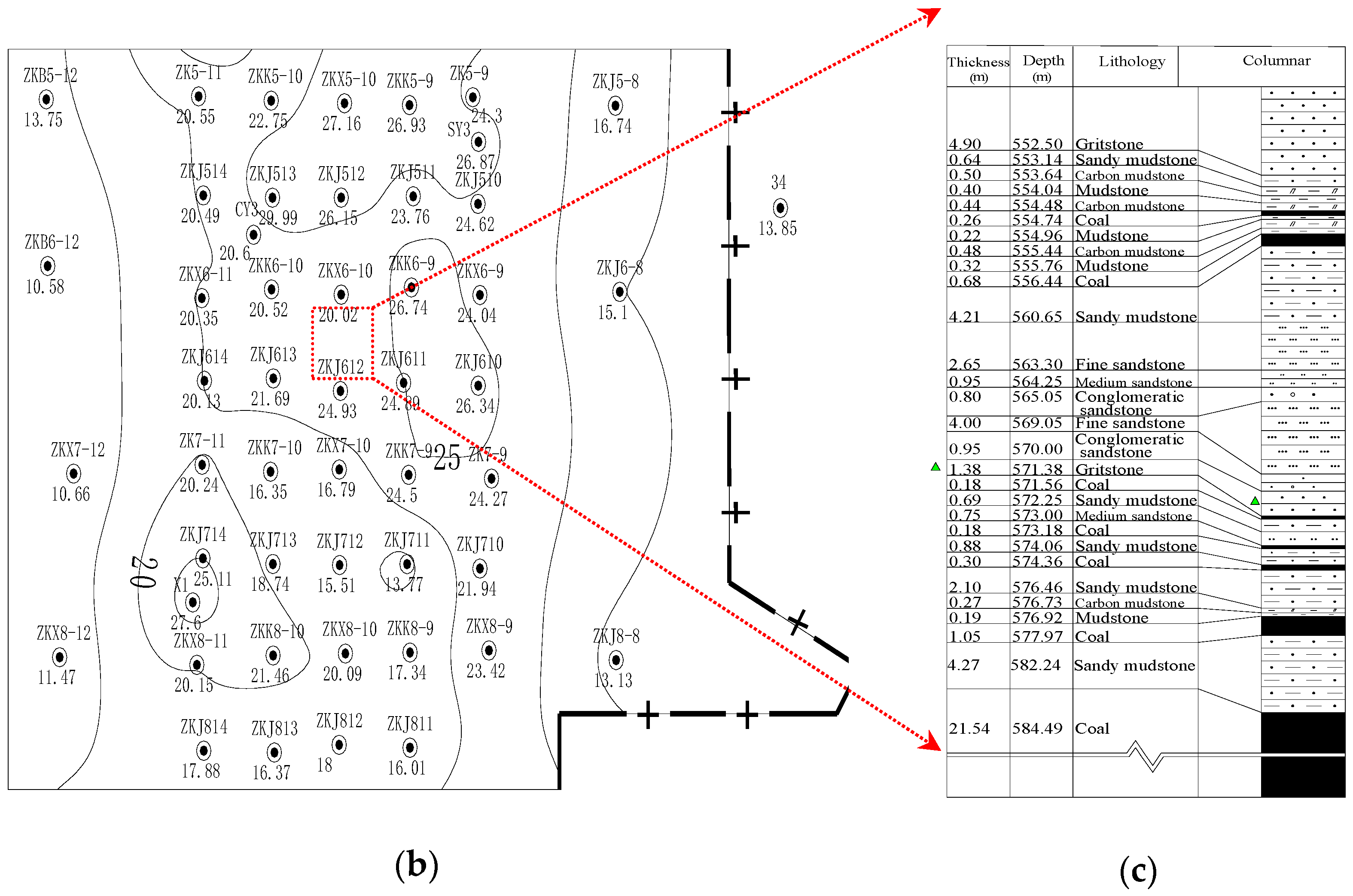
2.1. Study Case
2.2. Contact Constitutive Model
2.3. Numerical Simulation Model Construction
2.3.1. Numerical Model Parameter Validation
2.3.2. Hydraulic Parameter Fitting
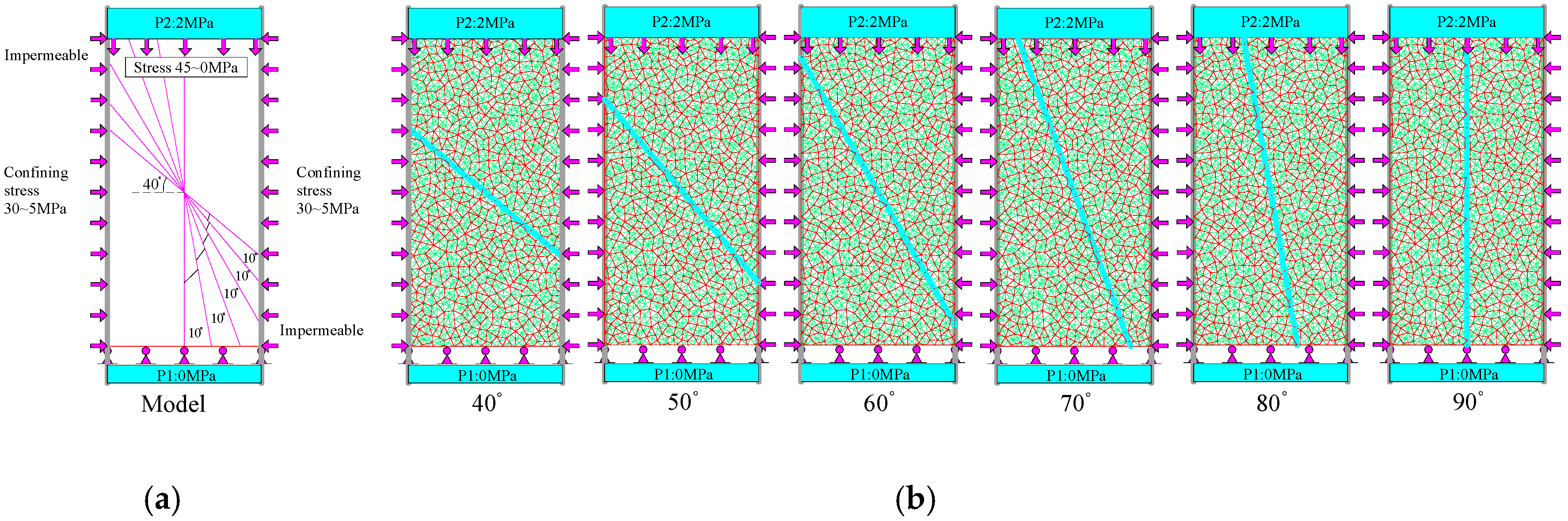
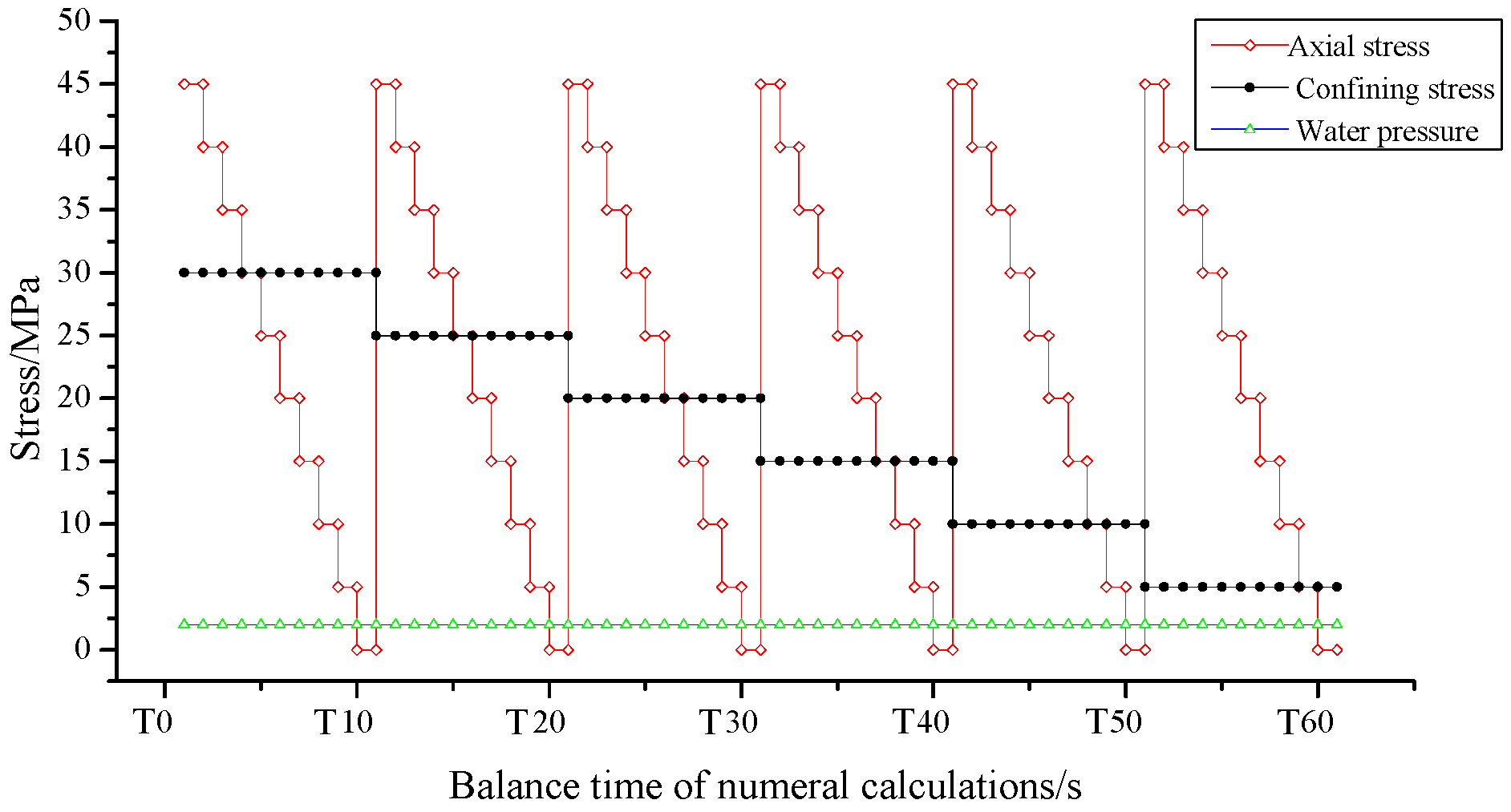
2.3.3. Determination of Numerical Simulation Scheme
3. Results and Discussion
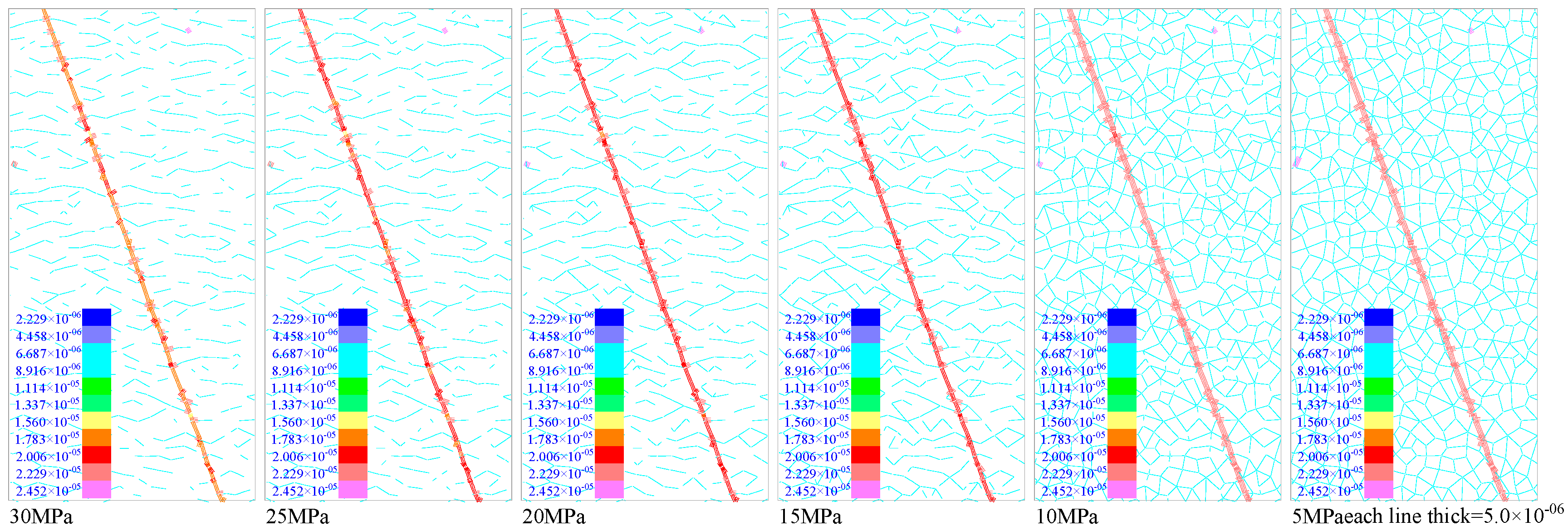
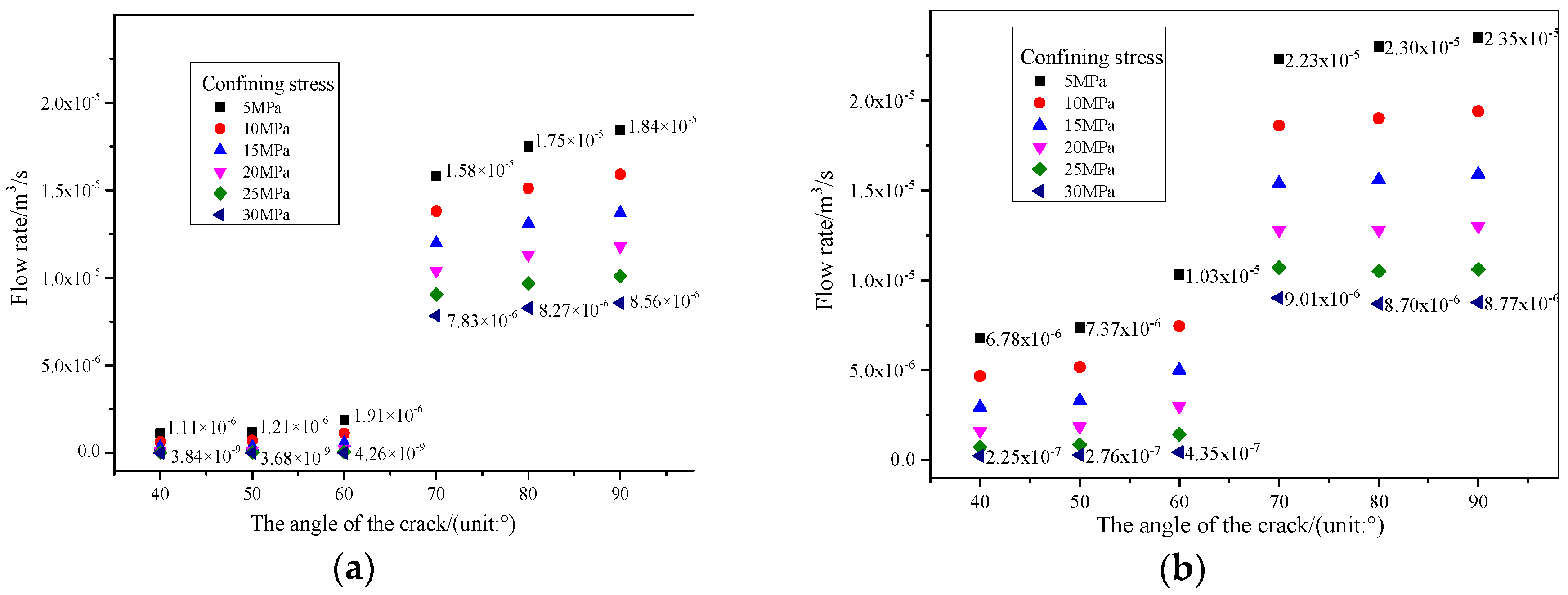
3.1. Experimental Results of Single-Crack Specimens with Different Angles
3.1.1. Fixed Angle
3.1.2. Fixed Axial Pressure
3.1.3. Fixed Confining Pressure
3.2. Average Joint Aperture of the Single Crack Model with Different Angles
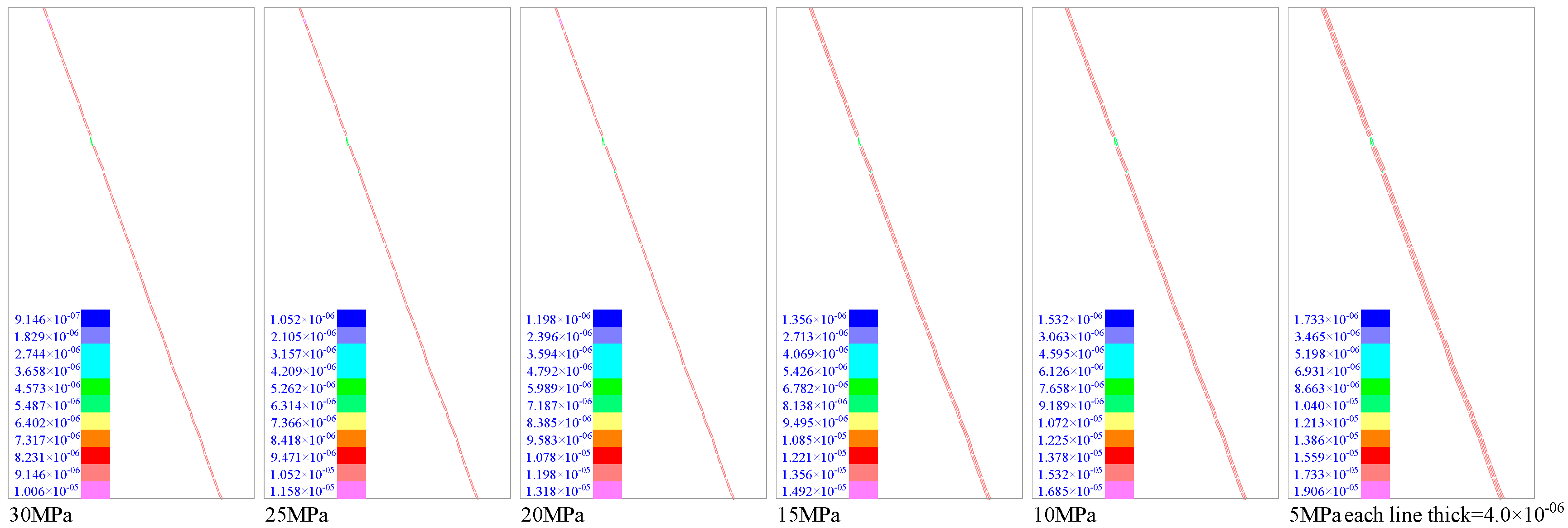
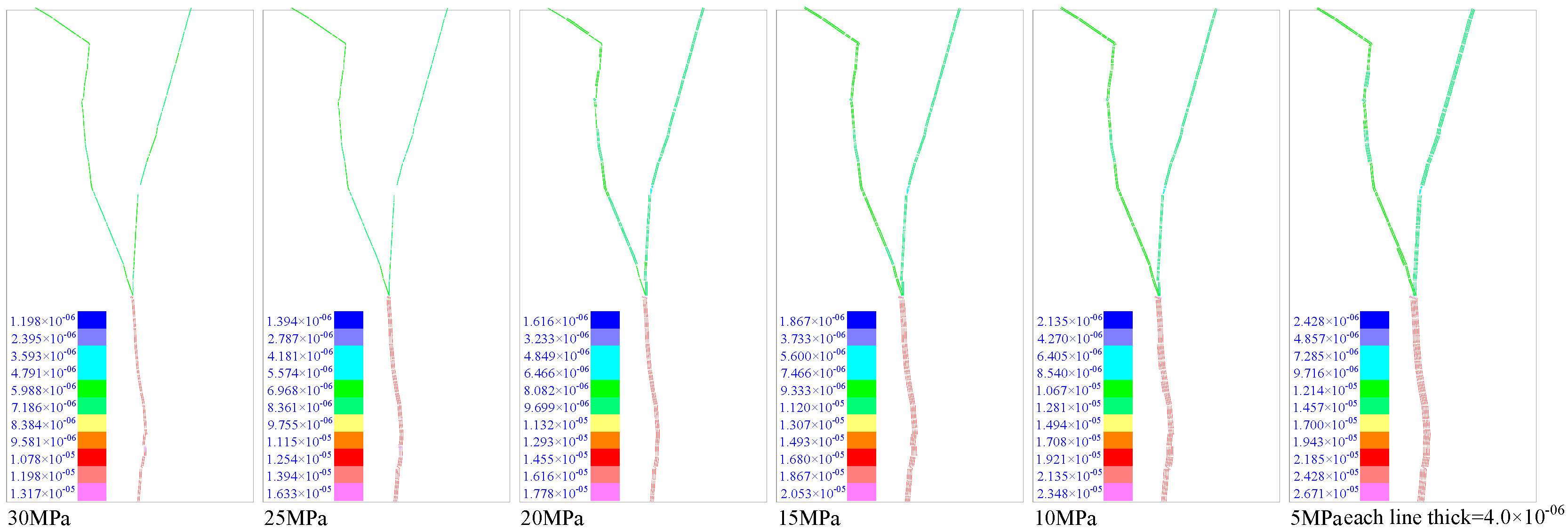
3.3. Experimental Results for the Four Typical Crack Models
3.3.1. Simulation Results of the “Type Y” Crack Model
3.3.2. Fixed Axial Pressure
3.3.3. Fixed Confining Pressure
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Terminology
| T | Joint tensile strength |
| τs | Joint shear stress |
| q | Flow rate |
| a | Width of the joint |
| W | Fluid viscosity |
| l | Length of the joint |
| ∆P | Pressure between the domains |
| k | Permeability coefficient of the joints |
| σn | Normal stress on the joint |
| kn | Stiffness of the joints |
| K | Intact bulk modulus |
| G | Intact shear modulus |
| kn | Normal stiffness of contacts |
| ks | Shear stiffness of contacts |
| a0 | Contact hydraulic aperture at zero normal stress |
| ares | Residual hydraulic aperture |
| amax | Maximum hydraulic aperture |
| CHA | Contact hydraulic aperture |
| FHA | Fracture hydraulic aperture |
| R | Ratio of FHA to CHA |
References
- Zheng, S.H.; Zhao, Y.S.; Duan, K.L. An experimental study on the permeability law of natural fracture under 3-d stresses. Chin. J. Rock Mech. Eng. 1999, 18, 133–136. [Google Scholar] [CrossRef]
- Forster, I.; Enever, J. Hydrogeological Response of Overburden Strata to Underground Mining; Report 1; Office of Energy: Washington, DC, USA, 1992; p. 104. [Google Scholar]
- Choi, S.K.; Wold, M.; Wood, J. Modelling of interburden gas flows at Appin Colleiry. In Proceedings of the Symposium on Safety on Mines: The Role of Geology, Newcastle, UK, 24–25 November 1997; pp. 105–117. [Google Scholar]
- Xue, Y.; Gao, F.; Liu, X.; Liang, X. Permeability and pressure distribution characteristics of the roadway surrounding rock in the damaged zone of an excavation. Int. J. Min. Sci. Technol. 2017, 27, 211–219. [Google Scholar] [CrossRef]
- Xia, B.; Zhang, X.; Yu, B.; Jia, J. Weakening effects of hydraulic fracture in hard roof under the influence of stress arch. Int. J. Min. Sci. Technol. 2018. [Google Scholar] [CrossRef]
- Zhao, Y.L. The fluid-solid coupling response in fractured rock mass and its engineering application. In The Introduction, 1st ed.; Science Press: Beijing, China, 2016; pp. 1–6. ISBN 978-7-03-046557-3. [Google Scholar]
- Pratt, H.R.; Swolfs, H.S.; Brace, W.F.; Black, A.D.; Handin, J.W. Elastic and transport properties of an in situ jointed granite. Int. J. Rock Mech. Min. 1977, 14, 35–45. [Google Scholar] [CrossRef]
- Kranz, R.L.; Frankel, A.D.; Engelder, T.; Scholz, C.H. The permeability of whole and jointed Barre granite. Int. J. Rock Mech. Min. 1979, 18, 225–234. [Google Scholar] [CrossRef]
- Chen, X.; Yu, J.; Tang, C.; Li, H.; Wang, S. Experimental and Numerical Investigation of Permeability Evolution with Damage of Sandstone Under Triaxial Compression. Rock Mech. Rock. Eng. 2017, 50, 1529–1549. [Google Scholar] [CrossRef]
- Zhu, W.; Wong, T.F. The transition from brittle faulting to cataclastic flow: Permeability evolution. J. Geophys. Res. 1997, 102, 3027–3041. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Montesi, L.G.J.; Wong, T.F. Shear-enhanced compaction and permeability reduction: Triaxial extension tests on porous sandstone. Mech. Mater. 1997, 25, 199–214. [Google Scholar] [CrossRef]
- Wang, J.A.; Park, H.D. Fluid permeability of sedimentary rocks in a complete stress-strain process. Eng. Geol. 2002, 63, S0013–S7952. [Google Scholar] [CrossRef]
- Huang, R.Q.; Huang, D. Experimental research on mechanical properties of granites under unloading condition. Chin. J. Rock Mech. Eng. 2008, 27, 2205–2213. [Google Scholar] [CrossRef]
- Jin, Y.U.; Hong, L.I.; Xu, C.; Cai, Y.Y.; Mu, K.; Zhang, Y.Z. Experimental study of permeability and acoustic emission characteristics of sandstone during processes of unloading confining pressure and deformation. Chin. J. Rock Mech. Eng. 2014, 33, 69–79. [Google Scholar] [CrossRef]
- Yin, G.; Jiang, C.; Wang, J.G.; Xu, J. Geomechanical and flow properties of coal from loading axial stress and unloading confining pressure tests. Int. J. Rock Mech. Min. 2015, 76, 155–161. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, T.; Yu, Q.; Xu, T.; Shi, W.; Li, S. Study of a Seepage Channel Formation Using the Combination of Microseismic Monitoring Technique and Numerical Method in Zhangmatun Iron Mine. Rock Mech. Rock. Eng. 2016, 49, 1–10. [Google Scholar] [CrossRef]
- Qu, Q.; Xu, J.; Wu, R.; Qin, W.; Hu, G. Three-zone characterisation of coupled strata and gas behaviour in multi-seam mining. Int. J. Rock Mech. Min. 2015, 78, 91–98. [Google Scholar] [CrossRef]
- Adhikary, D.P.; Guo, H. Modelling of Longwall Mining-Induced Strata Permeability Change. Rock Mech. Rock. Eng. 2015, 48, 345–359. [Google Scholar] [CrossRef]
- Lisjak, A.; Grasselli, G. A review of discrete modeling techniques for fracturing processes in discontinuous rock masses. J. Rock Mech. Geotech. Eng. 2014, 6, 301–314. [Google Scholar] [CrossRef] [Green Version]
- Jing, L.; Hudson, J.A. Numerical methods in rock mechanics. Int. J. Rock Mech. Min. Sci. 2002, 39, 409–427. [Google Scholar] [CrossRef]
- Bai, Q.S.; Tu, S.H.; Zhang, C. DEM investigation of the fracture mechanism of rock disc containing hole(s) and its influence on tensile strength. Theor. Appl. Fract. Mech. 2016, 86. [Google Scholar] [CrossRef]
- Ghazvinian, E.; Diederichs, M.S.; Quey, R. 3D random Voronoi grain-based models for simulation of brittle rock damage and fabric-guided microfracturing. J. Rock Mech. Geotech. Eng. 2014, 6, 506–521. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. UDEC: Universal Distinct Element Code; Version 5.0; ICG: Minneapolis, MN, USA, 2011. [Google Scholar]
- Damjanac, B.; Fairhurst, C. Evidence for a long-term strength threshold in crystalline rock. Rock Mech. Rock Eng. 2010, 43, 513–531. [Google Scholar] [CrossRef]
- Kazerani, T.; Yang, Z.Y.; Zhao, J.A. discrete element model for predicting shear strength and degradation of rock joint by using compressive and tensile test data. Rock Mech. Rock Eng. 2012, 45, 695–709. [Google Scholar] [CrossRef]
- Abdollahipour, A.; Marji, M.F.; Bafghi, A.Y. DEM simulation of confining pressure effects on crack opening displacement in hydraulic fracturing. Int. J. Min. Sci. Technol. 2016, 26, 557–561. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, S.J.; Zhang, D.S.; Fan, G.W.; Wang, Z. Determination of the Height of the Water-Conducting Fractured Zone in Difficult Geological Structures: A Case Study in Zhao Gu No. 1 Coal Seam. Sustainability 2017, 9, 1077. [Google Scholar] [CrossRef]
- Yao, C.; Jiang, Q.H.; Shao, J.F. Numerical simulation of damage and failure in brittle rocks using a modified rigid block spring method. Comput. Geotech. 2015, 64, 48–60. [Google Scholar] [CrossRef]
- Zhang, C.; Tu, S.; Zhang, L.; Chen, M. A study on effect of seepage direction on permeability stress test. Arab. J. Sci. Eng. 2016, 41, 1–14. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, D.; Wang, Z.; Chen, M. Influence of stress and water pressure on the permeability of fissured sandstone under hydromechanical coupling. Mine Water Environ. 2018, 37, 1–12. [Google Scholar] [CrossRef]
- Gao, F.Q.; Stead, D. The application of a modified Voronoi logic to brittle fracture modelling at the laboratory and field scale. Int. J. Rock Mech. Min. 2014, 68, 1–14. [Google Scholar] [CrossRef]
- Gao, F.Q. Simulation of Failure Mechanisms Around Underground Coal Mine Openings Using Discrete Element Modelling. Ph.D. Dissertation, Simon Fraser University, Burnaby, BC, Canada, 2013. [Google Scholar]
- Bai, Q.S.; Tu, S.H.; Zhang, C. Discrete element modeling of progressive failure in a wide coal roadway from water-rich roofs. Int. J. Coal Geol. 2016, 167, 215–229. [Google Scholar] [CrossRef]
- Wang, Z. Study on Permeability Evolution Law of Overlying Strata under Ultra-Thick Seam Mining in Laosangou Coal Mine. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2017. [Google Scholar]
- Xie, H.P.; Chen, Z.D. Analysis of Rock Fracture Micro-Mechanism. J. China Coal Soc. 1989, 14, 57–67. [Google Scholar] [CrossRef]
- Ramandi, H.L.; Mostaghimi, P.; Armstrong, R.; Saadatfar, M.; Pinczewski, W.V. Porosity and permeability characterization of coal: A micro-computed tomography study. Int. J. Coal Geol. 2016, 154–155, 57–68. [Google Scholar] [CrossRef]

























| Properties | Values |
|---|---|
| Intact bulk modulus, K (GPa) | 6.5 |
| Intact shear modulus, G (GPa) | 2.8 |
| Normal stiffness of contacts, kn (GPa/m) | 6100.0 |
| Shear stiffness of contacts, ks (GPa/m) | 2440.0 |
| Contact cohesion, ccont (MPa) | 29.4 |
| Contact friction angle, Φcont (◦) | 29.0 |
| Contact tensile strength, σtcont (MPa) | 6.9 |
| Residual cohesion (MPa) | 2.0 |
| Residual friction (°) | 15.0 |
| Residual tension (MPa) | 0.0 |
| Contact hydraulic aperture at zero normal stress, a0 (m) | 7.02 × 10−6 |
| Residual hydraulic aperture, ares (m) | 1 × 10−7 |
| Lithology | Confining Pressure | Osmotic Pressure Difference | Peak Stress | Post-Peak Permeability |
|---|---|---|---|---|
| gritstone | 12 MPa | 2 MPa | 82 MPa | 4.0 × 10−13 cm2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, G.; Zhang, D.; Zhang, S.; Zhao, Q.; Yu, W.; Liang, S. Influence of Stress and Crack Patterns on the Sensitive Characteristics of Fissure Sandstone Permeability under Hydromechanical Coupling. Appl. Sci. 2019, 9, 641. https://doi.org/10.3390/app9040641
Fan G, Zhang D, Zhang S, Zhao Q, Yu W, Liang S. Influence of Stress and Crack Patterns on the Sensitive Characteristics of Fissure Sandstone Permeability under Hydromechanical Coupling. Applied Sciences. 2019; 9(4):641. https://doi.org/10.3390/app9040641
Chicago/Turabian StyleFan, Gangwei, Dongsheng Zhang, Shuai Zhang, Qiang Zhao, Wei Yu, and ShuaiShuai Liang. 2019. "Influence of Stress and Crack Patterns on the Sensitive Characteristics of Fissure Sandstone Permeability under Hydromechanical Coupling" Applied Sciences 9, no. 4: 641. https://doi.org/10.3390/app9040641
APA StyleFan, G., Zhang, D., Zhang, S., Zhao, Q., Yu, W., & Liang, S. (2019). Influence of Stress and Crack Patterns on the Sensitive Characteristics of Fissure Sandstone Permeability under Hydromechanical Coupling. Applied Sciences, 9(4), 641. https://doi.org/10.3390/app9040641





