Numerical Modelling of the Fire Extinguishing Gas Retention in Small Compartments
Abstract
:Featured Application
Abstract
1. Introduction
1.1. Fire Protection in Industrial Safety
1.2. Use of Gaseous Fire Extinguishing Systems
1.3. Limitations of Standardised Models
- Model with a sharp interface between extinguishing gas and air, presented in NFPA2001 [22];
2. Materials and Methods
2.1. Experimental Study on Extinguishing Gas Retention Time
2.2. Numerical Modelling of Gaseous Fire-Extinguishing Systems
- -
- Difference of buoyancy between gas and air, and the phenomena that take part at the interface of the buoyant layer (e.g., diffusion, turbulent mixing);
- -
- Flow of clean air into to the protected compartment through leakages;
- -
- Flow of extinguishing gas out of the protected compartment through leakages;
- -
- The temperature gradient in and out of the protected compartment.
- -
- Forced ventilation inside of the protected compartment;
- -
- The non-uniform release of the gas and the use of local pressure relief dampers;
- -
- Heat sources in the compartment (e.g., server heat sinks);
- -
- Pressure gradient outside of the chamber (e.g., due to wind effects);
- -
- The source of fire itself.
2.3. General Description of the CFD Method
2.4. Numerical Model—Assumptions
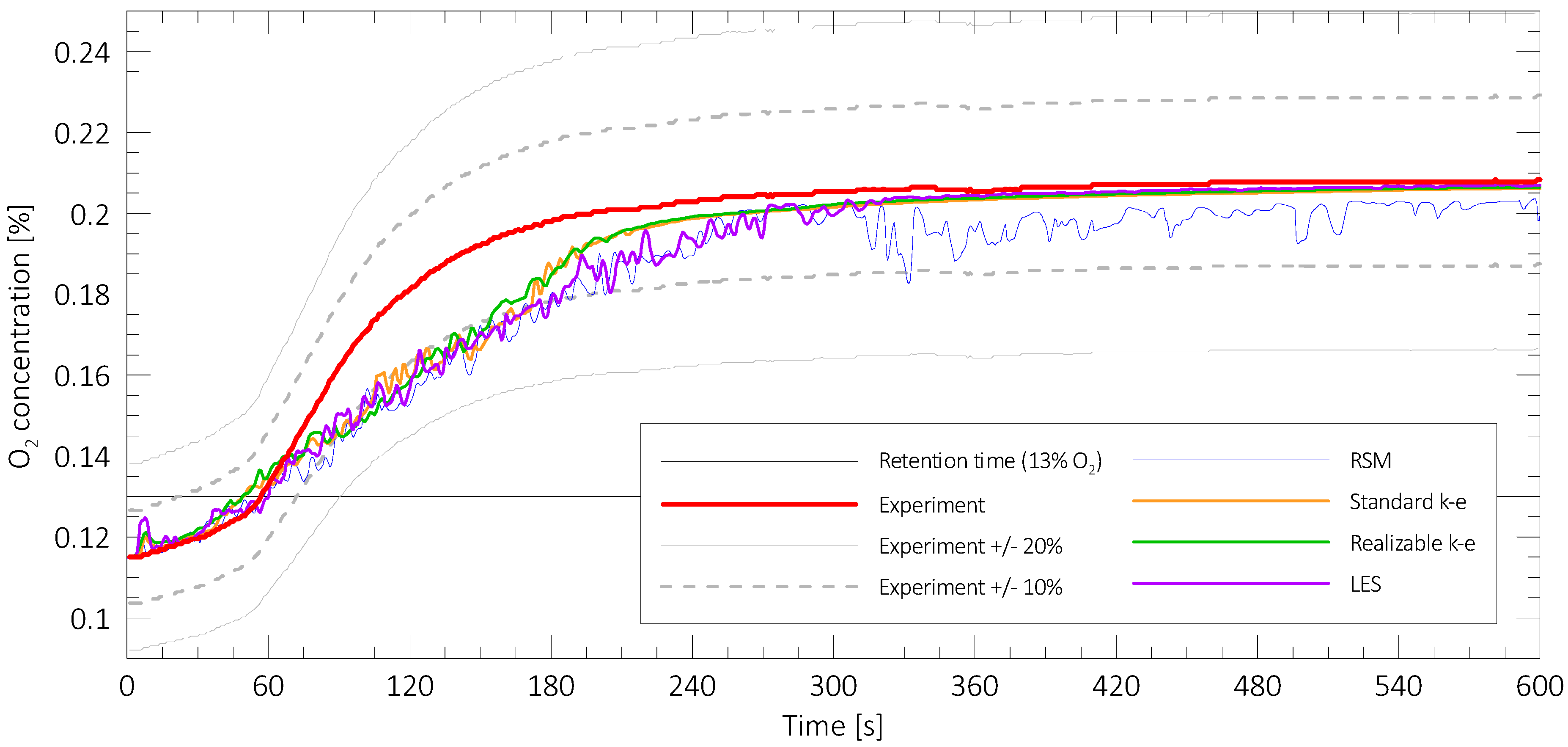
2.5. Turbulent Flow Sub-Model Sensitivity Study
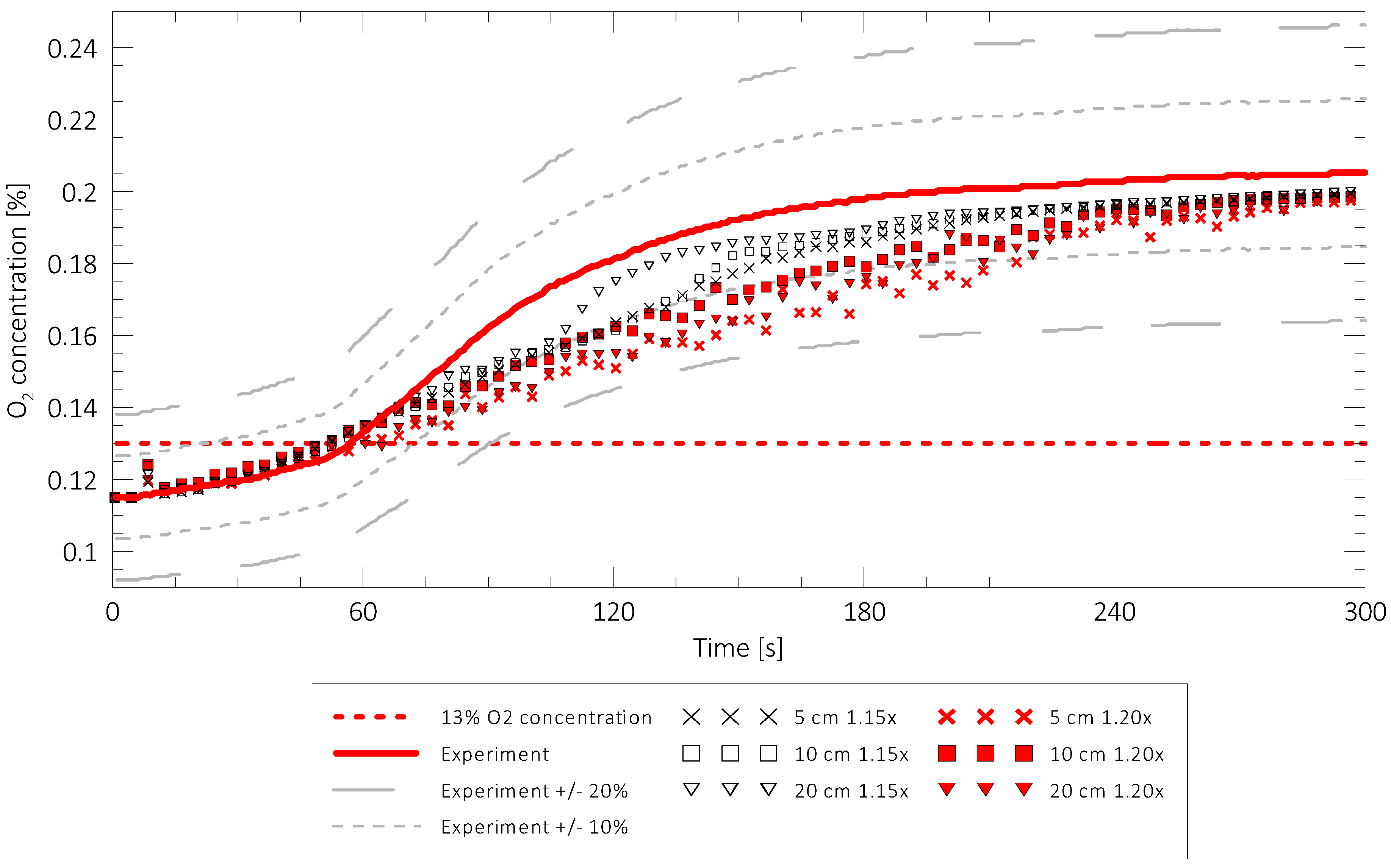
2.6. Mesh Sensitivity Study
3. Results
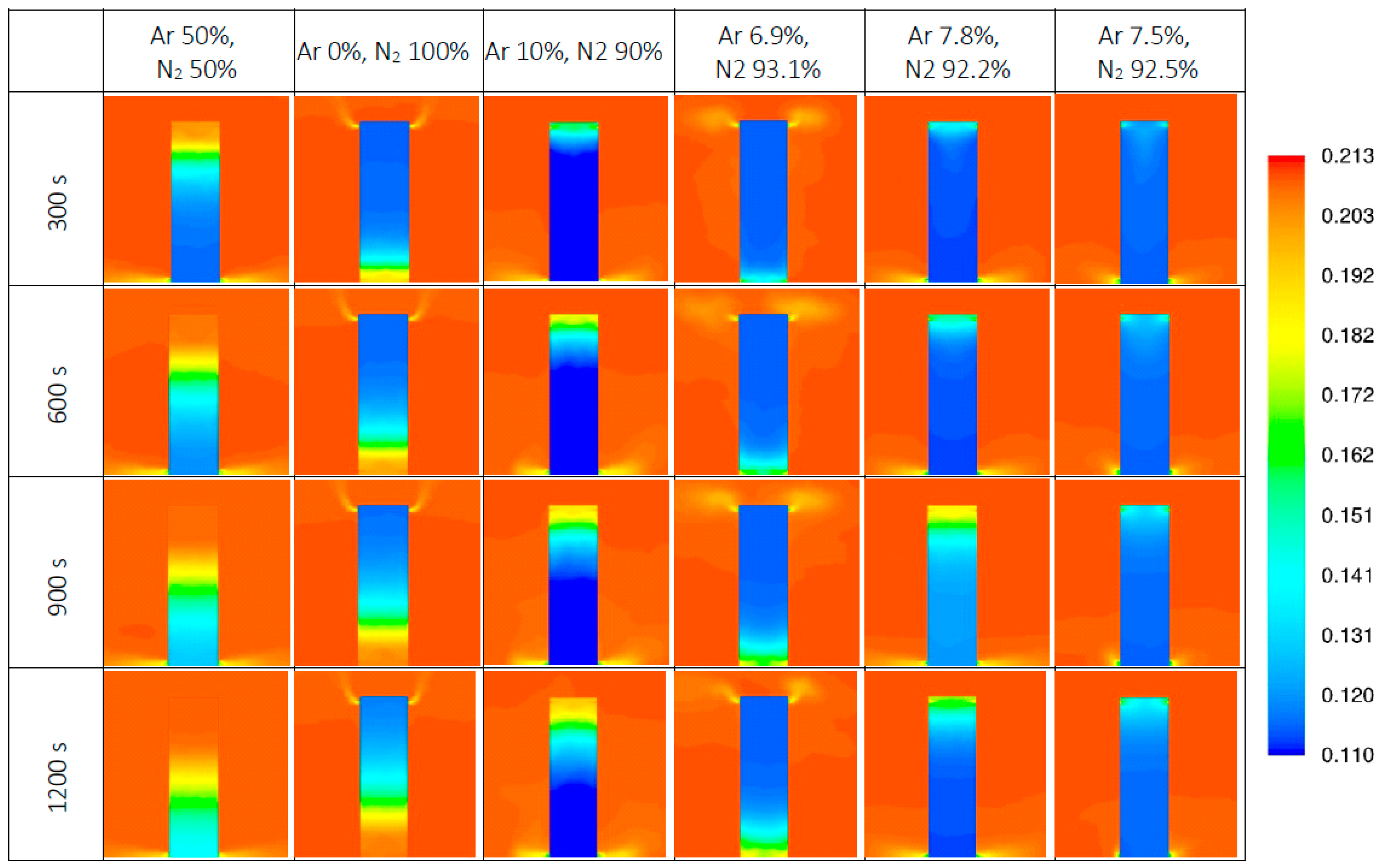
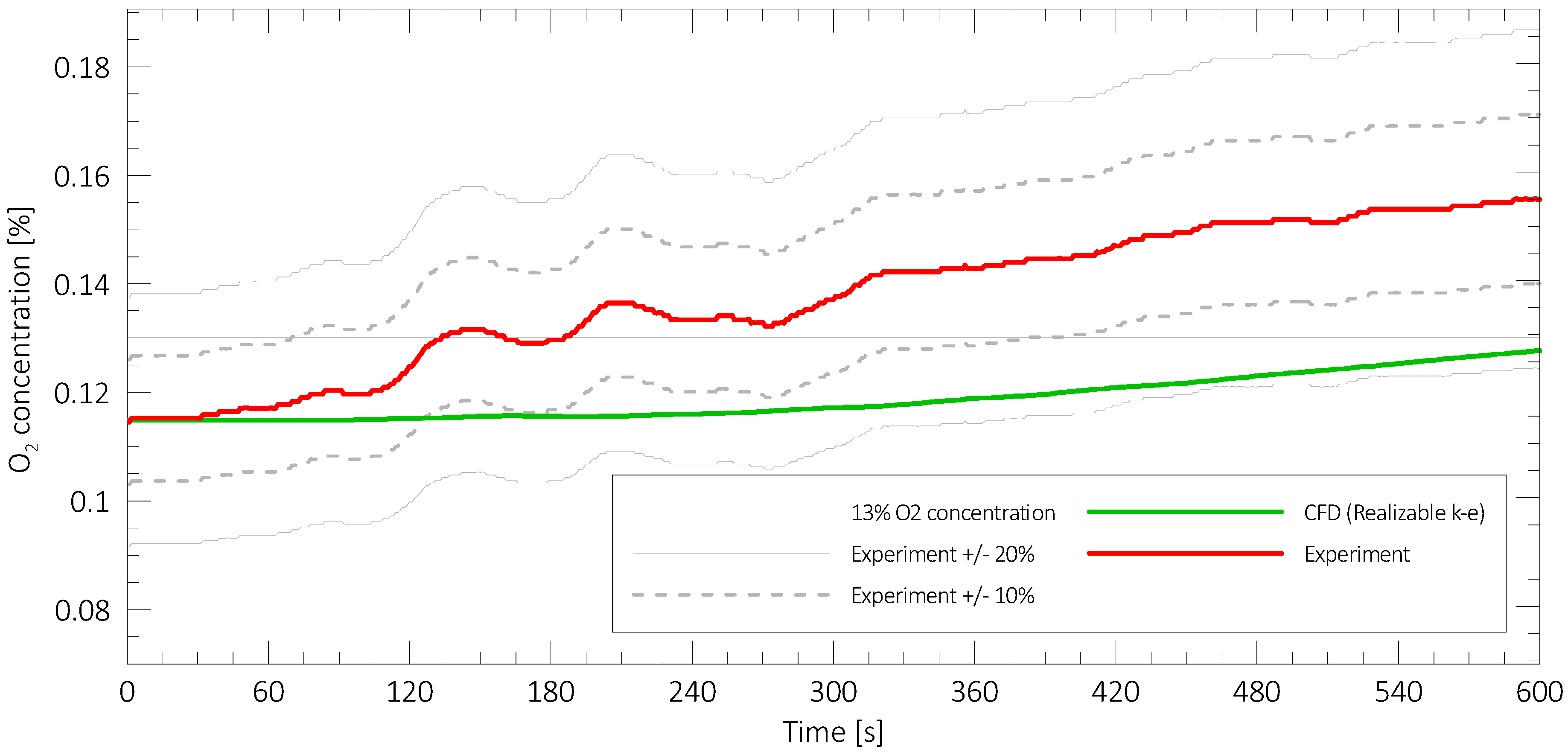
3.1. Overview of the Results of Numerical Modelling
3.2. The results for Standard Mixtures
3.3. The results for Mixtures with a Small Value of Δρ
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Milke, J. Fire protection as the underpinning of good process safety programs. J. Loss Prev. Process Ind. 2016, 40, 329–333. [Google Scholar] [CrossRef]
- Węgrzyński, W.; Sulik, P. The philosophy of fire safety engineering in the shaping of civil engineering development. Bull. Pol. Acad. Sci. Tech. Sci. 2016, 64, 719–730. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Rao, Z.; Xie, Q.; Wola, P. Brief review on passive and active methods for explosion and detonation suppression in tubes and galleries. J. Loss Prev. Process Ind. 2017, 49, 280–290. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, W.; Wang, Q. Optimization of water mist droplet size by using CFD modeling for fire suppressions. J. Loss Prev. Process Ind. 2016, 44, 626–632. [Google Scholar] [CrossRef]
- Jenft, A.; Collin, A.; Boulet, P.; Pianet, G.; Breton, A.; Muller, A. Experimental and numerical study of pool fire suppression using water mist. Fire Saf. J. 2014, 67, 1–12. [Google Scholar] [CrossRef]
- Rie, D.-H.; Lee, J.-W.; Kim, S. Class B Fire-Extinguishing Performance Evaluation of a Compressed Air Foam System at Different Air-to-Aqueous Foam Solution Mixing Ratios. Appl. Sci. 2016, 6, 191. [Google Scholar] [CrossRef]
- Buchlin, J. Mitigation of industrial hazards by water spray curtains. J. Loss Prev. Process Ind. 2017, 50, 91–100. [Google Scholar] [CrossRef]
- Węsierski, T.; Majder-Łopatka, M. Comparison of Water Curtain Effectiveness in the Elimination of Airborne Vapours of Ammonia, Acetone, and Low-Molecular Aliphatic Alcohols. Appl. Sci. 2018, 8, 1971. [Google Scholar] [CrossRef]
- Abramowicz, M.; Kowalski, R. The influence of short time water cooling on the mechanical properties of concrete heated up to high temperature. J. Civ. Eng. Manag. 2005, 11, 85–90. [Google Scholar] [CrossRef]
- Węgrzyński, W.; Vigne, G. Experimental and numerical evaluation of the influence of the soot yield on the visibility in smoke in CFD analysis. Fire Saf. J. 2017, 91, 389–398. [Google Scholar] [CrossRef]
- Kubica, P.; Czarnecki, L.; Boroń, S.; Węgrzyński, W. Maximizing the retention time of inert gases used in fixed gaseous extinguishing systems. Fire Saf. J. 2016, 80, 1–8. [Google Scholar] [CrossRef]
- Du, D.; Shen, X.; Feng, L.; Hua, M.; Pan, X. Efficiency characterization of fire extinguishing compound superfine powder containing Mg(OH)2. J. Loss Prev. Process Ind. 2019, 57, 73–80. [Google Scholar] [CrossRef]
- Shebeko, A.Y.; Shebeko, Y.N.; Zuban, A.V.; Navzenya, V.Y. An experimental investigation of an inertization effectiveness of fluorinated hydrocarbons in relation to premixed H2-N2O and CH4-N2O flames. J. Loss Prev. Process Ind. 2013, 26, 1639–1645. [Google Scholar] [CrossRef]
- Chaudhari, P.; Mashuga, C.V. Partial inerting of dust clouds using a modified standard minimum ignition energy device. J. Loss Prev. Process Ind. 2017, 48, 145–150. [Google Scholar] [CrossRef]
- Ouyang, D.; Liu, J.; Chen, M.; Wang, J. Investigation into the Fire Hazards of Lithium-Ion Batteries under Overcharging. Appl. Sci. 2017, 7, 1314. [Google Scholar] [CrossRef]
- Ouyang, D.; Liu, J.; Chen, M.; Weng, J.; Wang, J. An Experimental Study on the Thermal Failure Propagation in Lithium-Ion Battery Pack. J. Electrochem. Soc. 2018, 165, A2184–A2193. [Google Scholar] [CrossRef]
- Chen, M.; Liu, J.; Dongxu, O.; Cao, S.; Wang, Z.; Wang, J. A Simplified Analysis to Predict the Fire Hazard of Primary Lithium Battery. Appl. Sci. 2018, 8, 2329. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Fluent 14.5.0—Technical Documentation; ANSYS: Canonsburg, PA, USA, 2014. [Google Scholar]
- Boroń, S.; Kubica, P. Application of Computational Fluid Dynamics CFD for Modeling of Protection of Premises by Fixed Gaseous Extinguishing System (in Polish). Bezpieczeństwo Tech. Pożarnicza 2016, 42, 151–157. [Google Scholar]
- Wnęk, W.; Kubica, P. Analysis of distribution of oxygen concentrations during fire extinction in the enclosure by nitrogen with forced air condition. Bezpieczeństwo Tech. Pożarnicza 2011, 24, 65–79. (In Polish) [Google Scholar]
- Kubica, P. Retention Time of Gaseous Extinguishing Systems in the Fire Safety of Compartments; Instytut Techniki Budowlanej: Warsaw, Poland, 2014. (In Polish) [Google Scholar]
- NFPA 2001 Standard on Clean Agent Fire Extinguishing Systems; NFPA: Quincy, MA, USA, 2012.
- ISO 14520-1 Gaseous Fire-Extinguishing Systems—Physical Properties and System Design—Part 1: General Requirements; ISO: Geneva, Switzerland, 2015.
- BS EN 15004-1:2008 Fixed Firefighting Systems—Gas Extinguishing Systems. Design, Installation and Maintenance; BSI: London, UK, 2008.
- Genge, C. Clean agent enclosurer desgin optimization for peak pressures and agent retention. In Proceedings of the SFPE Engineering Technology Conference, Portland, OR, USA, 24–25 October 2011. [Google Scholar]
- OECD. NEA Best Practice Guidelines for the Use of CFD in Nuclear Reactor Safety Application—Revision. In NEA/CSNI/R(2014)11; OECD: Paris, France, 2015. [Google Scholar]
- McGrattan, K.; Miles, S. Modeling Fires Using Computational Fluid Dynamics (CFD). In SFPE Handbook of Fire Protection Engineering; Springer: New York, NY, USA, 2016; pp. 1034–1065. [Google Scholar]
- Merci, B.; Beji, T. Fluid Mechanics Aspects of Fire and Smoke Dynamics in Enclosures; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Chung, T.J. Computational Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: New York, NY, USA, 2002. [Google Scholar]
- McGrattan, K.; McDermott, R.; Floyd, J.; Hostikka, S.; Forney, G.; Baum, H. Computational fluid dynamics modelling of fire. Int. J. Comput. Fluid Dyn. 2012, 26, 349–361. [Google Scholar] [CrossRef]
- Wahlqvist, J.; van Hees, P. Implementation and validation of an environmental feedback pool fire model based on oxygen depletion and radiative feedback in FDS. Fire Saf. J. 2016, 85, 35–49. [Google Scholar] [CrossRef]
- Król, M.; Król, A. Multi-criteria numerical analysis of factors influencing the efficiency of natural smoke venting of atria. J. Wind Eng. Ind. Aerodyn. 2017, 170, 149–161. [Google Scholar] [CrossRef]
- Król, A.; Król, M. Study on Hot Gases Flow in Case of Fire in a Road Tunnel. Energies 2018, 11, 590. [Google Scholar] [CrossRef]
- Tauseef, S.M.; Rashtchian, D.; Abbasi, S.A. CFD-based simulation of dense gas dispersion in presence of obstacles. J. Loss Prev. Process Ind. 2011, 24, 371–376. [Google Scholar] [CrossRef]
- Dong, L.; Zuo, H.; Hu, L.; Yang, B.; Li, L.; Wu, L. Simulation of heavy gas dispersion in a large indoor space using CFD model. J. Loss Prev. Process Ind. 2017, 46, 1–12. [Google Scholar] [CrossRef]
- Yang, S.; Jeon, K.; Kang, D.; Han, C. Accident analysis of the Gumi hydrogen fluoride gas leak using CFD and comparison with post-accidental environmental impacts. J. Loss Prev. Process Ind. 2017, 48, 207–215. [Google Scholar] [CrossRef]
- Luo, T.; Yu, C.; Liu, R.; Li, M.; Zhang, J.; Qu, S. Numerical simulation of LNG release and dispersion using a multiphase CFD model. J. Loss Prev. Process Ind. 2018, 56, 316–327. [Google Scholar] [CrossRef]
- Middha, P.; Hansen, O.R.; Storvik, I.E. Validation of CFD-model for hydrogen dispersion. J. Loss Prev. Process Ind. 2009, 22, 1034–1038. [Google Scholar] [CrossRef]
- Mcnay, J.; Hilditch, R. Evaluation of computational fluid dynamics (CFD) vs. target gas cloud for indoor gas detection design. J. Loss Prev. Process Ind. 2017, 50, 75–79. [Google Scholar] [CrossRef]
- Blocken, B. LES over RANS in building simulation for outdoor and indoor applications: A foregone conclusion? Build. Simul. 2018, 11, 821–870. [Google Scholar] [CrossRef]
- Gibson, M.M.M.; Launder, B.E.E. Ground effects on pressure fluctuations in the atmospheric boundary layer. J. Fluid Mech. 1978, 86, 491–511. [Google Scholar] [CrossRef]
- Launder, B.E. Second-moment closure: Present… and future? Int. J. Heat Fluid Flow 1989, 10, 282–300. [Google Scholar] [CrossRef]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries Inc.: La Cañada, CA, USA, 2006. [Google Scholar]
- Peacock, R.D.; Reneke, P.A.; Davis, W.D.; Jones, W.W. Quantifying fire model evaluation using functional analysis. Fire Saf. J. 1999, 33, 167–184. [Google Scholar] [CrossRef]
- Węgrzyński, W.; Lipecki, T.; Krajewski, G. Wind and Fire Coupled Modelling—Part II: Good Practice Guidelines. Fire Technol. 2018, 54, 1443–1485. [Google Scholar] [CrossRef]


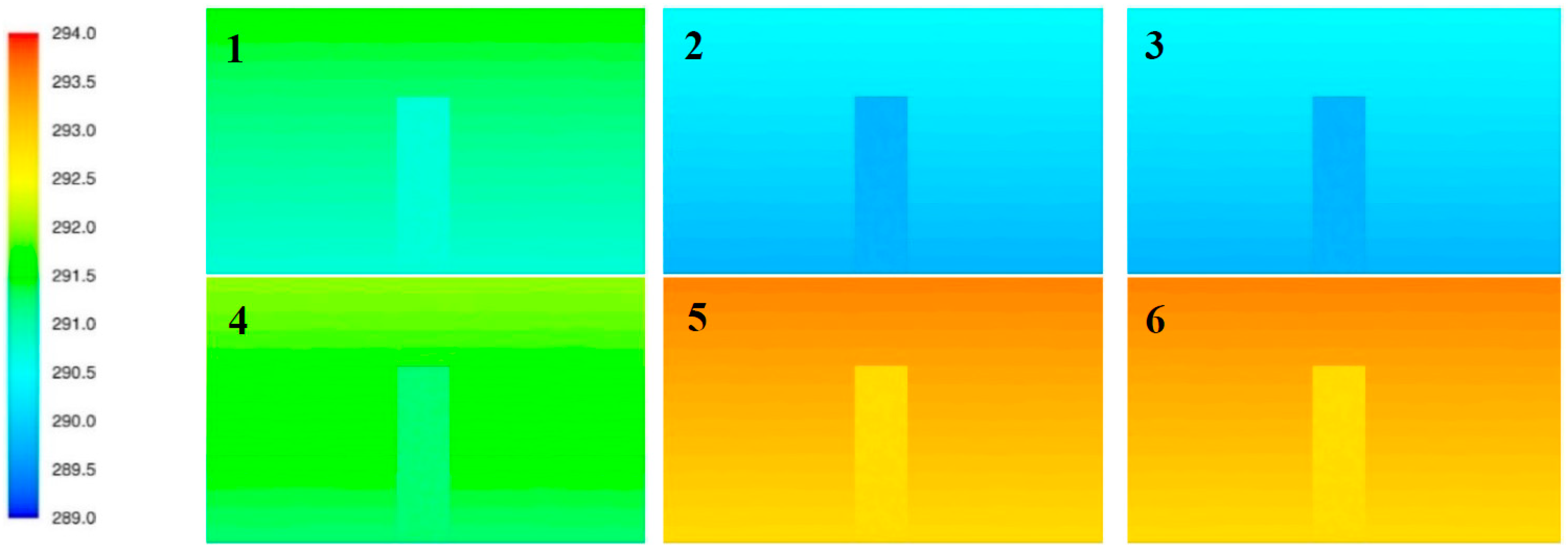










| No. | Ar [%v/v] | N2 [%v/v] | Δρ = dm − d0 [kg/m3] | Gas Molar Mass M | Volume Fraction Oxygen | Volume Fraction Gas | Temp. (out.) [K] | Temp. (ins.) [K] | p [hPa] |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 50 | 0.192 | 33.557 | 0.115 | 0.45 | 289.75 | 288.45 | 1003 |
| 2 | 0 | 100 | −0.039 | 28.013 | 0.115 | 0.45 | 288.75 | 289.25 | 1003 |
| 3 | 10 | 90 | 0.007 | 29.122 | 0.105 | 0.50 | 293.15 | 29415 | 1010 |
| 4 | 6.9 | 93.1 | −0.007 | 28.778 | 0.115 | 0.45 | 290.25 | 291.55 | 1002 |
| 5 | 7.8 | 92.2 | −0.003 | 28.878 | 0.113 | 0.46 | 292.65 | 292.05 | 1008 |
| 6 | 7.5 | 92.5 | −0.004 | 28.845 | 0.115 | 0.45 | 292.85 | 294.35 | 995 |
| No. | Ar [%v/v] | N2 [%v/v] | Δρ = dm − d0 [kg/m3] | Retention Time (Experiment) TR [s] | Retention Time (Stand. Model) tRn [s] | Retention Time—CFD [s] | Relative Errors in Relation to the Experiment [11] | |
|---|---|---|---|---|---|---|---|---|
| Standard Model | CFD | |||||||
| 1 | 50 | 50 | (+) 0.192 | 57 | 60.8 | 50 | −6.67 | 12.28 |
| 2 | 0 | 100 | (−) 0.039 | 119 | 136.7 | 135 | −14.87 | −13.45 |
| 3 | 10 | 90 | (+) 0.007 | 768 | 272 | 338 | 64.58 | 55.99 |
| 4 | 6.9 | 93.1 | (−) 0.007 | 186 | 325.1 | 654 | −74.78 | −251.61 |
| 5 | 7.8 | 92.2 | (−) 0.003 | 255 | 1563 | 396 | −512.94 | −55.29 |
| 6 | 7.5 | 92.5 | (−) 0.004 | 210 | 640.6 | 869 | −205.05 | −313.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boroń, S.; Węgrzyński, W.; Kubica, P.; Czarnecki, L. Numerical Modelling of the Fire Extinguishing Gas Retention in Small Compartments. Appl. Sci. 2019, 9, 663. https://doi.org/10.3390/app9040663
Boroń S, Węgrzyński W, Kubica P, Czarnecki L. Numerical Modelling of the Fire Extinguishing Gas Retention in Small Compartments. Applied Sciences. 2019; 9(4):663. https://doi.org/10.3390/app9040663
Chicago/Turabian StyleBoroń, Sylwia, Wojciech Węgrzyński, Przemysław Kubica, and Lech Czarnecki. 2019. "Numerical Modelling of the Fire Extinguishing Gas Retention in Small Compartments" Applied Sciences 9, no. 4: 663. https://doi.org/10.3390/app9040663
APA StyleBoroń, S., Węgrzyński, W., Kubica, P., & Czarnecki, L. (2019). Numerical Modelling of the Fire Extinguishing Gas Retention in Small Compartments. Applied Sciences, 9(4), 663. https://doi.org/10.3390/app9040663







