Effect of Slag Particle Size on Fracture Toughness of Concrete
Abstract
:1. Introduction
2. Research Significance
3. Experimental Details
3.1. Materials
3.2. Mixture Proportions
3.3. Specimen Fabrication
3.4. Testing Procedure
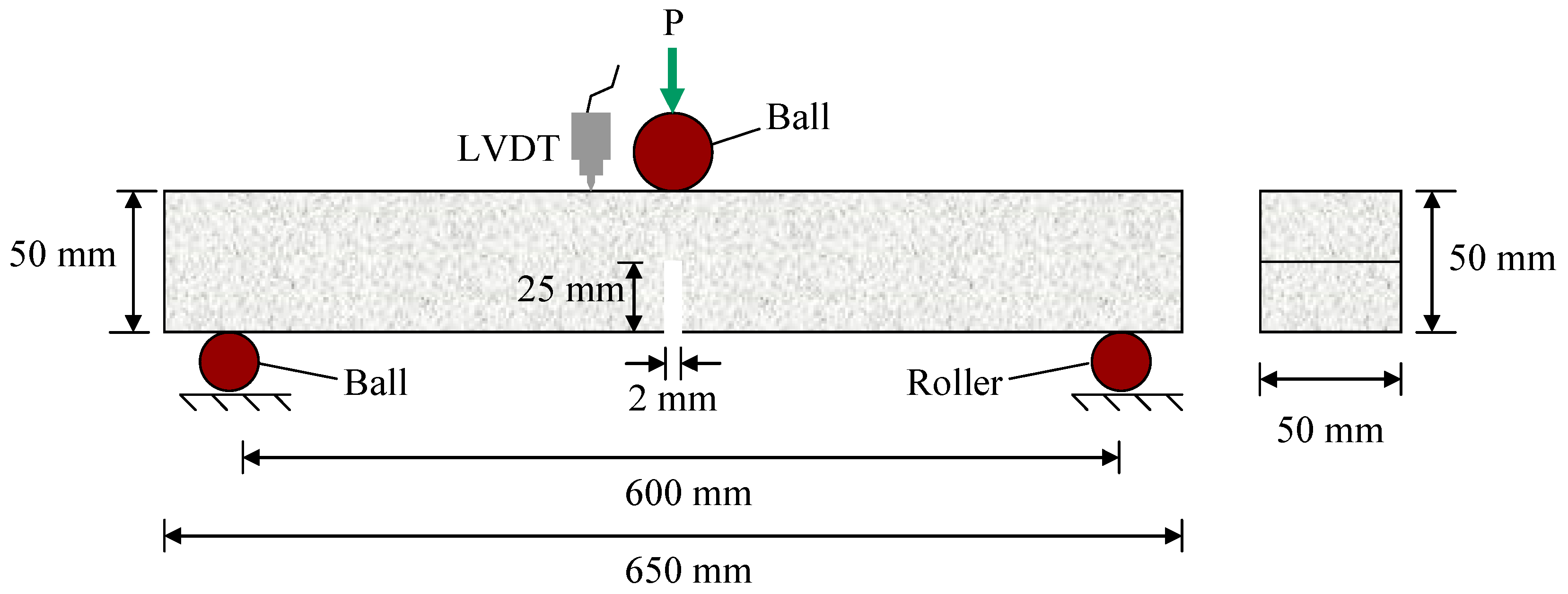
3.4.1. The Test for Determining GF
- where W0 = area under the load-deflection curve (N-m);
- m = mass of the beam between the supports (kg);
- g = acceleration due to gravity;
- δ0 = final deflection of the beam (m);
- A = cross-sectional area of the beam above the notch (m2).
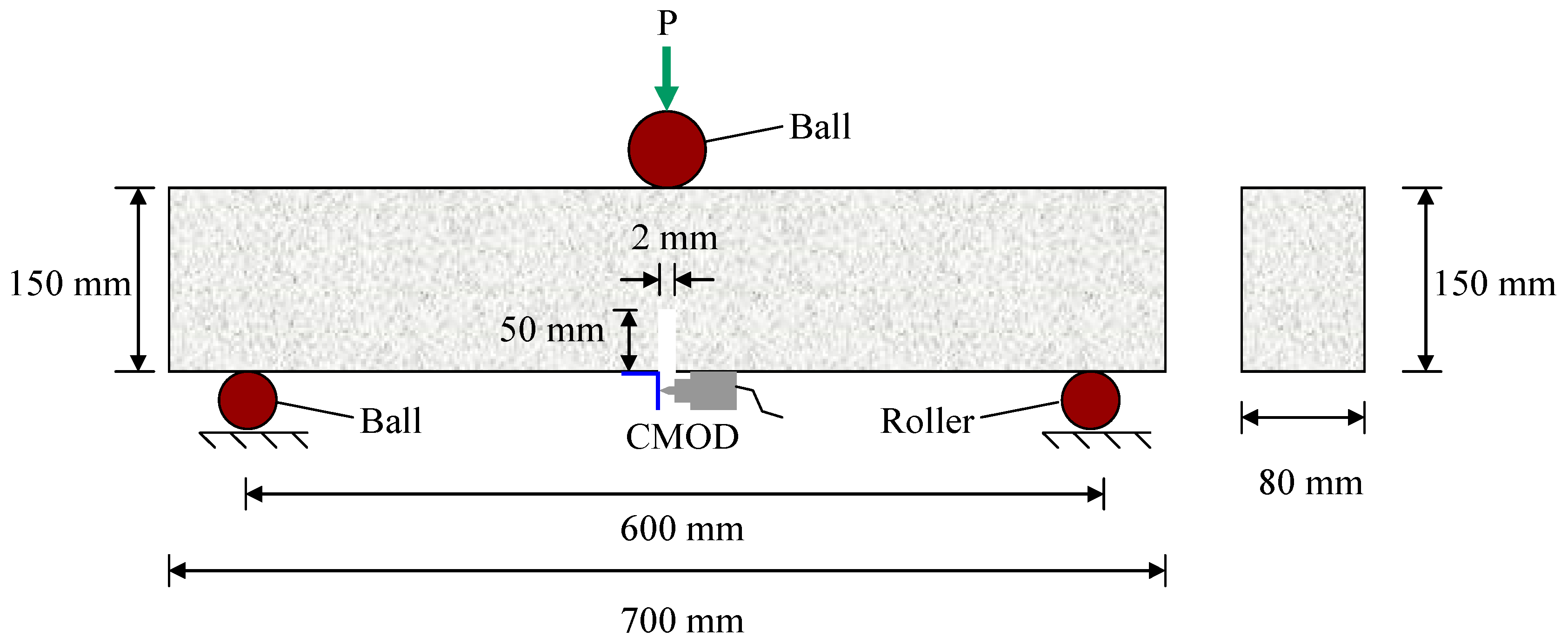
3.4.2. Test for Determining KSIC
- where Pmax = the measured maximum load (N);
- S = the span of the beam; b = beam width; d = beam depth;
- αc = critical effective crack length;
- α = αc/d.
4. Results and Discussion
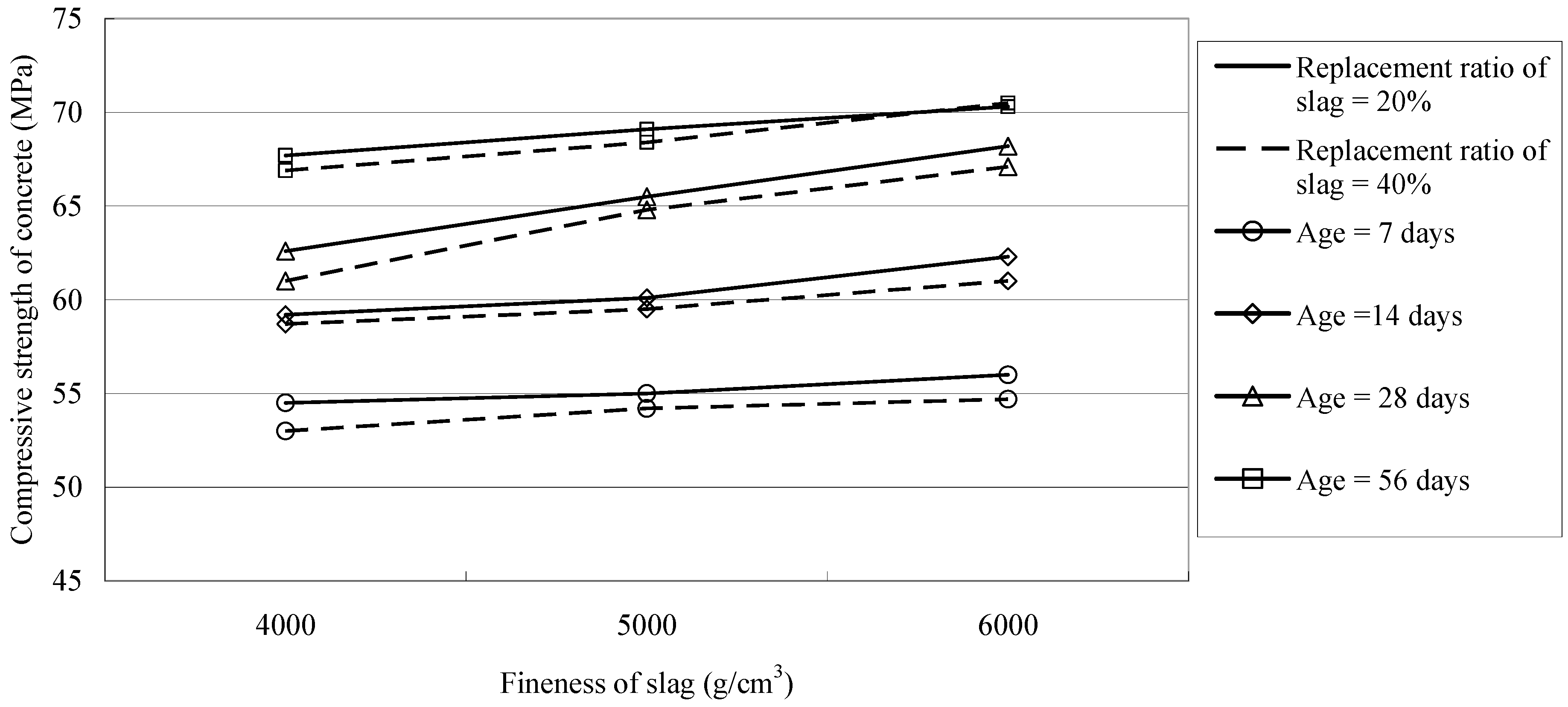
4.1. Compressive Strength
4.2. Fracture Energy
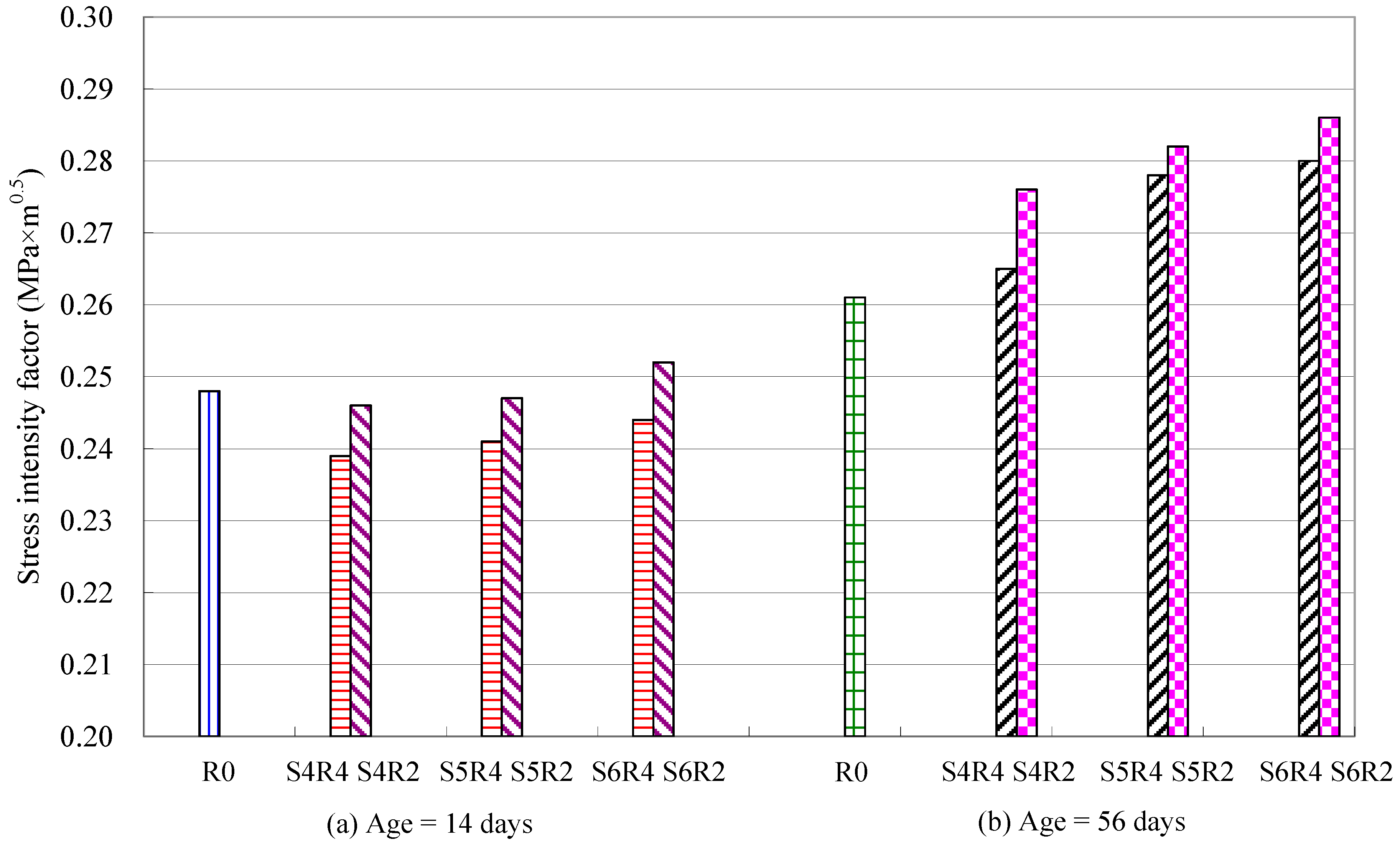
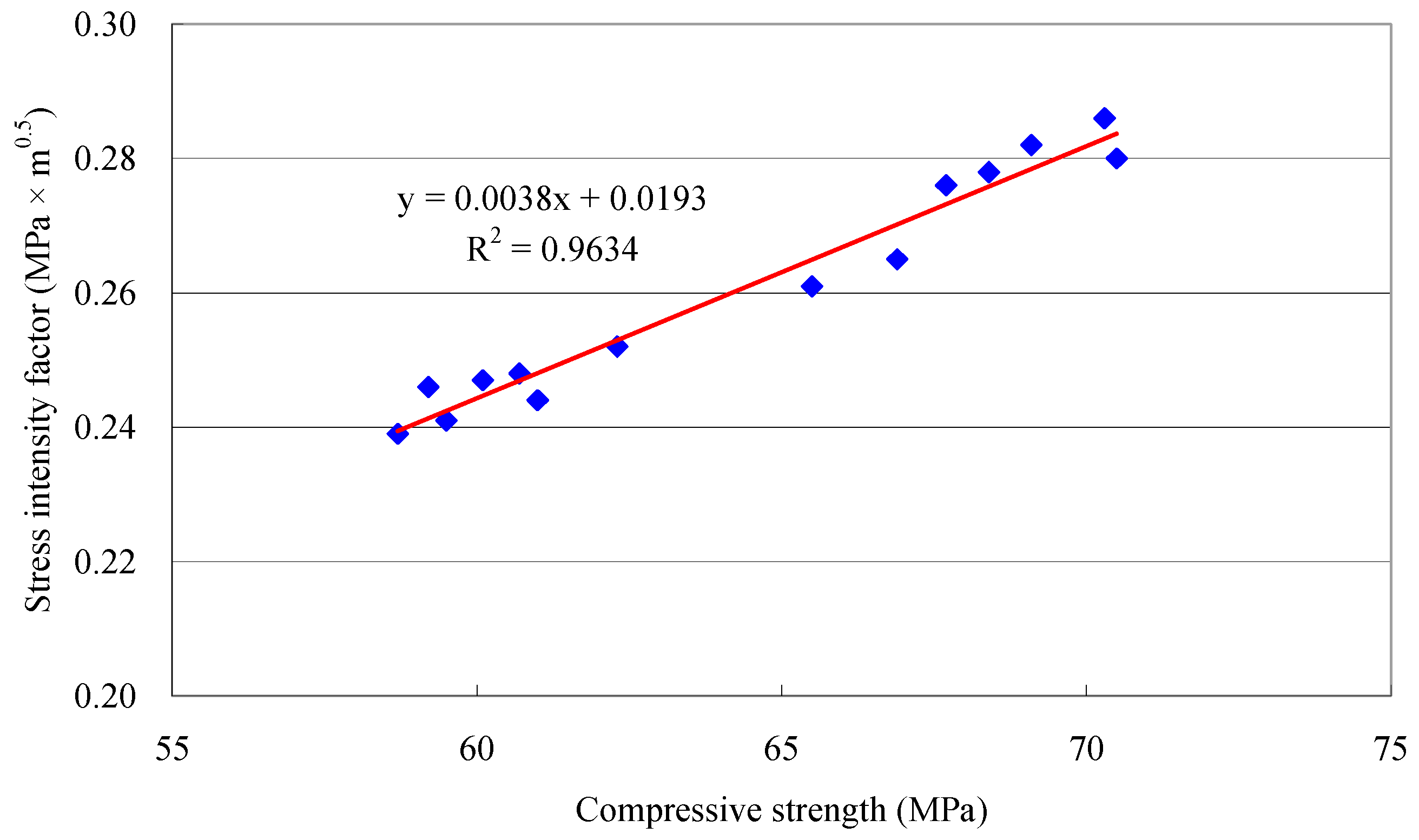
4.3. Critical Stress Intensity Factor
5. Conclusions
- The filling effect and the reactivity of slag can be improved by reducing its particle size. Incorporating finer slag into concrete may lead to larger early strength gains and larger strength increments of the concrete at later ages. The compressive strength of slag concrete was found to increase in conjunction with the fineness level of the slag incorporated into the mixture.
- The use of finer slag presents a beneficial effect on the fracture energy (GF) of concrete, even at early ages (14 days), due to superior filling effect. Increasing the fineness level of the incorporated slag leads to an increase of the GF value of concrete or an enhanced fracture toughness.
- The increment of the fracture energy of all the slag concretes measured in this study from 14–56 days was attained by 18–24%, which is found much higher than that of reference concrete (10.1%), and accordingly, the GF of the slag mixtures at 56 days almost exceeds that of the reference mixture.
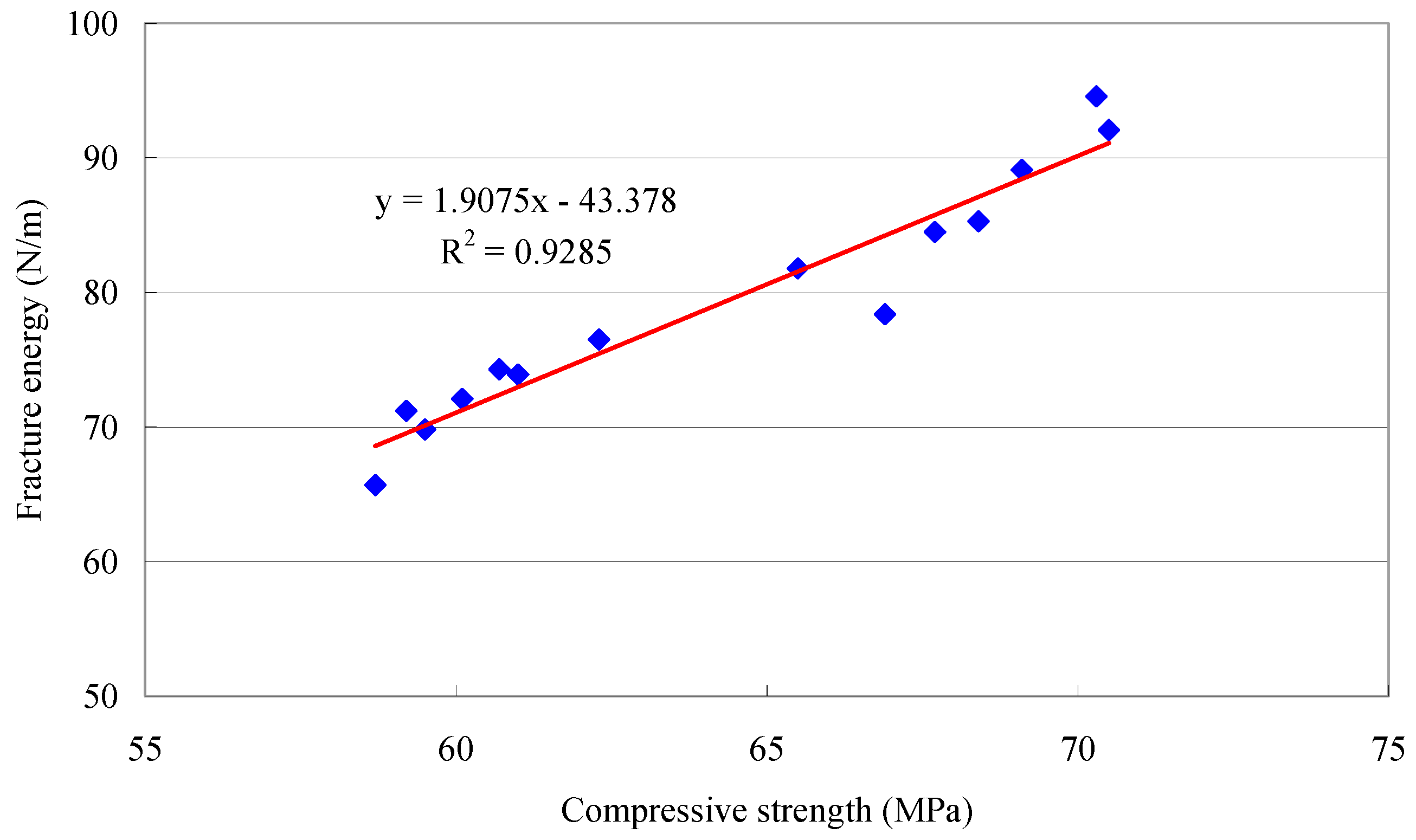
- An increase in compressive strength of slag concrete of 10% resulted in a fracture energy increase of around 18%. This raise rate is significantly higher than that previously found in high-strength concretes without slag, indicating that use of the finer slag can have a unique effect on the enhancement of the fracture resistance of concrete.
- The related tendency of the critical stress intensity factor (KSIC) of the slag concretes is similar to that of the fracture energy. At early ages (14 days), the KSIC values of slag concrete are less than that of the reference concrete (R0) but exceed that of R0 after 56 days.
- Concretes incorporating finer slag exhibit larger KSIC, and the KSIC increases in conjunction with the fineness level of the slag. This also implies an increase in the fracture resistance of the concrete.
Author Contributions
Funding
Conflicts of Interest
References
- Babu, K.G.; Kumar, V.S.R. Efficiency of GGBS in Concrete. Cem. Concr. Res. 2000, 30, 1031–1036. [Google Scholar] [CrossRef]
- Mehta, P.K. Pozzolanic and Cementitious By-products as Mineral Admixtures for Concrete—A Critical Review. Int. Concr. Abstr. Portal 1983, 79, 1–46. [Google Scholar]
- Malhotra, V.M.; Mehta, P.K. Pozzolanic and Cementitious Materials. In Advances in Concrete Technology; Gordon and Breach: London, UK, 1996. [Google Scholar]
- Babu, K.G.; Kumar, V.S.R. Performance of GGBS in Cementitious Composites. In Proceedings of the Sixth NCB International Seminar on Cement and Building Materials, New Delhi, India, 24–27 November 1998; p. XIII-76. [Google Scholar]
- Tan, K.; Pu, X. Strengthening Effects of Finely Ground Fly Ash, Granulated Blast Furnace Slag, and Their Combination. Cem. Concr. Res. 1998, 28, 1819–1825. [Google Scholar] [CrossRef]
- Mantel, D.G. Investigation into the Hydraulic Activity of Five Granulated Blast Furnace Slags with Eight Different Portland Cements. ACI Mater. J. 1994, 91, 471–477. [Google Scholar]
- Yűksel, I.; Özkan, Ö.; Bilir, I. Use of Granulated Blast Furnace Slag in Concrete as Fine Aggregate. ACI Mater. J. 2006, 103, 203–208. [Google Scholar]
- Duan, P.; Shui, S.; Chen, W.; Shen, C. Effects of Metakaolin, Silica Fume and Slag on Pore Structure, Interfacial Transition Zone and Compressive Strength of Concrete. Constr. Build. Mater. 2013, 44, 1–6. [Google Scholar] [CrossRef]
- Gao, J.M.; Qian, C.X.; Lin, H.F.; Wang, B.; Li, L. ITZ Microstructure of Concrete containing GGBS. Cem. Concr. Res. 2005, 35, 1299–1304. [Google Scholar] [CrossRef]
- Chinaprasirt, P.; Homwuttiwong, S.; Sirivivantananon, V. Influence of Fly Ash Fineness on Strength, Drying Shrinkage and Sulfate Resistance of Blended Cement Mortar. Cem. Concr. Res. 2004, 34, 1087–1092. [Google Scholar] [CrossRef]
- Zhu, J.; Zhong, Q.; Chen, F.; Li, D. Effect of Particle Size of Blast Furnace Slag on Properties of Portland Cement. Procedia Eng. 2012, 27, 231–236. [Google Scholar] [CrossRef]
- Nadeau, J.C. A Multiscale Model for Effective Moduli of Concrete Incorporating ITZ Water-Cement Ratio Gradients, Aggregate Size Distributions and Entrapped Voids. Cem. Concr. Res. 2003, 33, 103–113. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modeer, M.; Petersson, P.E. Analysis of Crack Formation and Crack Growth in Concrete by Means of Fracture Mechanics and Finite Elements. Cem. Concr. Res. 1976, 6, 773–782. [Google Scholar] [CrossRef]
- Petersson, P.E. Crack Growth and Development of Fracture Zones in Plain Concrete and Similar Materials; Rep. TVBM-1006; Division of Building Materials, Lund Institute of Technology: Lund, Sweden, 1981. [Google Scholar]
- Hillerborg, A. The Theoretical Basis of a Method to Determine the Fracture Energy GF of Concrete. Mater. Struct. 1985, 18, 291–296. [Google Scholar] [CrossRef]
- Rao, G.A.; Raghu Prasad, B.K. Size Effect and Fracture Properties of HPC. In Proceedings of the 14th Engineering Mechanics International Conference (ASCE), Austin, TX, USA, 21–24 May 2000; p. 104. [Google Scholar]
- Rao, G.A. Fracture Energy and Softening Behavior of High-Strength Concrete. Cem. Concr. Res. 2001, 32, 247–252. [Google Scholar] [CrossRef]
- Surendra, P.S. Determination of the Fracture Parameters (KSIC and CTODC) of Plain Concrete Using Three-Point Bend Test. Mater. Struct. 1990, 23, 457–460. [Google Scholar]
- Jenq, Y.S.; Shah, S.P. Two Parameters Fracture Model for Concrete. J. Eng. Mech. ASCE 1985, 111, 1227–1241. [Google Scholar] [CrossRef]
- Jensen, E.A.; Hansen, W. Fracture Energy Test for Highway Concrete—Determining the Effect of Coarse Aggregate on Crack Propagation Resistance. Transp. Res. Rec. 2001, 1730, 10–16. [Google Scholar] [CrossRef]
- RILEM Technical Committee 50-FMC, Proposed RILEM Recommendation. Determination of The Fracture Energy of Mortar and Concrete by Means of Three-Point Bend Tests on Notched Beams. Mater. Struct. 1985, 18, 285–290. [Google Scholar]
- Giaccio, G.; Rocco, C.; Zerbino, R. The Fracture Energy (GF) of High-Strength Concretes. Mater. Struct. 1993, 26, 381–386. [Google Scholar] [CrossRef]
- Gettu, R.; Bažant, Z.P.; Karr, M.E. Fracture Properties and Brittleness of High-Strength Concrete. ACI Mater. J. 1990, 87, 608–617. [Google Scholar]
- Xie, J.; Elwi, A.E.; MacGregor, J.G. Mechanical Properties of Three High-Strength Concretes Containing Silica Fume. ACI Mater. J. 1995, 92, 135–145. [Google Scholar]


| Chemical Analysis (%) | SiO2 | Al2O3 | Fe2O3 | CaO | MgO | SO3 | Na2O | K2O | LOI |
|---|---|---|---|---|---|---|---|---|---|
| Cement | 20.9 33.1 | 5.62 15.6 | 3.21 0.33 | 63.6 40.7 | 2.52 7.7 | 2.16 0.1 | 0.27 - | 0.52 - | 0.92 0.12 |
| GGBS |
| Mixture No. | w/cm | Water | Cement | Slag | Sand | Aggregate | SP. | Slump | Slump Flow |
|---|---|---|---|---|---|---|---|---|---|
| kg | mm | mm | |||||||
| R0 | 0.35 | 182 | 520 | 0 | 850 | 783 | 8.1 | 230 | 625 |
| S4R2 | 416 | 104 | 850 | 803 | 7.5 | 230 | 625 | ||
| S4R4 | 312 | 208 | 870 | 773 | 6.8 | 265 | 580 | ||
| S5R2 | 416 | 104 | 850 | 803 | 7.8 | 250 | 620 | ||
| S5R4 | 312 | 208 | 860 | 783 | 6.8 | 255 | 610 | ||
| S6R2 | 416 | 104 | 850 | 803 | 7.5 | 255 | 585 | ||
| S6R4 | 312 | 208 | 840 | 793 | 7.0 | 235 | 580 | ||
| Mixture No. | w/cm | Compressive Strength (MPa) | |||
|---|---|---|---|---|---|
| 7 Days | 14 Days | 28 Days | 56 Days | ||
| S0 | 0.35 | 56.2 (100%) | 60.7 (108.0%) | 63.2 (112.5%) | 65.5 (116.5%) |
| S4R2 | 54.5 (100%) | 59.2 (108.6%) | 62.6 (114.9%) | 67.7 (124.2%) | |
| S4R4 | 53.0 (100%) | 58.7 (110.8%) | 61.0 (115.1%) | 66.9 (126.2%) | |
| S5R2 | 55.0 (100%) | 60.1 (109.3%) | 65.5 (119.1%) | 69.1 (125.6%) | |
| S5R4 | 54.2 (100%) | 59.5 (109.8%) | 64.8 (119.6%) | 68.4 (126.2%) | |
| S6R2 | 56.0 (100%) | 62.3 (111.3%) | 68.2 (121.8%) | 70.3 (125.5%) | |
| S6R4 | 54.7 (100%) | 61.0 (111.5%) | 67.1 (122.7%) | 70.5 (128.9%) | |
| Mixture No. | Compressive Strength (MPa) | Fracture Energy (N/m) | |||
|---|---|---|---|---|---|
| 14 Days | 56 Days | 14 Days | 56 Days | Increment N/m (%) | |
| S0 | 60.7 | 65.5 | 74.3 | 81.8 | 7.5 (10.1) |
| S4R2 | 59.2 | 67.7 | 71.2 | 84.5 | 13.3 (18.7) |
| S4R4 | 58.7 | 66.9 | 65.7 | 78.4 | 12.7 (19.3) |
| S5R2 | 60.1 | 69.1 | 72.1 | 89.1 | 17.0 (23.5) |
| S5R4 | 59.5 | 68.4 | 69.8 | 85.3 | 15.5 (22.2) |
| S6R2 | 62.3 | 70.3 | 76.5 | 94.6 | 18.1 (23.7) |
| S6R4 | 61.0 | 70.5 | 73.9 | 92.1 | 18.2 (24.6) |
| Mixture No. | Compressive Strength (MPa) | Critical Stress Intensity Factor (MPa×m0.5) | ||
|---|---|---|---|---|
| 14 Days | 56 Days | 14 Days | 56 Days | |
| S0 | 60.7 | 65.5 | 0.248 | 0.261 |
| S4R2 | 59.2 | 67.7 | 0.246 | 0.276 |
| S4R4 | 58.7 | 66.9 | 0.239 | 0.265 |
| S5R2 | 60.1 | 69.1 | 0.247 | 0.282 |
| S5R4 | 59.5 | 68.4 | 0.241 | 0.278 |
| S6R2 | 62.3 | 70.3 | 0.252 | 0.286 |
| S6R4 | 61.0 | 70.5 | 0.244 | 0.280 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.-H.; Wu, C.-H.; Lin, S.-K.; Yen, T. Effect of Slag Particle Size on Fracture Toughness of Concrete. Appl. Sci. 2019, 9, 805. https://doi.org/10.3390/app9040805
Huang C-H, Wu C-H, Lin S-K, Yen T. Effect of Slag Particle Size on Fracture Toughness of Concrete. Applied Sciences. 2019; 9(4):805. https://doi.org/10.3390/app9040805
Chicago/Turabian StyleHuang, Chung-Ho, Chung-Hao Wu, Shu-Ken Lin, and Tsong Yen. 2019. "Effect of Slag Particle Size on Fracture Toughness of Concrete" Applied Sciences 9, no. 4: 805. https://doi.org/10.3390/app9040805
APA StyleHuang, C.-H., Wu, C.-H., Lin, S.-K., & Yen, T. (2019). Effect of Slag Particle Size on Fracture Toughness of Concrete. Applied Sciences, 9(4), 805. https://doi.org/10.3390/app9040805





