An Adaptive Neuro-Fuzzy Inference Model to Predict Punching Shear Strength of Flat Concrete Slabs
Abstract
:1. Introduction
2. ANFIS: Literature Review
3. Existing Equations Used for Two-Way Flat Slabs
3.1. ACI 318-14 Building Code Equations
3.2. Model Code 2010
3.3. British Code: BS-8110-97
3.4. Euro-Code 2 (EC2)
4. ANFIS: An Introduction
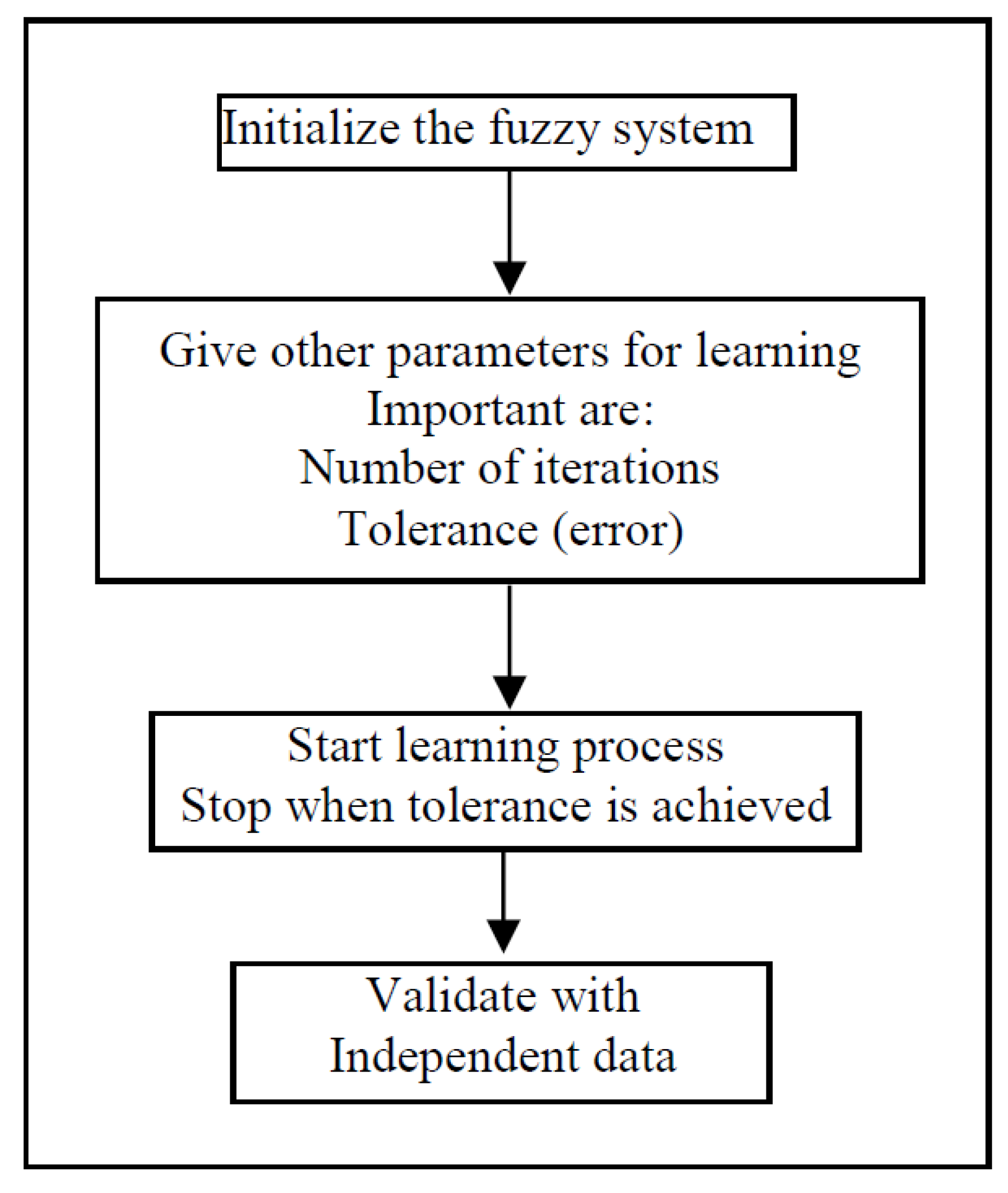
5. ANFIS: This Study
6. ANFIS: Results and Comparison
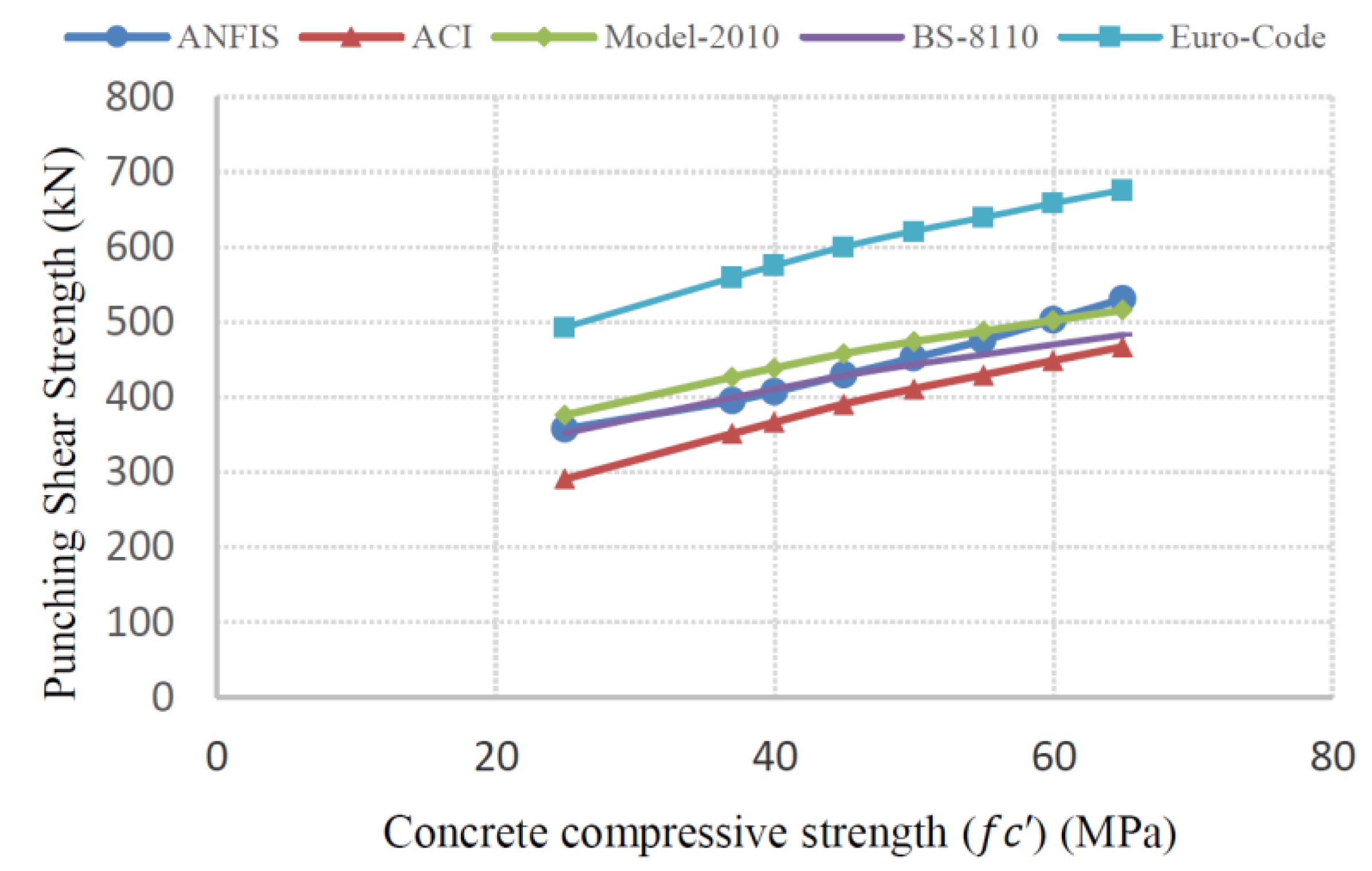
7. Parametric Studies
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Test No. | Reference | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 118 | 25.2 | 332 | 1.16 | 254 | 365 | [43] |
| 2 | 118 | 36.8 | 332 | 1.16 | 254 | 351 | |
| 3 | 118 | 20.3 | 332 | 1.16 | 254 | 356 | |
| 4 | 114 | 19.5 | 321 | 2.5 | 254 | 400 | |
| 5 | 114 | 37.4 | 321 | 2.5 | 254 | 467 | |
| 6 | 114 | 27.9 | 321 | 2.5 | 254 | 512 | |
| 7 | 114 | 22.6 | 321 | 3.74 | 254 | 445 | |
| 8 | 114 | 26.5 | 321 | 3.74 | 254 | 534 | |
| 9 | 114 | 34.5 | 321 | 3.74 | 254 | 547 | |
| 10 | 118 | 26.1 | 332 | 1.18 | 356 | 400 | |
| 11 | 114 | 25 | 321 | 3.74 | 356 | 498 | |
| 12 | 121 | 26.2 | 294 | 0.55 | 356 | 236 | |
| 13 | 114 | 14.2 | 324 | 0.48 | 254 | 178 | |
| 14 | 114 | 47.6 | 321 | 0.48 | 254 | 200 | |
| 15 | 114 | 43.9 | 341 | 2 | 254 | 505 | |
| 16 | 114 | 50.5 | 325 | 3.02 | 254 | 578 | |
| 17 | 118 | 29 | 332 | 1.16 | 254 | 356 | |
| 18 | 114 | 27.8 | 321 | 2.5 | 356 | 534 | |
| 19 | 114 | 47.7 | 303 | 1.01 | 254 | 334 | |
| 20 | 114 | 27.5 | 400 | 1.38 | 305 | 394 | [44] |
| 21 | 114 | 23.2 | 400 | 1.06 | 254 | 390 | |
| 22 | 114 | 22 | 400 | 1.03 | 254 | 356 | |
| 23 | 114 | 23.8 | 400 | 1.13 | 254 | 334 | |
| 24 | 114 | 25.3 | 400 | 1.02 | 254 | 379 | |
| 25 | 114 | 35.1 | 400 | 1.13 | 254 | 374 | |
| 26 | 114 | 20.4 | 400 | 1.13 | 254 | 312 | |
| 27 | 114 | 24.2 | 400 | 1.06 | 203 | 379 | |
| 28 | 114 | 23 | 400 | 1.5 | 305 | 433 | |
| 29 | 114 | 26.5 | 400 | 1.38 | 152 | 312 | |
| 30 | 114 | 24.4 | 400 | 1.06 | 254 | 393 | |
| 31 | 114 | 22.1 | 400 | 1.06 | 203 | 343 | |
| 32 | 51 | 21.1 | 386 | 1.1 | 152 | 79 | [41] |
| 33 | 51 | 15.5 | 386 | 1.1 | 203 | 93 | |
| 34 | 50 | 27.2 | 386 | 2.2 | 203 | 133 | |
| 35 | 51 | 22.9 | 386 | 2.2 | 254 | 152 | |
| 36 | 51 | 23 | 386 | 1.1 | 305 | 114 | |
| 37 | 51 | 27.7 | 386 | 1.1 | 356 | 139 | |
| 38 | 51 | 25 | 386 | 2.2 | 356 | 184 | |
| 39 | 51 | 24.9 | 386 | 1.1 | 406 | 145 | |
| 40 | 50 | 24.6 | 386 | 2.2 | 406 | 185 | |
| 41 | 50 | 27 | 386 | 1.1 | 152 | 102 | |
| 42 | 50 | 28.5 | 386 | 1.1 | 102 | 86 | |
| 43 | 50 | 24.9 | 386 | 2.2 | 102 | 102 | |
| 44 | 50 | 53.8 | 386 | 2.2 | 152 | 172 | |
| 45 | 50 | 21.1 | 386 | 1.1 | 152 | 99 | |
| 46 | 50 | 17 | 386 | 2.2 | 152 | 105 | |
| 47 | 51 | 18 | 336 | 2.2 | 152 | 99 | |
| 48 | 51 | 23.3 | 336 | 1.1 | 254 | 109 | |
| 49 | 50 | 26.4 | 386 | 2.2 | 305 | 159 | |
| 50 | 50 | 20 | 386 | 1.1 | 152 | 112 | |
| 51 | 100 | 35.7 | 706 | 0.8 | 125 | 216 | [42] |
| 52 | 99 | 28.6 | 701 | 0.81 | 125 | 194 | |
| 53 | 199 | 28.6 | 670 | 0.89 | 250 | 600 | |
| 54 | 200 | 30.3 | 657 | 0.8 | 250 | 603 | |
| 55 | 98 | 33.3 | 720 | 0.35 | 125 | 145 | |
| 56 | 99 | 31.4 | 712 | 0.34 | 125 | 148 | |
| 57 | 200 | 31.7 | 668 | 0.34 | 250 | 489 | |
| 58 | 197 | 30.2 | 664 | 0.35 | 250 | 444 | |
| 59 | 77 | 23.3 | 500 | 1.2 | 200 | 176 | [45] |
| 60 | 77 | 33.4 | 500 | 0.92 | 200 | 194 | |
| 61 | 79 | 21.7 | 480 | 0.75 | 200 | 165 | |
| 62 | 79 | 31.2 | 480 | 0.8 | 200 | 186 | |
| 63 | 200 | 36.3 | 530 | 0.98 | 250 | 825 | |
| 64 | 128 | 34.5 | 485 | 0.98 | 160 | 390 | |
| 65 | 64 | 34.5 | 480 | 0.98 | 80 | 117 | |
| 66 | 128 | 35.7 | 485 | 0.98 | 160 | 365 | |
| 67 | 64 | 35.7 | 480 | 0.98 | 80 | 105 | |
| 68 | 64 | 37.8 | 480 | 0.98 | 80 | 105 | |
| 69 | 41 | 31.5 | 530 | 0.42 | 100 | 36 | [46] |
| 70 | 41 | 31.5 | 530 | 0.69 | 100 | 49 | |
| 71 | 41 | 36.2 | 530 | 0.82 | 100 | 56 | |
| 72 | 41 | 36.2 | 530 | 1.03 | 100 | 66 | |
| 73 | 41 | 30.4 | 530 | 1.16 | 100 | 71 | |
| 74 | 41 | 30.4 | 530 | 1.29 | 100 | 71 | |
| 75 | 41 | 30.4 | 530 | 1.45 | 100 | 79 | |
| 76 | 41 | 30.6 | 530 | 0.52 | 100 | 44 | |
| 77 | 41 | 30.6 | 530 | 0.8 | 100 | 55 | |
| 78 | 41 | 35.3 | 530 | 0.6 | 100 | 49 | |
| 79 | 41 | 35.3 | 530 | 0.69 | 100 | 52 | |
| 80 | 41 | 35.3 | 530 | 1.99 | 100 | 85 | |
| 81 | 47 | 29.4 | 530 | 0.44 | 100 | 45 | |
| 82 | 47 | 29.4 | 530 | 0.69 | 100 | 66 | |
| 83 | 47 | 31.7 | 530 | 1.99 | 100 | 97 | |
| 84 | 35 | 39.6 | 530 | 0.42 | 100 | 29 | |
| 85 | 35 | 39.6 | 530 | 0.69 | 100 | 38 | |
| 86 | 35 | 31.7 | 530 | 1.99 | 100 | 73 | |
| 87 | 54 | 28.3 | 530 | 0.42 | 100 | 63 | |
| 88 | 54 | 33.5 | 530 | 0.69 | 100 | 88 | |
| 89 | 41 | 31.5 | 530 | 0.56 | 100 | 49 | |
| 90 | 41 | 36.2 | 530 | 0.88 | 100 | 57 | |
| 91 | 41 | 30.6 | 530 | 1.11 | 100 | 67 | |
| 92 | 47 | 29.4 | 530 | 1.29 | 100 | 90 | |
| 93 | 35 | 39.6 | 530 | 1.29 | 100 | 57 | |
| 94 | 54 | 33.5 | 530 | 1.29 | 100 | 124 | |
| 95 | 54 | 28.3 | 530 | 1.99 | 100 | 126 | |
| 96 | 76 | 24.1 | 430 | 2.05 | 102 | 129 | [47] |
| 97 | 76 | 22.6 | 430 | 2.05 | 102 | 136 | |
| 98 | 113 | 22.6 | 430 | 2.14 | 152 | 311 | |
| 99 | 113 | 24.8 | 430 | 2.14 | 203 | 357 | |
| 100 | 122 | 24.8 | 430 | 0.66 | 203 | 271 | |
| 101 | 73 | 25 | 430 | 5.01 | 152 | 202 | |
| 102 | 86 | 23.2 | 430 | 0.45 | 152 | 107 | |
| 103 | 81 | 25.5 | 430 | 1.47 | 102 | 121 | |
| 104 | 123 | 22.1 | 430 | 0.47 | 203 | 271 | |
| 105 | 113 | 15.1 | 430 | 2.14 | 203 | 278 | |
| 106 | 81 | 14.5 | 430 | 1.47 | 152 | 108 | |
| 107 | 73 | 52.1 | 430 | 5.01 | 203 | 323 | |
| 108 | 81 | 52.1 | 430 | 1.47 | 152 | 243 | |
| 109 | 76 | 24.6 | 430 | 2.05 | 102 | 129 | |
| 110 | 81 | 25 | 430 | 1.47 | 152 | 160 | |
| 111 | 122 | 16.1 | 430 | 0.66 | 203 | 230 | |
| 112 | 122 | 52.1 | 430 | 0.66 | 203 | 306 | |
| 113 | 86 | 52.1 | 430 | 0.45 | 152 | 148 | |
| 114 | 95 | 42 | 490 | 1.47 | 150 | 320 | [40] |
| 115 | 95 | 67 | 490 | 0.49 | 150 | 178 | |
| 116 | 95 | 70 | 490 | 0.84 | 150 | 249 | |
| 117 | 95 | 69 | 490 | 1.47 | 150 | 356 | |
| 118 | 90 | 66 | 490 | 2.37 | 150 | 418 | |
| 119 | 120 | 30 | 490 | 0.94 | 150 | 396 | |
| 120 | 125 | 68 | 490 | 0.64 | 150 | 365 | |
| 121 | 120 | 69 | 490 | 1.11 | 150 | 436 | |
| 122 | 120 | 74 | 490 | 1.61 | 150 | 543 | |
| 123 | 120 | 80 | 490 | 2.33 | 150 | 645 | |
| 124 | 70 | 75 | 490 | 1.52 | 150 | 258 | |
| 125 | 70 | 68 | 490 | 1.87 | 150 | 267 | |
| 126 | 95 | 72 | 490 | 1.47 | 220 | 498 | |
| 127 | 95 | 74 | 490 | 1.19 | 150 | 356 | |
| 128 | 120 | 70 | 490 | 0.94 | 150 | 489 | |
| 129 | 70 | 70 | 490 | 0.95 | 150 | 196 | |
| 130 | 95 | 71 | 490 | 1.47 | 300 | 560 | |
| 131 | 275 | 64 | 500 | 1.49 | 200 | 2050 | [48] |
| 132 | 275 | 112 | 500 | 1.49 | 200 | 2450 | |
| 133 | 275 | 90 | 500 | 2.55 | 200 | 2400 | |
| 134 | 200 | 88 | 500 | 1.75 | 150 | 1100 | |
| 135 | 200 | 87 | 500 | 1.75 | 150 | 1300 | |
| 136 | 200 | 119 | 500 | 1.75 | 150 | 1400 | |
| 137 | 275 | 84 | 500 | 1.49 | 200 | 2250 | |
| 138 | 200 | 70 | 500 | 1.75 | 150 | 1200 | |
| 139 | 200 | 90 | 500 | 2.62 | 150 | 1450 | |
| 140 | 200 | 98 | 500 | 2.62 | 150 | 1450 | |
| 141 | 200 | 80 | 500 | 2.62 | 150 | 1250 | |
| 142 | 200 | 108 | 500 | 2.62 | 150 | 1550 | |
| 143 | 88 | 85 | 500 | 1.4 | 100 | 330 | |
| 144 | 200 | 90 | 643 | 0.8 | 250 | 965 | [50] |
| 145 | 200 | 91 | 627 | 0.8 | 250 | 1021 | |
| 146 | 200 | 92 | 596 | 1.19 | 250 | 1041 | |
| 147 | 201 | 109 | 633 | 0.6 | 250 | 960 | |
| 148 | 202 | 84 | 634 | 0.33 | 250 | 565 | |
| 149 | 194 | 86 | 620 | 0.82 | 250 | 889 | |
| 150 | 198 | 95 | 631 | 0.8 | 250 | 944 | |
| 151 | 98 | 88.2 | 550 | 0.58 | 150 | 224 | [49] |
| 152 | 98 | 56.2 | 550 | 0.58 | 150 | 212 | |
| 153 | 98 | 26.9 | 550 | 0.58 | 150 | 169 | |
| 154 | 98 | 101.8 | 550 | 0.58 | 150 | 233 | |
| 155 | 98 | 60.4 | 550 | 1.28 | 150 | 319 | |
| 156 | 98 | 43.4 | 550 | 1.28 | 150 | 297 | |
| 157 | 98 | 98.4 | 550 | 1.28 | 150 | 362 | |
| 158 | 98 | 41.9 | 650 | 1.28 | 150 | 286 | |
| 159 | 98 | 84.2 | 650 | 1.28 | 150 | 405 | |
| 160 | 100 | 56.4 | 650 | 0.87 | 150 | 341 | |
| 161 | 100 | 37.6 | 650 | 1.27 | 150 | 294 | |
| 162 | 98 | 58.7 | 550 | 0.58 | 150 | 233 | |
| 163 | 98 | 60.8 | 550 | 1.28 | 150 | 341 | |
| 164 | 100 | 32.9 | 650 | 1.27 | 150 | 244 | |
| 165 | 102 | 33.7 | 650 | 1.03 | 150 | 227 | |
| 166 | 100 | 39.4 | 488 | 0.97 | 200 | 330 | [51] |
| 167 | 150 | 39.4 | 465 | 0.9 | 200 | 583 | |
| 168 | 200 | 39.4 | 465 | 0.83 | 200 | 904 | |
| 169 | 300 | 39.4 | 468 | 0.76 | 200 | 1381 | |
| 170 | 400 | 39.4 | 433 | 0.76 | 300 | 2224 | |
| 171 | 500 | 39.4 | 433 | 0.76 | 300 | 2681 | |
| 172 | 210 | 27.6 | 400 | 1.5 | 260 | 1024 | [52] |
| 173 | 210 | 28.5 | 400 | 0.25 | 260 | 445 | |
| 174 | 464 | 32.4 | 400 | 0.33 | 520 | 2153 | |
| 175 | 210 | 32.2 | 400 | 0.25 | 260 | 408 | |
| 176 | 210 | 29.3 | 400 | 0.33 | 260 | 550 | |
| 177 | 96 | 34.7 | 400 | 1.5 | 130 | 236 | |
| 178 | 100 | 34.7 | 400 | 0.75 | 130 | 243 | |
| 179 | 102 | 34.7 | 400 | 0.25 | 130 | 118 | |
| 180 | 210 | 40.5 | 400 | 0.25 | 260 | 439 | |
| 181 | 102 | 34.7 | 400 | 0.33 | 130 | 141 | |
| 182 | 210 | 28.5 | 400 | 0.33 | 260 | 540 | |
| 183 | 100 | 24 | 718 | 0.8 | 250 | 270 | [53] |
| 184 | 100 | 24.4 | 718 | 0.8 | 250 | 250 | |
| 185 | 125 | 27.2 | 718 | 0.64 | 150 | 265 | |
| 186 | 124 | 33.1 | 488 | 1.54 | 250 | 483 | [54] |
| 187 | 190 | 33.5 | 531 | 1.3 | 300 | 825 | |
| 188 | 260 | 31 | 524 | 1.1 | 350 | 1046 | |
| 189 | 158 | 35 | 490 | 2.17 | 250 | 678 | [55] |
| 190 | 128 | 70 | 490 | 2.68 | 250 | 801 | |
| 191 | 158 | 66.7 | 490 | 1.67 | 250 | 802 | |
| 192 | 113 | 70 | 490 | 1.88 | 250 | 480 | |
| 193 | 163 | 33 | 490 | 0.52 | 250 | 479 | |
| 194 | 138 | 68.5 | 490 | 2.48 | 250 | 788 | |
| 195 | 158 | 61.2 | 490 | 1.13 | 250 | 811 | |
| 196 | 105 | 34 | 490 | 0.4 | 250 | 228 | |
| 197 | 105 | 44.7 | 400 | 0.45 | 250 | 219 | [56] |
| 198 | 183 | 35 | 400 | 0.35 | 250 | 438 | |
| 199 | 183 | 70 | 400 | 0.35 | 250 | 574 | |
| 200 | 218 | 40 | 400 | 0.73 | 250 | 882 | |
| 201 | 220 | 76 | 400 | 0.43 | 250 | 886 | |
| 202 | 268 | 75 | 400 | 1.13 | 400 | 1721 | |
| 203 | 263 | 65 | 400 | 1.44 | 400 | 2090 | |
| 204 | 313 | 40 | 400 | 1.57 | 400 | 2234 | |
| 205 | 313 | 60 | 400 | 1.57 | 400 | 2513 | |
| 206 | 153 | 50.2 | 400 | 0.55 | 250 | 491 | |
| 207 | 218 | 64.7 | 400 | 0.73 | 250 | 1023 |
References
- Menetrey, P. Synthesis of punching failure in reinforced concrete. Cem. Concr. Compos. 2002, 24, 497–507. [Google Scholar] [CrossRef]
- Abbasi, M.; Baluch, M.H.; Azad, A.K.; Abdelrahman, H. Nonlinear finite element modelling of failure modes in RC slabs. Comp. Struct. 1992, 42, 815–823. [Google Scholar] [CrossRef]
- Theodorakopoulos, D.; Swamy, R. Ultimate punching shear strength analysis of slab–column connections. Cem. Concr. Compos. 2002, 24, 509–521. [Google Scholar] [CrossRef]
- Metwally, I.M.; Issa, M.S.; El-Betar, S.A. Punching shear resistance of normal and high strength reinforced concrete flat slabs. Civ. Eng. Res. Mag. 2008, 30, 982–1004. [Google Scholar]
- Micallef, K.; Sagaseta, J.; Ruiz, M.F.; Muttoni, A. Assessing punching shear failure in reinforced concrete flat slabs subjected to localised impact loading. Int. J. Impact Eng. 2014, 71, 17–33. [Google Scholar] [CrossRef] [Green Version]
- ACI. Building Code Requirements for Reinforced Concrete; American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- BS. Structural Use of Concrete. Part I: Code of Practice for Design and Construction; British Standards Institution: London, UK, 1997. [Google Scholar]
- FIB, M.C. Model Code 2010–Final Draft, Vol, 1; Bulletins: Lausanne, Switzerland, 2010. [Google Scholar]
- De Normalisation, C.E. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Shoorehdeli, M.A.; Teshnehlab, M.; Sedigh, A.K. Identification using ANFIS with intelligent hybrid stable learning algorithm approaches. Neural Comput. Appl. 2009, 18, 157–174. [Google Scholar] [CrossRef]
- Kasperkiewicz, J.; Racz, J.; Dubrawski, A. HPC strength prediction using artificial neural network. J. Comput. Civ. Eng. 1995, 9, 279–284. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 1, 116–132. [Google Scholar] [CrossRef]
- Topçu, İ.B.; Sarıdemir, M. Prediction of rubberized concrete properties using artificial neural network and fuzzy logic. Constr. Build. Mater. 2008, 22, 532–540. [Google Scholar] [CrossRef] [Green Version]
- Bilgehan, M. Comparison of ANFIS and NN models—With a study in critical buckling load estimation. Appl. Soft Comput. 2011, 11, 3779–3791. [Google Scholar] [CrossRef]
- Tesfamariam, S.; Najjaran, H. Adaptive network–fuzzy inferencing to estimate concrete strength using mix design. J. Mater. Civ. Eng. 2007, 19, 550–560. [Google Scholar] [CrossRef]
- Akbulut, S.; Hasiloglu, A.S.; Pamukcu, S. Data generation for shear modulus and damping ratio in reinforced sands using adaptive neuro-fuzzy inference system. Soil Dyn. Earthq. Eng. 2004, 24, 805–814. [Google Scholar] [CrossRef]
- Inan, G.; Göktepe, A.B.; Ramyar, K.; Sezer, A. Prediction of sulfate expansion of PC mortar using adaptive neuro-fuzzy methodology. Build. Environ. 2007, 42, 1264–1269. [Google Scholar] [CrossRef]
- Fonseca, E.T.; g da s Vellasco, P.C.; Vellasco, M.M.B.R.; de Andrade, S.A.L. A neuro-fuzzy evaluation of steel beams patch load behaviour. Adv. Eng. Softw. 2008, 39, 558–572. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Elhag, T.M. An adaptive neuro-fuzzy inference system for bridge risk assessment. Expert Syst. Appl. 2008, 34, 3099–3106. [Google Scholar] [CrossRef]
- Bateni, S.; Jeng, D.-S. Estimation of pile group scour using adaptive neuro-fuzzy approach. Ocean Eng. 2007, 34, 1344–1354. [Google Scholar] [CrossRef]
- Mashrei, M.A. Prediction of the Shear Strength of Concrete Beams Reinforced with Fiber Reinforced Polymer Bars Using Artificial Neural Networks Model. Thi-Qar Univ. J. Eng. Sci. 2011, 2, 45–63. [Google Scholar]
- Bilgehan, M.; Kurtoğlu, A.E. ANFIS-based prediction of moment capacity of reinforced concrete slabs exposed to fire. Neural Comput. Appl. 2016, 27, 869–881. [Google Scholar] [CrossRef]
- Mansouri, I.; Kisi, O.; Sadeghian, P.; Lee, C.-H.; Hu, J.W. Prediction of ultimate strain and strength of FRP-confined concrete cylinders using soft computing methods. Appl. Sci. 2017, 7, 751. [Google Scholar] [CrossRef]
- Naderpour, H.; Poursaeidi, O.; Ahmadi, M. Shear Resistance Prediction of Concrete Beams Reinforced by FRP Bars Using Artificial Neural Networks. Measurement 2018. [Google Scholar] [CrossRef]
- Basarir, H.; Bin, H.; Fourie, A.; Karrech, A.; Elchalakani, M. An adaptive neuro fuzzy inference system to model the uniaxial compressive strength of cemented hydraulic backfill. Min. Miner. Depos. 2018, 12, 1–12. [Google Scholar] [CrossRef]
- Dönmez, A.; Bažant, Z.P. Size effect on punching strength of reinforced concrete slabs with and without shear reinforcement. ACI Struct. J. 2017, 114, 875. [Google Scholar] [CrossRef]
- Shehata, I.A. Simplified model for estimating the punching resistance of reinforced corete slabs. Mater. Struct. 1990, 23, 364–371. [Google Scholar] [CrossRef]
- Regan, P.E. Behaviour of Reinforced Concrete Flat Slabs; Construction Inudstry Research and Information Association: London, UK, 1981. [Google Scholar]
- Gardner, N. Size Effect on Punching Strength of Reinforced Concrete Slabs with and without Shear Reinforcement. ACI Struct. J. 2018, 115, 897–899. [Google Scholar]
- Bazant, Z.P.; Kim, J.K. Size effect in shear failure of longitudinally reinforced beams. J. Am. Concr. Inst. 1984, 81, 456–468. [Google Scholar]
- Demirkaya, S. Deformation analysis of an arch dam using ANFIS. In Proceedings of the Second International Workshop on Application of Artificial Intelligence and Innovations in Engineering Geodesy, Braunschweig, Germany, June 2010. [Google Scholar]
- Chang, F.J.; Chang, Y.T. Adaptive neuro-fuzzy inference system for prediction of water level in reservoir. Adv. Water Resour. 2006, 29, 1–10. [Google Scholar] [CrossRef]
- Xu, J.; Wang, X.L. Prediction of Concrete Strength Using Fuzzy Neural Networks. Adv. Mater. Res. 2011, 243, 6121–6126. [Google Scholar] [CrossRef]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Mamdani, E.H. Application of fuzzy algorithms for control of simple dynamic plant. Proc. Electr. Eng. 1974, 121. [Google Scholar] [CrossRef]
- Sugeno, M.; Tanaka, K. Successive identification of a fuzzy model and its applications to prediction of a complex system. Fuzzy Sets Syst. 1991, 42, 315–334. [Google Scholar] [CrossRef]
- Sugeno, M.; Kang, G. Structure identification of fuzzy model. Fuzzy Sets Syst. 1988, 28, 15–33. [Google Scholar] [CrossRef]
- Zadeh, L.A. Information and control. Fuzzy Sets 1965, 8, 338–353. [Google Scholar]
- MATLAB, V. 8.1. 0.604 (R2013a); MathWorks: Natick, MA, USA, 2013.
- Marzouk, H.; Hussein, A. Experimental investigation on the behavior of high-strength concrete slabs. ACI Struct. J. 1991, 88, 701–713. [Google Scholar]
- Mowrer, R.; Vanderbilt, M. Shear strength of lightweight aggregate reinforced concrete flat plates. J. Am. Concr. Inst. 1967, 64, 722–729. [Google Scholar]
- Kinnunen, S.; Nylander, H.; Tolf, P. Investigations on Punching at the Division of Building Statics and Structural Engineering. Nordisk Betong 1978, 3, 25–27. [Google Scholar]
- Elstner, R.C.; Hognestad, E. Shearing strength of reinforced concrete slabs. J. Proc. 1956, 53, 29–58. [Google Scholar]
- Moe, J. Shearing Strength of Reinforced Concrete Slabs and Footings under Concentrated Loads; Portland Cement Association, Research and Development Laboratories: Chicago, IL, USA, 1961. [Google Scholar]
- Regan, P.; Walker, P.; Zakaria, K. Tests of Reinforced Concrete Flat Slabs; CIRIA Project RP; Polytechnic of Central: London, UK, 1979; 220p. [Google Scholar]
- Rankin, G.; Long, A. Predicting the Punching Strength of Conventional Slab-Column Specimens. Proc. Inst. Civ. Eng. 1987, 82, 327–346. [Google Scholar] [CrossRef]
- Gardner, N. Relationship of the punching shear capacity of reinforced concrete slabs with concrete strength. Struct. J. 1990, 87, 66–71. [Google Scholar]
- Tomaszewicz, A. Punching Shear Capacity of Reinforced Concrete Slabs; Trondheim SINTEF: Trondheim, Norway, 1993; 36p. [Google Scholar]
- Ramdane, K. Punching shear of high performance concrete slabs. In Proceedings of the Fourth International Symposium on Utilization of High-Strength/High Performance Concrete, Paris, France, 29–31 May 1996. [Google Scholar]
- Hallgren, M. Punching Shear Capacity of Reinforced High Strength Concrete Slabs; KTH Byggvetenskap: Stockholm, Sweden, 1996. [Google Scholar]
- Kevin, K. Influence of Size on Punching Shear Strength of Concrete Slabs; McGill University: Montreal, QC, Canada, 2000; p. 92. [Google Scholar]
- Guandalini, S.; Muttoni, A. Symmetrical Punching Tests on Slabs without Transverse Reinforcement; Test Report; de Lausanne Institut: Lausanne, Switzerland, 2004. [Google Scholar]
- Sundquist, H.; Kinnunen, S. The Effect of Column Head and Drop Panels on the Punching Capacity of Flat Slabs; Bulletin No. 82; Department of Civil and Architectural Engineering, Royal Institute of Technology: Stockholm, Sweden, 2004. [Google Scholar]
- Birkle, G.; Dilger, W.H. Influence of slab thickness on punching shear strength. ACI Struct. J. 2008, 105, 180–188. [Google Scholar]
- Marzouk, H.; Hossin, M. Crack Analysis of Reinforced Concrete Two-Way Slabs; Research Report; Faculty of Engineering and Applied Science, Memorial University of Newfoundland: St. John’s, NL, Canada, 2007. [Google Scholar]
- Marzouk, R.; Rizk, E. Punching Analysis of Reinforced Concrete Two-Way Slabs; Research Report RCS01; Faculty of Engineering and Applied Science, Memorial University of Newfoundland: St. John’s, NL, Canada, 2009. [Google Scholar]
- Chiu, S.L. Fuzzy model identification based on cluster estimation. J. Int. Fuzzy Syst. 1994, 2, 267–278. [Google Scholar]
- Mashrei, M.A.; Abdulrazzaq, N.; Abdalla, T.Y.; Rahman, M.S. Neural networks model and adaptive neuro-fuzzy inference system for predicting the moment capacity of ferrocement members. Eng. Struct. 2010, 32, 1723–1734. [Google Scholar] [CrossRef]





















| Parameters | Range |
|---|---|
| The slab effective depth (mm) | 35–550 |
| Concrete cylinder compressive strength () (MPa) | 14.2–119 |
| Reinforcement ratio (%) | 0.25–5.01 |
| Yield strength of reinforcement (MPa) | 294–720 |
| Width of square loaded area (mm) | 80–500 |
| Specimens | No. | Average of Vni/Vne | STDEV of Vni/Vne | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ANFIS | ACI-14 Code | Model-Code 2010 | BS-8110 Code | Euro-Code 2 | ANFIS | ACI-14 Code | Model-Code 2010 | BS-8110 Code | Euro Code 2 | ||
| Training set | 164 | 1.0 | 0.88 | 1.10 | 1.01 | 1.45 | 0.11 | 0.30 | 0.16 | 0.14 | 0.20 |
| Testing set | 43 | 1.01 | 0.84 | 1.07 | 0.98 | 1.42 | 0.13 | 0.26 | 0.15 | 0.13 | 0.19 |
| Type | Correlation (R) | RSME % | |||
|---|---|---|---|---|---|
| Training | Testing | All Data | Training | Testing | |
| ANFIS | 0.996 | 0.995 | 0.995 | 0.45 | 0.52 |
| ACI 318-14 Code | 0.927 | 0.952 | 0.927 | 2.06 | 2.05 |
| Model-Code-2010 | 0.986 | 0.992 | 0.986 | 0.93 | 0.72 |
| BS-8110-97 | 0.986 | 0.992 | 0.987 | 0.83 | 0.93 |
| Euro-Code 2 | 0.985 | 0.993 | 0.986 | 3.12 | 2.70 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mashrei, M.A.; Mahdi, A.M. An Adaptive Neuro-Fuzzy Inference Model to Predict Punching Shear Strength of Flat Concrete Slabs. Appl. Sci. 2019, 9, 809. https://doi.org/10.3390/app9040809
Mashrei MA, Mahdi AM. An Adaptive Neuro-Fuzzy Inference Model to Predict Punching Shear Strength of Flat Concrete Slabs. Applied Sciences. 2019; 9(4):809. https://doi.org/10.3390/app9040809
Chicago/Turabian StyleMashrei, Mohammed A., and Alaa M. Mahdi. 2019. "An Adaptive Neuro-Fuzzy Inference Model to Predict Punching Shear Strength of Flat Concrete Slabs" Applied Sciences 9, no. 4: 809. https://doi.org/10.3390/app9040809
APA StyleMashrei, M. A., & Mahdi, A. M. (2019). An Adaptive Neuro-Fuzzy Inference Model to Predict Punching Shear Strength of Flat Concrete Slabs. Applied Sciences, 9(4), 809. https://doi.org/10.3390/app9040809





