Influence of Initial Phase Modulation on the Sensitivity of the Optical Fiber Sagnac Acoustic Emission Sensor
Abstract
:1. Introduction
2. Theoretical Analysis
2.1. Relationship between the Initial Phase and the Phase Sensitivity
2.2. Numerical Simulation
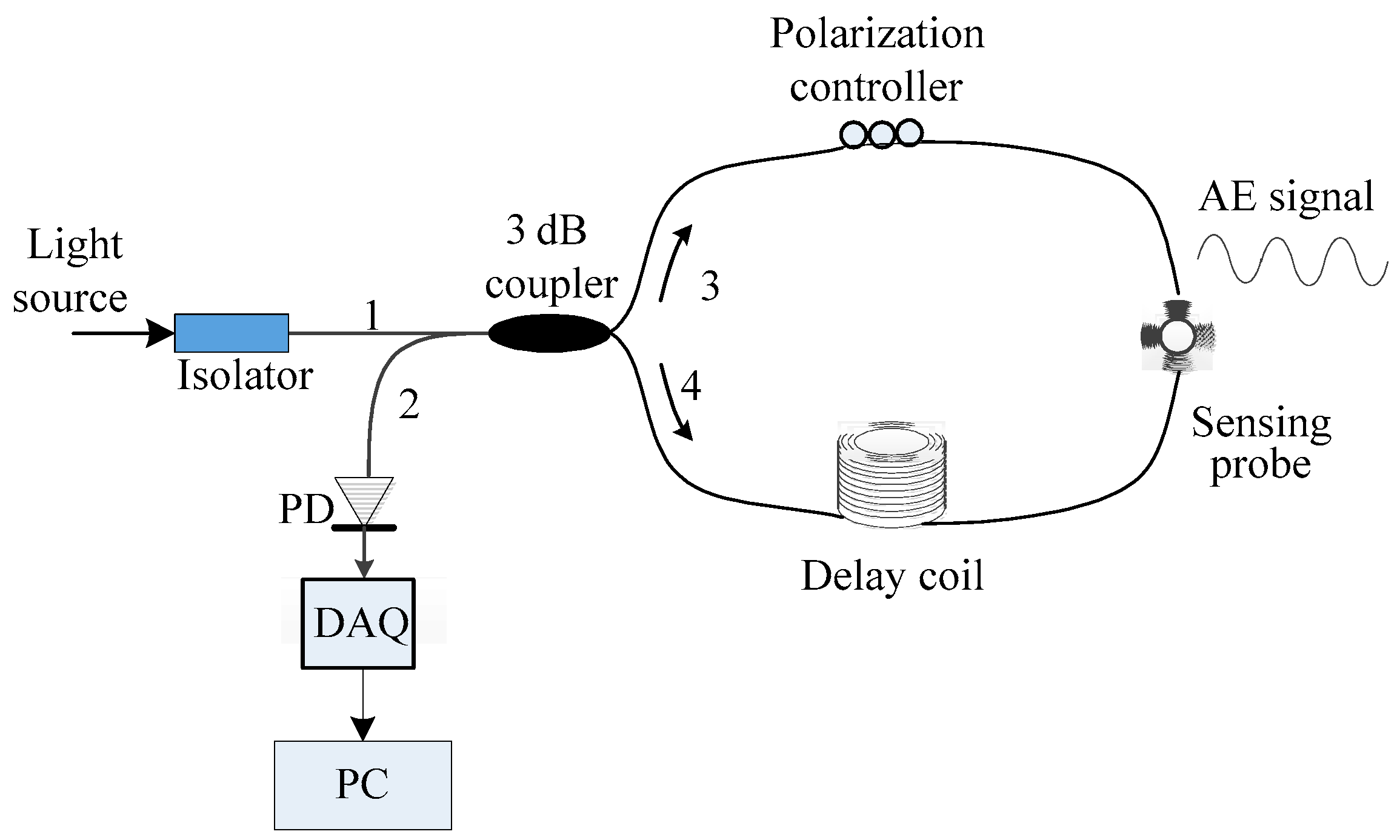
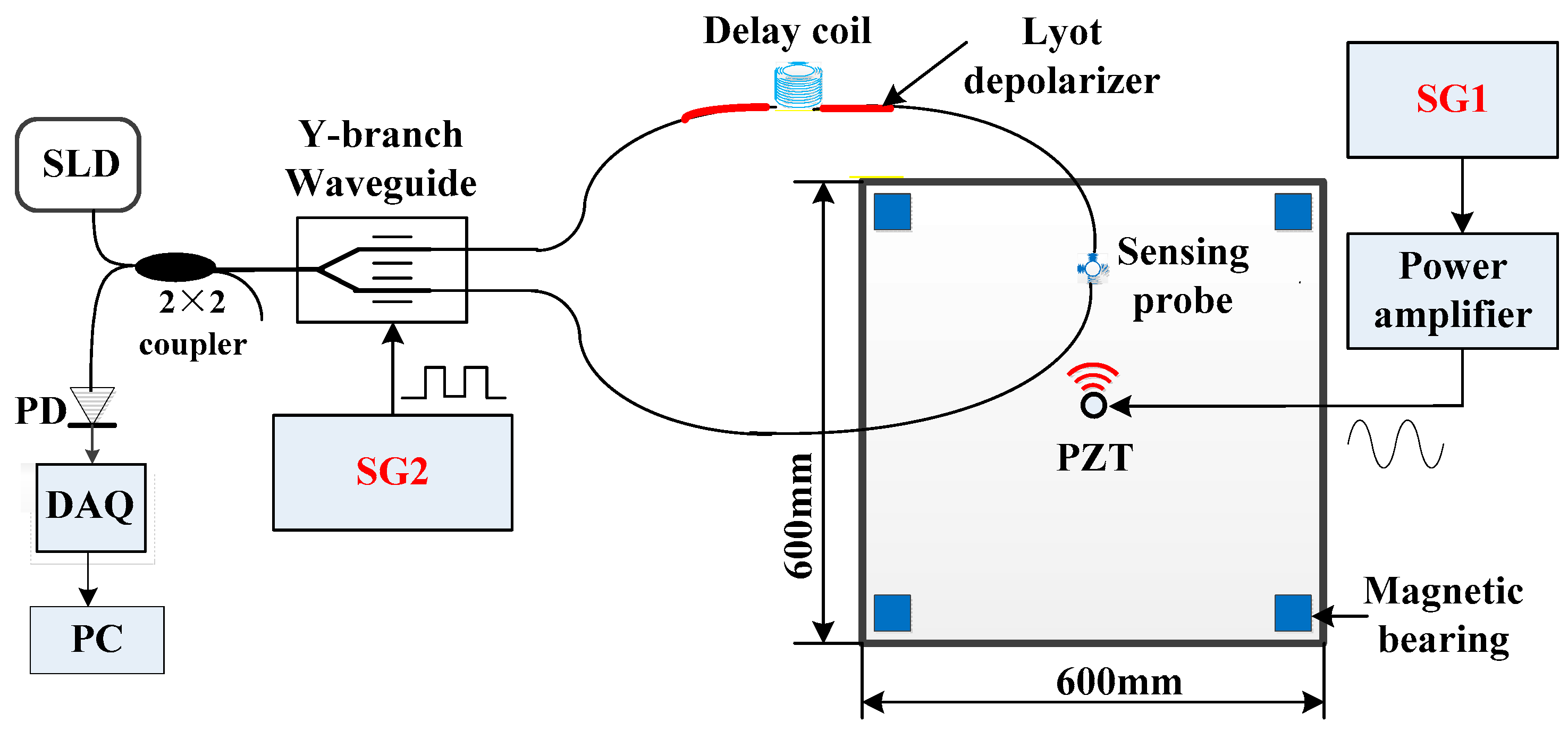
3. Experimental Setup
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Eaton, M.; Pearson, M.; Lee, W.; Pullin, R. Accurate damage location in complex composite structures and industrial environments using acoustic emission. In Proceedings of the 11th International Conference on Damage Assessment of Structures, Ghent, Belgium, 24–26 August 2015. [Google Scholar]
- He, J.J.; Guan, X.F.; Peng, T.S.; Liu, Y.M.; Saxena, A.; Celaya, J.; Goebel, K. A multi-feature integration method for fatigue crack detection and crack length estimation in riveted lap joints using Lamb waves. Smart Mater. Struct. 2013, 22, 105007. [Google Scholar] [CrossRef]
- Jaroszewicz, L.R.; Krajewski, Z.; Solarz, L.; Teisseyer, R. Application of the fibre-optic Sagnac interferometer in the investigation of seismic rotational waves. Meas. Sci. Technol. 2006, 17, 1186–1193. [Google Scholar] [CrossRef]
- Qian, S.; Chen, H.; Xu, Y.; Su, L. High Sensitivity Detection of Partial Discharge Acoustic Emission within Power Transformer by Sagnac Fiber Optic Sensor. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 2313–2320. [Google Scholar] [CrossRef]
- Sohaib, M.; Islam, M.; Kim, J.Y.; Jeon, D.C.; Kim, J.M. Leakage Detection of a Spherical Water Storage Tank in a Chemical Industry Using Acoustic Emissions. Appl. Sci. 2019, 9, 196. [Google Scholar] [CrossRef]
- Ghosh, R.; Chatterjee, B.; Dalai, S. A method for the localization of partial discharge sources using partial discharge pulse information from acoustic emissions. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 237–245. [Google Scholar] [CrossRef]
- Chai, M.Y.; Zhang, J.; Zhang, Z.X.; Duan, Q.; Cheng, G.X. Acoustic emission studies for characterization of fatigue crack growth in 316LN stainless steel and welds. Appl. Acoust. 2017, 126, 101–113. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, P.F.; Zhang, Y.N. Acoustic Emission Based on Cluster and Sentry Function to Monito Tensile Progressive Damage of Carbon Fiber Woven Composites. Appl. Sci. 2018, 8, 2265. [Google Scholar] [CrossRef]
- Wu, Q.; Yu, F.M.; Okabe, Y.; Kobayashi, S. Application of a novel optical fiber sensor to detection of acoustic emissions by various damages in CFRP laminates. Smart Mater. Struct. 2015, 24, 015011. [Google Scholar] [CrossRef]
- Yalcinkaya, H.; Ozevin, D. The design and calibration of particular geometry piezoelectric acoustic emission transducer for leak detection and localization. Meas. Sci. Technol. 2013, 24, 095103–095112. [Google Scholar] [CrossRef]
- Perelli, A.; De Marchi, L.; Marzani, A.; Speciale, N. Acoustic emission localization in plates with dispersion and reverberations using sparse PZT sensors in passive mode. Smart Mater. Struct. 2012, 21, 025010. [Google Scholar] [CrossRef]
- Ciampa, F.; Meo, M. Acoustic emission source localization and velocity determination of the fundamental mode A0 using wavelet analysis and a Newton-based optimization technique. Smart Mater. Struct. 2010, 19, 045027. [Google Scholar] [CrossRef]
- Lee, J.R.; Lee, S.S.; Yoon, D.J. Simultaneous multipoint acoustic emission sensing using fibre acoustic wave grating sensors with identical spectrum. J. Opt. A Pure Appl. Opt. 2008, 10, 085307–085315. [Google Scholar] [CrossRef]
- Cho, S.I.; Lee, J.K.; Lee, J.O.; Jung, S.S.; Lee, D.H.; Seo, W.C. PZT transducer response to an epicentral acoustic emission signal during glass capillary breakage. J. Korean Phys. Soc. 2008, 53, 3213–3219. [Google Scholar] [CrossRef]
- Read, I.; Foote, P.; Murray, S. Optical fibre acoustic emission sensor for damage detection in carbon fibre composite structures. Meas. Sci. Technol. 2002, 13, 5–9. [Google Scholar] [CrossRef]
- Fu, T.; Liu, Y.; Li, Q.; Leng, J. Fiber optic acoustic emission sensor and its applications in the structural health monitoring of CFRP materials. Opt. Lasers Eng. 2009, 47, 1056–1062. [Google Scholar] [CrossRef]
- Matsuo, T.; Cho, H.; Takemoto, M. Optical fiber acoustic emission system for monitoring molten salt attack. Sci. Technol. Adv. Mater. 2006, 7, 104–110. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.H.; Shi, Y.K.; Shan, N.; Yuan, X.Q. Stabilized fiber-optic extrinsic Fabry-Perot sensor system for acoustic emission measurement. Opt. Laser. Technol. 2008, 40, 874–880. [Google Scholar] [CrossRef]
- Wang, L.T.; Fang, N.; Wu, C.X.; Qin, H.J.; Huang, Z.M. A Fiber Optic PD Sensor Using a Balanced Sagnac Interferometer and an EDFA-Based DOP Tunable Fiber Ring Laser. Sensors 2014, 14, 8398–8422. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.B. Aluminum alloy material structure impact Localization by using FBG Sensors. Photonic Sens. 2014, 4, 344–348. [Google Scholar] [CrossRef]
- Lam, P.M.; Lau, K.T.; Ling, H.Y.; Su, Z.Q.; Tam, H.Y. Acousto-ultrasonic sensing for delaminated GFRP composites using an embedded FBG sensor. Opt. Lasers Eng. 2009, 47, 1049–1055. [Google Scholar] [CrossRef]
- Fomitchov, P.A.; Krishnaswamy, S.; Achenbach, J.D. Compact phase-shifted Sagnac interferometer for ultrasound detection. Opt. Laser Technol. 1997, 29, 333–338. [Google Scholar] [CrossRef]
- Zhang, G.; Liang, Y.J.; Xi, C.; Zuo, H.G. Dual-Sagnac Optical Fiber Sensor Used in Acoustic Emission Source Location. In Proceedings of the 2011 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference, Harbin, China, 26–30 July 2011. [Google Scholar]
- Wei, P.; Han, X.L.; Xia, D.; Liu, T.L.; Lang, H. Novel fiber-optic ring acoustic emission sensor. Sensors 2018, 18, 215. [Google Scholar]
- Jang, T.S.; Lee, S.S.; Kim, Y.G. Surface-bonded fiber optic Sagnac sensors for ultrasound detection. Ultrasonics 2004, 42, 837–841. [Google Scholar] [CrossRef]
- Jang, T.S.; Lee, J.J.; Yoon, D.J.; Lee, S.S. Non-contact detection of laser-generated surface acoustic waves using fiber optic Sagnac interferometer. Ultrasonics 2002, 40, 803–807. [Google Scholar] [CrossRef]
- Liang, Y.J.; Mu, L.L.; Liu, J.F.; Yu, X.T. Combined optical fiber interferometric sensors for the detection of acoustic emission. Opt. Lett. 2008, 4, 0184–0187. [Google Scholar] [CrossRef]






| Amplitude of Fundamental Voltage | |
|---|---|
| 0 | 0.00660 |
| ±0.1 | 0.01910 |
| ±0.2 | 0.02873 |
| ±0.3 | 0.04117 |
| ±0.4 | 0.04509 |
| ±0.5 | 0.05245 |
| ±0.6 | 0.06120 |
| ±0.7 | 0.06305 |
| ±0.8 | 0.06194 |
| ±0.9 | 0.05681 |
| ±1.0 | 0.04740 |
| ±1.1 | 0.04076 |
| ±1.2 | 0.03112 |
| ±1.3 | 0.02242 |
| ±1.4 | 0.00960 |
| ±1.5 | 0.00276 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Zeng, J.; Liang, D.; Chang, C.; Wang, B. Influence of Initial Phase Modulation on the Sensitivity of the Optical Fiber Sagnac Acoustic Emission Sensor. Appl. Sci. 2019, 9, 1018. https://doi.org/10.3390/app9051018
Cheng Z, Zeng J, Liang D, Chang C, Wang B. Influence of Initial Phase Modulation on the Sensitivity of the Optical Fiber Sagnac Acoustic Emission Sensor. Applied Sciences. 2019; 9(5):1018. https://doi.org/10.3390/app9051018
Chicago/Turabian StyleCheng, Zhuming, Jie Zeng, Dakai Liang, Chen Chang, and Bing Wang. 2019. "Influence of Initial Phase Modulation on the Sensitivity of the Optical Fiber Sagnac Acoustic Emission Sensor" Applied Sciences 9, no. 5: 1018. https://doi.org/10.3390/app9051018
APA StyleCheng, Z., Zeng, J., Liang, D., Chang, C., & Wang, B. (2019). Influence of Initial Phase Modulation on the Sensitivity of the Optical Fiber Sagnac Acoustic Emission Sensor. Applied Sciences, 9(5), 1018. https://doi.org/10.3390/app9051018






