The Virial Effect—Applications for SF6 and CH4 Thermal Plasmas
Abstract
:1. Introduction
2. Equations and Methods
2.1. Partition Functions
- -
- m is the mass of the species;
- -
- kB is the Boltzmann constant;
- -
- T is the temperature;
- -
- h is Planck’s constant;
- -
- E0 is the energy of formation.
2.1.1. The Internal Partition Function of Monoatomic Species
- -
- gi is the statistical weight of an electronic level i, given by gi = 2.J + 1, where J is the angular momentum;
- -
- Ei is the energy of the electronic level i;
- -
- imax is the limitation of the summation over the electronic levels, to avoid the divergence of the summation at high temperatures. The limit of the summation is the energy of ionization Eion, which is reduced by the lowering of the ionization potential ΔE (imax ≤ Eion − ΔE). The lowering of the ionization potential (Equation (3)) is introduced in order to limit the number of electronic energy levels that are considered in the sum (Equation (2)), due to the electric and electromagnetic field effects created by the charged particles. This can be estimated from the Debye–Hückel formula (Equation (3)):
- -
- Z is the electrical charge of the considered species;
- -
- e is the electrical charge of the electron;
- -
- ε0 is the vacuum permittivity;
- -
- λD is the Debye length, given by Equation (4):
2.1.2. The Internal Partition Function for Molecules
- -
- Tr and Pr are the temperature and pressure, respectively, of the reference in the JANAF database;
- -
- Na is the Avogadro constant;
- -
- H(0) − H(Tr) represents the enthalpy at absolute zero;
- -
- [G − H(Tr)]/T is the Gibbs energy, which must be known for each temperature that is considered.
2.2. The Equation for the Calculation of the LTE Plasma Composition
2.2.1. Choices of Elements and Chemical Species
2.2.2. The Composition Matrix
2.2.3. The Chemical Base
- -
- The densities of the species in the base matrix must be the highest densities.
- -
- The species of the base matrix must be independent, in order to avoid |B| = 0 (the null determinant).
- -
- The species that are present at very low densities must not be included in the base matrix.
2.2.4. The Reaction Coefficient
2.2.5. Conservation Equations
- -
- Conservation of nuclei:with the atomic proportion ε.
- -
- Electric neutrality:where Zi is the electric charge of the species i (which can be directly expressed from Ci, charge).
- -
- ΔPDebye is the Debye–Hückel pressure correction:
- -
- ΔPvirial is the virial pressure correction. For its calculation, several coefficients describing the difference in behavior between real fluids and perfect gases are needed. Taking into account the second- and third-order corrections, the virial pressure correction is given in Equation (15):where B(T) and C(T) are the second and third virial coefficients, respectively, and they depend on the temperature. The methods to obtain them are described in Section 3 of this paper (cf. Section 3 « virial coefficient »).
2.2.6. The Equation for Out-of-Base Species Density
2.2.7. Numerical Methods and System of Equations
2.3. Automatization of the Tool
2.3.1. Data from the NIST and JANAF Tables
- -
- the name of the species, for a link between the initialization file and the data file;
- -
- the energy of formation, needed for the calculation of the total partition function;
- -
- the energy of ionization that is used in order to satisfy the limit condition of Equation (2);
- -
- the units for the energy levels, depending on the extracted data (in cm−1 or in eV);
- -
- the number of energy levels to consider, up to the ionization of the considered species;
- -
- the mass of the considered species.
2.3.2. The Initialization File
- -
- the number of gases considered in the composition.
- -
- the name(s) of the gas(es) in the composition (for instance, SF6, N2, and O2, Ar, and Cu, etc.).
- -
- the molar fraction of each gas in the melt (the sum of all of the fractions must equal unity; for example, it could be 1 SF6, 0.7885 N2 and 0.2115 O2, or 0.8 Ar and 0.2 Cu, etc.);
- -
- the number of atoms and species that come from the gas mixture, in order to define M and N (cf. Section 2.2.1);
- -
- the names of the species in the plasma;
- -
- the atomic proportions of each atom/nucleus for the considered mixture (for example, 100% SF6: 1 S and 6 F; 78.85% N2 and 21.15% O2: (0.7885 × 2) N and (0.2115 × 2) O);
- -
- the considered pressure;
- -
- the temperature range and the temperature step of the results.
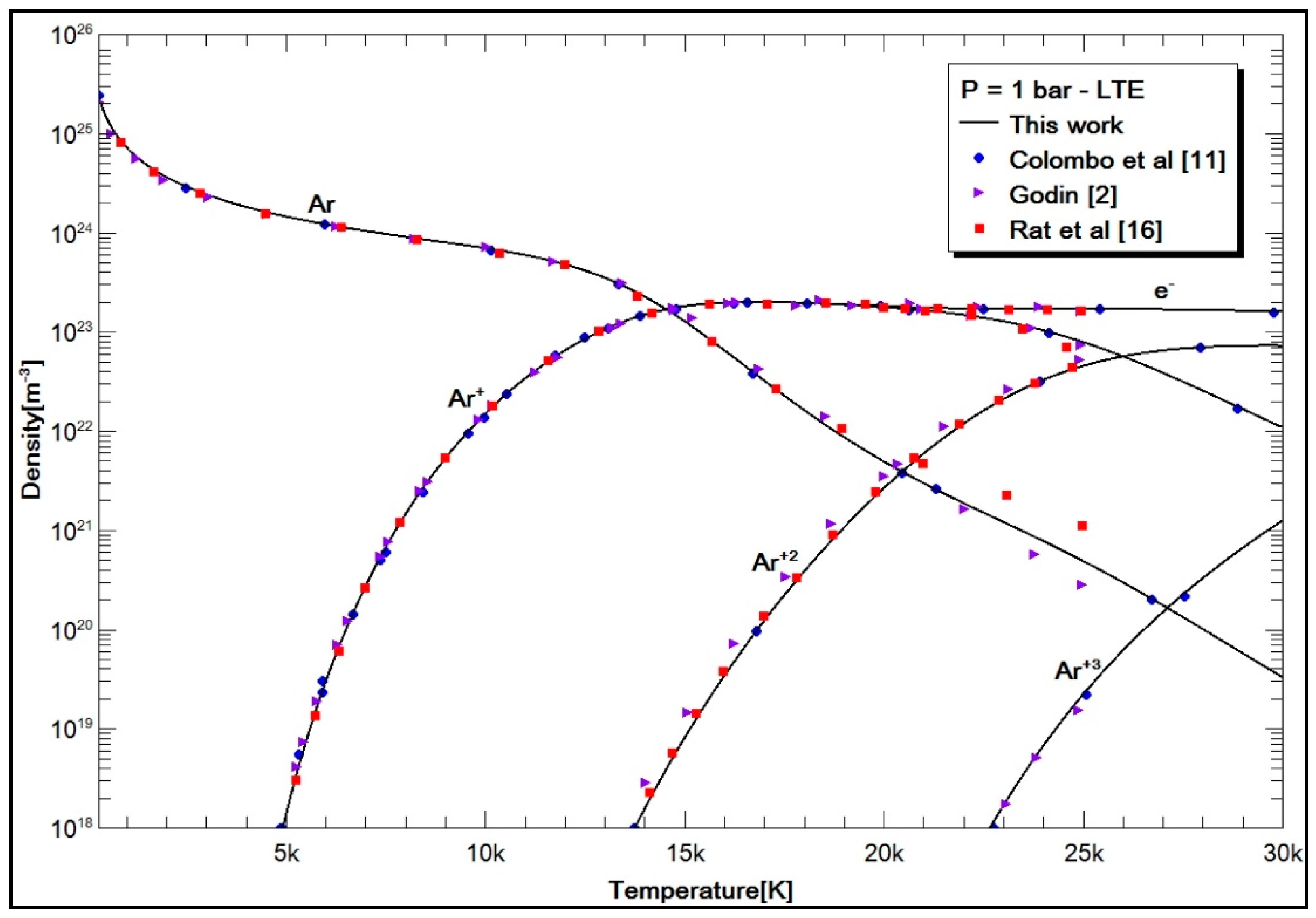
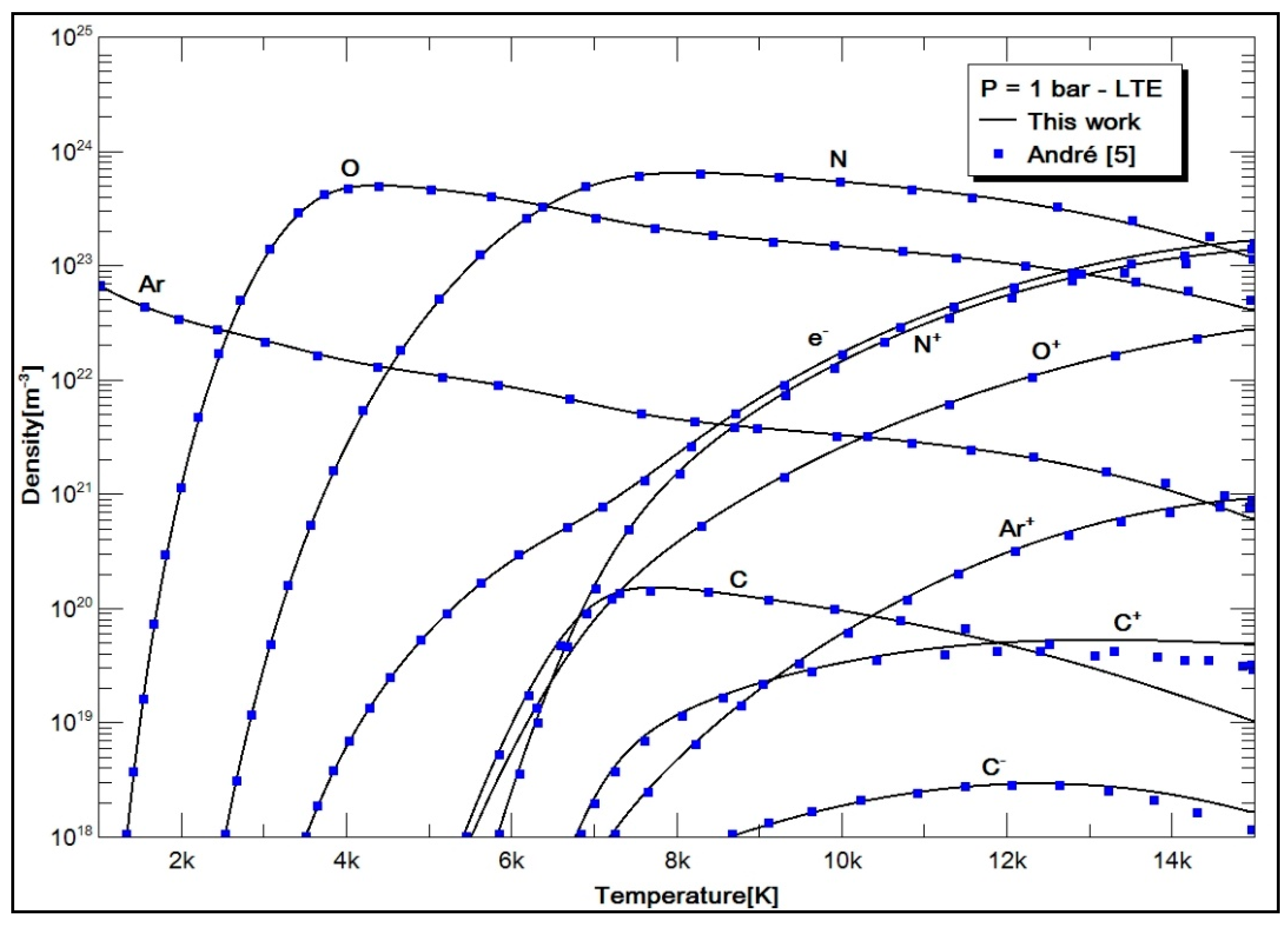
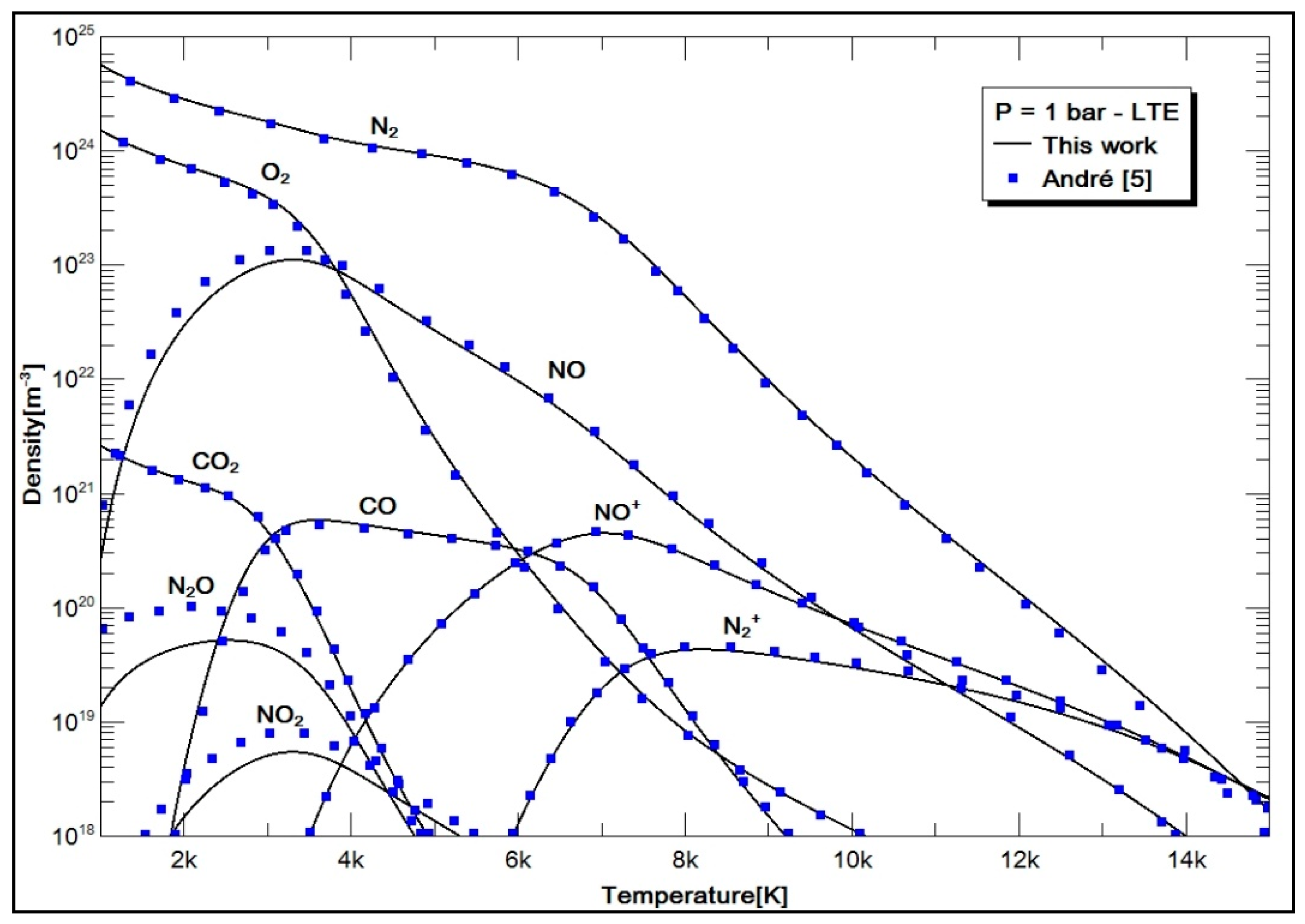
2.4. Results and Discussion
- -
- Case 1: pure argon;
- -
- Case 2: air with 78.084% N2, 20.946% O2, 0.036% CO2, and 0.934% Ar.
3. Virial Coefficients
- -
- m is the number of gas for mixing;
- -
- xi, xj, and xk are the respective molar fractions of species i, j, and k;
- -
- Bij is the binary interaction parameter;
- -
- Cijk is the ternary interaction parameter.
3.1. The Lennard–Jones Potential
3.1.1. Expression of the Potential
3.1.2. Potential Parameters σ and ε
3.2. Results and Discussion
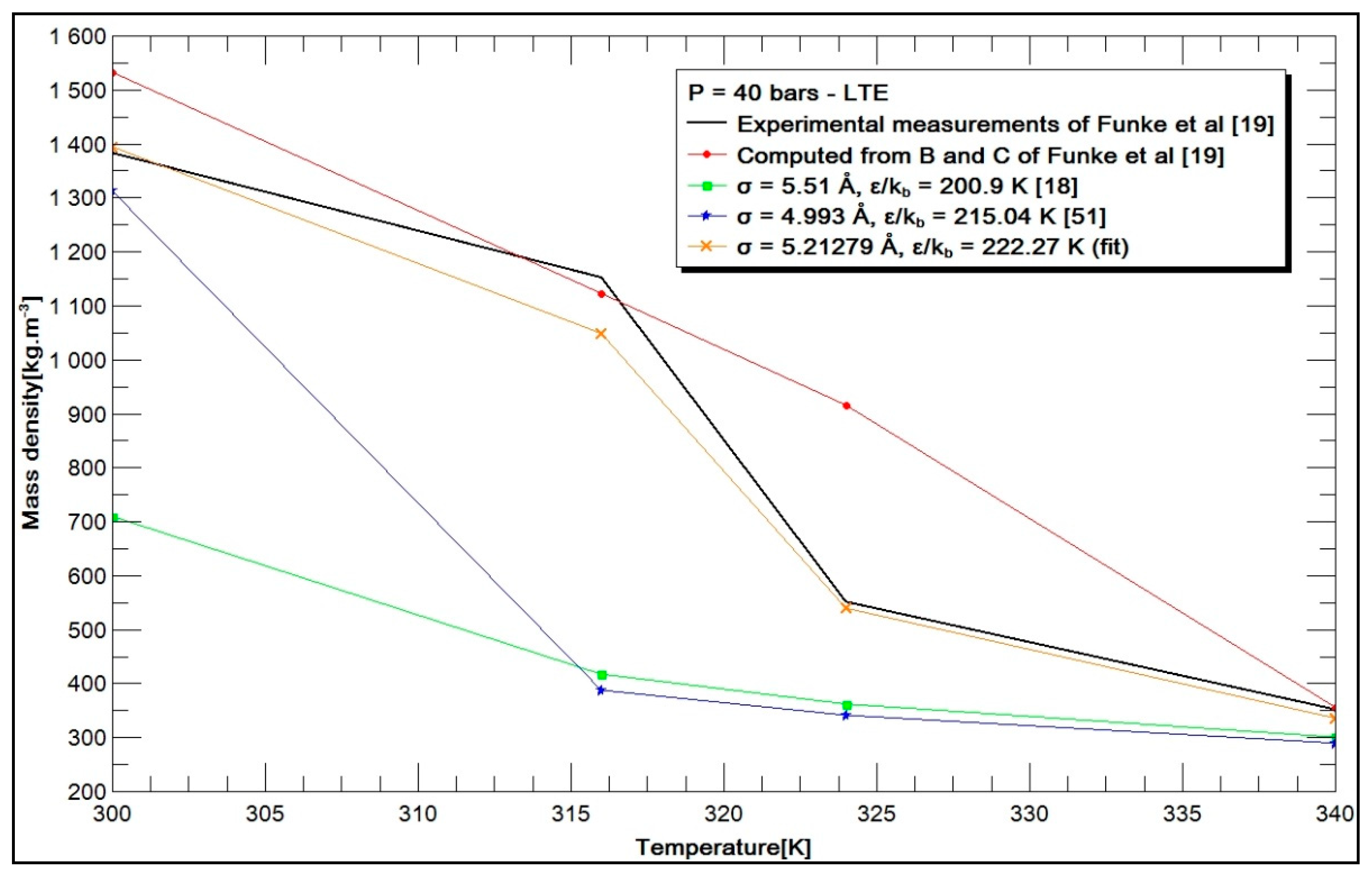
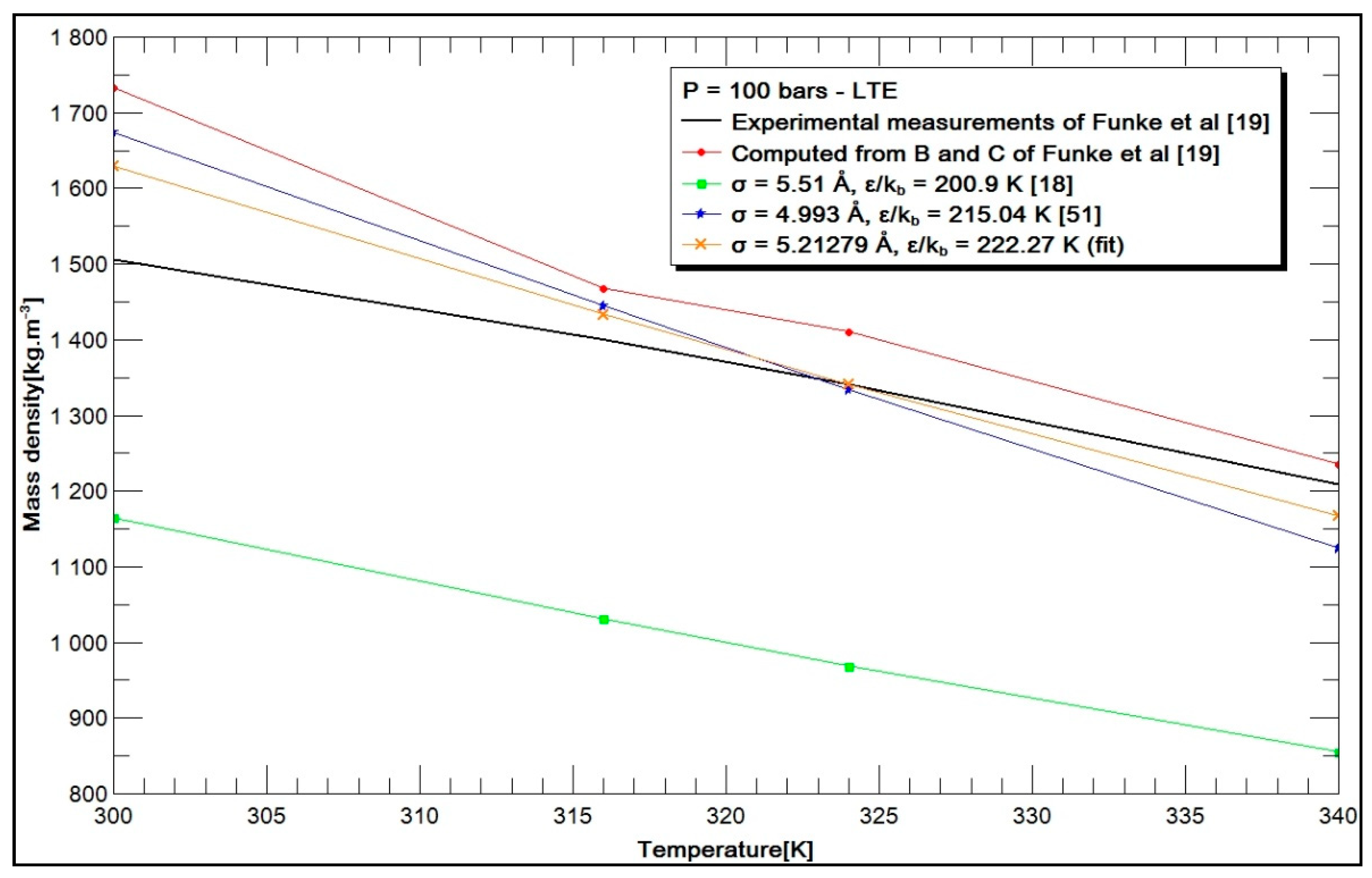
3.2.1. Choice of Parameters
- -
- the experimental mass densities measured by Funke [19];
- -
- the mass densities calculated from the second and third virial coefficients given by Funke [19];
- -
- the mass densities calculated from the values of σ and by Hirschfelder et al. [18];
- -
- the mass densities calculated from the values of σ and , deduced by the Stiel formulation [51];
- -
- the mass densities calculated from the values of σ and , deduced from the optimization process and named “fit”.
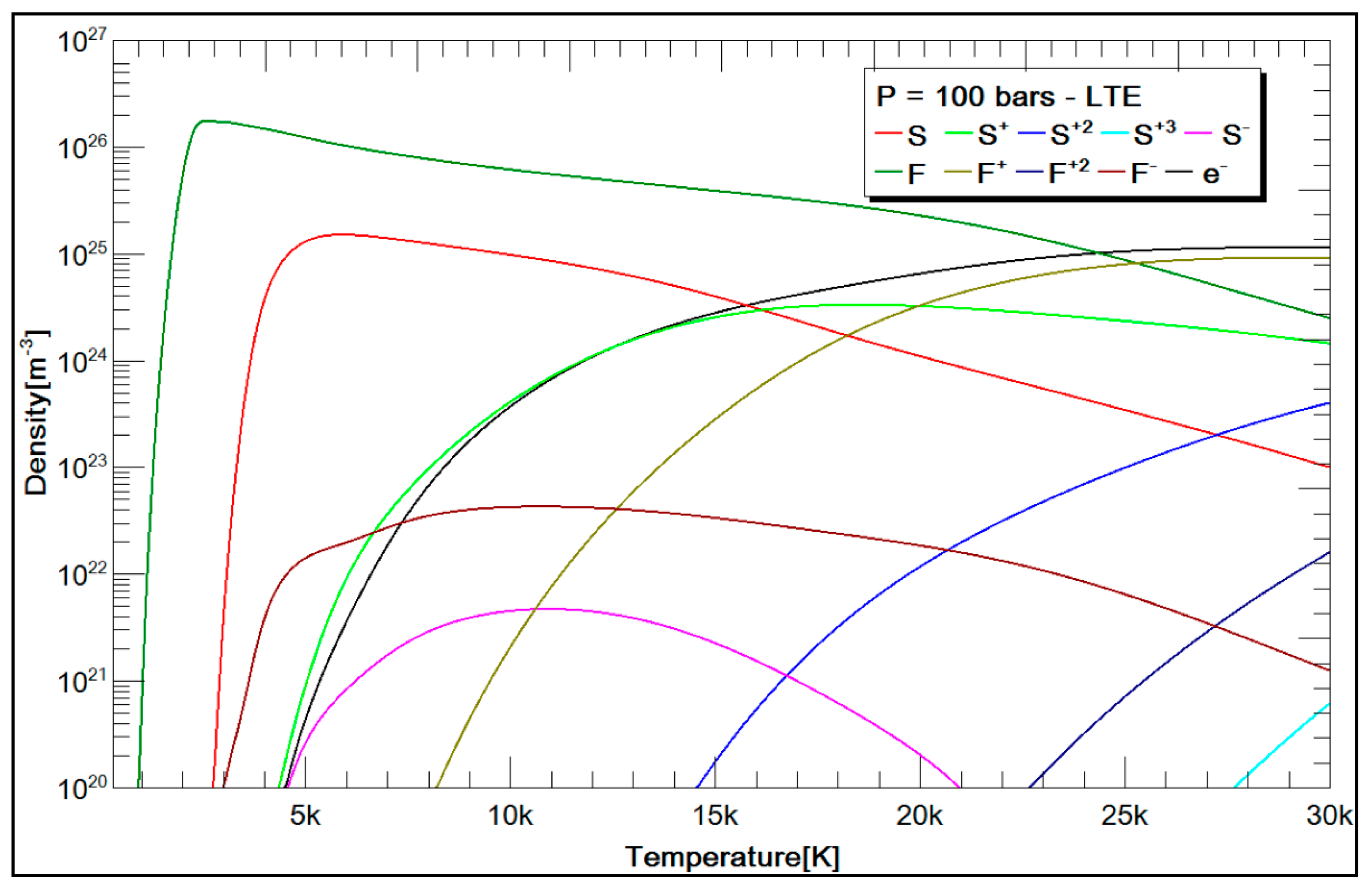
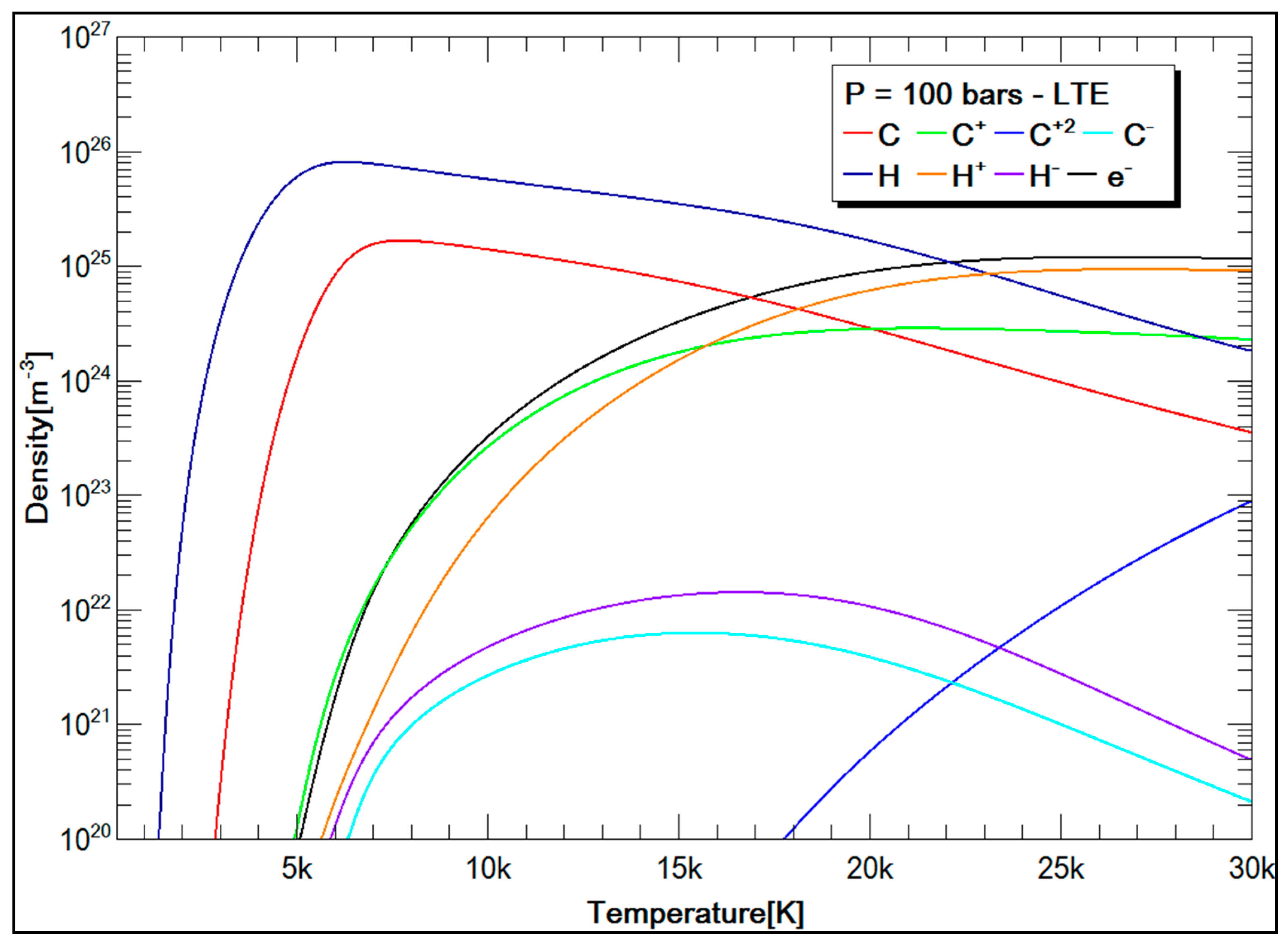
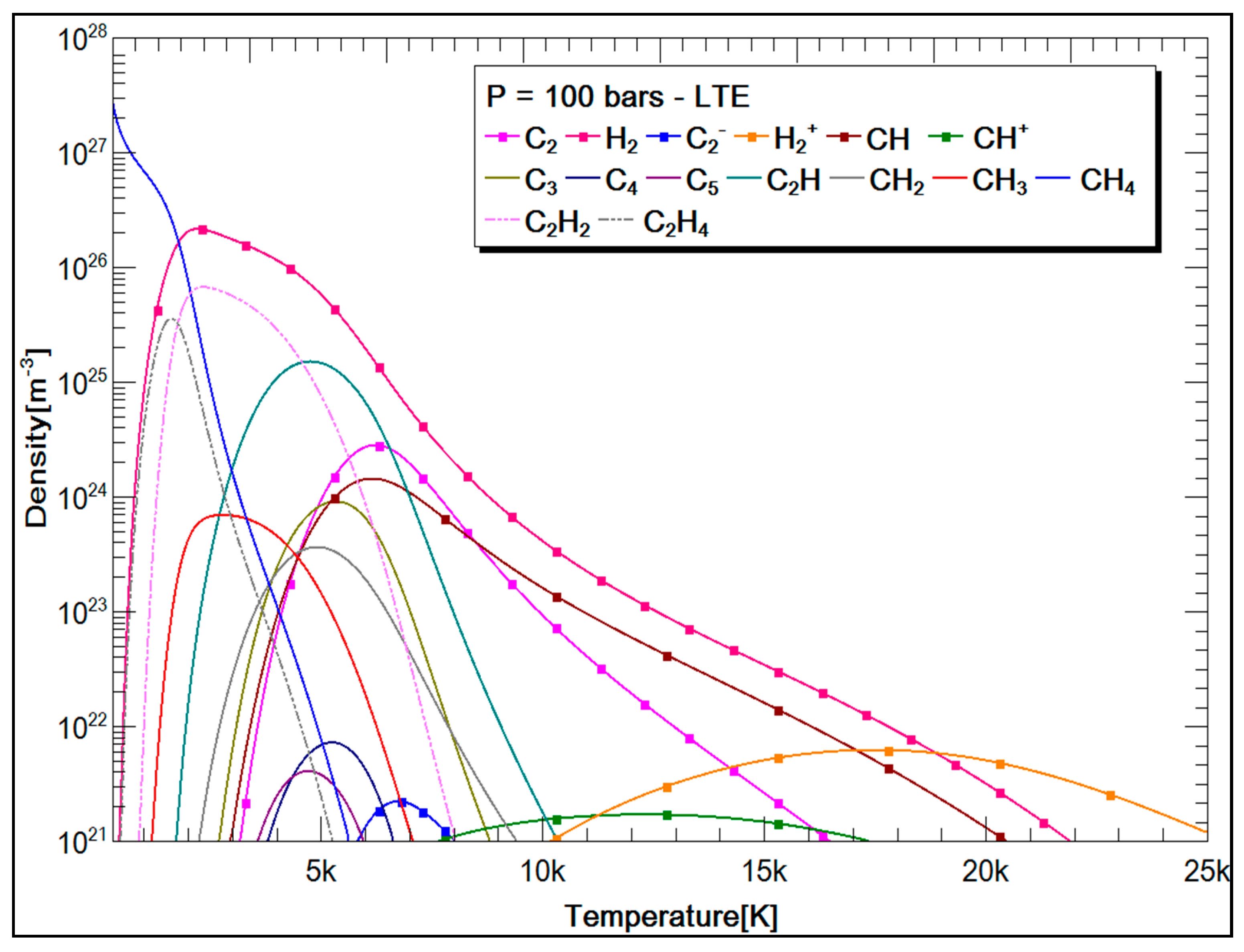
3.2.2. SF6 and CH4 Plasma Compositions
4. Conclusions
Plasma Compositions
Author Contributions
Funding
Conflicts of Interest
References
- White, W.B.; Johnson, S.M.; Dantzig, G.B. Chemical Equilibrium in Complex Mixtures. J. Chem. Phys. 1958, 28, 751–755. [Google Scholar] [CrossRef]
- Godin, D. Calcul de Compositions Chimiques de Plasmas à l’Equilibre Thermodynamique: Application à la Modélisation de l’Ablation dans les Disjoncteurs. Master’s Thesis, Université de Montréal—Ecole Polytechnique de Montréal, Montreal, QC, Canada, 1998; 239p. [Google Scholar]
- Godin, D.; Trépanier, J.Y. A Robust and Efficient Method for the Computation of Equilibrium Composition in Gaseous Mixtures. Plasma Chem. Plasma Process. 2004, 24, 447–473. [Google Scholar] [CrossRef]
- Ailas, S. Etude du Spectre Moléculaire Emis par un Plasma Thermique Formé de Mélange CH4-H2. Ph.D. Thesis, Université Abou-Bekr Belkaid, Tlemcen, Algerie, 2017. [Google Scholar]
- André, P. Etude de la Composition et des Propriétés Thermodynamiques des Plasmas Thermiques à l’Equilibre et Hors d’Equilibre Thermodynamique. Ph.D. Thesis, Université Blaise Pascal, Clermont-Ferrand, France, 1995; 123p. [Google Scholar]
- André, P.; Brunet, L.; Duffour, E.; Lombard, J.M. Composition, Pressure and Thermodynamic Properties Calculated in Plasma Formed in Insulator Vapours of PC and POM at fixed volume. Eur. Phys. J. Appl. Phys. 2002, 17, 53–64. [Google Scholar] [CrossRef]
- Aubreton, J. Etude des Propriétés Thermodynamiques et de Transport Dans les Plasmas à l’Equilibre et hors Equilibre Thermodynamique Appliquées aux Plasmas de Mélanges Ar-H2 et Ar-O2. Ph.D. Thesis, Université de Limoges, Limoges, France, 1985. [Google Scholar]
- Aubreton, A. Modélisation et Etude Expérimentale d’un Plasma Métallique Crée par Ablation Laser. Ph.D. Thesis, Université de Toulouse III, Paul Sabatier, Toulouse, France, 2002; 185p. [Google Scholar]
- Billoux, T. Elaboration d’une Base de Données Radiatives pour des Plasmas de Type CwHxOyNz et Application au Transfert Radiatif pour des Mélanges Air, CO2 et CO-H2. Ph.D. Thesis, Université de Toulouse III, Paul Sabatier, Toulouse, 2013; 180p. [Google Scholar]
- Cabrera, A.M. Modélisation de la Cinétique Chimique d’un Plasma en Extinction dans un Disjoncteur Basse Tension. Ph.D. Thesis, Université de Toulouse III, Paul Sabatier, Toulouse, France, 2003; 177p. [Google Scholar]
- Colombo, V.; Ghedini, E.; Sanibondi, P. Thermodynamic and Transport Properties in Non-Equilibrium Argon, Oxygen and Nitrogen Thermal Plasmas. Prog. Nuclear Energy 2008, 50, 921–933. [Google Scholar] [CrossRef]
- Colombo, V.; Ghedini, E.; Sanibondi, P. Two Temperature Thermodynamic and Transport Properties of Argon-Hydrogen and Nitrogen-Hydrogen plasma. J. Phys. D Appl. Phys. 2009, 42, 12. [Google Scholar] [CrossRef]
- Cressault, Y. Propriétés des Plasmas Thermiques dans des Mélanges Argon-Hydrogène-Cuivre. Ph.D. Thesis, Université de Toulouse III, Paul Sabatier, Toulouse, France, 2001; 167p. [Google Scholar]
- Cressault, Y.; Connord, V.; Hingana, H.; Teulet, P.; Gleizes, A. Transport properties of CF3I thermal plasmas mixed with CO2, air or N2 as an alternative to SF6 plasmas in high-voltage circuit breakers. J. Phys. D Appl. Phys. 2011, 44, 495202. [Google Scholar] [CrossRef]
- Hingana, H. Contribution à l’Etude des Propriétés des Plasmas à Deux Températures: Application A L’argon Et Air. Ph.D. Thesis, Université Toulouse III, Paul Sabatier, Toulouse, France, 2010; 143p. [Google Scholar]
- Rat, V.; André, P.; Aubreton, J.; Elchinger, M.F.; Fauchais, P.; Vacher, D. Transport coefficients including diffusion in a two-temperature argon plasma. J. Phys. D Appl. Phys. 2002, 35, 981–991. [Google Scholar] [CrossRef]
- Rochette, D.; Bussière, W.; André, P. Composition, Enthalpy, and Vaporization temperature, calculation of Ag-SiO2 plasmas with Air in the temperature range from 1000 to 6000 K and for pressure included between 1 and 50 bars. Plasma Chem. Plasma Process. 2004, 24, 475–492. [Google Scholar] [CrossRef]
- Hirschfelder, J.O.; Curtiss, C.F.; Bird, R.B. Molecular Theory of Gases and Liquids; J. Wiley and Sons Chapman and Hal, Inc.: New York, NY, USA, 1954. [Google Scholar]
- Funke, M.; Kleinrahm, R.; Wagner, W. Measurement and correlation of the (p, ρ, T) relation of sulphur hexafluoride. I. The homogeneous gas and liquid region in the temperature range from 225 K to 340 K at pressures up to 12 MPa. J. Chem. Thermodyn. 2002, 34, 717–734. [Google Scholar] [CrossRef]
- Gilgen, R.; Kleinrahm, R.; Wagner, W. Supplementary measurements of the (pressure, density, temperature) relation of carbon dioxide in the homogeneous region at temperatures from 220 K to 360 K and pressures up to 13 MPa. J. Chem. Thermodyn. 1992, 24, 1243–1250. [Google Scholar] [CrossRef]
- Hurly, J.J.; Defibaugh, D.R.; Moldover, M.R. Thermodynamic properties of sulfur hexafluoride. Int. J. Thermophys. 2000, 21, 739–765. [Google Scholar] [CrossRef]
- Zarkova, L.; Hohm, U. pVT—Second virial coefficients B(T), viscosity η(T), and self-diffusion ρD(T) of the gases: BF3, CF4, SiF4, CCl4, SiCl4, SF6, MoF6, WF6, UF6, C(CH3)4, and SI(CH3)4, determined by means of an isotopic temperature-dependent potential. J. Phys. Chem. Ref. Data 2002, 31, 183–216. [Google Scholar] [CrossRef]
- Sengers, J.M.H.L.; Klein, M.; Gallagher, J.S. Pressure-Volume-Temperature relationships of gases virial coefficients. In American Institute of Physics Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 1971. [Google Scholar]
- Wagner, W.; Ewers, J.; Schmidt, R. An equation of state for oxygen vapour—Second and third virial coefficients. Cryogenics 1984, 24, 37–43. [Google Scholar] [CrossRef]
- Zarkova, L.; Hohm, U.; Damyanova, M. Viscosity and pVT-Second virial coefficient of binary noble-globular gas and globular-globular gas mixtures, calculated by means of an isotropic temperature-dependent potential. J. Phys. Chem. Ref. Data 2003, 32, 1591–1705. [Google Scholar] [CrossRef]
- Zarkova, L.; Hohm, U.; Damyanova, M. Viscosity and pVT-Second virial coefficient, and diffusion of pure and mixed small alkanes CH4, C2H6, C3H8, n-C4H10, i-C4H10, n-C5H12, i-C5H12, and C(CH3)4, calculated by means of an isotopic temperature-dependent potential. I. Pure alkanes. J. Phys. Chem. Ref. Data 2006, 35, 1331–1364. [Google Scholar] [CrossRef]
- Petchanka, A.; Reichert, F.; Gonzalez, J.J.; Freton, P. Modelling of deformation of PTFE nozzles in high voltage circuit breaker due to multiple interruptions. J. Phys. D Appl. Phys. 2016, 49, 135201. [Google Scholar] [CrossRef]
- Reichert, F.; Petchanka, A.; Freton, P.; Gonzalez, J.J. Studies on the Thermal Re-ignition in SF6 High-Voltage Circuit-Breakers by means of Coupled Simulation. Plasma Phys. Technol. J. 2015, 2, 2336–2626. [Google Scholar]
- Gonzalez, J.J.; Freton, P.; Reichert, P.; Pechanka, A. PTFE vapor contribution to pressure changes in high voltage circuit breakers. IEEE Trans. Plasma Sci. 2015, 43, 2703–2714. [Google Scholar] [CrossRef]
- Laforest, Z.; Gonzalez, J.J.; Freton, P. Experimental study of a plasma bubble created by a wire explosion in water. Int. J. Res. Rev. Appl. Sci. 2018, 34, 93–105. [Google Scholar]
- Benmouffok, M.; Freton, P.; Gonzalez, J.J. Theoretical plasma characterization during current pulse. Int. J. Res. Rev. Appl. Sci. 2018, 34, 3. [Google Scholar]
- André, P.; Brunet, L.; Bussière, W.; Caillard, J.; Lombard, J.M.; Picard, J.P. Transport coefficients of plasmas consisting of insulator vapours: Application to PE, POM, PMMA, PA66 and PC. Eur. Phys. J. Appl. Phys. 2004, 25, 169–182. [Google Scholar] [CrossRef]
- Chervy, B.; Gleizes, A.; Razafinimanana, M. Thermodynamic properties and transport coefficients in SF6-Cu mixtures at temperatures of 300 K–30 kK and pressures of 0.1–1 MPa. J. Phys. D Appl. Phys. 1994, 27, 1193–1206. [Google Scholar] [CrossRef]
- Kravchik, T.; Sher, E.; Heywood, J.B. From spark ignition to flame initiation. Combust. Sci. Technol. 1995, 108, 1–30. [Google Scholar] [CrossRef]
- Maly, R.; Vogel, M. Initiation and Propagation of Flame Fronts in Lean Methane/Air Mixtures by the Three Modes of the Ignition Spark. In Symposium (International) on Combustion; Elsevier: New York, NY, USA, 1979; Volume 17, pp. 821–831. [Google Scholar]
- Zaepffel, C. Etude Expérimentale et Numérique d’une Décharge Electrique Appliquée à L’allumage d’un Milieu Réactif, Ph.D. Thesis, Université d’Orléans, Orléans, France, 2008. [Google Scholar]
- Chase, M.W.; Davies, C.A.; Downey, J.R.; Frurip, D.J.; McDonald, R.A.; Syverud, A.N. NIST-JANAF Thermochemical Tables (ver. 1.0), Online, Standard Reference Data Program; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1985. Available online: https://janaf.nist.gov/ (accessed on 7 November 2018). [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (ver. 5.5.6); Online; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. Available online: https://physics.nist.gov/PhysRefData/ASD/levels_form.html (accessed on 7 November 2018).
- Drawin, H.W.; Felenbok, P. Data of Plasmas in Local Thermodynamic Equilibrum; Editions Gauthier: Paris, France, 1965. [Google Scholar]
- Hryniewicki, M.K. Accurate and Efficient Evaluation of the Second Virial Coefficient Using Practical Intermolecular Potentials for Gases. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2011. [Google Scholar]
- Mamedov, B.A.; Somuncu, E. Analytical evaluation of third virial coefficient with Lennard-Jones (12-6) potential and its applications. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2016; pp. 020121-1–020121-4. [Google Scholar] [CrossRef]
- Rice, W.E.; Hirschfelder, J.O. Second virial coefficients of gases obeying a modified Buckingham (exp-6) potential. J. Chem. Phys. 1954, 22, 187–192. [Google Scholar] [CrossRef]
- Edalat, M.; Lan, S.S.; Pang, F.; Mansoori, G.A. Optimized parameters and exponents of Mie (n, m) intermolecular potential energy function based on the shape of molecules. Int. J. Thermophys. 1980, 1, 177–184. [Google Scholar] [CrossRef]
- Mahfouf, A. Calcul des Coefficients de Transport Dans des Plasmas Hors de L’équilibre. Ph.D. Thesis, Université Blaise Pascal, Clermont-Ferrand, France, 2016; 179p. [Google Scholar]
- Mouritz, F.M.; Rummens, F.H.A. A critical evaluation of Lennard-Jones and Stockmayer potential parameters and of some correlation methods. Can. J. Chem. 1977, 55, 3007–3020. [Google Scholar] [CrossRef]
- Youssef, A.; Hanna, M.M.; Saad, S.M. Determination of the Lennard-Jones force constants from diffusion measurements. Z. Phys. Chem. 1969, 241, 81–100. [Google Scholar] [CrossRef]
- Aziz, R.A.; Slaman, M.J. An improved intermolecular potential for sulfur hexafluoride. J. Chem. Phys. 1991, 94, 2. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; J. Wiley and Sons, Inc.: New York, NY, USA, 2002; ISBN 0-471-41077-5. [Google Scholar]
- Flynn, L.W.; Thodos, G. Lennard-Jones force constants from viscosity data: Their relationship to critical properties. AIChE J. 1962, 8, 362–365. [Google Scholar] [CrossRef]
- Hirschfelder, J.O.; Bird, R.B.; Spotz, E.L. The transport properties of gases and gaseous mixtures II. Chem. Rev. 1949, 44, 1205–1231. [Google Scholar] [CrossRef]
- Stiel, L.I.; Thodos, G. Lennard-Jones force constants predicted from critical properties. J. Chem. Eng. Data 1962, 7, 234–236. [Google Scholar] [CrossRef]
- Angus, S.; Armstrong, B.; Gosman, A.L.; McCarty, R.D.; Hust, J.G.; Vasserman, A.A.; Rabinovich, V.A. International Thermodynamic Tables of the Fluid State—1 Argon; Butterworths: London, UK, 1972. [Google Scholar]
- Angus, S.; de Reuck, K.M.; Armstrong, B.; Jacobsen, R.T.; Stewart, R.B. International Thermodynamic Tables of the Fluid State—6 Nitrogen; Pergamon Press: Pergamon, NY, USA, 1979.
- NIST Chemistry WebBook, NIST Standard Reference Database 69. Available online: https://webbook.nist.gov/chemistry/ (accessed on 7 November 2018).
- Makarevich, L.A.; Sokolova, E.S.; Sorina, G.A. Critical parameters of Sulfur Hexafluoride. Zh Fiz. Khim. 1968, 42, 3–22. [Google Scholar]
- Suehiro, Y.; Nakajima, M.; Yamada, K.; Uematsu, M. Critical parameters of {xCO2 + (1 − x)CHF3} for x = (1.0000, 0.7496, 0.5013, and 0.2522). J. Chem. Therm. 1996, 28, 1153–1164. [Google Scholar] [CrossRef]
- Claus, P.; Kleinrahm, R.; Wagner, W. Measurements of the (p, ρ, T) Relation of Ethylene, Ethane, and Sulphur Hexafluoride in the Temperature Range From 235 K to 520 K at Pressures Up to 30 MPa using an Accurate Single-Sinker Densimeter. J. Chem. Thermodyn. 2003, 35, 159–175. [Google Scholar] [CrossRef]
- Cristancho, D.E.; Mantilla, I.D.; Ejaz, S.; Hall, K.R. Accurate PρT data for methane from 300 to 450 K up to 180 MPa. J. Chem. Eng. 2010, 55, 826–829. [Google Scholar]
- Balester, P.J.; Carter, J.N. Real-parameter Genetic Algorithms for finding Multiple Optimal Solutions in Multi-modal Optimization. In Proceedings of the Genetic and Evolutionary Computation Conference GECCO 2003, Chicago, IL, USA, 12–16 July 2003; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2003; Volume 2723. [Google Scholar]
- Chervy, B. Calcul des Propriétés de Transport et Etude du Pouvoir de Coupure des Mélanges Hexafluorure de Soufre (SF6)-Fluorure de Carbone (CF4 ou C2F6) et Hexafluorure de Soufre—Vapeurs de Cuivre. Ph.D. Thesis, Université Toulouse III, Paul Sabatier, Toulouse, France, 1995; 165p. [Google Scholar]
- Belhaouari, J.B. Modélisation de l’Extinction d’un Arc de SF6 Hors Equilibre Thermodynamique Local. Ph.D. Thesis, Université de Toulouse III, Paul Sabatier, Toulouse, France, 1997; 180p. [Google Scholar]
- Brand, K.P.; Kopainsky, J. Particle densities in a decaying SF6 plasma. Appl. Phys. 1978, 6, 425–432. [Google Scholar] [CrossRef]


| Conservation Equation | Al,i | Number of Equations | |
|---|---|---|---|
| Atomic nuclei | 0 | M-2 | |
| Electric neutrality | 0 | 1 | |
| Pressure | 1 | 1 |
| Gas | Chemical Species |
|---|---|
| Argon | Ar, Ar +, Ar +2, Ar +3, e−. |
| Air | N, N+, N+2, O, O+, O+2, O−, C, C+, C+2, C−, Ar, Ar+, Ar+2, N2, N2+, NO, NO+, O2, O2+, C2, CO, N2O, NO2, CO2, e−. |
| Species | σ [Å] | References | |
|---|---|---|---|
| Ar | 2.83–3.48 | 110.2–124 | [18,45,46] |
| N2 | 3.681–4.21 | 26.9–95.9 | [18,45,46] |
| O2 | 3.30–3.58 | 88–118 | [18,45,46] |
| SF6 | 4.8–6.5 | 155–414.81 | [18,22,45,47] |
| CH4 | 3.22–3.882 | 137–176.8 | [18,45,46] |
| CO2 | 2.84–4.486 | 152–594.4 | [18,45,46] |
| Species | Reference | Reference | ||||
|---|---|---|---|---|---|---|
| Ar | 3.451 | 116.035 | [52] | 3.465 | 116 | [18] |
| N2 | 3.694 | 94.837 | [53] | 3.681 | 91.5 | [18] |
| O2 | 3.474 | 115.008 | [54] | 3.433 | 113 | [18] |
| SF6 | 4.993 | 215.04 | [55] | 5.199 | 212 | [45] |
| CH4 | 3.828 | 143.02 | [51] | 3.796 | 144 | [18] |
| CO2 | 3.993 | 191.143 | [56] | 3.996 | 190 | [18] |
| SF6 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Sources | Funke et al. [19] | Claus et al. [57] | This Work with the Stiel Formulation | |||||
| T [K] | Plit [bar] | Plit [bar] | ||||||
| with Virial | % Error | without Virial | % Error | |||||
| 300 | 100.1876 | 1505.417 | 100.613 | 1505.939 | 1673.43 | 11.2% | 585.554 | 61.1% |
| 40.1390 | 1382.802 | - | - | 1312.44 | 5.1% | 234.222 | 83.1% | |
| 20.0346 | 162.945 | - | - | 147.34 | 9.6% | 117.111 | 28.1% | |
| 316 | 100.2052 | 1399.646 | - | - | 1444.65 | 3.2% | 555.906 | 60.3% |
| 40.6363 | 1152.050 | - | - | 387.055 | 66.4% | 222.362 | 80.7% | |
| 20.0334 | 142.452 | - | - | 133.724 | 6.1% | 111.181 | 22.0% | |
| 324 | 100.0588 | 1340.546 | - | - | 1333.7 | 0.5% | 542.18 | 59.6% |
| 40.6180 | 550.994 | - | - | 340.594 | 38.2% | 216.872 | 60.6% | |
| 19.9775 | 134.527 | - | - | 128.128 | 4.8% | 108.436 | 19.4% | |
| 340 | 100.0395 | 1208.301 | 100.618 | 1210.5 | 1124.27 | 7.0% | 516.665 | 57.2% |
| 41.2991 | 351.610 | - | - | 288.904 | 17.8% | 206.666 | 41.2% | |
| 19.8607 | 121.89 | - | - | 118.652 | 2.7% | 103.333 | 15.2% | |
| 360 | - | - | 100.512 | 1019.111 | 897.537 | 11.9% | 487.962 | 52.1% |
| - | - | 19.9922 | 111.689 | 109.6 | 1.9% | 97.592 | 12.6% | |
| 375 | - | - | 100.31 | 872.05 | 768.606 | 11.9% | 468.443 | 46.3% |
| - | - | 39.9242 | 241.556 | 230.316 | 4.7% | 187.377 | 22.4% | |
| - | - | 20.1877 | 111.689 | 113.597 | 1.7% | 93.688 | 16.1% | |
| 410 | - | - | 102.462 | 644.85 | 583.902 | 9.5% | 428.454 | 33.6% |
| - | - | 40.7729 | 206.536 | 196.906 | 4.7% | 171.382 | 17.0% | |
| - | - | 20.2447 | 93.8963 | 91.6877 | 2.4% | 85.690 | 8.7% | |
| 460 | - | - | 100.829 | 469.477 | 452.405 | 3.6% | 381.883 | 18.7% |
| - | - | 40.5095 | 170.138 | 166.066 | 2.4% | 152.753 | 10.2% | |
| - | - | 20.2695 | 81.2073 | 79.7085 | 1.8% | 76.376 | 5.9% | |
| 490 | - | - | 101.215 | 415.62 | 404.055 | 2.8% | 358.503 | 13.7% |
| - | - | 20.0561 | 74.4856 | 74.0648 | 0.6% | 71.700 | 3.7% | |
| CH4 | ||||||
|---|---|---|---|---|---|---|
| Cristancho et al. [58] | This Work with the Stiel Formulation | |||||
| Tlit [K] | P [bar] | [kg/m3] | [kg/m3] | |||
| with virial | % Error | without Virial | % Error | |||
| 305.236 | 50.01 | 34.173 | 34.011 | 0.5% | 31.636 | 7.4% |
| 305.231 | 99.93 | 72.932 | 72.321 | 0.8% | 63.216 | 13.3% |
| 338.049 | 50 | 29.983 | 29.848 | 0.5% | 28.542 | 4.8% |
| 338.037 | 69.05 | 42.093 | 41.821 | 0.6% | 39.416 | 6.4% |
| 338.103 | 99.69 | 62.054 | 62.391 | 0.5% | 56.907 | 8.3% |
| 400.015 | 100.02 | 49.746 | 49.807 | 0.1% | 48.246 | 3.0% |
| 450.115 | 344.92 | 136.647 | 136.563 | 0.061% | 147.891 | 7.6% |
| SF6 | ||||||
|---|---|---|---|---|---|---|
| Sources | Funke et al. [19] | This Work | ||||
| T [K] | B [cm3/mol] | C [cm3/mol]2 | P [Bar] | % Error | ||
| 300 | −271.2 ± 0.8 | 18,160 ± 1250 | 100.1876 | 1505.417 | 1732.788 | 15.1% |
| 40.1390 | 1382.802 | 1532.088 | 10.8% | |||
| 20.0346 | 162.945 | 162.913 | 0.01% | |||
| 316 | −241.1 ± 0.8 | 17,850 ± 1000 | 100.2052 | 1399.646 | 1467.539 | 4.9% |
| 40.6363 | 1152.050 | 1122.203 | 2.6% | |||
| 20.0334 | 142.452 | 142.439 | 0.0% | |||
| 324 | −227.4 ± 0.6 | 16,950 ± 750 | 100.0588 | 1340.546 | 1410.368 | 5.2% |
| 40.6180 | 550.994 | 915.276 | 66.1% | |||
| 19.9775 | 134.527 | 134.572 | 0.03% | |||
| 340 | −202.9 ± 0.6 | 15,860 ± 750 | 100.0395 | 1208.301 | 1235.266 | 2.2% |
| 41.2991 | 351.610 | 355.637 | 1.1% | |||
| 19.8607 | 121.89 | 121.912 | 0.01% | |||
| σ [Å] | ||
|---|---|---|
| SF6 | 5.21279 | 222.27 |
| CH4 | 4.083 | 143.57 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harry Solo, A.; Freton, P.; Gonzalez, J.-J. The Virial Effect—Applications for SF6 and CH4 Thermal Plasmas. Appl. Sci. 2019, 9, 929. https://doi.org/10.3390/app9050929
Harry Solo A, Freton P, Gonzalez J-J. The Virial Effect—Applications for SF6 and CH4 Thermal Plasmas. Applied Sciences. 2019; 9(5):929. https://doi.org/10.3390/app9050929
Chicago/Turabian StyleHarry Solo, Andriniaina, Pierre Freton, and Jean-Jacques Gonzalez. 2019. "The Virial Effect—Applications for SF6 and CH4 Thermal Plasmas" Applied Sciences 9, no. 5: 929. https://doi.org/10.3390/app9050929
APA StyleHarry Solo, A., Freton, P., & Gonzalez, J.-J. (2019). The Virial Effect—Applications for SF6 and CH4 Thermal Plasmas. Applied Sciences, 9(5), 929. https://doi.org/10.3390/app9050929




