Three-Dimensional Optical Spin Angular Momentum Flux of a Vector Beam with Radially-Variant Polarization in Near Field
Abstract
:1. Introduction
2. Theoretical Formulation
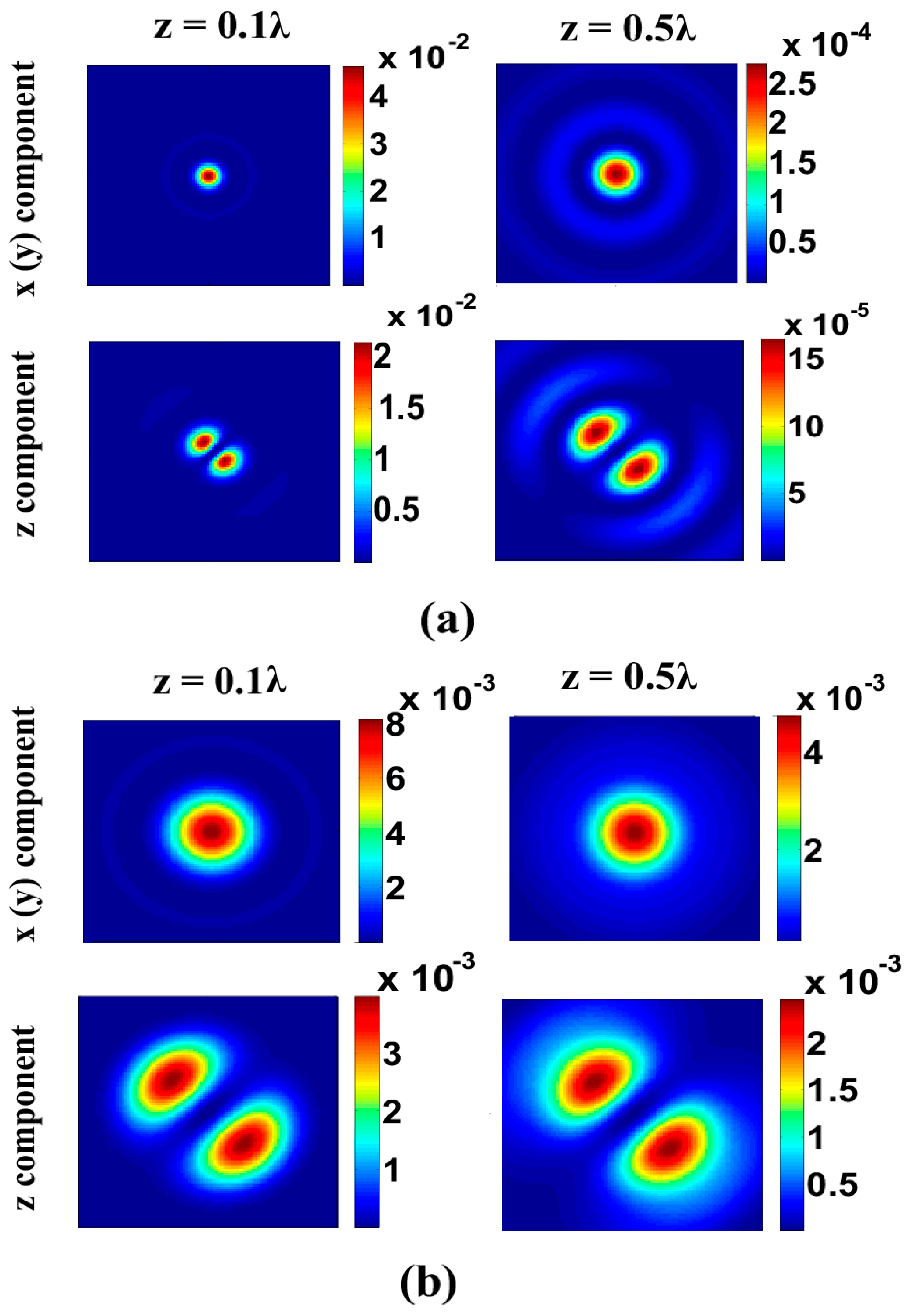
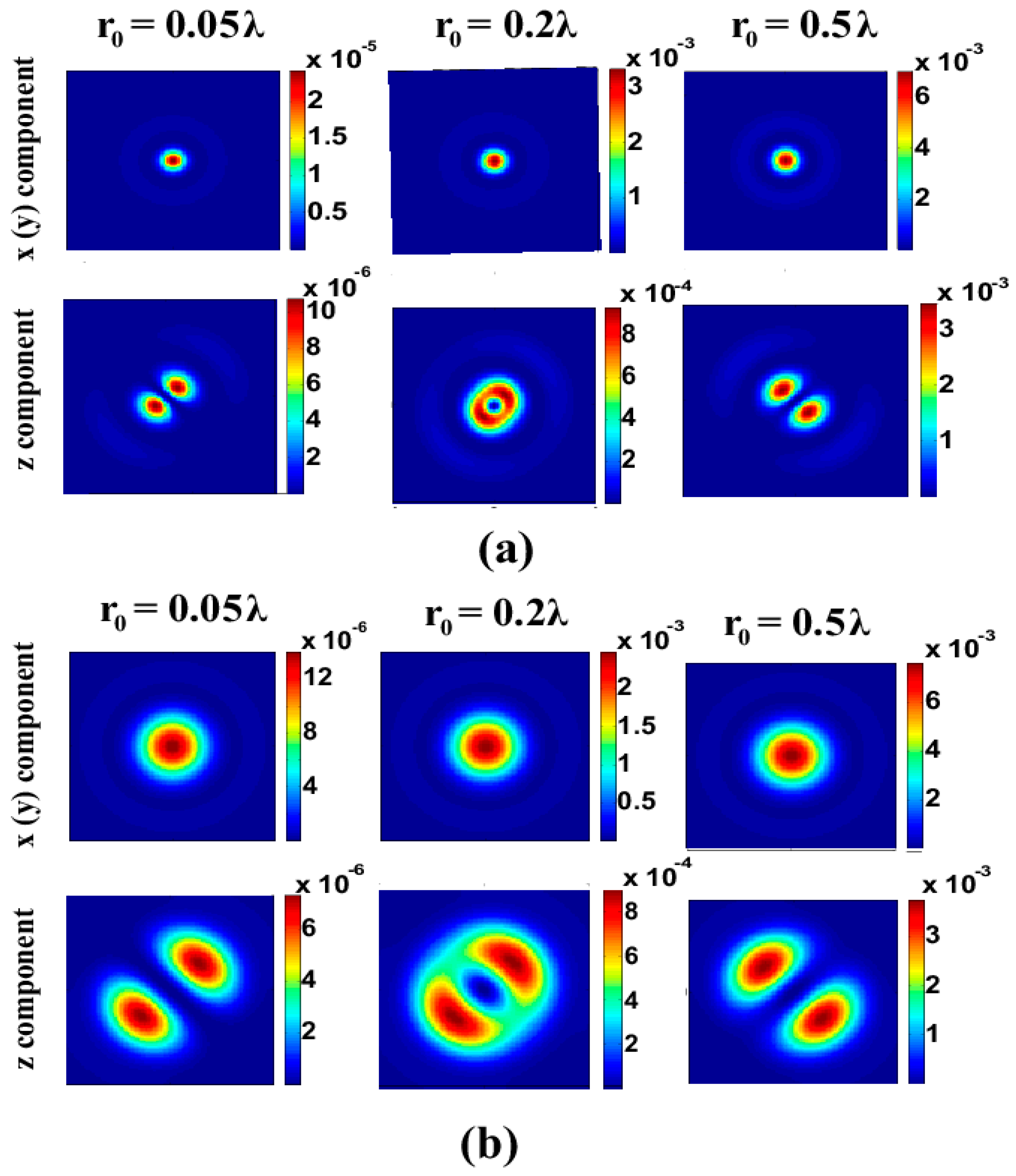
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, R.P.; Chen, Z.; Gao, Y.; Ding, J.; He, S. Flexible manipulation of the polarization conversions in a structured vector field in free space. Laser Photonics Rev. 2017, 11, 1700165. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Chen, R.P.; Chen, Z.; Chew, K.H.; Li, P.G.; Yu, Z.; Ding, J.; He, S. Structured caustic vector vortex optical field: Manipulating optical angular momentum flux and polarization rotation. Sci. Rep. 2015, 5, 10628. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.P.; Zhong, L.X.; Chew, K.H.; Zhao, T.Y.; Zhang, X. Collapse dynamics of a vector vortex optical field with inhomogeneous states of polarization. Laser Phys. 2015, 25, 075401. [Google Scholar] [CrossRef]
- Chen, R.P.; Zhong, L.X.; Chew, K.H.; Gu, B.; Zhou, G.; Zhao, T. Effect of a spiral phase on a vector optical field with hybrid polarization states. J. Opt. 2015, 17, 065605. [Google Scholar] [CrossRef]
- Wang, X.L.; Li, Y.N.; Chen, J.; Guo, C.S.; Ding, J.P.; Wang, H.T. A new type of vector fields with hybrid states of polarization. Opt. Express 2010, 18, 10786–10795. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Q.; Leger, J.R. Focus shaping using cylindrical vector beams. Opt. Express 2002, 10, 324–331. [Google Scholar] [CrossRef] [PubMed]
- Dorn, R.; Quabis, S.; Leuchs, G. Sharper focus for a radially polarized light beam. Phys. Rev. Lett. 2003, 91, 233901. [Google Scholar] [CrossRef] [PubMed]
- Ruffner, D.B.; Grier, D.G. Optical forces and torques in nonuniform beams of light. Phys. Rev. Lett. 2012, 108, 173602. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.P.; Dai, C.Q. Vortex solitons of the (3 + 1)-dimensional spatially modulated cubic-quintic nonlinear Schrödinger equation with the transverse modulation. Nonlinear Dyn. 2017, 90, 1563–1570. [Google Scholar] [CrossRef]
- Chen, R.P.; Chew, K.H.; Zhou, G.; Dai, C.Q.; He, S. Vectorial effect of hybrid polarization states on the collapse dynamics of a structured optical field. Opt. Express 2016, 24, 28143. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.P.; Dai, C.Q. Three-dimensional vector solitons and their stabilities in a Kerr medium with spatially inhomogeneous nonlinearity and transverse modulation. Nonlinear Dyn. 2017, 88, 2807–2816. [Google Scholar] [CrossRef]
- Chen, R.P.; Chew, K.H.; Dai, C.Q.; Zhou, G. Optical spin-to-orbital angular momentum conversion in the near field of a highly nonparaxial optical field with hybrid states of polarization. Phys. Rev. A 2017, 96, 053862. [Google Scholar] [CrossRef]
- Fornel, F.D. Evanescent Waves: From Newtonian Optics to Atomic Optics; Springer: Berlin, Germany, 2001. [Google Scholar]
- Agrawal, G.P.; Lax, M. Free-space wave propagation beyond the paraxial approximation. Phys. Rev. A 1983, 27, 1693–1695. [Google Scholar] [CrossRef]
- Grbic, A.; Jiang, L.; Merlin, R. Near-field plates: Subdiffraction focusing with patterned surfaces. Science 2008, 320, 511–513. [Google Scholar] [CrossRef] [PubMed]
- Merlin, R. Radiationless electromagnetic interference: Evanescent-field lenses and perfect focusing. Science 2007, 317, 927–929. [Google Scholar] [CrossRef] [PubMed]
- Lerman, G.M.; Avner, Y.; Uriel, L. Demonstration of nanofocusing by the use of plasmonic lens illuminated with radially polarized light. Nano Lett. 2009, 9, 2139–2143. [Google Scholar] [CrossRef] [PubMed]
- Helseth, L.E. Radiationless electromagnetic interference shaping of evanescent cylindrical vector waves. Phys. Rev. A 2008, 78, 013819. [Google Scholar] [CrossRef]
- Martínez-Herrero, R.; Mejías, P.M.; Juvells, I.; Carnicer, A. Transverse and longitudinal components of the propagating and evanescent waves associated to radially polarized nonparaxial fields. Appl. Phys. B 2012, 106, 151–159. [Google Scholar] [CrossRef]
- Martínez-Herrero, R.; Mejías, P.M.; Carnicer, A. Evanescent field of vectorial highly non-paraxial beams. Opt. Express 2008, 16, 2845–2858. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.P.; Li, G. The evanescent wavefield part of a cylindrical vector beam. Opt. Express 2013, 21, 22246–22254. [Google Scholar] [CrossRef] [PubMed]
- Jackson, J.D.; Levitt, L.C. Classical electrodynamics. Phys. Today 1999, 52, 78. [Google Scholar]
- Enk, S.J.V.; Nienhuis, G. Commutation Rules and Eigenvalues of Spin and Orbital Angular Momentum of Radiation Fields. Opt. Acta Int. J. Opt. 1994, 41, 963–977. [Google Scholar] [Green Version]
- Maucher, F.; Skupin, S.; Gardiner, S.A.; Hughes, I.G. Creating complex optical longitudinal polarization structures. Phys. Rev. Lett. 2018, 120, 163903. [Google Scholar] [CrossRef] [PubMed]
- Bauer, T.; Banzer, P.; Karimi, E.; Orlov, S.; Rubano, A.; Marrucci, L.; Santamato, E.; Boyd, R.W.; Leuchs, G. Observation of optical polarization Möbius strips. Science 2015, 347, 126635. [Google Scholar] [CrossRef] [PubMed]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Y.; Zhong, L.-X.; Qian, C.; Chen, R.-P. Three-Dimensional Optical Spin Angular Momentum Flux of a Vector Beam with Radially-Variant Polarization in Near Field. Appl. Sci. 2019, 9, 960. https://doi.org/10.3390/app9050960
Guan Y, Zhong L-X, Qian C, Chen R-P. Three-Dimensional Optical Spin Angular Momentum Flux of a Vector Beam with Radially-Variant Polarization in Near Field. Applied Sciences. 2019; 9(5):960. https://doi.org/10.3390/app9050960
Chicago/Turabian StyleGuan, Ying, Li-Xin Zhong, Chaoyang Qian, and Rui-Pin Chen. 2019. "Three-Dimensional Optical Spin Angular Momentum Flux of a Vector Beam with Radially-Variant Polarization in Near Field" Applied Sciences 9, no. 5: 960. https://doi.org/10.3390/app9050960
APA StyleGuan, Y., Zhong, L. -X., Qian, C., & Chen, R. -P. (2019). Three-Dimensional Optical Spin Angular Momentum Flux of a Vector Beam with Radially-Variant Polarization in Near Field. Applied Sciences, 9(5), 960. https://doi.org/10.3390/app9050960






