A Review of Super-Resolution Imaging through Optical High-Order Interference [Invited]
Abstract
:1. Introduction
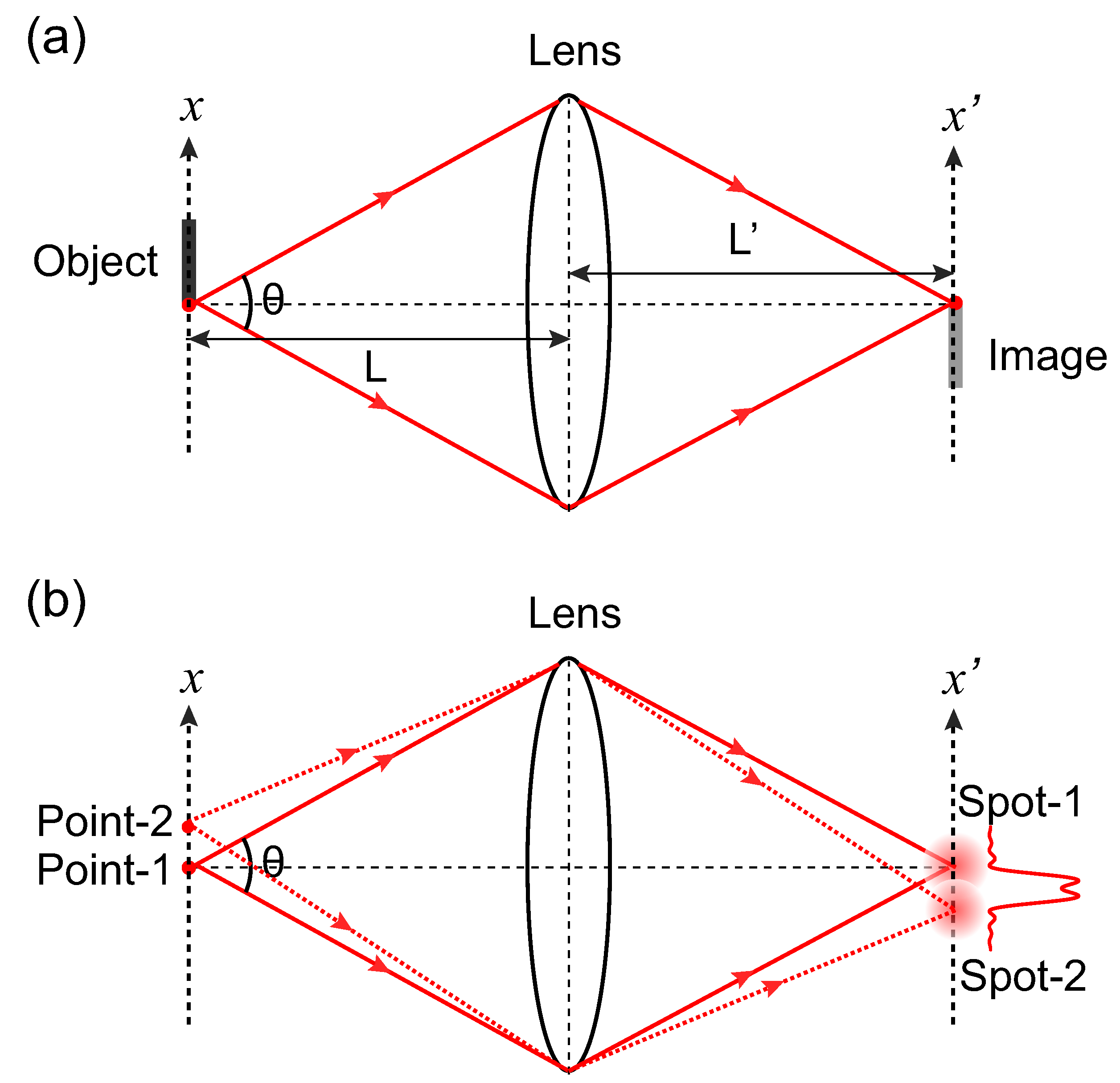
2. Rayleigh Resolution Limit
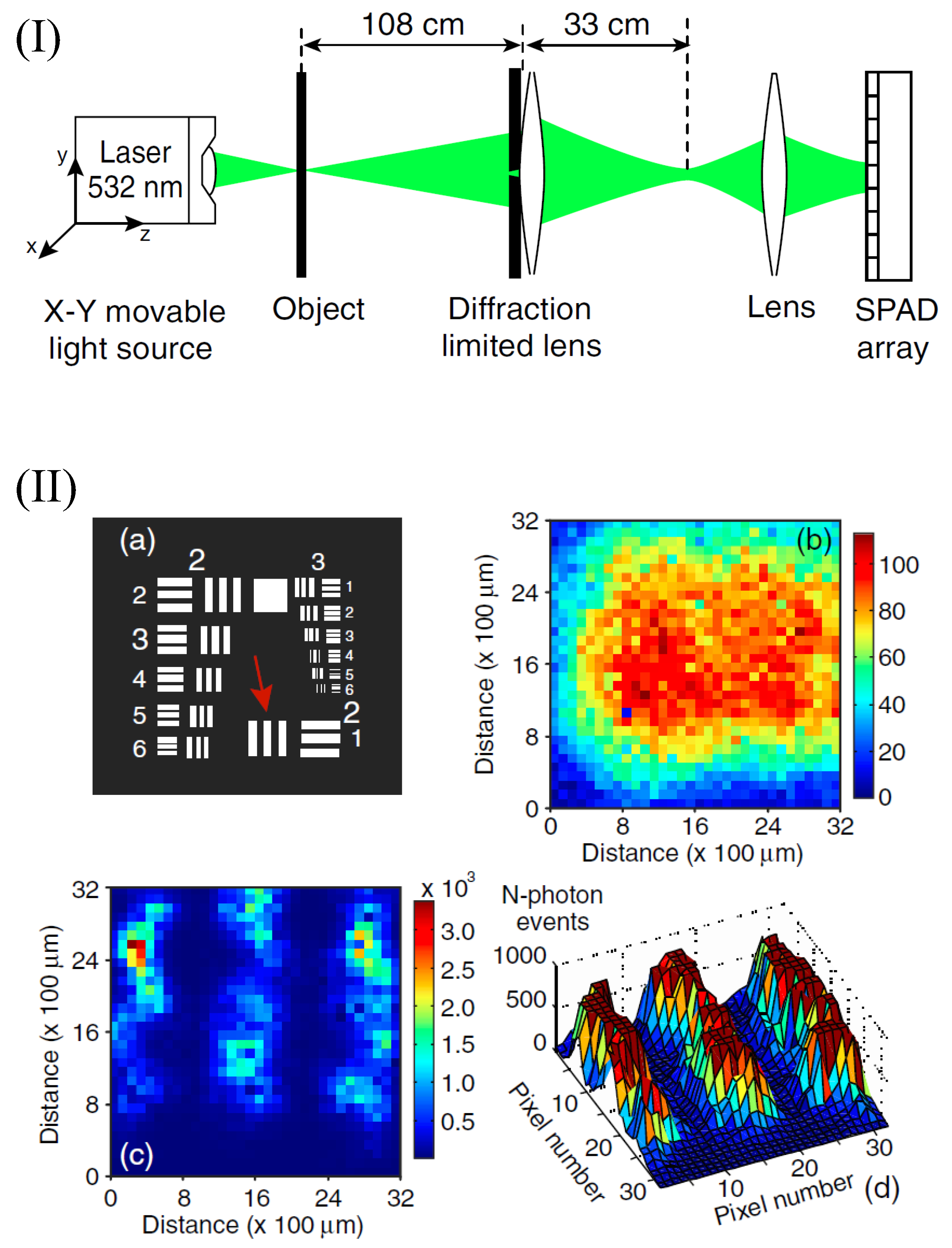
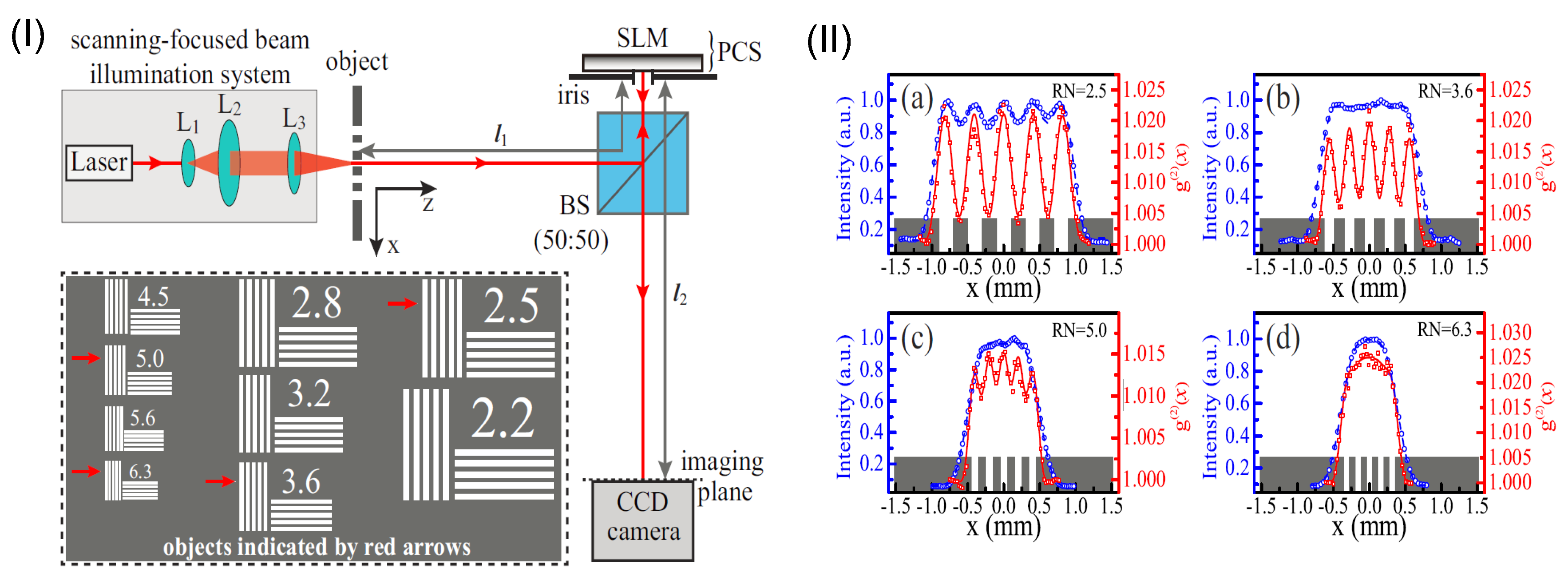
3. Super-Resolution with Scanning Focused Beam
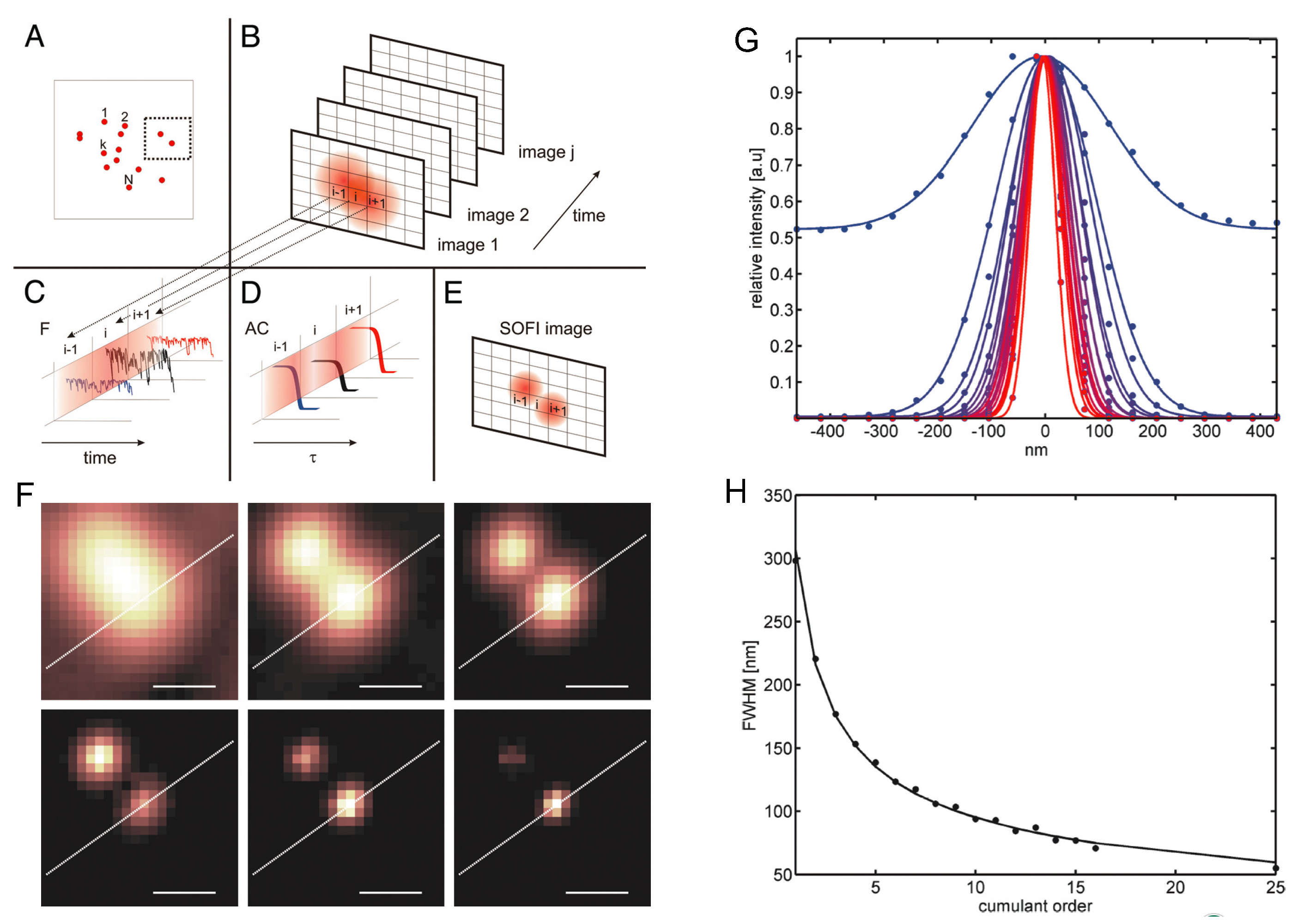
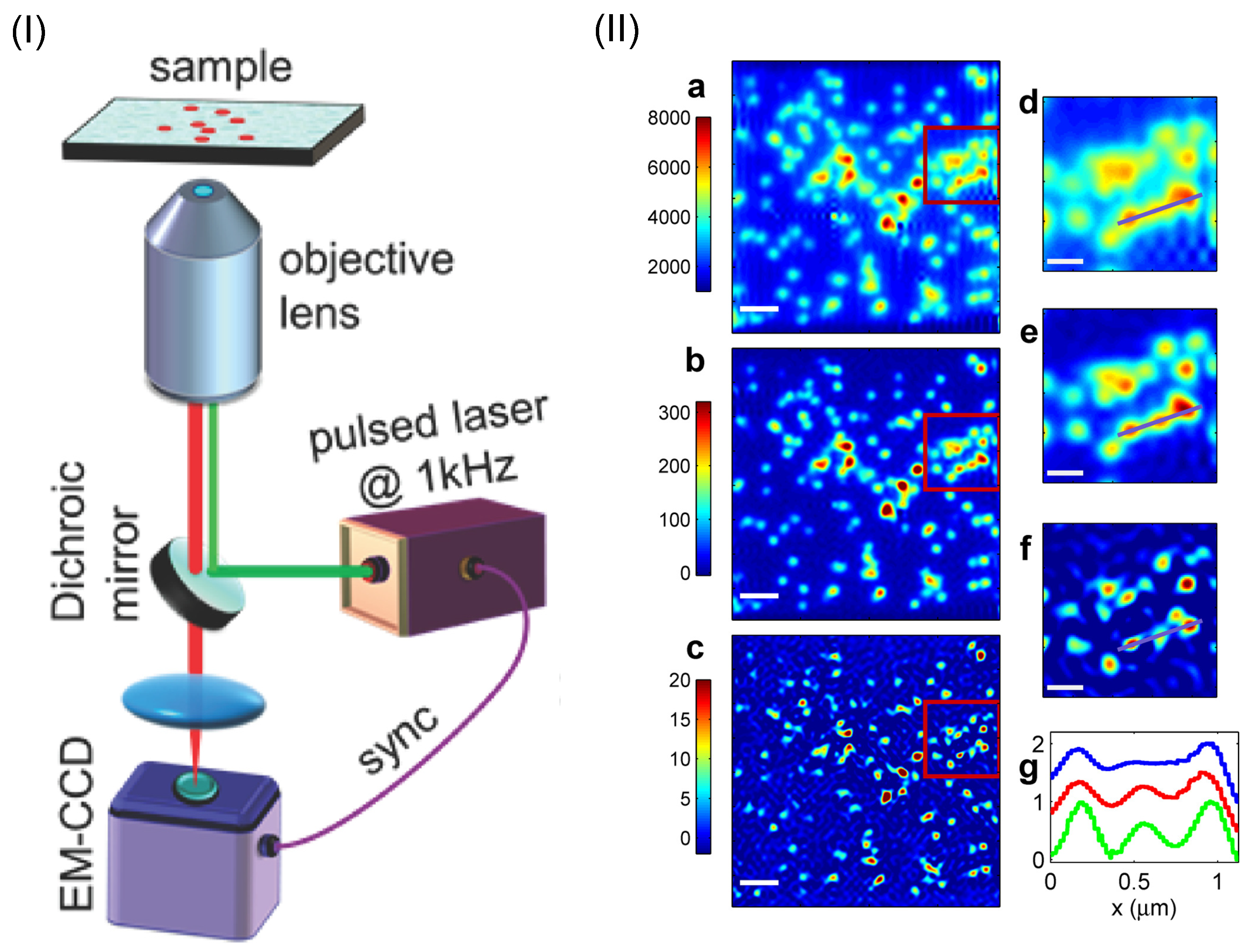
4. Super-Resolution via Bunching Effect
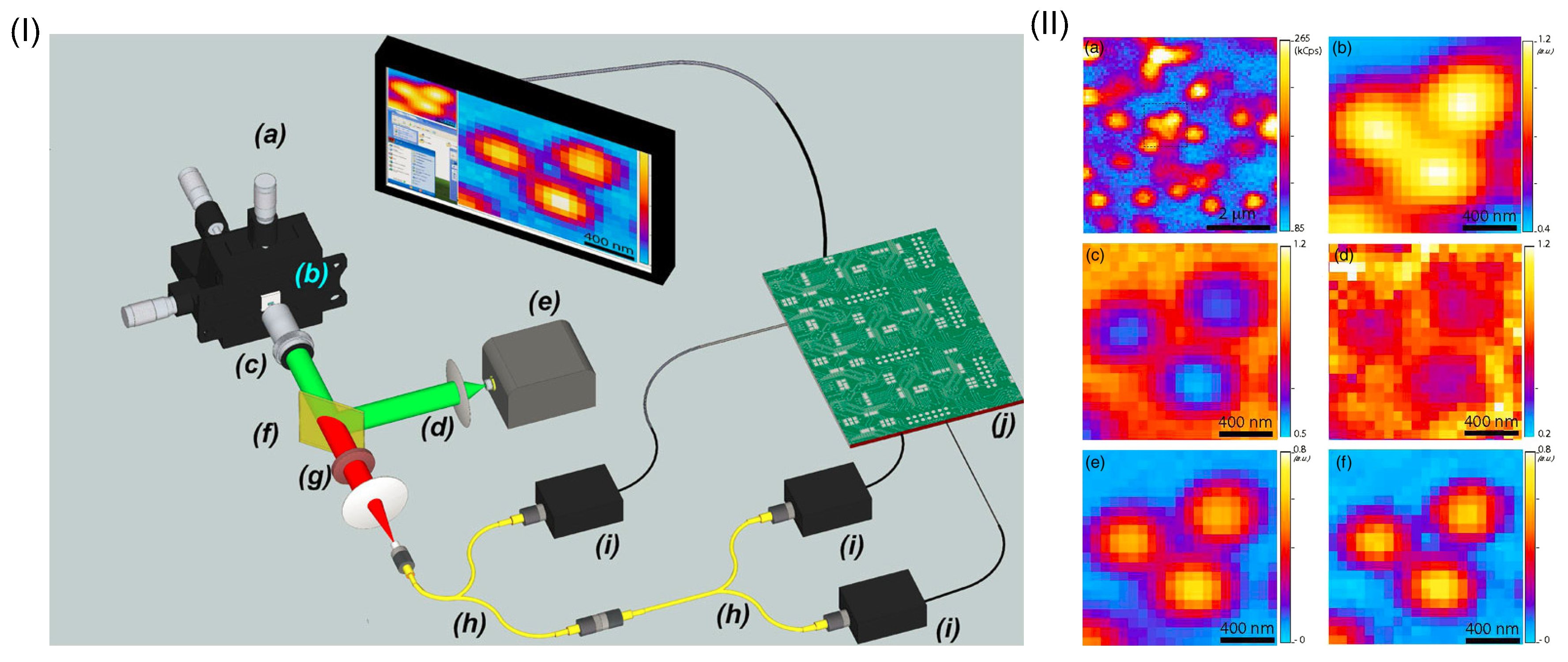
5. Super-Resolution via Quantum Antibunching Effect
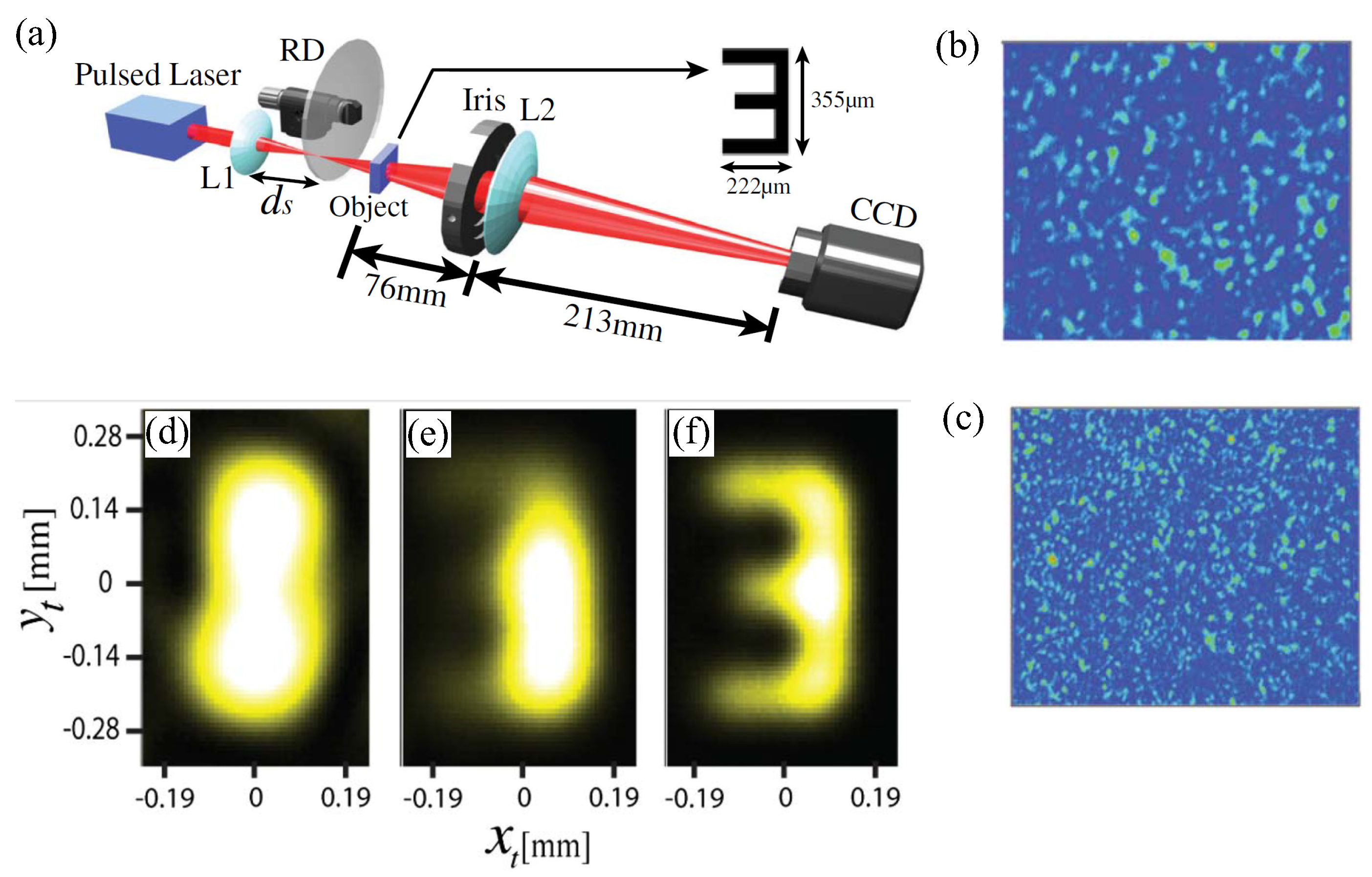
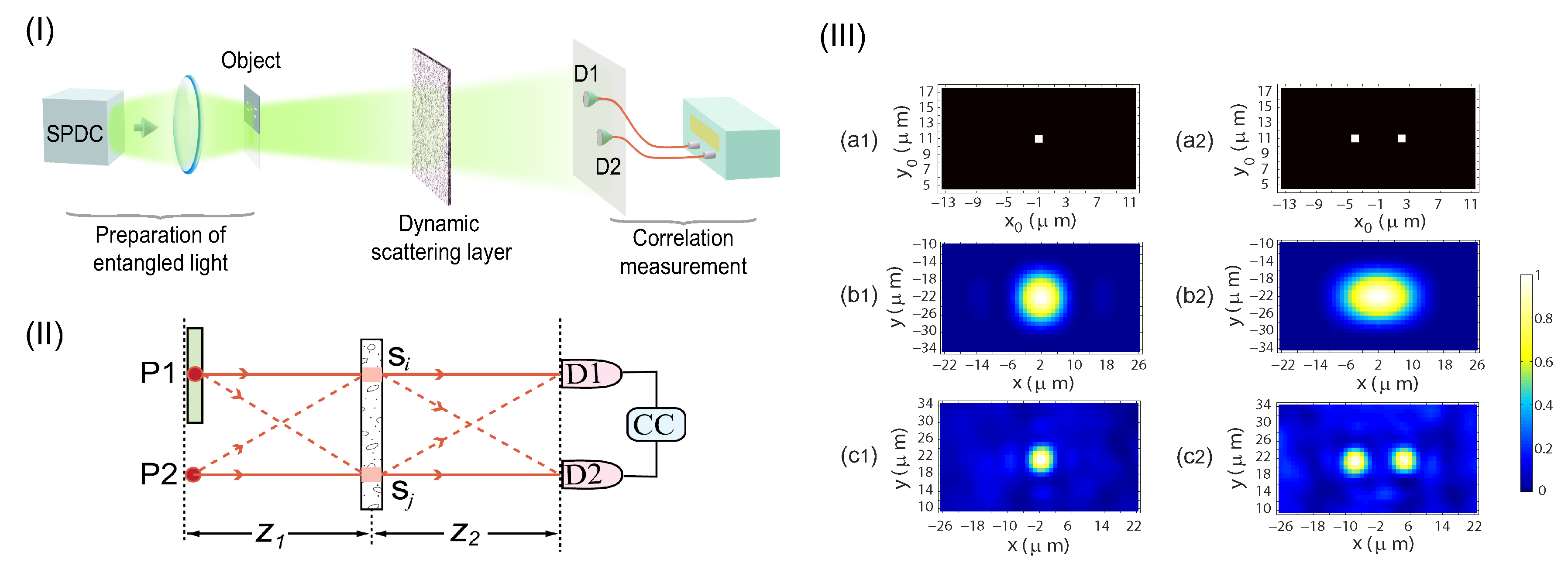
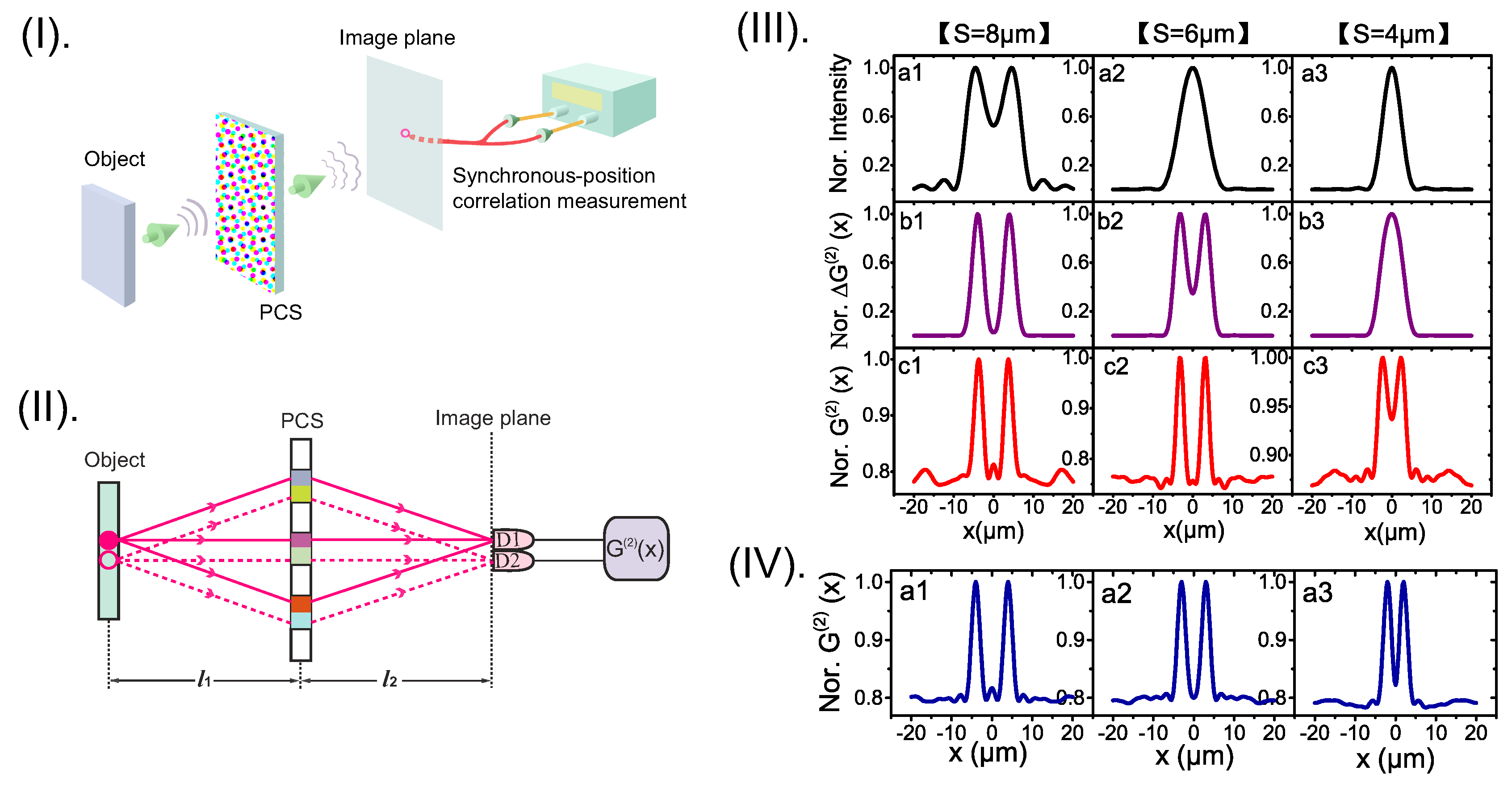
6. Super-Resolution via Quantum Entanglement
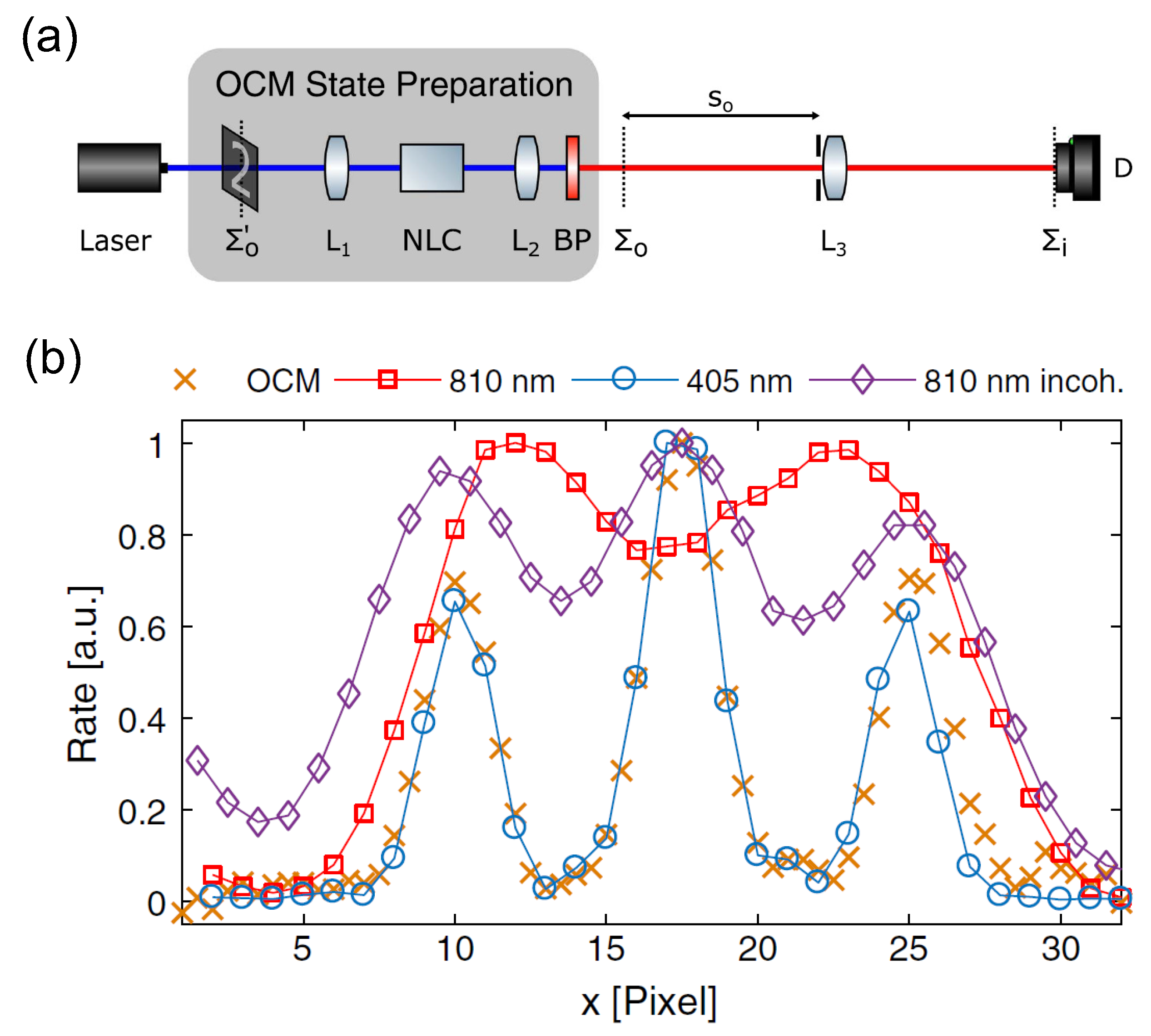
7. Super-Resolution via Dynamic Phase Control
8. Discussion and Perspectives
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SQL | Standard quantum limit |
| HL | Heisenberg limit |
| CCD | Charge-coupled device |
References
- Born, M.; Wolf, E. Principles of Optics, 7th (expanded) ed.; Cambridge U. Press: Cambridge, UK, 1999; Volume 890. [Google Scholar]
- Hell, S.W.; Wichmann, J. Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 1994, 19, 780–782. [Google Scholar] [CrossRef] [PubMed]
- Gustafsson, M.G. Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy. J. Microsc. 2000, 198, 82–87. [Google Scholar] [CrossRef]
- Betzig, E.; Patterson, G.H.; Sougrat, R.; Lindwasser, O.W.; Olenych, S.; Bonifacino, J.S.; Davidson, M.W.; Lippincott-Schwartz, J.; Hess, H.F. Imaging intracellular fluorescent proteins at nanometer resolution. Science 2006, 313, 1642–1645. [Google Scholar] [CrossRef]
- Rust, M.J.; Bates, M.; Zhuang, X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat. Methods 2006, 3, 793–796. [Google Scholar] [CrossRef]
- Courjon, D.; Bainier, C. Near field microscopy and near field optics. Rep. Prog. Phys. 1994, 57, 989. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966. [Google Scholar] [CrossRef] [PubMed]
- Kawata, S.; Inouye, Y.; Verma, P. Plasmonics for near-field nano-imaging and superlensing. Nat. Photonics 2009, 3, 388–394. [Google Scholar] [CrossRef]
- Brown, R.H.; Twiss, R. A test of a new type of stellar interferometer on Sirius. Nature 1956, 178, 1046–1048. [Google Scholar] [CrossRef]
- Glauber, R.J. The quantum theory of optical coherence. Phys. Rev. 1963, 130, 2529. [Google Scholar] [CrossRef]
- Paul, H. Interference between independent photons. Rev. Mod. Phys. 1986, 58, 209. [Google Scholar] [CrossRef]
- Jacobson, J.; Björk, G.; Chuang, I.; Yamamoto, Y. Photonic de Broglie waves. Phys. Rev. Lett. 1995, 74, 4835. [Google Scholar] [CrossRef]
- Fonseca, E.; Monken, C.; Pádua, S. Measurement of the de Broglie wavelength of a multiphoton wave packet. Phys. Rev. Lett. 1999, 82, 2868. [Google Scholar] [CrossRef]
- Boto, A.N.; Kok, P.; Abrams, D.S.; Braunstein, S.L.; Williams, C.P.; Dowling, J.P. Quantum interferometric optical lithography: exploiting entanglement to beat the diffraction limit. Phys. Rev. Lett. 2000, 85, 2733. [Google Scholar] [CrossRef]
- Edamatsu, K.; Shimizu, R.; Itoh, T. Measurement of the photonic de Broglie wavelength of entangled photon pairs generated by spontaneous parametric down-conversion. Phys. Rev. Lett. 2002, 89, 213601. [Google Scholar] [CrossRef]
- Mitchell, M.W.; Lundeen, J.S.; Steinberg, A.M. Super-resolving phase measurements with a multiphoton entangled state. Nature 2004, 429, 161–164. [Google Scholar] [CrossRef]
- D’Angelo, M.; Chekhova, M.V.; Shih, Y. Two-photon diffraction and quantum lithography. Phys. Rev. Lett. 2001, 87, 013602. [Google Scholar] [CrossRef]
- Walther, P.; Pan, J.W.; Aspelmeyer, M.; Ursin, R.; Gasparoni, S.; Zeilinger, A. De Broglie wavelength of a non-local four-photon state. Nature 2004, 429, 158. [Google Scholar] [CrossRef] [PubMed]
- Afek, I.; Ambar, O.; Silberberg, Y. High-NOON states by mixing quantum and classical light. Science 2010, 328, 879–881. [Google Scholar] [CrossRef]
- Scarcelli, G.; Valencia, A.; Shih, Y. Two-photon interference with thermal light. Europhys. Lett. 2004, 68, 618. [Google Scholar] [CrossRef]
- Wang, K.; Cao, D.Z. Subwavelength coincidence interference with classical thermal light. Phys. Rev. A 2004, 70, 041801. [Google Scholar] [CrossRef]
- Xiong, J.; Cao, D.Z.; Huang, F.; Li, H.G.; Sun, X.J.; Wang, K. Experimental observation of classical subwavelength interference with a pseudothermal light source. Phys. Rev. Lett. 2005, 94, 173601. [Google Scholar] [CrossRef] [PubMed]
- Cao, D.Z.; Ge, G.J.; Wang, K. Two-photon subwavelength lithography with thermal light. Appl. Phys. Lett. 2010, 97, 051105. [Google Scholar] [CrossRef]
- Zhai, Y.H.; Chen, X.H.; Zhang, D.; Wu, L.A. Two-photon interference with true thermal light. Phys. Rev. A 2005, 72, 043805. [Google Scholar] [CrossRef]
- Pe’er, A.; Dayan, B.; Vucelja, M.; Silberberg, Y.; Friesem, A.A. Quantum lithography by coherent control of classical light pulses. Opt. Express 2004, 12, 6600–6605. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhang, G. Unified interpretation for second-order subwavelength interference based on Feynman’s path-integral theory. Phys. Rev. A 2010, 82, 013822. [Google Scholar] [CrossRef]
- Hong, P.; Zhang, G. Subwavelength interference with an effective entangled source. Phys. Rev. A 2013, 88, 043838. [Google Scholar] [CrossRef]
- Hong, P.; Zhang, G. Synchronous position two-photon interference of random-phase grating. J. Opt. Soc. Am. A 2015, 32, 1256–1261. [Google Scholar] [CrossRef]
- Hong, P.; Zhang, G. Super-resolved optical lithography with phase controlled source. Phys. Rev. A 2015, 91, 053830. [Google Scholar] [CrossRef]
- Hong, P.; Li, L.; Liu, J.; Zhang, G. Active control on high-order coherence and statistic characterization on random phase fluctuation of two classical point sources. Sci. Rep. 2016, 6, 23614. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L.; Shapiro, J.H. Sub-Rayleigh-diffraction-bound quantum imaging. Phys. Rev. A 2009, 79, 013827. [Google Scholar] [CrossRef]
- Guerrieri, F.; Maccone, L.; Wong, F.N.; Shapiro, J.H.; Tisa, S.; Zappa, F. Sub-Rayleigh imaging via N-photon detection. Phys. Rev. Lett. 2010, 105, 163602. [Google Scholar] [CrossRef] [PubMed]
- Dertinger, T.; Colyer, R.; Iyer, G.; Weiss, S.; Enderlein, J. Fast, background-free, 3D super-resolution optical fluctuation imaging (SOFI). Proc. Natl. Acad. Sci. USA 2009, 106, 22287–22292. [Google Scholar] [CrossRef] [PubMed]
- Oh, J.E.; Cho, Y.W.; Scarcelli, G.; Kim, Y.H. Sub-Rayleigh imaging via speckle illumination. Opt. Lett. 2013, 38, 682–684. [Google Scholar] [CrossRef] [PubMed]
- Zhang, E.; Lin, H.; Liu, W.; Li, Q.; Chen, P. Sub-Rayleigh-diffraction imaging via modulating classical light. Opt. Express 2015, 23, 33506–33513. [Google Scholar] [CrossRef]
- Schwartz, O.; Oron, D. Improved resolution in fluorescence microscopy using quantum correlations. Phys. Rev. A 2012, 85, 033812. [Google Scholar] [CrossRef]
- Schwartz, O.; Levitt, J.M.; Tenne, R.; Itzhakov, S.; Deutsch, Z.; Oron, D. Superresolution microscopy with quantum emitters. Nano Lett. 2013, 13, 5832–5836. [Google Scholar] [CrossRef]
- Monticone, D.G.; Katamadze, K.; Traina, P.; Moreva, E.; Forneris, J.; Ruo-Berchera, I.; Olivero, P.; Degiovanni, I.; Brida, G.; Genovese, M. Beating the Abbe diffraction limit in confocal microscopy via nonclassical photon statistics. Phys. Rev. Lett. 2014, 113, 143602. [Google Scholar] [CrossRef]
- Xu, D.Q.; Song, X.B.; Li, H.G.; Zhang, D.J.; Wang, H.B.; Xiong, J.; Wang, K. Experimental observation of sub-Rayleigh quantum imaging with a two-photon entangled source. Appl. Phys. Lett. 2015, 106, 171104. [Google Scholar] [CrossRef]
- Hong, P. Two-photon imaging assisted by a thin dynamic scattering layer. Appl. Phys. Lett. 2018, 113, 101109. [Google Scholar] [CrossRef]
- Unternährer, M.; Bessire, B.; Gasparini, L.; Perenzoni, M.; Stefanov, A. Super-Resolution Quantum Imaging at the Heisenberg Limit. Optica 2018, 5, 1150–1154. [Google Scholar] [CrossRef]
- Hong, P.; Zhang, G. Heisenberg-resolution imaging through a phase-controlled screen. Opt. Express 2017, 25, 22789–22796. [Google Scholar] [CrossRef]
- Li, L.; Hong, P.; Zhang, G. Experimental realization of Heisenberg-limit resolution imaging through a phase-controlled screen with classical light. Opt. Express 2018, 26, 18950–18956. [Google Scholar] [CrossRef]
- Classen, A.; von Zanthier, J.; Scully, M.O.; Agarwal, G.S. Superresolution via structured illumination quantum correlation microscopy. Optica 2017, 4, 580–587. [Google Scholar] [CrossRef]
- Brooker, G.; Brooker, G. Modern Classical Optics; Oxford University Press: Oxford, UK, 2003; Volume 8. [Google Scholar]
- Guerrieri, F.; Tisa, S.; Tosi, A.; Zappa, F. Single-photon camera for high-sensitivity high-speed applications. In Proceedings of the Sensors, Cameras, and Systems for Industrial/Scientific Applications XI, International Society for Optics and Photonics, San Jose, CA, USA, 25 January 2010; Volume 7536, p. 753605. [Google Scholar]
- Arecchi, F.; Berné, A.; Bulamacchi, P. High-order fluctuations in a single-mode laser field. Phys. Rev. Lett. 1966, 16, 32. [Google Scholar] [CrossRef]
- Fitch, M.; Jacobs, B.; Pittman, T.; Franson, J. Photon-number resolution using time-multiplexed single-photon detectors. Phys. Rev. A 2003, 68, 043814. [Google Scholar] [CrossRef]
- Twiss, R.; Little, A.; Brown, R.H. Correlation between photons, in coherent beams of light, detected by a coincidence counting technique. Nature 1957, 180, 324–326. [Google Scholar] [CrossRef]
- Morgan, B.; Mandel, L. Measurement of photon bunching in a thermal light beam. Phys. Rev. Lett. 1966, 16, 1012. [Google Scholar] [CrossRef]
- Frantsuzov, P.; Kuno, M.; Janko, B.; Marcus, R.A. Universal emission intermittency in quantum dots, nanorods and nanowires. Nat. Phys. 2008, 4, 519–522. [Google Scholar] [CrossRef]
- Martienssen, W.; Spiller, E. Coherence and fluctuations in light beams. Am. J. Phys. 1964, 32, 919–926. [Google Scholar] [CrossRef]
- Hong, P.; Liu, J.; Zhang, G. Two-photon superbunching of thermal light via multiple two-photon path interference. Phys. Rev. A 2012, 86, 013807. [Google Scholar] [CrossRef]
- Scarcelli, G.; Valencia, A.; Shih, Y. Experimental study of the momentum correlation of a pseudothermal field in the photon-counting regime. Phys. Rev. A 2004, 70, 051802. [Google Scholar] [CrossRef]
- Kimble, H.J.; Dagenais, M.; Mandel, L. Photon antibunching in resonance fluorescence. Phys. Rev. Lett. 1977, 39, 691. [Google Scholar] [CrossRef]
- Short, R.; Mandel, L. Observation of sub-Poissonian photon statistics. Phys. Rev. Lett. 1983, 51, 384–391. [Google Scholar] [CrossRef]
- Edgar, M.P.; Tasca, D.S.; Izdebski, F.; Warburton, R.E.; Leach, J.; Agnew, M.; Buller, G.S.; Boyd, R.W.; Padgett, M.J. Imaging high-dimensional spatial entanglement with a camera. Nat. Commun. 2012, 3, 984. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.L.; Chen, L.K.; Li, W.; Huang, H.L.; Liu, C.; Chen, C.; Luo, Y.H.; Su, Z.E.; Wu, D.; Li, Z.D.; et al. Experimental ten-photon entanglement. Phys. Rev. Lett. 2016, 117, 210502. [Google Scholar] [CrossRef]
- Shih, Y. Entangled biphoton source-property and preparation. Rep. Prog. Phys. 2003, 66, 1009. [Google Scholar] [CrossRef]
- Fano, U. Quantum theory of interference effects in the mixing of light from phase-independent sources. Am. J. Phys. 1961, 29, 539–545. [Google Scholar] [CrossRef]
- Mandel, L. Quantum effects in one-photon and two-photon interference. Rev. Mod. Phys. 1999, 71, S274. [Google Scholar] [CrossRef]
- Tsang, M. Quantum imaging beyond the diffraction limit by optical centroid measurements. Phys. Rev. Lett. 2009, 102, 253601. [Google Scholar] [CrossRef]
- Shin, H.; Chan, K.W.C.; Chang, H.J.; Boyd, R.W. Quantum spatial superresolution by optical centroid measurements. Phys. Rev. Lett. 2011, 107, 083603. [Google Scholar] [CrossRef]
- Neuman, K.C.; Chadd, E.H.; Liou, G.F.; Bergman, K.; Block, S.M. Characterization of photodamage to Escherichia coli in optical traps. Biophys. J. 1999, 77, 2856–2863. [Google Scholar] [CrossRef]
- Smith, A.M.; Mancini, M.C.; Nie, S. Bioimaging: Second window for in vivo imaging. Nat. Nanotechnol. 2009, 4, 710–711. [Google Scholar] [CrossRef]
- Brida, G.; Genovese, M.; Berchera, I.R. Experimental realization of sub-shot-noise quantum imaging. Nat. Photonics 2010, 4, 227–230. [Google Scholar] [CrossRef]
- Lemos, G.B.; Borish, V.; Cole, G.D.; Ramelow, S.; Lapkiewicz, R.; Zeilinger, A. Quantum imaging with undetected photons. Nature 2014, 512, 409–412. [Google Scholar] [CrossRef]
- Pittman, T.; Shih, Y.; Strekalov, D.; Sergienko, A. Optical imaging by means of two-photon quantum entanglement. Phys. Rev. A 1995, 52, R3429–R3432. [Google Scholar] [CrossRef]
- Gatti, A.; Brambilla, E.; Bache, M.; Lugiato, L.A. Ghost imaging with thermal light: comparing entanglement and classicalcorrelation. Phys. Rev. Lett. 2004, 93, 093602. [Google Scholar] [CrossRef]
- Shapiro, J.H. Computational ghost imaging. Phy. Rev. A 2008, 78, 061802. [Google Scholar] [CrossRef]
- Katz, O.; Bromberg, Y.; Silberberg, Y. Compressive ghost imaging. Appl. Phys. Lett. 2009, 95, 131110. [Google Scholar] [CrossRef]
- Ferri, F.; Magatti, D.; Lugiato, L.; Gatti, A. Differential ghost imaging. Phys. Rev. Lett. 2010, 104, 253603. [Google Scholar] [CrossRef] [PubMed]


| Light Source | Resolution Limit | Illumination | Experiment | Detectors | Imaging Element | Ref. |
|---|---|---|---|---|---|---|
| Laser | SQL | Scanning focused beam | Y | SPAD-array (32 × 32) | Lens | [31,32] |
| HL | CCD | Phase-controlled screen | [42,43] | |||
| Fluctuating light | SQL | Wide field | Y | CCD, EMCCD for fluorescent imaging | Lens | [33,34,35] |
| HL | Scanning focused-beam | CCD | Phase-controlled screen | [42,43] | ||
| Single- photon emitters | SQL | Wide field | Y | EMCCD | Lens | [36,37,38] |
| Confocal scanning | SPADs | |||||
Entangled two- photon light | SQL | Wide field | Y | SPADs | Lens | [31,39] |
| HL | N | - | Phase-controlled screen | [42] | ||
| Y | SPAD-array (32 × 32) | Lens | [41] | |||
| N | - | Random scattering layer | [40] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, P.; Zhang, G. A Review of Super-Resolution Imaging through Optical High-Order Interference [Invited]. Appl. Sci. 2019, 9, 1166. https://doi.org/10.3390/app9061166
Hong P, Zhang G. A Review of Super-Resolution Imaging through Optical High-Order Interference [Invited]. Applied Sciences. 2019; 9(6):1166. https://doi.org/10.3390/app9061166
Chicago/Turabian StyleHong, Peilong, and Guoquan Zhang. 2019. "A Review of Super-Resolution Imaging through Optical High-Order Interference [Invited]" Applied Sciences 9, no. 6: 1166. https://doi.org/10.3390/app9061166
APA StyleHong, P., & Zhang, G. (2019). A Review of Super-Resolution Imaging through Optical High-Order Interference [Invited]. Applied Sciences, 9(6), 1166. https://doi.org/10.3390/app9061166





