JIT Production Strategy and Maintenance for Quality Deteriorating Systems
Abstract
:Featured Application
Abstract
1. Introduction
2. Industrial Motivation
3. Problem Statement
3.1. Production Inventory Control Problem
3.2. Major Maintenance Policy
3.3. Optimization Problem
4. Simulation–Optimization Approach
- ▪
- Step 1-Mathematical model: In this step, we provide rigorous modeling to analytically formulate the production system under study, and define the decision variables, the objective function to be minimized, and the control parameters of the joint control policy.
- ▪
- Step 2-Simulation model: We develop a combined discrete–continuous simulation model that uses the control parameters as inputs to evaluate the stochastic behavior and the performance of the production system, defined in this case by the total incurred cost. The complete description of the simulation model is provided in the next section.
- ▪
- Step 3-Statistical analysis: In this step, we perform a design of experiments (DOE) to fit the total incurred cost reported from the simulation model with a second-order regression model. Additionally, the obtained regression model is statistically analyzed to determine the main effects and significant interactions that must be included in the optimization phase.
- ▪
- Step 4-Optimization: The obtained cost regression model is optimized in this step within the feasible domain of the control parameters, defining the optimal values of and the optimal total cost. In this step, the optimal control policy is also analyzed extensively in a sensitivity analysis to validate the obtained results.
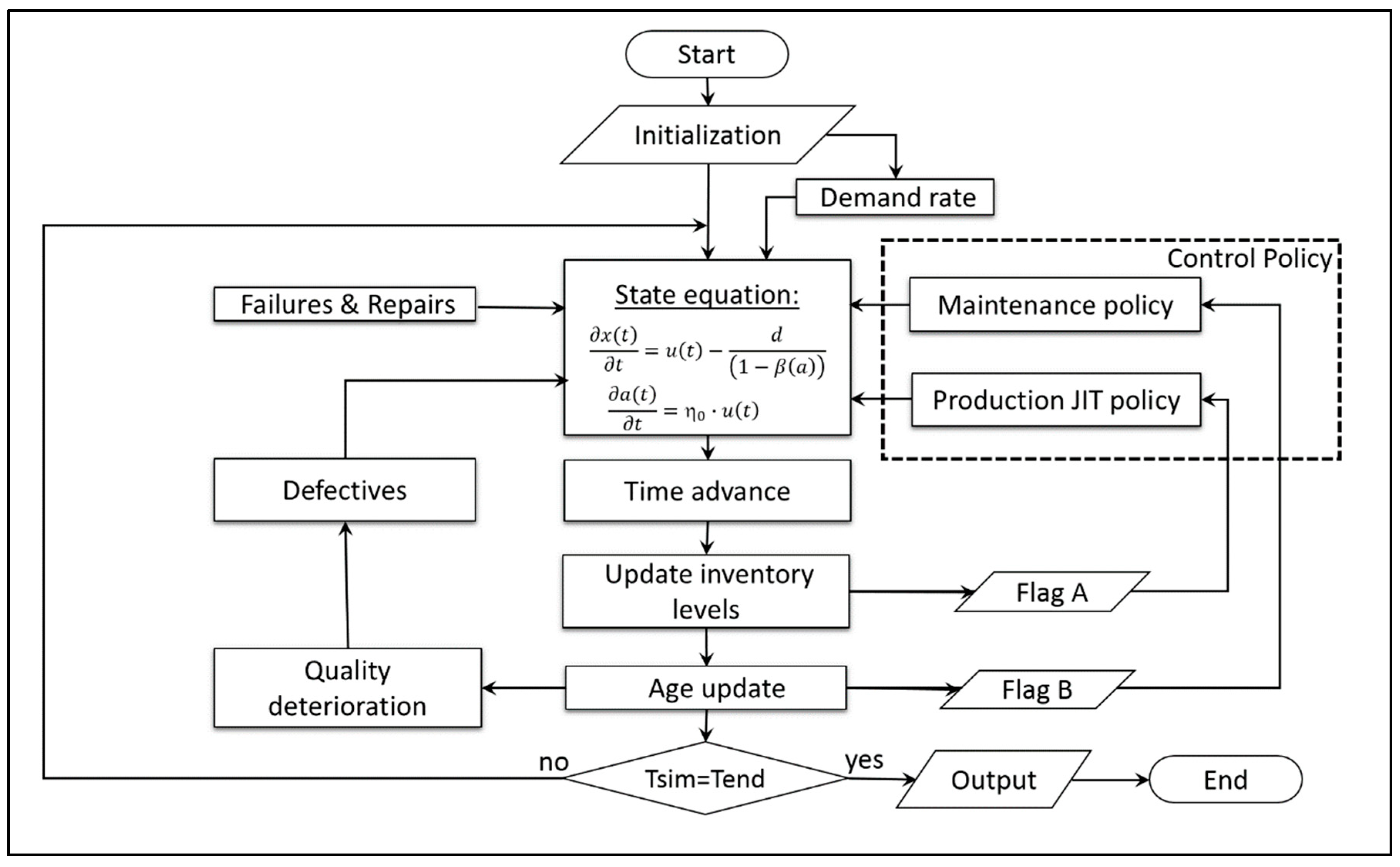
4.1. Simulation Model
4.2. Simulation Model
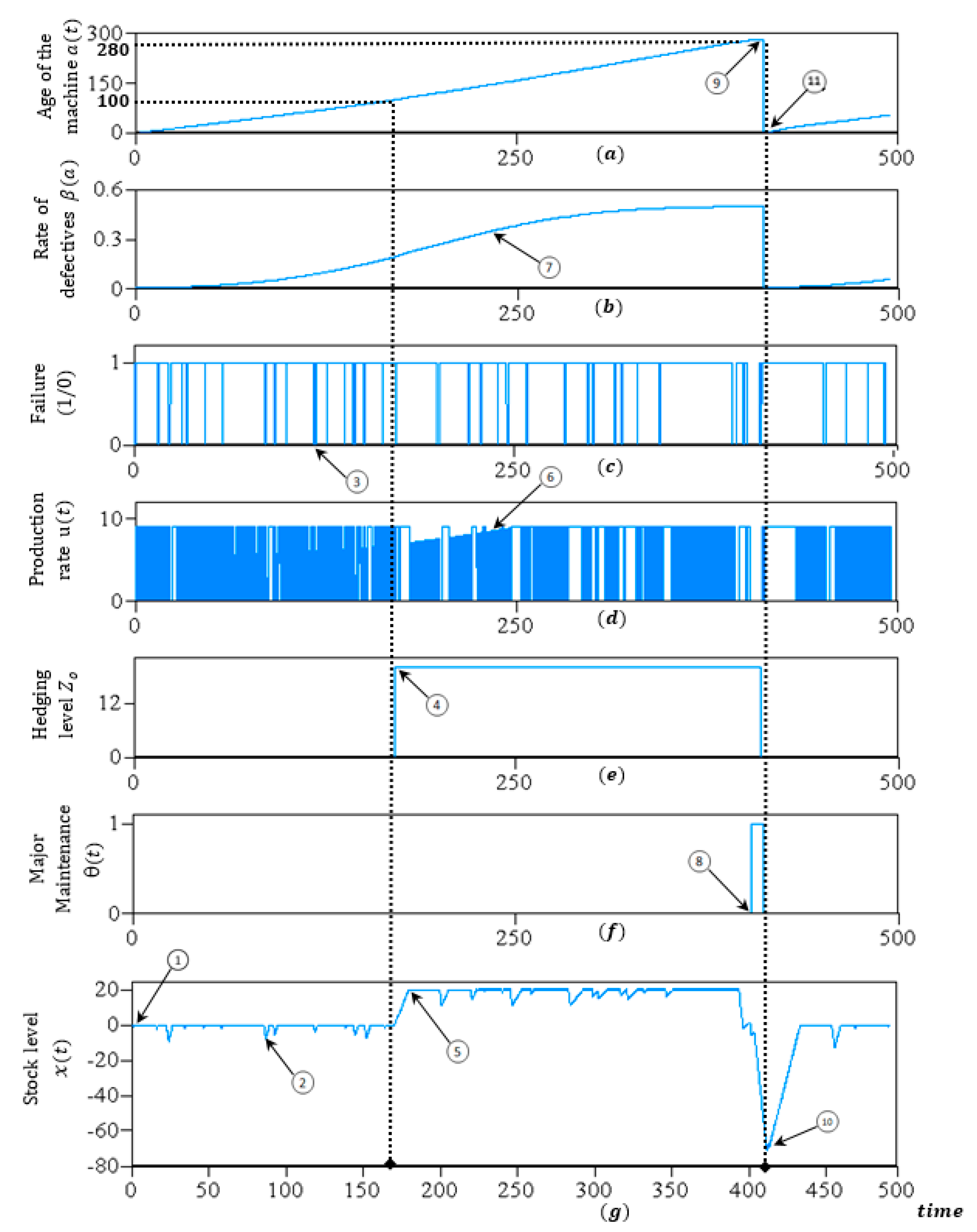
5. Numerical Example
6. Sensitivity and Results Analysis
- ▪
- Variation of the inventory cost: When the inventory cost increases (case II), the proposed policy reacts by decreasing the production threshold , since the inventory of products is more penalized. With the increase of such penalization, we also notice that product inventory is limited to the bare minimum, and so the system extends the JIT policy for a longer period of time, thus increasing age . By examining the results, we observe that the increment of promotes the conduction of more frequent major maintenance as a countermeasure to ensure the production of flawless units. Thus, at increasing , the critical age for major maintenance reduces. When the inventory cost decreases, we note the opposite effects (case I).
- ▪
- Variation of the backlog cost: When the backlog cost increases (case IV), the shortages of products are more penalized, and thus the production threshold increases as a protection against the lack of product. Additionally, we note that product deficiency is also tackled by reducing the critical age , and with this measure the unit applies less time the JIT policy, thus keeping product inventory for a longer period of time. Upon further investigation, the increment of the backlog cost exerts considerably more pressure to the unit performance, and hence major maintenance is conducted more frequently to mitigate the presence of defective units. The decrement of the backlog cost leads to the inverse effects (case III).
- ▪
- Variation of the minimal repair cost: With the increment of the repair cost (case VI), major maintenance must be performed more frequently, since the true usefulness of such maintenance is its ability to mitigate the presence of defective units, so the critical age reduces. Furthermore, we note that at reducing age , the unit will remain operational for less time, and thus the production threshold becomes less restricted, increasing as a countermeasure to ensure enough product availability to satisfy customers’ demand. Additionally, product availability is increased by reducing the period of time where the JIT policy is applied, since we note that at increasing , the critical age reduces. When the repair cost decreases, we observe the inverse effects (case V).
- ▪
- Variation of the major maintenance cost: The increase of the major maintenance cost (case VIII) is expected to delay the conduction of major maintenance, thus increasing age . This is because the production unit must attain higher levels of deterioration to justify the expensive cost of a major maintenance. Moreover, the intended consequence of delaying the major maintenance is that the unit will be operational for more time, increasing its responsiveness to customers’ demand, and also reducing the need for inventory, decreasing the production threshold . Furthermore, with more time available for production, the JIT policy is implemented for a longer period of time, and this increases age . The reduction of the major maintenance cost has the inverse effects (case VII).
- ▪
- Variation of the defectives cost: When increasing the defectives cost (case X), it is logical to observe that major maintenances are conducted more frequently to restore the unit faster and, most importantly, reduce the amount of defective units that reach the final customer. Moreover, a close examination of the increment of shows that the system opts to increase the production threshold to ensure that customers are satisfied with flawless units. This previous measure is complemented with the reduction of the critical age to limit the implementation of the JIT policy to a shorter period of time. With this measure, more inventory is available to replace defective units if necessary. The opposite occurs when the defective cost decreases (case IX).
7. Comparative Study
- ▪
- Policy-II: This paper is derived from the results of Bouslah et al. [30], where the production planning does not implement a JIT strategy. The production strategy consists only of the determination of an optimal inventory threshold level which is constant during the entire time horizon. In this Policy-II, the control parameter is disregarded. The control parameters of Policy-II are then , which are jointly optimized.
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, J.; Gershwin, S.B. Integrated quality and quantity modeling of a production line. OR Spectr. 2005, 27, 287–314. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Gershwin, S.B. Analysis of long flow lines with quality and operational failures. IIE Trans. 2008, 40, 284–296. [Google Scholar] [CrossRef] [Green Version]
- Colledani, M.; Tolio, T. Integrated analysis of quality and production logistics performance in manufacturing lines. Int. J. Prod. Res. 2011, 49, 485–518. [Google Scholar] [CrossRef] [Green Version]
- Colledani, M.; Ebrahimi, D.; Tolio, T. Integrated quality and production logistics modelling for the design of selective and adaptive assembly systems. CIRP Ann. Manuf. Technol. 2014, 63, 453–456. [Google Scholar] [CrossRef]
- Hajji, A.; Mhada, F.; Gharbi, A.; Pellerin, R.; Malhamé, R. Integrated product specifications and productivity decision making in unreliable manufacturing systems. Int. J. Prod. Econ. 2011, 129, 32–42. [Google Scholar] [CrossRef] [Green Version]
- Bouslah, B.; Gharbi, A.; Pellerin, R. Joint optimal lot sizing and production control policy in an unreliable and imperfect manufacturing system. Int. J. Prod. Econ. 2013, 144, 143–156. [Google Scholar] [CrossRef] [Green Version]
- Mhada, F.; Malhamé, R.; Pellerin, R. Joint assignment of buffer sizes and inspection points in unreliable transfer lines with scrapping of defective parts. Prod. Manuf. Res. 2013, 1, 79–101. [Google Scholar] [CrossRef]
- Rivera-Gómez, H.; Lara, J.; Montaño-Arango, O.; Hernández-Gress, E.S.; Corona-Armenta, J.R.; Santana-Robles, F. Joint production and repair efficiency planning of a multiple deteriorating system. Flex. Serv. Manuf. J. 2018. [Google Scholar] [CrossRef]
- Kumar-Sharma, R.; Kumar, D.; Kumar, P.F.M. A pragmatic tool to model, analyse and predict complex behavior of industrial systems. Eng. Comput. 2007, 24, 319–345. [Google Scholar] [CrossRef]
- Hajej, Z.; Turki, S.; Rezg, N. Modelling and analysis for sequentially optimizing production, maintenance and delivery activities taking into account product returns. Int. J. Prod. Res. 2015, 53, 4694–4719. [Google Scholar] [CrossRef]
- Nourelfath, M.; Nahas, N.; Ben-Daya, M. Integrated preventive maintenance and production decisions for imperfect processes. Reliab. Eng. Syst. Saf. 2016, 148, 21–31. [Google Scholar] [CrossRef]
- Dellagi, S.; Chelbi, A.; Trabelsi, W. Joint integrated production-maintenance policy with production plan smoothing through production rate control. J. Manuf. Syst. 2017, 42, 262–270. [Google Scholar] [CrossRef]
- Callahan, R.; Hubbard, K.; Strong, S. Computational methods for planning and developing flexible manufacturing systems. Eng. Comput. 2007, 22, 958–971. [Google Scholar] [CrossRef]
- Dehayem Nodem, F.; Kenné, J.P.; Gharbi, A. Simultaneous control of production, repair/replacement and preventive maintenance of deteriorating manufacturing systems. Int. J. Prod. Econ. 2011, 134, 271–282. [Google Scholar] [CrossRef] [Green Version]
- Hajej, Z.; Dellagi, S.; Nidhal, R. Optimal integrated maintenance/production policy for randomly failing systems with variable failure rate. Int. J. Prod. Res. 2011, 49, 5695–5712. [Google Scholar] [CrossRef]
- Khatab, A.; Ait-Kadi, D.; Rezg, N. Availability optimization for stochastic degrading systems under imperfect preventive maintenance. Int. J. Prod. Res. 2011, 52, 4132–4141. [Google Scholar] [CrossRef]
- Ayed, S.; Hajej, Z.; Turki, S.; Rezg, N. FPA method for optimal production planning under availability/degradation machine and subcontracting constraint. Int. J. Prod. Res. 2017, 55, 2135–2148. [Google Scholar] [CrossRef]
- Gharbi, A.; Hajji, A.; Dhouib, K. Production rate control of an unreliable manufacturing cell with adjustable capacity. Int. J. Prod. Res. 2011, 49, 6539–6557. [Google Scholar] [CrossRef] [Green Version]
- Berthaut, F.; Gharbi, A.; Dhouib, K. Joint modified block replacement and production/inventory control policy for a failure-prone manufacturing cell. Omega 2011, 39, 642–654. [Google Scholar] [CrossRef] [Green Version]
- Hlioui, R.; Gharbi, A.; Hajji, A. Integrated quality strategy in production and raw material replenishment in a manufacturing-oriented supply chain. Int. J. Adv. Manuf. Technol. 2015, 81, 335–348. [Google Scholar] [CrossRef] [Green Version]
- Tolio, T.; Ratti, A. Performance evaluation of two-machine lines with generalized thresholds. Int. J. Prod. Res. 2018, 56, 926–949. [Google Scholar] [CrossRef]
- Green, K.W., Jr.; Inman, R.A.; Birou, L.M.; Whitten, D. Total JIT (T-JIT) and its impact on supply chain competency and organizational performance. Int. J. Prod. Econ. 2014, 147, 125–135. [Google Scholar] [CrossRef]
- Fullerton, R.; McWatters, C. The production performance benefits from JIT implementation. J. Oper. Manag. 2001, 19, 81–96. [Google Scholar] [CrossRef]
- Alcaraz, J.L.; Macías, A.A.; Luevano, D.J.; Fernández, J.B.; López, A.D.; Macías, E.J. Main benefits obtained from a successful JIT implementation. Int. J. Adv. Manuf. Technol. 2016, 86, 2711–2722. [Google Scholar] [CrossRef]
- Kouedeu, A.F.; Kenne, J.P.; Dejax, P.; Songmene, V.; Polotski, V. Production and maintenance planning for a failure-prone deteriorating manufacturing system: A hierarchical control approach. Int. J. Adv. Manuf. Tech. 2016, 76, 1607–1619. [Google Scholar] [CrossRef]
- Amendola, L.; Artacho-Ramirez, M.A.; Depool, T. Analysis of key factors to improve maintenance management in the oil & gas industry in latin america. DYNA Ing. Ind. 2017, 92, 567–571. [Google Scholar] [CrossRef]
- Rivera-Gómez, H.; Gharbi, A.; Kenné, J.P.; Montaño-Arango, O.; Hernández-Gress, E.S. Subcontracting strategies with production and maintenance policies for a manufacturing system subject to progressive deterioration. Int. J. Prod. Econ. 2018, 200, 103–118. [Google Scholar] [CrossRef]
- Goti, A.; Oyarbide-Zubillaga, A.; Sánchez, A. Optimizing preventive maintenance by combining discrete event simulation and genetic algorithms. Hydrocarb. Process. 2007, 86, 115–122. [Google Scholar]
- Oyarbide-Zubillaga, A.; Goti, A.; Sanchez, A. Preventive maintenance optimization of multi-equipment manufacturing systems by combining discrete event simulation and multi-objective evolutionary algorithms. Prod. Plan. Control 2008, 19, 342–355. [Google Scholar] [CrossRef]
- Bouslah, B.; Gharbi, A.; Pellerin, R. Joint production, quality and maintenance control of a two-machine line subject to operation-dependent and quality-dependent failures. Int. J. Prod. Econ. 2018, 195, 210–226. [Google Scholar] [CrossRef]
| Parameter: | 12 (1/time units) | 21 (1/time units) | 13 (1/time units) | 31 (1/time units) | |
| Value: | 0.1 | 1.5 | 5 | 0.15 | 0.08 |
| Parameter: | (product/time units) | (product/time units) | |||
| Value: | 9 | 5.5 | 0.1 | 0.01 | 0.49 |
| Parameter: | |||||
| Value: | 15 × 10−6.2 | 2.4 |
| Parameter: | ($/Products/Time Units) | ($/Products/Time Units) | ($/Repair) | ($/Major Intervention) | ($/Product) |
|---|---|---|---|---|---|
| Value: | 1 | 50 | 100 | 3000 | 20 |
| Factor | Low Level | High Level | Description |
|---|---|---|---|
| 10 | 150 | Production threshold | |
| 0.1 | 0.9 | Critical value for increasing the stock level to | |
| 40 | 300 | Critical age for triggering major maintenance |
| Source | Sum of Squares | Df | Mean Square | F-Ratio | P-Value |
|---|---|---|---|---|---|
| A:Zo | 255,280.0 | 1 | 255,280.0 | 154.07 | 0.0000 |
| B:k | 55,583.3 | 1 | 55,583.3 | 33.55 | 0.0000 |
| C:Ao | 23,986.3 | 1 | 23,986.3 | 14.48 | 0.0004 |
| AA | 60,400.7 | 1 | 60,400.7 | 36.45 | 0.0000 |
| AB | 8,948.1 | 1 | 8,948.1 | 5.40 | 0.0249 |
| AC | 115,969.0 | 1 | 115,969.0 | 69.99 | 0.0000 |
| BB | 35,500.0 | 1 | 35,500.0 | 21.43 | 0.0000 |
| BC | 6,744.12 | 1 | 6,744.12 | 4.07 | 0.0499 |
| CC | 31,414.9 | 1 | 31,414.9 | 18.96 | 0.0001 |
| blocks | 1,348.02 | 1 | 1,348.02 | 0.81 | 0.3721 |
| Total error | 71,248.0 | 43 | 1,656.93 | ||
| Total (corr.) | 666,423.0 | 53 |
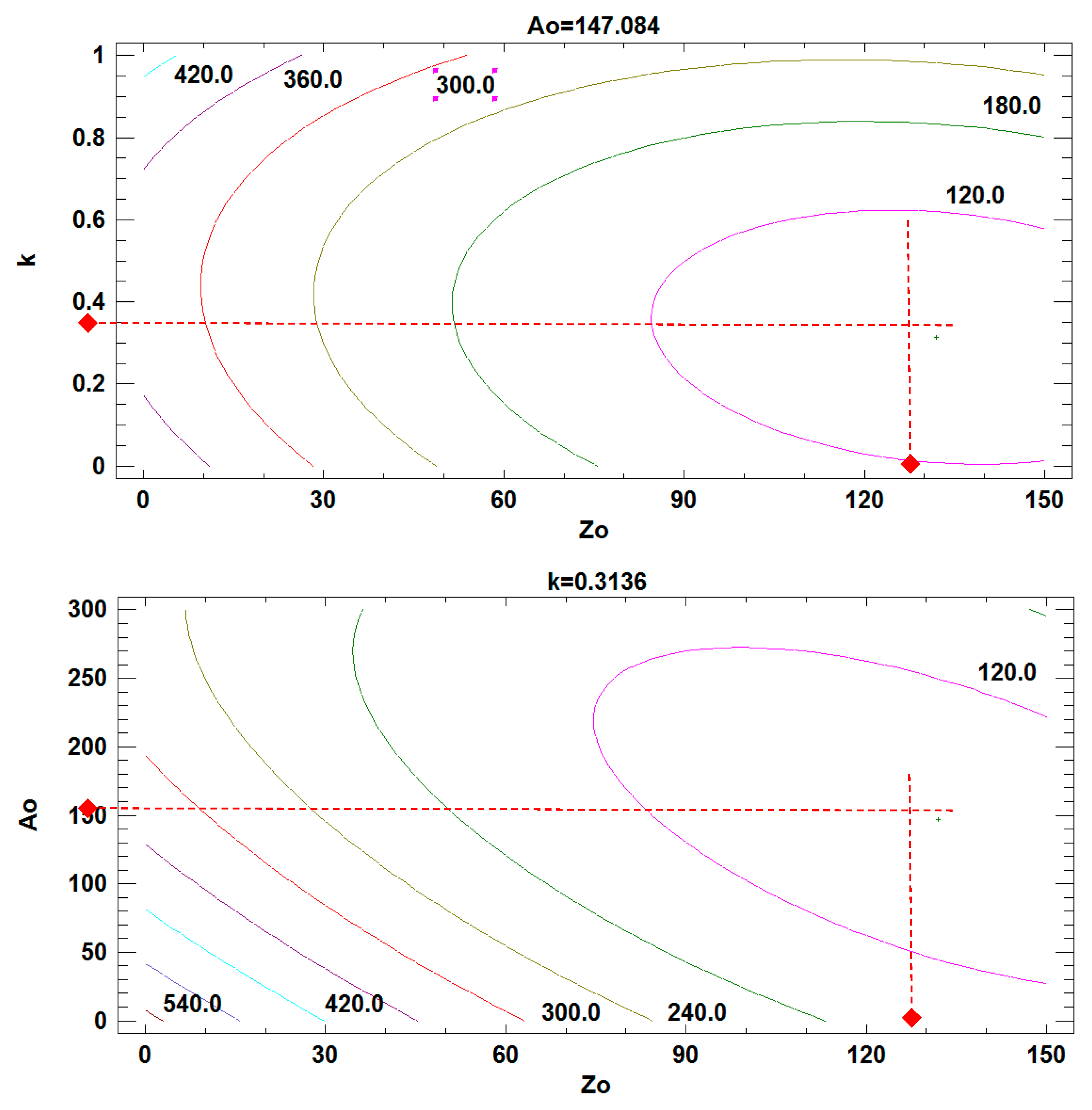
| Total Cost Estimate | Cross-Check Confidence Interval (95%) | ||||
|---|---|---|---|---|---|
| Factor | 132.02 | 0.3136 | 147.084 | 88.13 |
| Cost Variations | ||||||
|---|---|---|---|---|---|---|
| Cases | Cost Parameter | |||||
| Basic case | − | 1 | 50 | 100 | 3000 | 20 |
| Case I | 0.5 | 25 | 100 | 3000 | 20 | |
| Case II | 2 | 150 | 100 | 3000 | 20 | |
| Case III | 1 | 20 | 100 | 3000 | 20 | |
| Case IV | 1 | 70 | 100 | 3000 | 20 | |
| Case V | 1 | 50 | 20 | 3000 | 20 | |
| Case VI | 1 | 50 | 300 | 3000 | 20 | |
| Case VII | 1 | 50 | 100 | 1000 | 20 | |
| Case VIII | 1 | 50 | 100 | 5000 | 20 | |
| Case IX | 1 | 50 | 100 | 3000 | 5 | |
| Case X | 1 | 50 | 100 | 3000 | 50 | |
| Control Parameters Variations | Total Cost Variations | ||||||
|---|---|---|---|---|---|---|---|
| Par. | Cases | Remark | |||||
| - | Basic case | 132.04 | 0.3136 | 46.12 | 147.08 | 88.13 | Base for the comparison |
| Case I | 140.84 | 0.1978 | 29.63 | 149.83 | 55.78 | ||
| Case II | 122.17 | 0.4670 | 66.32 | 142.03 | 133.08 | ||
| Case III | 117.52 | 0.5215 | 78.19 | 149.95 | 82.70 | ||
| Case IV | 136.92 | 0.2509 | 36.87 | 146.98 | 109.89 | ||
| Case V | 131.88 | 0.3135 | 46.28 | 147.65 | 80.88 | ||
| Case VI | 132.05 | 0.3137 | 45.67 | 145.60 | 106.28 | ||
| Case VII | 139.40 | 0.3178 | 37.13 | 116.85 | 77.63 | ||
| Case VIII | 127.25 | 0.3110 | 51.80 | 166.58 | 96.27 | ||
| Case IX | 126.58 | 0.3078 | 51.74 | 168.11 | 75.58 | ||
| Case X | 143.99 | 0.3256 | 32.74 | 100.56 | 107.35 | ||
| Control Parameters | Total Cost * | Cost Difference Δ-Cost (%) | |||
|---|---|---|---|---|---|
| Description | |||||
| Policy-I | 132.02 | 46.12 | 147.08 | 88.13 | - |
| Policy-II | 117.38 | - | 163.26 | 121.09 | +37.39% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rivera-Gómez, H.; Montaño-Arango, O.; Corona-Armenta, J.R.; Garnica-González, J.; Ortega-Reyes, A.O.; Anaya-Fuentes, G.E. JIT Production Strategy and Maintenance for Quality Deteriorating Systems. Appl. Sci. 2019, 9, 1180. https://doi.org/10.3390/app9061180
Rivera-Gómez H, Montaño-Arango O, Corona-Armenta JR, Garnica-González J, Ortega-Reyes AO, Anaya-Fuentes GE. JIT Production Strategy and Maintenance for Quality Deteriorating Systems. Applied Sciences. 2019; 9(6):1180. https://doi.org/10.3390/app9061180
Chicago/Turabian StyleRivera-Gómez, Héctor, Oscar Montaño-Arango, José Ramón Corona-Armenta, Jaime Garnica-González, Antonio Oswaldo Ortega-Reyes, and Gustavo Erick Anaya-Fuentes. 2019. "JIT Production Strategy and Maintenance for Quality Deteriorating Systems" Applied Sciences 9, no. 6: 1180. https://doi.org/10.3390/app9061180
APA StyleRivera-Gómez, H., Montaño-Arango, O., Corona-Armenta, J. R., Garnica-González, J., Ortega-Reyes, A. O., & Anaya-Fuentes, G. E. (2019). JIT Production Strategy and Maintenance for Quality Deteriorating Systems. Applied Sciences, 9(6), 1180. https://doi.org/10.3390/app9061180





