Quantitative Reconstruction of Absorption Coefficients for Photoacoustic Tomography
Abstract
:1. Introduction
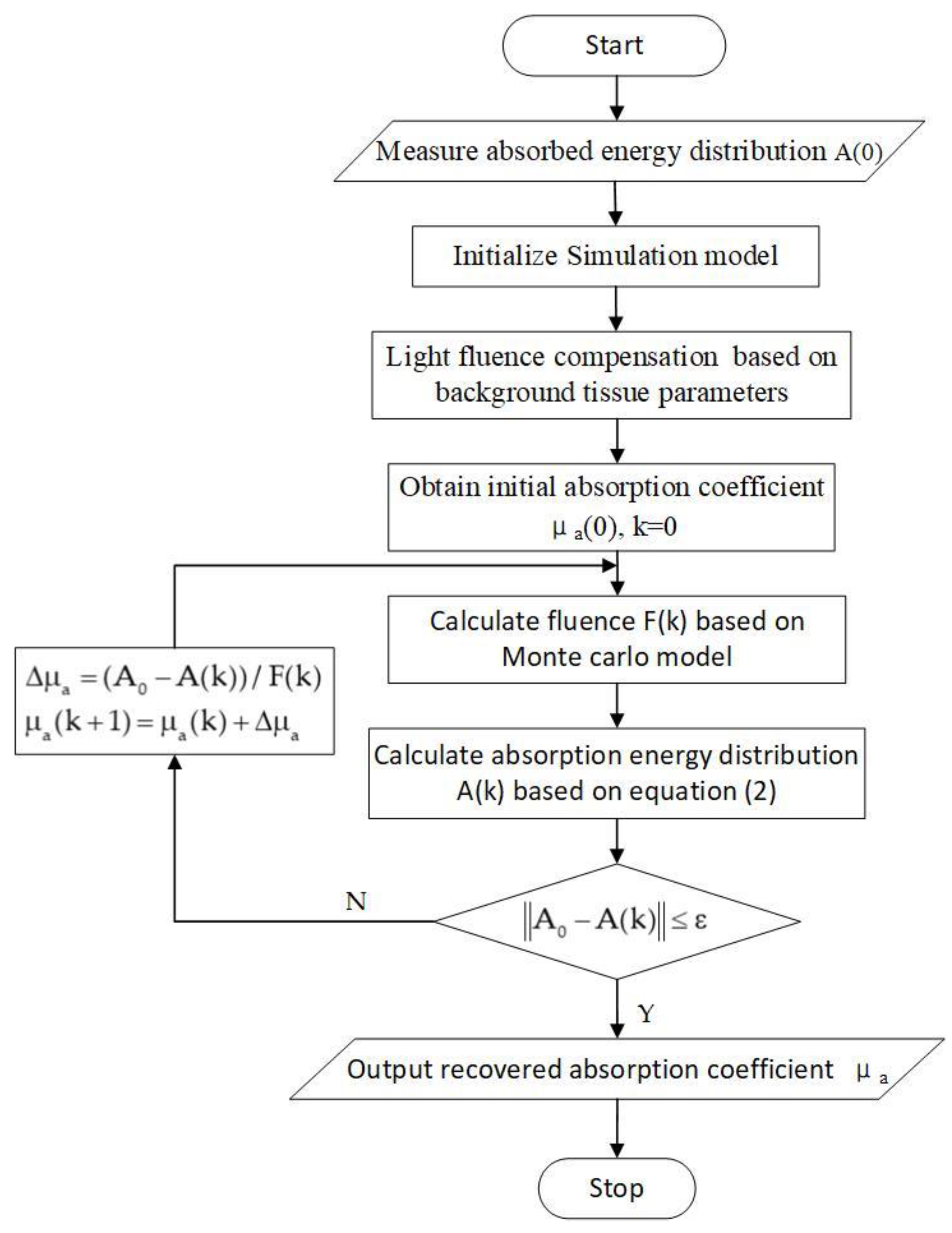
2. Methods
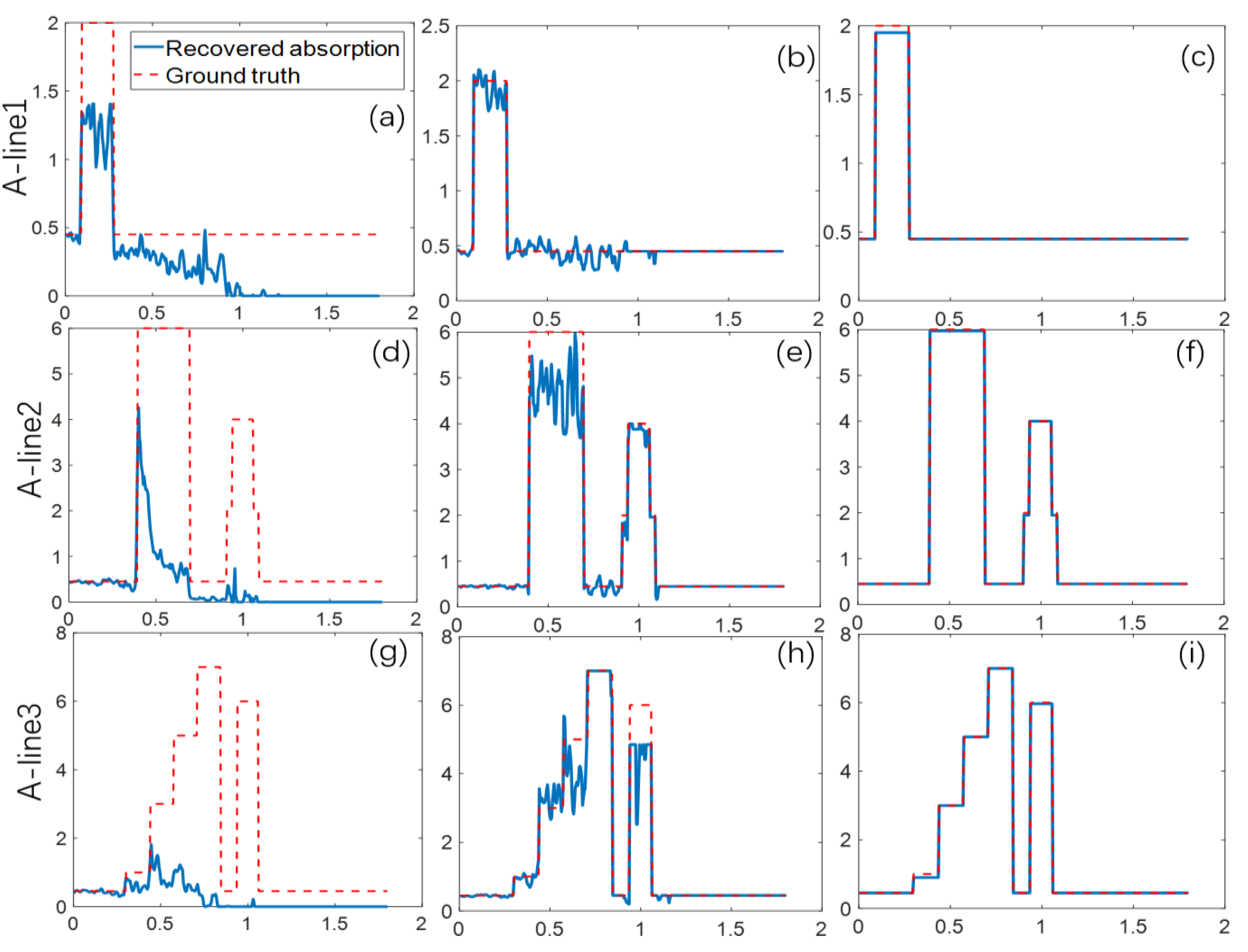
3. Numerical Simulation
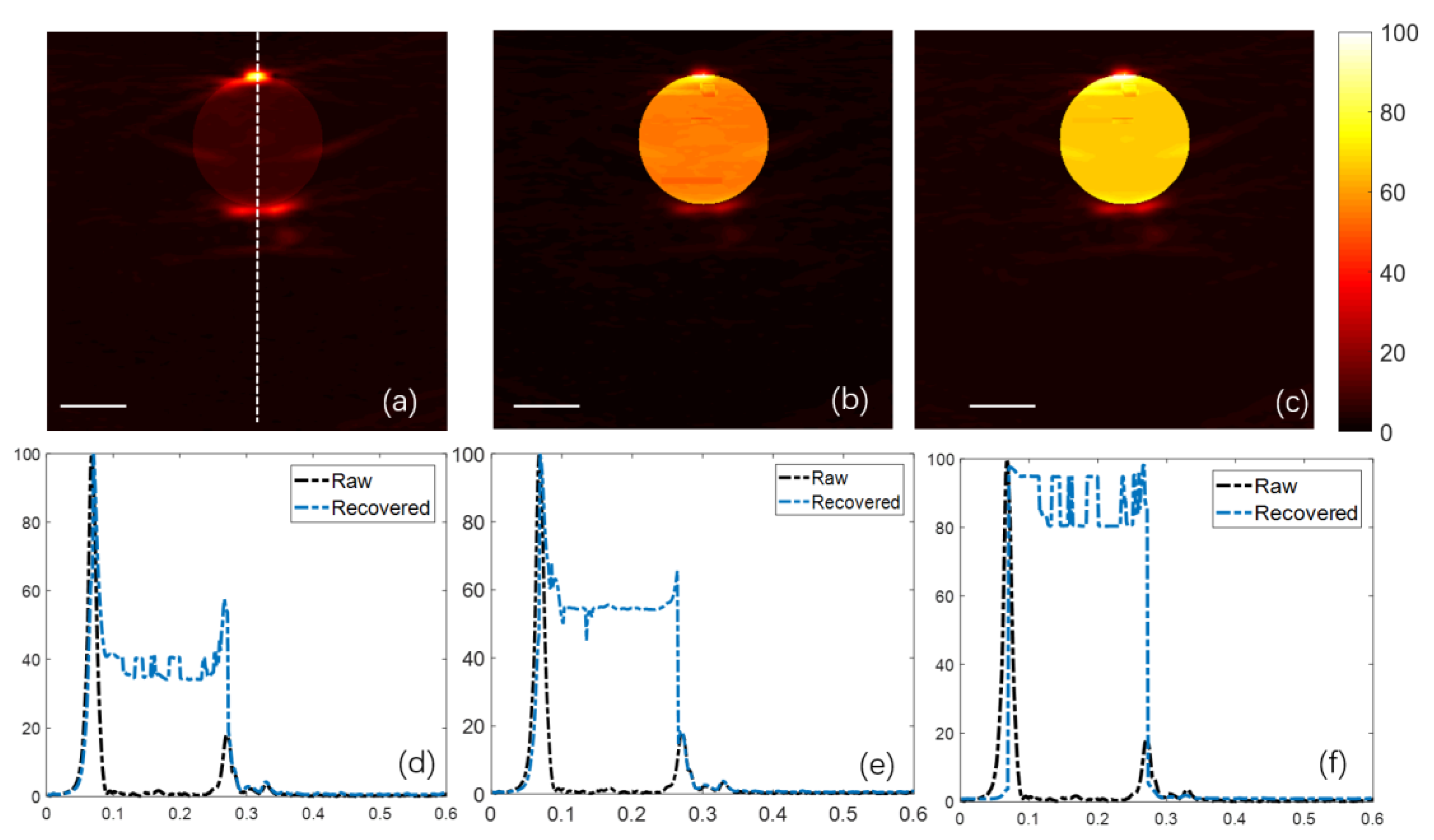
4. Phantom Experiment
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, L.V.; Hu, S. Photoacoustic Tomography: In Vivo Imaging from Organelles to Organs. Science 2012, 335, 1458–1462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, M.; Wang, L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006, 77, 305–598. [Google Scholar] [CrossRef]
- Beard, P. Biomedical photoacoustic imaging. Interface Focus 2011, 1, 602–631. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Pang, Y.; Ku, G.; Xie, X.; Stoica, G.; Wang, L.V. Noninvasive laser-induced photoacoustic tomography for structural and functional in vivo imaging of the brain. Nat. Biotechnol. 2003, 21, 803. [Google Scholar] [CrossRef]
- Zerda, A.D.L.; Zavaleta, C.; Keren, S.; Vaithilingam, S.; Bodapati, S.; Liu, Z.; Levi, J.; Smith, B.R.; Ma, T.-J.; Oralkan, O.; et al. Carbon nanotubes as photoacoustic molecular imaging agents in living mice. Nat. Nanotechnol. 2008, 3, 557. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V.; Wu, H. Biomedical optics: Principles and imaging. J. Biomed. Opt. 2008, 13, 049902. [Google Scholar] [CrossRef]
- Jacques, S.L. Coupling 3D Monte Carlo light transport in optically heterogeneous tissues to photoacoustic signal generation. Photoacoustics 2014, 2, 137–142. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Sun, M.; Feng, N.; Wu, Z.; Shen, Y. Multiscale Hessian filter-based segmentation and quantification method for photoacoustic microangiography. Chin. Opt. Lett. 2015, 13, 091701. [Google Scholar]
- Lin, X.; Sun, M.; Feng, N.; Hu, D.; Shen, Y. Monte Carlo light transport-based blood vessel quantification using linear array photoacoustic tomography. Chin. Opt. Lett. 2017, 15, 111701. [Google Scholar]
- Wang, X.; Roberts, W.W.; Carson, P.L.; Wood, D.P.; Fowlkes, J.B. Photoacoustic tomography: A potential new tool for prostate cancer. Biomed. Opt. Express 2010, 1, 1117–1126. [Google Scholar] [CrossRef]
- Zhou, Y.; Xing, W.; Maslov, K.I.; Cornelius, L.A.; Wang, L.V. Handheld photoacoustic microscopy to detect melanoma depth in vivo. Opt. Lett. 2014, 39, 4731–4734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heijblom, M.; Piras, D.; Xia, W.; van Hespen, J.C.; Klaase, J.M.; Van den Engh, F.M.; van Leeuwen, T.G.; Steenbergen, W.; Manohar, S. Visualizing breast cancer using the Twente photoacoustic mammoscope: What do we learn from twelve new patient measurements? Opt. Express 2012, 20, 11582. [Google Scholar] [CrossRef]
- Li, R.; Wang, P.; Lan, L.; Lloyd, F.P.; Goergen, C.J.; Chen, S.; Cheng, J.X. Assessing breast tumor margin by multispectral photoacoustic tomography. Biomed. Opt. Express 2015, 6, 1273. [Google Scholar] [CrossRef] [PubMed]
- Tzoumas, S.; Nunes, A.; Olefir, I.; Stangl, S.; Symvoulidis, P.; Glasl, S.; Bayer, C.; Multhoff, G.; Ntziachristos, V. Eigenspectra optoacoustic tomography achieves quantitative blood oxygenation imaging deep in tissues. Nat. Commun. 2016, 7, 12121. [Google Scholar] [CrossRef] [Green Version]
- Cox, B.; Laufer, J.G.; Beard, P.C.; Arridge, S.R. Quantitative spectroscopic photoacoustic imaging: A review. J. Biomed. Opt. 2012, 17, 061202. [Google Scholar] [CrossRef]
- Cox, B.T.; Arridge, S.R.; Kostli, K.P.; Beard, P.C. Quantitative photoacoustic imaging: Fitting a model of light transport to the initial pressure distribution. Photons Plus Ultrasound Imaging Sens. Sixth Conf. Biomed. Thermoacoust. 2005, 5697, 49–56. [Google Scholar]
- Cox, B.T.; Arridge, S.R.; Köstli, K.P.; Beard, P.C. Two-dimensional quantitative photoacoustic image reconstruction of absorption distributions in scattering media by use of a simple iterative method. Appl. Opt. 2006, 45, 1866–1875. [Google Scholar] [CrossRef] [PubMed]
- Cox, B.T.; Arridge, S.R.; Beard, P.C. Estimating chromophore distributions from multiwavelength photoacoustic images. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2009, 26, 443–455. [Google Scholar] [CrossRef]
- Cox, B.; Shao, P.; Zemp, R.J. Estimating optical absorption, scattering, and Grueneisen distributions with multiple-illumination photoacoustic tomography. Appl. Opt. 2011, 50, 3145–3154. [Google Scholar]
- Hochuli, R. Monte Carlo Methods in Quantitative Photoacoustic Tomography. Ph.D. Thesis, University College London, London, UK, 2016. [Google Scholar]
- Rosenthal, A.; Razansky, D.; Ntziachristos, V. Quantitative Optoacoustic Signal Extraction Using Sparse Signal Representation. IEEE Trans. Med. Imaging 2009, 28, 1997–2006. [Google Scholar] [CrossRef]
- Rosenthal, A.; Razansky, D.; Ntziachristos, V. Sparse signal representation at the service of quantitative optoacoustic tomography. Photons Plus Ultrasound Imaging Sens. Int. Soc. Opt. Photonics 2010, 7564, 75640S. [Google Scholar]
- Rosenthal, A.; Razansky, D.; Ntziachristos, V. Fast semi-analytical model-based acoustic inversion for quantitative optoacoustic tomography. IEEE Trans. Med. Imaging 2010, 29, 1275–1285. [Google Scholar] [CrossRef] [PubMed]
- Zemp, R.J. Quantitative photoacoustic tomography with multiple optical sources. Appl. Opt. 2010, 49, 3566–3572. [Google Scholar] [CrossRef] [PubMed]
- Mastanduno, M.A.; Gambhir, S.S. Quantitative photoacoustic image reconstruction improves accuracy in deep tissue structures. Biomed. Opt. Express 2016, 7, 3811. [Google Scholar] [CrossRef]
- Jetzfellner, T.; Razansky, D.; Rosenthal, A.; Schulz, R.; Englmeier, K.H.; Ntziachristos, V. Performance of iterative optoacoustic tomography with experimental data. Appl. Phys. Lett. 2009, 95, 013703. [Google Scholar] [CrossRef]
- Brochu, F.M.; Brunker, J.; Joseph, J.; Tomaszewski, M.R.; Morscher, S.; Bohndiek, S.E. Towards Quantitative Evaluation of Tissue Absorption Coefficients Using Light Fluence Correction in Optoacoustic Tomography. IEEE Trans. Med. Imaging 2017, 36, 322–331. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, B.; Bagchi, S.; Vasu, R.M.; Roy, D. Quantitative photoacoustic tomography from boundary pressure measurements: Noniterative recovery of optical absorption coefficient from the reconstructed absorbed energy map. JOSA A 2008, 25, 2347–2356. [Google Scholar] [CrossRef]
- Bauer, A.Q.; Nothdurft, R.E.; Culver, J.P.; Erpelding, T.N.; Wang, L.V. Quantitative photoacoustic imaging: Correcting for heterogeneous light fluence distributions using diffuse optical tomography. J. Biomed. Opt. 2011, 16, 096016. [Google Scholar] [CrossRef]
- Bu, S.; Liu, Z.; Shiina, T.; Kondo, K.; Yamakawa, M.; Fukutani, K.; Someda, Y.; Asao, Y. Model-Based Reconstruction Integrated with Fluence Compensation for Photoacoustic Tomography. IEEE Trans. Biomed. Eng. 2012, 59, 1354–1363. [Google Scholar]
- Yuan, Z.; Wang, Q.; Jiang, H. Reconstruction of optical absorption coefficient maps of heterogeneous media by photoacoustic tomography coupled with diffusion equation based regularized Newton Method. Opt. Express 2007, 15, 18076–18081. [Google Scholar] [CrossRef]
- Yuan, Z.; Jiang, H. Three-dimensional finite-element-based photoacoustic tomography: Reconstruction algorithm and simulations. Med. Phys. 2007, 34, 538–546. [Google Scholar] [CrossRef]
- Yao, L.; Jiang, H. Finite-element-based photoacoustic tomography in time domain. J. Opt. A Pure Appl. Opt. 2009, 11, 085301. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, H.; Yuan, Z. Two schemes for quantitative photoacoustic tomography based on Monte Carlo simulation. Med. Phys. 2016, 43, 3987–3997. [Google Scholar] [CrossRef] [PubMed]
- Rabanser, S.; Neumann, L.; Haltmeier, M. Stochastic Proximal Gradient Algorithms for Multi-Source Quantitative Photoacoustic Tomography. Entropy 2018, 20, 121. [Google Scholar] [CrossRef]
- Xia, J.; Danielli, A.; Liu, Y. Calibration-free quantification of absolute oxygen saturation based on the dynamics of photoacoustic signals. Opt. Lett. 2013, 38, 2800–2803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, Z.; Anastasio, M.A.; Riviere, P.J.; Wang, L.V. Effects of different imaging models on least-squares image reconstruction accuracy in photoacoustic tomography. IEEE Trans. Med. Imaging 2009, 28, 1781–1790. [Google Scholar]
- Bu, S.; Kondo, K.; Yamakawa, M.; Shiina, T.; Fukutani, K.; Someda, Y.; Asao, Y. Adaptive and Quantitative Reconstruction Algorithm for Photoacoustic Tomography. Proc. SPIE Int. Soc. Opt. Eng. 2011, 7899, 78992G. [Google Scholar]
- Razansky, D.; Buehler, A.; Ntziachristos, V. Volumetric real-time multispectral optoacoustic tomography of biomarkers. Nat. Protoc. 2011, 6, 1121–1129. [Google Scholar] [CrossRef]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; pp. 1398–1402. [Google Scholar]
- Mandal, S.; Viswanath, P.S.; Yeshaswini, N.; Dean-Ben, X.L.; Razansky, D. Multiscale edge detection and parametric shape modeling for boundary delineation in optoacoustic images. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 707–710. [Google Scholar]
- Kazakeviciute, A.; Ho CJ, H.; Olivo, M. Multispectral photoacoustic imaging artifact removal and denoising using time series model-based spectral noise estimation. IEEE Trans. Med. Imaging 2016, 35, 2151–2163. [Google Scholar] [CrossRef]
- Van Staveren, H.J.; Moes, C.J.; van Marie, J.; Prahl, S.A.; Van Gemert, M.J. Light scattering in lntralipid-10% in the wavelength range of 400–1100 nm. Appl. Opt. 1991, 30, 4507–4514. [Google Scholar] [CrossRef]
- Kirillin, M.; Perekatova, V.; Turchin, I.; Subochev, P. Fluence compensation in raster-scan optoacoustic angiography. Photoacoustics 2017, 8, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Matthews, T.P. Image Reconstruction of the Speed of Sound and Initial Pressure Distributions in Ultrasound Computed Tomography and Photoacoustic Computed Tomography. Available online: https://openscholarship.wustl.edu/eng_etds/286 (accessed on 14 March 2019).
- Mandal, S.; Deán-Ben, X.L.; Razansky, D. Visual quality enhancement in optoacoustic tomography using active contour segmentation priors. IEEE Trans. Med. Imaging 2016, 35, 2209–2217. [Google Scholar] [CrossRef] [PubMed]
- Tarvainen, T.; Pulkkinen, A.; Cox, B.T.; Kaipio, J.P.; Arridge, S.R. Bayesian image reconstruction in quantitative photoacoustic tomography. IEEE Trans. Med. Imaging 2013, 32, 2287–2298. [Google Scholar] [CrossRef] [PubMed]
- Prakash, J.; Mandal, S.; Razansky, D.; Ntziachristos, V. Maximum entropy based non-negative optoacoustic tomographic image reconstruction. IEEE Trans. Biomed. Eng. 2019. [Google Scholar] [CrossRef] [PubMed]

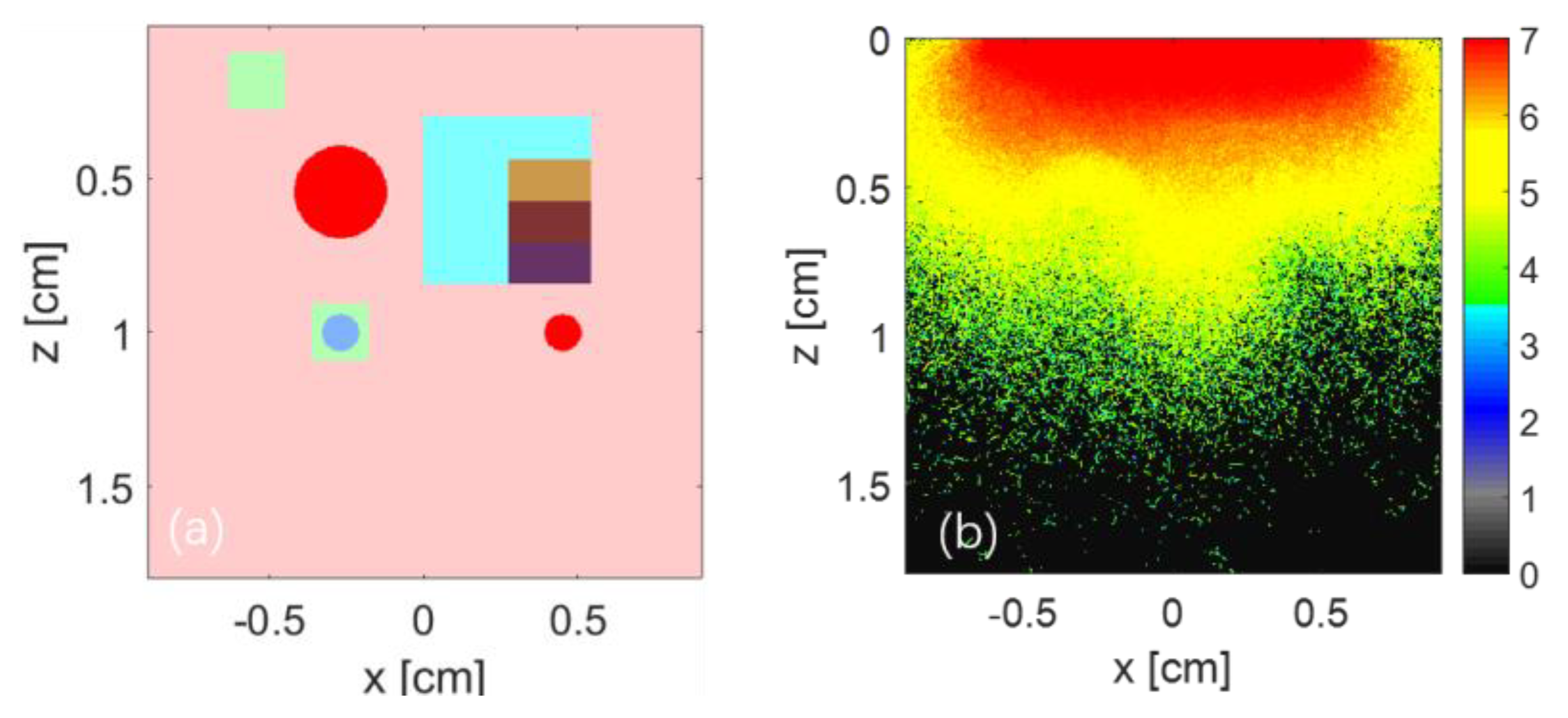
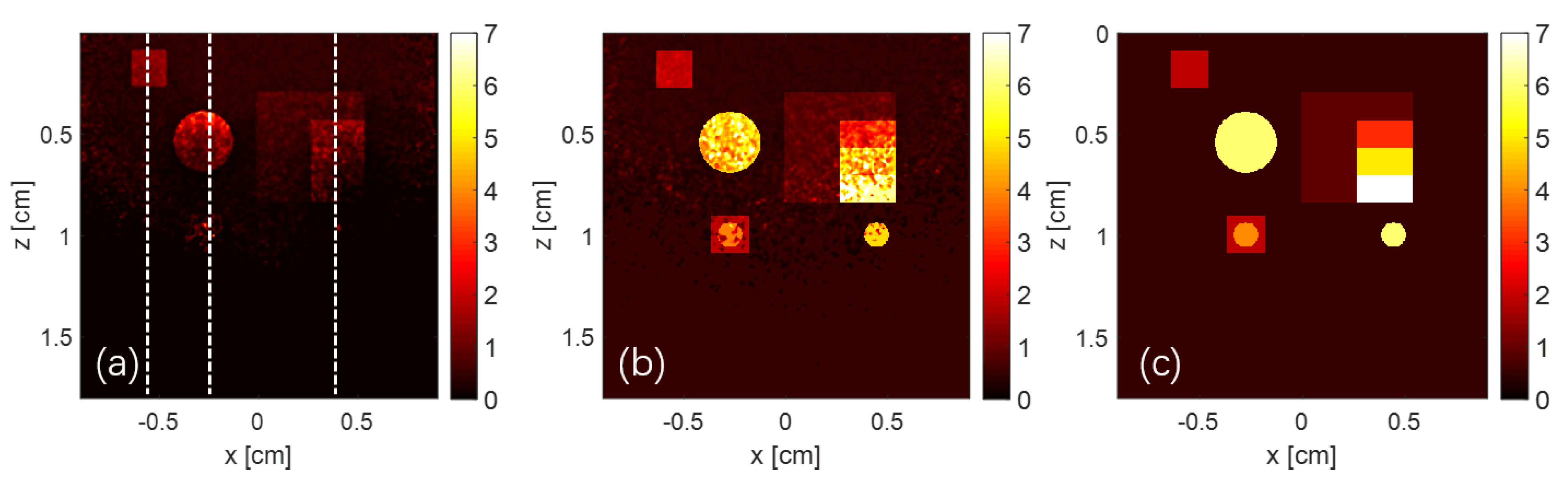
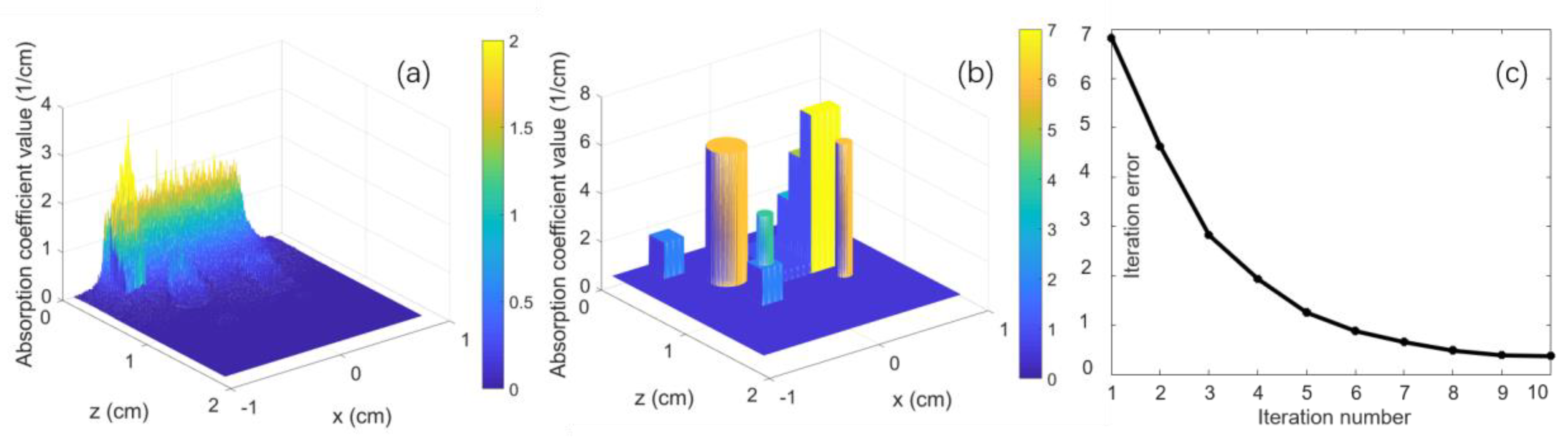

| Target Name | Target Structure | Target Size (x × y × z) (cm3) | μa (cm−1) | μs (cm−1) | g |
|---|---|---|---|---|---|
| target1 | cube | (0.18 × 0.18 × 0.18) | 2.00 | 100.00 | 0.90 |
| target2 | sphere | dia. 0.30 | 6.00 | 100.00 | 0.90 |
| target3- layer1 | Cube -layer1 | (0.27 × 0.54 × 0.135) | 1.00 | 100.00 | 0.90 |
| target3- layer2 | Cube -layer2 | (0.27 × 0.54 × 0.135) | 3.00 | 100.00 | 0.90 |
| target3- layer3 | Cube -layer3 | (0.27 × 0.54 × 0.135) | 5.00 | 100.00 | 0.90 |
| target3- layer4 | Cube -layer4 | (0.27 × 0.54 × 0.135) | 7.00 | 100.00 | 0.90 |
| target4 | cube + sphere | (0.18 × 0.18 × 0.18), dia. 0.12 | 2.00, 4.00 | 150.00 | 0.90 |
| target5 | small sphere | dia. 0.12 | 6.00 | 100.00 | 0.90 |
| background | cube | (1.80 × 1.80 × 1.80) | 0.45 | 356.00 | 0.90 |
| Target | Raw Data | Recovered | Ground Truth | SSIM1 | SSIM2 | Accuracy |
|---|---|---|---|---|---|---|
| target1 | 1.30 | 1.95 | 2.00 | 0.932036 | 0.999868 | 97.50% |
| target2 | 0.96 | 5.97 | 6.00 | 0.627773 | 0.999995 | 99.50% |
| target3- layer1 | 0.39 | 0.92 | 1.00 | 0.907882 | 0.998892 | 92.00% |
| target3- layer2 | 0.20 | 3.02 | 3.00 | 0.539483 | 0.999917 | 99.33% |
| target3- layer3 | 0.15 | 5.03 | 5.00 | 0.318427 | 0.999921 | 99.40% |
| target3- layer4 | 0.10 | 7.01 | 7.00 | 0.220775 | 0.999925 | 98.57% |
| target4 | 0.13 | 1.95, 3.97 | 2.00, 4.00 | 0.670044 | 0.999933 | 97.50%, 99.25% |
| target5 | 0.16 | 5.97 | 6.00 | 0.441811 | 0.999992 | 99.50% |
| Index | SSIM | RMSE | PSNR |
|---|---|---|---|
| Before recovery (Ground truth & Raw data) | 0.913498 | 1.45105 | 31.4724 dB |
| After recovery (Ground truth & Recovered) | 0.999927 | 0.0253681 | 112.403 dB |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Sun, M.; Liu, T.; Ma, Y.; Hu, D.; Li, C.; Feng, N. Quantitative Reconstruction of Absorption Coefficients for Photoacoustic Tomography. Appl. Sci. 2019, 9, 1187. https://doi.org/10.3390/app9061187
Liu Y, Sun M, Liu T, Ma Y, Hu D, Li C, Feng N. Quantitative Reconstruction of Absorption Coefficients for Photoacoustic Tomography. Applied Sciences. 2019; 9(6):1187. https://doi.org/10.3390/app9061187
Chicago/Turabian StyleLiu, Yang, Mingjian Sun, Ting Liu, Yiming Ma, Depeng Hu, Chao Li, and Naizhang Feng. 2019. "Quantitative Reconstruction of Absorption Coefficients for Photoacoustic Tomography" Applied Sciences 9, no. 6: 1187. https://doi.org/10.3390/app9061187
APA StyleLiu, Y., Sun, M., Liu, T., Ma, Y., Hu, D., Li, C., & Feng, N. (2019). Quantitative Reconstruction of Absorption Coefficients for Photoacoustic Tomography. Applied Sciences, 9(6), 1187. https://doi.org/10.3390/app9061187





