Seismic Response of High-Rise Buildings Equipped with Base Isolation and Non-Traditional Tuned Mass Dampers
Abstract
:1. Introduction
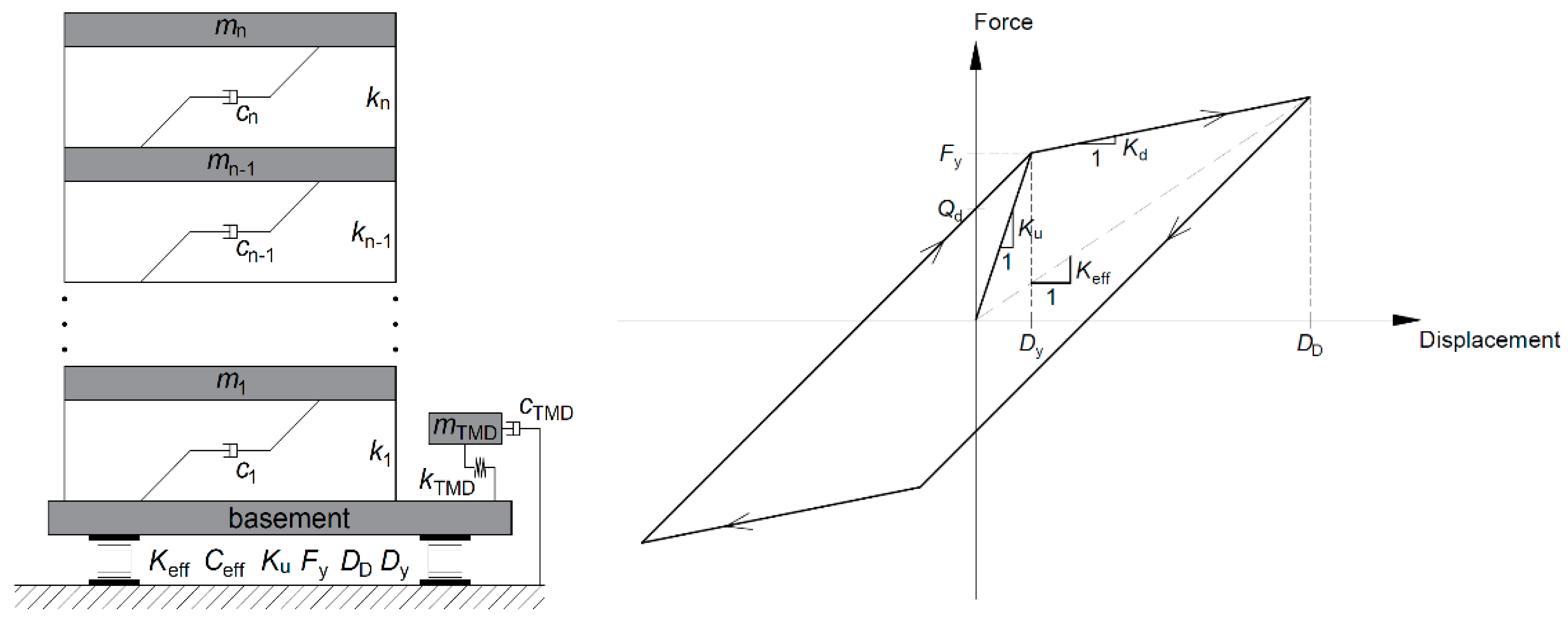
2. Materials and Methods
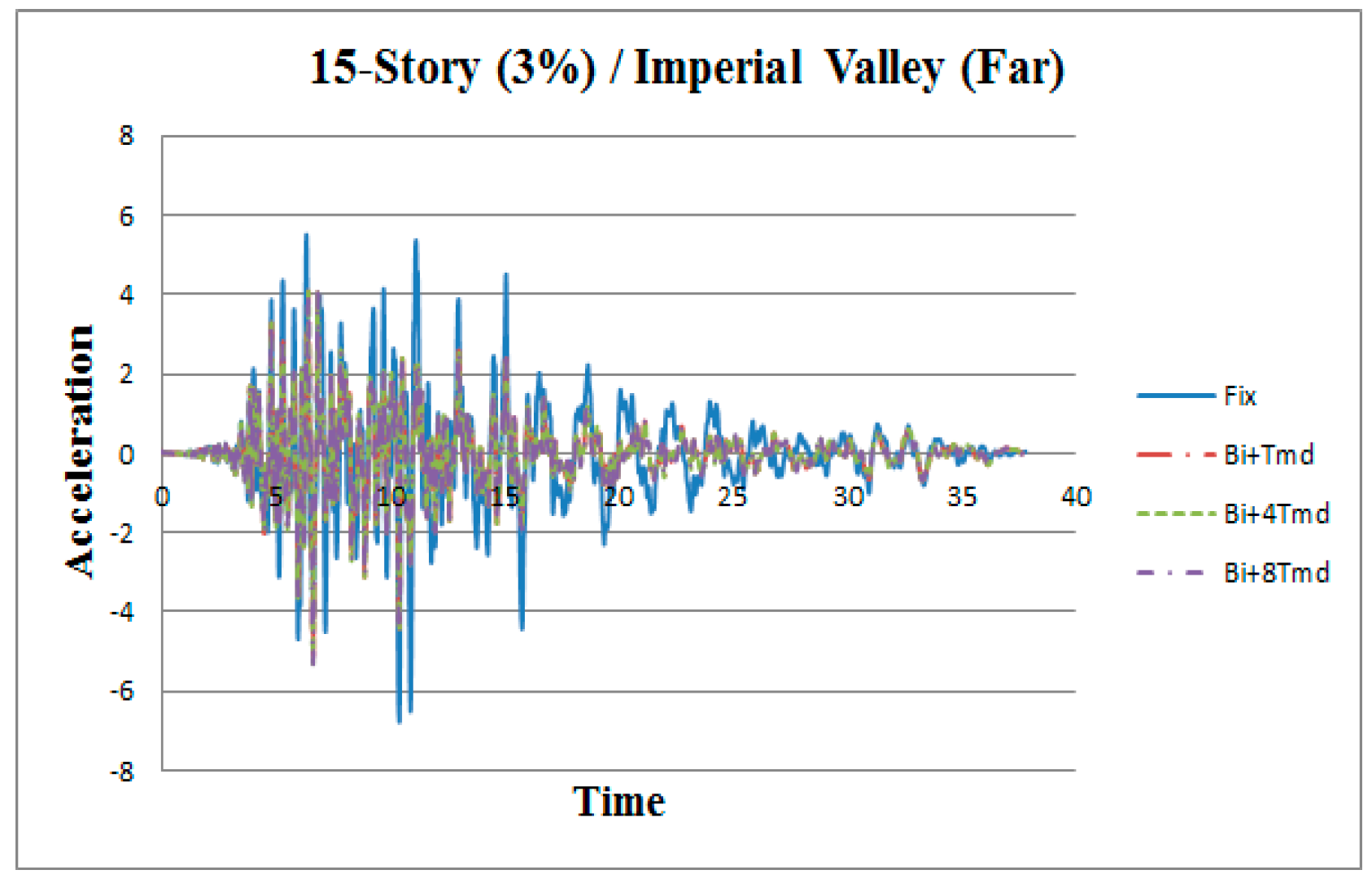
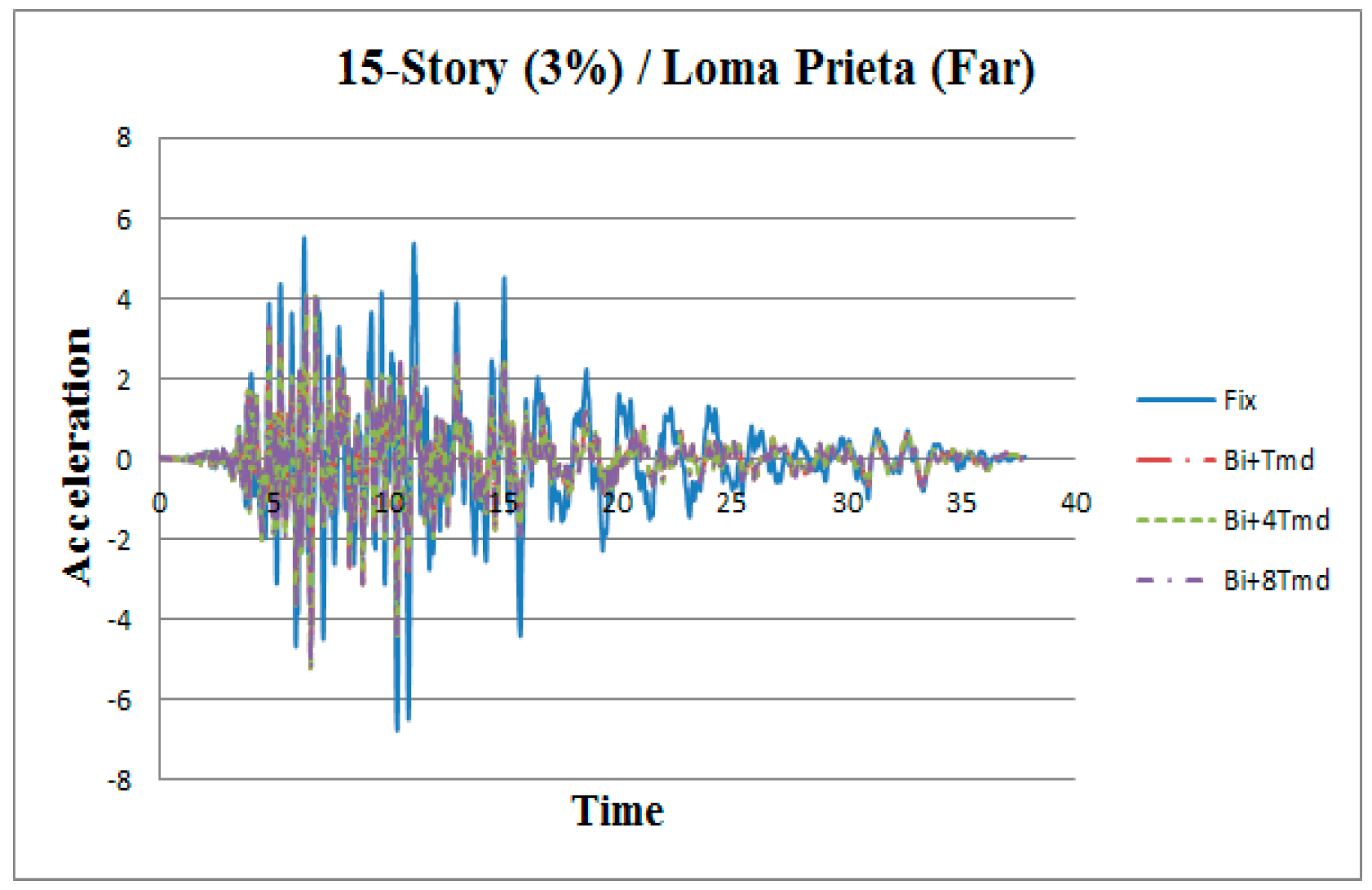
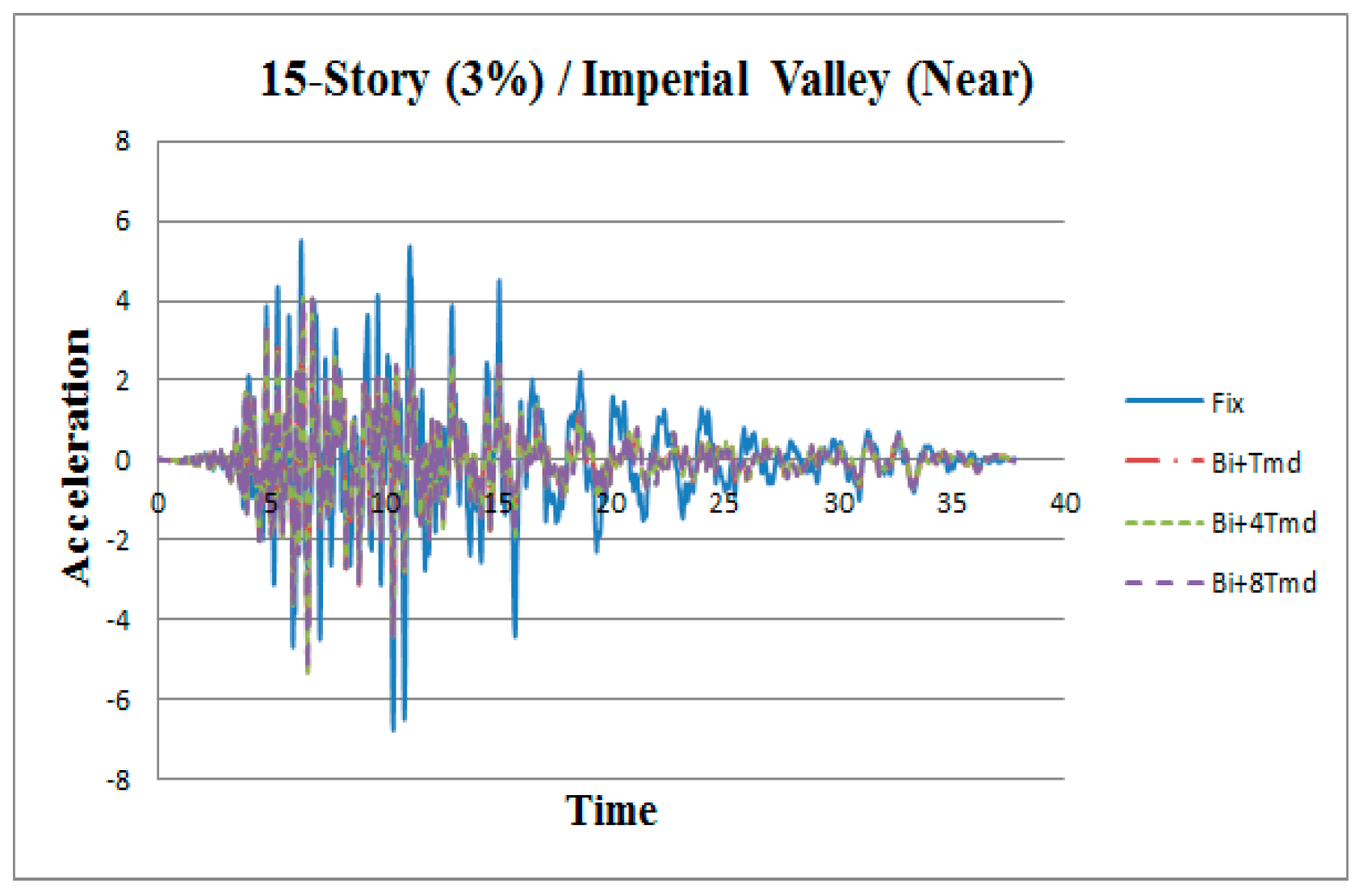
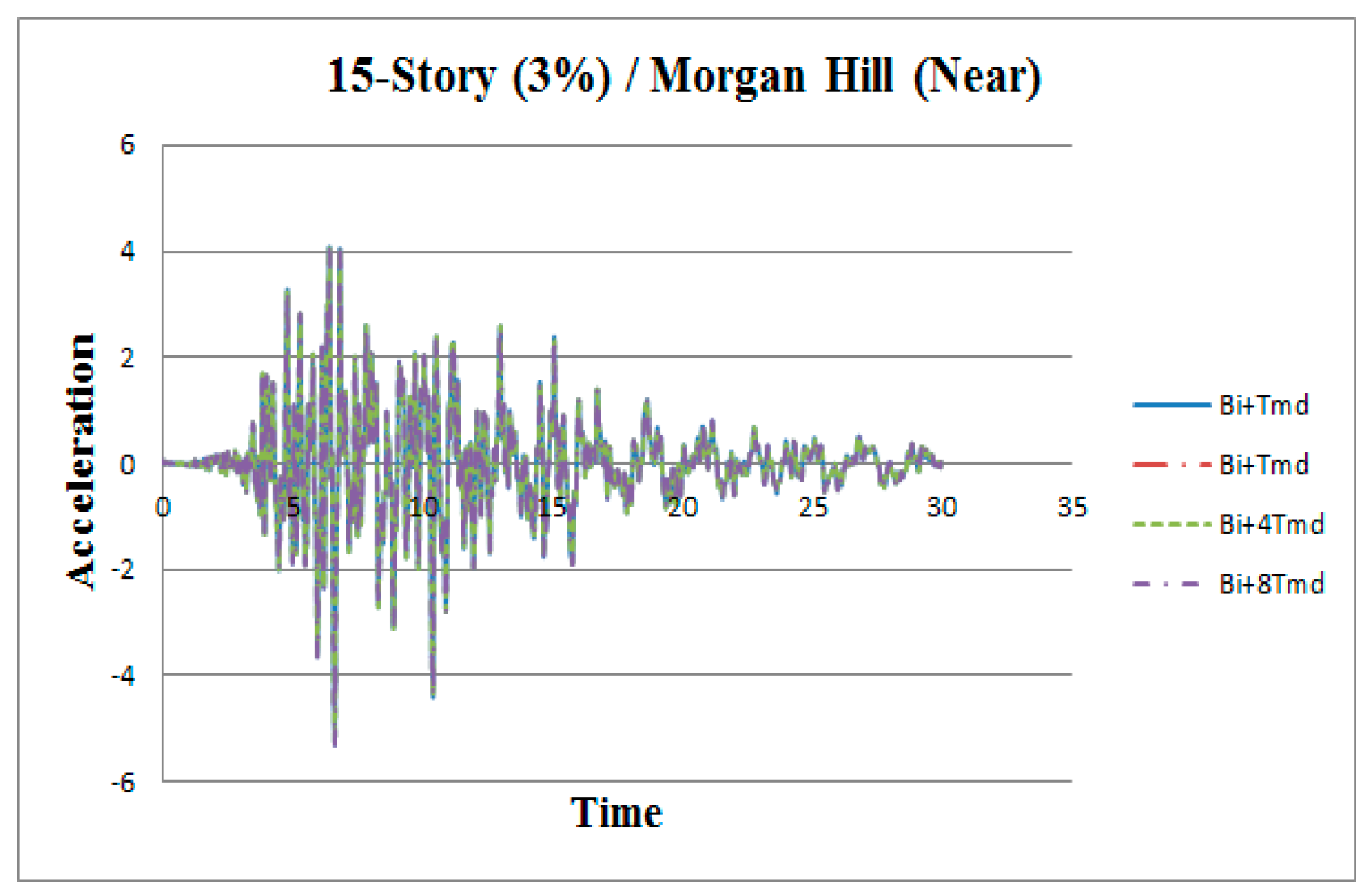
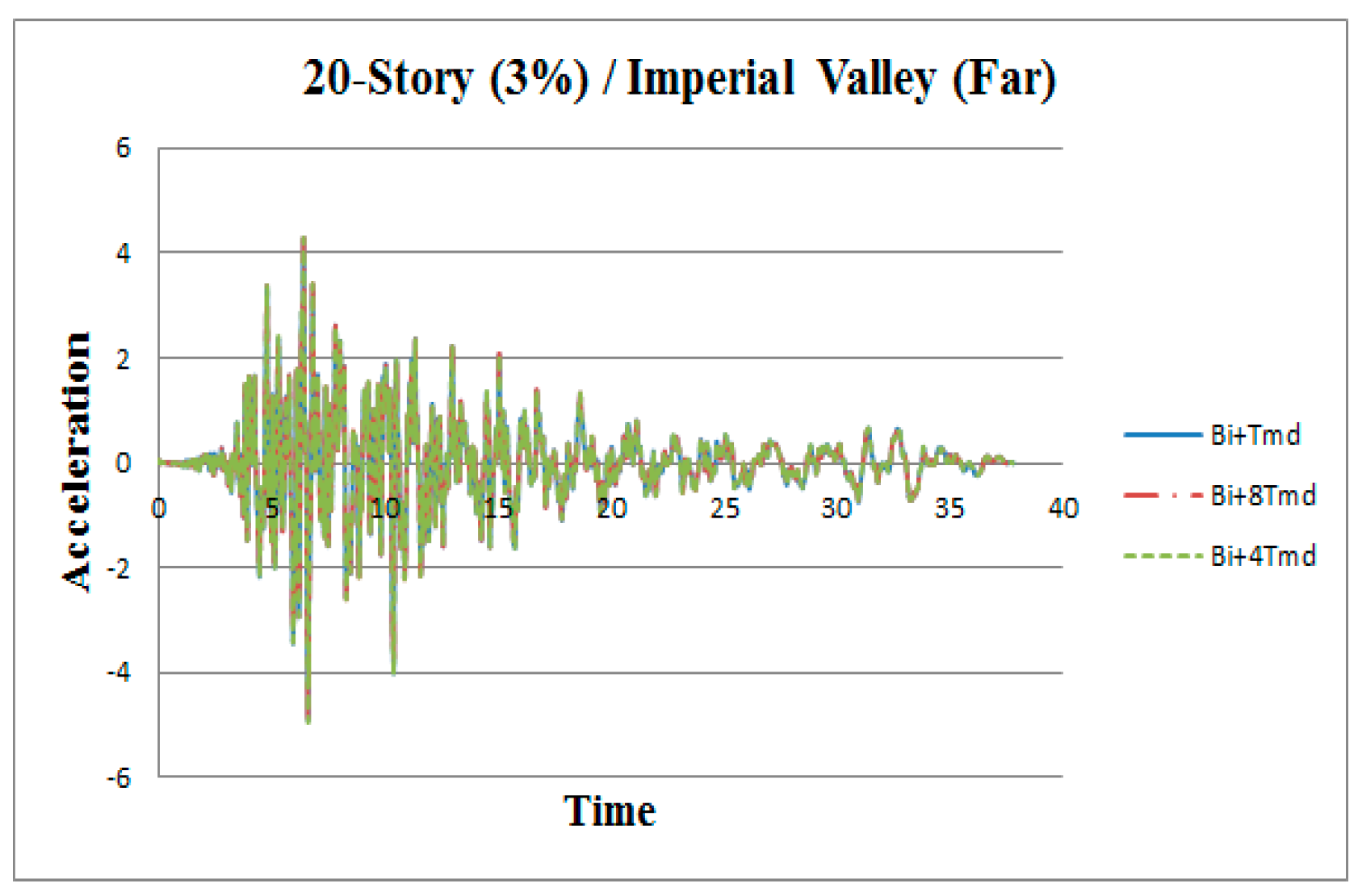
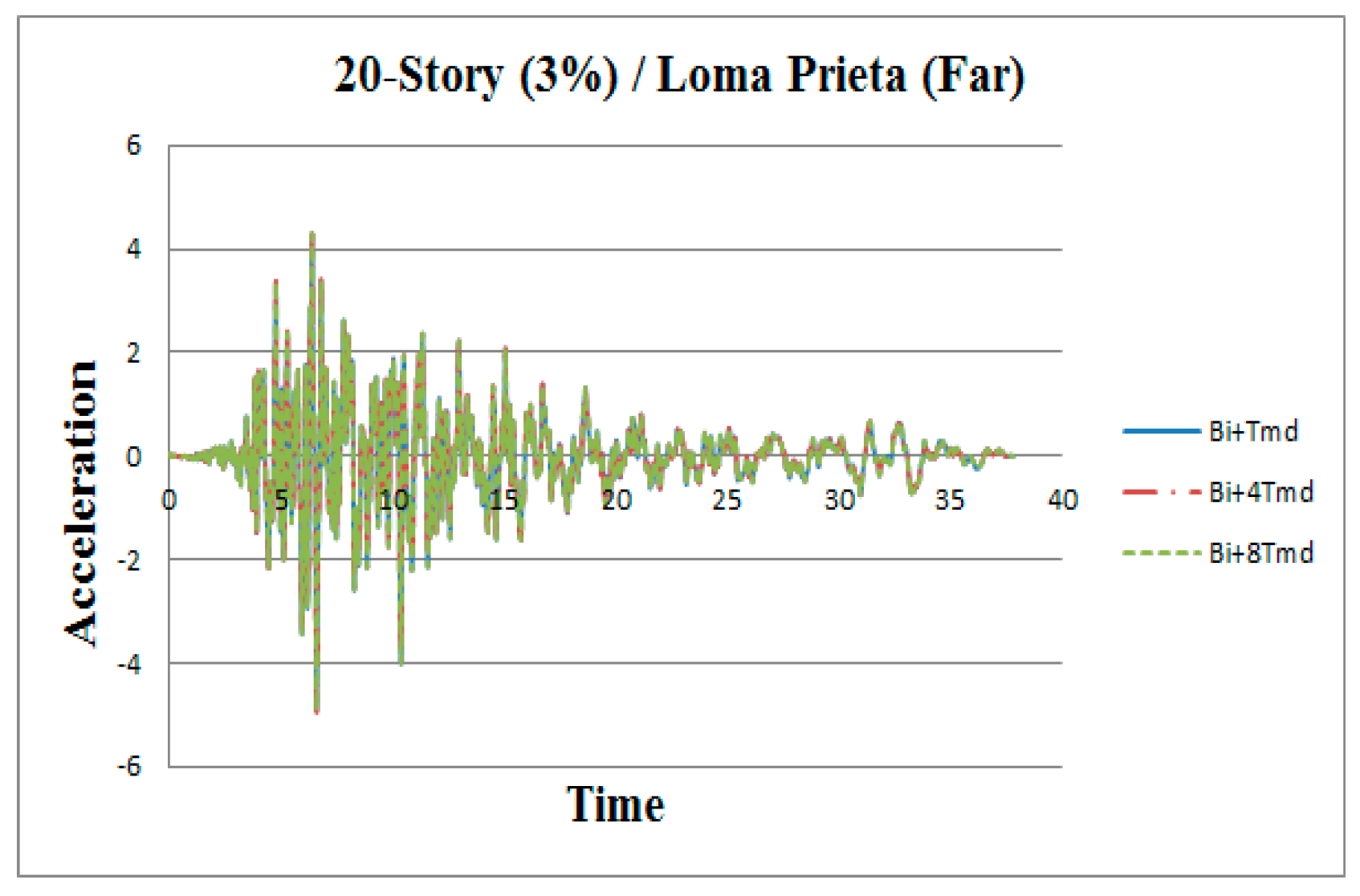
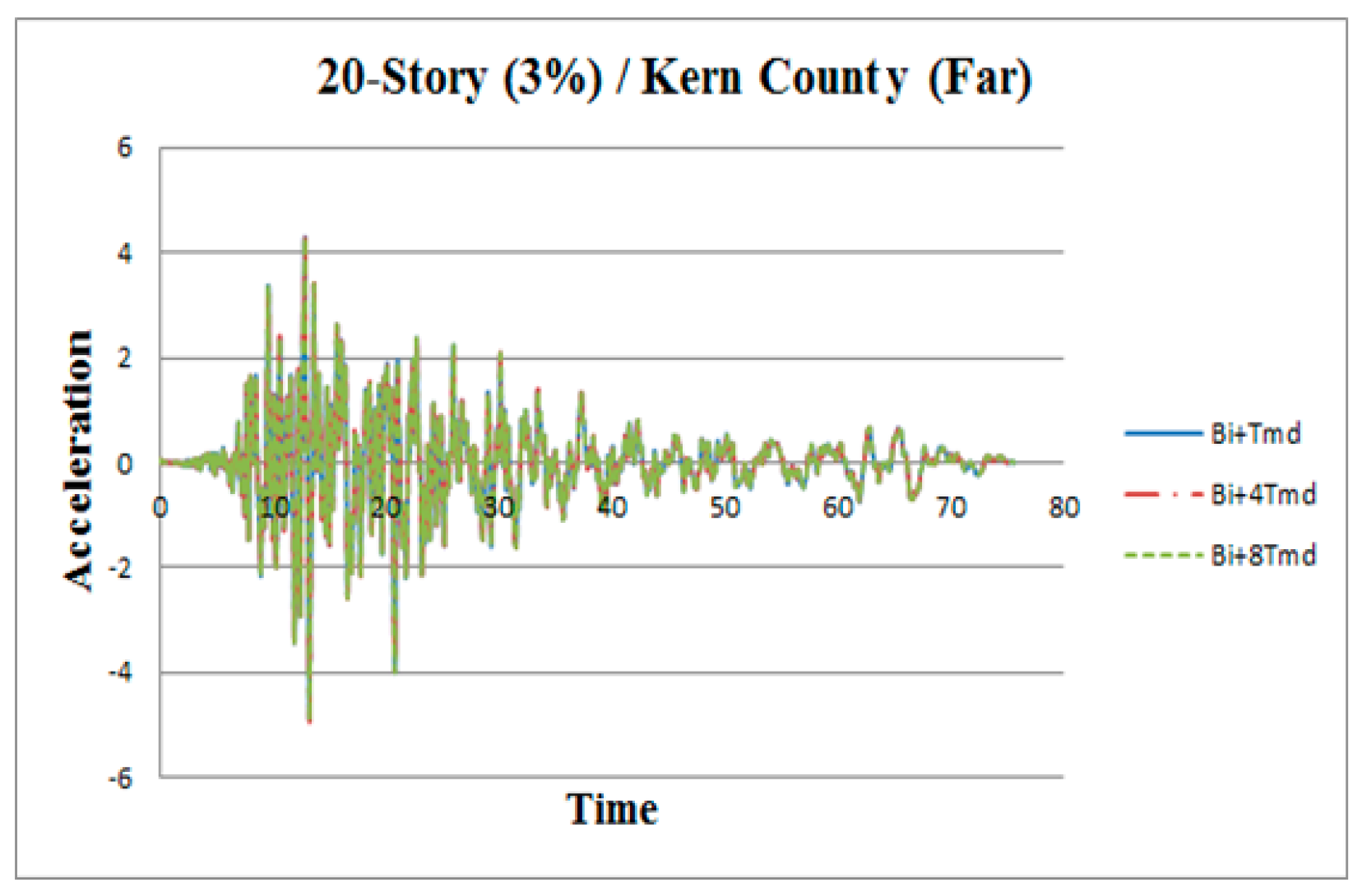
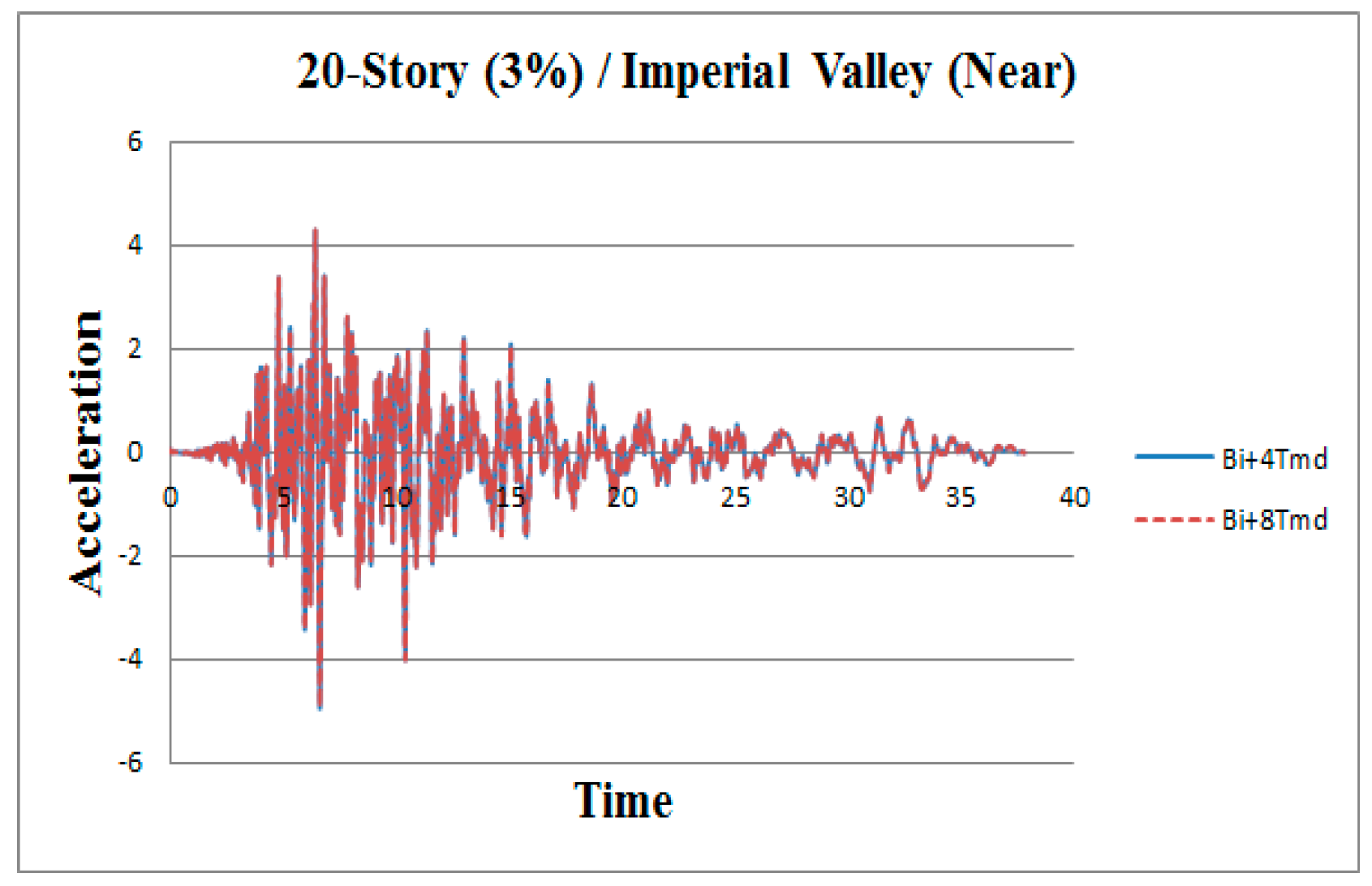
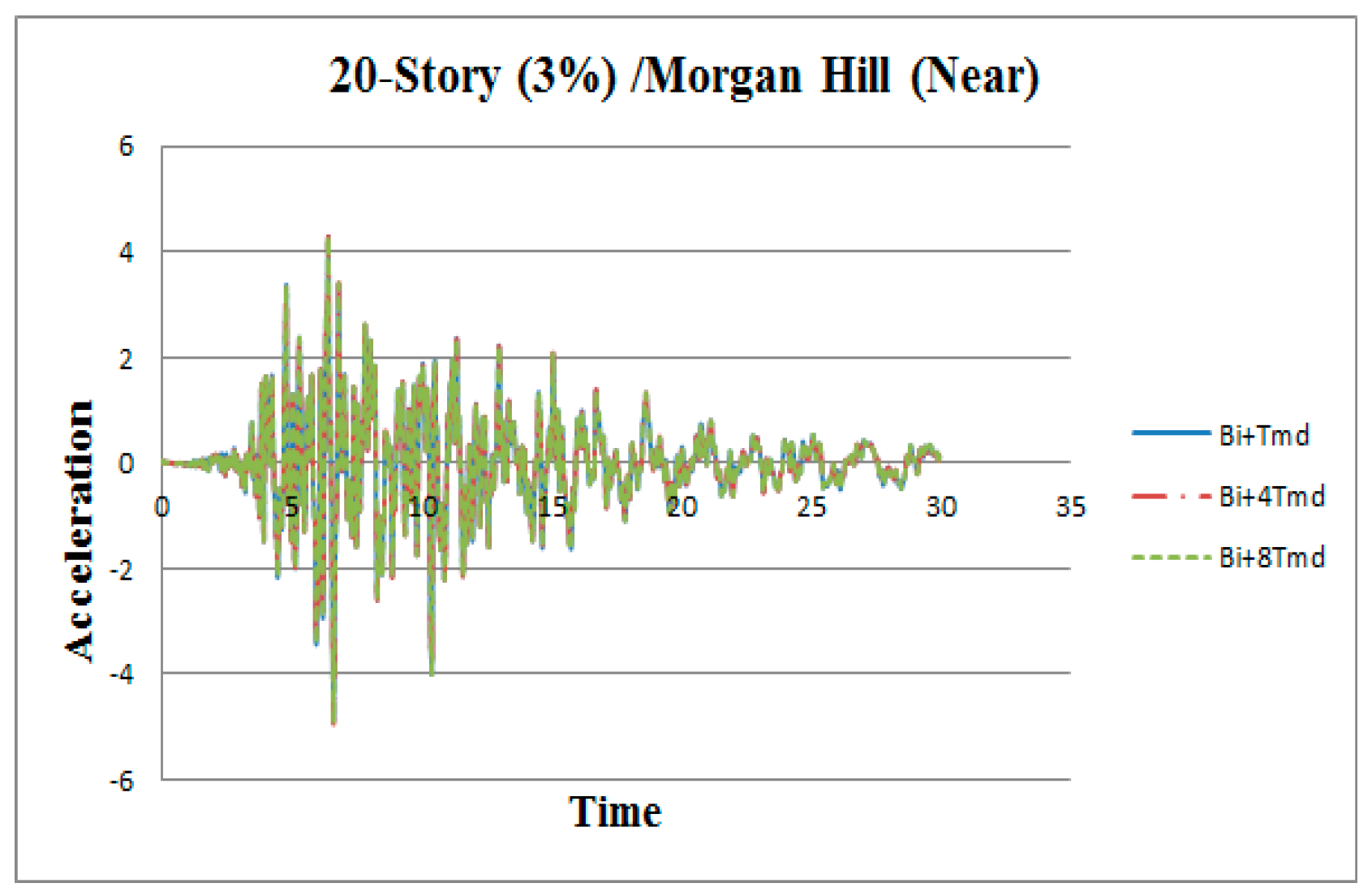
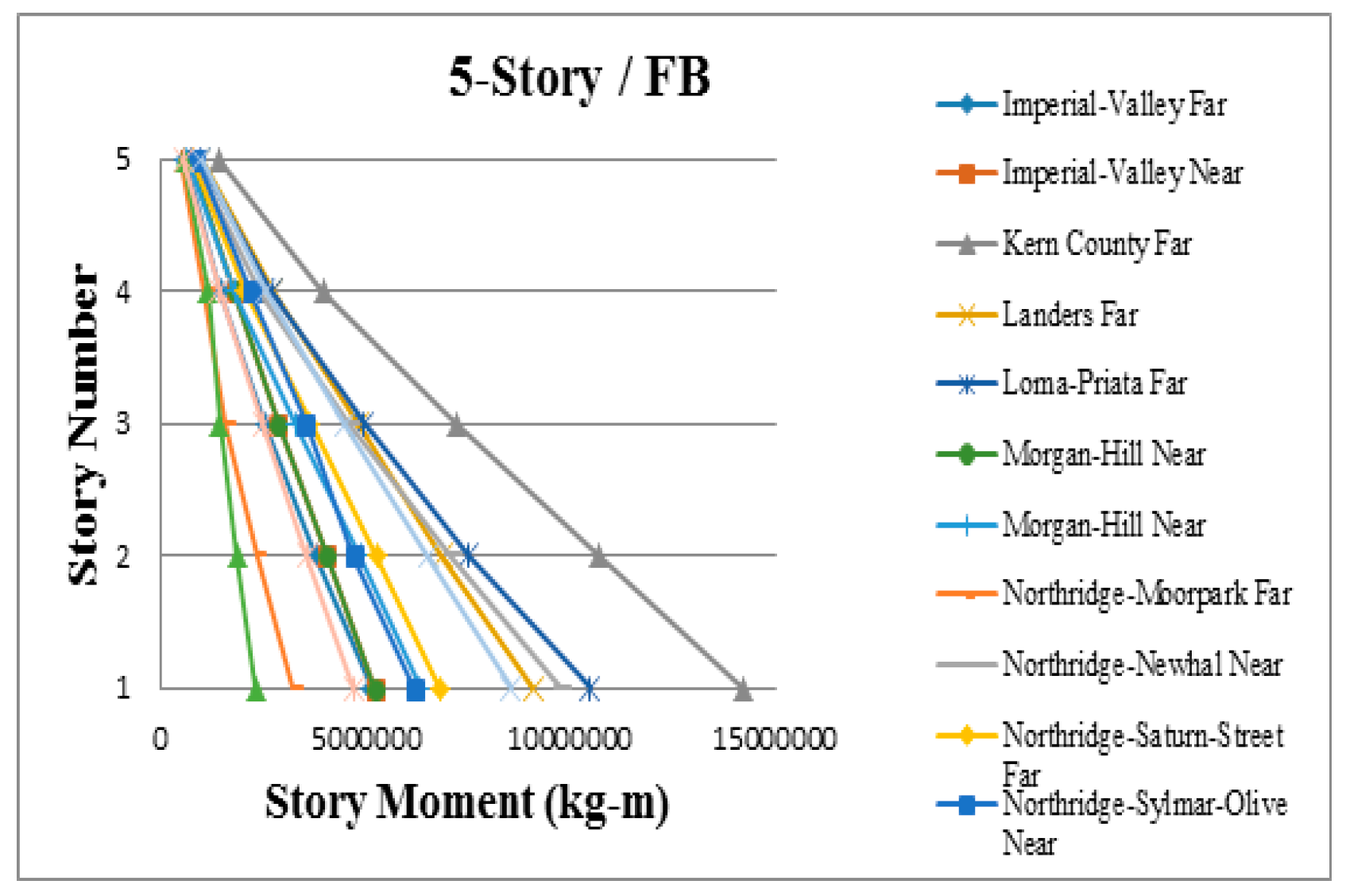
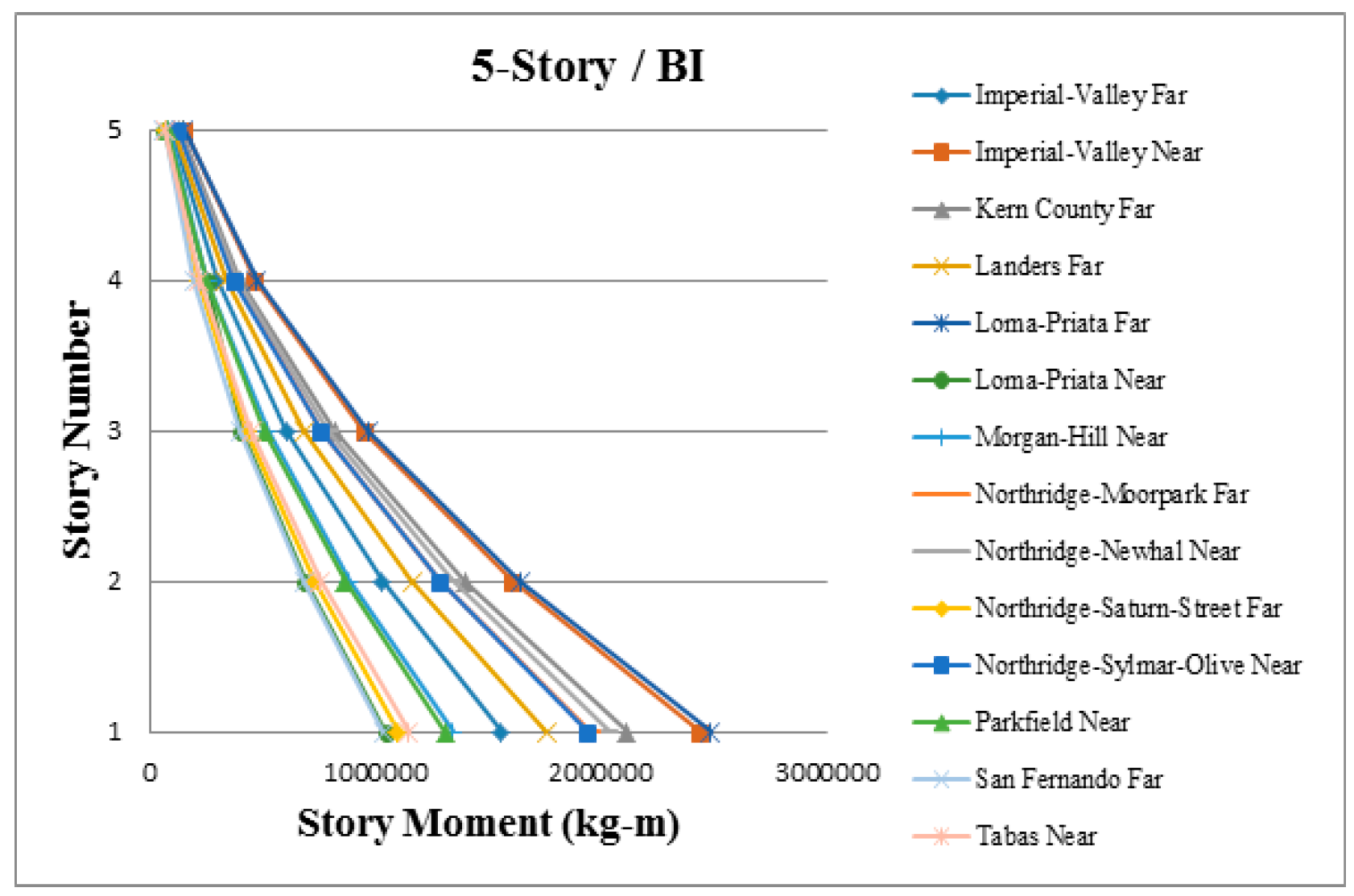
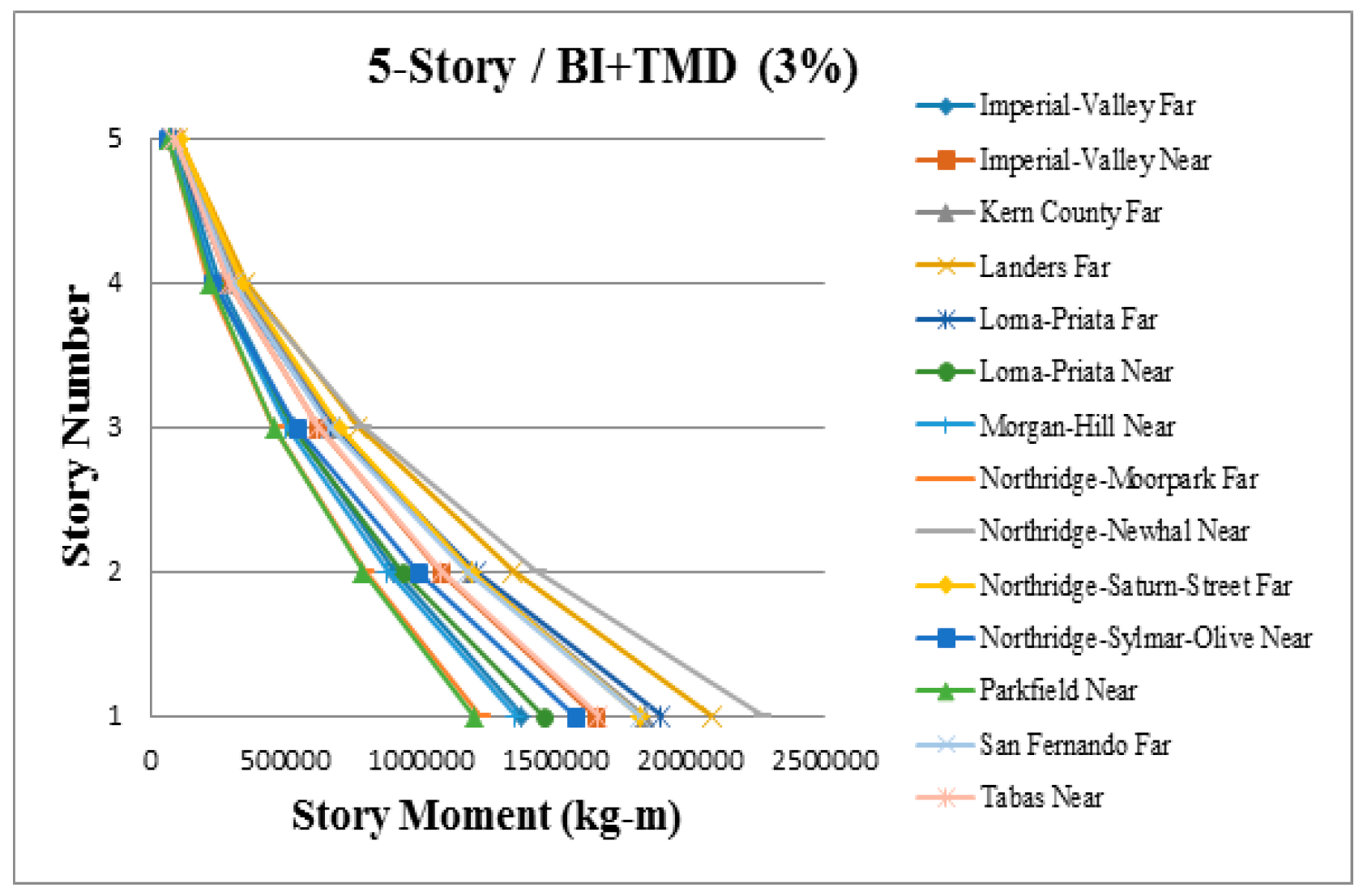
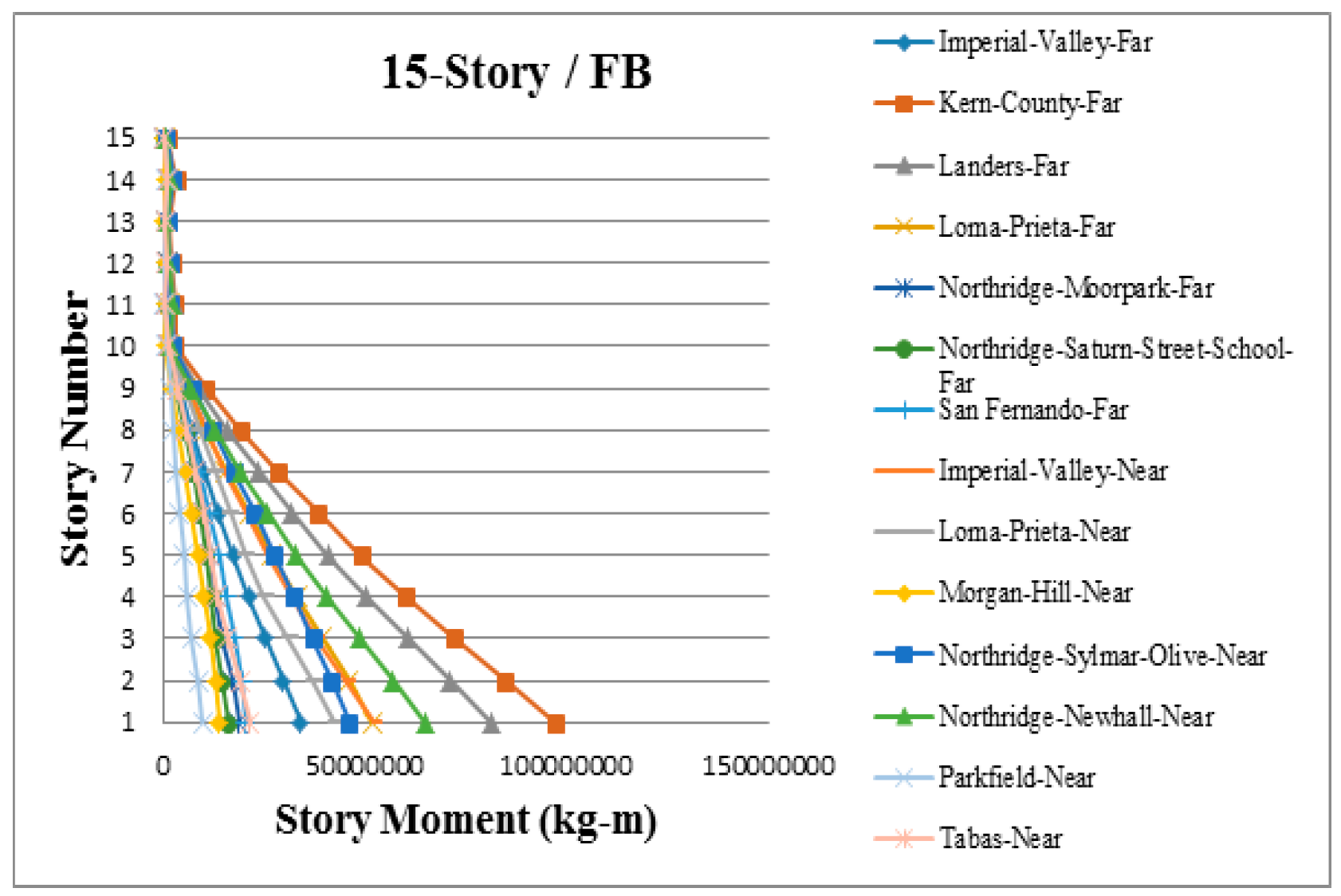
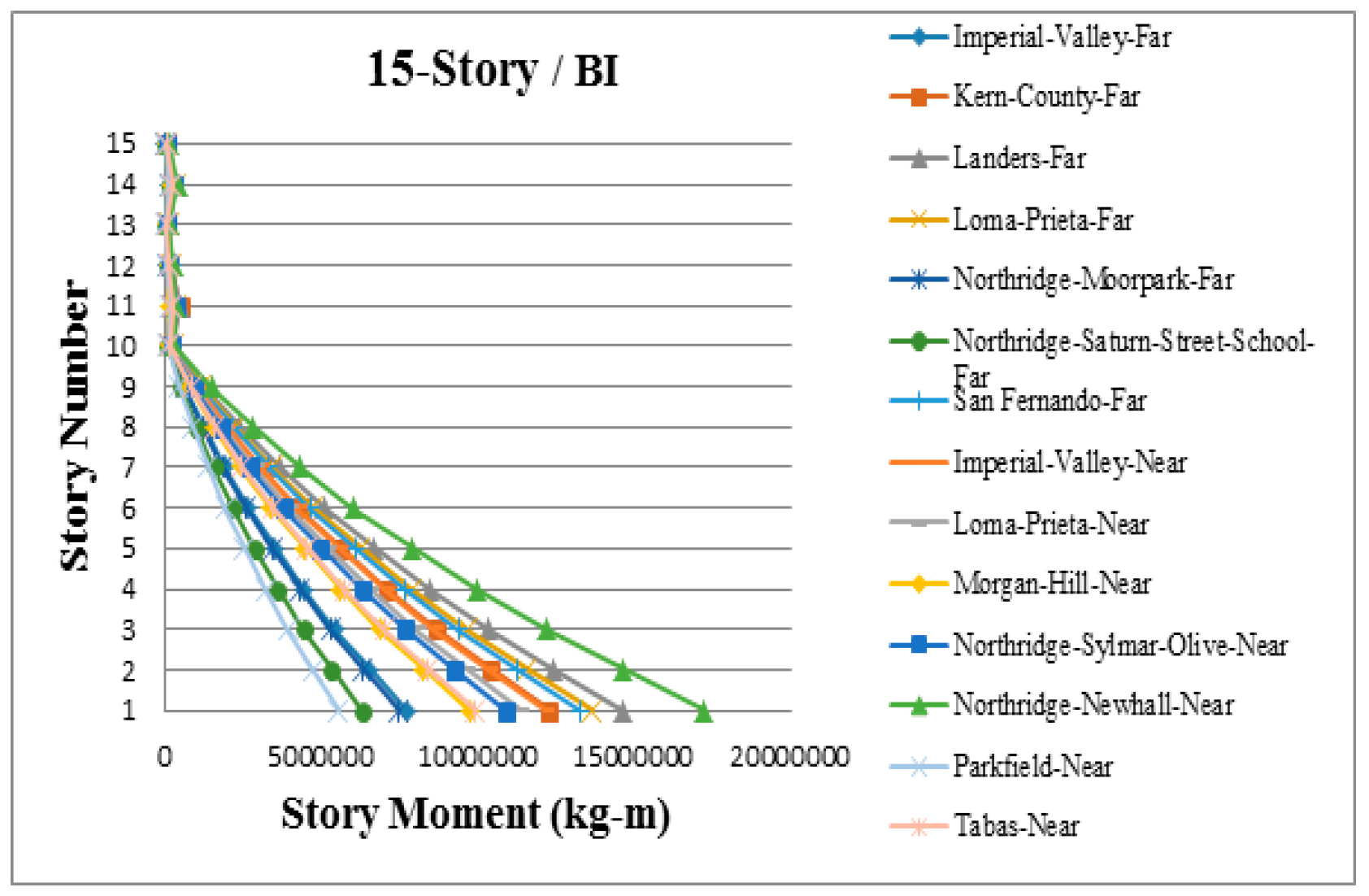
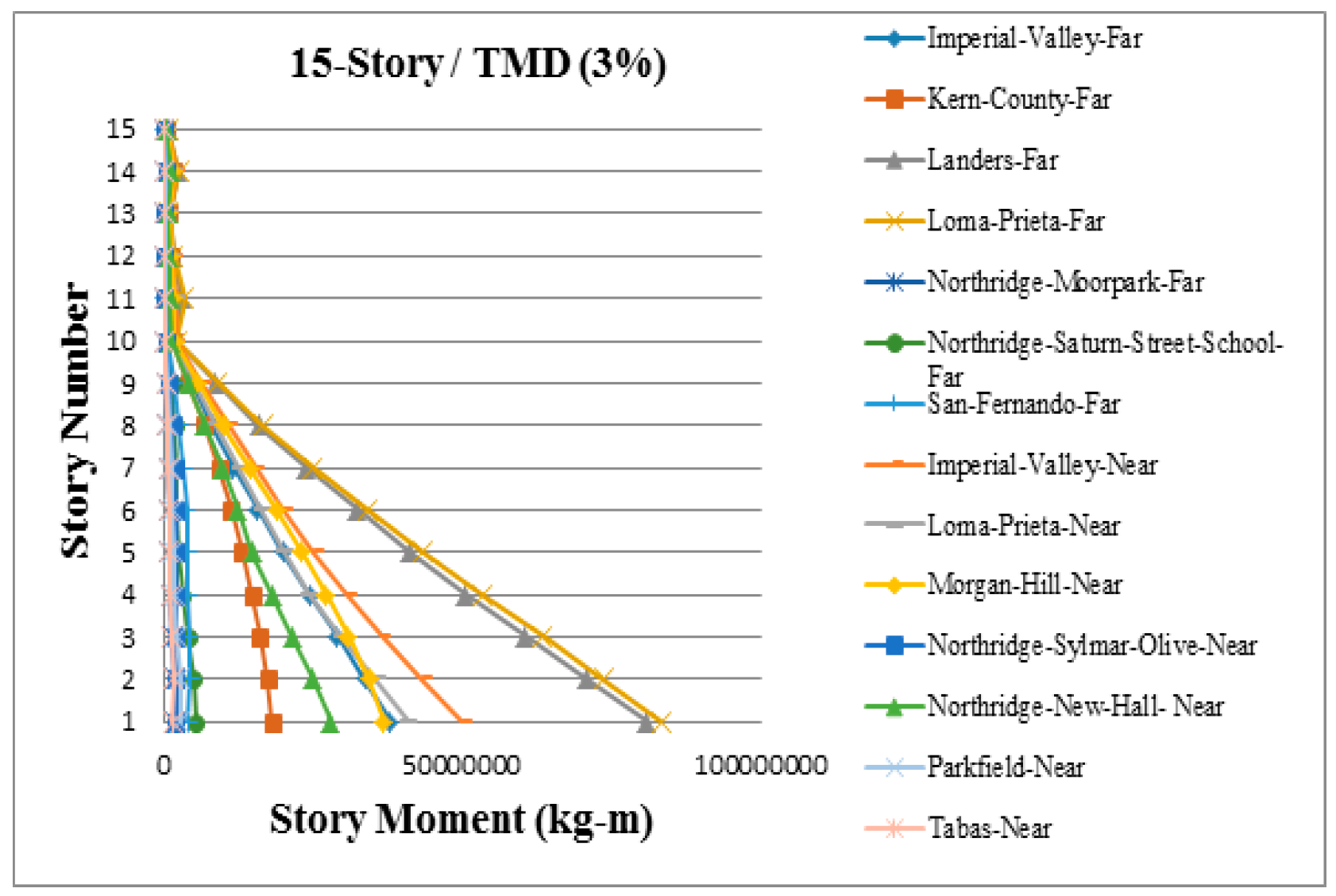
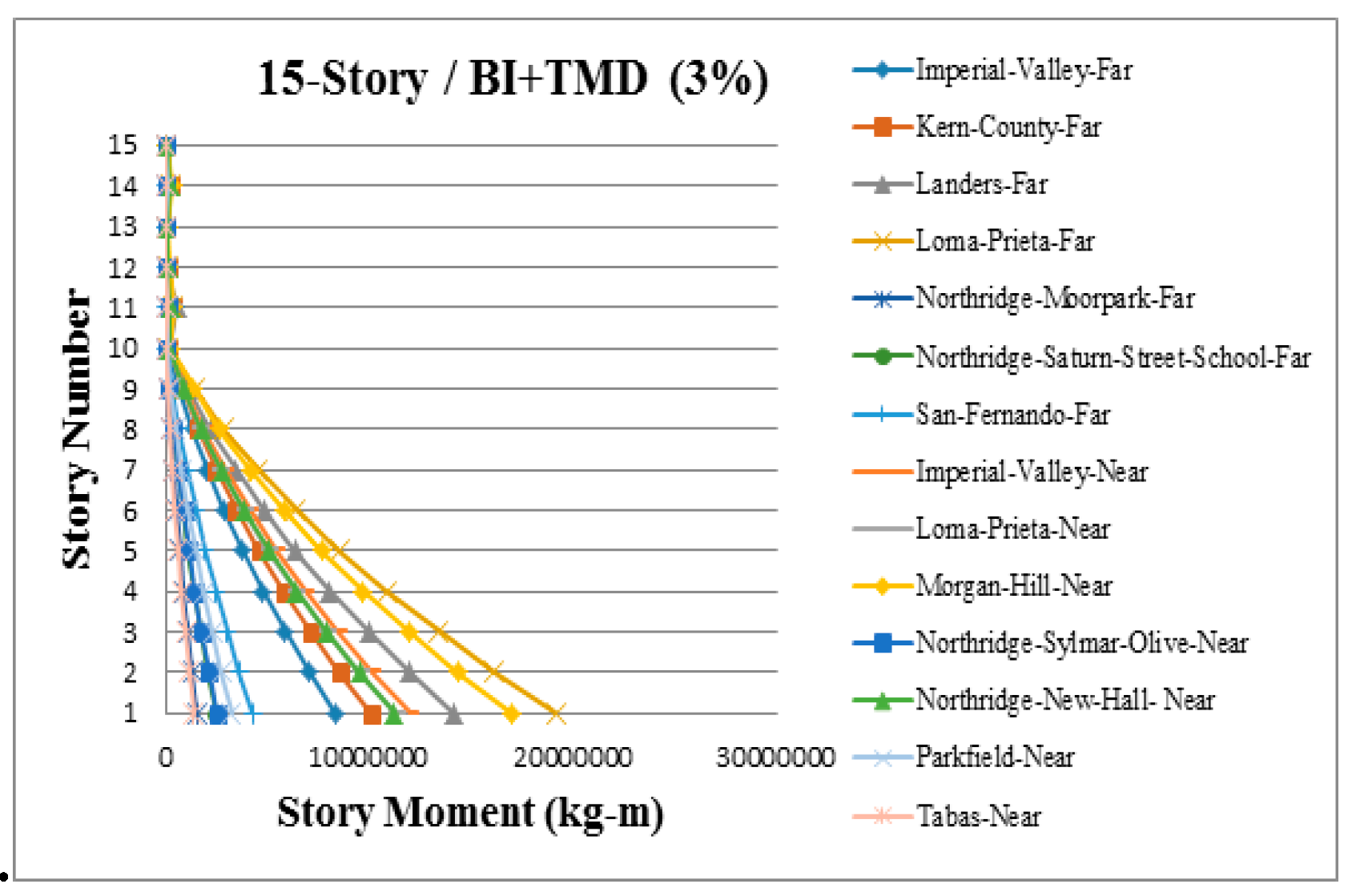
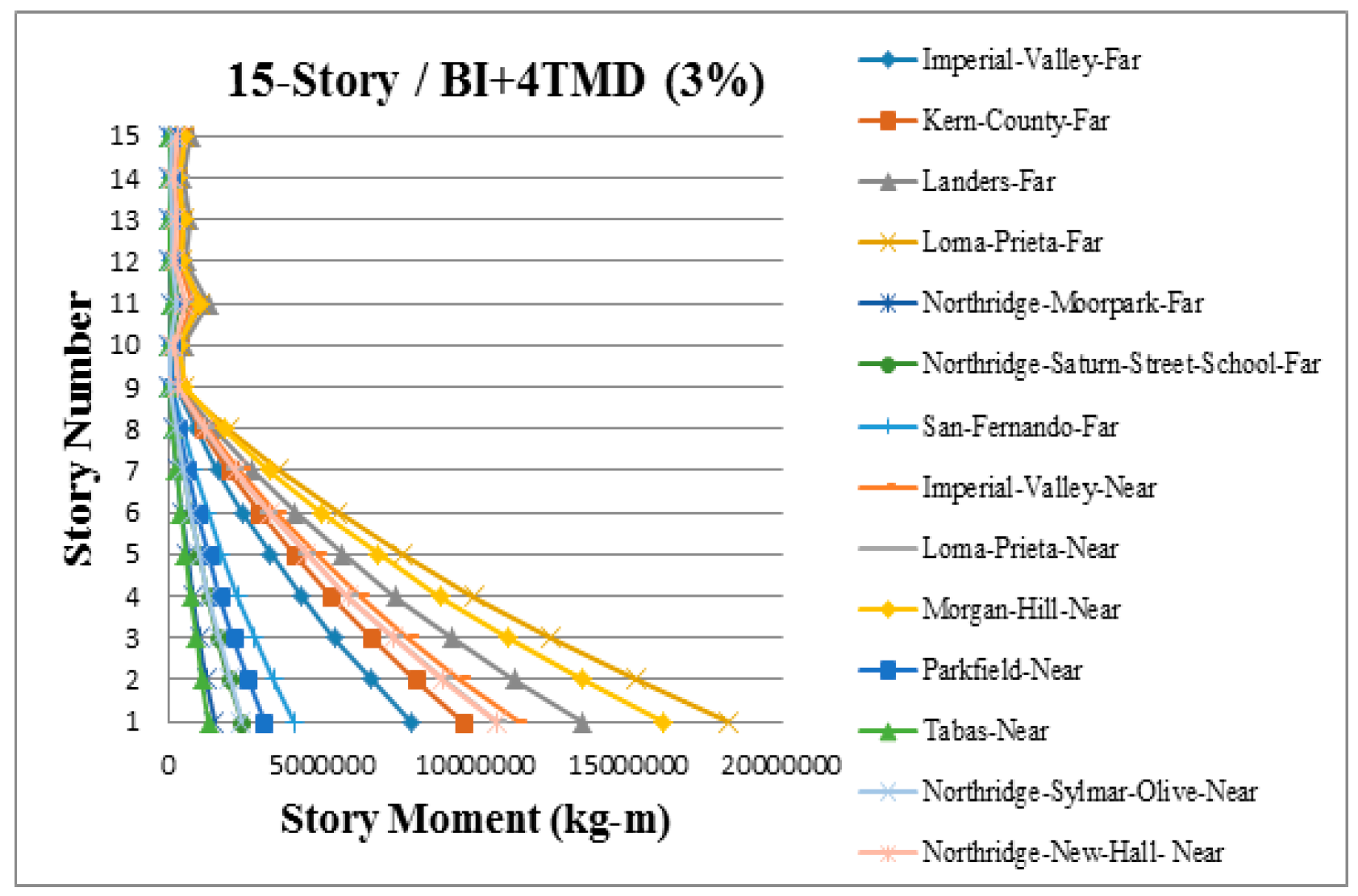
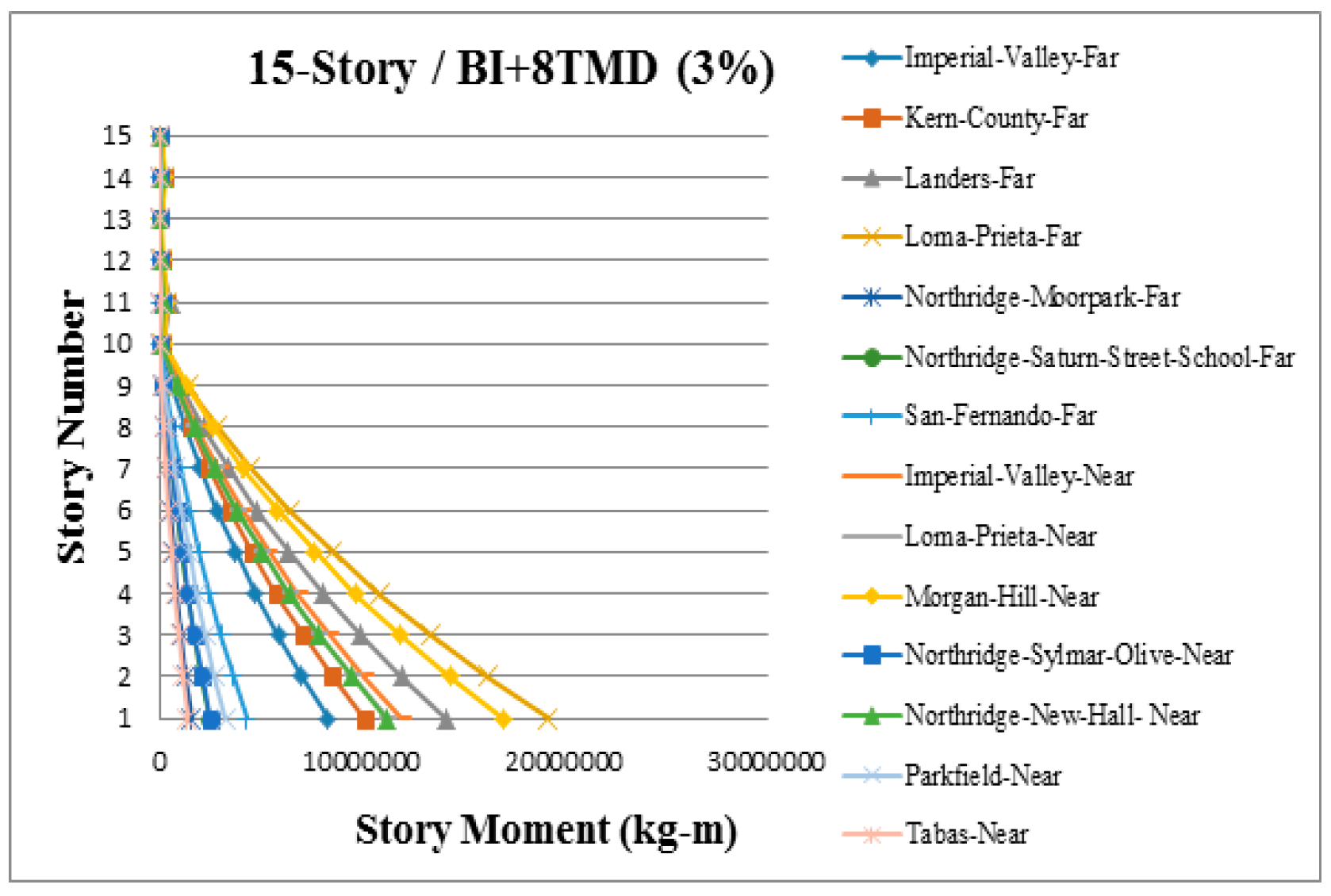
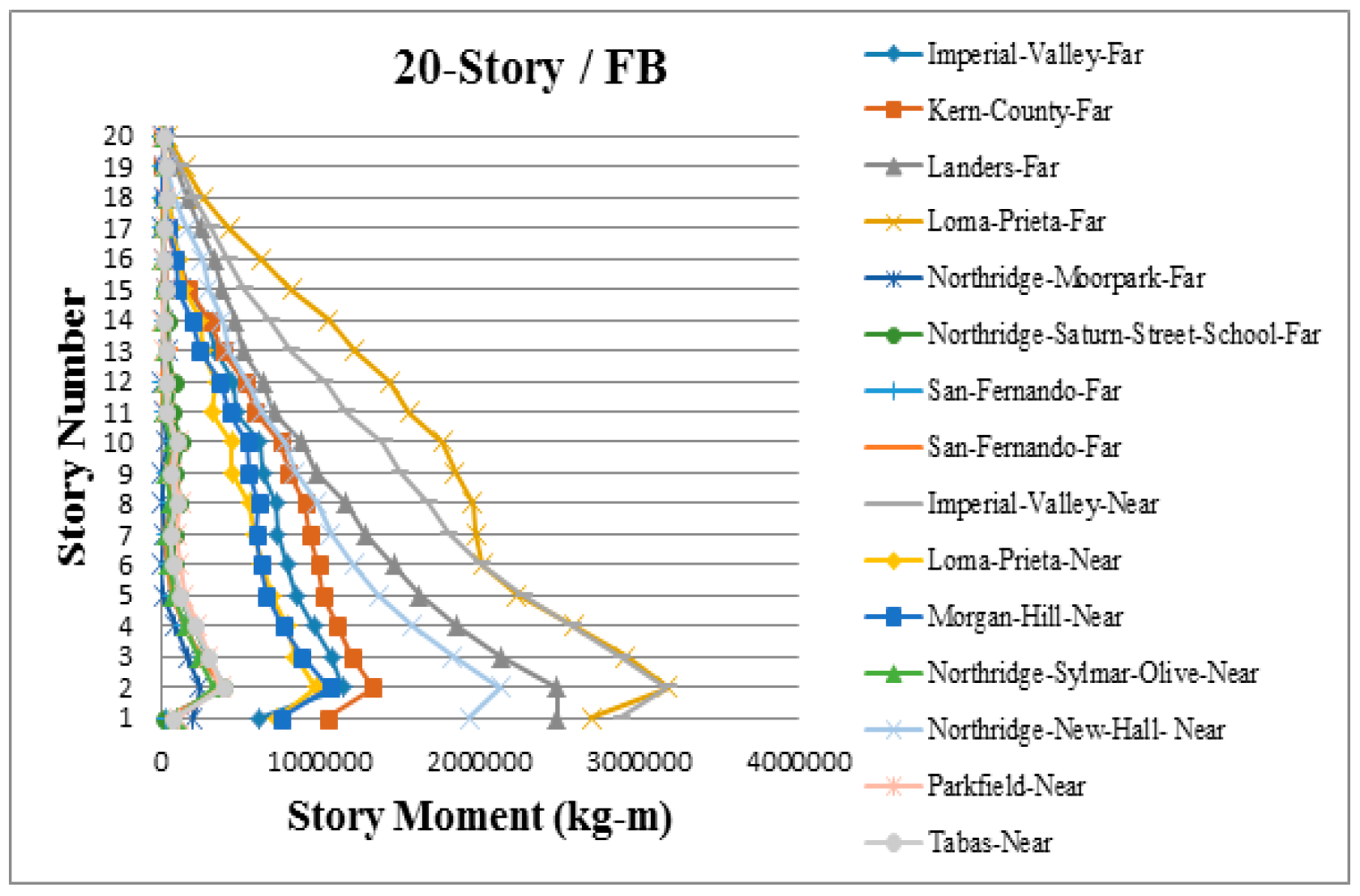
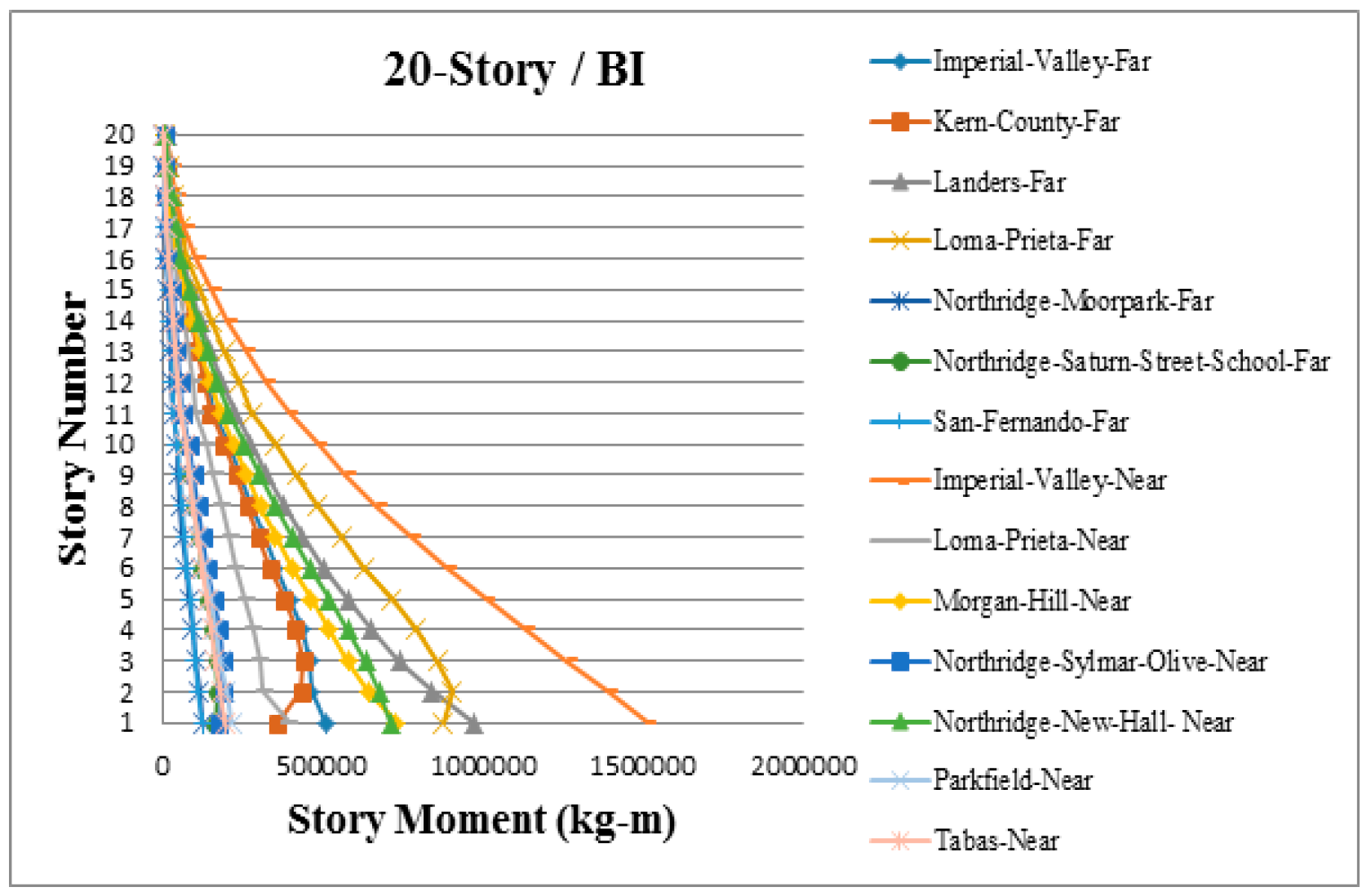
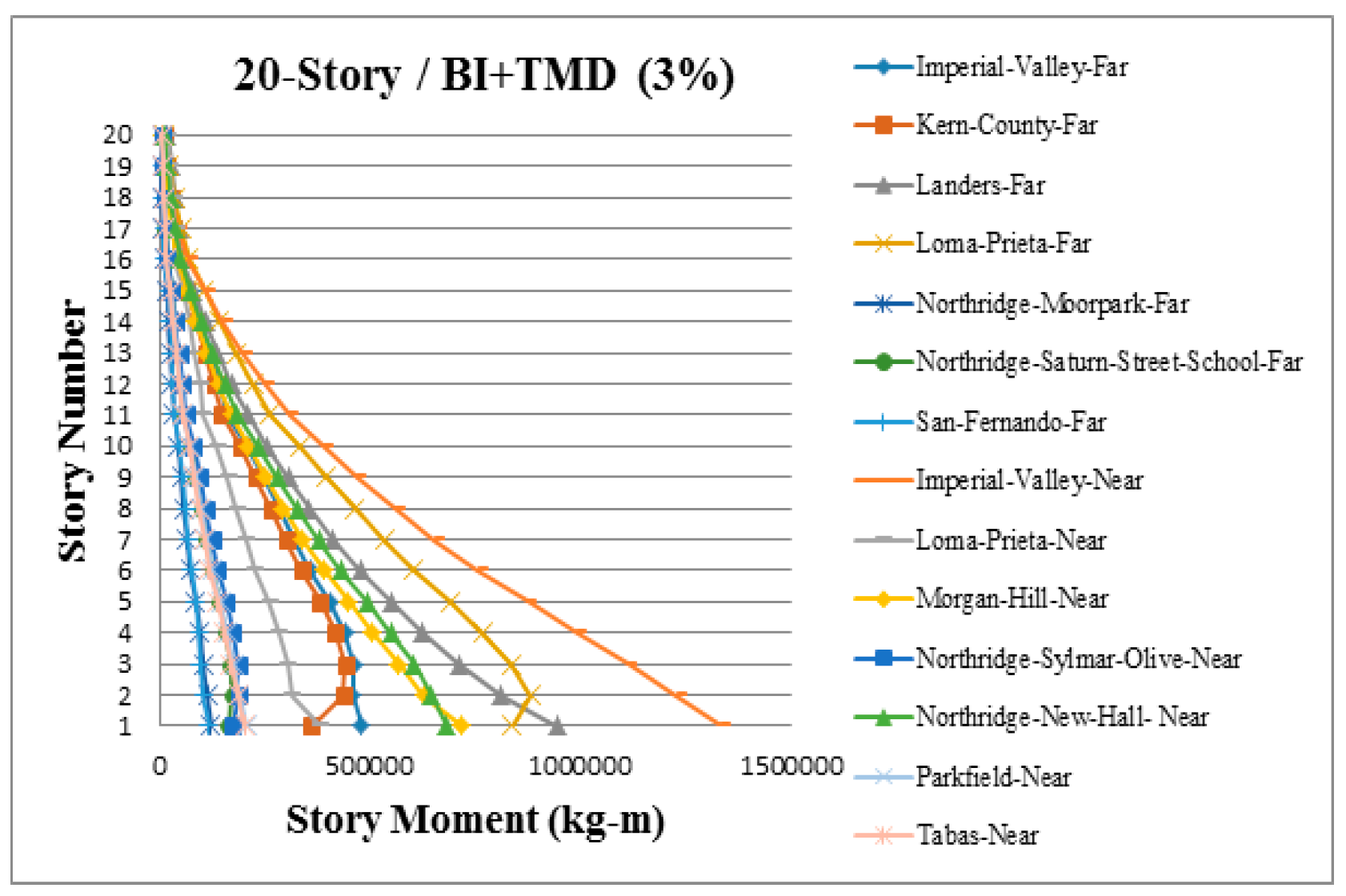
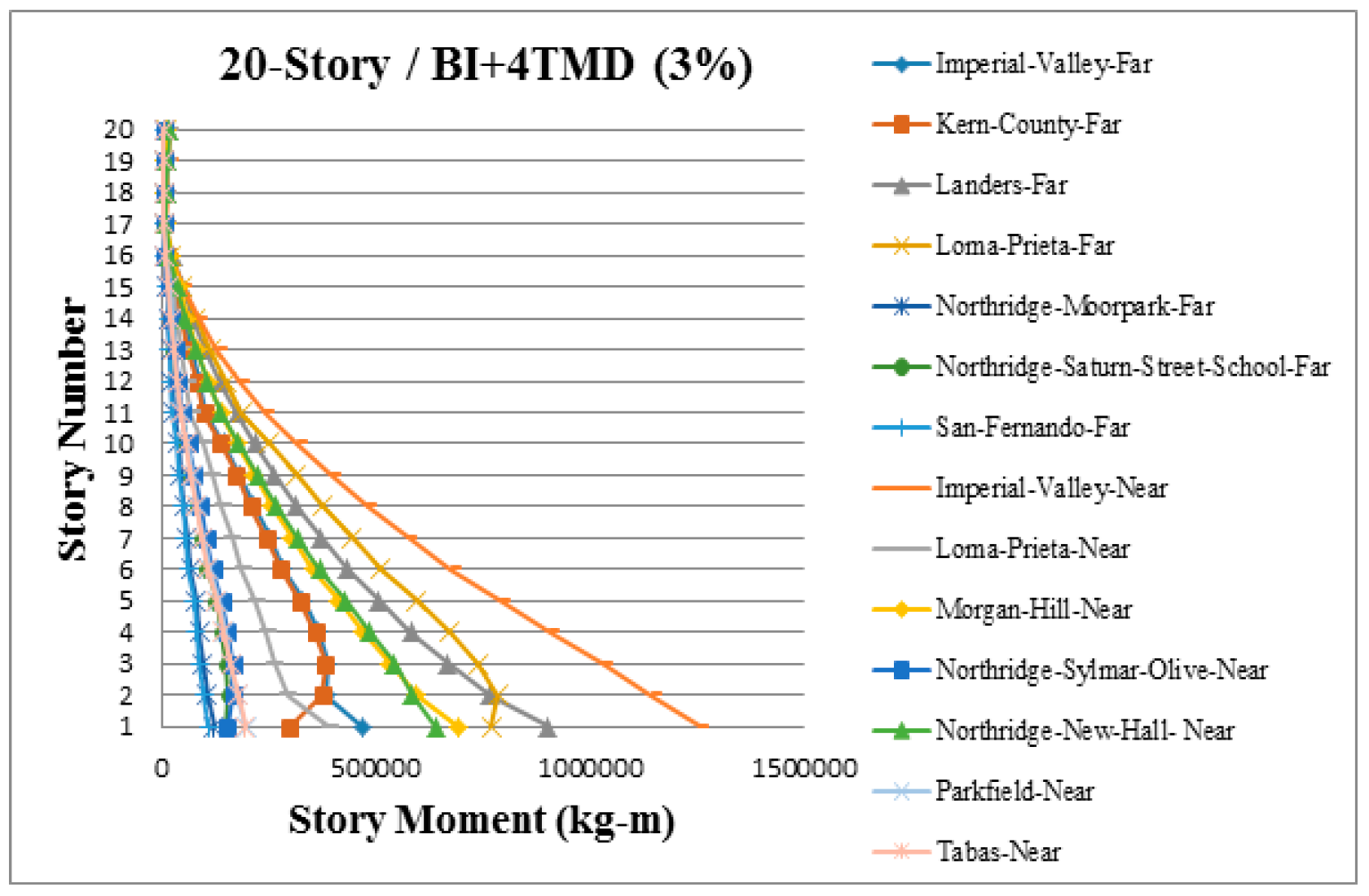
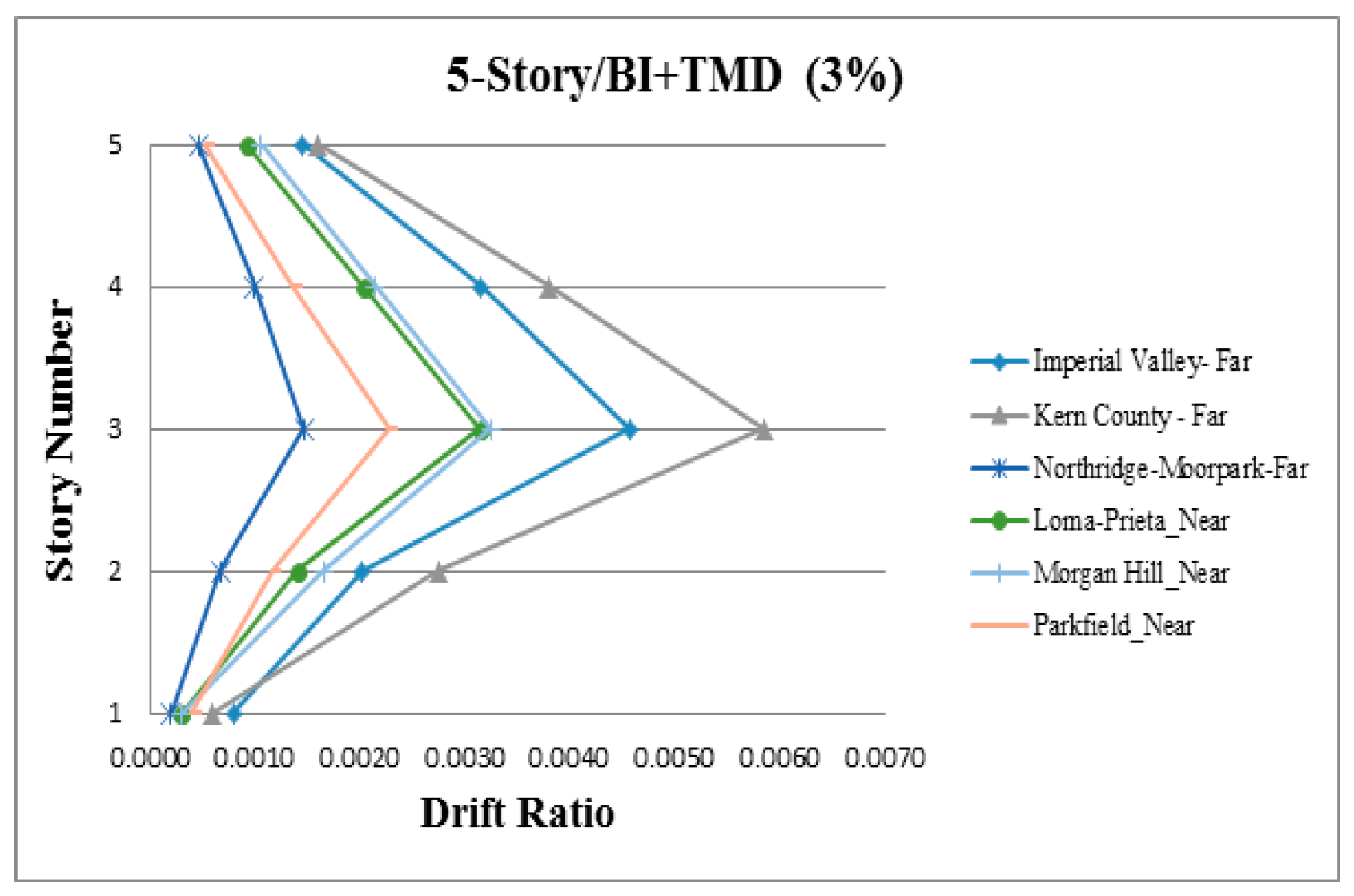
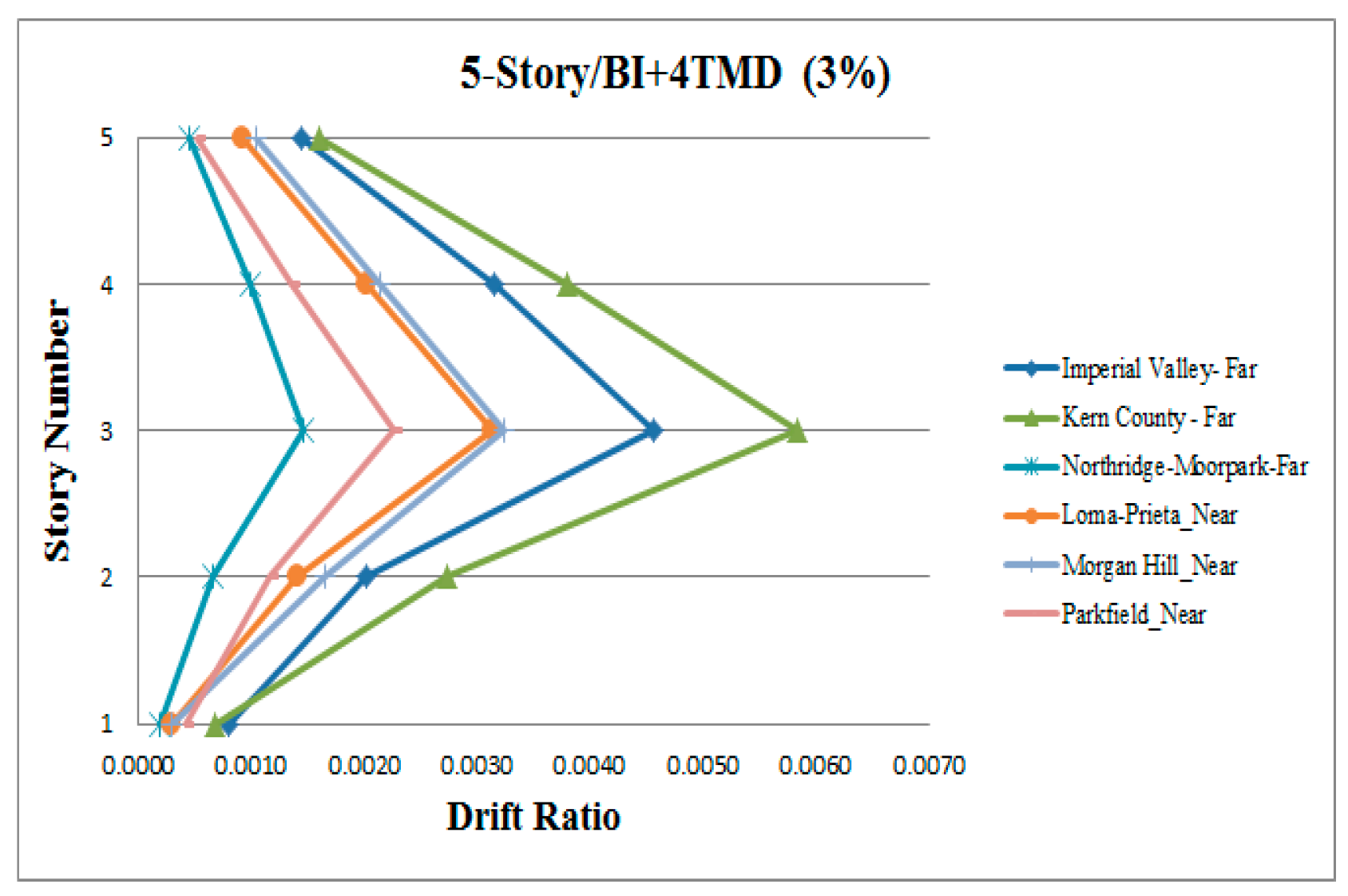
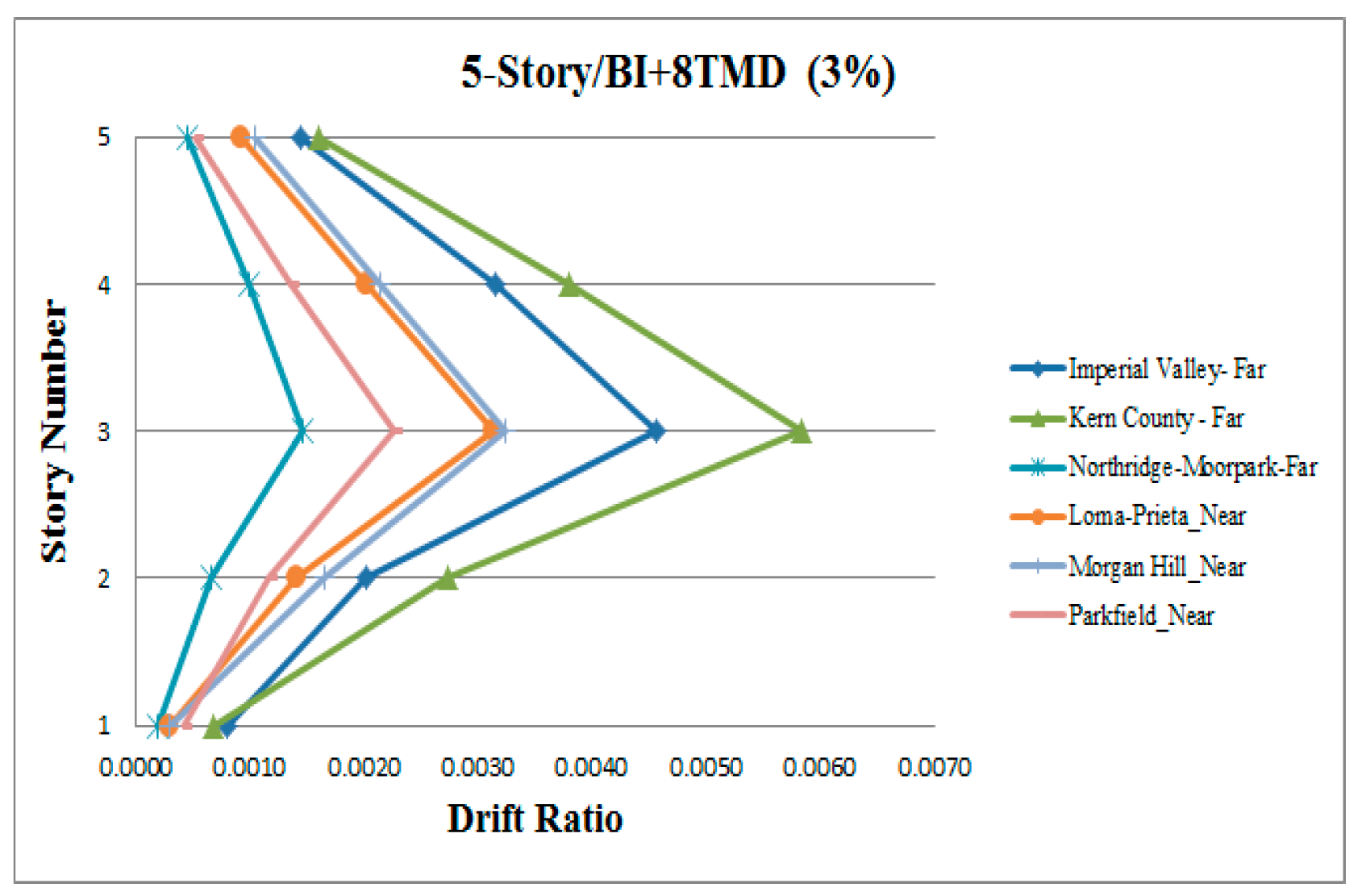
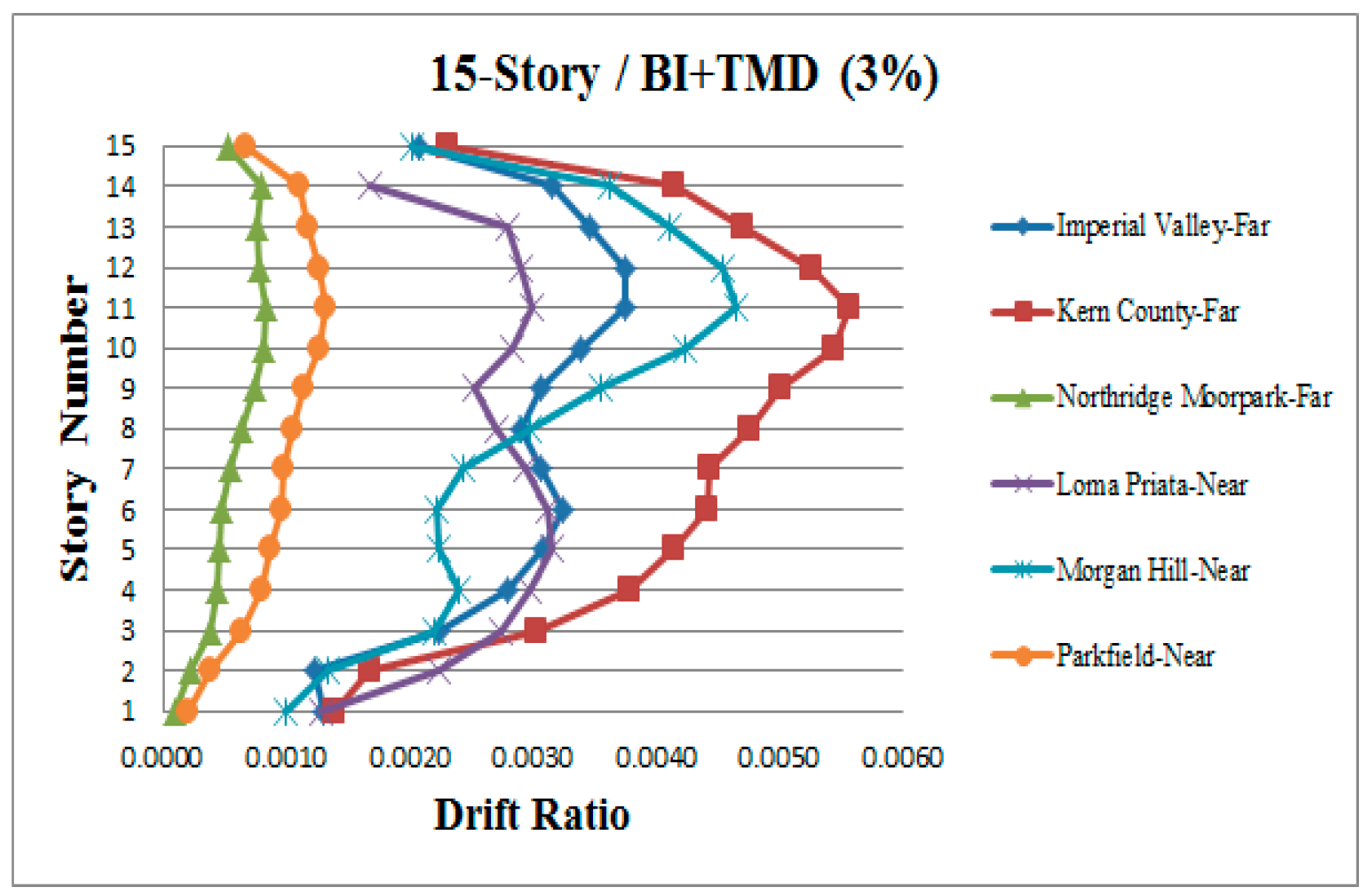
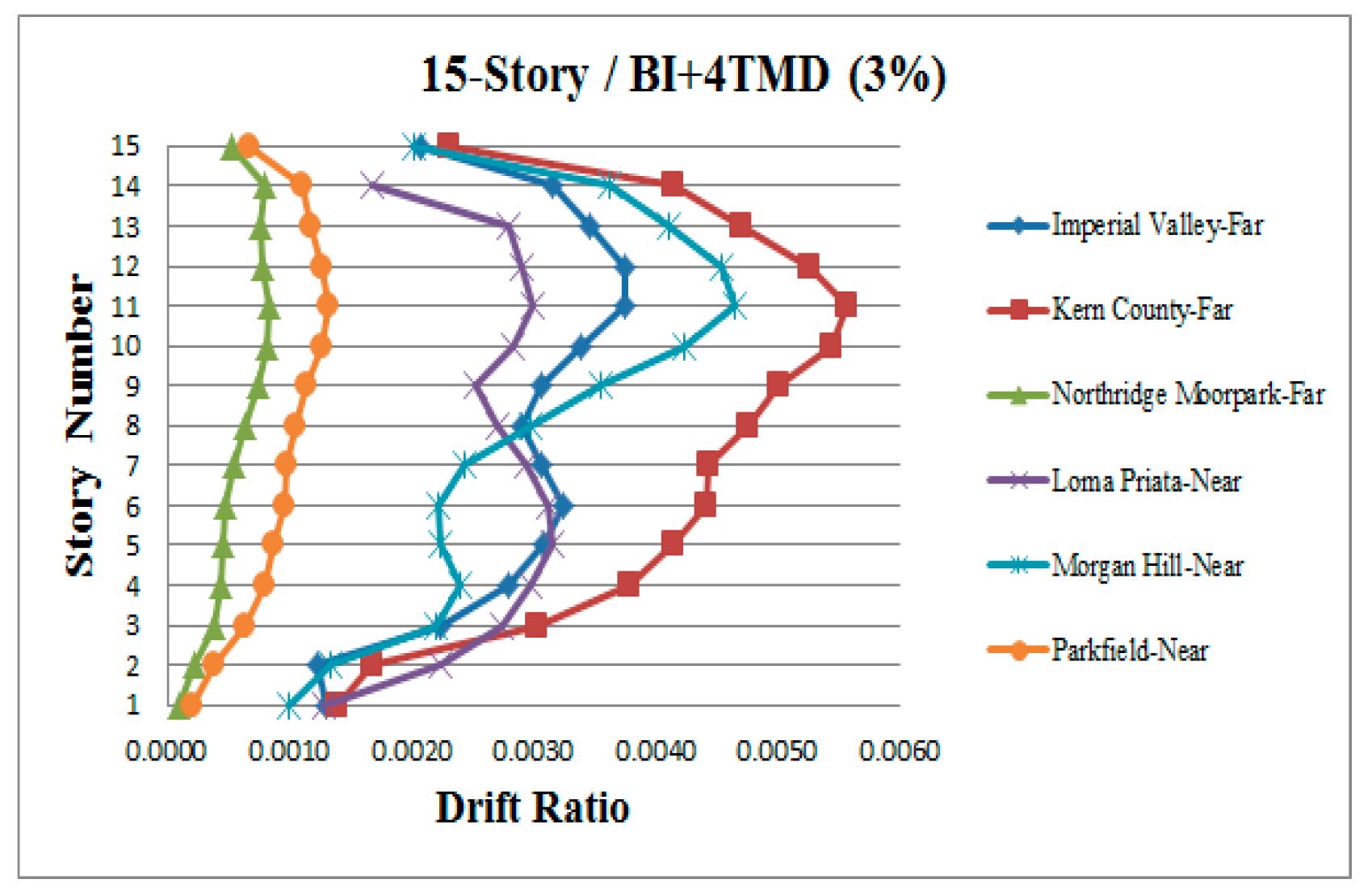
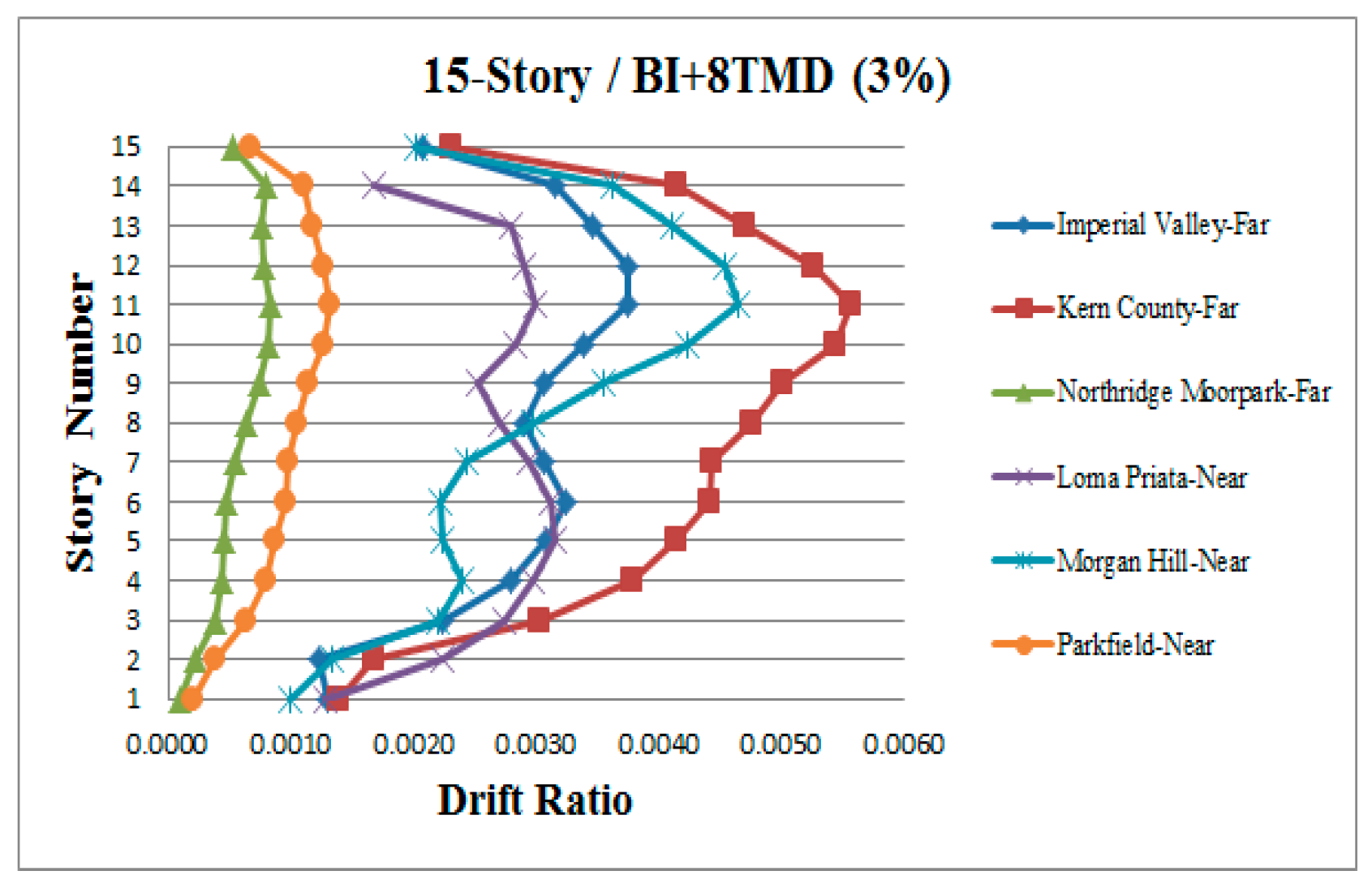
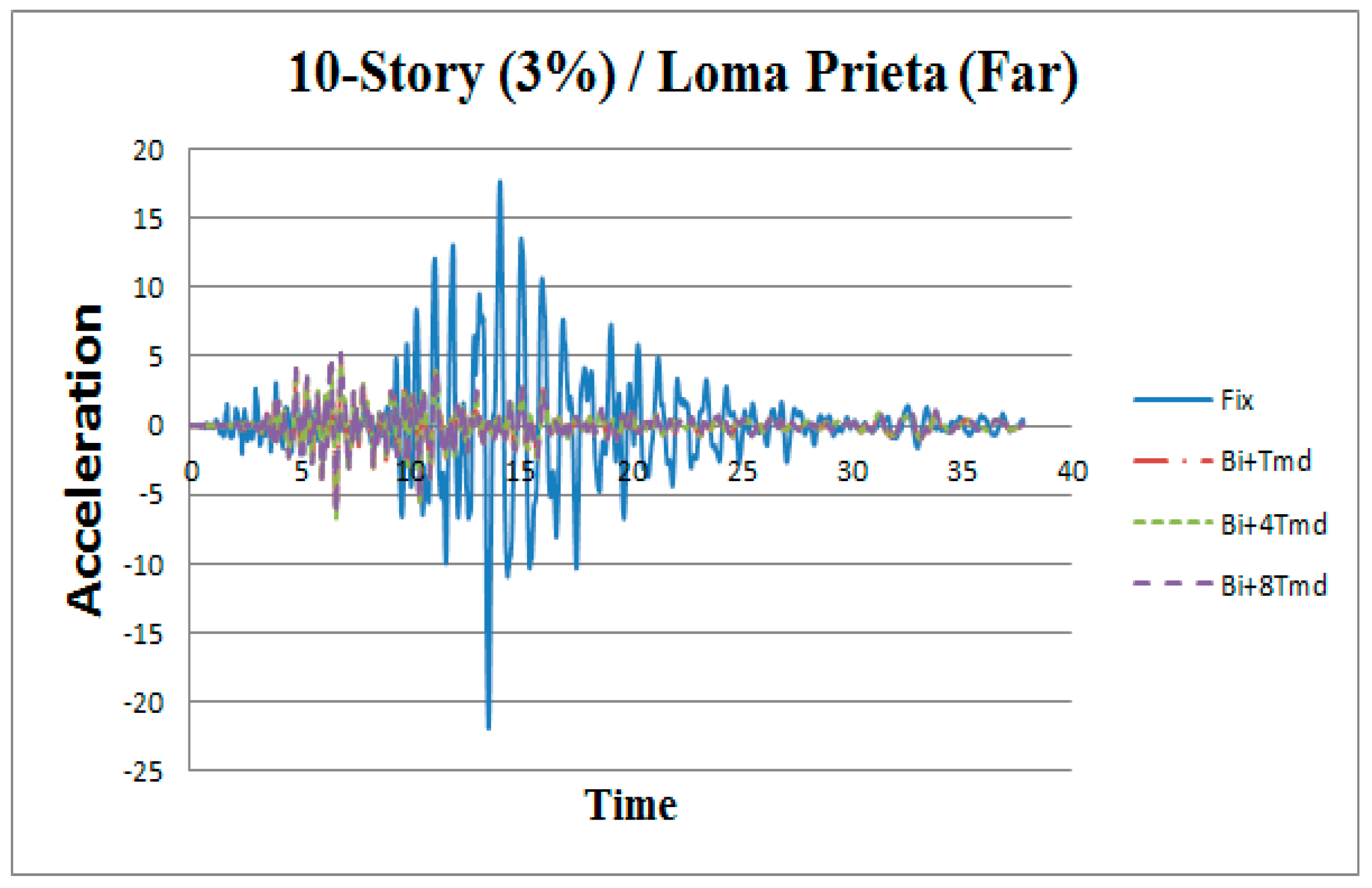
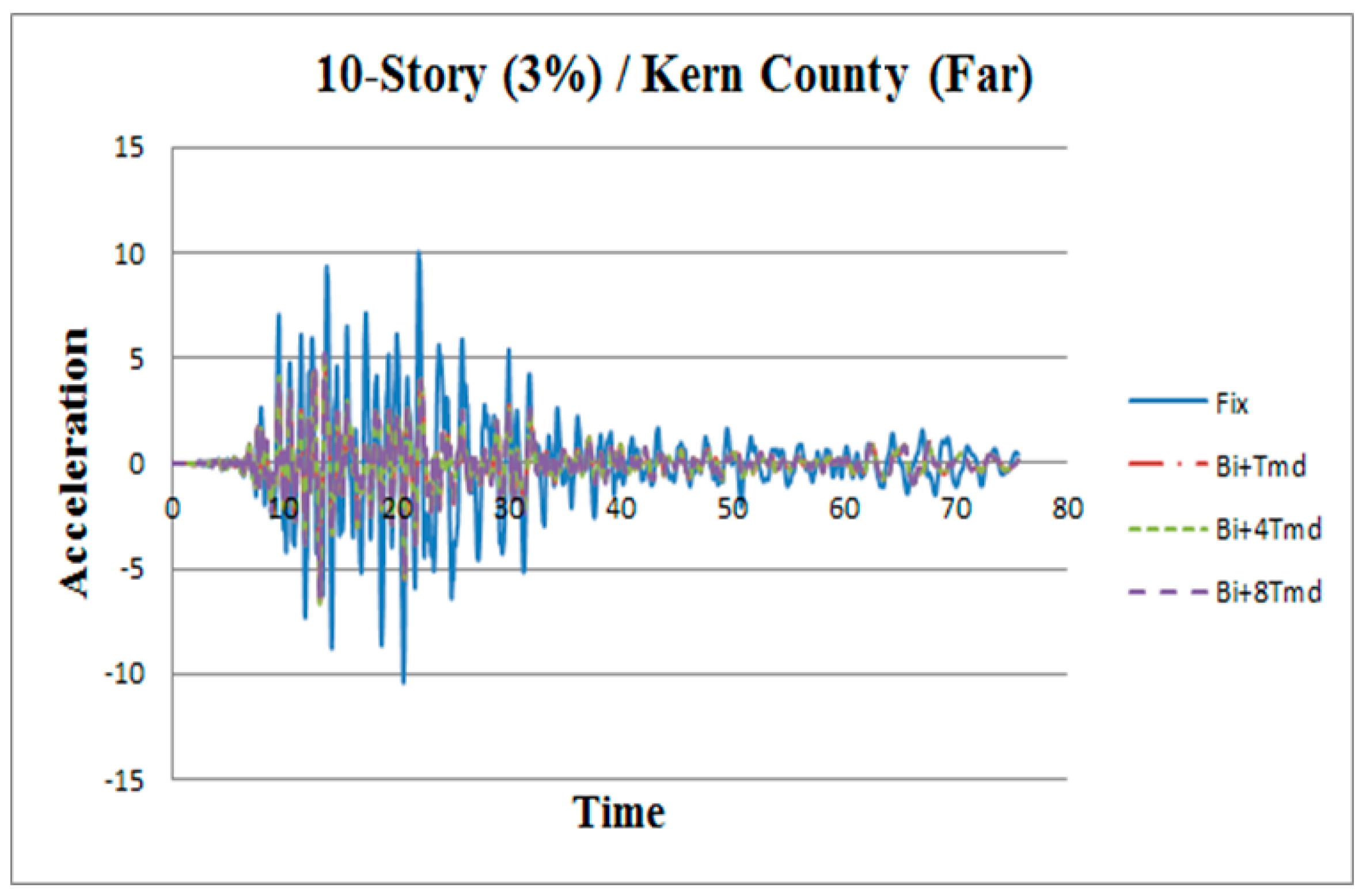
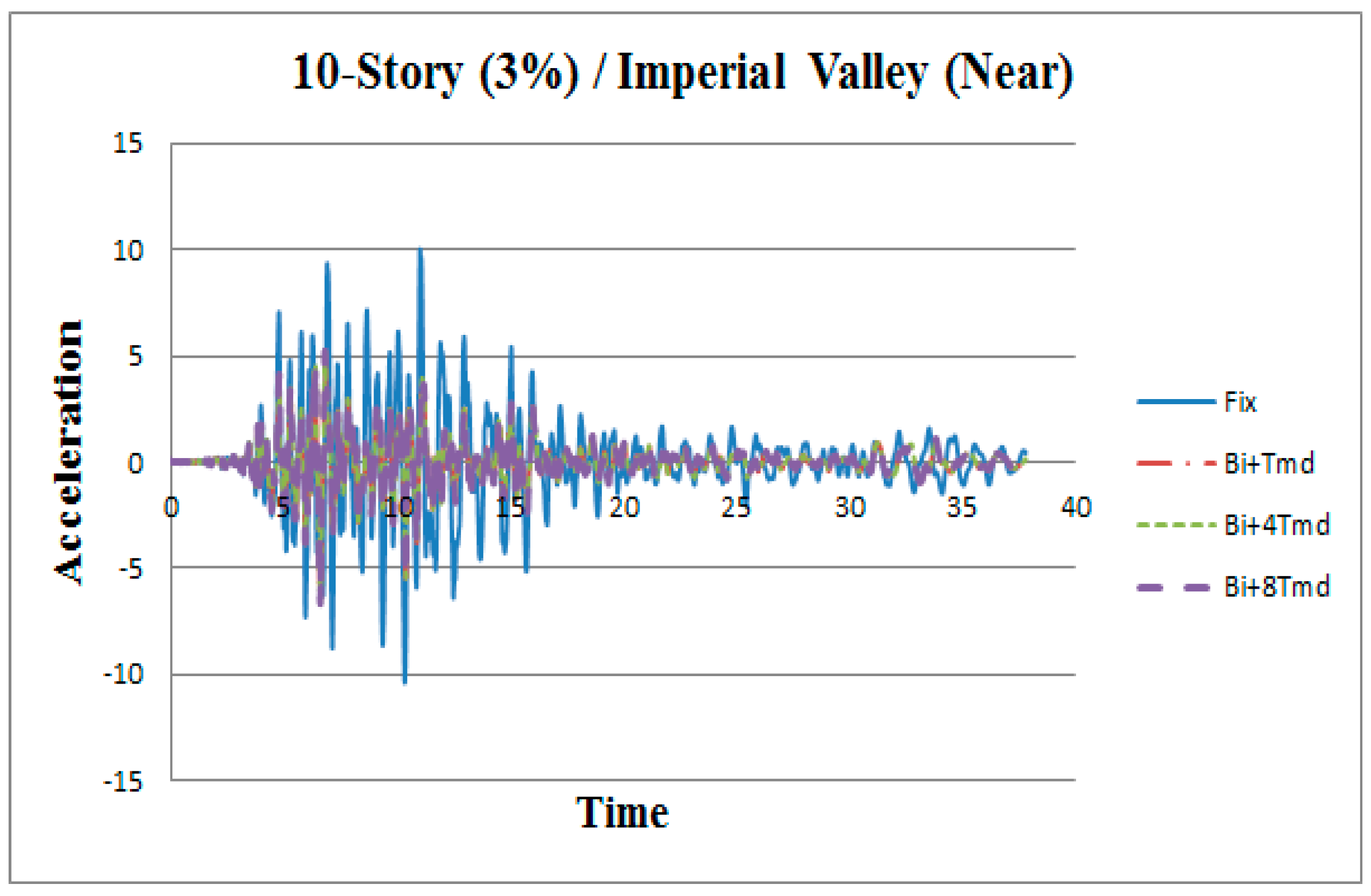
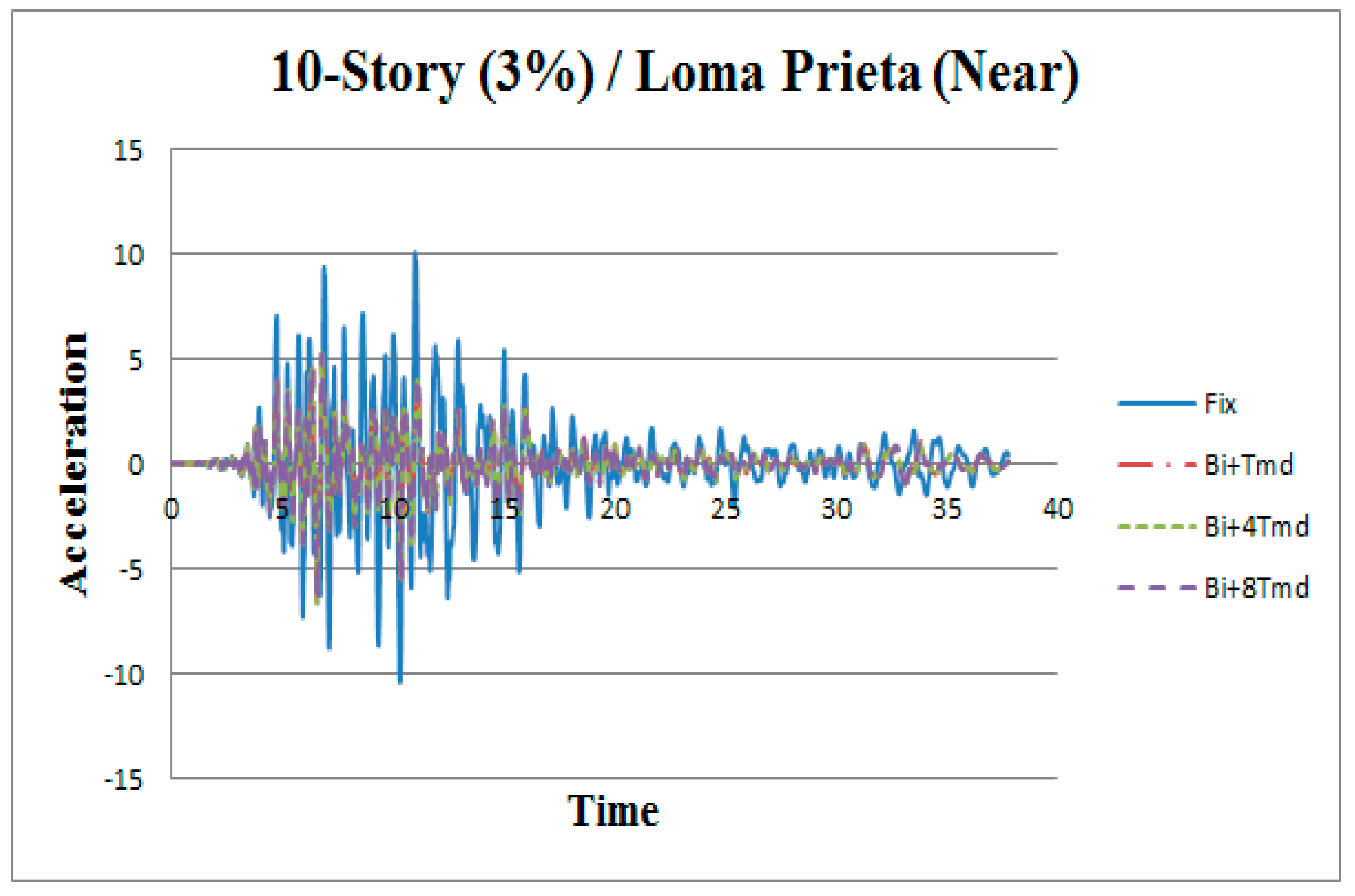
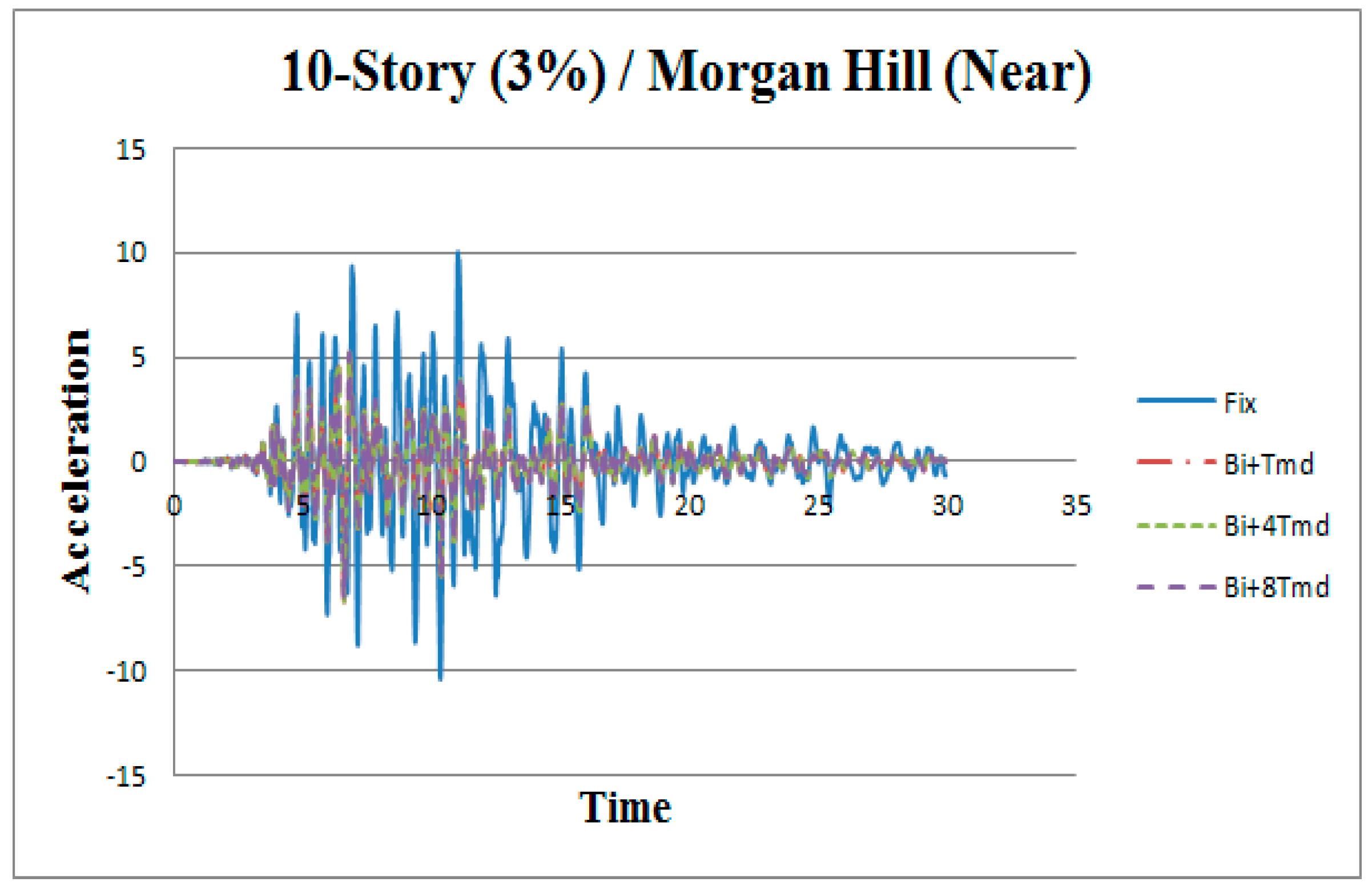
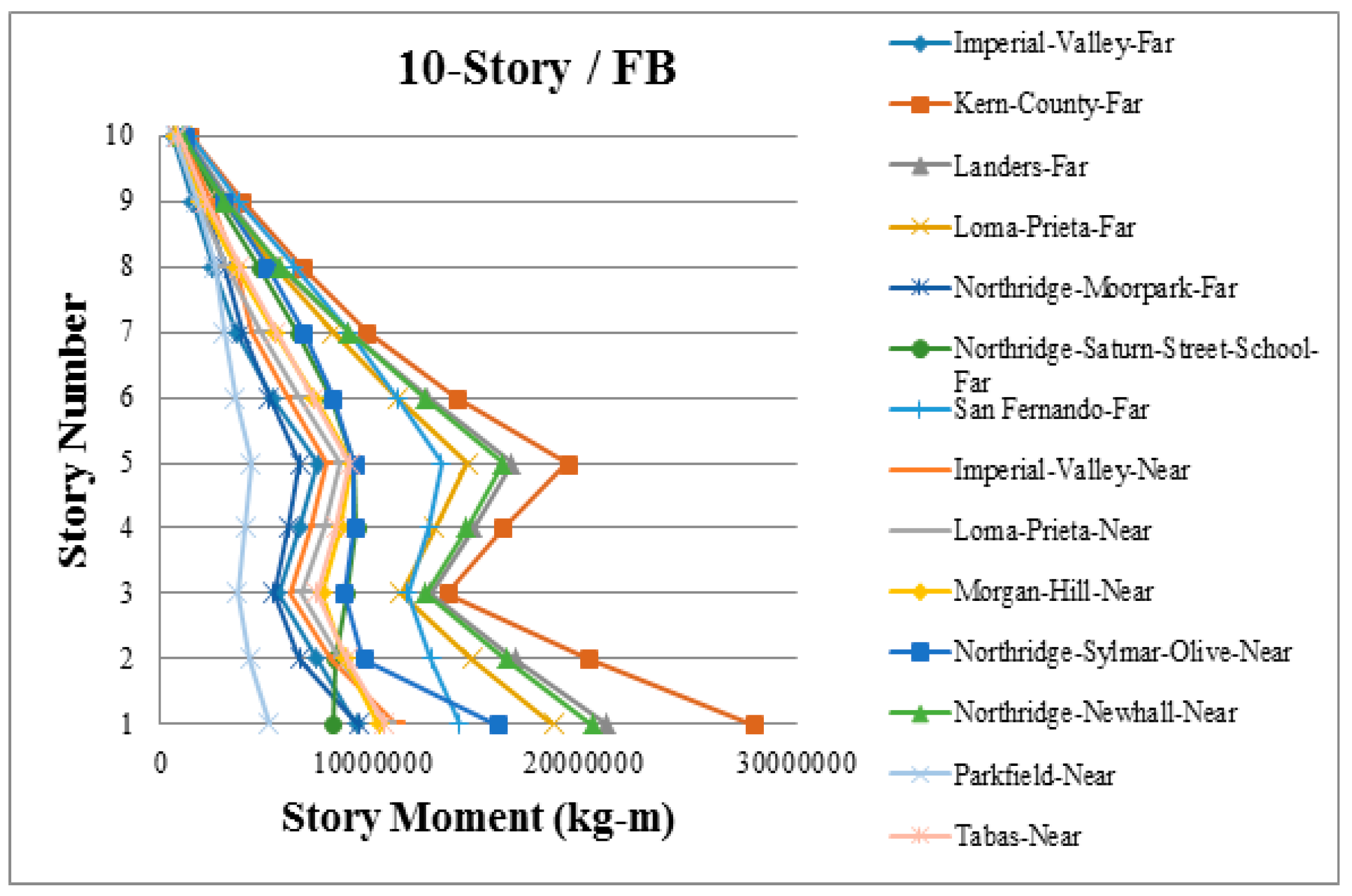
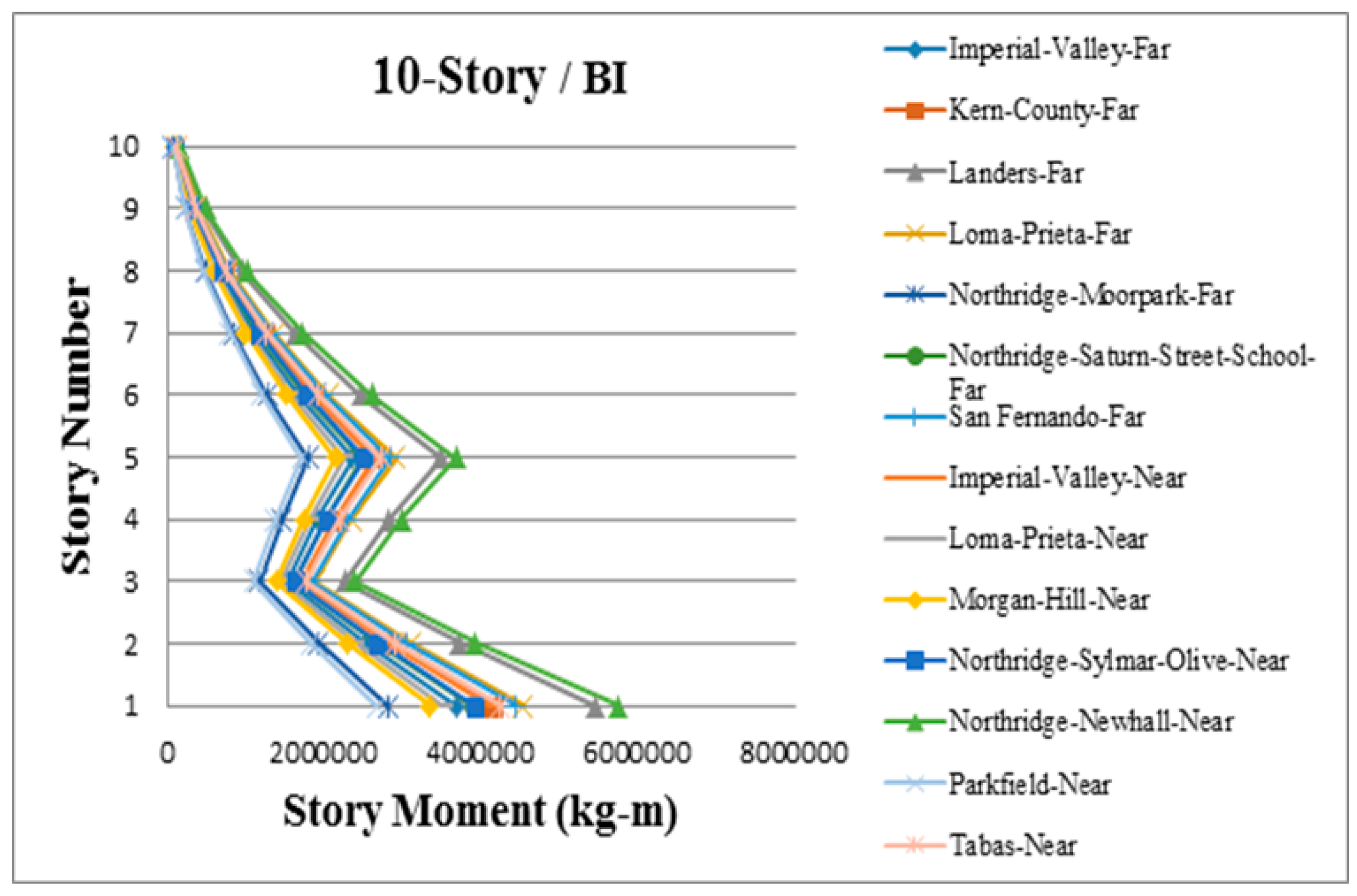
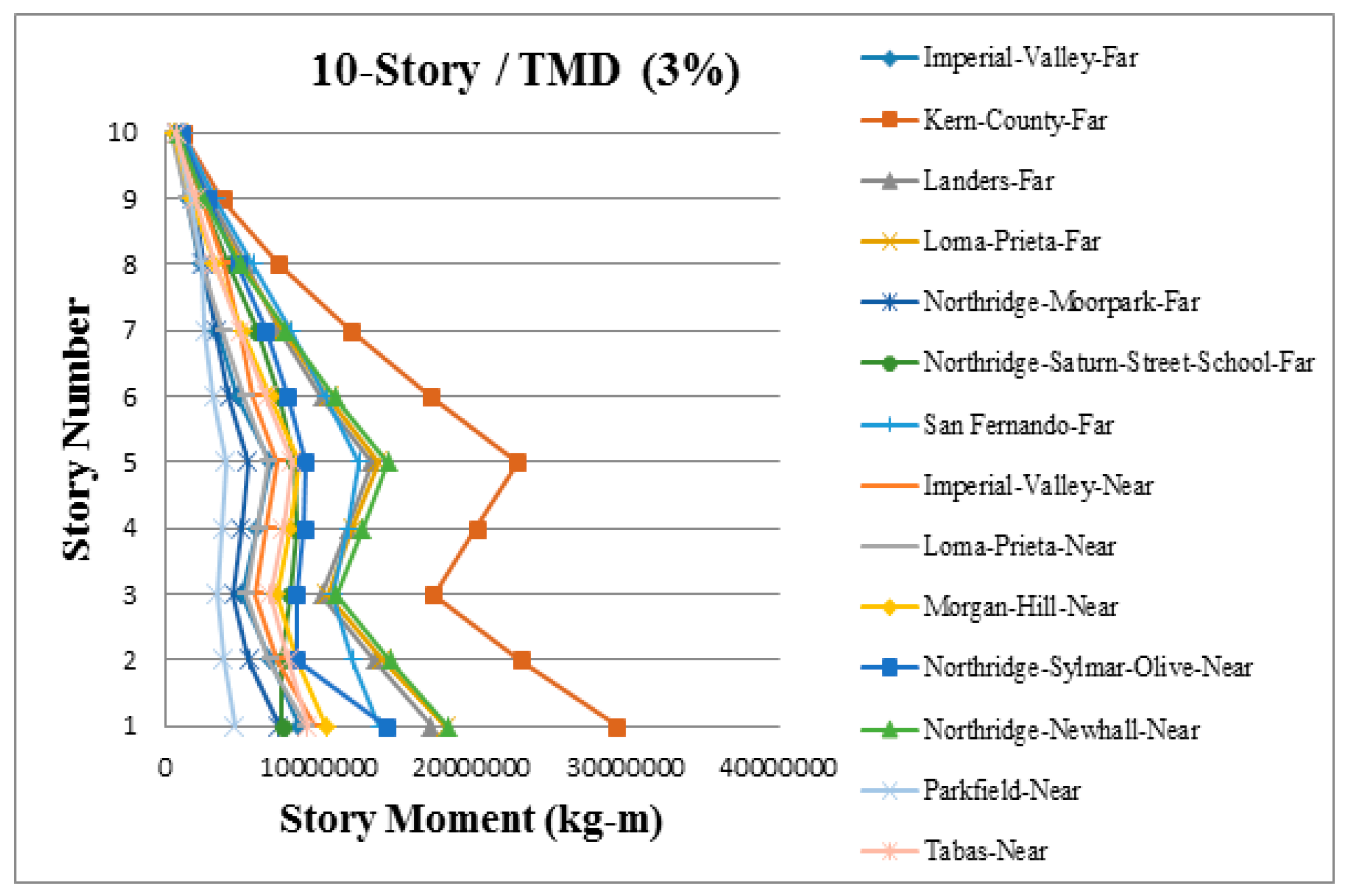
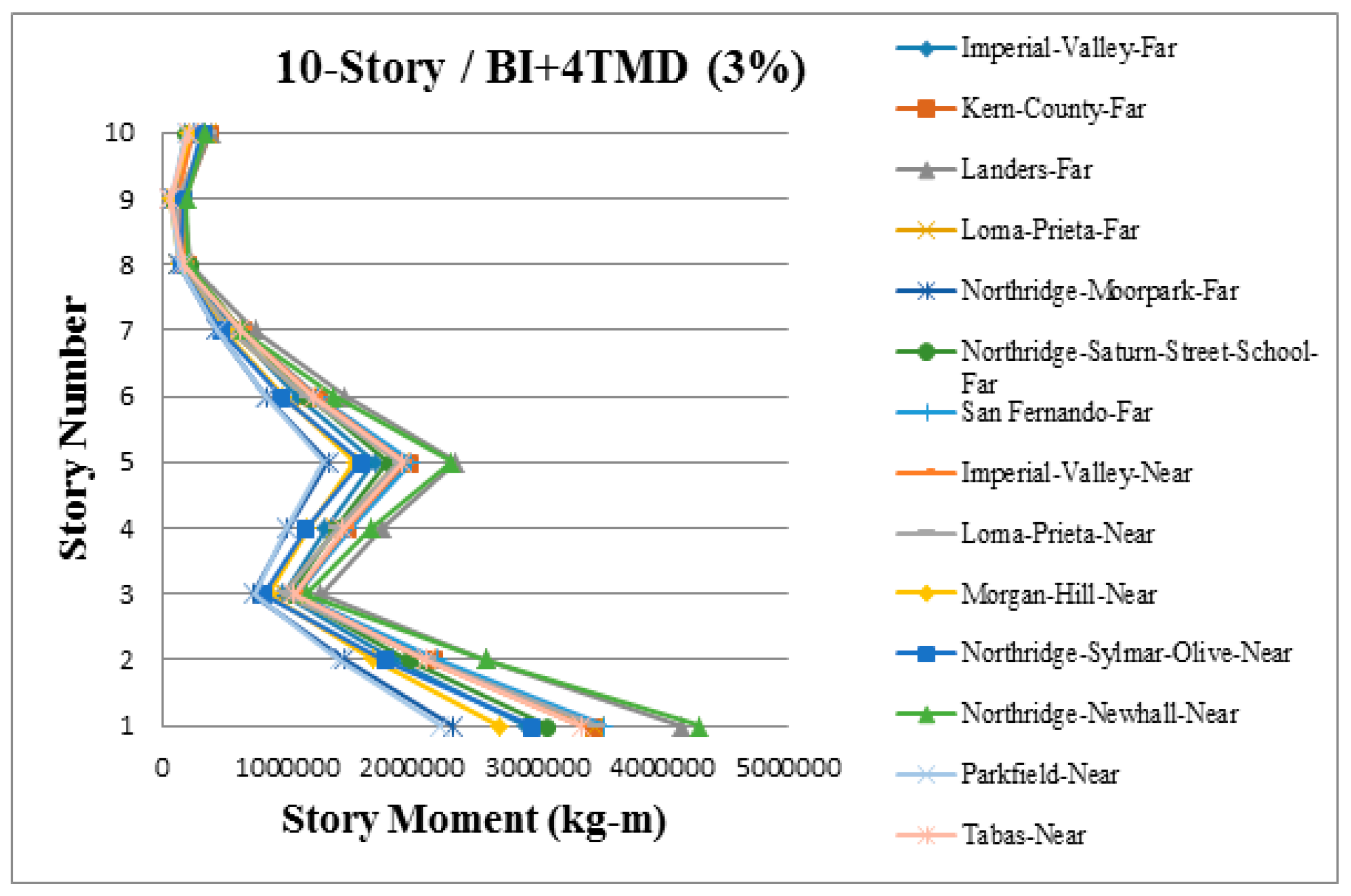
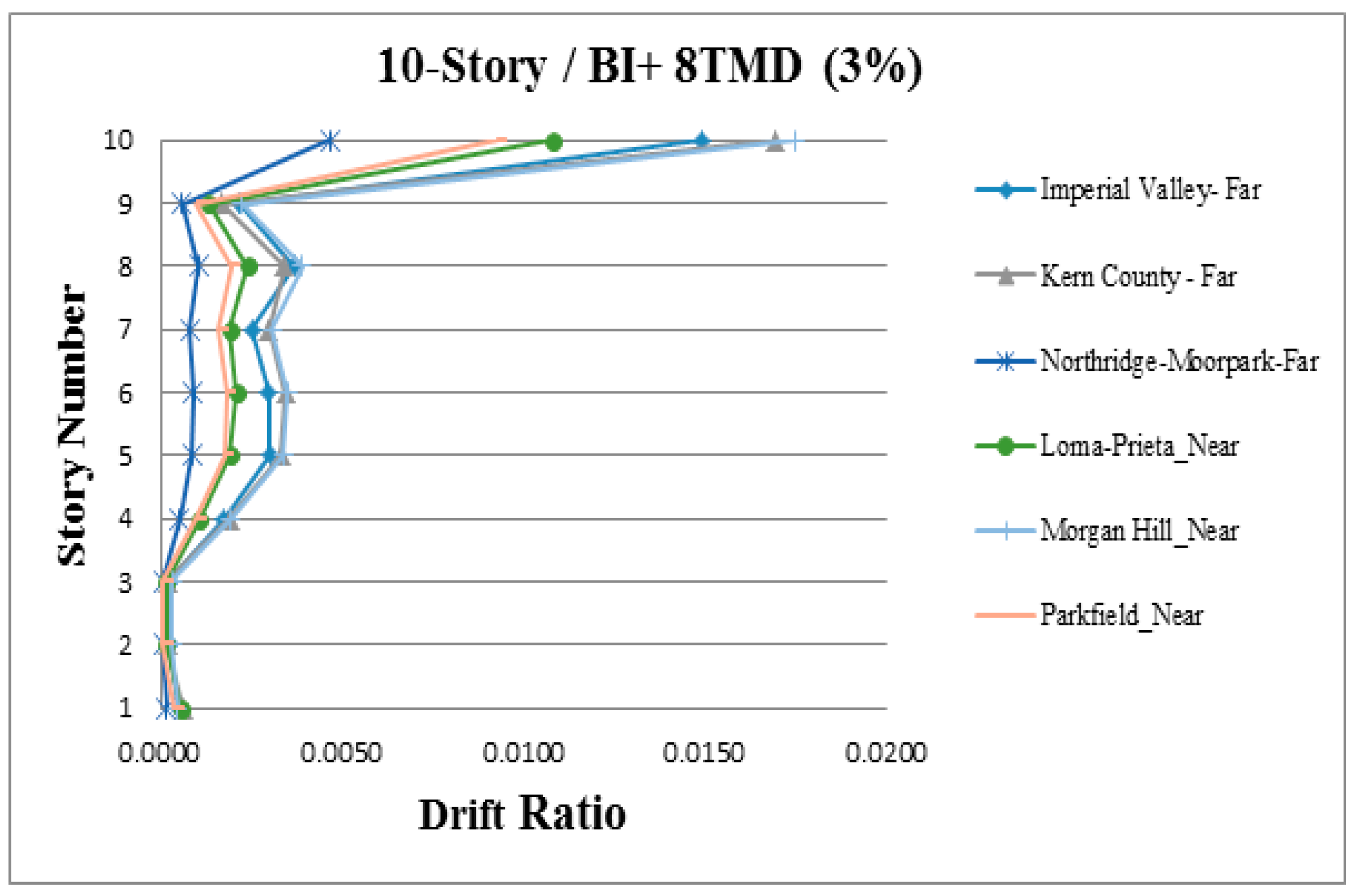
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A






References
- Naeim, F. The Seismic Design Handbook; Springer: Boston, MA, USA, 2001. [Google Scholar]
- Jankowski, R. Theoretical and experimental assessment of parameters for the non-linear viscoelastic model of structural pounding. J. Theor. Appl. Mech. 2007, 45, 931–942. [Google Scholar]
- Jankowski, R. Pounding between superstructure segments in multi-supported elevated bridge with three-span continuous deck under 3D non-uniform earthquake excitation. J. Earthq. Tsunami 2015, 9, 1550012. [Google Scholar] [CrossRef]
- Falborski, T.; Jankowski, R. Polymeric bearings - a new base isolation system to reduce structural damage during earthquakes. Key Eng. Mater. 2013, 569–570, 143–150. [Google Scholar] [CrossRef]
- Jankowski, R.; Mahmoud, S. Linking of adjacent three-storey buildings for mitigation of structural pounding during earthquakes. Bull. Earthq. Eng. 2016, 14, 3075–3097. [Google Scholar] [CrossRef]
- Kelly, J.M. Earthquake-Resistant Design with Rubber; Springer: London, UK, 1993. [Google Scholar]
- Soong, T.T.; Dargush, G.F. Passive Energy Dissipation Systems in Structural Engineering; John Wiley & Sons: London, UK, 1997. [Google Scholar]
- Komodromos, P. Seismic Isolation of Earthquake-Resistant Structures; WIT Press: Southampton, UK, 2000. [Google Scholar]
- Den Hartog, J.P. Mechanical Vibrations; Crastre Press: New York, NY, USA, 2008. [Google Scholar]
- Skinner, R.I.; McVerry, G.H. Base isolation for increased earthquake resistance of buildings. Bull. N. Z. Soc. Earthq. Eng. 1975, 8, 93–101. [Google Scholar]
- Kelly, J.M. Base isolation: Linear theory and design. Earthq. Spectra 1990, 6, 223–244. [Google Scholar] [CrossRef]
- Mahmoud, S.; Jankowski, R. Pounding-involved response of isolated and non-isolated buildings under earthquake excitation. Earthq. Struct. 2010, 1, 231–252. [Google Scholar] [CrossRef]
- Buckle, I.G.; Mayes, R.L. Seismic isolation: History, application, and performance—A world view. Earthq. Spectra 1990, 6, 161–201. [Google Scholar] [CrossRef]
- Skinner, R.I.; Robinson, W.H.; McVerry, G.H. An Introduction to Seismic Isolation; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Naeim, F.; Kelly, J.M. Design of Seismic Isolated Structures: From Theory to Practice; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Lashkari, B.; Kircher, C.A. Evaluation of SEAOC/UBC analysis procedures, Part 1: Stiff superstructure. Proceedings of a Seminar on Seismic Isolation, Passive Energy Dissipation and Active Control, Redwood, CA, USA, 11–12 March 1993. [Google Scholar]
- Constantinou, M.C.; Winters, C.W.; Theodossiou, D. Evaluation of SEAOC and UBC analysis procedures, Part 2: Flexible Superstructure. Proceedings of a Seminar on Seismic Isolation, Passive Energy Dissipation and Active Control, Redwood, CA, USA, 11–12 March 1993; Applied Technology Council: Redwood City, CA, USA, 1993. [Google Scholar]
- Kelly, J.M. The role of damping in seismic isolation. Earthq. Eng. Struct. Dyn. 1999, 28, 3–20. [Google Scholar] [CrossRef]
- Lin, G.L.; Kuo, T.C.; Lu, L.Y. Stiffness controllable isolation system for near-fault seismic isolation. Eng. Struct. 2008, 30, 747–765. [Google Scholar]
- Falborski, T.; Jankowski, R. Experimental study on effectiveness of a prototype seismic isolation system made of polymeric bearings. Appl. Sci. 2017, 7, 808. [Google Scholar] [CrossRef]
- Falborski, T.; Jankowski, R. Advanced hysteretic model of a prototype seismic isolation system made of polymeric bearings. Appl. Sci. 2018, 8, 400. [Google Scholar] [CrossRef]
- Falborski, T.; Jankowski, R.; Kwiecień, A. Experimental study on polymer mass used to repair damaged structures. Key Eng. Mater. 2012, 488–489, 347–350. [Google Scholar] [CrossRef]
- Rezaei Rad, A.; Banazadeh, M. Probabilistic risk-based performance evaluation of seismically base-isolated steel structures subjected to far-field earthquakes. Buildings 2018, 8, 128. [Google Scholar] [CrossRef]
- Nakai, A.; Sato, D.; Murakami, T.; Kasai, K. Evaluation of stiffness of base-isolation layer and superstructure of high-rise baseisolated building based on seismic observation recording. AIJ J. Technol. Des. 2018, 24, 571–576. [Google Scholar] [CrossRef]
- Du, D.; Wang, S.; Liu, W.; Shi, S.; Lee, C.; Xu, J. Modal property of base-isolated high-rise structure considering soil-structure interaction effect. Adv. Mech. Eng. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Wang, J.F.; Lin, C.C. Seismic performance of multiple tuned mass dampers for soil-irregular building interaction systems. Int. J. Solids Struct. 2005, 42, 5536–5554. [Google Scholar] [CrossRef]
- Loh, C.H.; Chao, C.H. Effectiveness of active tuned mass damper and seismic isolation on vibration control of multi-story building. J. Sound Vib. 1996, 193, 773–792. [Google Scholar] [CrossRef]
- Lin, C.C.; Ueng, J.M.; Huang, T.C. Seismic response reduction of irregular buildings using passive tuned mass dampers. Eng. Struct. 2000, 22, 513–524. [Google Scholar] [CrossRef]
- Pinkaew, T.; Lukkunaprasit, P.; Chatupote, P. Seismic effectiveness of tuned mass dampers for damage reduction of structures. Eng. Struct. 2003, 25, 39–46. [Google Scholar] [CrossRef]
- Ahlawat, A.S.; Ramaswamy, A. Multiobjective optimal absorber system for torsionally coupled seismically excited structures. Eng. Struct. 2003, 25, 941–950. [Google Scholar] [CrossRef]
- Sladek, J.E.; Klingner, R.E. Effect of tuned-mass dampers on seismic response. J. Struct. Eng. 1983, 109, 2004–2009. [Google Scholar] [CrossRef]
- Bernal, D. Influence of ground motion characteristics on the effectiveness of tuned mass dampers. In Proceedings of the Eleventh World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- Xiang, P.; Nishitani, A. Optimum design for more effective tuned mass damper system and its application to base-isolated buildings. Struct. Control Health Monit. 2014, 21, 98–114. [Google Scholar] [CrossRef]
- Alhan, C.; Altun, M. Performance of non-linear base isolation systems designed according to uniform building code. In Proceedings of the 5th International Advanced Technologies Symposium, Karabuk, Turkey, 13–15 May 2009; pp. 1–6. [Google Scholar]
- MHUD. Iranian National Building Code (Part 6): Loading; Ministry of Housing and Urban Development: Tehran, Iran, 2009.
- Building and Housing Research Center. Iranian Code of Practice for Seismic Resistance Design of Buildings, Standard No. 2800, 3rd ed.; BHRC: Tehran, Iran, 2005. [Google Scholar]
- Uniform Building Code; International Conference of Building Officials: Whittier, CA, USA, 1994.
- IBC. International Building Code; International Code Council: Illinois, IL, USA, 2006. [Google Scholar]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- PEER Ground Motion Database; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2019. Available online: https://ngawest2.berkeley.edu (accessed on February 2019).





| Building | (ton) | |||||||
|---|---|---|---|---|---|---|---|---|
| 5-story | 184.075 | 29.10 | 7.0 | 189.0 | 3.29 | 0.229 | 0.017 | 0.5 |
| 10-story | 335.348 | 53.59 | 12.8 | 348.1 | 6.06 | 0.215 | 0.017 | 1 |
| 15-story | 460.916 | 78.08 | 18.6 | 507.2 | 8.84 | 0.200 | 0.017 | 2 |
| 20-story | 596.275 | 102.57 | 24.5 | 666.3 | 11.61 | 0.206 | 0.017 | 3 |
| Building | |||
|---|---|---|---|
| 5-story with 1 TMD | 0.6903 | 12.3291 | 0.6144 |
| 5-story with 4 TMDs | 2.7612 | 49.3162 | 2.4575 |
| 5-story with 8 TMDs | 5.5223 | 98.6324 | 4.9150 |
| 10-story with 1 TMD | 1.2576 | 21.5204 | 1.0956 |
| 10-story with 4 TMDs | 5.0302 | 86.0816 | 4.3824 |
| 10-story with 8 TMDs | 10.0604 | 172.1632 | 8.7647 |
| 15-story with 1 TMD | 1.7284 | 13.5266 | 1.0183 |
| 15-story with 4 TMDs | 6.9138 | 54.1063 | 4.0733 |
| 15-story with 8 TMDs | 13.8275 | 108.2126 | 8.1465 |
| 20-story with 1 TMD | 2.2360 | 15.0643 | 1.2223 |
| 20-story with 4 TMDs | 8.9442 | 60.2573 | 4.8892 |
| 20-story with 8 TMDs | 17.8883 | 120.5145 | 9.7783 |
| Earthquake | Year | Magnitude | Station | Characteristics | PGA-X (g) | PGA-Y (g) | PGV (cm/s) | PGD (cm) |
|---|---|---|---|---|---|---|---|---|
| Imperial Valley | 1979 | 6.5 | El Centro Diff. Array | Near-fault | 0.3521 | 0.4798 | 55.32 | 33.04 |
| Tabas | 1978 | 7.4 | 9102 Dyhook | Near-fault | 0.3279 | 0.4061 | 28.24 | 9.03 |
| Loma Prieta | 1989 | 7.0 | Gilroy Array #3 | Near-fault | 0.5550 | 0.3674 | 43.11 | 11.83 |
| Morgan Hill | 1984 | 6.1 | Coyote Lake Dam | Near-fault | 0.7109 | 1.2982 | 68.35 | 10.21 |
| Northridge | 1994 | 6.7 | Sylmar Olive View Hospital | Near-fault | 0.6045 | 0.8433 | 95.38 | 21.94 |
| Northridge | 1994 | 6.7 | Newhall Pico Canyon | Near-fault | 0.4549 | 0.3254 | 79.07 | 30.21 |
| Parkfield | 2004 | 6.4 | Cholame #5 | Near-fault | 0.4416 | 0.3670 | 23.92 | 3.85 |
| Northridge | 1994 | 6.7 | Moorpark (Ventura Fire Station) | Far-fault | 0.1931 | 0.2919 | 22.31 | 4.13 |
| Northridge | 1994 | 6.7 | Saturn Street School | Far-fault | 0.4745 | 0.4386 | 35.34 | 5.96 |
| San Fernando | 1971 | 6.6 | Castaic. Old Ridge Route | Far-fault | 0.3239 | 0.2681 | 19.83 | 3.29 |
| Imperial Valley | 1979 | 6.5 | Calexico Fire Station | Far-fault | 0.2748 | 0.2019 | 18.52 | 9.2 |
| Landers | 1992 | 7.3 | Morango Valley | Far-fault | 0.1879 | 0.1405 | 18.63 | 8.04 |
| Kern County | 1952 | 7.5 | Santa Barbara Courthouse | Far-fault | 0.0871 | 0.1267 | 13.67 | 3.08 |
| Loma Prieta | 1989 | 7.0 | Presidio | Far-fault | 0.0995 | 0.1999 | 20.33 | 4.98 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naderpour, H.; Naji, N.; Burkacki, D.; Jankowski, R. Seismic Response of High-Rise Buildings Equipped with Base Isolation and Non-Traditional Tuned Mass Dampers. Appl. Sci. 2019, 9, 1201. https://doi.org/10.3390/app9061201
Naderpour H, Naji N, Burkacki D, Jankowski R. Seismic Response of High-Rise Buildings Equipped with Base Isolation and Non-Traditional Tuned Mass Dampers. Applied Sciences. 2019; 9(6):1201. https://doi.org/10.3390/app9061201
Chicago/Turabian StyleNaderpour, Hosein, Naghmeh Naji, Daniel Burkacki, and Robert Jankowski. 2019. "Seismic Response of High-Rise Buildings Equipped with Base Isolation and Non-Traditional Tuned Mass Dampers" Applied Sciences 9, no. 6: 1201. https://doi.org/10.3390/app9061201
APA StyleNaderpour, H., Naji, N., Burkacki, D., & Jankowski, R. (2019). Seismic Response of High-Rise Buildings Equipped with Base Isolation and Non-Traditional Tuned Mass Dampers. Applied Sciences, 9(6), 1201. https://doi.org/10.3390/app9061201






