Exploring the Optimal Safety Person–job Matching Method of Major Equipment Based on Human Reliability
Abstract
:1. Introduction
2. Literature Review
2.1. Safe Matching Decision-Making
2.2. Human Reliability Research
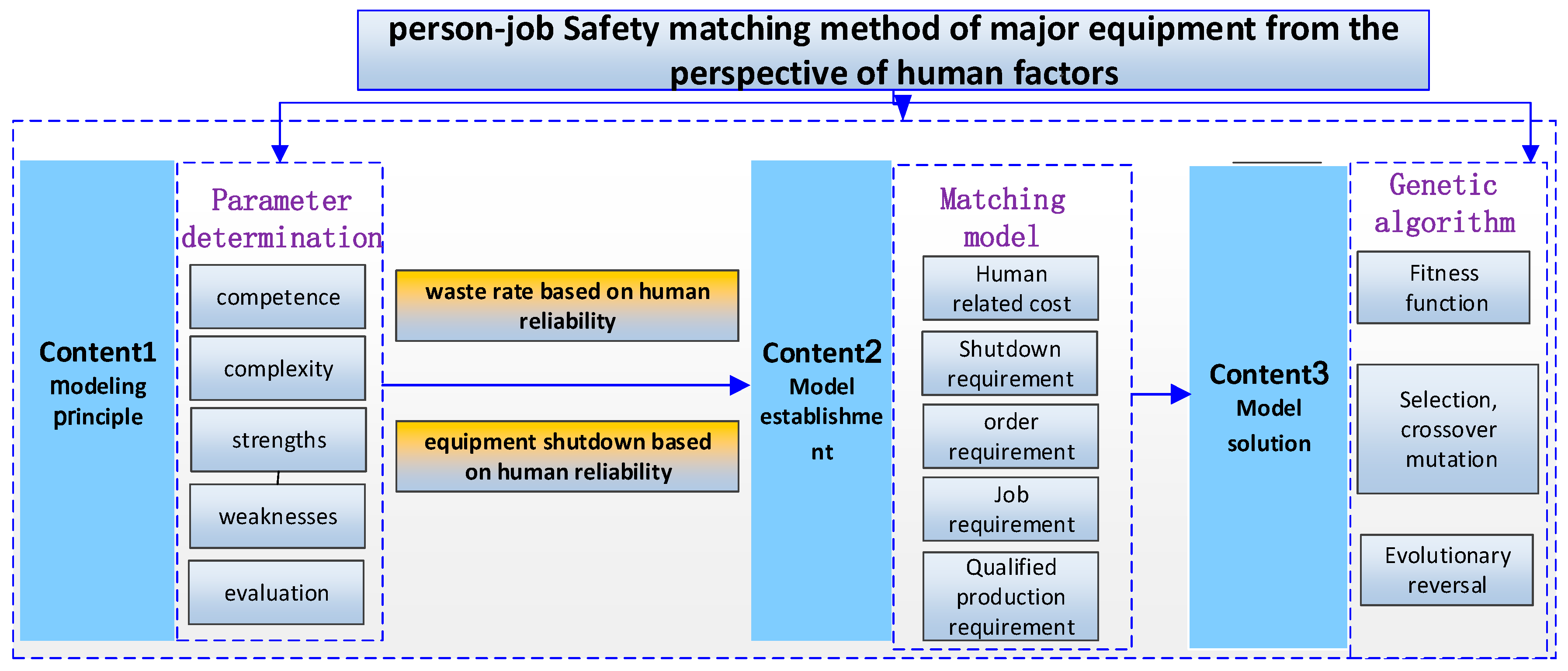
3. The Model of Safe Person–job Matching
3.1. Definition of the Variables
3.2. Matching Modelling Based on Competency and Complexity Strengths and Weaknesses
3.3. Genetic Algorithm
3.4. Proposed Analytical Procedures
4. Case Study
Case Information
5. Implications
5.1. Theoretical Implications
5.2. Management Implications
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, G.; Yang, H.X.; Yuan, C.M.; Eckhoff, R.K. A catastrophic aluminium-alloy dust explosion in China. J. Loss Prev. Process Ind. 2016, 39, 121–130. [Google Scholar] [CrossRef]
- Jiang, L.; Lavaysse, L.M.; Probst, T.M. Safety climate and safety outcomes: A meta-analytic comparison of universal vs. industry-specific safety climate predictive validity. Work Stress 2019, 33, 41–57. [Google Scholar] [CrossRef]
- Huang, C.; Xu, L.D.; Cai, H.; Li, G.; Du, J.; Jiang, L. A context-based service matching approach towards functional reliability for industrial systems. Enterp. Inf. Syst. 2019, 13, 196–218. [Google Scholar] [CrossRef]
- Eastwick, P.W.; Finkel, E.J.; Simpson, J.A. Best practices for testing the predictive validity of ideal partner preference-matching. Personal. Soc. Psychol. Bull. 2019, 45, 167–181. [Google Scholar] [CrossRef]
- Musharraf, M.; Smith, J.; Khan, F.; Veitch, B.; MacKinnon, S. Incorporating individual differences in human reliability analysis: an extension to the virtual experimental technique. Saf. Sci. 2018, 107, 216–223. [Google Scholar] [CrossRef]
- Gale, D.; Shapley, L.S. College admissions and the stability of marriage. Am. Math. Mon. 1962, 69, 9–15. [Google Scholar] [CrossRef]
- Lowalekar, M.; Varakantham, P.; Jaillet, P. Online spatio-temporal matching in stochastic and dynamic domains. Artif. Intell. 2018, 261, 71–112. [Google Scholar] [CrossRef]
- Okumura, Y. A one-sided many-to-many matching problem. J. Math. Econ. 2017, 72, 104–111. [Google Scholar] [CrossRef]
- Boudreau, J.W.; Knoblauch, V. A marriage matching mechanism menagerie. Oper. Res. Lett. 2017, 45, 68–71. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X. Integer k-matchings of graphs. Discret. Appl. Math. 2018, 235, 118–128. [Google Scholar] [CrossRef]
- Gourvès, L.; Monnot, J.; Pascual, F.; Vanderpooten, D. Bi-objective matchings with the triangle inequality. Theor. Comput. Sci. 2017, 670, 1–10. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, X. Understanding many-to-many matching relationship and its correlation with joint response. Transp. Res. Part B Methodol. 2018, 108, 249–260. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Mondal, A.; Murthy, T.S. Problems on matchings and independent sets of a graph. Discret. Math. 2018, 341, 1561–1572. [Google Scholar] [CrossRef]
- Erdil, A.; Ergin, H. Two-sided matching with indifferences. J. Econ. Theory 2017, 171, 268–292. [Google Scholar] [CrossRef]
- Monge, A.E.; Elkan, C. The field matching problem: algorithms and applications. KDD 1996, 2, 267–270. [Google Scholar]
- Gopalakrishnan, H.; Kosanovic, D. Operational planning of combined heat and power plants through genetic algorithms for mixed 0–1 nonlinear programming. Comput. Oper. Res. 2015, 56, 51–67. [Google Scholar] [CrossRef]
- Touat, M.; Bouzidi-Hassini, S.; Benbouzid-Sitayeb, F.; Benhamou, B. A hybridization of genetic algorithms and fuzzy logic for the single-machine scheduling with flexible maintenance problem under human resource constraints. Appl. Soft Comput. 2017, 59, 556–573. [Google Scholar] [CrossRef]
- Metawa, N.; Hassan, M.K.; Elhoseny, M. Genetic algorithm based model for optimizing bank lending decisions. Expert Syst. Appl. 2017, 80, 75–82. [Google Scholar] [CrossRef]
- Zhang, L.; Wong, T.N. An object-coding genetic algorithm for integrated process planning and scheduling. Eur. J. Oper. Res. 2015, 244, 434–444. [Google Scholar] [CrossRef]
- Painton, L.; Campbell, J. Genetic algorithms in optimization of system reliability. IEEE Trans. Reliab. 1995, 44, 172–178. [Google Scholar] [CrossRef]
- da Mata, S.H.; Guardieiro, P.R. Resource allocation for the LTE uplink based on Genetic Algorithms in mixed traffic environments. Comput. Commun. 2017, 107, 125–137. [Google Scholar] [CrossRef]
- Faia, R.; Pinto, T.; Vale, Z.; Corchado, J.M.; Soares, J.; Lezama, F. Genetic algorithms for portfolio optimization with weighted sum approach. IEEE Symp. Ser. Comput. Intell. 2018, 18, 1823–1829. [Google Scholar]
- Younas, I.; Kamrani, F.; Bashir, M.; Schubert, J. Efficient genetic algorithms for optimal assignment of tasks to teams of agents. Neurocomputing 2018, 314, 409–428. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, Y.; Zhang, L.; Wu, D.; Li, M.; Xie, T.; Li, P.; Dai, L.; Li, P.; Shi, X.; et al. A cognitive reliability model research for complex digital human-computer interface of industrial system. Saf. Sci. 2018, 108, 196–202. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Ciarapica, F.E. Human factor risk management in the process industry: A case study. Reliab. Eng. Syst. Saf. 2018, 169, 149–159. [Google Scholar] [CrossRef]
- Kim, Y.; Park, J.; Jung, W.; Choi, S.Y.; Kim, S. Estimating the quantitative relation between PSFs and HEPs from full-scope simulator data. Reliab. Eng. Syst. Saf. 2018, 173, 12–22. [Google Scholar] [CrossRef]
- McDonnell, D.; Balfe, N.; Pratto, L.; O’Donnell, G.E. Predicting the unpredictable: Consideration of human and organisational factors in maintenance prognostics. J. Loss Prev. Process Ind. 2018, 54, 131–145. [Google Scholar] [CrossRef]
- Olivares, R.D.C.; Rivera, S.S.; Leod, J.E.N.M. A novel qualitative prospective methodology to assess human error during accident sequences. Saf. Sci. 2018, 103, 137–152. [Google Scholar] [CrossRef]
- Islam, R.; Khan, F.; Abbassi, R.; Garaniya, V. Human error assessment during maintenance operations of marine systems What are the effective environmental factors? Saf. Sci. 2018, 107, 85–98. [Google Scholar] [CrossRef]
- Park, J.; Jung, J.Y.; Heo, G.; Kim, Y.; Kim, J.; Cho, J. Application of a process mining technique to identifying information navigation characteristics of human operators working in a digital main control room–feasibility study. Reliab. Eng. Syst. Saf. 2018, 175, 38–50. [Google Scholar] [CrossRef]
- Ribeiro, A.C.; Sousa, A.L.; Duarte, J.P.; e Melo, P.F. Human reliability analysis of the Tokai-Mura accident through a THERP–CREAM and expert opinion auditing approach. Saf. Sci. 2016, 87, 269–279. [Google Scholar] [CrossRef]
- Ergai, A.; Cohen, T.; Sharp, J.; Wiegmann, D.; Shappell, S. Assessment of the human factors analysis and classification system (HFACS): Intra-rater and inter-rater reliability. Saf. Sci. 2016, 82, 393–398. [Google Scholar] [CrossRef]
- Rasmussen, M.; Standal, M.I.; Laumann, K. Task complexity as a performance shaping factor: A review and recommendations in Standardized Plant Analysis Risk-Human Reliability Analysis (SPAR-H) adaption. Saf. Sci. 2015, 76, 228–238. [Google Scholar] [CrossRef]
- Kabir, S.; Papadopoulos, Y. A review of applications of fuzzy sets to safety and reliability engineering. Int. J. Approx. Reason. 2018, 100, 29–55. [Google Scholar] [CrossRef]
- Wiegmann, D.A.; Shappell, S.A. A Human Error Approach to Aviation Accident Analysis: The Human Factors Analysis and Classification System; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Zwirglmaier, K.; Straub, D.; Groth, K.M. Capturing cognitive causal paths in human reliability analysis with Bayesian network models. Reliab. Eng. Syst. Saf. 2017, 158, 117–129. [Google Scholar] [CrossRef]
- Zhou, Q.; Wong, Y.D.; Loh, H.S.; Yuen, K.F. A fuzzy and Bayesian network CREAM model for human reliability analysis—The case of tanker shipping. Saf. Sci. 2018, 105, 149–157. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W. Dependence assessment in human reliability analysis using an evidential network approach extended by belief rules and uncertainty measures. Ann. Nucl. Energy 2018, 117, 183–193. [Google Scholar] [CrossRef]
- Liu, H.C.; Li, Z.; Zhang, J.Q.; You, X.Y. A large group decision-making approach for dependence assessment in human reliability analysis. Reliab. Eng. Syst. Saf. 2018, 176, 135–144. [Google Scholar] [CrossRef]
- Zhao, X.; Zhu, C.; Wang, Y.; Jia, J. The Theory Method and Application of Competitive Evaluation; Science Press (China): Beijing, China, 2012. [Google Scholar]
- Zhao, X.; Wang, Q.; Lv, Y. Evaluation and judgement method of leader talent based on individual advantage analysis. Oper. Res. Manag. Sci. 2012, 21, 239–248. [Google Scholar]
- Kolus, A.; Wells, R.; Neumann, P. Production quality and human factors engineering: A systematic review and theoretical framework. Appl. Ergon. 2018, 73, 55–89. [Google Scholar] [CrossRef] [PubMed]
- Biajoli, F.L.; Chaves, A.A.; Lorena, L.A. A biased random-key genetic algorithm for the two-stage capacitated facility location problem. Expert Syst. Appl. 2019, 115, 418–426. [Google Scholar] [CrossRef]





| Symbol | Definition |
|---|---|
| basic layer indicator weight, expressing degrees of strength or weakness | |
| the k-th operator or job | |
| the i-th expert who gives each basic indicator values | |
| the -th middle layer factor | |
| value of t-th factor of middle layer calculated according to i-th expert evaluation score | |
| ideal value of the j-th basic indicator under the -th middle layer factor | |
| the -th basic layer index value of the -th intermediate layer index of the -the object to be analyzed by the -th expert | |
| j-th basic layer index of the t-th middle layer factor | |
| the number of basic layer indicator under the t-th middle layer factor | |
| x: | value of complexity and competency at the grassroots level |
| the -th basic layer index weight of the -th intermediate layer index of the -th object to be analyzed by the -th expert | |
| t-th middle layer index value | |
| ideal value of t-th middle layer factor | |
| t-th middle layer index value according to the i-th expert who gives each basic indicator values for the k-th operator or job | |
| middle layer indicator weight expresses the degree of strength or weakness | |
| number of middle layer indicators | |
| t-th middle layer indicator weight, which can express the degree of strength or weakness according to the i-th expert who gives each basic indicator values for the k-th operator or job | |
| m | m stands for the mth job |
| n | n denotes the nth operator |
| evaluating indicator of highest level of complexity and competence | |
| middle level evaluating indicator of complexity and competency | |
| X: | value of complexity and competency at the grassroots level |
| number of measurement indicators that support the middle layer ym | |
| : | profit from unit-qualified products |
| : | profit from scrap and defective products |
| : | production amount per hour |
| calendar time | |
| planned maintenance time | |
| : | j-th operator’s monthly stoppage at station i, () |
| 0-1 decision variable that indicates that the j-th person takes 1 in the i-th job and is 0 otherwise | |
| : | i-th job non-qualified product coefficient, |
| : | r-th competence indicator ideal value, |
| actual value of the r-th competence indicator of the j-th person, | |
| weight coefficient of the r-th competence index of the j-th person | |
| k-th indicator complexity value of the i-th job, | |
| : | i-th job k-th indicator complexity weight |
| : | fixed salary of the j-th person in the i-th job |
| : | unit time evaluation coefficient |
| downtime for the i-th job | |
| : | annual total wage cost lower limit |
| : | annual scrap limit |
| total labor cost limit | |
| annual order quantity |
| Before Crossing | Crossing | After Crossing |
|---|---|---|
| 6 3 7 8 5 1 2 4 9 | * 3 8 5 6 9 2 4 * | 7 3 8 5 6 9 2 4 1 |
| 7 2 8 5 6 9 4 1 3 | * 2 7 8 5 1 4 * 3 | 6 2 7 8 5 1 4 9 3 |
| Before Mutation | After Mutation |
|---|---|
| 6 3 7 8 5 1 2 4 9 | 6 3 1 8 5 7 2 4 9 |
| Before Reversal | After Reversal |
|---|---|
| 6 3 7 8 5 1 2 4 9 | 6 3 1 5 8 7 2 4 9 |
| Fitting Index | χ2 | df | p | χ2/df | NNFI | CFI | RMSEA |
|---|---|---|---|---|---|---|---|
| Output results | 2426.580 | 1020 | 0.067 | 2.379 | 0.916 | 0.907 | 0.071 |
| Measurement Index | Factor | COEFFICIENT | C.R. | P | Standard Coefficient | Measurement Index | Factor | Coefficient | C.R. | P | Standard Coefficient | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Task structure Task order | ← | Knowledge | 1 | 0.61 | Ideal state multipath | ← | Target path | 1 | 0.63 | ||||
| ← | Knowledge | 1.11 | 7.872 | *** | 0.61 | Multiple final states/targets | ← | Target path | 0.12 | 8.622 | *** | 0.66 | |
| Task organization | ← | Knowledge | 1.43 | 8.819 | *** | 0.71 | Competition path | ← | Target path | 0.16 | 10.194 | *** | 0.82 |
| Conflict rules | ← | Knowledge | 1.67 | 9.128 | *** | 0.74 | Multiple conflicting goals | ← | Target path | 0.12 | 7.715 | *** | 0.58 |
| Logical relationship | ← | Knowledge | 1.55 | 8.85 | *** | 0.71 | Path target conflict | ← | Target path | 0.16 | 9.714 | *** | 0.77 |
| Structural diversity | ← | Knowledge | 1.02 | 7.001 | *** | 0.53 | Error prone | ← | Target path | 0.12 | 7.738 | *** | 0.58 |
| Domain knowledge | ← | Knowledge | 1.2 | 7.985 | *** | 0.62 | Target number | ← | Target path | 0.13 | 8.949 | *** | 0.69 |
| Depth of knowledge | ← | Knowledge | 1.15 | 7.827 | *** | 0.61 | Number of tasks | ← | Target path | 0.14 | 7.724 | *** | 0.58 |
| Decision knowledge | ← | Knowledge | 1.17 | 7.712 | *** | 0.59 | Number of similar tasks | ← | Target path | 0.17 | 8.925 | *** | 0.69 |
| Quantity of behavior | ← | Workload | 1 | 0.7 | Path/process and result uncertainty | ← | Uncertainty | 1 | 0.65 | ||||
| Number of steps | ← | Workload | 0.87 | 9.417 | *** | 0.66 | Transcendental decision method | ← | Uncertainty | 0.11 | 9.429 | *** | 0.75 |
| Amount of input | ← | Workload | 0.36 | 4.54 | *** | 0.51 | Known factor number | ← | Uncertainty | 0.11 | 8.118 | *** | 0.63 |
| Output quantity | ← | Workload | 0.97 | 10.412 | *** | 0.73 | Known connection numbers | ← | Uncertainty | 0.13 | 8.229 | *** | 0.64 |
| Number of programs | ← | Workload | 1.08 | 10.281 | *** | 0.72 | Information/task transparency | ← | Uncertainty | 0.13 | 7.957 | *** | 0.61 |
| Number of actions | ← | Workload | 0.87 | 10.249 | *** | 0.72 | Information integrity | ← | Uncertainty | 0.12 | 7.346 | *** | 0.56 |
| Time urgency | ← | Workload | 0.84 | 9.981 | *** | 0.7 | Number of task elements | ← | Factor relation | 1 | 0.63 | ||
| Time length | ← | Workload | 80 | 9.489 | *** | 0.66 | Information prompt quantity | ← | Factor relation | 0.11 | 8.692 | *** | 0.67 |
| Number of personal interactions | ← | Interpersonal dependence | 1 | 0.61 | Quantity of information | ← | Factor relation | 0.16 | 10.194 | *** | 0.82 | ||
| Amount of collective communication | ← | Interpersonal dependence | 1.01 | 7.372 | *** | 0.62 | Information intensity | ← | Factor relation | 0.12 | 7.715 | *** | 0.58 |
| Amount of collective communication | ← | Interpersonal dependence | 1.23 | 8.319 | *** | 0.69 | Size of question space | ← | Factor relation | 0.16 | 9.714 | *** | 0.77 |
| Everyone’s Dependence | ← | Interpersonal dependence | 1.77 | 9.425 | *** | 0.75 | Subtask number | ← | Factor relation | 0.12 | 7.738 | *** | 0.58 |
| Misleading | ← | Interface | 1 | 0.71 | Number of variables | ← | Factor relation | 0.13 | 8.949 | *** | 0.69 | ||
| Lack of information | ← | Interface | 0.09 | 7.895 | *** | 0.64 | Memory requirements | ← | Factor relation | 0.14 | 7.724 | *** | 0.58 |
| Homogeneity | ← | Interface | 0.13 | 8.138 | *** | 0.83 | Relationship between elements | ← | Factor relation | 0.17 | 8.925 | *** | 0.69 |
| Logical presentation | ← | Interface | 0.17 | 0.621 | 0.535 | 0.05 | Input-output relationship | ← | Factor relation | 0.15 | 7.954 | *** | 0.65 |
| Operation information | ← | Interface | 0.16 | -0.76 | 0.447 | -0.06 | Element connection number | ← | Factor relation | 0.11 | 9.429 | *** | 0.75 |
| Element connection strength | ← | Factor relation | 0.11 | 8.118 | *** | 0.63 |
| Staff | wi1 | wi2 | wi3 | wi4 | wi5 | wi6 | wi7 | wi8 | wi9 | wi10 | wi11 | wi12 | wi13 | wi14 | wi15 | wi16 | wi17 | wi18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.1 | 0 | 0.1 | 0.1 | 0 | 0.1 | 0 | 0.1 | 0 | 0 | 0 | 0.1 | 0.1 | 0.1 | 0 | 0.1 | 0 | 0.1 |
| 2 | 0 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 |
| 3 | 0.045 | 0.061 | 0.061 | 0.061 | 0.061 | 0.045 | 0.061 | 0.061 | 0.076 | 0.045 | 0.045 | 0.076 | 0.061 | 0.061 | 0.045 | 0.061 | 0.061 | 0.015 |
| 4 | 0.045 | 0.061 | 0.061 | 0.061 | 0.061 | 0.045 | 0.061 | 0.061 | 0.076 | 0.045 | 0.045 | 0.076 | 0.061 | 0.061 | 0.045 | 0.061 | 0.061 | 0.015 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0.125 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 |
| 7 | 0 | 0 | 0 | 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 |
| 8 | 0 | 0 | 0 | 0.25 | 0 | 0 | 0 | 0 | 0.25 | 0 | 0 | 0.25 | 0.25 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0.1 | 0 | 0.1 | 0.1 | 0 | 0 | 0.1 | 0 | 0.1 | 0.1 | 0.1 | 0 | 0 | 0 | 0.1 | 0.1 | 0 | 0.1 |
| Staff | Comprehensive Evaluation Value | Staff | Comprehensive Evaluation Value | Staff | Comprehensive Evaluation Value | Staff | Comprehensive Evaluation Value | Staff | Comprehensive Evaluation Value |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.09894 | 11 | 0.06390 | 21 | 0.04925 | 31 | 0.05776 | 41 | 0.10682 |
| 2 | 0.07366 | 12 | 0.09514 | 22 | 0.06598 | 32 | 0.14674 | 42 | 0.10682 |
| 3 | 0.10682 | 13 | 0.08354 | 23 | 0.05354 | 33 | 0.09714 | 43 | 0.10682 |
| 4 | 0.10682 | 14 | 0.05849 | 24 | 0.04965 | 34 | 0.19529 | 44 | 0.10682 |
| 5 | 0.11452 | 15 | 0.10845 | 25 | 0.08220 | 35 | 0.16380 | 45 | 0.06085 |
| 6 | 0.07960 | 16 | 0.09040 | 26 | 0.06492 | 36 | 0.16247 | 46 | 0.07375 |
| 7 | 0.11249 | 17 | 0.07898 | 27 | 0.07829 | 37 | 0.10682 | 47 | 0.05815 |
| 8 | 0.09658 | 18 | 0.06101 | 28 | 0.05269 | 38 | 0.10682 | 48 | 0.08033 |
| 9 | 0.08749 | 19 | 0 | 29 | 0.10964 | 39 | 0.10682 | 49 | 0.07277 |
| 10 | 0.08320 | 20 | 0.03861 | 30 | 0 | 40 | 0.10682 |
| Job | Factor 1 | Factor 2 | Factor3 | Factor 4 | Factor 5 | Factor 6 | Factor 7 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0.2 | 0.2 | 0 | 0.2 | 0.2 | 0.2 |
| 2 | 0.143 | 0.143 | 0.143 | 0.143 | 0.143 | 0.143 | 0.143 |
| 3 | 0.167 | 0.167 | 0.167 | 0.167 | 0 | 0.167 | 0.167 |
| 4 | 0.167 | 0.167 | 0.167 | 0.167 | 0 | 0.167 | 0.167 |
| 5 | 0.143 | 0.143 | 0.143 | 0.143 | 0.143 | 0.143 | 0.143 |
| 6 | 0.167 | 0.167 | 0.167 | 0.167 | 0.167 | 0 | 0.167 |
| 7 | 0.2 | 0.2 | 0.2 | 0 | 0 | 0.2 | 0.2 |
| 8 | 0.333 | 0 | 0.333 | 0 | 0 | 0.333 | 0 |
| 9 | 0.2 | 0 | 0.2 | 0 | 0.2 | 0.2 | 0.2 |
| Job | Evaluation Value | Job | Evaluation Value | Job | Evaluation Value | Job | Evaluation Value | Job | Evaluation Value |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.17936 | 11 | 0.16418 | 21 | 0.05073 | 31 | 0.22105 | 41 | 0.21493 |
| 2 | 0.10192 | 12 | 0.21157 | 22 | 0.09203 | 32 | 0.26238 | 42 | 0.11541 |
| 3 | 0.11950 | 13 | 0.11247 | 23 | 0.20843 | 33 | 0.20488 | 43 | 0.09867 |
| 4 | 0.16417 | 14 | 0.20605 | 24 | 0.10222 | 34 | 0.21949 | 44 | 0.16750 |
| 5 | 0.09918 | 15 | 0.08890 | 25 | 0.09201 | 35 | 0.12193 | 45 | 0.23186 |
| 6 | 0.11348 | 16 | 0.11514 | 26 | 0.20135 | 36 | 0.14264 | 46 | 0.05992 |
| 7 | 0.14171 | 17 | 0.27778 | 27 | 0.17924 | 37 | 0.32119 | 47 | 0.08991 |
| 8 | 0.21129 | 18 | 0.24278 | 28 | 0.22081 | 38 | 0.25532 | 48 | 0.21254 |
| 9 | 0.13527 | 19 | 0.27888 | 29 | 0.13795 | 39 | 0.25957 | 49 | 0.20469 |
| 10 | 0.18522 | 20 | 0.04401 | 30 | 0.11712 | 40 | 0.25966 |
| Serial Number | Category | Numerical Value |
|---|---|---|
| 1 | Profit per unit product | 405 yuan |
| 2 | Unit hour output | 500 ton |
| 3 | Scrap profit | −2370 yuan |
| 4 | Calendar time | 8760 h |
| 5 | Scheduled downtime | 588 h |
| 6 | The first job assessment downtime | 0.6 h |
| 7 | The job unreliable conversion into non-qualified product coefficient | 0.02 |
| 8 | man job fixed salary | 3000 yuan |
| 9 | Annual total fixed wages | 324,000 yuan |
| 10 | Unit time assessment coefficient | 6000 yuan/hour |
| 11 | Annual order quantity | 3,000,000 ton |
| 12 | Annual total human shutdown ceiling | 70 h |
| 13 | Annual maximum number of rejected items | 408,600 ton |
| 14 | Total labor cost ceiling | 700,000 yuan |
| 15 | the length of a person’s downtime in job | Table 12 |
| P J | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.6294 | 1.8116 | 0.2540 | 1.8268 | 1.2647 | 0.1951 | 0.5570 | 1.0938 | 1.9150 | 1.9298 | 0.3152 | 1.9412 |
| 2 | 1.5094 | 0.5521 | 1.3594 | 1.3102 | 0.3252 | 0.2380 | 0.9967 | 1.9195 | 0.6808 | 1.1705 | 0.4476 | 1.5025 |
| 3 | 0.0238 | 0.6742 | 0.3244 | 1.5886 | 0.6224 | 1.0571 | 0.3313 | 1.2040 | 0.5259 | 1.3082 | 1.3784 | 1.4963 |
| 4 | 0.2466 | 0.3678 | 0.4799 | 0.8345 | 0.0993 | 1.8054 | 1.8896 | 0.9817 | 0.9785 | 0.6754 | 1.8001 | 0.7385 |
| 5 | 1.0170 | 1.0215 | 1.6353 | 1.5897 | 1.2886 | 0.7572 | 1.6232 | 1.0657 | 0.7015 | 1.8780 | 1.7519 | 1.1003 |
| 6 | 1.4607 | 0.9772 | 1.1571 | 0.4745 | 0.9177 | 1.9262 | 1.0936 | 1.0423 | 0.4632 | 0.9778 | 1.2481 | 1.3583 |
| 7 | 0.9798 | 0.3359 | 1.9574 | 1.4254 | 1.0009 | 0.9422 | 0.1192 | 1.3639 | 0.0849 | 0.1429 | 1.0433 | 0.1935 |
| 8 | 1.4757 | 0.5382 | 0.8457 | 1.0957 | 1.8855 | 0.8355 | 1.9661 | 0.6029 | 1.4022 | 1.3327 | 1.0783 | 1.3962 |
| 9 | 1.6355 | 0.5215 | 1.1887 | 0.0450 | 0.8505 | 0.6254 | 0.3230 | 0.3575 | 0.8458 | 0.1885 | 1.1970 | 0.9418 |
| 10 | 0.4481 | 1.3357 | 1.6888 | 0.6889 | 1.5610 | 1.3507 | 0.0134 | 1.2043 | 0.7735 | 1.8320 | 0.0023 | 0.9249 |
| 11 | 0.9175 | 1.3239 | 1.5406 | 0.7004 | 1.3240 | 0.8323 | 1.6839 | 1.6658 | 0.5129 | 1.2269 | 1.1645 | 1.0815 |
| 12 | 1.0401 | 0.6954 | 0.3000 | 1.1722 | 0.5243 | 0.0889 | 1.5099 | 0.4856 | 0.8848 | 1.3756 | 0.7185 | 1.4727 |
| Staff Job | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.0175 | 0.0156 | 0.0163 | 0.0173 | 0.0155 | 0.0161 | 0.0169 | 0.0179 | 0.0167 | 0.0176 | 0.0173 | 0.0179 |
| 2 | 0.0181 | 0.0167 | 0.0172 | 0.0180 | 0.0167 | 0.0171 | 0.0177 | 0.0184 | 0.0175 | 0.0182 | 0.0184 | 0.0170 |
| 3 | 0.0173 | 0.0153 | 0.0160 | 0.0171 | 0.0151 | 0.0158 | 0.0166 | 0.0177 | 0.0164 | 0.0174 | 0.0171 | 0.0177 |
| 4 | 0.0173 | 0.0153 | 0.0160 | 0.0171 | 0.0151 | 0.0158 | 0.0166 | 0.0177 | 0.0164 | 0.0174 | 0.0171 | 0.0177 |
| 5 | 0.0171 | 0.0149 | 0.0157 | 0.0169 | 0.0148 | 0.0155 | 0.0164 | 0.0176 | 0.0162 | 0.0172 | 0.0169 | 0.0176 |
| 6 | 0.0180 | 0.0165 | 0.0170 | 0.0178 | 0.0164 | 0.0168 | 0.0175 | 0.0183 | 0.0173 | 0.0181 | 0.0178 | 0.0183 |
| 7 | 0.0172 | 0.0150 | 0.0158 | 0.0169 | 0.0149 | 0.0155 | 0.0164 | 0.0176 | 0.0163 | 0.0173 | 0.0169 | 0.0176 |
| 8 | 0.0176 | 0.0157 | 0.0164 | 0.0173 | 0.0156 | 0.0162 | 0.0169 | 0.0179 | 0.0168 | 0.0176 | 0.0173 | 0.0179 |
| 9 | 0.0178 | 0.0161 | 0.0167 | 0.0176 | 0.0160 | 0.0165 | 0.0172 | 0.0181 | 0.0171 | 0.0179 | 0.0176 | 0.0181 |
| 10 | 0.0179 | 0.0163 | 0.0169 | 0.0177 | 0.0162 | 0.0167 | 0.0174 | 0.0182 | 0.0172 | 0.0180 | 0.0177 | 0.0182 |
| 11 | 0.0184 | 0.0172 | 0.0176 | 0.0182 | 0.0171 | 0.0175 | 0.0180 | 0.0186 | 0.0179 | 0.0184 | 0.0182 | 0.0186 |
| 12 | 0.0176 | 0.0158 | 0.0164 | 0.0174 | 0.0157 | 0.0162 | 0.0170 | 0.0180 | 0.0168 | 0.0177 | 0.0174 | 0.0180 |
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| j | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 8 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 17 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 22 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 24 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 31 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 32 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 37 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 38 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 41 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 42 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 43 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 44 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 45 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 46 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 47 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 48 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 49 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Parameter | ||||
|---|---|---|---|---|
| Parameter Change Rate (%) | −50/0/+50 | −50/0/+50 | −50/0/+50 | |
| The corresponding cost of different parameter changes (10,000 yuan) | Human failure downtime cost | 1469/3034/3741 | 2974/3034/3045 | 3034/3034/3034 |
| Cost of defective products | 18,882/18,837/19,063 | 9493/18,837/28,197 | 18,837/18,837/18,837 | |
| Labor cost | 345/298/277 | 298/298/298 | 240/298/347 | |
| Total cost | 20,696/22,169/23,081 | 12,765/22,169/31,540 | 22,043/22,169/22,432 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Li, Z.; Wu, K.-J.; Yang, W. Exploring the Optimal Safety Person–job Matching Method of Major Equipment Based on Human Reliability. Appl. Sci. 2019, 9, 1219. https://doi.org/10.3390/app9061219
Zhang L, Li Z, Wu K-J, Yang W. Exploring the Optimal Safety Person–job Matching Method of Major Equipment Based on Human Reliability. Applied Sciences. 2019; 9(6):1219. https://doi.org/10.3390/app9061219
Chicago/Turabian StyleZhang, Lili, Zhengfeng Li, Kuo-Jui Wu, and Wenwen Yang. 2019. "Exploring the Optimal Safety Person–job Matching Method of Major Equipment Based on Human Reliability" Applied Sciences 9, no. 6: 1219. https://doi.org/10.3390/app9061219
APA StyleZhang, L., Li, Z., Wu, K.-J., & Yang, W. (2019). Exploring the Optimal Safety Person–job Matching Method of Major Equipment Based on Human Reliability. Applied Sciences, 9(6), 1219. https://doi.org/10.3390/app9061219






