Fatigue Behaviour of Textile Reinforced Cementitious Composites and Their Application in Sandwich Elements
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Characteristics
2.1.1. Mortar
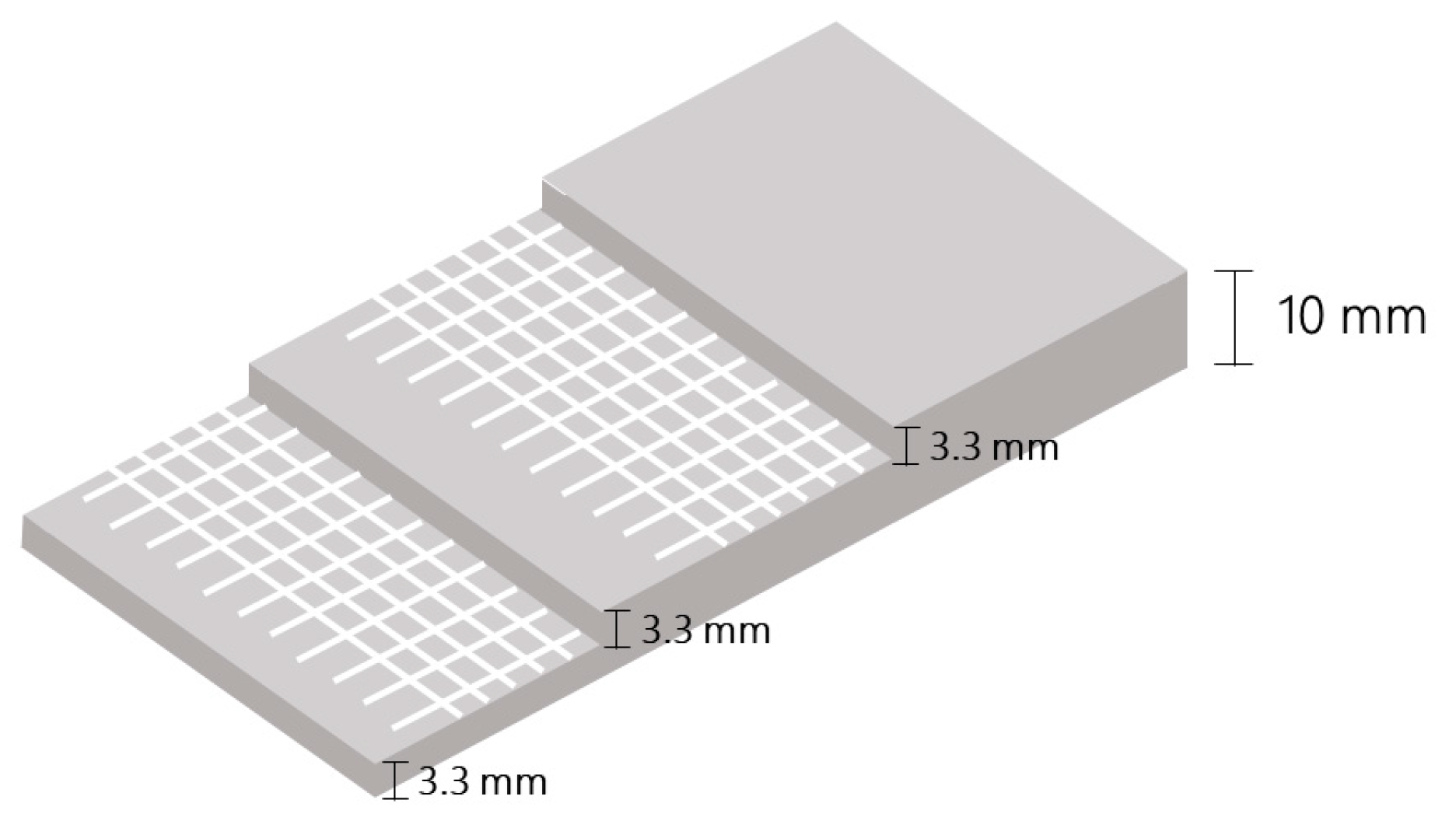
2.1.2. Textile Reinforcement
2.1.3. Expanded Polystyrene
2.2. Specimen Preparation
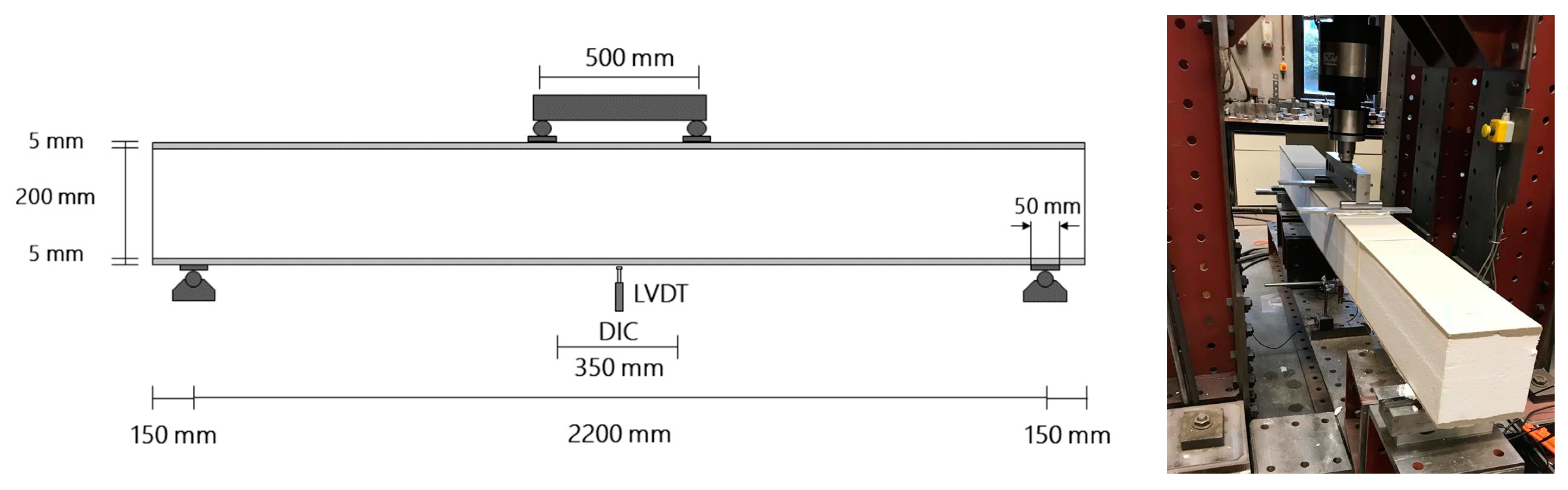
2.3. Test Set-Up
2.3.1. Uniaxial Tensile Tests
2.3.2. Four-Point Bending Tests
2.3.3. Digital Image Correlation
3. Results and Discussion
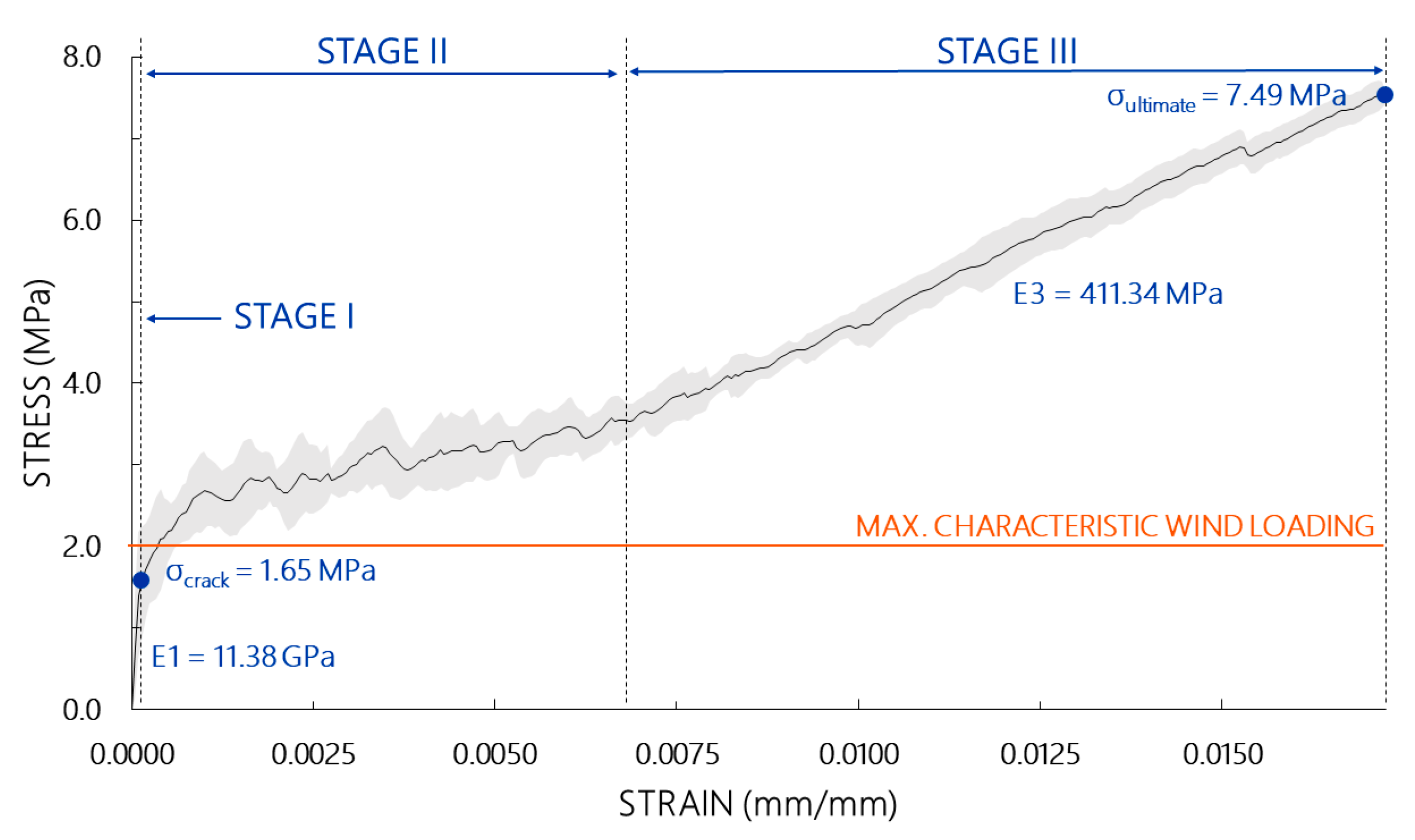
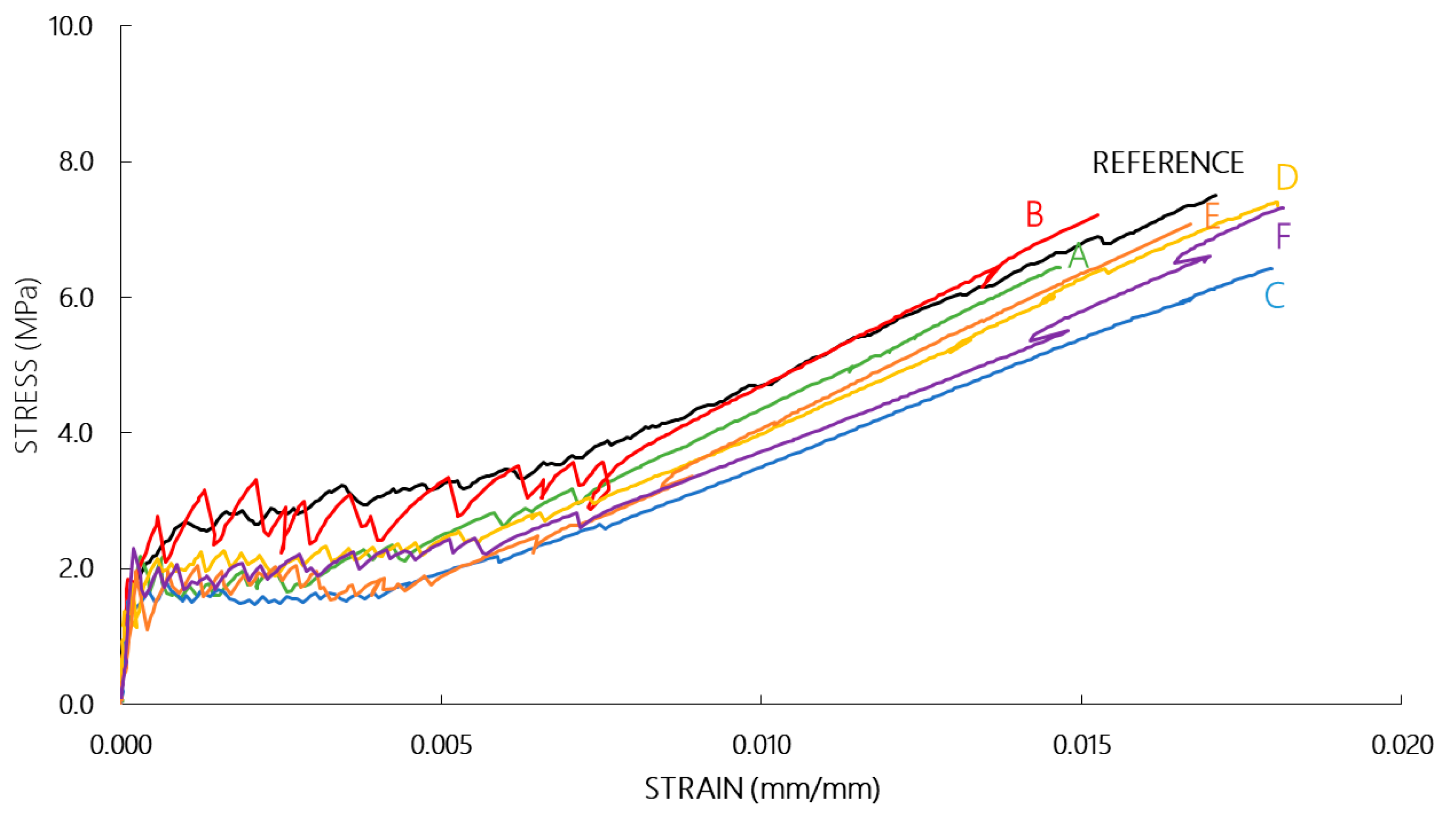
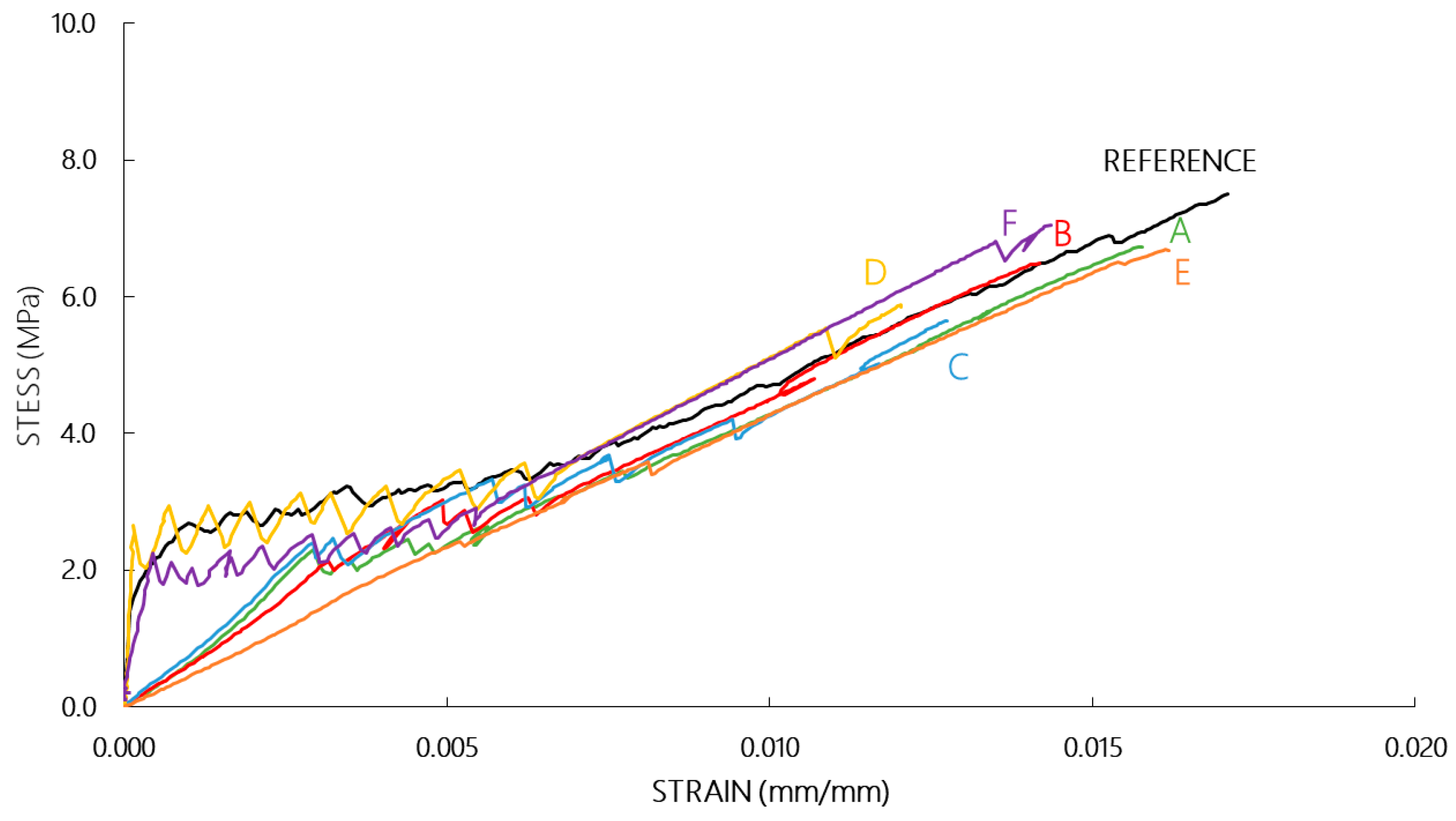
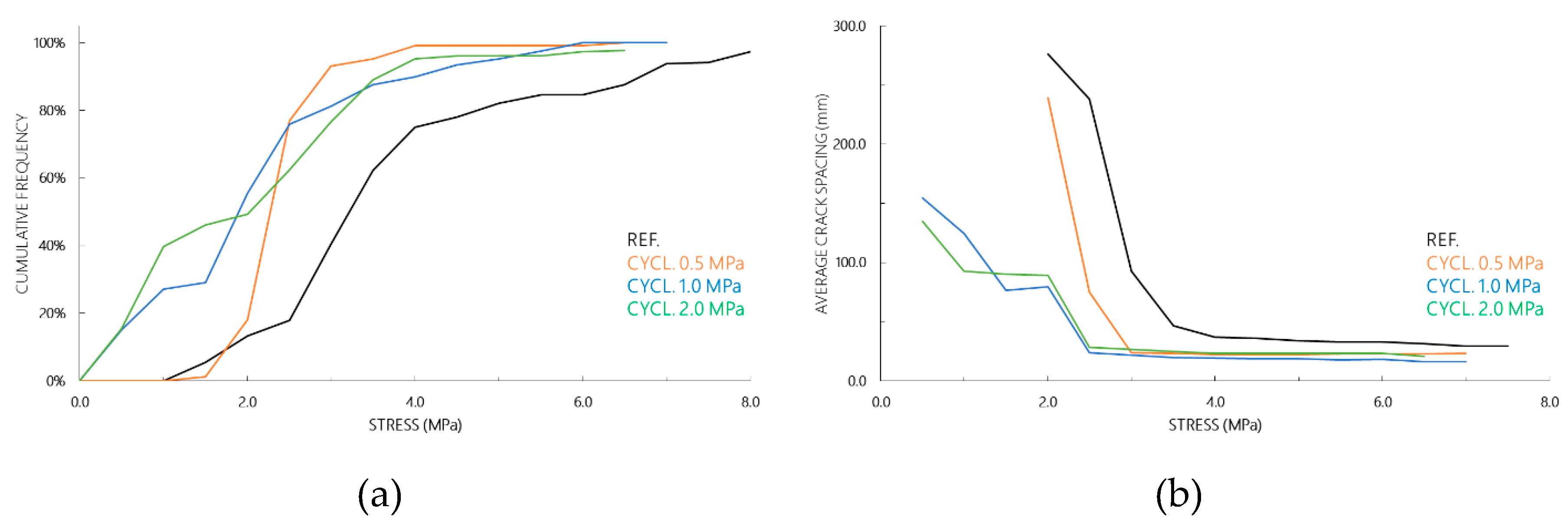
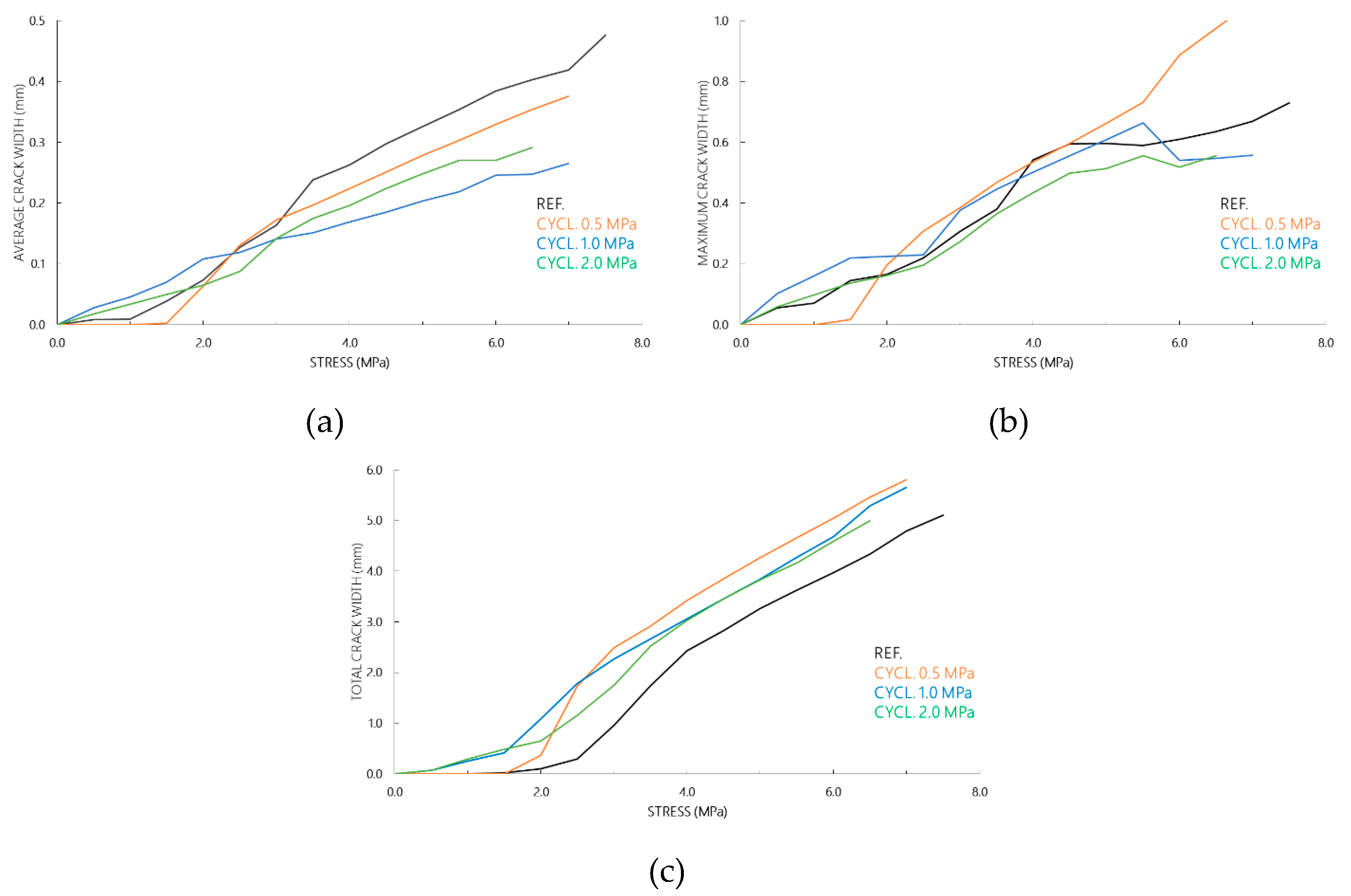
3.1. Investigations on TRC Coupons
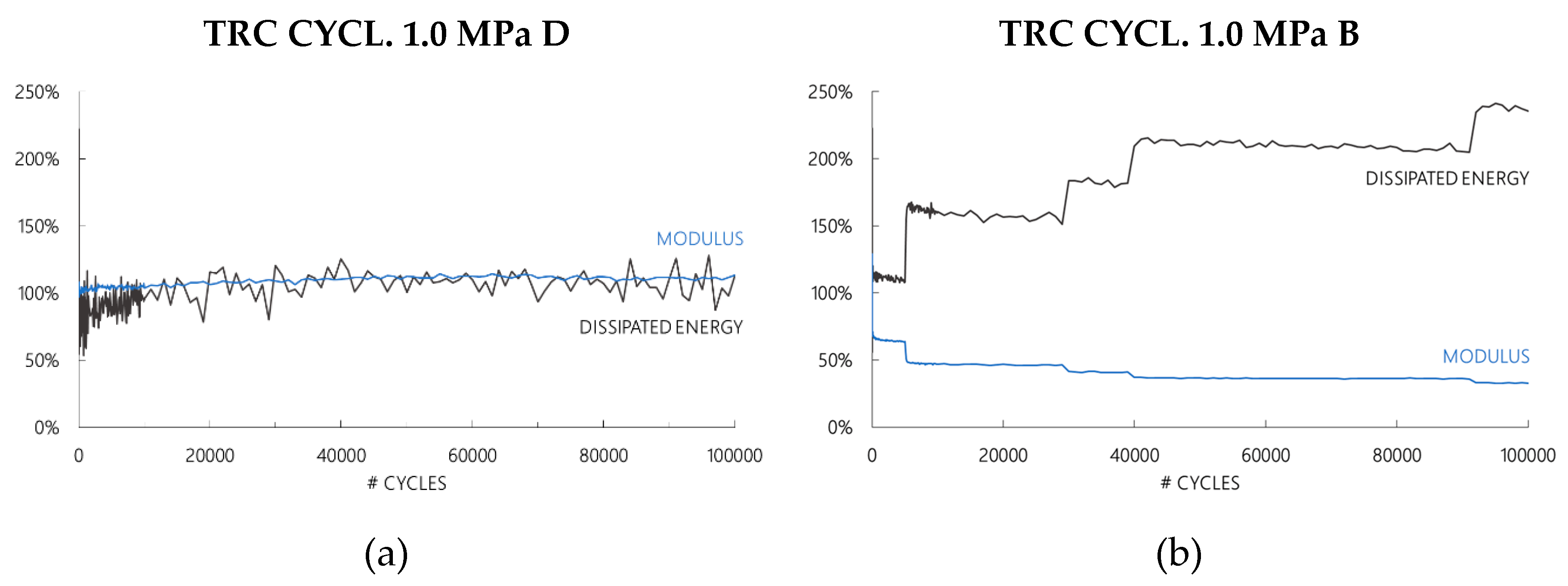
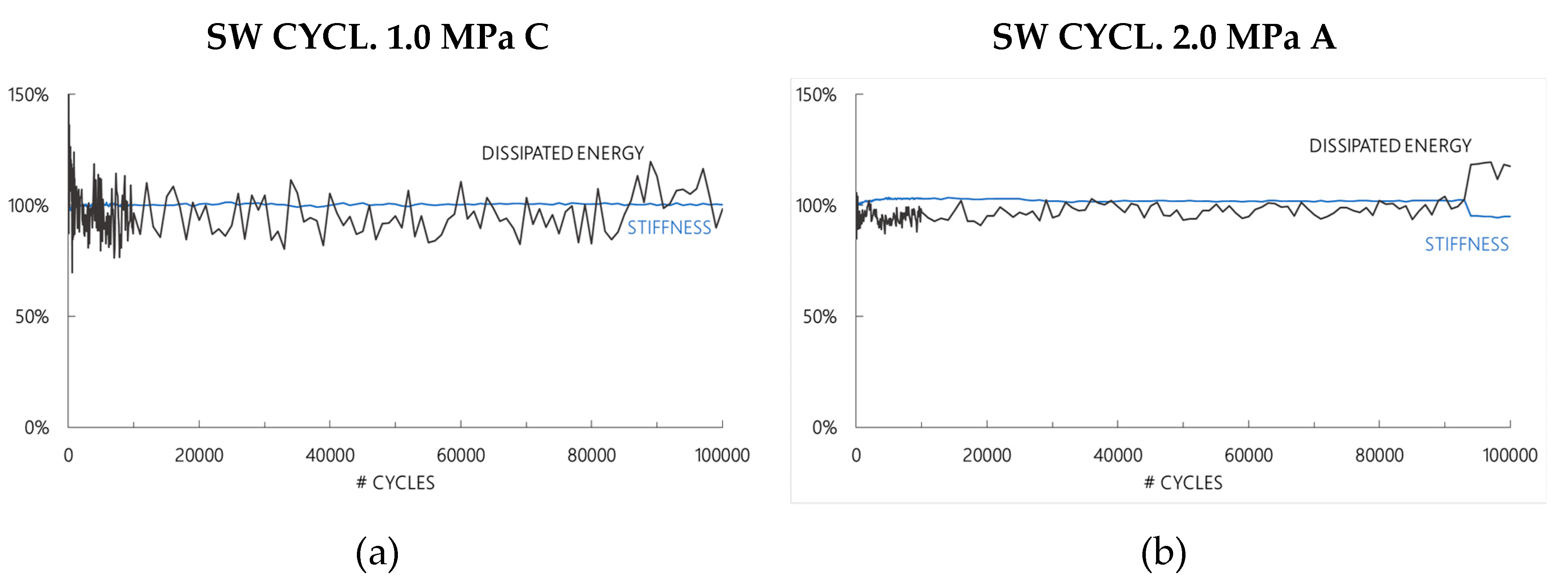
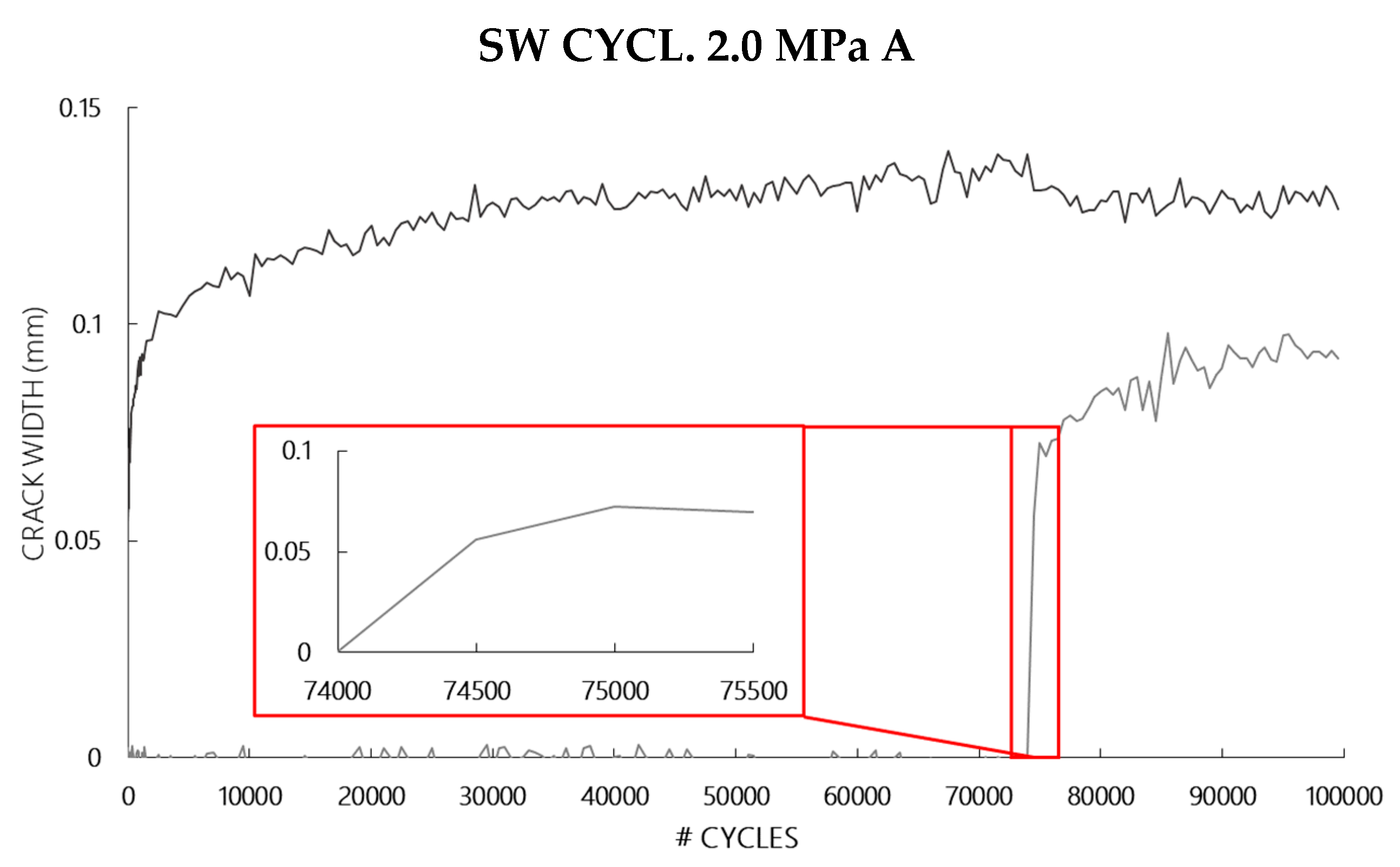
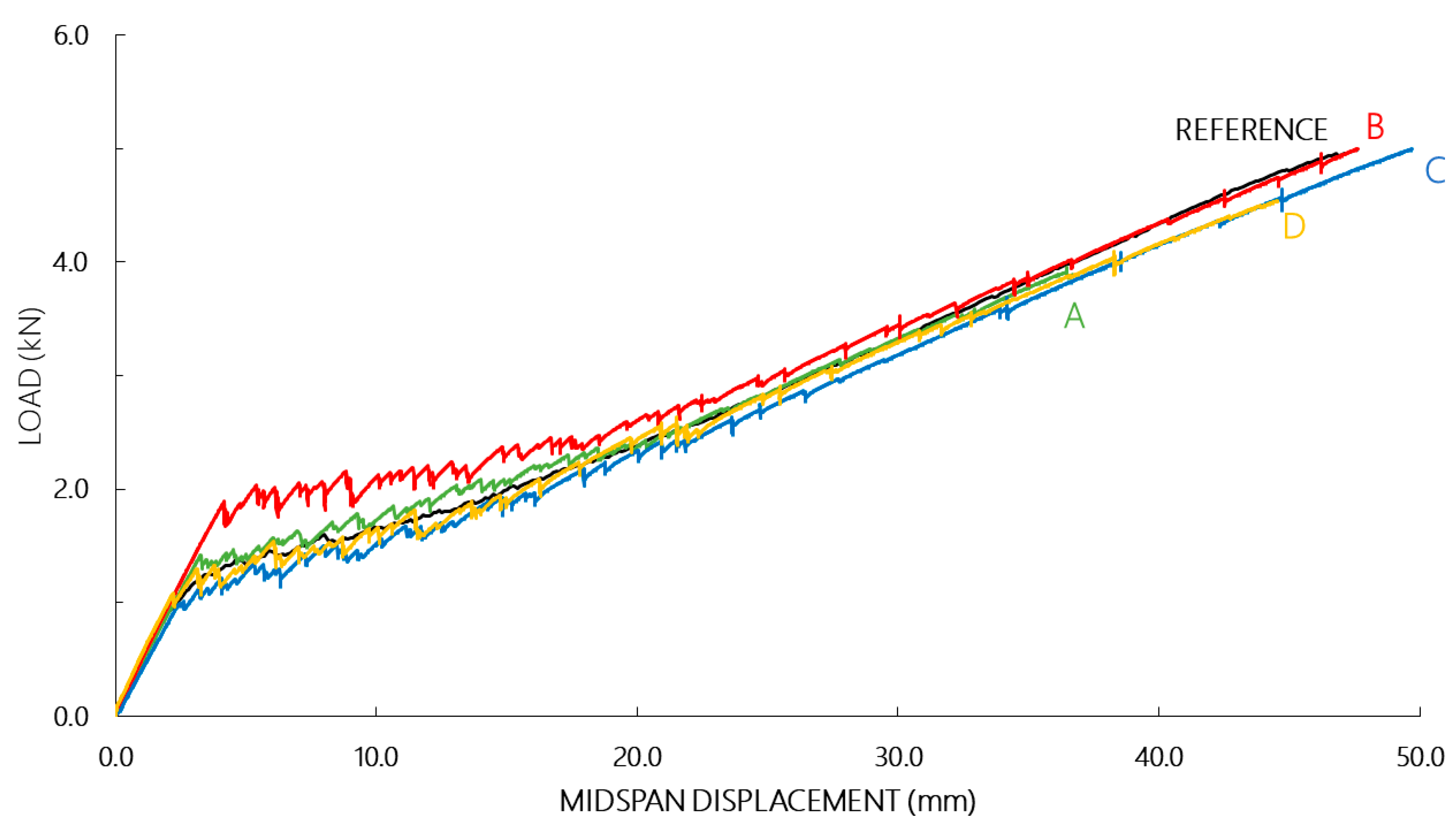
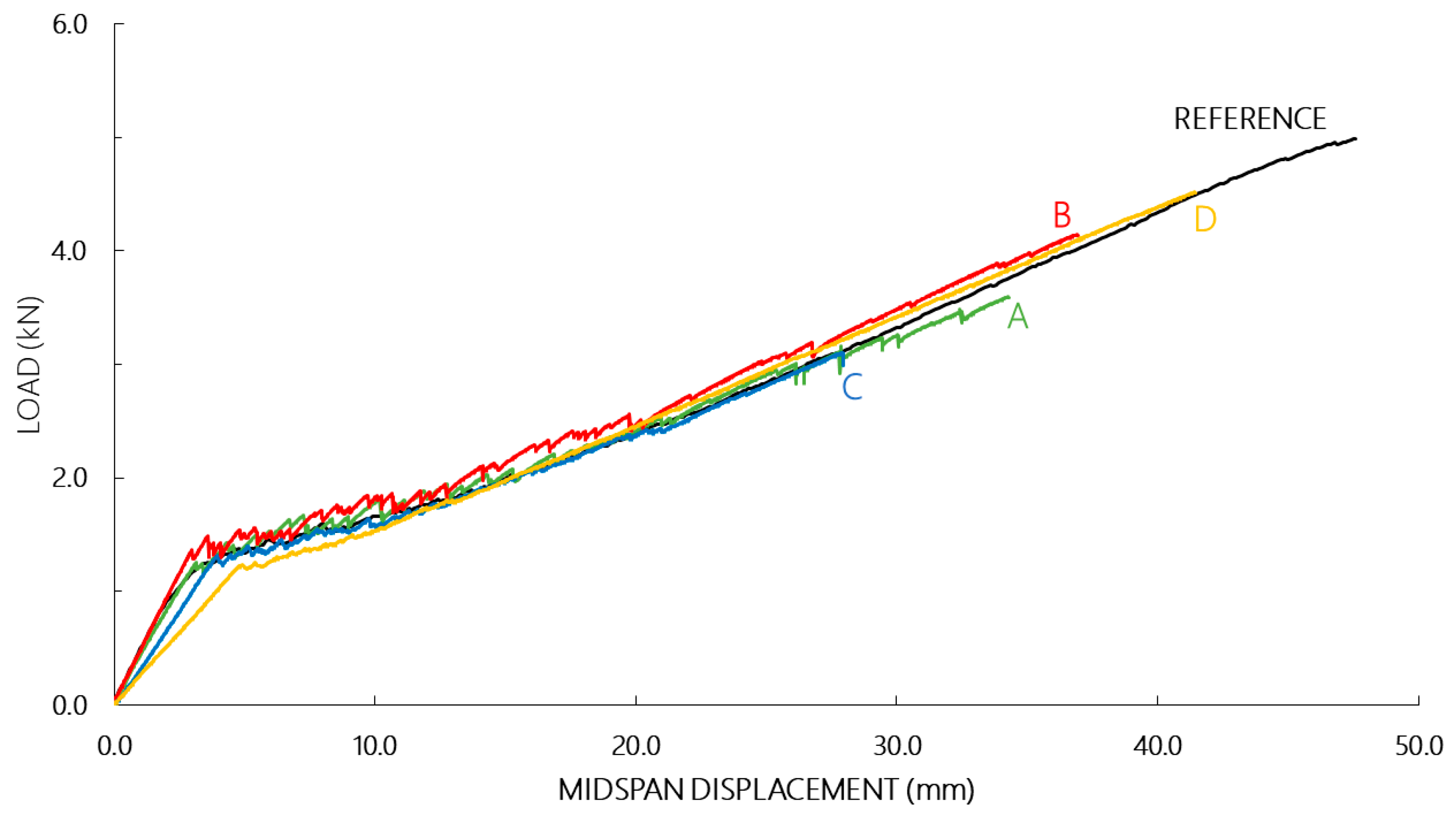
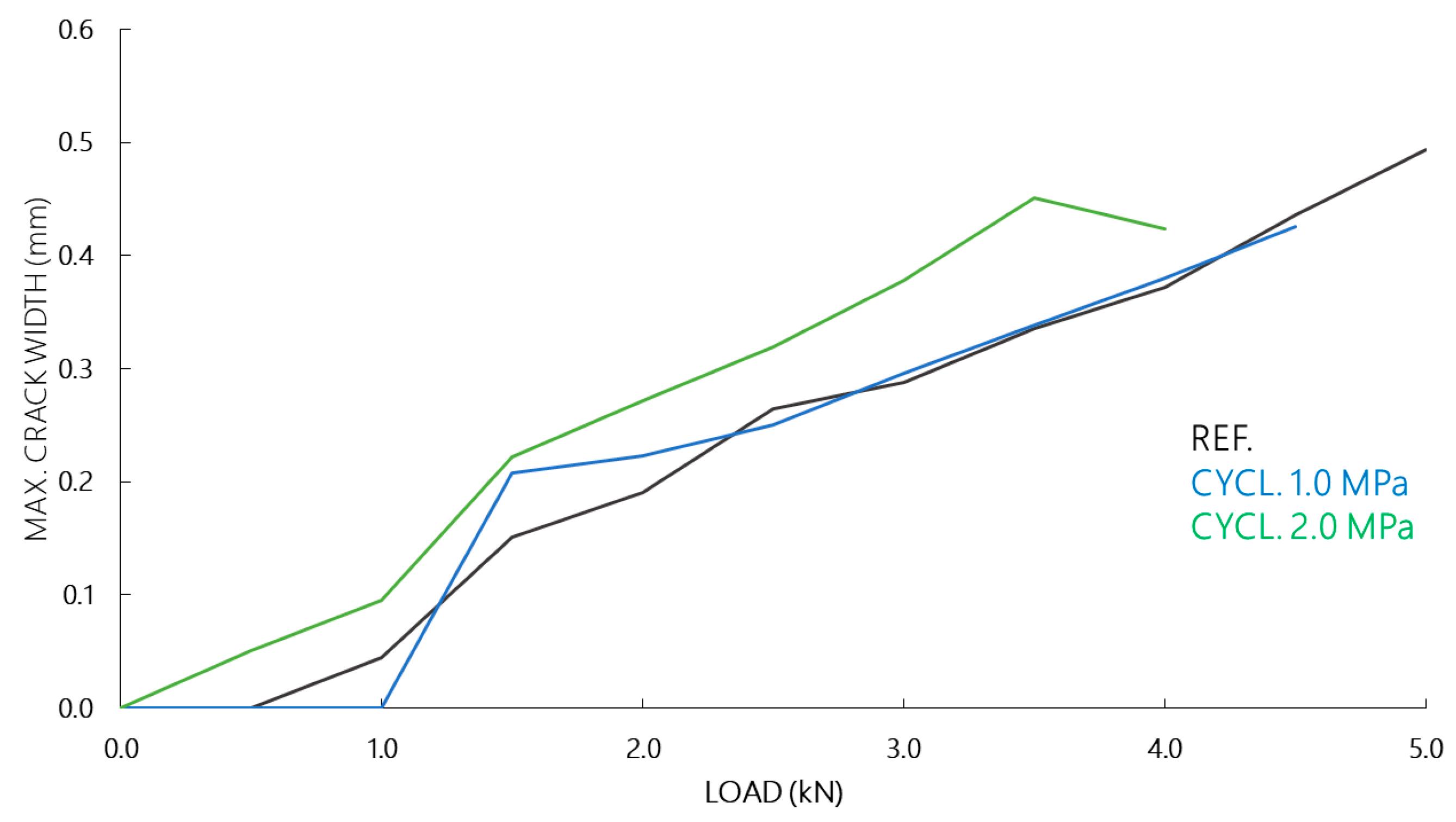
3.2. Investigations on Sandwich Beams
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Davies, J.M. Lighweight Sandwich Construction; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Larbi, A.S.; Contamine, R.; Ferrier, E.; Hamelin, P. Shear strengthening of RC beams with textile reinforced concrete (TRC) plate. Constr. Build. Mater. 2010, 24, 1928–1936. [Google Scholar] [CrossRef]
- Verbruggen, S.; Tysmans, T.; Wastiels, J. TRC or CFRP strengthening for reinforced concrete beams: An experimental study of the cracking behaviour. Eng. Struct. 2014, 77, 49–56. [Google Scholar] [CrossRef]
- Papanicolaou, C.G.; Triantafillou, T.C.; Papathanasiou, M.; Karlos, K. Textile reinforced mortar (TRM) versus FRP as strengthening material of URM walls: Out-of-plane cyclic loading. Mater. Struct. Constr. 2008, 41, 143–157. [Google Scholar] [CrossRef]
- Parisi, F.; Lignola, G.P.; Augenti, N.; Prota, A.; Manfredi, G. Rocking response assessment of in-plane laterally-loaded masonry walls with openings. Eng. Struct. 2013, 56, 1234–1248. [Google Scholar] [CrossRef]
- Hegger, J.; Voss, S. Investigations on the bearing behaviour and application potential of textile reinforced concrete. Eng. Struct. 2008, 30, 2050–2056. [Google Scholar] [CrossRef]
- Nguyen, V.A.; Jesse, F.; Curbach, M. Experiments about load bearing behaviour of lightweight sandwich beams using textile reinforced and expanded polystyrene concrete. Struct. Concr. 2015, 17, 760–767. [Google Scholar] [CrossRef]
- Colombo, I.G.; Colombo, M.; Prisco, M. Bending behaviour of Textile Reinforced Concrete sandwich beams. Constr. Build. Mater. 2015, 95, 675–685. [Google Scholar] [CrossRef]
- Portal, N.W.; Flansbjer, M.; Zandi, K.; Wlasak, L.; Malaga, K. Bending behaviour of novel Textile Reinforced Concrete-foamed concrete (TRC-FC) sandwich elements. Compos. Struct. 2017, 177, 104–118. [Google Scholar] [CrossRef]
- Cuypers, H.; Wastiels, J. Analysis and verification of the performance of sandwich panels with textile reinforced concrete faces. J. Sandw. Struct. Mater. 2011, 3, 589–603. [Google Scholar] [CrossRef]
- Junes, A.; Larbi, A.S. An indirect non-linear approach for the analysis of sandwich panels with TRC facings. Constr. Build. Mater. 2016, 112, 406–415. [Google Scholar] [CrossRef]
- Shams, A.; Hegger, J.; Horstmann, M. An analytical model for sandwich panels made of textile-reinforced concrete. Constr. Build. Mater. 2014, 64, 451–459. [Google Scholar] [CrossRef]
- Finzel, J.; Häussler-Combe, U. Textile reinforced concrete sandwich panels: Bending tests and numerical analyses. In Proceedings of the Euro-C 2010, Schladming, Austria, 15–18 March 2010; pp. 789–795. [Google Scholar]
- Miccoli, L.; Fontana, P. Numerical modelling of UHPC and TRC sandwich elements for building envelopes Façade element components. Int. Assoc. Bridge Struct. Eng. 2015, 105, 1–9. [Google Scholar]
- Djamai, Z.I.; Bahrar, M.; Salvatore, F.; Larbi, A.S.; El Mankibi, M. Textile reinforced concrete multiscale mechanical modelling: Application to TRC sandwich panels. Finite Elem. Anal. Des. 2017, 135, 22–35. [Google Scholar] [CrossRef]
- Contamine, R.; Larbi, A.S.; Hamelin, P. Contribution to direct tensile testing of textile reinforced concrete (TRC) composites. Mater. Sci. Eng. A 2011, 528, 8589–8598. [Google Scholar] [CrossRef]
- De Andrade Silva, F.; Butler, M.; Mechtcherine, V.; Zhu, D.; Mobasher, B. Strain rate effect on the tensile behaviour of textile-reinforced concrete under static and dynamic loading. Mater. Sci. Eng. A 2011, 528, 1727–1734. [Google Scholar] [CrossRef]
- Barhum, R.; Mechtcherine, V. Effect of short, dispersed glass and carbon fibres on the behaviour of textile-reinforced concrete under tensile loading. Eng. Fract. Mech. 2012, 92, 56–71. [Google Scholar] [CrossRef]
- Hartig, J.; Jesse, F.; Schicktanz, K.; Häußler-Combe, U. Influence of experimental setups on the apparent uniaxial tensile load-bearing capacity of Textile Reinforced Concrete specimens. Mater. Struct. Constr. 2012, 45, 433–446. [Google Scholar] [CrossRef]
- Hegger, J.; Will, N.; Curbach, M.; Jesse, F. Tragverhalten von textilbewehrtem Beton: Verbund, Ribbildung und Tragverhalten. Beton-Und Stahlbetonbau 2004, 99, 452–455. [Google Scholar] [CrossRef]
- El Kadi, M.; Tysmans, T.; Verbruggen, S.; Vervloet, J.; de Munck, M.; Wastiels, J.; van Hemelrijck, D. A layered-wise, composite modelling approach for fibre textile reinforced cementitious composites. Cem. Concr. Compos. 2018, 94, 107–115. [Google Scholar] [CrossRef]
- Bertolesi, E.; Carozzi, F.G.; Milani, G.; Poggi, C. Numerical modeling of Fabric Reinforce Cementitious Matrix composites (FRCM) in tension. Constr. Build. Mater. 2014, 70, 531–548. [Google Scholar] [CrossRef]
- Promis, G.; Gabor, A.; Hamelin, P. Analytical modeling of the bending behavior of textile reinforced mineral matrix composite beams. Compos. Struct. 2011, 93, 792–801. [Google Scholar] [CrossRef]
- Tysmans, T.; Wozniak, M.; Remy, O.; Vantomme, J. Finite element modelling of the biaxial behaviour of high-performance fi bre-reinforced cement composites (HPFRCC) using Concrete Damaged Plasticity. Finite Elem. Anal. Des. 2015, 100, 47–53. [Google Scholar] [CrossRef]
- Cuypers, H. Analysis and Design of Sandwich Panels with Brittle Matrix Composite Faces for Building Applications. Ph.D. Thesis, Vrije Universiteit Brussel, Brussels, Belgium, 2002. [Google Scholar]
- Mesticou, Z.; Bui, L.; Junes, A.; Larbi, A.S. Experimental investigation of tensile fatigue behaviour of Textile-Reinforced Concrete (TRC): Effect of fatigue load and strain rate. Compos. Struct. 2017, 160, 1136–1146. [Google Scholar] [CrossRef]
- Remy, O. Lightweight Stay Formwork: A Concept for Future Building Applications. Ph.D. Thesis, Vrije Universiteit Brussel, Brussels, Belgium, 2012. [Google Scholar]
- Cuypers, H.; Gu, J.; Croes, K.; Dumortier, S.; Wastiels, J. Evaluation of fatigue and durability properties of E-glass fibre reinforced phosphate cementitious composite. Int. Symp. Brittle Matrix Compos. 2000, 6, 127–136. [Google Scholar]
- Belgian Bureau for Standardisation (NBN). NBN EN 196-1:2016 Methods of Testing Cement-Part 1: Determination of Strength; Belgian Bureau for Standardisation (NBN): Brussels, Belgium, 2016. [Google Scholar]
- Knauf. Gitex, Glasvezelwapening Technische Fiche. 2018. Available online: http://www.knauf.be/nl/product/gitex-glasvezelwapening (accessed on 18 January 2018).
- Kemisol. Technische Documentatie EPS. 2004. Available online: http://www.kemisol.be/ (accessed on 15 March 2018).
- Sutton, M.A.; Orteu, J.J.; Schreier, H. Image Correlation for Shape, Motion and Deformation Measurements; Springer: New York, NY, USA, 2009. [Google Scholar]
- De Munck, M.; Vervloet, J.; El Kadi, M.; Verbruggen, S.; Wastiels, J.; Remy, O.; Tysmans, T. Modelling and experimental verification of flexural behaviour of textile reinforced cementitious composite sandwich renovation panels. In Proceedings of the 12th fib International PhD Symposium in Civil Engineering, Prague, Czech Republic, 29–31 August 2018; pp. 179–186. [Google Scholar]






| fct,f MPa | fcc MPa | |
|---|---|---|
| Average | 6.35 | 23.17 |
| Standard Deviation | 0.45 | 1.59 |
| Density kg/m3 | E-Modulus MPa | Bending Strength kPa |
|---|---|---|
| 20 | 10 | 250 |
| TRC Coupons | Sandwich Beams | |
|---|---|---|
| subset | 21 pxs | 21 pxs |
| step | 7 pxs | 7 pxs |
| filter size | 11 | 11 |
| area of interest | 250 × 45 mm | 250 × 190 mm |
| Type of Camera | CCD |
|---|---|
| lenses size | 8 mm |
| resolution | 2546 × 2048 pxs |
| Specimen | TRC CYCL 0.5 MPa | TRC CYCL 1.0 MPa | TRC CYCL 2.0 MPa |
|---|---|---|---|
| A | 0 | 22 | 7 |
| B | 0 | 8 | 12 |
| C | 0 | 0 | 10 |
| D | 0 | 0 | 0 |
| E | 0 | 5 | 16 |
| F | 0 | 1 | 1 |
| Specimen | E1 GPa | E3 GPa | σcrack MPa | σultimate MPa | # Cracks | ||
|---|---|---|---|---|---|---|---|
| After Cyclic Preloading | At Failure | ||||||
| REF | avg | 11.38 | 0.41 | 1.65 | 7.49 | - | 13 |
| st dev | 1.94 | 0.018 | 0.54 | 0.52 | - | 2 | |
| CYCL. 0.5 MPa | A | 8.99 | 0.45 | 2.19 | 6.44 | 0 | 14 |
| B | 15.32 | 0.49 | 1.85 | 7.22 | 0 | 11 | |
| C | 11.74 | 0.37 | 1.49 | 6.43 | 0 | 19 | |
| D | 14.60 | 0.43 | 1.38 | 7.40 | 0 | 19 | |
| E | 9.22 | 0.48 | 1.96 | 7.07 | 0 | 14 | |
| F | 12.64 | 0.43 | 2.30 | 7.32 | 0 | 17 | |
| avg | 12.08 | 0.44 | 1.86 | 6.98 | - | 16 | |
| st dev | 2.42 | 0.038 | 0.34 | 0.40 | - | 3 | |
| Specimen | E1 GPa | E3 GPa | σcrack MPa | σultimate MPa | # Cracks | ||
|---|---|---|---|---|---|---|---|
| After Cyclic Preloading | At Failure | ||||||
| REF | avg | 11.38 | 0.41 | 1.65 | 7.49 | - | 13 |
| st dev | 1.94 | 0.018 | 0.54 | 0.52 | - | 2 | |
| CYCL. 1.0 MPa | A | 0.48 | 0.48 | - | 5.55 | 22 | 24 |
| B | 0.92 | 0.49 | 2.41 | 5.92 | 8 | 14 | |
| C | 8.37 | 0.39 | 1.53 | 5.49 | 0 | 22 | |
| D | 12.27 | 0.45 | 1.63 | 7.20 | 0 | 14 | |
| E | 0.91 | 0.41 | 1.70 | 8.25 | 5 | 29 | |
| F | 2.59 | 0.41 | 1.20 | 7.41 | 1 | 28 | |
| avg | - | 0.44 | 1.69 | 6.64 | - | 22 | |
| st dev | - | 0.037 | 0.40 | 1.04 | - | 6 | |
| Specimen | E1 GPa | E3 GPa | σcrack MPa | σultimate MPa | # Cracks | ||
|---|---|---|---|---|---|---|---|
| After Cyclic Preloading | At Failure | ||||||
| REF | avg | 11.38 | 0.41 | 1.65 | 7.49 | - | 13 |
| st dev | 1.94 | 0.018 | 0.54 | 0.52 | - | 2 | |
| CYCL. 2.0 MPa | A | 0.84 | 0.42 | 2.30 | 6.74 | 7 | 22 |
| B | 0.65 | 0.48 | 2.13 | 6.48 | 12 | 19 | |
| C | 0.81 | 0.43 | 2.41 | 5.65 | 10 | 20 | |
| D | 13.06 | 0.47 | 2.66 | 5.88 | 0 | 10 | |
| E | 0.48 | 0.42 | 2.42 | 6.68 | 16 | 24 | |
| F | 4.76 | 0.48 | 2.24 | 7.13 | 1 | 11 | |
| avg | - | 0.45 | 2.36 | 6.43 | - | 18 | |
| st dev | - | 0.029 | 0.17 | 0.51 | - | 5 | |
| Specimen | SW CYCL 1.0 MPa | SW CYCL 2.0 MPa |
|---|---|---|
| A | 0 | 2 |
| B | 0 | 1 |
| C | 0 | 2 |
| D | 0 | 6 |
| Specimen | S1 kN/mm | S3 kN/mm | Pcrack kN | Pultimate kN | # Cracks | ||
|---|---|---|---|---|---|---|---|
| After CyclicPreloading | At Failure | ||||||
| REF | avg | 0.451 | 0.098 | 1.12 | 4.99 | - | 17 |
| st dev | 0.009 | 0.002 | 0.27 | 0.45 | - | 4 | |
| SW CYCL. 1.0 MPa | A | 0.437 | 0.091 | 1.42 | 3.95 | 0 | 12 |
| B | 0.474 | 0.090 | 1.89 | 5.14 | 0 | 13 | |
| C | 0.418 | 0.091 | 0.98 | 5.35 | 0 | 13 | |
| D | 0.488 | 0.090 | 1.04 | 4.62 | 0 | 13 | |
| avg | 0.454 | 0.090 | 1.34 | 4.76 | - | 13 | |
| st dev | 0.028 | 0.000 | 0.36 | 0.54 | - | 0 | |
| Specimen | S1 kN/mm | S3 kN/mm | Pcrack kN | Pultimate kN | # Cracks | ||
|---|---|---|---|---|---|---|---|
| After CyclicPreloading | At Failure | ||||||
| REF | avg | 0.451 | 0.098 | 1.12 | 4.99 | - | 17 |
| st dev | 0.009 | 0.002 | 0.27 | 0.45 | - | 4 | |
| SW CYCL. 2.0 MPa | A | 0.412 | 0.082 | 1.25 | 3.60 | 2 | 9 |
| B | 0.455 | 0.097 | 1.36 | 4.15 | 1 | 10 | |
| C | 0.336 | 0.086 | 1.32 | 3.11 | 2 | 15 | |
| D | 0.254 | 0.096 | 1.22 | 4.52 | 6 | 24 | |
| avg | - | 0.090 | 1.29 | 3.84 | - | 15 | |
| st dev | - | 0.006 | 0.055 | 0.54 | - | 6 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Munck, M.; Tysmans, T.; Wastiels, J.; Kapsalis, P.; Vervloet, J.; El Kadi, M.; Remy, O. Fatigue Behaviour of Textile Reinforced Cementitious Composites and Their Application in Sandwich Elements. Appl. Sci. 2019, 9, 1293. https://doi.org/10.3390/app9071293
De Munck M, Tysmans T, Wastiels J, Kapsalis P, Vervloet J, El Kadi M, Remy O. Fatigue Behaviour of Textile Reinforced Cementitious Composites and Their Application in Sandwich Elements. Applied Sciences. 2019; 9(7):1293. https://doi.org/10.3390/app9071293
Chicago/Turabian StyleDe Munck, Matthias, Tine Tysmans, Jan Wastiels, Panagiotis Kapsalis, Jolien Vervloet, Michael El Kadi, and Olivier Remy. 2019. "Fatigue Behaviour of Textile Reinforced Cementitious Composites and Their Application in Sandwich Elements" Applied Sciences 9, no. 7: 1293. https://doi.org/10.3390/app9071293
APA StyleDe Munck, M., Tysmans, T., Wastiels, J., Kapsalis, P., Vervloet, J., El Kadi, M., & Remy, O. (2019). Fatigue Behaviour of Textile Reinforced Cementitious Composites and Their Application in Sandwich Elements. Applied Sciences, 9(7), 1293. https://doi.org/10.3390/app9071293






